CAN INFANTS BE “TAUGHT” TO ATTEND TO A NEW PHYSICAL VARIABLE IN AN EVENT CATEGORY? THE CASE OF HEIGHT IN COVERING EVENTS

Abstract

As they observe or produce events, infants identify variables that help them predict outcomes in each category of events. How do infants identify a new variable? An explanation-based learning (EBL) account suggests three essential steps: (1) observing contrastive outcomes relevant to the variable; (2) discovering the conditions associated with these outcomes; and (3) generating an explanation for the condition-outcome regularity discovered. In Experiments 1–3, 9-month-old infants watched events designed to “teach” them the variable height in covering events. After watching these events, designed in accord with the EBL account, the infants detected a height violation in a covering event, three months earlier than they ordinarily would have. In Experiments 4–6, the “teaching” events were modified to remove one of the EBL steps, and the infants no longer detected the height violation. The present findings thus support the EBL account and help specify the processes by which infants acquire their physical knowledge.

1. Introduction

When wrapping gifts for the winter holidays, we readily attend to size and shape information in selecting a box for each gift: a thin rectangular box for Uncle Albert’s new tie, a small square box for Aunt Emma’s fancy bath salts, and a large rectangular box for Baby Jane’s new doll. In this task as in many others, our intuitive knowledge of the physical world directs our attention to the most relevant information, often in the absence of explicit awareness.

A wealth of evidence suggests that infants’ knowledge of the physical world increases steadily during the first year of life (e.g., Aguiar & Baillargeon, 2002; Dan, Omori, & Tomiyasu, 2000; Huettel & Needham, 2000; Kotovsky & Baillargeon, 1998; Wang, Kaufman, & Baillargeon, 2003; Wilcox, 1999; for recent reviews, see Baillargeon, Li, Luo, & Wang, 2006; Baillargeon, Li, Ng, & Yuan, in press). Infants learn, for example, that a wide object cannot be lowered inside a narrow container (e.g., Aguiar & Baillargeon, 1998; Sitskoorn & Smitsman, 1995; Wang, Baillargeon, & Brueckner, 2004), and that a tall object cannot become fully hidden behind a short screen (e.g., Baillargeon & DeVos, 1991; Baillargeon & Graber, 1987; Hespos & Baillargeon, 2001a) or inside a short container (e.g., Hespos & Baillargeon, 2001a, 2006; Wang, Baillargeon, & Paterson, 2005). The present research examined the process by which infants acquire such expectations.

The point of departure for our research was the finding that infants younger than 12 months of age do not yet realize that the height of an object relative to that of a cover (i.e., a rigid, inverted container) determines whether the object can be fully or only partly hidden under the cover: they search for a tall object under either a short or a tall cover (e.g., McCall, 2001; Wang & Kohne, in press), and they are not surprised¹ when shown an event in which a tall object becomes fully hidden under a short cover (e.g., Wang & Baillargeon, 2005; Wang et al., 2005). Here we attempted to “teach” 9-month-old infants to attend to height information in covering events, by exposing them to appropriate observations in the laboratory. We reasoned that this approach, if successful, would allow us to manipulate the contents of the observations, to determine what information is necessary and sufficient to support learning in infancy.

In the following sections, we first review recent findings on the development of infants’ physical knowledge. We next introduce a recent account of how infants acquire their physical expectations, the explanation-based learning (EBL) account (e.g., Baillargeon et al., 2006, in press). This account provided the “recipe” for our teaching experiments, by suggesting what ingredients might be essential for infants to acquire a new expectation.

1.1. The development of infants’ physical knowledge

Investigations of the development of infants’ physical knowledge over the past 15 years have yielded four main findings relevant to the present research (for recent reviews, see Baillargeon et al., 2006, in press). First, from an early age, infants form distinct event categories, which capture simple spatial or mechanical relations between objects (e.g., Aguiar & Baillargeon, 2003; Baillargeon & Wang, 2002; Casasola & Cohen, 2002; Casasola, Cohen, & Chiarello, 2003; Hespos & Baillargeon, 2001a, 2006; McDonough, Choi, & Mandler, 2003; Quinn, 2007; Wang & Baillargeon, 2006; Wang et al., 2005; Wang & Kohne, in press; Wilcox & Chapa, 2002). Examples of infants’ event categories include occlusion events (i.e., an object is placed behind another object, or occluder), containment events (i.e., an object is placed inside a container), tube events (i.e., an object is placed inside a tube), covering events (i.e., a cover is placed over an object), support events (i.e., an object is released on another object), and collision events (i.e., an object hits another object).

Second, each event category comprises one or more vectors, which correspond to distinct problems that infants must solve in order to fully predict outcomes within the category. For example, in the case of occlusion events, infants must learn to predict whether an object will be fully or only partly hidden when behind an occluder, and how soon an object that moves behind an occluder will emerge from behind it (e.g., Aguiar & Baillargeon, 1999; Baillargeon & DeVos, 1991; Baillargeon & Graber, 1987; Hespos & Baillargeon, 2001a; Kochukhova & Gredebäck, in press; Luo & Baillargeon, 2005; Spelke, Kestenbaum, Simons, & Wein, 1995a; Wilcox & Schweinle, 2003). Similarly, in the case of containment events, infants must learn to predict whether an object can be lowered inside a container, and how much of an object that is lowered inside a container will protrude above it (e.g., Aguiar & Baillargeon, 1998, 2003; Hespos & Baillargeon, 2001a, 2001b, 2006; Sitskoorn & Smitsman, 1995; Wang et al., 2004, 2005).

Third, for each vector of an event category, infants identify one or more variables that enable them to better predict outcomes (e.g., Aguiar & Baillargeon, 2002; Hespos & Baillargeon, 2001a; Kotovsky & Baillargeon, 1998; Luo & Baillargeon, 2005; Sitskoorn & Smitsman, 1995; Wang et al., 2003, 2005; Wilcox, 1999). A variable is defined as a two-facet knowledge structure that (1) calls infants’ attention to a certain type of information in an event and (2) provides a causal rule for interpreting this information. For example, the variable height in an occlusion event calls infants’ attention to the relative heights of the object and occluder, and specifies that the object can become fully hidden behind the occluder if it is shorter but not taller than the occluder. After infants identify this variable, at about 3.5 months of age (e.g., Baillargeon & DeVos, 1991), they begin to consistently attend to height information in occlusion events: as a result, they search for a tall object behind a tall as opposed to a short occluder (e.g., Hespos & Baillargeon, 2006), and they are surprised when a tall object becomes fully hidden behind a short occluder (e.g., Baillargeon & Graber, 1987; Hespos & Baillargeon, 2001a). In vectors with multiple variables, each new variable revises and refines predictions from earlier variables. This process can be illustrated by a decision tree: with each new variable—or each new node in the decision tree—infants’ predictions slowly approximate those of older children and adults.

Finally, variables identified in the context of one event category are not generalized to other categories, even when equally relevant: infants learn separately about each event category. In some cases, a variable may be identified at about the same age in different categories; in other cases, however, several months may separate the identification of the same variable in different categories. A good case in point is the variable height, which is identified at about 3.5 months in occlusion events (e.g., Baillargeon & DeVos, 1991), but only at about 7.5 months in containment events (e.g., Hespos & Baillargeon, 2001a, 2006), 12 months in covering events (e.g., McCall, 2001; Wang & Baillargeon, 2006; Wang et al., 2005), and 14 months in tube events (e.g., Wang et al., 2005).

1.2. How do infants reason about variables?

How does infants’ physical reasoning change as they form event categories and identify the vectors and variables relevant for predicting outcomes in each category? In a recent account of infants’ physical reasoning (e.g., Baillargeon et al., 2006, in press; Wang et al., 2005), we proposed that, when infants watch a physical event, their Physical-Reasoning System—an abstract computational system dedicated to monitoring events and predicting and interpreting their outcomes—builds a specialized representation of the event, which we call a physical representation.

The information infants include in their physical representation of an event becomes subject to a few core principles (e.g., Baillargeon et al., 2006, in press; Carey & Spelke, 1994; Leslie, 1994, 1995; Spelke, 1994; Spelke, Breinlinger, Macomber, & Jacobson, 1992; Spelke, Phillips, & Woodward, 1995b). Of most relevance to the present research is the principle of persistence, which states that objects exist continuously in time and space, retaining all of their physical properties as they do so (e.g., Baillargeon, in press; Baillargeon et al., in press). The principle of persistence has many corollaries: for example, that stationary objects, whether visible or hidden, exist continuously in time; that moving objects, whether visible or hidden, follow continuous paths; that two objects, whether visible or hidden and whether stationary or moving, cannot occupy the same space at the same time; and that an object of a particular size, shape, pattern, and color, whether stationary or moving and whether visible or hidden, cannot spontaneously become an object of a different size, shape, pattern, or color.

When watching an event, infants begin by representing the basic information about the event (e.g., Cheries, Wynn, & Scholl, 2006; Feigenson & Spelke, 2003; Hespos & Baillargeon, 2001b; Kestenbaum, Termine, & Spelke, 1987; Luo, Kaufman, & Baillargeon, 2007; Needham, 2000; Slater, 1995; Spelke, 1982; Wynn, 1992; Yonas & Granrud, 1984). This basic information comprises both spatiotemporal and identity information. The spatiotemporal information specifies how many objects are involved in the event (up to some small number), and how their spatial arrangement changes as the event unfolds. The identity information provides key categorical or ontological information about each object, such as whether it is self- or nonself-propelled, and whether it is closed or open (e.g., is the object open at the top to form a container, open at the bottom to form a cover, or open at both ends to form a tube?).

Next, infants use the basic information they represent about the event to categorize it. Infants then tap their knowledge of the category selected, which lists all of the variables that have been identified as relevant for predicting outcomes in the category. Information about each variable is then included in the physical representation of the event and is interpreted in accord with the variable rule. Events whose outcomes are inconsistent with the variable rules are flagged as violations.

To illustrate, consider once again the finding that infants aged 3.5 months and older are surprised when a tall object becomes fully hidden behind a short occluder (e.g., Baillargeon & DeVos, 1991; Baillargeon & Graber, 1987; Hespos & Baillargeon, 2001a). When watching this event, infants represent the basic information about the event, categorize it as an occlusion event, and tap their knowledge of this event category. Because at 3.5 months this knowledge comprises the variable height, infants include information about the relative heights of the object and occluder in their physical representation of the event. This information is then interpreted in terms of the variable rule. Because the outcome of the event contradicts this rule—the object is taller than the occluder and yet becomes fully hidden—the event is flagged as a violation. Infants younger than 3.5 months, who have not yet identified height as an occlusion variable, typically do not include height information in their physical representations of occlusion events (e.g., Aguiar & Baillargeon, 2002; Baillargeon & DeVos, 1991; Luo & Baillargeon, 2005). (This is not to say that young infants watching an occlusion event will represent no information at all about the heights of the object and occluder; we return to this point in the General Discussion).

1.3. How do infants identify variables?

The evidence reviewed in the preceding sections suggests that infants’ physical representations of events are initially crude and become more sophisticated as infants identify more and more of the variables relevant for predicting outcomes in each event category. But how do infants come to identify these variables?

We have proposed that the process by which infants identify a new variable in an event category is one of explanation-based learning (EBL) (e.g., Baillargeon et al., 2006, in press; for a computational description of EBL in the machine learning literature, see DeJong, 1993). This process involves three main steps. First, infants notice contrastive outcomes relevant to the variable. This occurs when infants build similar physical representations for two or more events—and notice that the events’ outcomes differ along some vector. For example, consider the variable height in covering events, which is typically identified at about 12 months of age (e.g., McCall, 2001; Wang & Baillargeon, 2006; Wang et al., 2005; Wang & Kohne, in press). We suppose that at some point prior to 12 months of age, infants begin to notice—either as they themselves manipulate covers and objects, or as they observe others do so—that when a cover is lowered over an object, the object sometimes remains partly visible beneath the cover and sometimes does not. Infants thus notice contrastive outcomes they cannot predict based on their current variable knowledge: similar physical representations (“cover lowered over object”) lead to contrastive outcomes (“object remains partly visible beneath cover” versus “object becomes fully hidden”), suggesting that some crucial piece of information is missing from the representations.

At this point, infants begin to search for the conditions that map onto these contrastive outcomes. Specifically, infants attempt to determine under what condition one outcome is observed, and under what condition the other outcome is observed. Eventually, infants uncover a regularity linking each outcome with a distinct condition.² In the case of the variable height in covering events, infants detect that objects remain partly visible when placed under covers that are shorter than the objects, and become fully hidden when placed under covers that are as tall as or taller than the objects.

Finally, infants attempt to supply an explanation for the observed condition-outcome regularity, based on their prior knowledge. According to the EBL process, only condition-outcome regularities for which causal explanations can be provided—or condition-outcome regularities which can be described as causal rules—are recognized as new variables. These explanations are typically shallow (e.g., Keil, 1995; Wilson & Keil, 2000), but nevertheless serve to integrate new variables with infants’ existing causal knowledge. In the case of the variable height in covering events, the principle of persistence provides a ready explanation for infants’ observations: because an object continues to exist and retains its height when under a cover, it can become fully hidden only if its height is equal to, or shorter than, that of the cover.

After infants have identified a variable in an event category, they begin to routinely include information about the variable in their physical representation of any event from the category, thus ensuring powerful generalization of the variable to all events within the category.

1.4. New and existing vectors

In the case discussed in the last section, the identification of the variable height went hand in hand with the formation of a new vector for covering events (“When is an object under a cover hidden?”). In other cases, the new variable may be added to an existing vector, revising predictions from earlier variables. The EBL process is assumed to operate in essentially the same manner whether infants identify the first variable in a vector or add a variable to an existing vector. Nevertheless, there is a critical difference between the two situations, having to do with whether infants are likely to view the contrastive outcomes for the new variable as expected or as unexpected.

When infants are in the process of identifying the first variable in a vector, they typically look equally at the contrastive outcomes for the variable, because neither outcome is inconsistent with their existing knowledge (e.g., Li, Baillargeon, & Needham, 2006). Thus, we would expect infants who have not yet identified the variable height in covering events to look equally when a tall object becomes partly hidden under a short cover or becomes fully hidden under a tall cover: at that point, infants do not possess a definite expectation that all objects should be partly hidden, or that all objects should be fully hidden, when under covers—they simply have no expectation as to whether objects should be partly or fully hidden when under covers. This not to say that infants have no expectations at all about covering events: even young infants expect an object to continue to exist under a cover (e.g., Leslie, 1995; Wang et al., 2005). However, knowing that an object will continue to exist under a cover is not sufficient to determine whether it should be fully or only partly hidden.

The situation is very different when infants are in the process of adding a variable to an existing vector: here, infants will possess definite expectations about the contrastive outcomes for the new variable. To illustrate, consider once again the variable height in occlusion events, which is identified at about 3.5 months of age (e.g., Baillargeon & DeVos, 1991). This variable is added to an existing vector, “When is an object behind an occluder hidden?”. By about 3 months of age, infants have already identified at least one variable in this vector, lower-edge-discontinuity: when an object moves behind an occluder whose lower edge is not continuous with the surface on which it rests, creating an external opening between the occluder and surface, infants expect the object to appear in this opening; conversely, when an objects moves behind an occluder whose lower edge is continuous with the surface on which its rests, they expect the object to be fully hidden when behind the occluder (e.g., Aguiar & Baillargeon, 2002; Luo & Baillargeon, 2005). In time, infants come to observe contrastive outcomes for the variable height: they notice that when an object moves behind an occluder with no external opening, the object sometimes is fully hidden, but sometimes remains partly visible above the occluder. The first outcome is consistent with the variable lower-edge-discontinuity and thus expected—but the second outcome is inconsistent with the variable and thus unexpected. We have used the phrase errors of commission to refer to situations where infants view as unexpected events that are physically possible and even ordinary (such as a tall object protruding above a short occluder), but happen to contradict their limited and hence faulty knowledge (e.g., Luo & Baillargeon, 2005; Wang & Baillargeon, 2007). Through the EBL process, infants eventually discover the conditions that map onto these contrastive outcomes and identify the variable height: they now expect an object that moves behind an occluder to remain partly visible if it is taller but not shorter than the occluder.

1.5. The present research

The EBL account suggests that infants’ identification of a new variable in an event category involves three main steps: (1) noticing contrastive outcomes relevant to the variable (this first step serves to trigger the learning process); (2) uncovering the conditions associated with these contrastive outcomes; and (3) building an explanation for this condition-outcome regularity. The EBL account also suggests how infants might be helped to identify a new variable in an event category—or, to put it differently, how infants might be “taught” such a variable—through exposure, in the home or laboratory, to appropriate observations.

There already exists preliminary evidence that infants can be helped to identify a new variable in an event category through a brief teaching session in the laboratory (e.g., Baillargeon, 1998, 1999; Baillargeon, Fisher, & DeJong, 2000). These experiments focused on the variable weight distribution in support events, which is typically not identified until about 12.5 months of age (e.g., Baillargeon, 1995). According to this variable, an asymmetrical object that is released on a platform will remain stable only if the portion of the object on the platform is heavier than that off the platform. Infants younger than 12.5 months typically expect any object, whether symmetrical or asymmetrical, to remain stable as long as half or more of its bottom surface rests on the platform. In one experiment, 11-month-old infants gave evidence that they had identified weight distribution as a support variable after receiving three pairs of teaching trials. Each pair consisted of a box-stays and a box-falls event. In both events, an asymmetrical box was deposited on a platform in such a way that half of the box’s bottom surface rested on the platform. In the box-stays event, the larger end of the box was placed on the platform, and the box remained stable when released; in the box-falls event, the smaller end of the box was placed on the platform, and the box fell when released. Three different asymmetrical boxes were used in the three pairs of teaching trials. Next, the infants saw two static test displays in which a novel, L-shaped box rested on a platform with its larger end (adequate-support display) or smaller end (inadequate-support display) supported. The infants looked reliably longer at the inadequate- than at the adequate-support test display, suggesting that the teaching trials had helped them identify weight distribution as a support variable.

The present research sought to extend this research to a different event category and to younger infants. In Experiments 1 to 3, we attempted to teach the variable height in covering events to 9-month-old infants; recall that this variable is typically not identified until about 12 months of age (e.g., McCall, 2001; Wang & Baillargeon, 2006; Wang et al., 2005). In Experiments 4 to 6, we began to manipulate the contents of our teaching events, both to determine what information was necessary for learning and to address alternative interpretations of our findings.

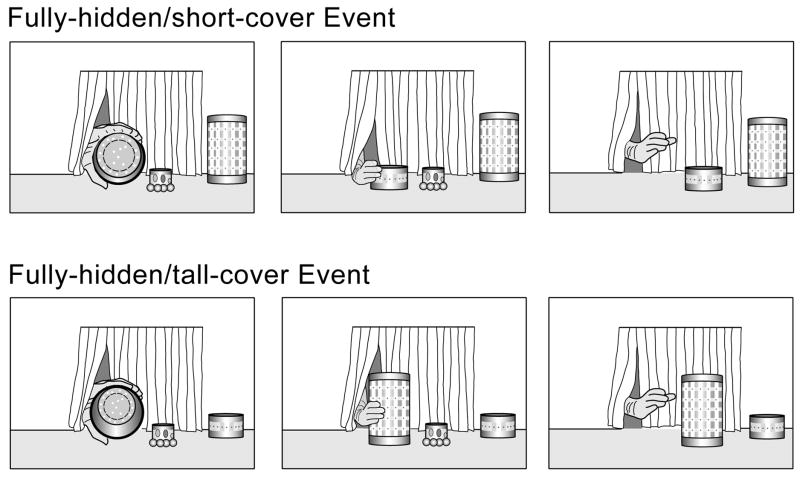
2. Experiment 1: Three pairs of teaching trials

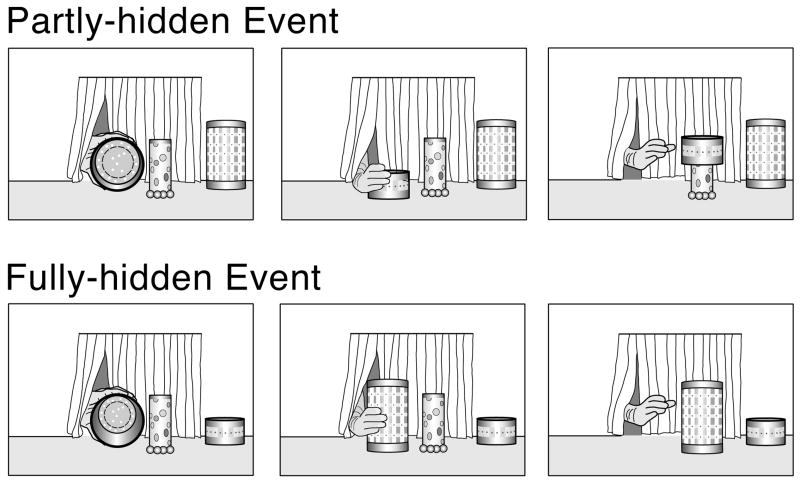
The infants in Experiment 1 received three pairs of teaching trials; in each pair, the infants saw a partly-hidden event in one trial and a fully-hidden event in the other trial (see Fig. 1). At the beginning of each trial, a cover stood next to a tall object on an apparatus floor; the cover was shorter than the object in the partly-hidden event and taller than the object in the fully-hidden event. Whichever cover was not in use was placed against the back wall of the apparatus, to provide the infants with a possible comparison point. An experimenter’s gloved hand first rotated the cover upward 90 degrees to show its hollow interior; the hand then returned the cover to the apparatus floor. Next, the hand lifted the cover, lowered it over the object, and released it. In the partly-hidden event, a portion of the object remained visible beneath the short cover; in the fully-hidden event, the object became fully hidden under the tall cover. After a pause, the hand grasped the cover, lifted it, and returned it to its original position on the apparatus floor. The hand then again lifted the cover to begin a new event cycle; cycles were repeated until the trial ended.

Figure 1.

Schematic depiction of the first pair of teaching events shown in Experiment 1.

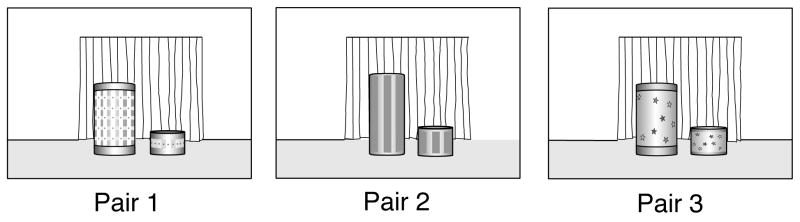
Within each pair of teaching trials, the short and tall covers were identical except for their heights; across pairs, the covers differed in height, pattern, and color (see Fig. 2). The same tall object was used in all six teaching trials.

Figure 2.

Schematic depiction of the teaching covers used in the three pairs of teaching trials in Experiment 1.

The teaching events were designed in accord with the EBL account. First, the infants were presented with contrastive outcomes for the variable height: when the cover was lowered over the object, the object sometimes remained partly visible beneath the cover and sometimes became fully hidden. Second, the events were designed to make it easy for the infants to identify the conditions that mapped onto these contrastive outcomes: the short and tall covers used in each pair of teaching trials differed only in height, and in each trial the infants could easily compare the relative heights of the cover and object when they stood side by side on the apparatus floor.³ Finally, the infants’ principle of persistence suggested a ready explanation for the condition-outcome regularity they observed: because a tall object continues to exist and retains its height when under a cover, it can become fully hidden under a tall but not a short cover.

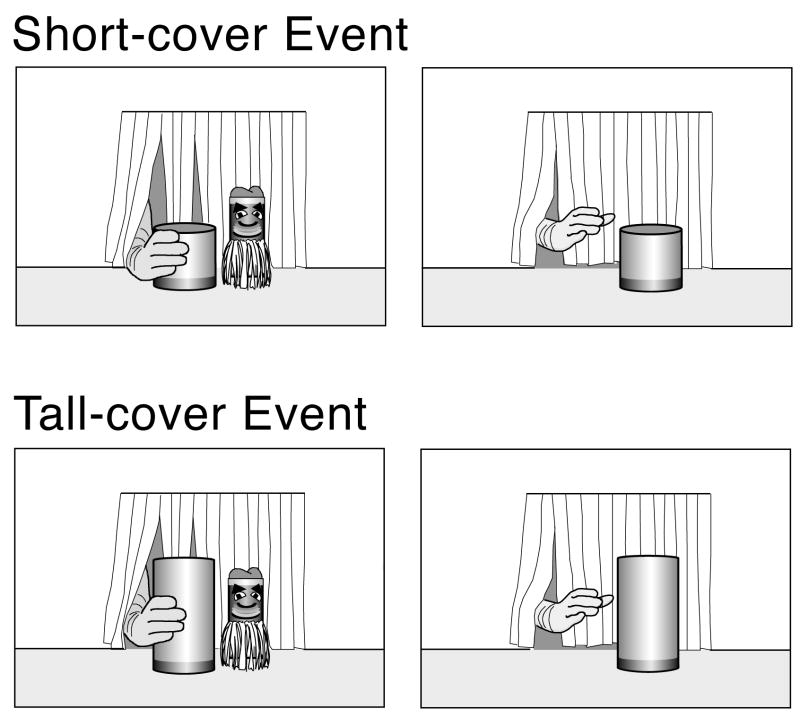
Following the teaching trials, the infants received two test trials in which they saw a short- and a tall-cover event; these events involved a novel short and tall cover and a novel tall object (see Fig. 3). At the beginning of the short-cover event, the short cover stood next to the object. To start, the experimenter’s gloved hand lifted the cover and lowered it over the object until it contacted the apparatus floor and thus fully hid the object. Because the cover was shorter than the object, it should have been impossible for the cover to fully hide the object. After a pause, the hand again grasped the cover and returned it to its original position next to the object. As in the teaching trials, event cycles were repeated until the trial ended. The tall-cover event was similar to the short-cover event, except that the cover was taller and could fully hide the object.

Figure 3.

Schematic depiction of the test events shown in Experiment 1.

We reasoned that if exposure to the teaching events enabled the infants to identify height as a covering variable, then they should include information about the relative heights of the cover and object when watching each test event. This information should then be interpreted in terms of the variable rule, allowing the infants to detect the violation in the short-cover event: the object was taller than the short cover and yet became fully hidden under it. The infants should thus look reliably longer at the short- than at the tall-cover event.

On the other hand, if exposure to the teaching events was not sufficient to enable the infants to identify height as a covering variable, then they should respond as infants under 12 months of age typically do in such situations (e.g., Wang & Baillargeon, 2005; Wang et al., 2005): they should fail to include height information in their physical representations of the test events, and hence they should fail to detect the violation in the short-cover event. The infants should thus look about equally at the short- and tall-cover events.

2.1. Method

2.1.1. Participants

Participants were 16 healthy term infants, 9 male and 7 female (range: 8 months, 25 days to 9 months, 29 days, M = 9 months, 6 days). An additional 7 infants were tested but eliminated, 6 because they were fussy (4) or distracted (2), and 1 because she looked for the maximum amount of time allowed (60 s) on both test trials.

The infants’ names in this and in the following experiments were obtained from local hospitals or from birth announcements published in the local newspaper. Parents were contacted by letters and follow-up phone calls; they were offered reimbursement for their travel expenses but were not compensated for their participation.

2.1.2. Apparatus

The apparatus consisted of a wooden display booth 106 cm high, 100 cm wide, and 46 cm deep, that was mounted 76 cm above the room floor. The infants faced an opening 41 cm high and 95 cm wide in the front of the apparatus; between trials, a muslin-covered wooden frame, 61 cm high and 99.5 cm wide, was lowered in front of this opening. The back wall of the apparatus was made of white foam board and the side walls were painted white. A primary experimenter introduced her/his right hand (wearing a yellow rubber glove) into the apparatus through a window 36 cm high and 43 cm wide in the back wall. The window was filled with a muslin fringe and extended from the lower edge of the back wall, 25 cm from the right wall.

Two layers of foam board, each 0.5 cm thick and covered with black contact paper, were placed on the apparatus floor. The upper layer had no hole and was used during the teaching trials. Between the teaching and test trials, the experimenter quickly and quietly removed the upper layer; the bottom layer had a hole 7 cm wide which was used to produce the short- and tall-cover events (see below).

The object used during the teaching trials (or “teaching object”) was 14.5 cm tall, 5.5 cm in diameter, made of cardboard, and covered with a white contact paper with large pastel dots. The top of the object was decorated with a red horizontal stripe, and the bottom sported four fuzzy orange pom-poms on the front.

The three pairs of covers used during the teaching trials (or “teaching covers”) were all 10.5 cm in diameter and made of cardboard 0.2 cm thick. The interior of each cover was covered with red contact paper; a second, ring-shaped layer of red contact paper covered the circumference of the interior top surface, leaving a slight circular depression 6.5 cm in diameter at the center.⁴ The whole interior surface was decorated with white dots. The short and tall covers used in the first pair of teaching trials were 6 cm and 17.5 cm tall, respectively; they were covered with a green and white checker-patterned contact paper and decorated with dark green horizontal stripes at the top and bottom. The covers used in the second pair of teaching trials were 11 cm and 20 cm tall; they were covered with yellow construction paper and decorated with brown vertical stripes as well as with golden horizontal stripes at the top and bottom. Finally, the covers used in the third pair of teaching trials were 7.5 cm and 15 cm tall; they were covered with ivory construction paper and decorated with silver star-shaped stickers and with gray horizontal stripes at the top and bottom. The heights of the teaching covers were chosen to ensure that, when lowered over the teaching object, the short cover in each pair only partly hid the object and the tall cover fully hid the object.

The object used during the test trials (or “test object”) was collapsible and composed of an outer and an inner cylinder made of cardboard 0.2 cm thick. The outer cylinder was 6.5 cm in diameter and 24 cm tall. The bottom 14.5 cm portion of the outer cylinder was not visible to the infants: it protruded through the hole in the apparatus floor. The top 9.5 cm portion of the outer cylinder was covered with red contact paper and was decorated with a white fringe. Several layers of rubber bands were attached to the bottom of this portion (at that point, the outer cylinder was 8 cm wide); the bands hid the hole in the bottom layer of the apparatus floor and also prevented the outer cylinder from falling through the hole. The inner cylinder was closed at the top and was 5.5 cm in diameter and 32 cm tall. The bottom 24 cm portion of the inner cylinder was not visible to the infants: it stood hidden inside the outer cylinder and was covered with thin sponges. These sponges filled the space between the inner and outer cylinders, preventing the inner cylinder from falling through the outer cylinder (and the hole in the apparatus floor). The top 8 cm portion of the inner cylinder was again covered with red contact paper and decorated with a colorful clown face. The fringe on the outer cylinder hid the small gap between the inner and outer cylinders, and also concealed the rubber bands.

A non-collapsible replica of the test object was shown to the infants prior to the experiment (see Procedure).

The short and tall covers used during the test trials (or “test covers”) were both 10 cm in diameter and made of cardboard 0.2 cm thick; their interior was covered with white construction paper. The short cover was 9.5 cm tall, covered with green construction paper, and decorated at the bottom with a dark green horizontal stripe. The tall cover was 18.5 cm tall, covered with blue construction paper, and decorated at the bottom with a dark blue horizontal stripe.

At the start of each test event, the test object was 17.5 cm tall (8 cm inner cylinder and 9.5 cm outer cylinder). When the short cover was lowered over the object in the short-cover event, the inner cylinder was pressed downward by the cover’s interior top surface; the inner cylinder glided silently and smoothly inside the outer cylinder, making it possible for the object to become fully hidden. As the cover was lifted, a secondary experimenter pushed the inner cylinder upward until its bottom edge was flush with that of the outer cylinder, thus restoring the test object to its initial height. Because the outer cylinder remained stationary, and the downward or upward displacement of the inner cylinder took place out of view inside the cover, the infants saw no motion involving either the outer or the inner cylinder of the test object. In the tall-cover event, a block was inserted in the tall cover so that its interior depth was the same as that of the short test cover (because the cover was shown to the infants prior to the experiment and was not rotated forward at the beginning of each test trial, the infants could not know that the interior depth of the tall test cover did not match its exterior height). The tall-cover event was thus produced in the same manner as the short-cover event.

The infants were tested in a brightly lit room. One 150-W, one 60-W, and three 40-W lamps attached to the front and back wall of the apparatus provided additional light. Two wooden frames, each 183 cm and 71 cm wide and covered with fabric, stood at an angle on either side of the apparatus; these frames served to isolate the infants from the experimental room.

2.1.3. Events

Two experimenters worked in concert to produce the events: the primary experimenter wore the yellow rubber glove and manipulated the tall and short covers in full view of the infants; the secondary experimenter was hidden from view and helped produce the short- and tall-cover test events by pushing up the test object’s inner cylinder. To help the experimenters adhere to the events’ prescribed scripts, a metronome beat softly once per second. A camera mounted behind and next to the infant projected an image of the events onto a TV screen in a different part of the test room; a supervisor monitored the events to confirm that they followed the scripts. In the next sections, the numbers in parentheses indicate the time taken by the experimenters to perform the actions described. All events are described from the infants’ perspective.

Teaching events

The infants saw a partly- and a fully-hidden event in each pair of teaching trials. At the beginning of each partly-hidden event, the short cover used in the pair stood 45 cm from the left wall and 23 cm from the front of the apparatus; the primary experimenter’s gloved hand grasped the left side of the cover. The teaching object stood centered 4 cm to the right of the cover, 35 cm from the right wall and 25.5 cm from the front of the apparatus. The tall cover stood against the back wall of the apparatus 12.5 cm to the right and 4.5 cm to the back of the object; this made it easy for the infants to compare the appearance of the two covers, if they so chose.⁵ The fully-hidden event shown in each pair of teaching trials was similar to the partly-hidden event, except that the locations of the tall and short covers were reversed.

Each teaching event began with two pretrials. During the first pretrial, the hand rotated the cover upward 90 degrees (2 s) and then paused; this pretrial ensured that the infant had the opportunity to see the hollow interior of the cover. When the computer signaled that the infant had looked at this paused scene for 2 cumulative seconds, the experimenter rotated the cover back to its starting position (2 s), and paused again; this second pretrial ensured that the infant had the opportunity to inspect the cover and object and to compare their heights. When the computer signaled that the infant had looked at this paused scene for 2 cumulative seconds, the event proper began.

To start, the hand lifted the cover 17 cm (2 s) and moved it to the right until it was centered 2.5 cm above the object (1 s). Next, the hand lowered the cover over the object (2 s), released it (1 s), and then paused a short distance to the left of the cover (1 s). In the partly-hidden events, varying portions of the object remained visible to the infant; in the fully-hidden events, the object became fully hidden. Next, the hand again grasped the cover (1 s), lifted it above the object (2 s), moved it to the left (1 s), lowered it to its starting position on the apparatus floor (2 s), and then paused for 1 s. Each cycle of the teaching event thus lasted about 14 s; cycles were repeated until the trial ended (see below).

Test events

At the beginning of each test event, the short (short-cover event) or tall (tall-cover event) test cover stood 43.5 cm from the left wall and 28.5 cm from the front of the apparatus; the primary experimenter’s gloved hand grasped the left side of the cover; and the test object stood centered 2.5 cm to the right of the cover, 36 cm from the right wall and 29.5 cm from the front of the apparatus. Each test trial began with a static pretrial, to give the infants the opportunity to inspect the cover and object and to compare their heights. When the computer signaled that the infant had looked at this paused scene for 2 cumulative seconds, the event proper began.

To start, the experimenter lifted the cover 20 cm (2 s) and then moved it to the right until it was centered 2.5 cm above the object (1 s). Next, the hand lowered the cover over the object until it became fully hidden (3 s); the interior top surface of the cover depressed the inner cylinder of the object inside its outer cylinder, smoothly and silently. The hand then released the cover (1 s) and paused a short distance to the left of the cover (1 s). Following this pause, the hand again grasped the cover (1 s) and lifted it above the object (3 s); as the hand lifted the cover, the secondary experimenter pushed the inner cylinder of the object upward inside its outer cylinder, thus surreptitiously restoring the object to its initial height. Next, the hand moved the cover to the left (1 s), lowered it to its starting position on the apparatus floor (2 s), and paused for 1 s. Each cycle of the test event thus lasted about 16 s; cycles were repeated until the trial ended (see below).

2.1.4. Procedure

During the experiment, each infant sat on a parent’s lap, centered 45 cm in front of the apparatus. Parents were instructed to remain silent and neutral during the experiment and to close their eyes during the test trials.

Prior to the start of the experiment, the primary experimenter first showed the infant her glove. Next, she introduced the replica of the test object. To demonstrate to the infant that the replica was not collapsible, the primary experimenter held its bottom with one hand and tapped its top about five times with the other hand. Finally, the primary experimenter showed the infant the short and tall test covers, one at the time, in each case calling the infant’s attention to the cover’s closed top and hollow interior.

The infants first received three pairs of teaching trials. Within each pair, half of the infants saw the partly-hidden event first, and half saw the fully-hidden event first. Each teaching trial ended when the infants either (1) looked away from the event for 2 consecutive seconds after having looked at it for at least 14 cumulative seconds or (2) looked for 60 cumulative seconds without looking away for 2 consecutive seconds. The 14-s minimal value was chosen to ensure that the infants had the opportunity to observe at least one cycle of each teaching event.

Following the teaching trials, the infants saw the tall- and short-cover test events on two successive trials. The infants who saw the partly-hidden event first in each pair of teaching trials saw the short-cover event first; the infants who saw the fully-hidden event first in each pair of teaching trials saw the tall-cover event first. Each test trial ended when the infants either (1) looked away from the event for 1 consecutive second after having looked at it for at least 8 cumulative seconds or (2) looked at the event for 60 cumulative seconds without looking away for 1 consecutive second. The 8-s minimum value was chosen to ensure that the infants had the opportunity to observe the outcome of each test event at least once.

Each infant’s looking behavior was monitored by two observers who viewed the infant through peepholes in the cloth-covered frames on either side of the apparatus. The observers were not told, and could not determine, in what order the events were presented during the teaching and test trials. Each observer held a button linked to a computer and depressed the button when the infant looked at the event. The looking times recorded by the primary observer were used to determine when a trial had ended.

To assess interobserver agreement during the test trials, each trial was divided into 100-ms intervals, and the computer determined in each interval whether the two observers agreed on whether the infant was or was not looking at the event. Percent agreement was calculated for each trial by dividing the number of intervals in which the observers agreed by the total number of intervals in the trial. Agreement was measured for 15 of the 16 infants (only one observer was present for one infant) and averaged 96% per trial per infant.

Preliminary analyses in this and in the following experiments revealed no significant interaction involving event and either order or sex during the teaching or the test trials; the data were therefore collapsed across order and sex in subsequent analyses.

2.2. Results

Teaching trials

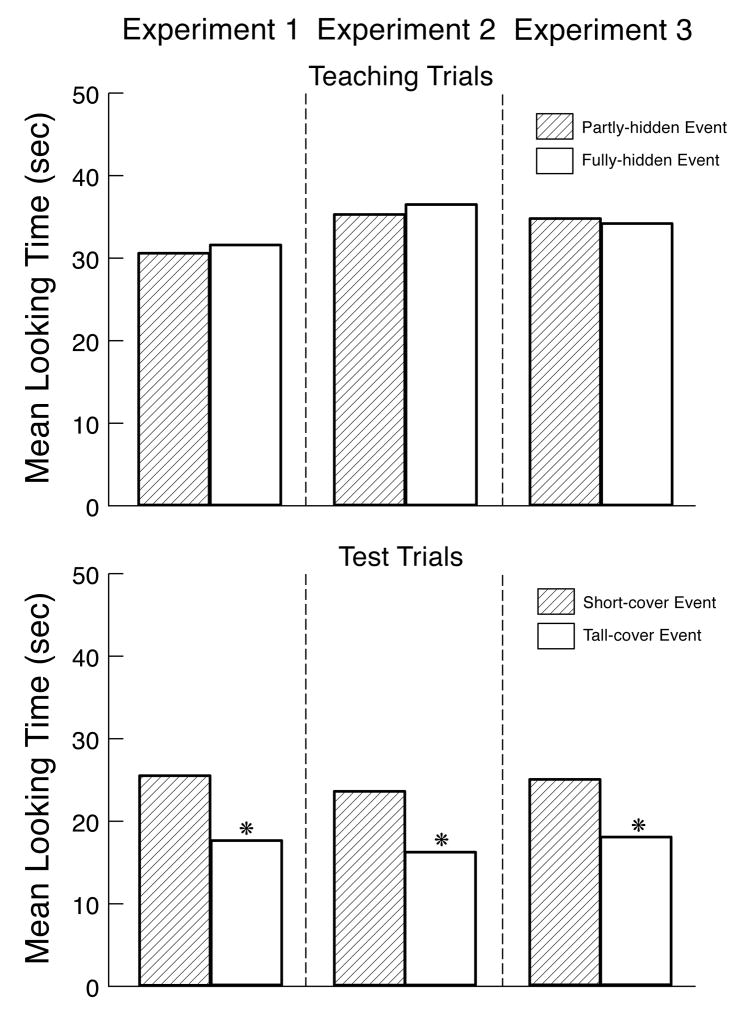
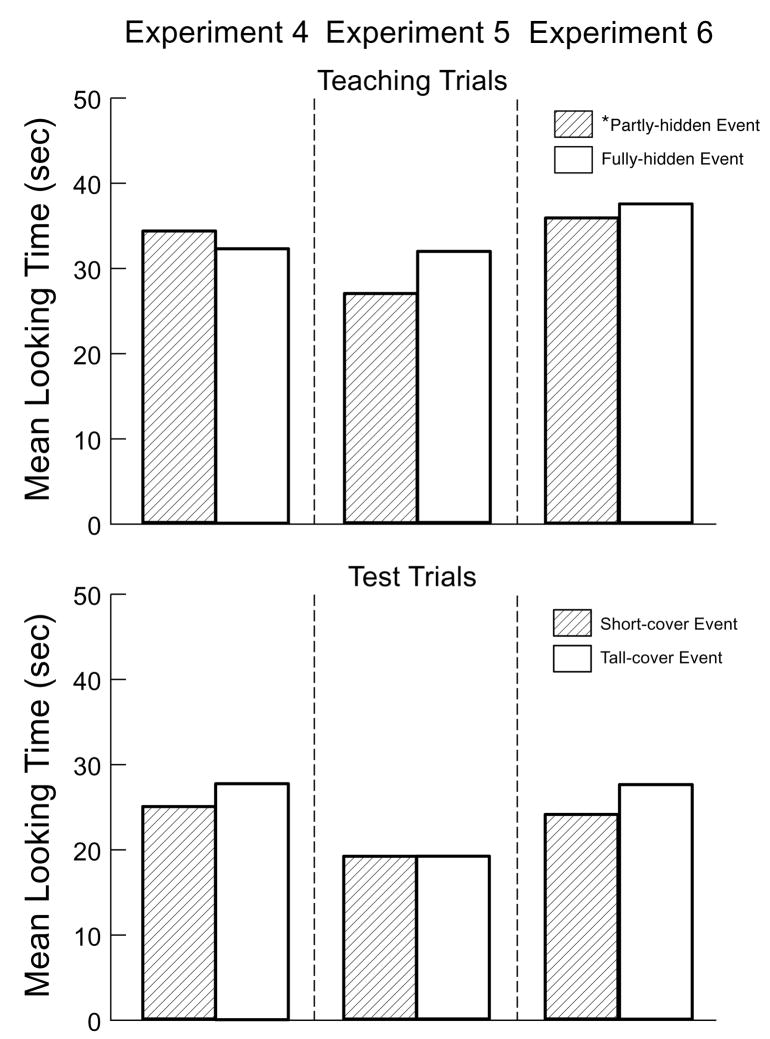
The infants’ looking times during the three pairs of teaching trials (see Fig. 4) were averaged across pairs and analyzed by means of a one-way analysis of variance (ANOVA) with event (partly- or fully-hidden) as a within-subject factor. The main effect of event was not significant, F(1, 15) = 0.28, suggesting that the infants looked about equally at the partly- (M = 30.5, SD = 11.0) and fully-hidden (M = 31.5, SD = 9.4) events. Because each event cycle in the teaching trials lasted about 14 s, the infants saw about two event cycles per trial.

Figure 4.

Mean looking times of the infants in Experiments 1 to 3 at the teaching and test events.

Test trials

The infants’ looking times during the two test trials (see Fig. 4) were analyzed by means of a one-way ANOVA with event (short- or tall-cover) as a within-subject factor. The analysis revealed a significant main effect of event, F(1, 15) = 9.25, p < 0.01, indicating that the infants looked reliably longer at the short- (M = 25.4, SD = 13.3) than at the tall-cover (M = 17.5, SD = 8.3) event. Inspection of the individual infants’ looking times revealed that 13 of the 16 infants showed this pattern, Wilcoxon signed-ranks test, T = 18, p < .01.

2.3. Discussion

During the teaching trials, the infants looked about equally at the partly- and fully-hidden events, suggesting that they viewed neither event as unexpected. Thus, consistent with the analysis offered above (section 1.4), the infants did not bring to the task an expectation that all objects should be partly hidden, or that all objects should be fully hidden, when under covers. Although the infants no doubt expected the teaching object to continue to exist when under the covers (e.g., Leslie, 1995; Wang et al., 2005), they had no prior expectation as to whether it should be partly or fully hidden.

During the test trials, the infants looked reliably longer at the short- than at the tall-cover test event, suggesting that they (1) identified height as a covering variable when watching the teaching events; (2) included information about the relative heights of the cover and object in their physical representation of each test event; and hence (3) detected the violation in the short-cover test event, about three months before infants typically detect such a violation (e.g., Wang et al., 2005).

In the next two experiments, we attempted to confirm and extend the findings of Experiment 1. In Experiment 2, infants received fewer teaching trials; in Experiment 3, a delay was introduced between the teaching and test trials.

3. Experiment 2: Two pairs of teaching trials

The goal of Experiment 2 was two-fold: one was to confirm the results of Experiment 1, and the other was to determine whether infants would still succeed in identifying height as a covering variable if given two, instead of three, pairs of teaching trials.

3.1. Method

3.1.1. Participants

Participants were 16 healthy term infants, 9 male and 7 female (range: 8 months, 26 days to 10 months, 5 days, M = 9 months, 17 days). An additional 6 infants were tested but eliminated, 4 because they were fussy (2) or distracted (2), and 2 because the differences in their looking times during the two test trials were over 3 SD from the mean of their condition.

3.1.1. Apparatus, events, and procedure

The apparatus, events, and procedure used in Experiment 2 were similar to those in Experiment 1 with one exception: the infants received only the first two pairs of teaching trials. Interobserver agreement during the test trials was measured for 15 of the 16 infants and averaged 96% per trial per infant.

3.2. Results

Teaching trials

The infants’ looking times during the teaching trials were analyzed as in Experiment 1 (see Fig. 4). The main effect of event was not significant, F (1, 15) = 0.10, suggesting that the infants tended to look equally at the partly- (M = 35.2, SD = 12.1) and fully-hidden (M = 36.4, SD = 12.9) events. Because each event cycle in the teaching trials lasted about 14 s, the infants saw about 2.5 event cycles per trial.

Test trials

The infants’ looking times during the test trials were analyzed as in Experiment 1 (see Fig. 4). The ANOVA yielded a significant main effect of event, F(1, 15) = 9.35, p < 0.01, indicating that the infants looked reliably longer at the short- (M = 23.5, SD = 8.5) than at the tall-cover (M = 16.1, SD = 7.4) event. Of the 16 infants in Experiment 2, 12 showed this pattern, T = 10, p < .01.

3.3. Discussion

The 9-month-old infants in Experiment 2, like those in Experiment 1, looked reliably longer at the short- than at the tall-cover test event. These results suggested that two (Experiment 2) or three (Experiment 1) pairs of teaching trials were sufficient to enable the infants to identify height as a covering variable. As a result, when watching each test event, the infants included information about the relative heights of the cover and object, and they interpreted this information in accord with their new variable rule: an object can become fully hidden under a cover if it is shorter but not taller than the cover. Because the short-cover event violated this rule, the infants responded to the event with increased attention.

The preceding analysis suggested that infants might still succeed at detecting the violation in the short-cover test event if a substantial time interval separated the teaching and test trials. After all, if infants identify height as a covering variable during the teaching trials, and add this variable to their knowledge of covering events, then height should still be listed as a relevant variable the next time infants encounter covering events and tap their knowledge of this event category. This is not to say that some amount of repetition or practice may not be necessary for the permanent consolidation of height as a covering variable (e.g., Alibali & Goldin-Meadow, 1993). Nevertheless, within some broad limits, we might expect infants to succeed at detecting the violation in the short-cover event not only immediately following the teaching trials, but also after a delay of several hours.

Experiment 3 was designed to examine this possibility. Parents brought their infants to the lab on two consecutive days, at about the same time each day; the infants received the teaching trials the first day, and the test trials the second day. A 24-hour delay thus separated the infants’ exposure to the teaching and test events.

4. Experiment 3: 24-hour delay

4.1. Method

4.1.1. Participants

Participants were 16 healthy term infants, 9 male and 7 female (range: 8 months, 29 days to 9 months, 27 days, M = 9 months, 16 days). An additional 7 infants were tested but eliminated, 3 because of fussiness, 2 because the differences in their looking times during the two test trials were over 3 SD from the mean of their condition, 1 because of parental interference, and 1 because she did not return to complete the test session after the 24-hour delay.

4.1.2. Apparatus, events, and procedure

The apparatus, events, and procedure used in Experiment 3 were similar to those in Experiment 1 with the following exceptions. On their first visit to the lab, the infants received only the three pairs of teaching trials; prior to the session, the primary experimenter showed the infants only her gloved hand. On their second visit to the lab, approximately 24 hours later, the infants received the two test trials; prior to the session, the experimenter showed the infants her gloved hand, the non-collapsible replica of the test object, and the test covers, in the same manner as in Experiment 1. Interobserver agreement during the test trials was measured for 15 of the 16 infants and averaged 97% per trial per infant.

4.2. Results

Teaching trials

The infants’ looking times during the teaching trials (see Fig. 4) were analyzed as in Experiment 1. The main effect of event was not significant, F(1, 15) = 0.07, indicating that the infants looked about equally at the partly- (M = 34.7, SD = 9.4) and fully-hidden (M = 34.1, SD = 9.4) events. Because each event cycle in the teaching trials lasted about 14 s, the infants saw about 2.5 event cycles per trial.

Test trials

The infants’ looking times during the test trials (see Fig. 4) were analyzed as in Experiment 1. The analysis yielded a significant main effect of event, F(1, 15) = 4.89, p < 0.05, indicating that the infants looked reliably longer at the short- (M = 24.9, SD = 11.1) than at the tall-cover (M = 17.9, SD = 10.2) event. Of the 16 infants in Experiment 2, 12 showed this pattern, T = 28, p < .05.

4.3. Discussion

The infants in Experiment 3, like those in Experiments 1 and 2, looked reliably longer at the short- than at the tall-cover test event, suggesting that they detected the violation in the short-cover event: they realized that the object was too tall to become fully hidden under the short cover. These results stand in marked contrast to previous findings that infants under 12 months of age typically do not attend to height information in tasks involving covering events (e.g., McCall, 2001; Wang & Baillargeon, 2006; Wang et al., 2005).

The results of Experiments 1 to 3 provide three separate demonstrations that infants can be taught the variable height in covering events through exposure in the laboratory to appropriate teaching events. Infants detected the violation in the short-cover event when tested immediately after receiving three (Experiment 1) or two (Experiment 2) pairs of teaching trials, and when tested 24 hours after receiving three pairs of teaching trials (Experiment 3).

Our interpretation of these results, consistent with the EBL account, is that the infants noticed, when watching the teaching trials, that the object sometimes remained partly visible beneath the cover and sometimes became fully hidden. Because the infants’ physical representations of these covering events did not include height information, the infants could not make sense of their observations: the same physical representations (“cover lowered over object”) led to contrastive outcomes (“object remains partly visible beneath cover” versus “object becomes fully hidden”). Exposure to these unexplained contrastive outcomes served to trigger learning. At that point, the infants began to look for the conditions that mapped onto the different outcomes, and soon noticed that the object remained partly visible when the cover was shorter than the object, and became fully hidden when the cover was taller than the object. The infants’ principle of persistence allowed them to readily make sense of this condition-outcome regularity, and height was then added to the list of variables relevant for predicting outcomes in covering events. When the infants next saw the test events, either immediately following the teaching trials or the next day, they categorized the events as covering events, and tapped their knowledge of this event category. Because height was now listed as a relevant variable (even after 24 hours, in the case of the infants in Experiment 3), the infants included information about the relative heights of the cover and object in their physical representation of each test event. This information was then interpreted in accord with the variable rule, and the short-cover test event was flagged as a violation.

The preceding analysis makes several interesting predictions about the circumstances under which infants should fail to identify height as a covering variable, and hence should fail to detect the violation in the short-cover test event. Experiments 4 to 6 began to examine some of these predictions.

Our general strategy was to modify our teaching events by introducing a single modification at a time; according to the EBL account, each of the modifications introduced should disrupt learning. In all three experiments, the infants received three pairs of modified teaching trials immediately followed by the same two test trials as in Experiments 1 to 3. If the modification introduced in the teaching trials disrupted learning, as predicted, then the infants should fail to identify height as a covering variable, and hence should look about equally at the short- and tall-cover test events.

We reasoned that the results of Experiments 4 to 6 would not only help make clear which aspects of our teaching events were essential for learning, but would also help address an alternative, low-level interpretation of the positive findings obtained in Experiments 1 to 3. In all three experiments, the infants looked reliably longer at the short- than at the tall-cover test event. One could argue that the infants did so, not because they identified height as a covering variable during the teaching trials, but because they found the short-cover event intrinsically more attractive than the tall-cover event. Perhaps our short-cover event differed from those used in previous experiments (e.g., Wang & Baillargeon, 2006; Wang et al., 2005) in subtle ways that made it particularly attractive for these 9-month-old infants. Evidence in Experiments 4 to 6 that the infants tended to look equally at the short- and tall-cover events would rule out such a possibility.

5. Experiment 4: Teaching events without contrastive outcomes

According to the EBL account, the first step in infants’ identification of a new variable in an event category is noticing contrastive outcomes relevant to the variable that cannot be predicted or interpreted by infants’ current physical knowledge; this first step serves to trigger learning. The purpose of Experiment 4 was to examine whether this assumption was indeed correct.

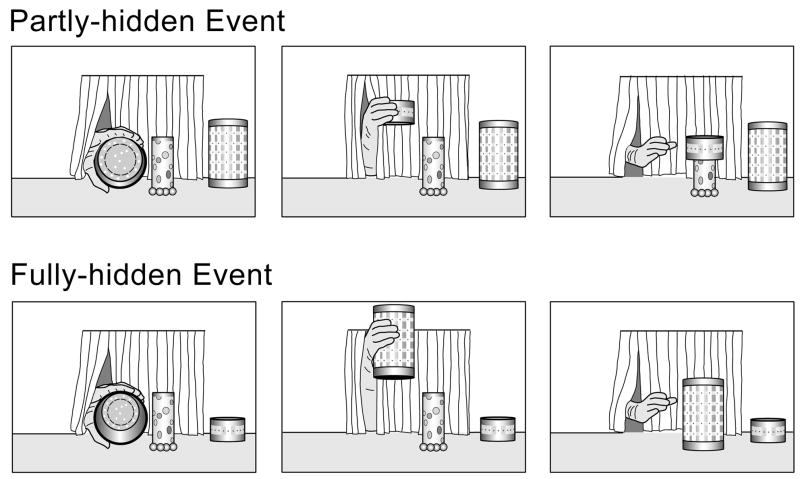
In their teaching experiments on the support variable weight distribution, Baillargeon and her colleagues (e.g., Baillargeon, 1999; Baillargeon et al., 2000) addressed this same issue by presenting infants with only the box-stays or only the box-falls teaching events. Consistent with the EBL account, they found that infants no longer identified weight distribution as a variable. In the present research we adopted a different tack, which made the teaching trials shown in Experiment 4 more similar to those shown in our previous experiments. Specifically, the infants were tested using the same procedure as in Experiment 1, except that the teaching object was much shorter and became fully hidden under the short as well as the tall cover in each pair of teaching trials (see Fig. 5). Across trials, the infants thus saw both short and tall covers being placed over the teaching object, as before. However, all of these events now resulted in the same outcome: the object became fully hidden under the cover. In each pair of teaching trials, the infants thus saw a fully-hidden event involving a short cover (fully-hidden/short-cover event) and a fully-hidden event involving a tall cover (fully-hidden/tall-cover event). Following the teaching trials, the infants received two test trials in which they saw the short- and tall-cover test events, as in the previous experiments.

Figure 5.

Schematic depiction of the first pair of teaching events shown in Experiment 4.

According to the EBL account, exposure to contrastive outcomes is necessary to trigger learning. Therefore, we predicted that the infants in Experiment 4, who saw similar (fully-hidden) outcomes in all teaching trials, would fail to identify height as a covering variable, and hence would look about equally at the short- and tall-cover test events. However, other predictions were possible: one could imagine alternative learning accounts in which variation in outcome would play little or no role. For example, one might propose that, when watching similar physical events, infants look for invariants across the events, and extract more and more subtle invariants over time (e.g., Gibson, 1969). According to this invariant-extraction account, infants might still be able to extract a height invariant when shown the modified teaching events in Experiment 4: after all, the object was always shorter than the cover, and always became fully hidden under it. If the infants extracted this invariant, then they should detect the violation in the short-cover test event—the object was now taller than the cover, and yet became fully hidden under it—and they should thus look reliably longer at the short- than at the tall-cover event.

5.1. Method

5.1.1. Participants

Participants were 16 healthy term infants, 10 male and 6 female (range: 8 months, 25 days to 9 months, 29 days, M = 9 months, 11 days). An additional 3 infants were tested but eliminated, 2 because they were fussy and 1 because the difference in her looking times during the two test trials was over 3 SD from the mean of her condition.

5.1.2. Apparatus, events, and procedure

The apparatus, events, and procedure used in Experiment 4 were similar to those in Experiment 1, except that the teaching object was 5.5 cm tall, instead of 14.5 cm tall, and became fully hidden under all of the teaching covers. Interobserver agreement during the test trials was calculated for all 16 infants and averaged 97% per trial per infant.

5.2. Results

Teaching trials

The infants’ looking times during the three pairs of teaching trials (see Fig. 6) were averaged across pairs and compared by means of a one-way ANOVA with event (fully-hidden/short-cover or fully-hidden/tall-cover) as a within-subject factor. The main effect of event was not significant, F(1, 15) = 0.68, indicating that the infants looked about equally at the fully-hidden/short-cover (M = 34.2, SD = 13.5) and the fully-hidden/tall-cover (M = 32.2, SD = 12.1) events. Because each event cycle in the teaching trials lasted about 14 s, the infants saw between 2 and 2.5 event cycles per trial.

Figure 6.

Mean looking times of the infants in Experiments 4 to 6 at the teaching and test events.

*The striped bar of Experiment 4 represents the infants’ looking time at the fully-hidden/short-cover teaching events, and the white bar represents the fully-hidden/tall-cover teaching events.

The infants’ looking times during the teaching trials were also compared to those of the infants in Experiment 1 by means of a 2 × 2 ANOVA with experiment (1 or 4) as a between-subjects factor and event (with short or tall covers) as a within-subject factor. The main effect of experiment was not significant, F(1, 30) = 0.33, nor was the experiment × event interaction, F(1, 30) = 0.95, suggesting that the infants in Experiments 1 and 4 were equally attentive during the teaching trials.

Test trials

The infants’ looking times during the two test trials (see Fig. 6) were analyzed as in Experiment 1. The main effect of event was not significant, F(1, 15) = 0.79, indicating that the infants looked about equally at the short- (M = 24.9, SD = 15.4) and tall-cover (M = 27.7, SD = 17.6) events. Of the 16 infants in the experiment, only 6 looked longer at the short- than at the tall-cover event, T = 48.5, p > .10.

The infants’ test responses were also compared to those of the infants in Experiment 1 by means of a 2 × 2 ANOVA with experiment (1 or 4) as a between-subjects factor and event (short- or tall-cover) as a within-subject factor. The analysis revealed only a significant experiment × event interaction, F(1, 30) = 6.85, p < .025. Planned comparisons confirmed that, whereas the infants in Experiment 1 looked reliably longer at the short- (M = 25.4, SD = 13.3) than at the tall-cover (M = 17.5, SD = 8.3) event, F(1, 30) = 7.46, p < .025, those in Experiment 4 tended to look equally at the two events, F(1, 30) = 0.95.

5.3 Discussion

In contrast to the infants in the preceding experiments, the infants in Experiment 4 looked about equally at the two test events, suggesting that they failed to detect the violation in the short-cover event. These results are important for two reasons. First, they rule out a possible low-level interpretation (mentioned earlier) of the positive findings obtained in Experiments 1 to 3. Had the infants in these experiments looked reliably longer at the short-cover event simply because they found it intrinsically more attractive than the tall-cover event, then the same response pattern should have been observed in Experiment 4. However, this was not the case: although the infants in Experiment 4 saw exactly the same test events as the infants in Experiments 1 to 3, they tended to look equally at the events.

Second, the results of Experiment 4 make clear that exposure to contrastive outcomes is important for learning, at least in the context of a brief laboratory session. In Experiment 4, the teaching object always became fully hidden under the teaching covers, so that the infants saw similar outcomes across all six teaching trials; when next shown the short- and tall-cover test events, the infants gave no evidence that they had identified height as a covering variable.

Why is variation in outcome important for learning? According to the EBL account, such variation helps trigger learning by making infants aware, at some level, that their current physical knowledge does not allow them to predict or interpret the observed outcomes. Similar physical representations (“cover lowered over object”) lead to contrastive outcomes (“object remains partly visible beneath cover” versus “object becomes fully hidden”), signaling that some critical information is missing from the representations.

It might be objected that exposure to contrastive outcomes could be helpful for a simpler reason: perhaps infants merely tend to look longer at events that present contrastive outcomes, thus increasing their opportunity to learn about the events or extract their invariants. However, recall that no reliable difference was found between the looking times of the infants in Experiments 1 and 4 during the teaching trials. Indeed, infants’ mean total looking times at the teaching events were very similar in Experiments 1 (186.1 s) and 4 (199.3 s). Thus, it seems likely that the infants in Experiment 4 failed to identify height as a covering variable, not because they were less attentive to the modified teaching events they were shown, but because these events lacked a crucial ingredient to trigger learning.

The results of Experiment 4 thus support the EBL account’s assumption that noticing contrastive outcomes relevant to a variable is an important first step in identifying the variable. Future experiments using an eye-tracking device might shed additional light on the effects of exposure to contrastive outcomes, by comparing infants’ eye movements when such outcomes are present versus absent. According to the EBL account, once infants notice contrastive outcomes they cannot predict or interpret based on their current physical knowledge, they begin to search for the conditions that map onto these outcomes. Thus, in the context of the present research, we might expect infants who are exposed to contrastive outcomes during the teaching events to spend more time comparing the heights of the cover and object in each event, than infants who are not exposed to such outcomes.

6. Experiment 5: Teaching events without relative height information

According to the EBL account, the second step in infants’ identification of a new variable in an event category involves discovering what conditions map onto the observed contrastive outcomes. In Experiments 1 to 3, discovering the relevant condition-outcome regularity was particularly easy, for two reasons. First, within each pair of teaching trials, the short and tall covers differed only in height: they were identical in width, shape, pattern, and color. Second, within each teaching trial, the infants could directly compare the heights of the cover and object as they stood next to each other on the apparatus floor. Prior research (e.g., Baillargeon, 1991, 1995) indicates that, when infants begin to reason about a continuous variable such as height or width in an event category, they can do so qualitatively, but not quantitatively. The distinction between quantitative and qualitative reasoning is derived from computational models of everyday physical reasoning (e.g., Forbus, 1984). Quantitative reasoning requires one to encode and remember information about absolute quantities (e.g., object A is “this” tall, where “this” stands for some absolute measure of A’s height). Qualitative reasoning, in contrast, requires one to encode and remember information about only relative quantities (e.g., object A is taller than object B). In order to encode the heights of covers and objects qualitatively, infants must compare them as they stand side by side. Since at the start of each event cycle in each teaching trial the cover and object stood side by side on the apparatus floor, the infants in the preceding experiments had ample opportunity to encode information about their relative heights.

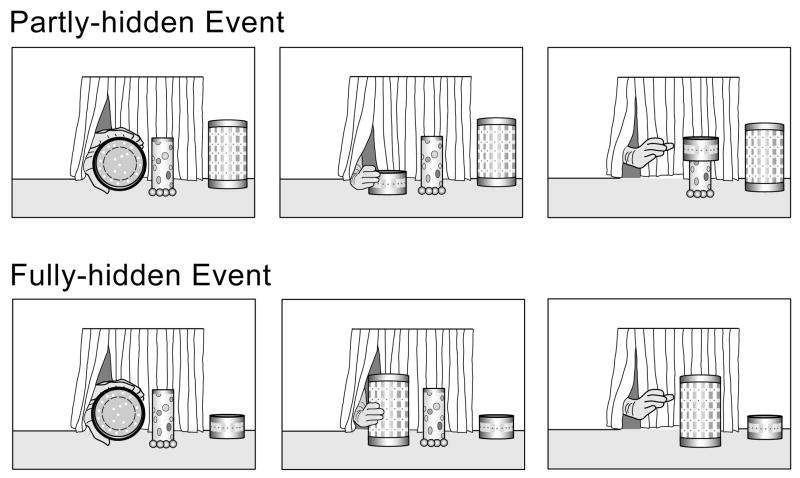
In Experiment 5, we made it impossible for the infants to directly compare the heights of the cover and object in each teaching trial. Throughout the entire teaching session, the cover was never placed on the apparatus floor next to the object. At the beginning of each event cycle, the primary experimenter’s gloved hand held the cover next to and above the object (see Fig. 7). Thus, although the infants could still encode the absolute heights of the cover and object, they could no longer encode their relative heights and judge whether the cover was taller or shorter than the object through a direct visual comparison.

Figure 7.

Schematic depiction of the first pair of teaching events shown in Experiment 5.

If the infants in Experiments 1 to 3 succeeded in identifying height as a covering variable in the teaching trials in part because they (1) noticed that the object became sometimes partly and sometimes fully hidden under the cover, and then (2) uncovered a condition-outcome regularity having to do with the relative heights of the cover and object, then Experiment 5 might yield negative results. Although the infants could still observe that the object became sometimes partly and sometimes fully hidden under the cover, they could no longer detect a condition-outcome regularity having to do with the relative heights of the cover and object.

We reasoned that negative results in Experiment 5 would be helpful on several counts. First, they would support the EBL account’s assumption that, after noticing unexplained contrastive outcomes, infants look for the conditions that map onto these outcomes.

Second, negative results in Experiment 5 would provide evidence that the infants in Experiments 1 to 3 detected a condition-outcome regularity having to do with the relative heights of the cover and object, rather than some other, more arbitrary, condition-outcome regularity. During the teaching trials of Experiments 1 to 3, there were other regularities the infants could detect. For example, in the partly-hidden teaching events, the infants could learn that the object became partly hidden when the cover was 6 to 11 cm tall, or was not much larger than the primary experimenter’s gloved hand. Had the infants in Experiments 1 to 3 learned such regularities, they might have looked reliably longer at the short-cover test event simply because it violated these regularities: the short cover was 9.5 cm tall, and was not much larger than the gloved hand, but still fully hid the object. Since the infants in Experiment 5 could detect these same regularities, negative results would suggest that the infants in Experiments 1 to 3 detected a condition-outcome regularity having to do with the relative heights of the cover and object in each event, rather than these more arbitrary regularities.

Finally, negative results in Experiment 5, like those in Experiment 4, would contradict the possibility that the infants in Experiments 1 to 3 simply found the short-cover test event intrinsically more attractive than the tall-cover test event.

6.1. Method

6.1.1. Participants

Participants were 16 healthy term infants, 7 male and 9 female (range: 8 months, 25 days to 9 months, 23 days, M = 9 months, 11 days). An additional 3 infants were tested but eliminated, 2 because of parental interference and 1 because the difference in her looking times during the two test trials was over 3 SD from the mean of her condition.

6.1.2. Apparatus, events, and procedure

The apparatus, events, and procedure used in Experiment 5 were similar to those in Experiment 1 with one exception: each teaching event started with the primary experimenter’s hand holding the cover 2.5 cm above and 4 cm to the left of the object. Both the object and the cover not in use (i.e., the other cover from the same pair of teaching trials) were placed at the same locations as in Experiment 1.

As in Experiment 1, each teaching event began with two pretrials. During the first pretrial, the primary experimenter’s gloved hand rotated the cover 90 degrees (2 s) and then paused, to show the infant the hollow interior of the cover. When the computer signaled that the infant had looked at this paused scene for 2 cumulative seconds, the hand rotated the cover back to its starting position above and next to the object (2 s), and paused again; this second pretrial gave the infant the opportunity to inspect the cover and object (however, the infants could no longer directly compare their heights because the cover and object did not stand side by side). When the computer signaled that the infant had looked at this paused scene for 2 cumulative seconds, the event proper began. This event was similar to that shown in Experiment 1 but was 4 s shorter, because the hand did not lift (2 s) or lower (2 s) the cover next to the object at the start and end of the event cycle. Each event cycle thus lasted 10 s, instead of 14 s as in Experiment 1; cycles were repeated until the computer signaled that the trial had ended.

Because each teaching trial had a shorter event cycle, a teaching trial now ended when the infants either (1) looked away from the event for 2 consecutive seconds after having looked at it for at least 10 cumulative seconds or (2) looked for 60 cumulative seconds without looking away for 2 consecutive seconds. The 10-s minimal value was chosen to ensure that the infants had the opportunity to observe at least one cycle of each teaching event.

The test trials shown in Experiment 5 were identical those in the preceding experiments. At the beginning of each event cycle, as before, the cover stood next to the object on the apparatus floor, allowing the infants to directly compare their heights.

Interobserver agreement during the test trials was calculated for 14 of the 16 infants and averaged 97% per trial per infant.

6.2. Results

Teaching trials

The infants’ looking times during the teaching trials (see Fig. 6) were analyzed as in Experiment 1. The main effect of event was not significant, F(1, 15) = 2.20, p >.10, suggesting that the infants looked about equally at the partly- (M = 26.9, SD = 7.3) and fully-hidden (M = 31.8, SD = 9.9) events. Because each event cycle in the teaching trials lasted about 10 s, the infants saw about 2.5 to 3 event cycles per trial.

As in Experiment 4, the infants’ looking times during the teaching trials were also compared to those of the infants in Experiment 1. The main effect of experiment was not significant, F(1, 30) = 0.36, nor was the experiment × event interaction, F(1, 30) = 1.00, p > .10, suggesting that the infants in Experiments 1 and 5 were equally attentive during the teaching trials.

Test trials

The infants’ looking times during the test trials (see Fig. 6) were analyzed as in Experiment 1. The main effect of event was not significant, F(1, 15) = 0.00, indicating that the infants looked about equally at the short- (M = 19.1, SD = 6.7) and tall-cover (M = 19.1, SD = 8.7) events. Of the 16 infants in the experiment, 10 looked longer at the short-cover event, T = 55, p > .10.

As in Experiment 4, the infants’ test responses were also compared to those of the infants in Experiment 1. The analysis revealed a significant main effect of event, F(1, 30) = 6.15, p < .025, and a significant experiment × event interaction, F(1, 30) = 6.13, p < .025. Planned comparisons confirmed that, whereas the infants in Experiment 1 looked reliably longer at the short- (M = 25.4, SD = 13.3) than at the tall-cover (M = 17.5, SD = 8.3) event, F(1, 30) = 12.31, p < .0025, those in Experiment 5 tended to look equally at the two events, F(1, 30) = 0.00.

6.3. Discussion

The infants in Experiment 5 looked about equally at the two test events, suggesting that they failed to identify height as a covering variable during the teaching trials, and hence failed to detect the violation in the short-cover event.

These results, together with those of Experiment 4, support the EBL account’s claims that, in order to identify a new variable in an event category, infants must first notice contrastive outcomes relevant to the variable, and then uncover the conditions associated with these outcomes. Although the infants in Experiment 5 were exposed to the same contrastive outcomes as the infants in Experiments 1 to 3, they could not detect the conditions associated with these outcomes. Because in each teaching trial the cover was held next to and above the object, the infants could not directly compare their heights.⁶ As a result, the infants could not gather condition-outcome data having to do with the relative heights of the cover and object. Consequently, the infants did not discover that the object became partly hidden when placed under a cover that was shorter than the object, and became fully hidden when placed under a cover that was taller than the object.

The results of Experiment 5 thus provide further support for the distinction between qualitative and quantitative reasoning and for the developmental evidence that, when infants first identify a continuous variable as relevant to an event category, they can reason about it qualitatively, but not quantitatively (e.g., Baillargeon, 1991, 1995; Wang et al., 1994). Although the infants in Experiments 1 to 5 all had ample opportunity to encode the absolute heights of the cover and object in each teaching trial, only the infants in Experiments 1 to 3, who also had opportunity to encode the relative heights of the cover and object, succeeded in identifying height as a covering variable.

The negative results of Experiment 5 also provide evidence against the notion that the infants in Experiments 1 to 3 detected condition-outcome regularities having to do with other aspects of the teaching events. Had the infants in Experiments 1 to 3 looked reliably longer at the short-cover test event because they (1) noticed that the teaching object became partly hidden when the cover was 6 to 11 cm tall, or was slightly larger than the gloved hand, and became fully hidden otherwise, and (2) realized that the short-cover event deviated from this regularity (the short cover was 9.5 cm tall, and was not much larger than the gloved hand, but still fully hid the object), then the infants in Experiment 5 should have responded in the same manner, because these same regularities were again present in the teaching events. The fact that the infants in Experiment 5 did not in fact respond in the same manner suggests that the infants in Experiments 1 to 3 detected a condition-outcome regularity having to do specifically with the relative heights of the cover and teaching object.

In future experiments, we plan to use modified teaching trials in which infants can easily gather information about the relative heights of the cover and object—but in which other aspects of the teaching events present irrelevant variation (e.g., Baillargeon et al., 2000). For example, what if the infants were shown the same six teaching covers as in Experiment 1, but scrambled so that the short and tall covers in each pair of teaching trials no longer matched in pattern and color? Or what if the teaching covers remained the same, but the teaching object differed in shape, pattern, and color across trials? Would infants still be able to detect the condition-outcome regularity in these more varied events, or would they now require more than six teaching trials to do so? Answers to these and related questions will help us specify the mechanisms that underlie infants’ detection of condition-outcome regularities, and the limitations imposed by their information-processing resources.

7. Experiment 6: Teaching events without a plausible explanation

According to the EBL account, the third step in infants’ identification of a new variable in an event category involves building an explanation for the condition-outcome regularity that has been detected. In Experiments 1 to 3, this third step was straightforward, because the regularity the infants detected in the course of the teaching trials—the object became partly hidden when the cover was shorter than the object, and became fully hidden otherwise—was entirely consistent with the principle of persistence: because an object continues to exist and retains its height when under a cover, it can become fully hidden only if its height is equal to, or shorter than, that of the cover.

But is it really the case that infants build explanations, using their prior knowledge, for the condition-outcome regularities they observe? Is this third step truly necessary? One might propose that infants notice contrastive outcomes, find the conditions that map onto these outcomes—and then simply use this condition-outcome regularity to predict the outcomes of subsequent events. Why assume that infants engage in causal, as opposed to statistical, learning?

To our way of thinking, causal reasoning presents at least two major advantages for infants. One is that it ensures enormous, yet appropriate, generalization. Infants who understand why tall objects cannot become fully hidden under short covers, even if only at the most shallow level, should be able to reason correctly about height information in any covering event, however remote or dissimilar this event may be from the original learning events. Indeed, one of the striking features of infants’ physical reasoning is that infants who have identified a variable as relevant to an event category give evidence of attending to this variable when tested with very different events from the category. As an example, the variable height is identified at about 3.5 months in occlusion events, and infants aged 3.5 to 6 months (1) are surprised when a tall, self-propelled object moves back and forth behind a screen with a high window without appearing in the screen’s window (e.g., Baillargeon & DeVos, 1991; Baillargeon & Graber, 1987); (2) are surprised when a gloved hand lowers a tall object behind a short container until it becomes almost fully hidden (e.g., Hespos & Baillargeon, 2001a); and (3) search for a tall object behind a tall as opposed to a short screen (e.g., Hespos & Baillargeon, 2006). This sort of broad yet appropriate generalization is precisely what one would expect from infants who have acquired a causal rule involving height in occlusion events; it may be more difficult to explain such abstract generalization from the standpoint of statistical learning.

Another advantage of causal learning is that it helps protect infants from learning and generalizing spurious regularities (e.g., Newcombe, Sluzenski, & Huttenlocher, 2005). If it is the case that only condition-outcome regularities for which infants can provide explanations—or which infants can describe as causal rules—can become variables, then infants are unlikely to learn many false regularities along the way. This means, for example, that we could not easily teach infants in the laboratory that objects become partly hidden under round (or striped or red) covers, and become fully hidden under square (or dotted or green) covers. Infants might be able to learn such arbitrary regularities given a sufficient number of teaching trials, and they might use these arbitrary regularities to make predictions about the outcomes of similar events; however, one would expect learning to be slower, and generalization to be narrower, than with causal learning.

In the teaching experiments we mentioned earlier that focused on the support variable weight distribution (e.g., Baillargeon, 1998, 1999; Baillargeon et al., 2000), 11-month-old infants readily identified this variable when shown events designed to teach the correct causal rule. However, infants gave no evidence of learning when shown teaching events involving the reverse rule: in each pair of teaching trials, the asymmetrical object now remained stable when its smaller end rested on the platform, and conversely fell when its larger end rested on the platform. Following exposure to these teaching events, the infants tended to look equally at the adequate- and inadequate-support test displays, suggesting that they did not expect the L-shaped box to fall when its larger end lay on the platform. Indeed, the infants appeared to have no expectation about these displays. These findings provide evidence consistent with the EBL account. If infants are simply in the business of detecting condition-outcome regularities, without attempting to make sense of them, why would they learn the correct, causal regularity, but not the incorrect, reverse regularity? Nevertheless, one potential limitation of these findings is that infants were presented with very different teaching events in the causal-rule and reverse-rule conditions, leaving open the possibility that the first regularity was simply easier to detect than the second one.

In Experiment 6, we attempted to create teaching events that were perceptually highly similar to those used in Experiments 1 and 3, but for which no causal explanation could be provided. Recall that at the start of each teaching trial in these experiments, the infants received a brief pretrial in which the gloved hand rotated the cover upward to show its hollow interior. In Experiment 6, all of the teaching covers were modified to be of the same depth: false tops inserted in the covers rendered them all 2.5 cm deep (see Fig. 8). Thus, when the cover was rotated upward at the start of each teaching trial, the infants could see that, whatever the cover’s exterior height, its interior height was only 2.5 cm (the infants could detect the mismatch between the cover’s exterior and interior height through direct visual comparison, by comparing the exterior and interior sidewall of the cover at any point along its circumference). After the cover was rotated back to its original position on the apparatus floor, the trial proceeded exactly as before: in each partly-hidden event, the short cover hid the top portion of the object, and in each fully-hidden event, the tall cover hid the whole object (the false top inserted in each cover could be altered surreptitiously to produce exactly the same outcome as when no false top was used). The infants in Experiment 6 thus saw exactly the same partly- and fully-hidden teaching events as in Experiments 1 and 3, except for the brief pretrial at the start of each teaching trial in which the cover’s interior was revealed.

Figure 8.

Schematic depiction of the first pair of teaching events shown in Experiment 6.

We reasoned that if the infants in Experiments 1 and 3 merely detected a condition-outcome regularity having to do with the relative heights of the cover and object—the object became partly hidden when the cover was shorter than the object, and became fully hidden otherwise—then the infants in Experiment 6, who were exposed to the same partly- and fully-hidden covering events, should also detect this regularity. The infants should thus look reliably longer at the short-cover test event, which deviated from this regularity.

On the other hand, if the infants in Experiments 1 and 3 not only detected a condition-outcome regularity having to do with the relative heights of the cover and object, but also built a causal explanation for this regularity using their prior knowledge, and more specifically their principle of persistence, then the infants in Experiment 6 might fail to identify height as a covering variable. To make sense of the regularity shown in the teaching events, the infants had to be able to reason that, because the object continued to exist and retained its height when under the covers, it could extend to its full height inside the tall but not the short covers. However, because the covers were now all shallow, no plausible explanation could be provided for the condition-outcome regularity present in the teaching events: it no longer made sense that the object became fully hidden under the tall (but shallow) covers. Thus, we expected that the infants in Experiment 6 would fail to identify height as a covering variable during the teaching trials. The infants should thus include no height information in their physical representations of the test events, and hence they should fail to detect the violation in the short-cover event.

7.1. Method

7.1.1. Participants

Participants were 16 healthy term infants, 8 male and 8 female (range: 8 months, 25 days to 9 months, 27 days, M = 9 months, 10 days). An additional 3 infants were tested but eliminated, because they were fussy (2) or distracted (1).

7.1.2. Apparatus, events, and procedure

The apparatus, events, and procedure used in Experiment 6 were similar to those in Experiment 1, with the following exceptions. To create the false top inside each teaching cover, an inner cover 2.5 cm tall and 10.4 cm in diameter was inserted just inside its opening. The sides of this inner cover fit tightly against those of the teaching cover and were not distinguishable from them. Thus, when each teaching cover was rotated upward, what the infants actually saw was the interior of the inner cover, with its interior top surface 2.5 cm deep.

From the infants’ perspective, except for the shallow interior of each teaching cover, which was revealed during the brief pretrial at the start of each teaching trial when the cover was rotated upward, all other aspects of the teaching events were identical to those in Experiments 1 and 3.

To make it possible to produce the partly- and fully-hidden teaching events, the top of the inner cover inside each teaching cover consisted of a magnetic outer ring surrounding a hole 7.5 cm in diameter; resting above this hole, against the outer ring, was a thin metal disc 9 cm in diameter. A thin magnet was also attached to the top of the teaching object, under the contact paper that covered it. In each teaching trial, when the short or tall teaching cover was lowered over the teaching object, the metal disc became attached to the top of the object, allowing the object to pass through the hole in the top of the inner cover and into the interior of the teaching cover proper. In each partly-hidden event, when the short teaching cover was released, its (actual) interior top surface rested on the metal disk attached to the top of the object; in each fully-hidden event, the tall teaching cover was taller than the object, and so its (actual) interior top surface did not come into contact with the metal disc attached to the top of the object. Finally, in each teaching trial, when the short or tall teaching cover was lifted, the metal disk became attached to the magnetic outer ring once more, so that the teaching object, when revealed, appeared exactly as before.

The outer ring and metal disc forming the top of the inner cover inside each teaching cover created the illusion of a solid top with a slight circular depression about 7.5 cm in diameter at its center (this two-layer arrangement was similar to that in the teaching covers used in the preceding experiments). The entire interior surface of the inner cover inside each teaching cover was covered with red contact paper and decorated with white dots, again as in previous experiments.

Interobserver agreement during the test trials was calculated for 13 of the 16 infants, and averaged 98% per trial per infant.

7.2. Results

Teaching trials

The infants’ looking times during the teaching trials (see Fig. 6) were analyzed as in Experiment 1. The main effect of event was not significant, F(1, 15) = 0.28, indicating that the infants tended to look equally at the partly- (M = 35.8, SD = 11.4) and fully-hidden (M = 37.4, SD = 12.7) events. Because each event cycle in the teaching trials lasted about 14 s, the infants saw about 2.5 event cycles per trial.

As in Experiments 4 and 5, the infants’ looking times during the teaching trials were also compared to those of the infants in Experiment 1. The main effect of experiment was not significant, F(1, 30) = 2.51, p > .10, nor was the experiment × event interaction, F(1, 30) = 0.02, suggesting that the infants in Experiment 6 were as attentive as those in Experiment 1 during the teaching trials.

Test trials

The infants’ looking times during the test trials (see Fig. 6) were analyzed as in the previous experiments. The main effect of event was not significant, F(1, 15) = 0.72, indicating that the infants looked about equally at the short- (M = 24.0, SD = 17.4) and tall-cover (M = 26.7, SD = 16.5) events. Of the 16 infants in the experiment, 8 looked longer at the short-cover event, T = 55.5, p > .10.

As in Experiments 4 and 5, the infants’ test responses were also compared with those of the infants in Experiment 1. The analysis revealed only a significant experiment × event interaction, F(1, 30) = 6.61, p < .025. Planned comparisons confirmed that, whereas the infants in Experiment 1 looked reliably longer at the short- (M = 25.4, SD = 13.3) than at the tall-cover (M = 17.5, SD = 8.3) event, F(1, 30) = 7.30, p < .025, those in Experiment 6 tended to look equally at the two events, F(1, 30) = 0.88.

7.3. Discussion

The infants in Experiment 6 looked about equally at the two test events, suggesting that they did not identify height as a covering variable during the teaching trials, and hence failed to detect the violation in the short-cover event.

These results, together with those of Experiments 4 and 5, support the EBL account’s claims that, in order to identify the variable height in covering events, infants must (1) notice that when covers are lowered over objects, the objects sometimes remain partly visible beneath the covers and sometimes become fully hidden; (2) discover that the objects remain partly visible when taller than the covers, and become fully hidden when shorter than the covers; and (3) build an explanation for this condition-outcome regularity using their prior knowledge. In Experiment 6, the infants were exposed to contrastive outcomes in the partly- and fully-hidden teaching events, and they could readily discover the conditions that mapped onto these outcomes: the teaching object remained partly visible when it was taller but not shorter than the cover. However, the infants could not generate a plausible explanation for this condition-outcome regularity: they realized that, despite the differences in their exterior heights, the short and tall teaching covers were all equally shallow, making it impossible to explain the contrastive outcomes of the partly- and fully-hidden events.

The preceding interpretation assumes that the infants in Experiment 6 failed to identify height as a covering variable because they could not build a plausible explanation for the teaching events. Another, weaker interpretation of the results in Experiment 6 assumes that the infants (1) recognized when the teaching covers were rotated upward that their interior heights did not match their exterior heights, but (2) could not remember after the teaching covers were rotated downward just how shallow they were. As a result, the infants could proceed no further. Although this second interpretation is weaker than the first, it still suggests that there is more to identifying variables than detecting condition-outcome regularities. The infants in Experiment 6 saw the same partly- and fully-hidden teaching events as those in Experiments 1 and 3. Only the infants’ causal knowledge could have led them to understand that, in order to make sense of the condition-outcome regularity in the events, they also needed information about the covers’ non-matching interior heights.

The first interpretation proposed above assumes that the infants recognized that the short and tall teaching covers were equally shallow, making it difficult to explain why the teaching object became partly hidden under the short covers but fully hidden under the tall covers; the second interpretation assumes that the infants did not have sufficient information about the teaching covers’ interior heights to proceed further (e.g., they had no opportunity to compare the interior height of each teaching cover to the height of the teaching object, to determine whether the latter could fit inside the former). Both interpretations are consistent with the EBL claim that the identification of a new variable in an event category requires more than statistical learning: condition-outcome regularities become variables only when infants can make sense of what they observe.

However, one other interpretation of the results in Experiment 6 is possible that provides no support for the EBL account. It might be suggested that their experiences with covers prior to coming to the laboratory led the infants in Experiment 6 to expect covers with matching exterior and interior heights. When faced with the unusual, shallow teaching covers used in the experiment, the infants became confused, processed the teaching events only superficially, and thus failed to detect the condition-outcome regularity in the events. As a result, they could not detect that the short-cover test event deviated from this regularity.

Although this interpretation is logically possible, examination of the infants’ looking times during the teaching trials provides little evidence for it. Had the infants in Experiment 6 found the shallow covers odd or unusual, they might have looked reliably longer during the teaching trials than the infants in Experiment 1 or 3. However, as reported above, no reliable differences were found between the looking times of the infants in Experiments 1 and 6 during the teaching trials. Furthermore, an analysis comparing the looking times of the infants in Experiments 3 and 6 during the teaching trials yielded similar results: the main effect of experiment was not significant, F(1, 30) = 0.42, nor was the experiment × event interaction, F(1, 30) = 0.34.

Much research remains to be done to determine whether and how infants causally interpret the condition-outcome regularities they detect. Future experiments will build on the present results in various ways. Some experiments will again use shallow teaching covers, to better understand how the infants in Experiment 6 perceived the shallow covers they were shown. For example, what if the short teaching covers were all 2.5 cm deep, as Experiment 6, but the tall covers were now all 10 cm deep? Evidence that infants now looked reliably longer at the short- than at the tall-cover test event would suggest that, as long as the short and tall covers differ in their interior heights (as they did in Experiments 1 to 3), infants can make sense of the contrastive outcomes of the partly- and fully-hidden teaching events.

Other experiments might introduce reverse rules, as in the support teaching experiments mentioned earlier (e.g., Baillargeon, 1998, 1999; Baillargeon et al., 2000; see also Newcombe et al., 2005). For example, what if the teaching object became partly hidden under the tall covers, and fully hidden under the short covers? Would infants now look reliably longer at the tall-cover test event? Or would they fail to give any evidence of learning, as predicted by the EBL account?

Finally, other experiments might focus on arbitrary, as opposed to reverse, regularities. Could infants learn that the teaching object becomes partly hidden under cylindrical (or dotted or red) covers, but becomes fully hidden under rectangular (or striped or green) covers? How many trials would infants require to learn such condition-outcome regularities? And how much generalization would be possible?

Answers to these and related questions should help us better understand the role of infants’ prior knowledge in their identification of variables.

8. Comparisons of Experiments 1–3 versus Experiments 4–6

We have argued that the infants in Experiments 1–3 looked reliably longer at the short- than at the tall-cover test event because they watched effective teaching events that allowed them to identify height as a covering variable; and that the infants in Experiments 4–6 tended to look equally at the two test events because they watched ineffective teaching events that did not allow them to identify height as a covering variable. However, this description tells us only about differences in the infants’ relative looking times at the two test events. In a final set of analyses, we compared the test responses of the two groups of infants to determine whether there were also differences in their absolute looking times at the two test events.

The infants’ test responses were compared by means of a 2 × 2 ANOVA with group (Experiments 1–3 or 4–6) as a between-subjects factor and event (short- or tall-cover test event) as a within-subject factor. The main effect of group was not significant, F(1, 94) = 1.41, p > .10. However, the main effect of event, F(1, 94) = 6.24, p < .025, and the group × event interaction, F(1, 94) = 17.28, p < .0001, were both significant. A first set of planned comparisons indicated that, as expected, the infants in Experiments 1–3 looked reliably longer at the short- (M = 24.6, SD = 11.0) than at the tall-cover (M = 17.2, SD = 8.6) event, F(1, 94) = 22.12, p < .0001, whereas those in Experiments 4–6 tended to look equally at the two events (short-cover: M = 22.6, SD = 13.9, tall-cover: M = 24.5, SD = 15.0, F(1, 94) = 1.37, p > .10). Additional comparisons revealed that (1) there was no reliable difference in the looking times at the short-cover event of the infants in Experiments 1–3 (M = 24.6, SD = 11.0) and 4–6 (M = 22.6, SD = 13.9), F(1, 94) = 1.54, p > .10; and (2) there was a reliable difference in the looking times at the tall-cover event of the infants in Experiments 1–3 (M = 17.2, SD = 8.6) and 4–6 (M = 24.5, SD = 15.0), F(1, 94) = 21.47, p < .0001.

Compared to the infants in Experiments 1–3, those in Experiments 4–6 thus tended to look equally, and equally long, at the short- and tall-cover test events. Why did they do so? One possible interpretation might be that, because the infants in Experiments 4–6 failed to identify height as a covering variable and thus viewed all of the covering events shown in the teaching and test trials as expected events, they tended to focus on the superficial similarities and differences among the events, and they readily detected the differences between the teaching and test events. Recall that during the test trials a novel object and novel covers were used; the covers differed from each other not only in height but also in color (the short cover was green and the tall cover blue); only one cover was present in the apparatus in each test trial; the cover used in each trial was not rotated forward at the start of the trial; and so on. Any or all of these differences could have led the infants in Experiments 4–6 to view the short- and tall-cover events as relatively novel, thus resulting in greater attention to both events.

In contrast, the infants in Experiments 1–3 presumably paid little attention to the superficial similarities and differences among the various covering events they were shown. After they identified height as a covering variable, the infants most likely focused on the relative heights of the cover and object in each new event, and examined whether the event unfolded in a manner consistent or inconsistent with this new height rule. The tall-cover test event was consistent with the rule, and as such received relatively little attention; in contrast, the short-cover test event violated the rule, and hence received greater attention. Future experiments can test the above speculation by gathering detailed information about infants’ eye movements during the short- and tall-cover test events.

9. General Discussion

Infants typically do not identify height as a relevant variable for predicting and interpreting the outcomes of covering events until they are about 12 months of age (e.g., McCall, 2001; Wang & Baillargeon, 2006; Wang et al., 2005). In the present research, 9-month-old infants were shown three (Experiments 1 and 3) or two (Experiment 2) pairs of teaching events designed to help them identify height as a covering variable. After watching these events, the infants detected a violation when a tall object became fully hidden under a short cover. The infants succeeded in detecting this violation when tested immediately following the teaching trials (Experiments 1 and 2) or after a 24-hour delay (Experiment 3). These results suggest that the infants identified height as a covering variable during the teaching trials, and retained this new knowledge for at least one day. When next shown the short- and tall-cover test events, the infants categorized each event as a covering event, and then tapped their knowledge of this event category. Because this knowledge now included the variable height, the infants included information about the relative heights of the cover and object in their physical representation of each event. This information was then interpreted in accord with the variable rule, and the short-cover test event, which violated the rule, was flagged as a violation.

The teaching events used in Experiments 1–3 were designed in accord with the EBL account described in the Introduction, and included three ingredients assumed to be essential for learning. First, the events presented infants with contrastive outcomes: the teaching object sometimes remained partly visible beneath the cover (partly-hidden events) and sometimes did not (fully-hidden events). Second, the events made it easy for infants to discover the conditions that mapped onto these outcomes: in each pair of teaching events, the short and tall covers differed only in height; furthermore, at the start of each event cycle, each cover was placed on the apparatus floor next to the teaching object, to facilitate qualitative height comparisons. Finally, infants’ core principle of persistence could provide a ready explanation for the condition-outcome regularity thus discovered: because an object continues to exist and retains its height under a cover, it can become fully hidden if it is shorter but not taller than the cover. According to the EBL account, only regularities which can be explained, or reconciled with infants’ prior causal knowledge, become variables. Newly identified variables are added to infants’ knowledge of the relevant event category, to be applied to all events from the category.

In contrast to the infants in Experiments 1–3, those in Experiments 4–6 failed to detect the violation in the short-cover test event, suggesting that the modified teaching events they were shown did not allow them to identify height as a covering variable. In these experiments, the three key ingredients described above were removed, one at a time, from the teaching events. In Experiment 4, the infants no longer saw contrastive outcomes: a small teaching object was used that became fully hidden under the short and tall covers in each pair of teaching events. In Experiment 5, the tall teaching object was again used and the infants saw the same contrastive outcomes as in Experiments 1–3, but qualitative height comparisons were no longer possible: in each teaching event, the cover was held next to and above the object, making it difficult for infants to gather information about their relative heights by a direct visual comparison. As a result, the infants were unable to identify the conditions that mapped onto the events’ contrastive outcomes. Finally, in Experiment 6, the infants had access to the same contrastive outcomes and the same condition data as in Experiments 1–3; however, the infants were given additional information that made it difficult for them to arrive at an explanation for the outcomes of the teaching events. When the cover was rotated forward at the start of each teaching trial, the infants could see that its exterior height did not match its interior height: all covers were shallow and appeared only 2.5 cm deep. One interpretation of the results of Experiment 6 (other interpretations were also considered earlier) is that the infants noticed that all the teaching covers were equally shallow, and so could not generate an explanation for the different outcomes of the partly- and fully-hidden events. As a result, the infants failed to identify height as a covering variable.

The results of Experiment 6 are particularly striking because the infants saw exactly the same partly- and fully-hidden teaching events as in Experiments 1–3, except for the 2-s interval at the start of each teaching trial in which they saw the interior of the cover. Had the infants in Experiments 1–3 simply detected a statistical regularity between certain conditions and outcomes—“object shorter than cover, object remains partly visible beneath cover”; “object taller than cover, object becomes fully hidden under cover”—we might have expected the infants in Experiment 6 to do the same: after all, they saw the same events, and they spent about equal amounts of time looking at the events. The fact that the infants in Experiment 6 responded differently during the test events provides tentative support for the notion that the infants in Experiments 1–3 did not simply detect a condition-outcome regularity: they also attempted to make sense of what they saw, and it was this ability to arrive at an explanation for the teaching events that enabled them to identify height as a covering variable.

Taken together, the present results support the EBL account and also demonstrate that infants can be “taught” to identify a new variable in an event category, through exposure in the laboratory (or presumably the home) to appropriate observations for the variable. Our teaching paradigm also allowed us to manipulate the observations available to infants, and as such to begin examining what information may be critical for learning, Our teaching paradigm thus appears to provide a useful tool for peering into the processes involved in infants’ identification of new physical variables and, more generally, in infants’ acquisition of their physical knowledge.

9.1. Using variable information in action tasks

We have proposed that, when infants identify a new variable as relevant to an event category, they consistently attend to this information when they encounter various events from the category. Consistent with this proposal, there is evidence that after infants identify height as a covering variable, at about 12 months of age, (1) they are surprised when a tall object becomes fully hidden under a short cover (e.g., Wang et al., 2005); (2) they are surprised when a short object becomes much taller while briefly hidden under a tall cover (e.g., Wang & Baillargeon, 2006); and (3) they search for a tall object under a tall but not a short cover (e.g., McCall, 2001; Wang & Kohne, in press).

This last finding is particularly interesting for two reasons. First, it makes clear that infants who identify a new variable in an event category are not simply learning to attend to new visual information in the events they observe: they also use the variable information to guide their actions on objects. Second, more generally, such findings support the view that the same physical knowledge underlies infants’ responses in violation-of-expectation and action tasks (e.g., Baillargeon et al., in press; Hespos & Baillargeon, 2006, 2007; Wang & Kohne, in press). Of course, infants sometimes fail to reveal in action tasks knowledge that they readily reveal in violation-of-expectation tasks (e.g., Ahmed & Ruffman, 1998; Diamond & Lee, 2000; Piaget, 1954; Shinskey & Munakata, 2001; Vishton, Ware, & Badger, 2005). When such discrepancies arise, one of at least three explanations may apply: (1) infants may have difficulty planning the necessary actions (e.g., Baillargeon, Graber, DeVos, & Black, 1990; Willatts, 1997); (2) poor motor control may make it difficult for infants to execute the necessary actions (e.g., Diamond & Gilbert, 1989; Diamond & Lee, 2000); and (3) infants may be able to plan and execute the necessary actions, but may fail to do so because the total demands of the task (which depend on the difficulty of both the physical reasoning and the actions involved) overwhelm their limited information-processing resources (e.g., Boudreau & Bushnell, 2000; Keen & Berthier, 2004).

The preceding discussion leads to a striking prediction: 9-month-old infants who are “taught” in the laboratory to identify height as a covering variable, using teaching events similar to those in Experiments 1–3, should succeed in demonstrating their knowledge of this variable not only in a violation-of-expectation task (as in the present research) but also in an action task, as long as the responses required are sufficiently easy for the infants to plan and execute.

To examine this prediction, Wang and Kohne (in press) recently tested 9-month-old infants in a simple action task; half of the infants were assigned to a teaching condition, and half to a baseline condition. The infants in the teaching condition first received the same three pairs of teaching trials as in Experiments 1 and 3. Following these trials, the infants were brought to a different room where they sat on a parent’s lap at a table, across from an experimenter. On the table were a short and a tall cover. A tall toy was placed between the two covers, to facilitate height comparisons; the short cover was only about half as tall as the toy, and the tall cover was slightly taller than the toy. The covers and toy differed in size, shape, pattern, and color from those used in the teaching trials. After the infants had the opportunity to inspect the covers and toy, a large screen was placed in front of them, to hide them from the infants’ view. Next, an experimenter lifted the two covers above the screen and lowered them again, as though to hide the toy; from the experimenter’s actions, it was not possible for the infants to determine which of the two covers was lowered over the toy. Finally, the screen was removed, revealing only the two covers; Wang and Kohne measured whether the infants contacted the tall or the short cover first. The infants in the baseline condition were tested using the same procedure except that they received no teaching trials.

As expected, the infants in the teaching condition were reliably more likely to choose the tall than the short cover, whereas those in the baseline condition were equally likely to choose either cover. Additional results indicated that 12-month-old infants tested in the baseline condition were reliably more likely to choose the tall cover, and that this effect disappeared when the tall toy was replaced with a shorter toy that could be fully hidden under either cover.

The above findings thus make clear that, once infants have identified a physical variable as relevant to an event category, they not only attend to information about the variable when observing events from the category: they also use this information to decide which actions to perform in response to events from the category.

9.2. Priming manipulations

We have argued throughout this article that the teaching events shown in Experiments 1–3 helped the infants identify height as a covering variable; and that the identification of this variable brought about a significant and lasting change in infants’ knowledge of covering events. This change was demonstrated in infants’ newfound ability (1) to detect a violation when a tall object became fully hidden under a short as opposed to a tall cover (Experiments 1–3), and (2) to retrieve a tall object from under a tall as opposed to a short cover (Wang & Kohne, in press).

However, it might be objected that there could be an alternative way of describing the present results. Recent research suggests that infants who have not yet identified a variable in an event category can sometimes be induced, through various contextual manipulations, to include information about this variable in their physical representations of events; this variable information, once represented, becomes subject to infants’ core knowledge, allowing them to detect violations involving the variable earlier than they would otherwise (e.g., Wang & Baillargeon, 2005; Wilcox & Chapa, 2004). Some of this research has involved priming manipulations designed to highlight a particular variable, or particular values of a variable. For example, Wilcox and Chapa (2004), in a seminal series of experiments, attempted to prime infants to attend to color information in occlusion events.

At 9.5 months of age, infants are not surprised when a green ball disappears behind a narrow screen (too narrow to hide two balls) and a red ball reappears from behind it (e.g., Wilcox, 1999; Wilcox & Chapa, 2004). Although width is identified as an occlusion variable by 4 months of age (e.g., Wang et al., 2004), color is not identified until about 11.5 months of age (e.g., Wilcox, 1999). As a result, young infants typically include no color information in their physical representation of the narrow-screen event, and assume that the same ball is moving back and forth behind the screen. Wilcox and Chapa (2004) asked whether 9.5-month-old infants could be primed to attend to the color information in this event.

The infants first received two pairs of priming trials. Each pair consisted of a pound event, in which a green cup was used to pound a peg, and a pour event, in which a red cup was used to pour salt. Different green and red cups were used in the two pairs of trials. Next, the infants saw a test event in which a green and a red ball appeared successively from behind a narrow (narrow-screen event) or a wide (wide-screen event) screen. The infants who saw the narrow-screen event looked reliably longer than those who saw the wide-screen event, suggesting that the infants perceived the association in the priming trials between the color and function of the cups (green-pound, red-pour). This association made the colors green and red more salient for the infants. As a result, the infants were more likely to include information about the colors of the green and red balls in their physical representations of the test events. This color information, once represented, became subject to the persistence principle, and the infants realized when watching the narrow-screen that the green ball (1) filled most of the space behind the narrow screen, and (2) could not spontaneously change from a green to a red ball.

In subsequent experiments, 9-month-old infants were tested using new color-function pairings in the priming trials: long-handled spoons of different colors were used to stir salt in a bowl or to lift a bowl by its hook (Wilcox & Wood, in press). The infants looked reliably longer at the narrow- than at the wide-screen event when the spoons used in the priming trials were the same colors as the balls (green and red), but not when they were different (yellow and blue). These results suggest that the effect of the priming manipulation was quite specific: because the colors green and red were paired with different object functions in the situation, the infants were more likely to attend to these same colors when they next encountered them in another, very different event. However, watching priming events involving yellow and blue spoons did not serve to make infants more likely to include information about the colors of the balls in the narrow- and wide-screen events. The priming manipulation thus served to highlight the colors green and red for the infants—not color information generally.

Could the present results and those of Wang and Kohne (in press) be described in an analogous manner? Is it possible that the teaching trials simply served to prime the infants to attend to height information? This information, once represented, would have become subject to the persistence principle, allowing the infants to detect the violation in the short-cover test event (Experiments 1–3), and to search for the tall toy under the tall cover (Wang & Kohne, in press). This interpretation differs substantially from the one offered here, because priming manipulations are thought to have little or no permanent effect on infants’ knowledge of the variables relevant to an event category. The pound and pour events used by Wilcox and Chapa (2004) were not expected to help the infants identify color as a relevant variable for predicting the outcomes of occlusion events: they were only intended to highlight, for a brief time, the colors green and red for the infants.

The results of Experiment 3 provide tentative evidence against the notion that our teaching trials simply served to prime the infants to attend to height information: one would not expect such priming effects to be long-lasting, and yet the infants in Experiment 3 succeeded in detecting the violation in the short-cover test event after a 24-hour delay.

To further test this alternative, priming interpretation, Wang and Kohne (in press) conducted an additional action experiment which built on the finding that the variable height is not identified as relevant to tube events until about 14 months of age (e.g., Wang & Baillargeon, 2006; Wang et al., 2005). As before, 9-month-old infants first received the three pairs of teaching trials used in Experiments 1–3. Next, the infants were brought to another room where they received an action task similar to that described earlier, with one exception: the short and tall covers were replaced with short and tall tubes (these were identical to the covers with their tops removed). If the teaching trials simply served to highlight height information, then the infants should be equally likely to succeed in an action task involving covers or tubes. After all, in the priming trials used by Wilcox and her colleagues (Wilcox & Chapa, 2004; Wilcox & Woods, in press), there was no similarity at all—other than the specific colors used—between the priming and test events: the infants saw events in which cups were used to pound or pour, or in which spoons were used to stir or lift, followed by events in which balls moved back and forth behind a screen. Thus, if the teaching trials simply served to prime the infants to attend to height information, there would be no reason to expect this priming effect to be limited to covering events.

In the action experiment reported earlier (Wang & Kohne, in press), 9-month-old infants who received the teaching trials were more likely to search for the tall toy under the tall as opposed to the short cover. In contrast, in the experiment described here, infants performed at chance: they were equally likely to reach for the tall or the short tube.

This negative result casts doubt on the notion that the teaching trials used in the present research and in Wang and Kohne (in press) simply served to prime the infants to attend to height information. Rather, it supports the interpretation that the teaching trials helped the infants identify height as a covering variable. When the infants next encountered a covering event, they tapped their knowledge of this event category. Because height was now listed as one of the variables known to be relevant to covering events, the infants included information about the variable in their physical representation of the event. This information made it possible for them to detect the violation in the short-cover test event (Experiments 1–3), and to appropriately search for the tall toy under the tall cover (Wang & Kohne, in press).

The preceding discussion thus makes clear that once infants have identified a physical variable as relevant to an event category, they will attend to information about the variable in tasks presenting different stimuli and calling for different responses—but only when the tasks involve events from the same event category. Infants’ learning processes are thus designed to ensure broad, yet circumscribed, generalization: a variable identified in an event category will be attended to in any event from the category—but only in events from the category.

9.3. A final caveat

In this article, we have suggested that (1) infants who have not yet identified a variable as relevant to an event category typically do not include information about this variable in their physical representations of events from the category; and (2) infants who are exposed to appropriate observations (such as the teaching events used in Experiments 1–3) identify the variable, and subsequently include information about the variable in their physical representations of events from the category.

Before ending this paper, we would like to emphasize the following point: we do not wish to claim that infants who have not yet identified a variable as relevant to an event category do not represent any information at all about the variable when they encounter events from the category. We have proposed that, when infants watch a physical event, two distinct computational systems form different representations simultaneously, for different purposes (e.g., Baillargeon et al., 2006; Wang & Baillargeon, 2006). On the one hand, infants’ Recognition System represents information about the properties of the objects in the event, for identification and related purposes (e.g., categorization, pattern detection). On the other hand, infants’ Physical-Reasoning System forms a physical representation of the event, to interpret and predict its outcome. On this view, infants who have not yet identified height as a covering variable, and do not include information about this variable in their physical representation of a covering event, may nevertheless encode information about the heights of the cover and object in their Recognition System.

Thus, from this perspective, the teaching events in Experiments 1–3 did not lead the infants to encode height information they would not (or could not) have encoded otherwise. Rather, our teaching events led the infants to recognize that height information is relevant for predicting the outcomes of covering events—it helps determine whether the object will be fully or only partly hidden under the cover—and as such should be included in physical representations of covering events. This interpretation is consistent with an incremental, explanation-based view of the development of infants’ physical reasoning: infants begin with sparse representations of physical events, containing only basic information, and learn to include additional information in these representations, category by category, vector by vector, and variable by variable, as they come to understand how each variable can be used to better predict outcomes.