Isolated interstitial nodal spaces may facilitate preferential solute and fluid mixing in the rat renal inner medulla

Abstract

Recent anatomic findings indicate that in the upper inner medulla of the rodent kidney, tubules, and vessels are organized around clusters of collecting ducts (CDs). Within CD clusters, CDs and some of the ascending vasa recta (AVR) and ascending thin limbs (ATLs), when viewed in transverse sections, form interstitial nodal spaces, which are arrayed at structured intervals throughout the inner medulla. These spaces, or microdomains, are bordered on one side by a single CD, on the opposite side by one or more ATLs, and on the other two sides by AVR. To study the interactions among these CDs, ATLs, and AVR, we have developed a mathematical compartment model, which simulates steady-state solute exchange through the microdomain at a given inner medullary level. Fluid in all compartments contains Na⁺, Cl⁻, urea and, in the microdomain, negative fixed charges that represent macromolecules (e.g., hyaluronan) balanced by Na⁺. Fluid entry into AVR is assumed to be driven by hydraulic and oncotic pressures. Model results suggest that the isolated microdomains facilitate solute and fluid mixing among the CDs, ATLs, and AVR, promote water withdrawal from CDs, and consequently may play an important role in generating the inner medullary osmotic gradient.

recent anatomic studies in the inner medulla (IM) of the rat kidney have revealed collecting duct (CD) clusters as the dominant organizing structural elements for the arrangement of tubules and vessels (30, 31). In the upper IM, the descending thin limbs (DTL) of the loops of Henle and the descending vasa recta (DVR) are nearly always located outside and surrounding the CD clusters. In contrast, the ascending thin limbs (ATLs) and ascending vasa recta (AVR) are arranged nearly uniformly across the IM, both inside and outside the CD clusters.

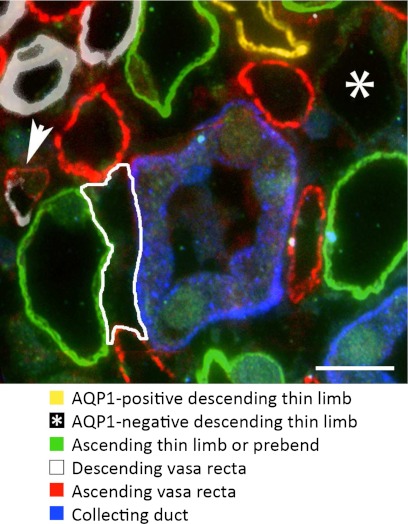
When CD clusters are viewed in transverse sections, CDs and some of the AVR and ATLs are observed to form interstitial nodal spaces (INS; see Fig. 1) or microdomains. These spaces are bordered on one side by a CD, on the opposite side by one or more ATLs, and the other two sides by AVR. These spaces continue along the cortico-medullary direction, forming columns running alongside CDs; however, the columns are likely divided at regular intervals by interstitial cells (31), giving rise to an arrangement of stacks of INS. Axial diffusion of fluids and solutes along the column would be impeded by the interstitial cells that form caps above and below each nodal space.

Fig. 1.

Interstitial nodal spaces associated with a single collecting duct (CD) in a transverse section from ∼400 μm below the OM-IM boundary. One nodal space is outlined (white). A single aquaporin-1-negative descending thin limb (AQP1-negative DTL) marked with an asterisk was identified with α-B crystallin. A descending vas rectum (DVR) merging into an ascending vasa recta (AVR) is marked with the arrow. Scale bar = 10 μm.

In previous reviews (7, 24, 33), we hypothesized that such repeating microdomains may facilitate interstitial solute and fluid mixing and thus play an important role in generating the IM osmotic gradient. Assuming that the ATLs bordering the INS have low urea permeability and high NaCl permeability, NaCl is reabsorbed from the ATL segments. With this assumption, the microdomains appear ideally configured to mix NaCl absorbed from loops with absorbate from the CDs (which consists mostly of water, urea, and NaCl) to produce isolated sites of high osmolality that will promote water withdrawal from adjoining CDs.

In this study, we use immunohistochemical techniques to quantify the degrees to which CDs, ATLs, and AVR are connected to the INS. We then incorporate those data into a compartment model of the INS and the associated tubules and vessels, and we use that model to assess the extent to which preferential interactions among the CDs, ATLs, and AVR contribute to urea sequestration within the CD clusters and facilitate water reabsorption from the CDs.

Hyaluronan is abundant in renal papillary interstitium. On a dry weight basis, hyaluronan content may reach as much as several hundredfold higher than in the cortex (13). Approximately 70% of IM hyaluronan exists in the deepest two-fifths below the base of the papilla (25). Hyaluronan has two properties that may be particularly relevant to the urine concentrating mechanism. First, it has viscoelastic properties that may play a role in peristaltic contractions, potentially influencing fluid and solute flow dynamics (18). Secondly, hyaluronan is not generally covalently linked to proteins and is not sulfated (40) and, as a consequence, provides binding sites for cations. This latter property is a focus of the present modeling study in which we investigate the effects of hyaluronan's fixed charges on solute-mixing within the interstitium of the IM.

EXPERIMENTAL METHOD

Animals.

Young male Munich-Wistar rats (average weight, 90 g) were purchased from Harlan (Indianapolis, IN). The animals were euthanized with sodium pentobarbital (0.2 ml/100 g body wt) or with CO₂. All experiments were conducted in accordance with the Guide for the Care and Use of Laboratory Animals (Washington, DC: National Academy Press, 1996) and approved by the Institutional Animal Care and Use Committee.

Tissue preparation and immunohistochemistry.

Kidneys from male Munich-Wistar rats were prepared for immunohistochemistry by retrograde perfusion through the aorta with PBS (pH 7.4) for 5 min, followed by periodate-lysineparaformaldehyde (0.01 M, 0.075 M, 2%) in PBS (pH 7.4) for 5 min before removal from the animal. The whole medulla was dissected free and immersion fixed for 3 h at 4°C and washed in PBS. The medullas were embedded in Spurrs resin, and several transverse sections (1-μm thick) were taken from each kidney, ∼400 μm below the OM-IM boundary. Immunohistochemistry was carried out as described previously (31, 32, 16) using the following primary antibodies: aquaporin-1 (AQP1) to label AQP1-positive DTL (chicken/Dan Stamer, University of Arizona and mouse/Abcam); α-B crystallin to label AQP1-negative DTL (mouse/Stressgen); ClC-K to label prebend segments and ascending thin limbs (rabbit/Chemicon and Alomone); UT-B to label DVR (rabbit/Jeff Sands and Janet Klein, Emory University); PV-1 to label fenestrated blood vessels (chicken/Radu Stan, Dartmouth University); and AQP2 to label CDs (goat/Santa Cruz). Sections were viewed with epifluorescence microscopy.

Image analysis.

Images of labeled sections were prepared either as single images or as double-image overlays with sections no more than ∼1 μm apart. For quantitative analyses of abutting tubular segments, the portions of abutting segments were outlined in transverse sections using Adobe PhotoShop. The lengths of these outlines were then determined with the Image Processing Toolkit (Reindeer Graphics). The volume shrinkage factor for ethanol dehydration of rat medullary tissue has been reported to be ∼20% (1), and the linear shrinkage factor has been reported to be ∼20–25% (12). Thus the linear distances that we report would underestimate the distances measured for fresh tissue by a maximum of ∼20–25%.

Statistical analyses.

Data combined from multiple samples are reported as means ± SE.

MATHEMATICAL MODEL

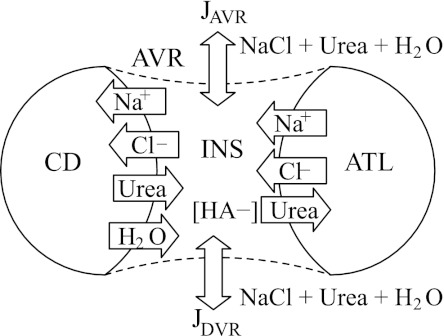
We have developed a compartment model that simulates steady-state solute exchanges through an INS at a cross-section of the upper IM, near the OM-IM boundary. The model represents cross-sections (perpendicular to the cortico-medullary axis) of CD, ATL, and AVR, which interact through the INS. Fractions of the CD and ATL epithelia are assumed to be in close contact with the AVR endothelia, and solute exchanges are assumed to occur (and water exchanges between CD and AVR). To model the limited interactions between the INS and extra-cluster structures, the cross-section of a DVR is also represented, and limited communications between the DVR and the INS are allowed. A schematic diagram of the model configuration is shown in Fig. 2. Fluids in all compartments contain Na⁺, Cl⁻, and urea. CD and DVR are assumed to be permeable to Na⁺, Cl⁻, urea, and water; ATL is permeable to Na⁺, Cl⁻, urea, but not water.

Fig. 2.

Schematic diagram of compartment model. Represented are cross-sections of CD, ascending thin limb (ATL), and AVR, which interact through the interstitial nodal space (INS). Fractions of the CD and ATL are assumed to be in direct contact with the AVR endothelium. Cross-section of a DVR is also represented to model limited interactions between intra- and extra-cluster structures. J_AVR and J_DVR, transmural water flux in AVR and DVR; HA, hyaluron.

Urea fluxes into the CD, ATL, or DVR arise from the transmural concentration gradient between the tubule and the INS or, in the case of the CD and ATL, also between the tubule and AVR

$$J_{i,j,\text{urea}}={\tilde{l}}_{i,j}{P}_{i,\text{urea}}(C_{j,\text{urea}}-C_{i,\text{urea}}),$$ (1)

for i = CD, ATL, or DVR, j = INS or AVR, where C_j,urea and C_i,urea denote urea concentration, P_i,urea denotes urea permeability of structure i, and ${\tilde{l}}_{i,j}$ is the fraction of the CD or ATL membrane circumference in contact with the INS or AVR. Since the DVR is assumed to have limited interactions with the INS only, J_DVR,AVR,urea = 0.

Transmural fluxes of a charged ion k into CD, ATL, or DVR arise from transmural concentration gradient and electrical potential,

$$J_{i,j,k}={\tilde{l}}_{i,j}{P}_{i,k}\beta (\frac{C_{j,k}-C_{i,k}{e}^{\beta }}{1-e^{\beta }}).\beta =\Delta {\psi }_{i,j}\frac{z_kℱ}{RT}.$$ (2)

where ℱ is the Faraday constant, RT is the product of gas constant and absolute temperature, z_k is the electrical valence of ion k (k = Na⁺ or Cl⁻), and Δψ_i,j is the electrical potential difference between tubule i and structure j (where j = INS or AVR, with J_DVR,AVR,k = 0).

The electrical potentials Δψ_i,j are the values at which there is zero net current flow into any of the compartments, thereby ensuring electroneutrality. In other words, the electroneutrality constraints are imposed by calculating barrier potentials across the CD and ATL that result in zero net current flow, as described by Latta et al. (20). Since the present model represents only two ionic species (Na⁺ and Cl⁻), the electroneutrality requirement simplifies to J_i,Na = J_i,Cl, where J_i,k denotes total transmural fluxes of solute k into CD or ATL given by

$$J_{i,k}=J_{i,\text{INS},k}+J_{i,\text{AVR},k},$$ (3)

for i = CD or ATL.

Water fluxes into the CD are assumed to be driven by transmural osmotic and hydraulic pressure. Water fluxes directed from the AVR into the CD are given by

$$\begin{gathered} J_{\text{CD},\text{AVR},V}={\tilde{l}}_{\text{CD},\text{AVR}}{L}_{\text{CD},p}[\Delta p_{\text{CD},\text{AVR}}+ \\ RT{\displaystyle \sum _{k=\text{Na},\text{Cl},\text{urea}}}{\varphi }_k(C_{\text{CD},k}-C_{\text{AVR},k})], \end{gathered}$$ (4)

where L_CD,p denotes the CD water permeability; Δp_CD,AVR is the hydrostatic force across the CD-AVR interface; and the summation represents osmotic driving force exerted by solutes. Water fluxes into the DVR, denoted by J_DVR,INS,V, is defined analogously. The total transmural water flux into the CD is given by

$$J_{\text{CD},V}=J_{\text{CD},\text{INS},V}+J_{\text{CD},\text{AVR},V}.$$ (5)

Water that enters the AVR lumen is driven by osmotic pressure across the CD epithelium in contact with the AVR endothelium or by transendothelial hydrostatic pressure and the oncotic pressure exerted by the plasma proteins in the AVR. Taken together,

$$J_{\text{AVR},V}=J_{\text{CD},\text{AVR},V}+J_{\text{AVR},\text{INS},V},$$ (6)

where

$$J_{\text{AVR},\text{INS,}V}={\tilde{l}}_{\text{AVR}}{L}_{\text{AVR},p}(\Delta p_{\text{AVR}}+\Delta {\displaystyle {\mathrm{\Pi }}_{\text{pr}}}).$$ (7)

L_AVR,p is the AVR water permeability, and ΔΠ_pr denotes the net oncotic pressure exerted by AVR plasma proteins. Thus the AVR serves as a sink for the reabsorbate. Solute fluxes that enter the AVR lumen from the INS are given by (22)

$$\begin{gathered} J_{\text{AVR},\text{INS,}k}=J_{\text{AVR},\text{INS,}V}(1-{\sigma }_k)[\frac{C_{\text{AVR},k}-C_{N,k}\text{exp}(-\text{Pe})}{1-\text{exp}(-\text{Pe})}], \\ \text{ Pe}=\frac{J_{\text{AVR},V}(1-{\sigma }_k)}{P_{\text{AVR},k}}, \end{gathered}$$ (8)

where σ_k is the reflection coefficient of the capillary wall to solute k, and Pe is the Péclet number. The total transmural fluxes of solute k into AVR are given by

$$J_{\text{AVR},k}=J_{\text{AVR},\text{INS,}k}-J_{\text{CD},\text{AVR},k}-J_{\text{ATL},\text{AVR,}k}.$$ (9)

The concentrations of Na⁺, Cl⁻, and urea in the CD, ATL, and DVR are assumed known a priori. Owing to the high AVR solute permeabilities, solute concentrations in the AVR and the INS tend to be nearly equal. Thus we do not specify solute concentrations in the AVR compartment directly. Instead, we specify upstream (i.e., toward the papilla) AVR luminal fluid solute concentrations, and we assume that AVR fluid solute concentrations decrease linearly. With these assumptions, AVR solute concentrations in the compartment are given by

$$F_{\text{AVR},V}^0{C}_{\text{AVR},k}^0-(F_{\text{AVR},V}^0-d_{\text{AVR}}{J}_{\text{AVR},V})C_{\text{AVR},k}=d_{\text{AVR}}{J}_{\text{AVR},k},$$ (10)

where d_AVR is the distance between the current IM level and the upstream position and the superscript 0 denotes upstream values.

The INS is assumed to be somewhat compliant, so fluid reabsorbed from the CD and DVR (i.e, −J_CD,INS,V and −J_DVR,INS,V, respectively) raises both the volume of the compartment (V_INS) and the pressure (p_INS) inside:

$$\begin{gathered} \frac{\partial }{\partial t}{V}_{\text{INS}}=-J_{\text{CD},\text{INS},V}-J_{\text{DVR},\text{INS},V}-J_{\text{AVR},\text{INT},V}, \\ {V}_{\text{INS}}\propto p_{\text{INS}}, \end{gathered}$$ (11)

where −J_AVR,V is water flux from the INS into the AVR and thus the rate of fluid drained away by the AVR. In the model, CD luminal hydrostatic pressure p_CD is assumed fixed. As water is reabsorbed from the CD, the model hydrostatic pressure p_INS will rise, and the transepithelial hydrostatic force Δp_CD,INS ≡ p_CD − p_INS will decrease, which, taken in isolation, will tend to impede water reabsorption from the CD.

Solute concentrations in the INS will be updated based on mass conservation, given by

$$\frac{\partial }{\partial t}(V_N{C}_{N,k})=-J_{\text{CD},\text{INS},k}-J_{\text{ATL},\text{INS},k}-J_{\text{DVR},\text{INT},k}-J_{\text{AVR},\text{INT},k}.$$ (12)

Representing hyaluronan.

In some of the simulations, we assume that the INS contains negative fixed charges that represent macromolecules (e.g., hyaluronan, HA⁻) balanced by Na⁺. In this case, the effect of the counterion, Na⁺, on solute and water fluxes must be taken into account. In the base case, transmural Na⁺ fluxes into CD, ATL, or DVR are given by Eq. 2. When hyaluronan is assumed to be present in the INS, and Na⁺ fluxes are affected by its counterion:

$$J_{i,\text{INS},\text{Na}}={\tilde{l}}_{i,\text{INS}}{P}_{i,\text{Na}}\beta (\frac{C_{\text{INS},\text{Na}}+C_{\text{INS},\text{HA}}-C_{i\text{,Na}}{e}^{\beta }}{1-e^{\beta }}),$$ (13)

where C_INS,HA denotes the fixed charge density. Additionally, the osmotic effect of counterion Na⁺ is represented by an additional osmotic term in the expression for CD water flux:

$$J_{\text{CD},\text{INS},V}={\tilde{l}}_{\text{CD},\text{INS}}{L}_{\text{CD,}p}[\Delta p_{\text{CD,INS}}+RT{\displaystyle \sum _{k=\text{Na},\text{Cl},\text{urea}}}{\varphi }_k(C_{\text{CD},k}-C_{\text{INS},k})+{\varphi }_{\text{Na}}{C}_{\text{INS},\text{HA}}].$$ (14)

RESULTS

Immunohistochemistry and image analysis.

Sections for all kidneys examined lie within ∼400 μm below the OM-IM boundary. Structure-to-structure abutments associated with each INS include the following: 1) CD/nodal space, 2) ATL/nodal space, 3) AVR/nodal space, 4) CD/AVR, and 5) ATL/AVR. The basal plasma membrane of the AVR that abut CDs has been shown to lie within ∼1 μm from the CD basal plasma membrane (2, 39, 31). ATLs whose basal plasma membrane lies within 2 μm from the basal plasma membrane of the AVR are considered to abut the AVR not the INS. No significant fluid flux occurs across the epithelium of the AQP1-negative DTL (5, 6). Substantial NaCl and urea fluxes have been measured across this segment (5); however, because AQP1-negative segments make a relatively minor contribution to the INS boundaries, compared with CD, ATL, and AVR, the AQP1-negative segments were excluded from the model.

CD circumference increases with depth along the corticopapillary axis as CDs coalesce; the CD circumferences that we measured along the corticopapillary axis for the Munich Wistar rat (32) are comparable to those reported for the Sprague-Dawley rat (17). The CD circumferences and the contact lengths between different structures that form boundaries of the INSs were determined for those structures surrounding five CDs from each of four medullas. On average, about four INSs are juxtaposed alongside each CD at this level (31). The mean circumference of a CD was determined to be 102 ± 4.9 μm (means ± SE, given per CD). Approximately 70% of the CD circumference (68.5 ± 3.9 μm) borders the approximately four to five INSs that exist around each CD. Table 1 shows the contact lengths among CD, AVR, ATL, AQP1-negative DTL segment, and INS; those lengths are given per INS.

Table 1.

Quantitative analysis of abutting tubular segments

	Contact Length, μm
CD-INS	18.1 ± 0.57
ATL-INS	16.4 ± 3.16
AVR-INS	12.0 ± 0.40
DTL*-INS	5.34 ± 0.23
CD-AVR	7.14 ± 0.25
ATL-AVR	4.79 ± 0.27
DTL*-AVR	2.54 ± 0.13

Values are means ± SE; n = 4. CD, collecting duct; INS, interstitial nodal space; ATL, ascending thin limb; AVR, ascending vasa recta; DTL, descending thin limb. Contact lengths are given per INS.

^*DTL segments are AQP1-negative.

Baseline simulation results.

The fraction of membrane area for a tubule or vessel in contact with the INS or AVR (i.e., ${\tilde{l}}_{i,j}$) is given by the contact lengths displayed in Table 1. The bordering length between DVR and INS is allowed to vary, to represent the degree of isolation of the CD cluster. Base-case parameters for transtubular transport, which are gleaned from literature, are given in Table 2. In addition, luminal solute concentrations of the CD and ATL are specified based on predictions of a modeling study (21) (see Table 2). AVR fluid flow rate and composition are specified at a location that is 500 μm upstream (i.e., d_AVR = 500 μm). The upstream AVR solute concentrations are given in Table 2; upstream AVR fluid flow rate is assumed to be 4 nl/min (21). Luminal hydraulic pressures in CD, AVR, and ATL and oncotic pressures in AVR are specified based on experimental measurements (36). Hydraulic pressure does not need to be specified for the ATL, which is assumed to be water impermeable.

Table 2.

Base-case transtubular transport parameters

	CD	ATL	AVR	DVR
Transport parameters
Pf, μm/s	450 (4)	0	5,260 (27)	1200
PNa, 10−5 cm/s	1	80	100	74 (29)
PCl, 10−5 cm/s	1	80	100	74 (29)
Purea, 10−5 cm/s	2	1	100	74 (29)
Luminal compositions
CNaCl, mM	140	317	322*	337
Curea, mM	500	133	178*	120
Osmolality, mosmol/kg H2O	742	712	765*	736
Pressures
Δπ, mmHg	—	—	10.3	—
p, mmHg	5.5	—	8.0	9.2

P_f, P_Na, P_Cl, P_urea, permeability of water, Na, Cl, and urea; C_NaCl and C_urea concentration of NaCl and urea; p, hydrostatic pressure; ΔΠ, oncotic pressure; DVR, descending vasa recta.

^*Upstream concentration values.

The base-case model is formulated for an INS located centrally in a CD cluster and is largely isolated from extra-cluster tubules and vessels. To simulate such a CD cluster, we set ${\tilde{l}}_{\mathrm{D}\mathrm{V}\mathrm{R},\text{INS}}$ to 1 μm. We assume zero fixed charge density for the base case, i.e., we set C_INS,HA = 0. Using the base-case parameter set, the model equations were solved, by means of the Newton's method, to obtain steady-state solutions, which include solute concentrations in the INS and in the AVR, interstitial hydraulic pressure, and transmural water and solute fluxes. These key results are displayed in Table 3.

Table 3.

Base-case model results

	CNaCl, mM	Curea, mM	Osmolality, mosmol/kg H2O	p, mmHg
INS	316	179	756	23.7
AVR	268	183	756	8.0*

	JNaCl, μmol/cm·s	Jurea, μmol/cm·s	JV, cm2/s
CD	3.11E-6	−1.13E-5	−1.85E-2
ATL	−1.10E-6	9.00E-7	0
AVR	−4.76E-7	6.00E-6	2.25E-2
DVR	−1.53E-6	4.40E-6	−4.08E-3

J_NaCl, J_urea, and J_V, transmural flux of NaCl, urea, and water secretion.

^*Prescribed.

Given the tubular fluid composition and permeabilities prescribed for the ATL and CD, the model predicts that NaCl is reabsorbed from the ATL and urea is reabsorbed from the CD. Because the CD is assumed to be moderately water permeable, water resorption follows. The model predicts that the mixing of the absorbate from CD and ATL yields an interstitial fluid that is substantially hyperosmotic compared with CD tubular fluid (756 vs. 742 mosmol/kgH₂O). That osmolality gradient (14 mosmol/kgH₂O) corresponds to an osmotic pressure of ∼272 mmHg, which renders the hydrostatic pressure difference of 18.2 mmHg negligible by comparison. The absorbate is drained by the AVR.

Fluid uptake by the AVR is assumed to be pressure driven. With the AVR luminal hydraulic pressure and transmural oncotic pressure taken to be 8 and 10.3 mmHg (36), respectively, the model predicts a nodal fluid pressure of 23.7 mmHg, which is substantially higher than measurements by Sanjana et al. in the papilla (36) and by Garcia-Estañ and Roman in the cortex (9). Thus our model's prediction suggests that local interstitial fluid pressure within the INS may be substantially higher than elsewhere and that AVR transmural hydrostatic pressure is inwardly directed and favors uptake of fluid by the AVR.

Preferential interactions among CDs, ATLs, and AVR facilitate water reabsorption from CDs.

The base-case configuration of the model assumes that the INSs, and the surrounding CDs, ATLs, and AVR, have only limited communications with the extra-cluster DVR. The model DVR is assumed to be in contact with the INS for a small fraction of its endothelium (1 μm). This assumption may be valid, to a large extent, for INSs that are located centrally within the CD clusters, but less so for INSs that lie in the periphery of the CD clusters, where there would be increased contact with DVR, which are more abundant at the periphery. Coupling with DVR may have substantial impacts on fluid composition of the INSs, because the vascular fluid osmolality of those DVR is likely substantially lower than those of the CDs and AVR, as predicted by our previous modeling studies (21, 23).

In a set of simulations, we investigate the impacts of coupling with extra-cluster DVR on water and solute absorption from the CDs, ATL, and AVR, by varying the fractional DVR endothelium in contact with the INS, denoted ${\tilde{l}}_{\mathrm{D}\mathrm{V}\mathrm{R},\text{INS}}$. By obtaining model results for differing values of ${\tilde{l}}_{\mathrm{D}\mathrm{V}\mathrm{R},\text{INS}}$, we can study the effect of extra-cluster fluid on water and solute absorption of the CD and ATL and assess the extent to which the INSs promote preferential interactions and specific solute mixing among the three surrounding structures.

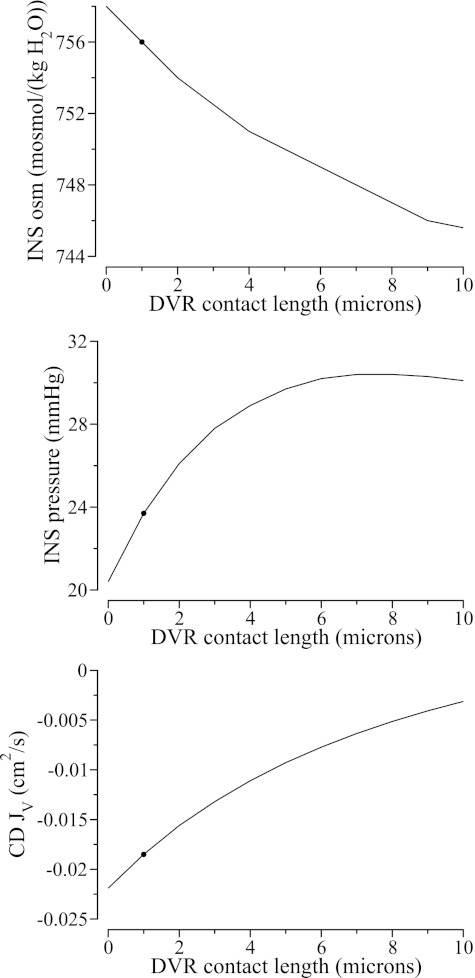
We obtained model solutions for a range of ${\tilde{l}}_{\mathrm{D}\mathrm{V}\mathrm{R},\text{INS}}$, from 0, which corresponds to a completely isolated INS, to 10 μm, which corresponds to an INS in the periphery of the CD cluster. Key predictions are summarized in Fig. 3. Because DVR luminal fluid osmolality is assumed to be substantially lower than CD, a less isolated INS (i.e., a stronger coupling with the inter-cluster DVR), which corresponds to a larger ${\tilde{l}}_{\mathrm{D}\mathrm{V}\mathrm{R},\text{INS}}$, is predicted to have a less concentrated interstitial fluid osmolality. The water reabsorbed from the DVR also raises interstitial fluid pressure, until for ${\tilde{l}}_{\mathrm{D}\mathrm{V}\mathrm{R},\text{INS}}$ at which point the effect of reduced CD water withdrawal begins to dominate and results in a slight drop in interstitial pressure. Together, the decrease in interstitial fluid osmolality and the generally higher interstitial hydrostatic pressure reduce water reabsorption from the CD from 2.19 × 10⁻² to 3.12 × 10⁻³ cm²/s.

Fig. 3.

Effects of coupling between INS and extra-cluster DVR on INS fluid composition and water absorption from CD. Shown are INS fluid osmolality (top), INS hydrostatic pressure (middle), and CD water reabsorption rate (bottom) as functions of DVR contact length. Because DVR luminal fluid is assumed to be dilute relative to CD, a stronger coupling between the INS and DVR results in more dilute INS fluid (see top) and, together with a higher INS hydraulic pressure (see middle), decreases water absorption from the CD (see bottom). ●, Base-case values. J_V, water flux.

Interstitial hyaluronan in the nodal spaces facilitates water reabsorption from the CDs.

A disproportionate concentration of Na⁺ may be found in the interstitial space where it balances fixed negative charges associated with hyaluronan. As a result, a chemical gradient is generated across the ATL epithelium that promotes Cl⁻ reabsorption from the ATLs, raises interstitial fluid osmolality, and promotes water reabsorption from the CDs. However, that absorbate will raise the interstitial fluid pressure, which may impede further water reabsorption. Thus, in the next set of simulations, we assess the extent to which that osmotic pressure is balanced by the interstitial fluid pressure that might be generated if the AVR fail to drain away the absorbate sufficiently rapidly.

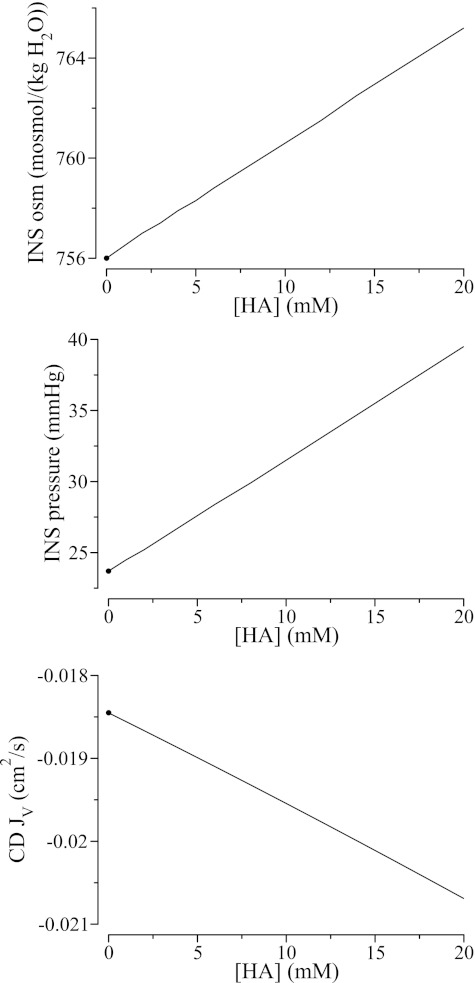
We computed model solutions for C_INS,HA = 0, … , 20 mM. Figure 4 displays the resulting INS fluid osmolality, INS hydraulic pressure, and CD water reabsorption. These results suggest that a higher fixed charge density increases INS fluid osmolality and increases water absorption from the CD and, to a smaller extent, from the DVR (DVR not shown). The higher water reabsorption rate raises interstitial fluid pressure, which, taken in isolation, should impede water movement, although its effect is dominated by the higher interstitial fluid osmolality.

Fig. 4.

Effects of interstitial fixed charges on INS fluid composition and water absorption from CD. Interstitial fixed charges induce a disproportionate concentration of counterions in the INS, thereby raising the effective interstitial fluid osmolality (top) and increases water absorption from the CD (bottom), despite a higher interstitial hydrostatic pressure (middle). ●, Base-case values.

ATL urea permeability.

ATLs associated with loops of Henle that turn within the first millimeter are located within the CD clusters, as are some of the ATLs associated with loops that reach into the mid-IM. Thus most of the ATLs bordering the INS are likely associated with the shorter long loops. The initial IM portion of ATLs that reach beyond the first millimeter is believed to be moderately urea permeable. However, the urea permeability of ATLs associated with the shorter long loops has not been measured. The model ATL is assumed to have low urea permeability (1 × 10⁻⁵ cm/s). In a set of simulations, we assess the sensitivity of model results to variations in ATL urea permeability.

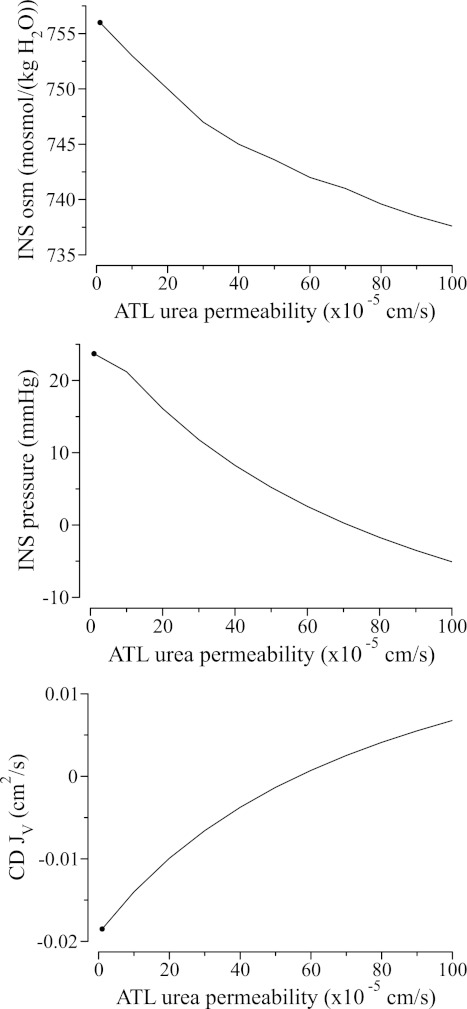
We varied ATL urea permeability from 0 to 100 × 10⁻⁵ cm/s and computed model results. All other model parameters were kept at base-case values. Because the ATL luminal fluid urea concentration was assumed to be low (133 mM), INS urea concentration, and thus osmolality, decreased when ATL urea permeability was increased, as the two compartments increasingly equilibrated (see Fig. 5, top). The lower interstitial fluid osmolality reduced water reabsorption from the CD. In fact, for ATL urea permeability above 57 × 10⁻⁵ cm/s, water was predicted to be secreted into the CD.

Fig. 5.

Effects of ATL urea permeability on INS fluid composition and water absorption from CD. Because ATL luminal urea concentration is assumed to be low, interstitial fluid urea concentration and osmolality decrease (see top) as ATL urea permeability increases and the two compartments increasingly equilibrate. Lower interstitial fluid osmolality lowers CD water reabsorption rate (bottom) and interstitial pressure (middle); at sufficiently high ATL urea permeability, water is secreted into CD. Positive CD J_V denotes water secretion into CD. ●, Base-case values.

If the ATLs bordering the INS are moderately or highly urea permeable, then it seems likely that its urea content is more nearly equilibrated with the AVR. Thus, in another set of simulations, we set ATL urea permeability to 80 × 10⁻⁵ cm/s and then varied ATL urea concentration from 130 to 180 mM. For such a high ATL urea permeability, interstitial fluid osmolality was predicted to be low (739 mM) and water is secreted into the CD when ATL urea concentration was set to a low value of 130 mM (Fig. 6). As ATL urea concentration increased, interstitial fluid urea concentration and osmolality increased, and for ATL urea concentration >145 mM, water was reabsorbed from the CD.

Fig. 6.

Effects of ATL luminal urea concentration on INS fluid composition and water absorption from CD. A high ATL urea permeability (80 × 10⁻⁵ cm/s) is assumed. As ATL urea concentration increases, interstitial fluid urea concentration and osmolality increase (see top), leading to increase in CD water reabsorption rate (see bottom). Middle, INS pressure. Positive CD J_V denotes water secretion into CD.

AVR hydrostatic pressure.

The hydrostatic pressure of the vascular fluid is not well characterized. Because the absorbate is driven, in part, by the hydrostatic pressure difference between the AVR and the INS, the pressures in the two compartments are linked. To assess the sensitivity of model results to variations in AVR hydrostatic pressure p_AVR, we obtained model solutions for p_AVR = 4, 5, … , 8 mmHg. Varying p_AVR by a factor of two has minimal effect on CD water reabsorption rate, INS osmolality, and all other model predictions, except for INS hydrostatic pressure, which exhibits an approximately linear dependence on p_AVR. The insensitivity of most model variables (except for INS hydrostatic pressure) to variations in p_AVR is expected: the processes that depend directly on p_AVR are CD and AVR water fluxes. As previously noted, CD water flux is dominated by osmotic pressure, which renders the effects of varying hydrostatic pressure gradient negligible. In contrast, a substantial portion of the water flux into AVR is driven by hydrostatic pressure; as a result, p_INS and p_AVR vary almost proportionally.

CD active Na⁺ transport.

The base-case model represents only passive transmural solute diffusion. To study the effects of CD active Na⁺ transport on model predictions, we added active reabsorption of Na⁺ into the CD Na⁺ flux equation (Eq. 2):

$$J_{\text{CD},j,\text{Na}}={\tilde{l}}_{\text{CD},j}{P}_{\text{CD,Na}}\beta (\frac{C_{j,\text{Na}}-C_{\text{CD},\text{Na}}{e}^{\beta }}{1-e^{\beta }})-J_{\text{act}},$$ (15)

where J_act denotes the active reabsorption of Na⁺ from the CD. When J_act was increased from 0 (base case) to 12 × 10⁻⁶ μmol/(cm·s), CD NaCl flux [in units of μmol/(cm·s)] reversed direction, from secretion at the base-case rate of 3.11 × 10⁻⁶, to reabsorption at the rate of −2.31 × 10⁻⁶. The active transport of Na⁺ generates a luminal negative potential on the CD membrane, which drives Na⁺ into the CD lumen. Thus, when J_act was set to the base-case CD NaCl secretion rate, the overall result was not zero flux but NaCl secretion into CD. The NaCl reabsorbed raised INS fluid osmolality, albeit only slightly by 2 mosmol/kgH₂O when J_act increased from 0 to 12 × 10⁻⁶ μmol/(cm·s), and increased water reabsorption from the CD (by 16%).

DISCUSSION

The objective of this study is to use mathematical modeling techniques to investigate the functional implications of experimental studies in which immunohistochemical methods were employed to reveal spatial relationships between vessels and tubules in the upper IM. CDs coalesce as they descend from the OM-IM boundary towards the tip of the papilla, forming distinct CD clusters. Loops of Henle and vasa recta are organized around these clusters in a regular fashion, along the corticopapillary axis. INSs are compartments of interstitial space that are created by the complex geometrical configurations arising from four or five tubular structures running parallel to each other along the corticopapillary axis. These structures include a single CD, two AVR, and one or two ATL or prebend segments. In some regions of the IM, especially in the region deeper than ∼3.5 mm below the OM, AQP1-negative DTLs may form part of the INS (34). A previous study (34) has shown that all prebend and equivalent-length postbend segments on the ascending side of the loop border the INSs. The depth below the OM-IM boundary at which AQP1-negative DTLs enter into the CD cluster has not been determined, although this depth is likely a function of loop length.

Immunohistochemical analysis of the present study revealed that ∼30% of the total CD circumference abuts AVR. This is less than a previous estimate of 54% (31), a discrepancy that likely reflects the higher resolution of the images prepared for the present study. That a large fraction (∼70%) of the CD circumference borders INSs indicates the potential for preferential interactions among the CDs and the ATLs. Based on these anatomical findings, we developed a mathematical compartment model that represents the radial organization of the vessels and tubules in a cross-section of the upper IM (∼400 μm below the OM-IM boundary). The model simulates steady-state solute and fluid exchange through the INSs.

INS fluid pressure.

Analysis by MacPhee and Michel (27) indicates that the oncotic pressure exerted by plasma proteins in the AVR is greater than the outwardly directed hydrostatic pressure of the AVR fluid and the oncotic pressure in the interstitium. This balance of forces favors uptake of fluid by the AVR. Estimates by MacPhee indicate that the interstitial fluid pressure is less than the outwardly directed hydrostatic pressure in the AVR, which suggests that the interstitial fluid hydrostatic pressure did not play an essential role in driving fluid uptake by the AVR (26). However, MacPhee's analysis did not consider microdomains. Indeed, our model predicts an interstitial fluid hydrostatic pressure in the microdomain of 23.7 mmHg, which substantially exceeds the sum of hydrostatic and oncotic pressures gradients for the AVR fluid, which are assumed to be 8 and 7 mmHg, respectively (27, 43). It should be noted that there are substantial uncertainties in the AVR hydrostatic pressure value and that our sensitivity study indicates that INS and AVR hydrostatic pressures are closely related. However, because the two pressures vary almost proportionally, it remains the case that INS hydrostatic pressure exceeds AVR hydrostatic and oncotic pressures. Taken together, these results suggest that, as a result of water reabsorption from tubules, the interstitial fluid pressure within these localized areas may be substantially higher than elsewhere.

Effects of hyaluronan.

Hyaluronan is a major component of the extracellular matrix. It is a glycosaminoglycan composed of repeating disaccharides of glucuronic acid and N-acetylglucosamine and plays an important role in tissue development and growth (40). In many tissues, including renal cells, hyaluronan interacts with the cell surface through surface receptors and thus can influence cell signaling and cell function. Hyaluronan can also participate in the formation of a pericellular hydrated zone.

Hyaluronan is believed to be abundant in the interstitial space of the IM (3, 8, 11, 18), but its concentration is not well characterized. Hällgren et al. (11) reported hyaluronan concentrations of 209 and 463 μg/g of dried tissues in the IM and papilla, respectively, of the rat kidney. Because hyaluronan is present in the interstitial spaces only, it is not obvious what fixed charge concentrations the above measurements correspond to. Other interstitial macromolecules bearing negative charges may contribute to the fixed charge concentration. Such molecules promote water reabsorption from the CD by functioning as external osmolytes. In this study, we chose a range of fixed charge concentrations that we believe to be reasonable, and then we performed sensitivity studies to assess the effect of differing fixed charge density on model predictions. Our model predicted that a moderate fixed charge concentration of 20 mM increased CD water reabsorption rate by ∼10%. Given the higher hyaluronan concentration in the papilla (11), the effects of fixed charges would potentially have a greater impact on solute and fluid mixing in that region. The architecture of the terminal ∼1.5 mm of the IM is substantially different from that of the upper IM; the organizational pattern of CD clusters is reduced, loop of Henle density is reduced, and INS volume increases in parallel with increased interstitial fractional volume (17, 32). Therefore, fluid and solute mixing in the deep papillary INSs could very well be substantially different from that which occurs in the upper IM.

Schmidt-Nielsen and colleagues (35, 37, 38) proposed that peristaltic contractions of the renal pelvic wall may play an important role in the production of a highly concentrated urine in rodents. In a review, Knepper et al. (18) suggested that the viscoelastic and chemical properties of hyaluronan may allow it to function as a mechanoosmotic transducer, converting energy from the contractions of the pelvic walls to an axial osmolality gradient in the IM. Specifically, during the contraction phase of the pelvocalyceal contraction-relaxation cycle, the compression of hyaluronan results in a lowering of the counterion activity, and a hypotonic fluid is drained by the AVR. During the relaxation phase, water is reabsorbed from the DTL as a result of the reduced hydrostatic pressure in the interstitium.

It is unclear whether the pelvic contractions in the rat kidney reach up to half a millimeter below the OM-IM border. Assuming that they do, we will use our model to assess the extent to which the compression and relaxation of hyaluronan facilitate water reabsorption from CDs (not DTL, because the DTL segments bordering the INS are AQP1-negative). Because many of the parameters needed below are unknown, we will choose values that seem reasonable. During the contraction phase, tubular and DVR lumen collapse. Owing to the presence of interstitial cells, the INS is likely compressed to a lesser extent, say 20% of its volume. We assume a fixed charge density of 20 mM and that the counterion activity is reduced by 50% when the hyaluronan is compressed. (For a fixed charge density of 20 mM, our sensitivity study computed an INS osmolality of 765.2 mosmol/kgH₂O and hydrostatic pressure of 39.5 mmHg; see Fig. 4, top and middle.) Then the osmolality of its free fluid is 765.2 − 0.5 × 20 = 755.2 mosmol/kgH₂O. After that free fluid is taken up by the AVR, the osmolality of the interstitial fluid at the beginning of the relaxation phase is (765.2 − 755.2 × 0.2)/0.8 = 767.7 mosmol/kgH₂O. That 2.5 mosmol/kgH₂O increase in interstitial fluid osmolality corresponds to an osmotic pressure of 48.5 mmHg. Now assume that at the end of the contraction phase, the INS hydrostatic pressure is 42 mmHg, which is 2.5 mmHg higher than the steady-state prediction without peristalsis. Because we assume that 20% of the interstitial fluid is drained during the compression phase, the INS hydrostatic pressure at the beginning of the relaxation phase is 42 × 0.8 = 33.6 mmHg, which corresponds to a reduction of 8.4 mmHg from the contraction phase and a reduction of 5.9 mmHg from the steady-state value. These pressure differences are small compared with the osmotic pressure. These calculations suggest that the contractions of the pelvic walls may facilitate water absorption from the CDs, in large part by raising the INS fluid osmolality during the relaxation phase, rather than by lowering INS hydrostatic pressure.

Urine concentrating mechanism.

In the context of a countercurrent system, we have previously suggested (7, 24, 33) that the absorbate from the CDs and ATL is carried via the AVR to higher levels within the CD cluster, where the local absorbate will likely have lower solute concentrations and lower osmolality and where the ascension in AVR fluid that is concentrated relative to local fluid would raise the osmolality of the CD tubular fluid and contribute to an optimization of concentrating efficiency. The model predicts that AVR fluid is hypotonic relative to tubular fluid in loops of Henle, CDs, and DVR. This prediction is in agreement with measurements in rat by Johnston et al. (15) and by Gelbart et al. (10). In contrast, two studies (28, 41) in hamster showed little or no difference between osmolality of AVR and ATL, either at the loop bend or at ∼1 mm above the bend, supporting the view that there are species-differences in the urine concentrating mechanism.

Model results of the present study support our hypothesis, described in previous reviews (7, 24, 33), that the countercurrent system in the CD cluster mixes NaCl absorbed from ATLs with absorbate from the CDs (which consists mostly of water, urea, and NaCl) to produce isolated sites of high osmolality that will promote water withdrawal from CDs. By isolating CDs from DVR, which carry relatively dilute fluid, the INSs increase water reabsorption from the CDs and raise the osmolality of its tubular fluid. Our model predicts that CD water reabsorption rate is approximately six- to sevenfold higher in a completely isolated CD cluster than one that is highly coupled with the model DVR (see Fig. 3). The model predicts that interstitial hydrostatic pressure suffices to drive fluid entry into the AVR fenestration. Because these fenestrations are extensive (19) and because AVR are more numerous than DVR (the number ratio of AVR to DVR is ∼4:1 in the papilla; Refs. 14, 42), resistance in the AVR to fluid entry may be relatively small.

The present study uses a compartment model that represents cross-sections of an INS and of the lumina of a CD, an ATL, an AVR, and a DVR. Axial flows are not represented, and the luminal fluid compositions are specified a priori. The advantage of the compartment approach is that it allows one to focus on the fluid and solute exchanges at a given medullary level, decoupled from tubular interactions elsewhere in the medulla. The limitation of this approach is that model results are sensitive to luminal compositions, which we specified based on predictions of a whole-medulla model (21). The model in Ref. 21 represents the isolation of CDs from DVR and DTL in the upper IM but does not explicitly represent hydraulic pressure, oncotic pressure, or interstitial fixed charges. Thus the question of whether the transmural fluxes predicted in the present model are consistent with the specified luminal fluid compositions will ultimately need to be tested in a more comprehensive model of the urine concentrating mechanism.

Indeed, taken in isolation, a higher water reabsorption rate from the CD would imply a more concentrated CD tubular fluid and, perhaps, eventually a higher urine osmolality. However, the isolation of the DVR from the CD clusters would also result in a more dilute DVR fluid. Also, in the final 1.5–2 mm of the IM, where the central and peripheral regions of the CD clusters can no longer be distinguished, the relatively dilute DVR might impose a load on the concentrating mechanism and lower the urine concentration. The effects of these competing factors, and the resulting impacts of INS on the urine concentrating mechanism, merit further investigation.

GRANTS

This research was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grants DK-089066 (to A. T. Layton) and DK-083338 (to T. L. Pannabecker) and National Science Foundation Grant DMS- 0701412 (to A. T. Layton).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

Glossary

d_AVR

distance between current IM level and the upstream position where AVR luminal composition is specified

Ƒ

Faraday constant

F_AVR,V⁰

upstream AVR fluid flow rate

J_i,j,k

transmural flux of solute k from compartment j into i

J_i,k

total transmural flux of solute k into compartment i

J_i,j,V

transmural water flux from compartment j into i

J_i,V

total transmural water flux into compartment i

L_i,p

water permeability of structure i

l̃_i,j

fraction of circumference of compartment i in contact with j

P_i,k

permeability of structure i to solute k

p_i

hydrostatic pressure in compartment i

R

gas constant

σ_k

reflection coefficient of capillary wall to solute k

T

absolute temperature

ϕ_k

osmotic coefficient of solute k

Δψ_i,j

electrical potential difference between compartments i and j

V_INS

INS volume

z_k

electrical valance of ion k