Geometric Correspondence for Ensembles of Nonregular Shapes

Abstract

An ensemble of biological shapes can be represented and analyzed with a dense set of point correspondences. In previous work, optimal point placement was determined by optimizing an information theoretic criterion that depends on relative spatial locations on different shapes combined with pairwise Euclidean distances between nearby points on the same shape. These choices have prevented such methods from effectively characterizing shapes with complex geometry such as thin or highly curved features. This paper extends previous methods for automatic shape correspondence by taking into account the underlying geometry of individual shapes. This is done by replacing the Euclidean distance for intrashape pairwise particle interactions by the geodesic distance. A novel set of numerical techniques for fast distance computations on curved surfaces is used to extract these distances. In addition, we introduce an intershape penalty term that incorporates surface normal information to achieve better particle correspondences near sharp features. Finally, we demonstrate this new method on synthetic and biological datasets.

1 Introduction

A well established method for performing statistics on an ensemble of shapes is to compare configurations of corresponding landmarks placed on the individual shapes. In recent years, several methods have proposed an automatic placement of landmarks in a way that captures statistical properties of an ensemble [1, 2]. The method of Cates et al [1] uses a formulation of ensemble entropy to deploy a dense set of landmarks, or particles, which assign correspondences between shapes within a population. The positions of the particles on the shape surfaces are optimized using a variational framework that tries to find a balance between model simplicity via minimum entropy, and geometric accuracy of the surface representation. However, medical or biological objects shapes are often composed of sharp features and regions of high curvature. In such cases, nearby particles in the ambient space may be separated by a large distance on the object’s surface (see Fig. 1). Thus, the Euclidean distance measure cannot capture correctly the underlying local geometry and prevents the method from producing a faithful shape representation. This limitation reflects a failure of Euclidean distance to account for the intrinsic distances between points on the surface, suggesting geodesic distance as a better choice. However, geodesic distances are generally not computable in closed form, and interparticle interactions are part of the inner loop of an interactive optimization process. Thus, the computational burden of geodesics are prohibitive. This paper makes several contributions that enable better modeling of ensembles composed of shapes with a complex geometric structure. First, we incorporate geodesic distance measures into the framework proposed by Cates, et al [1]. While accurate geodesic distance computation is unwieldy for implicit surfaces, very fast methods exist to compute geodesic distances between vertices of 3D mesh representations of shapes. Thus, we propose precomputing all pairwise distances on a somewhat fine 3D mesh of an input surface and interpolate, as required, in the process of optimizing intrashape particle interactions. To address mismatches of correspondences on highly curved features across different shapes, we introduce an intershape penalty that accounts for the behavior of normals on highly curved geometry. Hence, the second contribution of our paper is to integrate this intershape penalty term into the variational framework for model optimization given in [1] to improve particle correspondences near sharp features. As a final contribution we demonstrate the use of a correspondence-based method for the analysis of highly curved (or nonregular) shapes—the left ventricle myocardium of the human heart—which has, so far not feasible with point correspondences.

Fig. 1.

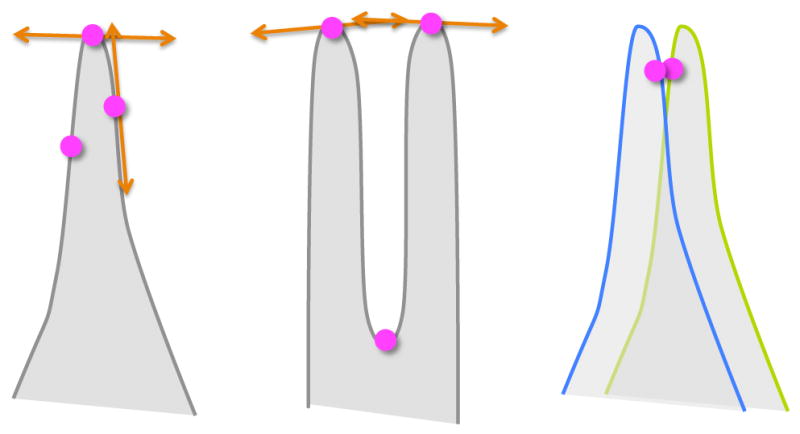
Points near sharp features (left) are not able to achieve good distributions with Euclidean distance, because they do not lie in the same tangent space, which is necessary for movement that is constrained to the surfaces. Points may be nearby and interact (center) even though they sample very different parts of the surface. Points on nearby features (right) on different shapes (blue and green) can come into incorrect correspondence if the system considers only distance.

2 Background

In the following section we provide a brief overview the particle-system correspondence optimization method as proposed in [1]. The general strategy of this method is to represent correspondences as point sets that are distributed across an ensemble of similar shapes by minimizing an objective function that quantifies the entropy of the system. We also describe an efficient, fine-grained algorithm for solving the eikonal equation on triangular meshes, as proposed by Fu et al [3]

Correspondence Optimization

Let us define a surface as a smooth, closed manifold of codimension one, which is a subset of ℝ^d (e.g., d = 3 for volumes). We sample the surface ⊂ ℝ^d using a discrete set of N points that are considered as random variables Z = (X₁, X₂, …, X_N)^T, X ∈ ℝ^d drawn from a probability density function (PDF), p(X). We denote a realization of this PDF with lower case, and thus we have z = (x₁, x₂, …, x_N)^T, where z ∈ . We refer to the positions x as particles, and to a set of particles as a particle system. The amount of information encoded in this random sampling is, in the limit, the differential entropy of the PDF, given by H[X] = −E{log p(X)}, where E{·} is the expectation. Approximating the expectation by the sample mean, we have $H[\mathbf{X}]\approx -\frac{1}{Nd}{\sum }_{i}logp({\mathbf{x}}_i)$. To determine the probability of a particle’s position, p(x_i), [1] uses a nonparametric Parzen-window density estimation given by a mixture of multivariate, isotropic Gaussian kernels with standard deviation σ that determines the strength of particles interaction with N neighbouring particles within the defined window. An ensemble comprised of M surfaces, 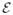= z¹, …, z^M can be described by a Nd × M matrix of particle positions $P=({\mathbf{x}}_j^k)$, where k = 1, …, M and j = 1, …, N. Let z^k ∈ ℝ^Nd be an instance of a random variable Z, then, the combined ensemble and shape cost function is defined by

$$Q=H(\mathbf{Z})-\sum _{k}H(P^k)$$ (1)

This cost function is composed of two interacting terms. The first term produces a compact distribution of samples in shape space, while the second term provides uniformly-distributed correspondence positions on the shape surfaces, to achieve a faithful shape representation. The optimization process of this cost function is defined via gradient descent as described in [1].

Fast Geodesic Distance Computation

The use of Euclidean distance between particles in the Parzen-window density estimation in [1] requires that nearby particles interact in the local tangent plane of the surface. However, it is not the case for thin structures with high curvature, such as the one illustrated in Fig. 1 (left). To address this, we replace the Euclidean distance in the kernel by the geodesic interparticle distance. However, this modification demands a large number of pairwise geodesic distance computations. Such computations are not feasible without the recent developments in fast, parallel algorithms for solving hyperbolic partial differential equations (PDEs) as well as extremely fast SIMD hardware in the form of graphics processors (GPUs). The distance between each point a on the surface and every other point, is given by the solution to the eikonal equation |∇u| = 1, as discussed in [4], using the boundary condition u(a) = 0. The computation of distances to many thousands of points on large ensembles of shapes is feasible only if the eikonal equation can be solved in a small fraction of a second. The fast iterative method (FIM) [4] for regular grids is not worst-case optimal, but is extremely efficient on parallel, SIMD architectures, such as GPUs. Here, we use an extension of the FIM for triangular meshes [3]. This algorithm computes, for instance, distances between nodes on a mesh with thousands of vertices in less than 30 seconds on a GPU.

3 Methodology

The input to the shape correspondence system is a collection of implicitly defined surfaces. For this paper, the input surfaces are binary segmentations, and we use the preprocessing, initialization, and particle optimization pipeline described in [1]. Here we describe the integration of the geodesic distance for inter-particle interactions and the surface normal based penalty term for intershape correspondence into the framework described in Sec. 2.

Particle Position Optimization using Geodesic Distances

A triangulation of each input surface is generated using the algorithm described in [5]. An example triangulation is shown in Fig. 2(a) along with the corresponding synthetic shape. The numerical technique for fast distance computation on 3D triangulated surfaces described at the end of Sec. 2 is then used to precompute geodesic distances between each vertex and all other vertices within a prescribed distance, d_max. The parameter d_max is chosen to coincide with the limited range of influence of the Gaussian kernels that control the range of influence of each particle. This truncation results in a sparse, symmetric matrix of geodesic distances. The entries in this matrix are then converted into a fixed point format and stored using a List of Lists (LIL) representation for efficient memory usage and fast access. We call this matrix M_G such that D_G(v₁, v₂) = M_G[v₁, v₂], where D_G(v₁, v₂) is the geodesic distance between vertices v₁, v₂. Geodesic distances between particle positions on the implicit surface can now be computed via a barycentric interpolation scheme described below.

Fig. 2.

(a) An example of a triangle mesh used for geodesic distance computations. (b) Configuration for two-layered interpolation of geodesic distance between arbitrary points: x and y are contained in triangles defined by vertices (x₁, x₂, x₃) and (y₁, y₂, y₃) respectively. The geodesic distances between vertices for all shapes are precomputed on a GPU.

To use this discrete set of distances between particles, which lie in the volume and are constrained to lie on the implicit surface, we interpolate the mesh-vertex distances to the faces of the triangles. This requires two layers of linear interpolation on the faces of the mesh. Let the barycentric coordinates of a point x in a triangle T_x defined by vertices (v₁, v₂, v₃) be given by (α, β, γ) such that the location of x can be given as x = αv₁ + βv₂ + γv₃ where α + β + γ = 1. Consequently, any function of x can be interpolated as f(x) = αf(v₁) + βf(v₂) + γf(v₃) provided its value is known at all vertices in the mesh. For the case of geodesic distances, the function f is the distance to another arbitrary point y, which can be evaluated on each vertex using this same interpolation scheme for the triangle T_x that contains y. To compute D_G(x, y) in a fast and efficient manner, we first determine the triangle faces on the mesh that contain points x and y, by projecting them onto the nearest face in the mesh. Let these triangles defined by vertices (x₁, x₂, x₃) and (y₁, y₂, y₃), as shown in Fig. 2. Since the geodesic distance is a function defined between every pair of vertices in the mesh, we can approximate the geodesic distance between points x and y as

$$\begin{array}{l}{D}_G(x,y)\approx \alpha D_G(x_1,y)+\beta D_G(x_2,y)+\gamma D_G(x_3,y),\\ D_G(x_i,y)\approx \alpha D_G(x_i,y_1)+\beta D_G(x_i,y_2)+\gamma D_G(x_i,y_3).\end{array}$$ (2)

Each D_G(x_i, y_i) is simply an entry in the matrix M_G as described above. Thus, using this two-layered interpolation scheme, we can approximate geodesic distances between particle positions on the implicit surface. The Gaussian forces of repulsion governing the motion of particles can then be computed as a function of these geodesic distances to improve sensitivity to the underlying geometry.

Correspondence Optimization with Surface Normals

The cost function described in Eq. 1 relies on particle positions to find a balance between a compact ensemble representation and a good distribution of particles on each surface. However, with an ensemble containing highly curved or convoluted surfaces, like those shown in Fig. 1, a reliance on only positional information may lead to incorrect correspondences. To address this shortcoming, we propose the addition of an intershape penalty term based on surface normals to disambiguate correspondences near highly curved features. Thus, we associate with each particle on each surface a pair of d-tuples (x_i, n_i) ∈ ℝd × S², where S² is the unit sphere.

We denote the total collection of N normals across M shapes as V. With the assumption that N > M. Assuming a Gaussian model with a covariance S, we can compute the entropy

$$H(V)\approx \frac{1}{2}log\mid \mathrm{\sum }\mid \approx \frac{1}{2}log\mid \sum _i\sum _k{\widehat{n}}_i^k·{({\widehat{n}}_i^k)}^T\mid$$ (3)

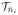
For the ith particle on the kth shape, ${\widehat{n}}_i^k=d(n_i^k,{\overline{n}}_i)$, where n̄_i is the Fréchet mean defined in [6]. Since the normals are points on the Riemannian manifold $\mathcal{M}\epsilon S^2,{\widehat{n}}_i^k={\mathit{Log}}_{{\overline{n}}_i}(n_i^k)$. [6]. In the tangent plane 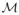, we have

$${\widehat{n}}_i^k={\mathit{Log}}_{{\overline{n}}_i}(n_i^k)=\frac{P_t(n_i^k-{\overline{n}}_i)arccos(n_i^k·{\overline{n}}_i)}{1-{(n_i^k·{\overline{n}}_i)}^2}$$ (4)

where P_t is the idempotent projection matrix given by ( $I-{\overline{n}}_i·{(n_i^k)}^T$). Since Σ will not have a full rank in practice, we implement a regularization similar to that described in [1] to introduce a lower bound on the eigenvalues. The optimization problem in Eq. 1 can now be reformulated as

$$Q=H(\mathbf{Z})-\sum _{k}H(P^k)+H(V)$$ (5)

The Riemannian distances are functions of normals; ${\widehat{n}}_i^k=f(n_i^k)$, which in turn are a function of position; $n_i^k=n(x_i^k)$, the gradient descent on H(V) with respect to particle position x_i is given by the chain rule:

$$\frac{\partial H(V)}{\partial x_i^k}=\frac{\partial H(V)}{\partial {\widehat{n}}_i^k}·\frac{\partial f(n_i^k)}{\partial n_i^k}·\frac{\partial n(x_i^k)}{\partial x_i^k}$$ (6)

This incremental update gets projected onto the tangent plane of the surface, as part of the algorithm described in Sec. 2, in order to maintain the constraint that particles remain on the surface. As with the geodesic distances, the curvature, $\partial n_i^k/\partial x_i^k$, is precomputed. Here we use the formulation of curvature for the level sets of the volume using finite differences (combined with a Gaussian kernel of standard deviation 1.0). The means of the normals are updated after each full iteration (one update for every particle on every shape).

4 Results and Discussion

This section details experiments designed to illustrate and validate the proposed method. First, we present an experiment with synthetically generated coffee bean shapes, that consist of an ellipsoid with a slot or indentation, creating a high-curvature feature that would confound the previous approaches. We also present an application to a study of group differences in the left ventricular myocardium.

Synthetic Data

Computational solid geometry methods were used to compute the intersection of a small ellipsoid with axes a, b and c, and a larger ellipsoid with axes A, B and C, to create a coffee bean shape. The slot was then moved and scaled stochastically, to create a population of 10 coffee bean shapes. The position of the slot was chosen from a uniform distribution in the range [−B/3, B/3], and its width was sampled from a Gaussian distribution of μ = 8 and σ = 2. Both, the method in [1] and the proposed method were applied to distribute 1024 correspondences across the ensemble. Both methods identified two dominant modes of variation, with significantly different amount of leakage into smaller modes. These modes are illustrated in Fig. 3 for both the methods, to 2 standard deviations. The proposed method lost 4% of the total variation into smaller modes, compared to 16% lost by the original method. Thus, the proposed method was able to characterize the variation in the population better than the original method, while remaining faithful to the original shape representation (as seen from the reconstructions in Fig. 3).

Fig. 3.

Mean shape computed from the proposed method (left) and the original method (right), projected onto the first (top) and second (bottom) PCA modes, and ±2 standard deviations

Application to Group Comparison

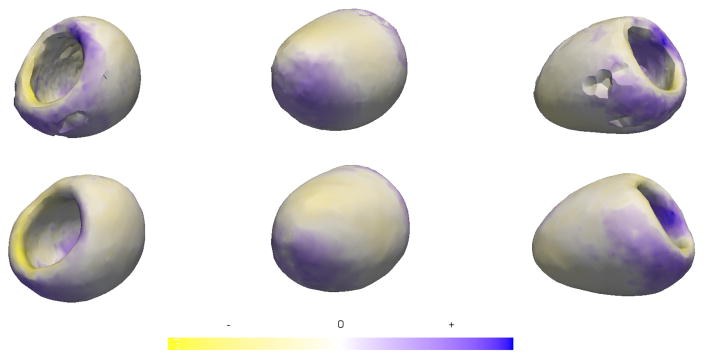
We applied the proposed methods to study group differences in the left ventricular myocardium of ischemic patients and non-ischemic controls, using segmented volumes of the left ventricular myocardium at end diastole (ED) as inputs. The proposed method was used to initialize and optimize 1024 correspondences across the ensemble of 21 (12 patients, 9 controls) shapes. We then used parallel analysis to project the correspondences into a lower dimensional space determined by choosing an optimal number of basis vectors from principal component analysis (PCA). A standard, parametric Hotelling T² test was used to test for group differences, with the null hypothesis that the two groups are drawn from the same distribution. In this case, the hypothesis test results in a highly significant p-value of 0.005, with 7 PCA modes chosen by parallel analysis. Fig. 4 (bottom row) shows the differences between the mean shape surfaces for the normal and ischemic groups. To visualize the group differences driving statistical results, we use the linear discriminant vector, rotated from PCA space into the full dimensional shape space, and mapped onto the mean group shape surfaces to give an indication of the significant morphological differences between groups. The above experiment was also conducted using the method described in [1]. The resulting group differences, visualized in Fig. 4 (top row), were also found to be statistically significant with a p-value of 0.005 using the Hotelling T² test. However, the shape differences obtained using the proposed method are found to be more consistent with previously published results presented in [7], as compared to those obtained using [1].

Fig. 4.

Visualizing mean differences between normal and ischemic groups (blue denotes expansion and yellow denotes contraction) using [1] (top row) and the proposed method (bottom row)

5 Conclusion and Future Work

This paper extends the method given by [1] to improve particle distribution and correspondences across an ensemble of highly convoluted surfaces. The first contribution is the inclusion of geodesic distance to compute the intrashape particle interactions, which results in improved sensitivity of the particle distribution to the underlying surface geometry. The second contribution is the introduction of an intershape penalty term based on surface normals, to improve correspondence near sharp features. Results on synthetic and real data indicate that the proposed method provides a practical solution to compute correspondence models of ensembles of highly convoluted surfaces in an efficient and robust manner.