Motion Compensated Magnetic Resonance Reconstruction Using Inverse-Consistent Deformable Registration: Application to Real-Time Cine Imaging

Abstract

Patient motion is a major limitation for magnetic resonance imaging. Recent theoretical advances incorporate explicit rigid and non-rigid motion compensation into conventional image reconstruction for multi-shot acquisitions and recover motion-free images by solving a general matrix inversion problem. Although the theory has been established, applications are rare due to the challenges of estimating motion field for every pixel of every shot. In this paper we propose a method to overcome this difficulty using the inverse-consistent deformable registration supplying both forward and backward deformations for matrix inversion. We further extend this framework for multi-coil motion compensated image reconstruction using the eigen-mode analysis. Both simulations and in vivo studies demonstrate the effectiveness of our approach.

1 Introduction

Patient motion during magnetic resonance imaging (MRI) causes blurring or ghosting that degrades image quality. The undesired effects of patient motion are introduced during the acquisition of Fourier domain or k-space data. Any inconsistencies in k-space can strongly influence every pixel in the image domain. Even slight motion will cause blurring in linearly acquired k-space or ghosting artifacts in interleaved k-space acquisitions. Significant movement may create artificial structures that may interfere with diagnostic interpretation of the image (Fig. 1).

Fig. 1.

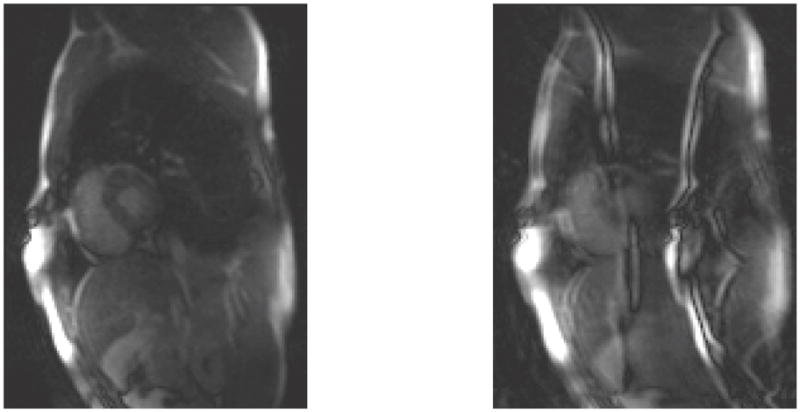
An illustration of motion induced artifacts. The left shows a cardiac cine frame whose k-space was divided into 2 shots by picking every the other line. Significant artifacts are induced on the right after two shots are shifted by 3 pixels.

Motion compensation in MRI is an active research area [1]. Published methods can be classified as either prospective or retrospective. Prospective approaches such as breath-holding, ECG synchronization or respiratory gating require additional clinical set-up, rely on patient cooperation, regular breathing and/or cardiac rhythm, and can lengthen the scan time. The majority of retrospective methods deals with rigid motion, and may be insufficient for applications like cardiac or liver imaging where significant deformation of organs could occur in addition to rigid motion.

Recently proposed methods aim to extend conventional MR reconstruction to incorporate explicit motion compensation for non-rigid deformations. Recent theoretical advances [2] elucidate that if a) the MR data acquisition is performed in a multi-shot or multi-segment manner, which is often the case for many cardiac and 3D imaging applications, and b) the motion between every shot is known, motion compensation can be achieved by solving a general matrix inversion problem [2]. A ‘shot’ here is defined as a subset of k-space, but can be extended to include the k-space data for an entire image; i.e., in dynamic single-shot or real-time acquisition. The assumption in [2] is that all k-space points within a shot are acquired during a sufficiently short period to be considered motion-free. Although the theory has been established, this methodology is rarely applied mainly due to the difficulty of estimating dense deformation fields for every shot. An attempt to bypass this problem was published in [3], where a motion model within the field of view is assumed and parameterized as a linear combination of selected input basis signals, e.g. navigator echoes or respiratory belts or signals derived from ECG. The optimization process is extended to interleave the estimation of a motion-free image and a motion model by consecutively solving two large linear systems. Although this approach avoids the estimation of deformation fields, it requires a more complicated matrix representation and couples motion estimation and compensation. Significant computational cost is thus incurred to converge to a solution.

With the aim to correct non-rigid motion, we propose an efficient algorithm as an extension of the motion compensation framework based on matrix inversion. The key feature is to estimate the pixel-wise forward and backward deformation fields using the inverse-consistent non-rigid registration algorithm, and to perform multi-coil reconstruction using eigen-mode analysis. In this way, the motion field can be interpreted as a prior, simplifying the solver and reducing total reconstruction times to the order of seconds. The algorithm was successfully applied to cardiac real-time cine imaging showing suppression of ghosting artifacts caused by chest-wall motion.

2 Methods

2.1 General Motion Compensation Framework

Suppose the MR acquisition consists of k_s shots, presenting a n₁ × n₂ image. The k-space sampling pattern for every shot is defined by the sampling matrix A_s(n₁n₂ × n₁n₂). The motion-free image S₀(n₁n₂ × 1) is corrupted by the motion field u_s(n₁n₂ × n₁n₂). Then the final image with motion artifacts S(n₁n₂ × 1) can be expressed by the following matrix equation, as proposed in [3]:

$$\mathit{S}=\left({\sum }_{\mathit{s}=\mathbf{0}}^{{\mathit{k}}_{\mathit{s}}-\mathbf{1}}{\mathit{F}}^{\mathit{H}}·{\mathit{A}}_{\mathit{s}}·\mathit{F}·{\mathit{u}}_{\mathit{s}}\right)·{\mathit{S}}_{\mathbf{0}}=\mathit{g}·{\mathit{S}}_{\mathbf{0}}$$ (1)

Here F(n₁n₂ × n₁n₂) is the Fourier transform and F^H is the inverse of F (hermitian conjugate). u_s is the image transform, corresponding to the deformation for shot s. We emphasize that u_s · S₀ represents the transformed image intensities and can be efficiently computed by image interpolation operation. For every pixel in S₀, its spatial position is calculated after applying the transform. The intensity at this position is estimated by performing an image interpolation. This process is repeated for all pixels in S₀ and the resulting transformed image is u_s · S₀. The task here is to estimate the motion-free image S₀, given the measured k-space data S, sampling pattern A_s and deformation field u_s. While the Eq. 1 is linear, it is fully capable to represent both rigid and non-rigid motion, because only transformed image intensities, not the motion itself, are needed.

To estimate the motion-free image S₀, the inversion of ghosting matrix g (here ‘ghosting’ means motion artifacts are introduced after applying this matrix to motion-free images) is necessary. Despite the large size of matrix g, the standard conjugate gradient solver such as LSQR only requires the computation of matrix-vector product g · S and g^H · S, as pointed out in [2]. These matrix-vector products can be efficiently computed using image pixel-wise operations, such as FFT and image interpolation.

Given the matrix description of motion compensation and its fast solver, the deformation field u_s for every shot is still missing. Besides, ${\mathit{g}}^{\mathit{H}}={\sum }_{\mathit{s}=\mathbf{0}}^{{\mathit{k}}_{\mathit{s}}-\mathbf{1}}{\mathit{u}}_{\mathit{s}}^{\mathit{H}}·{\mathit{F}}^{\mathit{H}}·{\mathit{A}}_{\mathit{s}}·\mathit{F}$ is needed since g^H · S is required by the LSQR solver. One way to get g^H is to explicitly compute g. But this will disable the fast algorithm using image based operations. Fortunately, as suggested in [2], if the inverse deformation ${\mathit{u}}_{\mathit{s}}^{-\mathbf{1}}$ is available in the sense of inverse consistency ${\mathit{u}}_{\mathit{s}}^{-\mathbf{1}}·{\mathit{u}}_{\mathit{s}}=\mathit{id}$, the ${\mathit{u}}_{\mathit{s}}^{\mathit{H}}$ can be replaced by ${\mathit{u}}_{\mathit{s}}^{-\mathbf{1}}$. Then, fast pixel-wise operations can be applied to computing g · S and g^H · S.

2.2 Inverse-Consistent Non-rigid Registration

Incorporating motion compensation into MR reconstruction requires the availability of both forward and backward deformation fields u_s and ${\mathit{u}}_{\mathit{s}}^{-\mathbf{1}}$ for every shot. While most non-rigid algorithms neither supply the inverse deformation field as the output nor maintain the inverse consistency, there are some researches in this topic [4,5]. To estimate both forward and backward deformation, we propose to utilize an inverse consistent non-rigid registration algorithm [6] which estimates both deformation fields using an interleaved optimization scheme and maintaining the symmetry and inverse-consistency of image alignment. In this optimization scheme, a symmetric energy functional is descended by alternating the registration direction after each iteration and enforcing the inverse consistency. This inverse-consistency optimization is added on top of a variational registration framework [6]. Although current algorithm is selected because of its great efficiency and ability to produce the pixel-wise deformation field which is required by the matrix description of motion compensation, other inverse consistent registration algorithms can be applied.

2.3 Motion Compensated MR Reconstruction with Multiple Coils

The usage of multiple phased array receiver coils has become essential in contemporary MR systems due to the success of parallel imaging. It is thus necessary to utilize the proposed technique in the context of multi-coil imaging using parallel image acquisition.

There are two approaches that extend the above-mentioned technique for multi-coil imaging. Firstly, one could repeat the solver to correct motion independently for every coil with the same deformation fields. After all coils are corrected, they can be combined to generate the final image. To estimate the deformation fields, non-rigid registration needs to be applied to the magnitude image of every shot. There are many possible ways to achieve this. In dynamic imaging, an initial round of parallel imaging reconstruction can be applied to generating images needed to estimate the deformation fields. In multi-segment 3D imaging, images for every shot could be computed by a rough re-gridding reconstruction. In 2D imaging, those images can be obtained by a simple SENSE reconstruction. Other alternatives include performing the registration on low-resolution pre-scan before running the intended protocol.

An apparent drawback of performing the solver on every coil is the increased computational cost since coils with 32 channels or more are commonly used in clinical settings. To avoid this, suppose a total of n_r coils are used for imaging, the ghosting matrix formula can be listed for every coil: ${\mathit{S}}_{\mathit{r}}=\left({\sum }_{\mathit{s}=\mathbf{0}}^{{\mathit{k}}_{\mathit{s}}-\mathbf{1}}{\mathit{F}}^{\mathit{H}}·{\mathit{A}}_{\mathit{s}}·\mathit{F}·{\mathit{u}}_{\mathit{s}}\right)·{\mathit{C}}_{\mathit{r}}·{\mathit{S}}_{\mathbf{0}}={\mathit{g}}_{\mathit{r}}·{\mathit{S}}_{\mathbf{0}}$ where C_r is the coil sensitivity for the channel r. The above matrix equation can be repeated for every coil and stacked together except S₀, ending up solving a linear system of n_rn₁n₂ × n₁n₂. The pixel-wise image operation can still be applied for efficiency. The main disadvantage here is that the coil sensitivity must be known beforehand, which can be achieved if a reference scan is feasible. However, in many applications a precise estimation of coil sensitivity is problematic due to motion of the chest-wall or abdomen that alters the coil sensitivity between the pre-scan and subsequent image acquisitions.

We propose to employ the so-called ‘eigen-coil’ method to reduce computational cost without affecting reconstruction accuracy. The eigen-coil images are computed by performing a Karhunen-Loeve Transform or principal component analysis on the multi-coil images [7]. Suppose a set of n_r coils, each coil acquires an image of n₁ · n₂ pixels at the same time. These n_r images can be represented by a n_r × n₁n₂ data matrix D. As the same object is imaged by all coils and there are overlaps between coil sensitivities, images from every coil bear redundancy. Therefore, the empirical covariance matrix of D, defined as DD^H/n₁n₂, has maximal n_r non-zero eigenvalues. The eigen-coil images are computed by multiplying the data matrix by corresponding eigenvectors. If we sort the eigenvalues by its magnitude and the first few eigen-coil images will occupy most image information, while those corresponding to small eigenvalues are basically representing noise. Therefore, it is adequate to only perform the motion compensation on the first few eigen-coil images without discernibly jeopardizing the accuracy. In this way, the computational cost can be largely reduced and coil sensitivity is not required.

2.4 Motion Compensated Real-Time Cine Imaging

Real-time cine imaging is a technique that captures cardiac motion without the need for breath-holding and regular cardiac rhythm; these are requirements of segmented multi-shot acquisition strategies. Temporal GRAPPA, i.e. TGRAPPA [8], and temporal SENSE, i.e. TSENSE [9] are state-of-the-art dynamic parallel imaging methods that acquire time-interleaved, undersampled k-space data and fuse information from adjacent frames in order to estimate the coil sensitivity for TSENSE or the autocalibrating signals (ACS) for TGRAPPA. This fusion of information from k-space data acquired in an interleaved fashion can lead to ghosting artifacts in the estimated coil sensitivity that might corrupt the reconstructed image. This can be especially problematic in the real-time stress imaging, where patient heart-rate and respiratory motion are at extremes, and there may be severe mismatches between the estimated coil sensitivity and the acquired image data. We propose here to apply the presented technique to correct the chest-wall motion between adjacent frames and suppress artifacts in the coil sensitivity estimation, which leads to an improved reconstruction. Fig. 2 illustrates the workflow of this reconstruction. In this scheme, an initial reconstruction was performed using standard TGRAPPA and the frame-to-frame deformation fields were estimated from the magnitude images. To reconstruct frame f, every R neighboring k-spaces around f were treated as R shots from a MR acquisition and a motion-compensated reference image was computed by solving the general matrix inversion with the deformation fields as inputs. This reference was fed into the GRAPPA computation to reconstruct frame f.

Fig. 2.

Motion compensation reconstruction for time-interleaved real-time cine imaging

3 Results

Proposed algorithm was implemented using Matlab (MathWorks, Natick, Massachusetts) and the non-rigid registration was programmed in C++. All computations were performed on a dual-core desktop with 3.00GHz CPU and 6GB RAM without utilizing multi-threading. Typical computation time needed for non-rigid registration is less than 0.1ms (320×80 pixels). The conjugate gradient solver costs ~1s for every eigen-coil image. In all following tests, the solver was fixed to iterate 15 times due to the observation that more iterations did not result in better results.

3.1 Simulation

To test feasibility, two simulations were performed. The first was designed to apply a known non-rigid deformation to a complex 32 channel cardiac cine image. Four artificial deformation fields were applied to warp this image to simulate a continuous chest-wall motion. K-space sub-sampling was restricted to the phase-encoding direction (horizontal axis in this case) and a regular sampling pattern with 4 times reduction was used and leads to 4 shots for every coil. After contaminating these 4 shots with corresponding deformation fields, the motion compensation solver was performed on each coil independently and thus repeated 32 times. Simulation results are shown in Fig. 3, presenting an accurate correction that is virtually identical to the ground truth. The second simulation was designed to perform motion compensation on the eigen-coil images. Fig. 4 shows the motion compensation results on eigen images where we empirically selected 0.05 as the cutoff of accumulated eigenvalue and kept 10 modes out of 32. Motion correction was applied to those kept and results were transformed back to original image space by multiplying the hermitian transpose of eigenvector matrix. As 95% of the total image content was actually compensated for motion, the corrected image was indiscernible compared to previous simulation with ~70% of processing time reduced.

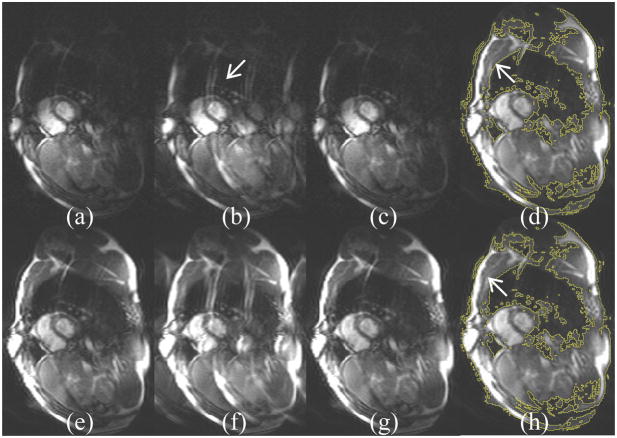
Fig. 3.

Simulation of non-rigid motion compensation for multi-coil complex image. K-space was divided into 4 shots and deformation fields were applied to mimic the chest wall motion. (a) Original image of the first coil; (b) Ghosting image of first coil due to non-rigid chest wall motion. (c) After motion compensation, the image content is completely recovered. (e–g) Sum-of-square original image, its ghosting version and recovered result. (d,h) Effect of chest wall motion.

Fig. 4.

Simulation of motion compensation using eigen-coil. (a) Ghosting artifacts appear on every coil; (b) All eigen modes bear ghosting artifacts, but only those corresponding to large eigenvalues need correction. (c) Eigen images after correction show good artifact removal. (d) Sum-of-square image after correcting 10 modes and leaving other 22 unchanged. Difference compared to Fig. 3(f) where all coils are processed is indiscernible with ~70% time-saving. The curve shows the accumulated eigen-values for all 32 channels.

3.2 In Vivo Study

18 volunteers (10 men, 8 women; mean age 36.7±15.2 years) underwent time-interleaved free-breathing real-time cine examinations. The study protocol was approved by the Institutional Review Board and all participants gave written informed consent. A clinical 1.5T MR scanner (MAGNETOM Avanto, Siemens) equipped with a 32 channel phased-array coil (Rapid MR International, Columbus, Ohio, USA) was used. MR sequence parameters included: balanced SSFP readout, TR=1.09/TE=0.9ms, acquired matrix 160×80 (interpolated to 160×120), flip angle 58°, interpolated in-plane resolution 2.44×2.44 mm², slice thickness 10mm, bandwidth 1420Hz/pixel and parallel imaging reduction factor of 4. For every patient, 9 slices were acquired to cover the left ventricle of the heart. Both standard TGRAPPA and motion compensated version were performed on all datasets. Image qualify was assessed by both noise and artifacts levels. To measure image noise, a retrospective signal-noise-ratio (SNR) estimation algorithm based on random matrix theory was applied [10]. This method has been validated for dynamic imaging. Although images reconstructed with or without motion compensation showed similar SNR (26.8 vs. 28.1), the advantage of propose method was that motion induced artifacts were clearly reduced when the chest all motion is severe during the image acquisition, as illustrated in Fig. 5. The motion compensation via eigen-coil method was found to be robust and visual equivalent to the per-coil strategy, while the reduction of reconstruction time is around 60~70%.

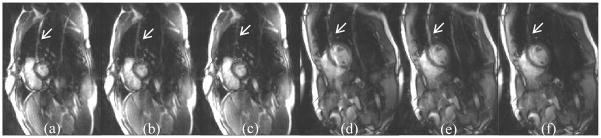
Fig. 5.

Example images generated using three different methods to estimate ACS signals for TGRAPPA reconstruction. (a,d) Averaging all undersampled k-space; (b,e) Moving averaging every 4 consecutive frames; (c,f) Moving averaging every 4 frames with motion compensation, where artifacts induced by chest wall motion were better suppressed.

4 Conclusion and Discussion

This paper describes a novel MR motion compensation algorithm based on inverse-consistent non-rigid registration and general matrix inversion. A practical realization of this method was proposed for real-time cine imaging. The proposed method requires a multi-shot interleaved k-space acquisition where each shot is free of motion inconsistency. In case this condition is violated, a longer shot can be divided into multiple shorter ones. The specific implementation for cardiac cine imaging relies on 2D image registration, implying that through-slice motion is not specifically handled. For future work, we plan to extend the proposed method to compensate multi-shot 3D imaging as the registration is not limited to 2D. Further validation studies are being pursued with emphasis on the clinical benefits of our technique.