Mitigating Errors in External Respiratory Surrogate-Based Models of Tumor Position

Abstract

Purpose

To investigate the impact of tumor site, measurement precision, tumor-surrogate correlation, training data selection, model design, and inter-patient and inter-fraction variations on the accuracy of external-marker based models of tumor position.

Methods and Materials

Cyberknife Synchrony^™ system log files comprising synchronously acquired positions of external markers and the tumor from 167 treatment fractions were analyzed. The accuracies of Synchrony^™, ordinary-least-squares (OLS) regression, and partial-least-squares (PLS) regression models for predicting tumor position from external markers were evaluated. Quantity and timing of data used to build the predictive model were varied. Effects of tumor-surrogate correlation and of the precision in both tumor and external surrogate position measurements were explored by adding noise to the data.

Results

Tumor position prediction errors increased over the duration of a fraction. Increasing training data quantities did not always lead to more accurate models. Adding uncorrelated noise to the external marker-based inputs degraded tumor-surrogate correlation models by 16% for PLS and 57% for OLS. External marker and tumor position measurement errors led to tumor position prediction changes 0.3 to 3.6 times the magnitude of measurement errors, varying widely with model algorithm. Tumor position prediction errors were significantly associated with patient index but not with fraction index or tumor site. PLS was as accurate as Synchrony^™ and more accurate than OLS.

Conclusions

The accuracy of surrogate-based inferential models of tumor position was affected by all of the investigated factors except tumor site and fraction index.

I. Introduction

Respiration-induced tumor motion degrades radiation therapy targeting accuracy.^1–3 While 4DCT and brief fluoroscopic movies can be used to measure tumor motion over a few respiratory cycles, accurately predicting the extent of tumor motion during treatment often cannot be accomplished because of day-to-day and breath-to-breath variations.⁴ Furthermore, a transient event such as a deep breath or a cough can cause the tumor to move out of its usual range of positions.^5–9 As a result, motion management technologies correcting for real-time tumor motion must accurately track the tumor.^8–11

Direct tracking systems, which measure the position of the tumor itself, either continuously image or electromagnetically localize the tumor. Fluoroscopically imaging over the entire treatment fraction¹² imparts unnecessary ionizing radiation to the healthy tissue. While electromagnetic signals can be used to track implanted fiducial markers without ionizing radiation,¹³ at the time of this writing the technology has only been approved for use in the prostate.

Indirect tracking systems rely on external surrogates of respiratory motion, such as optical markers affixed to the torso, to predict the position of the tumor.^{8–10,14–17} Tumor motion models based on the positions of multiple markers affixed to the torso show particular promise as alternatives to direct tracking systems.^{9–10,14–16}

Most studies to date of surrogate-based tumor localization do not explore potential variations in the model or explain sources of error. One notable exception is the study by Yan et al.,¹⁶ which considers both single and multiple marker models and quantifies the impact of shifting input data in time to account for marker-tumor phase offsets. While the literature has suggested that such issues as signal-to-noise ratio (SNR)¹⁸ and variations in the tumor-surrogate relationship^7,19–21 might lead to indirect tumor tracking system errors, to our knowledge no study to date has provided a systematic investigation of factors that may contribute to the accuracy of surrogate-based predictive models of tumor position. This information would make it possible to more accurately localize the tumor in real time.

In this study, we evaluate potential sources of error in tumor position prediction models. The primary purpose of this study was to investigate the impacts of: (1) tumor site, (2) tumor and external surrogate measurement precision, (3) tumor-surrogate correlation, (4) training data selection, (5) model design, (6) inter-patient variations, and (7) inter-fraction variations on the accuracy of external marker-based models of tumor position in the context of three modeling algorithms: ordinary-least-squares (OLS) regression, the Cyberknife Synchrony^™ algorithm, and partial-least-squares (PLS) regression. The secondary goal of this study was to evaluate PLS regression for modeling tumor motion from external surrogates. Preliminary studies¹⁰ have indicated that PLS may be more accurate than computationally simpler multiple-marker linear algorithms such as OLS and Synchrony^™ because of the collinearity in external markers’ motion.²²

II. Methods and Materials

II.A. Position Data

Data consisted of Synchrony^™ (Accuray Inc., Sunnyvale, CA) system log files comprising 113, 10, and 44 treatment fractions from 61, 5, and 22 lung, liver, and pancreas patients, respectively, who underwent stereotactic body radiation therapy at Georgetown University Hospital, Washington, DC. These data were obtained under an Institutional Review Board protocol. The files included 3D positions of: (1) the centroid of a set of 2–3 fiducials implanted in the tumor that were measured via stereoscopic x-rays, henceforth referred to as the tumor position; and (2) three markers affixed to the patient’s form-fitting vest that were tracked optically. The position of the tumor, identified as the centroid of the set of implanted fiducials, was aligned in time with those of the external markers according to the timestamps in the system log files. Each dataset included 40–112 (mean=62) concurrent tumor and marker localizations spaced at a mean interval of 66 sec. The log files also included the continuous real-time output of the Synchrony^™ inferential model.

II.B. Applying and Testing Inferential Models

For each fraction, a series of models were tested. First, a model was fit (Section II.C) to a training dataset of concurrent tumor and external marker positions. This model was used to predict tumor positions from other external marker measurements in the same treatment fraction. Each predicted tumor position, derived from marker measurements alone, was validated against the tumor position measured from stereoscopic x-rays. This process was repeated for training datasets of each set of N consecutive measurements in a treatment fraction, each time testing the model against the tumor localizations that were acquired during that fraction after the training dataset. Prediction error was defined as the magnitude of the vector displacement between the stereoscopic x-ray-measured tumor position and the modeled tumor position.

II.C. Model Design

II.C.1. Input Data Pre-processing

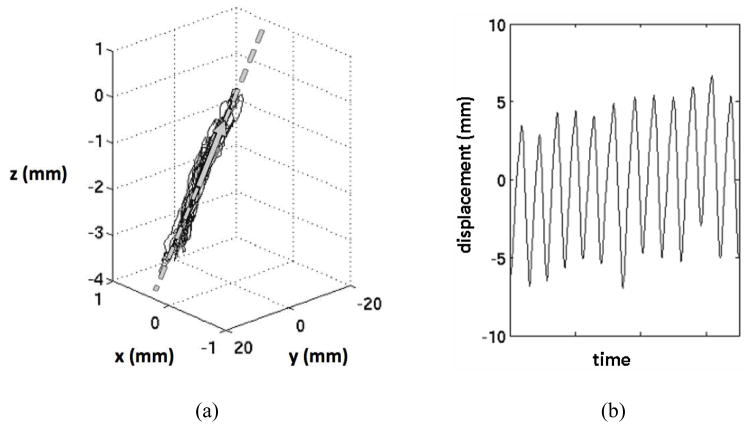
In addition to the raw external marker positions, an alternative input was created by projecting marker displacements onto a single dimension of motion, defined as r_i (Figure 1). The motivation for comparing raw 3D inputs to projected, 1D inputs was to better understand the impact of this data processing technique on the Cyberknife Synchrony^™ algorithm’s performance. As described by Sayeh et al.,²³ the Cyberknife Synchrony^™ system uses r_i as the inputs to its tumor position models.

Figure 1.

Example of (a) 3D surrogate marker motion data (solid) projected onto its first principle component (arrow) line (dashed) to obtain (b) a 1D representation of respiration-induced surrogate marker motion.

To calculate r_i(t) for a marker i, the projection line was determined from the three-column matrix of marker positions acquired during training data collection. The direction of the line was given by the first principal component vector of the marker positions, which is defined as the first eigenvector of the marker data covariance matrix.²⁴ The projection line also was designed to intersect the average 3D marker position, m_i, of the marker data. Each 3D marker position was then projected orthogonally onto the projection line. For each position (x_i(t), y_i(t), z_i(t)), r_i(t) was defined as the distance between the projected position of the sample on the line and m_i.

II.C.2. Model Algorithms

Three model fitting algorithms were considered: OLS regression, PLS regression, and the Synchrony^™ algorithm. OLS and PLS are mutlilinear models that operate according to Ŷ = X · B, where X is matrix of inputs (respiratory surrogate positions) with m measurements and n inputs, B is an n × 3 matrix of regression coefficients, and Ŷ is a matrix of m × 3 outputs (predicted tumor positions).

OLS defines B as the set of regression coefficients that minimizes the expression ||Y − X · B||². The OLS solution is given by B = X ⁺ · Y, where X ⁺ is the Moore-Penrose pseudo-inverse of X. For full-rank, real X, X ⁺ is defined as X ⁺ = (X ^T · X)⁻¹ · X^T. For rank-deficient, real X, X ⁺ = V · Σ⁺ · U^T, where U, Σ, and V are the matrices in the singular value decomposition of X given by X =U · Σ · V. The terms of Σ⁺ are given by ${\mathrm{\sum }}_{i,j}^{+}={({\mathrm{\sum }}_{i,j})}^{-1}$ for Σ_{i, j} ≠ 0 and ${\mathrm{\sum }}_{i,j}^{+}=0$ for Σ_{i, j} =0.

PLS regression finds the regression coefficients that minimize the expression $\frac{1}{2}{B}^T·X^{T}X·B-{(X^{T}Y)}^T·B$.²⁵ To accomplish this task, PLS regression first compresses the input data matrix, X, into an m × A matrix of scores, T = [t₁, t₂, …, t_A], where A is typically less than the number of variables in the raw input data. The scores, t_i, are orthogonal, linear combinations of the columns of X. The optimal number of scores, A, for each dataset was determined through a cross-validation process, in which models based on various numbers of scores were created, each time leaving one sample out of the training data and using it to evaluate the model. In most cases 1–3 scores were utilized in the PLS model. The SIMPLS algorithm²⁶ was applied to determine the PLS regression coefficients. The scores of Y, u_i for i = 1 to A, were linear combinations of the columns of Y that are chosen so as to maximize the covariance between t_i and u_i. The first X score, t₁, was given by t₁ = X · X^T · Y ₀/norm(X · X^T · Y), where Y₀ is mean-centered Y. The first X weight, r₁, and the first X basis, v₁, were both unity. The Y loadings and scores were calculated as $q_i=Y_0^T·t_i$ and u_i = Y₀ · q_i, respectively. The X basis was updated with each iteration as $v_i=v_{i-1}-V_{i-1}·(V_{i-1}^T·{(t^T·X)}^T)$, where V_i−1 = [v₁, v₂, …, v_i−1]. Subsequent X weights and scores were calculated as $r_i=(S_{i-1}-v_i·(v_i^T·S_{i-1}))·q_i$ and t_i =X · r_i. The regression coefficient matrix, B, was given by B =R · Q^T, where R = [r₁, r₂, …, r_A] and Q = [ q₁, q₂, …, q_A].

The inferential model in the Synchrony^™ system was reproduced for this study based on the description by Sayeh et al.²³ so that the training data and timing could be controlled for comparison to OLS and PLS results. The algorithm can be stated briefly as follows. Initially, separate linear, quadratic, or hybrid models were developed for each of the three markers. The linear and quadratic models were defined by Ŷ_i = A_1,ir_i + A_0,i and ${\widehat{Y}}_i=A_{2,i}{r}_i^2+A_{1.i}{r}_i+A_{0,i}$, respectively. For quadratic and hybrid models, separate coefficients were calculated for inhalation and exhalation. The final estimated tumor position was given by the average of the outputs of models using the three markers. The system selects between linear or quadratic models through a modified standard error function that selects for increased accuracy and reduced computational complexity.²³ In the clinical Cyberknife Synchrony^™ system, the operator selects both the number of images used to train the model and the frequency of images acquired during treatment. Our implementation of the Synchrony^™ model, SYNr, based on 15 tumor localizations (the typical training data length in the clinic from which our data originated) was validated against the actual logged 15-sample model output. In the SI, ML and AP directions, respectively, the mean (± standard deviation) distance between SYNr and actual Synchrony^™ outputs were 0.5 ± 1.2 mm, 0.5 ± 1.7 mm, and 0.3 ± 0.5 mm. For this study, only the linear form was considered, because more than 70% of cases in the database did not utilize quadratic models when the modified standard error function was applied.

Both the OLSr and the SYNr algorithms utilize an ordinary linear regression step. The SYNr algorithm differs from OLSr in that SYNr creates separate linear models for each of the 3 markers and averages their outputs to predict the tumor position. In contrast, the OLSr model regresses on one matrix comprising all of the marker data, leading to a different set of regression coefficients.

II.C.3. Summary of Models Evaluated

Five tumor position prediction models were considered: OLSxyz, OLSr, PLSxyz, PLSr, and SYNr. OLSxyz and PLSxyz models utilized the 3D marker data. OLSr, PLSr, and SYNr models utilized the projected marker data.

II.D. Training Data Selection

II.D.1. Quantity of Training Data

Training datasets of N = 6 to N = 35 samples of measured tumor and external surrogate positions were evaluated for their accuracy in inferring tumor positions that occurred subsequent to the training data. Mean and 95^th percentile errors over 20 minutes of data were evaluated.

II.D.2. Time Since Training Data Acquisition

Errors for models in which 6 samples of concurrent external marker and tumor positions comprised the training data were binned by time elapsed since the end of training data.

II.D.3. Tumor-Surrogate Correlation

The impact of uncorrelated external surrogate inputs on tumor position prediction model accuracy was explored in OLSr, PLSr, and SYNr models. For each model type, models with 6 samples of concurrent external marker and tumor positions were created. Then new models were trained on the same training data (6 samples × 3 inputs) plus an additional input vector of Gaussian noise (6 random values × 1 input) for a total of 4 inputs. The accuracy of models with and without the additional noise input were compared.

II.E. Inter-Patient and Inter-Fraction Variations

Each patient underwent 1–5 treatment fractions. The mean tumor-surrogate model prediction error for each treatment fraction was determined. Using the 46 patients for whom more than one treatment fraction of data was available, the Kruskal-Wallis one-way analysis of variance test was applied to determine whether the mean error of a fraction was significantly associated with either patient index or fraction index.

II.F. Measurement Precision

Tumor-surrogate models created from the training data were compared to models with simulated noise in either input (external marker) or output (tumor) measurements. In each case, models based on 6 training samples were evaluated on the testing dataset.

To simulate radiographic tumor localization uncertainties, noise from a Gaussian distribution was added to the radiographic tumor localizations. Noise levels were varied by randomly selecting the standard deviation of the Gaussian noise in each trial. Another set of models was then created from training data with noise and used to determine new predicted tumor positions in the testing dataset. This process was repeated for noise added to external marker localizations.

III. Results

III.A. Model Design

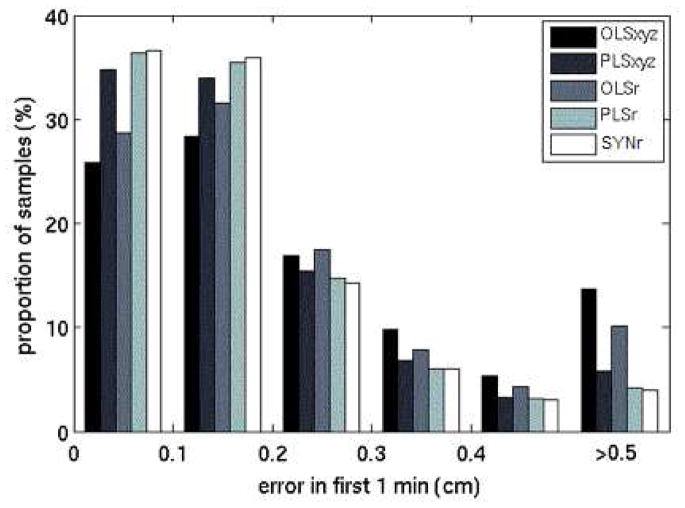
For OLSxyz, PLSxyz, OLSr, PLSr, and SYNr models trained on 6 samples, 22.8%, 12.7%, 19.0%, 9.1%, and 9.5% of the predictions, respectively, exceeded 0.5 cm (Figure 2). The OLSxyz, PLSxyz, and OLSr distributions peaked in the 0.1 cm to 0.2 cm range, and the PLSxyz, PLSr, and SYNr distributions peaked in the 0–0.1 cm range. PLSr and SYNr results did not differ significantly for any quantity of training points.

Figure 2.

Histogram of radial errors from the first minute of testing samples for models based on 6 training samples. The last bin comprises all errors greater than 0.5 cm.

III.B. Training Data Selection

III.B.1. Quantity of Training Data

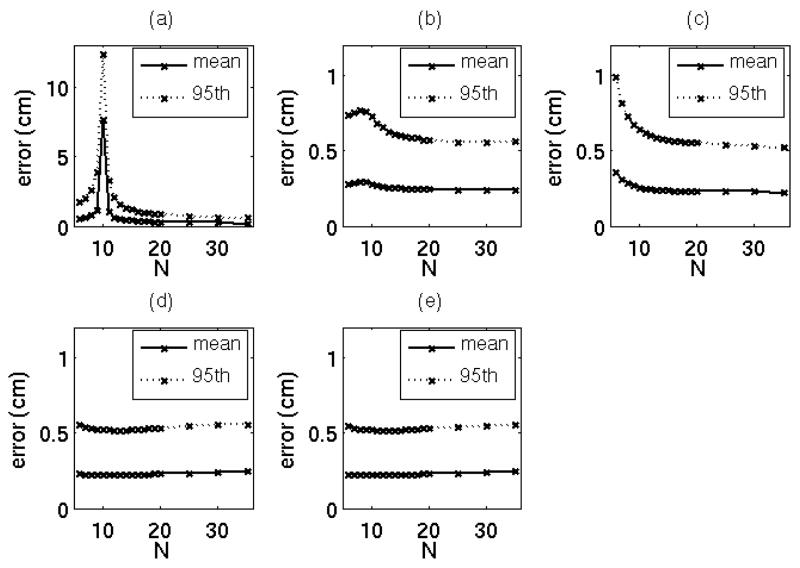
The 95^th percentile and mean tumor position prediction errors for each number of training samples are shown in Figure 3. The OLSxyz error peaked to an average of 7.7 cm at N = 10. OLSxyz, and OLSr 95^th percentile errors exceeded 1 cm for some values of N, but PLSxyz, PLSr, and SYNr 95^th percentile errors did not exceed 1 cm in the tested range of N. Mean errors for the six models converged to approximately 0.2 cm for N > 20.

Figure 3.

Mean and 95^th percentile tumor position model prediction errors in the test data acquired over 20 minutes for (a) OLSxyz, (b) PLSxyz, (c) OLSr, (d) PLSr, and (e) SYNr models. For clarity, the y-axis in (a) is scaled differently than that of (b–e).

III.B.2. Time Since Training Data Acquisition

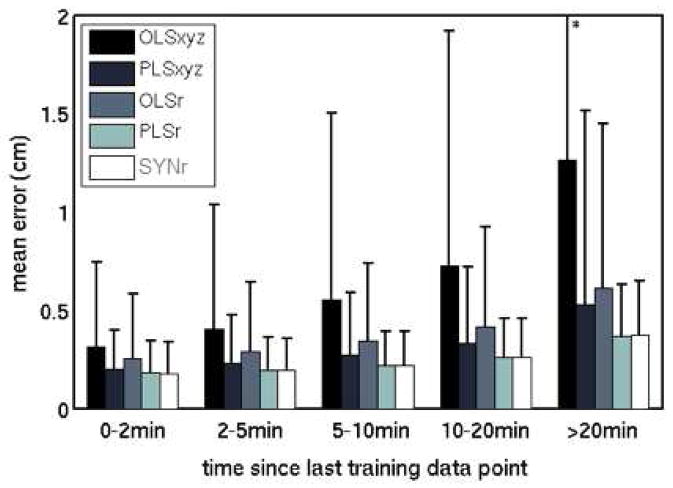
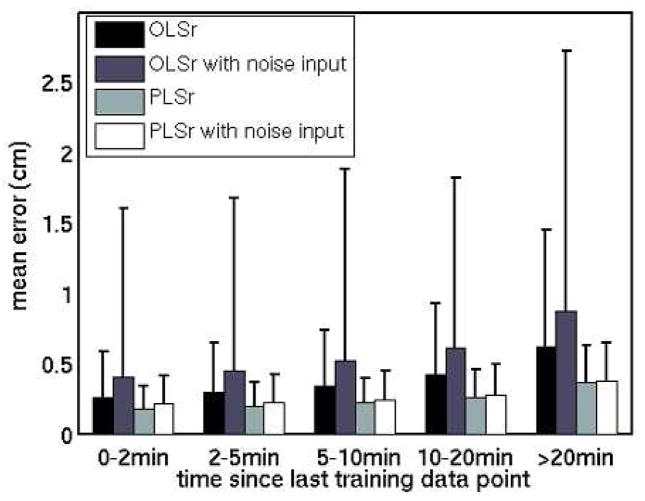
Average errors for each model type increased as time elapsed after the end of the training data (Figure 4). Mean errors in 0–2 min and in 10–20 min of data increased from 0.3 to 1.3 cm for OLSxyz, 0.2 to 0.5 cm for PLSxyz, 0.2 to 0.6 cm for OLSr, 0.2 to 0.4 cm for PLSr, and 0.2 cm to 0.4 cm for SYNr.

Figure 4.

Mean and standard deviation (error bars) of tumor position model prediction errors, binned by time elapsed since the end of training data collection.

* The standard deviation of the OLSxyz error bar in the >20 min bin is 2.3 cm.

III.C. Tumor-Surrogate Correlation

The uncorrelated (Gaussian noise) input degraded prediction models (Figure 5). Mean errors in the 0–2 min bin increased by 57% for OLSr and by 16% for PLSr.

Figure 5.

The impact of an uncorrelated (Gaussian noise) input variable in OLSr and PLSr models. Mean and standard deviation of model errors indicate that the additional input increased errors. In the 0–2 min bin, OLSr errors increased by 57%, and PLSr errors increased by 16%.

III.D. Tumor Site

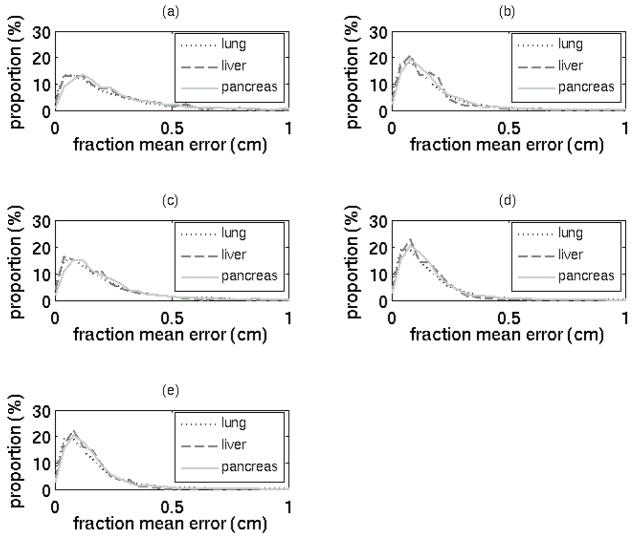
For each modeling algorithm, error distributions were comparable across the three tumor sites (Figure 6). Lung, liver, and pancreas mean errors were 2.2 mm, 1.9 mm, and 2.3 mm, respectively, and further details are described in Table I. Of the three sites, only the pancreas errors differed significantly (Kruskal-Wallis one-way ANOVA, p < 0.05) from errors of the other sites. However, it can be argued that the 0.1 mm mean error difference between lung and pancreas cases is not clinically significant. It is not clear whether liver results would differ significantly from lung results with a larger sample size.

Figure 6.

Histograms of mean error in each fraction by tumor site for (a) OLSxyz, (b) PLSxyz, (c) OLSr, (d) PLSr, and (e) SYNr models, each based on 6 training data points.

Table I.

Errors for models based on 6 training points, stratified by tumor site

	Mean ± standard deviation of error (mm)
Model	Lung	Liver	Pancreas
OLSxyz	3.0 ± 4.5	2.7 ± 2.7	3.3 ± 4.6
PLSxyz	1.9 ± 2.0	1.7 ± 1.3	2.0 ± 2.0
OLSr	2.5 ± 3.4	2.1 ± 2.6	2.6 ± 2.8
PLSr	1.8 ± 1.6	1.6 ± 1.1	1.8 ± 1.5
Synchrony	1.7 ± 1.6	1.6 ± 1.0	1.8 ± 1.5
Pooled results	2.2 ± 2.9	1.9 ± 1.9	2.3 ± 2.8

III.E. Inter-Patient and Inter-Fraction Variations

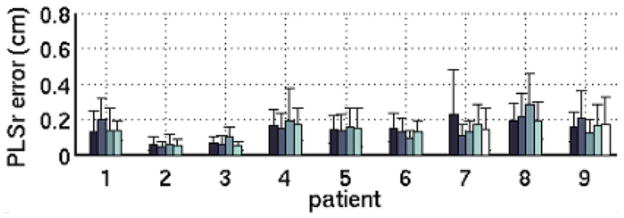
For each of the model types, the model error in a single fraction was significantly (p < 0.05) associated with the patient from whom the fraction was recorded. This pattern is evident in Figure 7, in which the mean errors of the four fractions of patient 2, for instance, cluster around a value that differs from the value associated with patient 8. The mean model error over a fraction was not significantly (p > 0.05) associated with the treatment fraction index.

Figure 7.

Mean and standard deviation of 9-training-datapoint PLSr in each fraction for 9 patients. Errors represent samples acquired within 20 minutes of the training dataset. For clarity, the figure is limited to the 9 patients with >3 treatment fractions available for analysis; the results for these patients are consistent with the dataset as a whole.

III.F. Measurement Precision

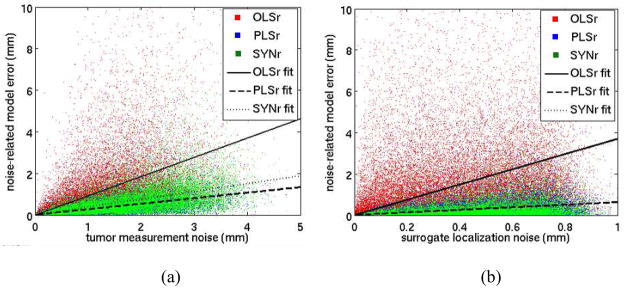
When noise was added to measurements of radiographic tumor positions in the training dataset (Figure 8), the resulting average error in the testing dataset varied as 1.1, 0.3, and 0.4 times the average noise for OLSr, PLSr, and SYNr, respectively; noise-to-error correlations ranged from 0.44 to 0.53. When noise was added to the measurement of the external surrogate position data, the resulting average error in the testing dataset varied as 3.7, 0.6, and 0.6 times the average noise for OLSr, PLSr, and SYNr, respectively, and noise-to-error correlations ranged from 0.09 to 0.32.

Figure 8.

(a) Tumor and (b) external marker localization noise (in the training data used to build the model that predict tumor position) versus tumor position prediction error. Best fit lines represent least-squared-error linear regression fits with an assumption of zero error for zero noise. OLSr regression lines have slopes of (a) 1.1 and (b) 3.7. The PLSr line overlies the SYNr line in (b).

IV. Discussion

In this study, a series of factors impacting the accuracy of respiratory surrogate models of tumor motion were explored. Model accuracy was affected by inter-patient variations, tumor and external surrogate measurement precision, tumor-surrogate correlation, training data selection, tumor-surrogate correlation, and model design. Tumor site and fraction index were not predictive of model accuracy. These results provide the reader with a framework for designing and evaluating a surrogate-based tumor position prediction model. In addition, PLS models were more accurate than OLS models and were as accurate as Synchrony^™ models.

Many studies reporting high tumor-surrogate correlations have evaluated only a few minutes of data.^21,27 The results of these studies may not be representative of the behavior of the model over entire treatment fractions. Analyses of datasets capturing motion over the duration of a treatment fraction have reported variations in the tumor-surrogate relationship.^7–8,19 In this study, model errors increased over time; we attribute this increasing error to tumor-surrogate relationship changes. In practice, this effect could be overcome by updating the model during the treatment fraction. Intra-fraction model updates have been utilized by tracking systems like Cyberknife Synchrony^™, but model updates are not common in gated treatment protocols.

In this work, projecting external marker motion onto a single dimension improved accuracy by increasing the correlation between surrogate signals and tumor motion. Shifting the surrogate signal in time relative to the tumor signal is a common method for increasing tumor-surrogate correlation.^{16,19,28–29} However, because of changes in the tumor-surrogate phase offset, these shifted surrogates are not likely to maintain their improved correlation over time.^7,19

PLSr and SYNr results did not differ significantly. We investigated other model designs (not described in detail here) but were unable to reduce model errors below those of the PLSr model. Because the continuous external marker motion in the data log files appears to indicate a high signal-noise ratio (SNR), we hypothesize that the accuracy of any model based on this dataset is limited by precision of the gold-standard radiographic tumor localizations. PLSr and SYNr represent the state-of-the-art in indirect tumor localization algorithms. In addition to their accuracy, each requires only milliseconds to derive tumor position from surrogate data. Subject to the limitations of SNR and the other factors investigated in this study, both PLSr and SYNr are candidates for real-time applications.

Decreased measurement precision in either gold-standard tumor localizations or external surrogate measurements was found to have considerable impact on model accuracy. For OLSr models, the errors in tumor position prediction induced by measurement precision limitations were 1–4 times as large as the measurement errors themselves. For PLSr and Synchrony^™ models, the errors in tumor position prediction were 0.3–0.6 times as large as the measurement errors. Many optical (surrogate) tracking systems are capable of achieving sub-millimeter accuracy,^30–31 but infrared tracking accuracies exceeding one millimeter have been reported in clinically available devices.³² Typical errors of x-ray-based localizations of bony anatomy or fiducial tracking are 0.6–2 mm.³²

Surprisingly, utilizing a larger quantity of training data, whether in dimensionality of marker motion or in number of training data points, did not improve the accuracy of tumor position predictions. In the case of OLS models, the error peaked at the transition between underdetermined and overdetermined systems. For any modeling algorithm, the optimal number of training points will also vary as a function of spacing between training samples. Training data captured over a period of minutes may encompass tumor-surrogate relationship changes that would not be present in training data captured in a shorter period of time.

PLS was consistently more accurate than OLS, a conclusion in agreement with the diaphragm tracking work of Qiu et al.¹⁰ OLS regression coefficients are volatile when inputs are collinear, tending to change considerably for different training samples from the same dataset.²² As a result, PLS has been described a superior alternative to OLS when the inputs are highly collinear.³³

Yan et al. has shown that multiple-surrogate models of tumor motion can be more accurate than single-marker models¹⁶ by overcoming the location effect, in which tumor-surrogate correlation varies with marker placement.¹⁵ Nevertheless, our results support the conclusion that incorporating additional surrogate-based inputs that are uncorrelated with tumor motion may actually degrade the model. Fortunately, respiration-induced tumor motion is correlated with such respiratory surrogates as markers affixed to the torso, spirometry, and bellows systems.^7,16,34

Finally, patient-specific, fraction-specific, and site-specific results were evaluated. Results did not differ between lung, liver, and pancreas cancers. Furthermore, the model error was not found to be significantly associated with fraction index. Patient index, on the other hand, was significantly associated with model accuracy. The practical implication of these results is that the design of a study to evaluate tumor motion models should use a large enough group of patients to obtain statistically significant results; multi-site and inter-fraction data are less important unless a model will be applied without revision on multiple treatment days.

V. Conclusions

The accuracy of tumor position prediction models using external surrogates was affected by inter-patient variations, measurement precision, tumor-surrogate correlation, training data selection, and model design, but tumor site and fraction index were not predictive of model accuracy. PLS regression models were more accurate OLS models and as accurate as Synchrony^™ models.