The longer-term effects of human capital enrichment programs on poverty and inequality: Oportunidades in Mexico

Abstract

Previous empirical research has shown that Mexico’s Oportunidades program has succeeded in increasing schooling and improving health of disadvantaged children. This paper studies the program’s potential longer-term consequences for the poverty and inequality of these children. It adapts methods developed in DiNardo, Fortin and Lemieux (1996) and incorporates existing experimental estimates of the program’s effects on human capital to analyze how Oportunidades will affect future earnings of program participants. We nonparametrically simulate earnings distributions, with and without the program, and predict that Oportunidades will increase future mean earnings but have only modest effects on poverty rates and earnings inequality.

1. Introduction

In recent years, governments in many Latin American countries have adopted conditional cash transfer (CCT) programs as a primary strategy for alleviating poverty and stimulating investment in human capital. These programs typically provide cash grants to poor families if they send their age-eligible children to school and subsidies for regularly visiting health clinics. Mexico and Brazil first adopted CCT programs in the 1990’s. Since then, programs with similar incentives have been introduced in Argentina, Chile, Colombia, Costa Rica, El Salvador, Ecuador, Honduras, Nicaragua, Peru and Uruguay¹.

The Mexican Oportunidades program (formerly called PROGRESA) was rigorously evaluated using both experimental and non-experimental evaluation designs. In the first two years (1998–1999) of its implementation in rural areas, the program was evaluated using a place-based social experiment that randomized 506 villages in or out of the program. The experimental results demonstrated statistically significant program impacts on increasing schooling enrollment and attainment, reducing child labor, improving health and nutrition outcomes and reducing poverty². Partly on the basis of these observed positive program impacts, the Mexican government expanded the program into urban areas in 2002. By 2005, the program covered five million families and had an annual budget of U.S. $2.1 billion. A non-experimental evaluation carried out in urban areas found statistically significant program impacts similar in magnitude to those found in rural areas.

As noted, previous evaluation studies of the Oportunidades program documented the program’s short-term impacts. This paper takes as a point of departure the observed impacts on education and nutrition and estimates the effects of these changes on the future earnings distributions of the children currently participating in the program. The question we consider is how the program’s impacts on human capital, as measured by years of schooling attained and increases in height (interpreted as an indicator of long-term nutritional status), will affect future earnings inequality and poverty of the younger generation. In the last decade, Mexico has ranked among the countries in Latin America with the highest income inequality. A study by Lopez-Acevedo (2004) finds that educational inequality accounts for the largest share of Mexico’s earnings inequality, suggesting that human capital enrichment programs could be an effective instrument for reducing inequality. Freije, Bando and Arce (2006) show that Oportunidades has significantly decreased the poverty rate among the current generation of recipients, but little is known about the longer-term effects of the program on poverty.

Our approach to simulating program impacts on earnings distributions adapts for use in program evaluation a nonparametric decomposition method originally developed in DiNardo, Fortin and Lemieux (1996) and extends this method to allow for probability mass at zero in earnings distributions. Existing micro-simulation approaches for predicting effects of conditional cash transfer programs have focused on the short-term and are mainly based on parametric modeling frameworks³. The parametric models can be quite rich, but they typically impose strong functional form assumptions. The goal in microsimulation studies is usually to forecast the effects of programs prior to their implementation, whereas our aim is to understand how program impacts that have already been estimated will affect future earnings and poverty. Our approach is fully nonparametric and does not impose any functional form assumptions on the earnings-height-education-work experience relationship, other than continuity and differentiability. We find evidence of nonlinearities in the estimated relationship that shows the benefits of flexibility with regard to model specification. We use the nonparametric simulation method to compare the earnings and employment distributions with and without the program and to compare our inferences to those that would be obtained using more standard parametric approaches.

The key implications from the analysis are that the program’s impacts on education and height will increase mean future earnings of beneficiaries but will likely have little impact on earnings inequality. The modest overall observed impacts on inequality are attributable to two main factors. First, the program targets children from poor family backgrounds, and family background is an imperfect predictor of future earnings. Children from poor backgrounds ultimately get distributed throughout the adult earnings distribution due to substantial intergenerational mobility. Second, we find important nonlinearities in the relationship between earnings, education and height, the most notable being that the returns to education are greater for post-primary years of education. Such nonlinearities imply that people who would obtain higher levels of schooling in the absence of the program tend to benefit more from the intervention, which contributes to widening rather than lessening inequality.

Our empirical analysis is based on the first wave of the Mexican Family Life Survey (MxFLS-1) which was collected in 2002. The survey collected data for all members of 8,440 households and includes information about labor force participation, income for both primary and secondary jobs (including self-employment), education, and health. It also contains measures of family background, that we use to simulate program targeting. Our final analyses use a subsample of 5,171 individuals age 25 to 40.

This paper proceeds as follows. Section two describes the nonparametric simulation method and how we adapt and use it to study how Oportunidades affects employment and the overall earnings distribution. Section three describes the Mexican Family Life Survey and our analysis samples. The empirical results are presented in section four. Section five concludes.

2. Methodology for Simulating Program Effects on Population Earnings Distributions

The simulation method that we use to study program effects on earnings and employment outcomes is adapted from a wage decomposition method originally proposed in DiNardo et al. (1996). Their study uses the method to investigate the effects of institutional and labor market factors on changes in the U.S. wage distribution over time. Their approach writes the overall wage density at time t, f_w = (w | t) in terms of the conditional wage densities, where conditioning is on a set of labor market or institutional factors, z, whose effects on earnings they analyze:

$$f_w(w\mid t)={\int }_z{f}_w(w\mid z,t)f_z(z\mid t)dz.$$

In their study, z includes variables indicating union status, industrial sector, and whether the wage falls above or below the minimum wage. Counterfactual wage densities are constructed by replacing f_z(z | t) by a different hypothetical conditional density, g_z(z | t).

We apply the DiNardo et al. (1996) method to simulate earnings densities with and without a program intervention, where the program intervention changes the distribution of z. We extend the method to account for simultaneous analysis of both employment and earnings by permitting the earnings distribution to have a mass point at zero due to nonparticipation. In this section, we first describe the simulation approach in general terms, and then how it applies to evaluating the effects of the Oportunidades program.

2.1. Basic method

Denote some outcome of interest (earnings) by y and define its density in terms of its conditional density (conditional on some observed characteristics x):

$$f(y)={\int }_{x}f(y,x)dx={\int }_{x}f(y\mid x)f(x)dx.$$

Suppose that the program intervention changes the distribution of x from f(x) to f̃(x) but that the distribution of y conditional on x stays the same (f̃(y | x) = f(y | x)). The new unconditional distribution of y would be given by:

$$\stackrel{\sim }{f}(y)={\int }_{x}f(y\mid x)\stackrel{\sim }{f}(x)dx.$$

We wish to simulate the effect of the program intervention on the outcome y as it operates through changing x. For example, suppose that the variable x represents years of schooling attained and height and that the program intervention increases schooling attainment and height by some amount, i.e. x̃ = x + Δ_x. Suppose also that we have a sample of size n drawn from the unconditional density, f(x). If we know Δ_x we can generate for each individual x̃_i = x_i + Δ_xi. We can simulate the post-program earnings density f̃(y) at a point y₀ by the average:

$$\begin{array}{l}\widehat{\stackrel{\sim }{f}}(y_0)=\frac{1}{n}\sum _{x_i\in X}\widehat{f}(y_0\mid {\stackrel{\sim }{x}}_i=x_i+{\mathrm{\Delta }}_{x_i})\\ =\frac{1}{n}\sum _{{\stackrel{\sim }{x}}_i\in \stackrel{\sim }{X}}\frac{\widehat{f}(y_0,{\stackrel{\sim }{x}}_i)}{\widehat{f}({\stackrel{\sim }{x}}_i)},\end{array}$$

where f̂(y, x_i ) and f̂(x_i) are nonparametric estimators of the unconditional densities computed from the original (pre-program) sample:

$$\begin{array}{l}\widehat{f}(y_0,x_i)=\frac{1}{{\alpha }_y{\alpha }_{x}n}\sum _{j=1}^{n}K\left(\frac{y_j-y_0}{{\alpha }_y}\right)K\left(\frac{x_j-x_i}{{\alpha }_x}\right)\widehat{f}(x_i)\\ =\frac{1}{{\alpha }_{x}n}\sum _{j=1}^{n}K\left(\frac{x_j-x_i}{{\alpha }_x}\right).\end{array}$$

α_y and α_x are bandwidths that are assumed to satisfy the usual requirements for consistent kernel density estimation⁴.

The MxFLS data are a stratified sample, so sampling weights are required to reweight the sample back to population proportions. Incorporating sampling weights into the simulation method is straightforward. Assume each observation has a sampling weight, ω_i, and that the weights are scaled so that Σ ω_i = n. The weights can be incorporated into the estimation of f̃(y) as follows:

$$\widehat{\stackrel{\sim }{f}}(y)=\frac{1}{n}\sum _{{\stackrel{\sim }{x}}_i\in \stackrel{\sim }{x}}{\omega }_i\frac{\widehat{f}(y,{\stackrel{\sim }{x}}_i)}{\widehat{f}({\stackrel{\sim }{x}}_i)},$$

and also into the estimation of the unconditional kernel densities:

$$\begin{array}{l}\widehat{f}(y_0,x_i)=\frac{1}{{\alpha }_y{\alpha }_{x}n}\sum _{j=1}^n{\omega }_{j}K\left(\frac{y_j-y_0}{{\alpha }_y}\right)K\left(\frac{x_j-x_i}{{\alpha }_x}\right)\\ \widehat{f}(x_i)=\frac{1}{{\alpha }_{x}n}\sum _{j=1}^n{\omega }_{j}K\left(\frac{x_j-x_i}{{\alpha }_x}\right).\end{array}$$

For expositional clarity, we suppress the weights in the remainder of the discussion, although we incorporate them in the estimation.

2.2. Accounting for probability mass at zero

Kernel density estimation can approximate well the distributions of continuous random variables, but in our data many people (especially women) report zero earnings. The program intervention could increase earnings among workers as well as change the probability of having positive earnings. We accommodate the mass point at zero in the earnings distribution by estimating the density of earnings as a mixture, where with some probability individuals earn zero and with the remaining probability they earn income drawn from the density of income conditional on its being positive, f_y>0(y). Both the probability of having positive earnings and the magnitude of earnings are potentially affected by the program.

Let ỹ be the random variable representing the distribution of income implied by the counterfactual distribution of x̃. Again, we assume the distribution of y conditional on x stays constant; in other words that the density of earnings conditional on schooling attainment and height is the same whether or not the program is in place. This implies that

$$\begin{array}{c}Pr(\stackrel{\sim }{y}=0\mid x)=Pr(y=0\mid x)\\ {\widehat{f}}_{\stackrel{\sim }{y}>0}(y\mid x)=f_{y>0}(y\mid x)\end{array}$$

The stability assumption implicitly rules out general equilibrium effects, because it assumes that increases in the population in schooling attainment or height do not affect the earnings premium for those characteristics.

We can obtain the probability of zero earnings, Pr(ỹ = 0), with the program intervention (under the counterfactual f̃(x) ) using the following:

$$\begin{array}{c}Pr(\stackrel{\sim }{y}=0)={\int }_{x}Pr(y=0\mid \stackrel{\sim }{x})\stackrel{\sim }{f}(x)dx,\\ \approx \frac{1}{n}\sum _{{\stackrel{\sim }{x}}_i\in X}\widehat{Pr}(y=0\mid {\stackrel{\sim }{x}}_i=x_i+{\mathrm{\Delta }}_x),\end{array}$$

where X is the support of x_i and where

$$\widehat{Pr}(y=0\mid x_i)=\frac{{\displaystyle \sum _{x_j\in X}}1(y_j=0)K\left(\frac{x_j-{\stackrel{\sim }{x}}_i}{{\alpha }_x}\right)}{{\displaystyle \sum _{x_j\in X}}K\left(\frac{x_j-{\stackrel{\sim }{x}}_i}{{\alpha }_x}\right)}.$$

In the last equation, 1(y_i = 0) is an indicator that denotes whether the individual has zero earnings.

Let f̃_ỹ>0(y) be the density of income conditional on its being positive. The counterfactual distribution of y conditional on y being positive is given by:

$$\begin{array}{l}{\stackrel{\sim }{f}}_{\stackrel{\sim }{y}>0}(y)={\int }_x{f}_{y>0}(y\mid x)\stackrel{\sim }{f}(x\mid \stackrel{\sim }{y}>0)\\ ={\int }_x{f}_{y>0}(y\mid x)\frac{Pr(y>0\mid x)}{Pr(\stackrel{\sim }{y}>0)}\stackrel{\sim }{f}(x).\end{array}$$

We estimate the conditional density by:

$$\begin{array}{l}{\widehat{\stackrel{\sim }{f}}}_{\stackrel{\sim }{y}>0}(y)=\frac{1}{n}\sum _{{\stackrel{\sim }{x}}_i\in X}{\widehat{f}}_{y>0}(y\mid {\stackrel{\sim }{x}}_i)\frac{\widehat{Pr}(y>0\mid {\stackrel{\sim }{x}}_i=x_i+{\mathrm{\Delta }}_x)}{\widehat{Pr}(y>0)}\\ =\frac{1}{n}\sum _{{\stackrel{\sim }{x}}_i\in X}\frac{{\widehat{f}}_{y>0}(y,{\stackrel{\sim }{x}}_i)}{{\widehat{f}}_{y>0}({\stackrel{\sim }{x}}_i)}\frac{\widehat{Pr}(y>0\mid x_i)}{\widehat{Pr}(\stackrel{\sim }{y}>0)}.\end{array}$$

We estimate the conditional densities at a point (y₀, x₀) using the standard kernel density estimator applied to the subset of data for which income is positive:

$$\begin{array}{l}{\widehat{f}}_{y>0}(y_0,x_0)=\frac{1}{{\alpha }_y{\alpha }_x{\displaystyle \sum _i}1(y_i>0)}\sum _{i=1}^{n}1(y_i>0)K\left(\frac{y_i-y_0}{{\alpha }_y}\right)K\left(\frac{x_i-x_0}{{\alpha }_x}\right)\\ {\widehat{f}}_{y>0}(x_0)=\frac{1}{{\alpha }_x{\displaystyle \sum _i}1(y_i>0)}\sum _{i=1}^{n}1(y_i>0)K\left(\frac{x_i-x_0}{{\alpha }_x}\right).\end{array}$$

We now have all the ingredients to simulate the post-intervention earnings distribution. Earnings is 0 with probability Pr (ỹ = 0) and is drawn from ${\widehat{\stackrel{\sim }{f}}}_{\stackrel{\sim }{y}>0}(y)$ with Pr(ỹ > 0).

2.3. Measures of poverty and inequality

After simulating the distribution of earnings with and without actual and hypothetical program impacts, it is possible to examine the effect of that the program intervention has on poverty and inequality using standard measures considered in the poverty measurement literature. Below, we briefly summarize the measures that we use in the empirical analysis as functions of the estimated densities, taking into account that densities may have probability mass at zero. For a recent discussion of the relative merits of alternative poverty and inequality measures, see Foster and Szekely (2007).

Headcount Ratio

The headcount ratio is the fraction of the population below a predefined poverty line. Denote the value of the poverty line by L.

$$\text{HCR}=Pr(y=0)+(1-Pr(y=0))F_{\mid y>0}(L)$$

Average Poverty Gap Ratio

The average poverty gap ratio is the mean shortfall between an individual’s income and the poverty line (with those above the poverty line having no shortfall) expressed as a fraction of the poverty line:

$$\text{APGR}=Pr(y=0)+(1-Pr(y=0)){\int }_0^L\frac{L-y}{L}{f}_{\mid y>0}(y)dy$$

Foster-Greer-Thorbecke (1984) Index

The Foster-Greer-Thorbecke (1984) index is a weighted version of the average poverty gap ratio that gives more weight to poorer individuals:

$$\text{FGT}=Pr(y=0)+(1-Pr(y=0)){\int }_0^L{\left(\frac{L-y}{L}\right)}^2{f}_{\mid y>0}(y)dy$$

Coefficient of variation

The coefficient of variation is a common measure of dispersion of a distribution, defined as

$$\text{coef}\text{of}\text{variation}=\frac{\sqrt{\text{Var}[y]}}{\text{E}[y]}$$

where

$$\begin{array}{l}\text{E}[y]=Pr(y=0)·0+(1-Pr(y=0)){\int }_0^{\infty }{yf}_{\mid y>0}(y)dy\\ =(1-Pr(y=0)){\int }_0^{\infty }{yf}_{\mid y>0}(y)dy\end{array}$$

$$\text{Var}[y]=Pr(y=0)\text{E}{[y]}^2+(1-Pr(y=0)){\int }_0^{\infty }{(y-\text{E}[y])}^2{f}_{\mid y>0}(y)dy$$

Inter-quantile ranges

Another common measure of the dispersion of a distribution is the interquartile range. The differences between quantiles of y can be computed directly from the empirical cdf:

$$\begin{array}{l}F(y)=Pr(y=0)\text{if}y=0\\ =Pr(y=0)+(1-Pr(y=0))F_{\mid y>0}(y)\text{if}y>0\end{array}$$

Gini Coefficient

The Gini coefficient is widely used as a measure of inequality of a distribution of income. Its values range between 0 and 1, with 0 corresponding to perfect equality and 1 corresponding to perfect inequality (one person has all the income).

$$G=1-\frac{1}{E[y]}{\int }_0^{\infty }{(1-F(y))}^{2}dy$$

Theil Entropy Coefficient

The Theil entropy coefficient can be computed from a set of observations by:

$$T=\frac{1}{n}\sum _{i=1}^n\frac{y_i}{\overline{y}}ln\frac{y_i}{\overline{y}}$$

If everyone has the same (i.e., mean) income, then the index equals 0. If one person has all the income, then the index equals ln n.

Taking the limit as n → ∞, we get the following formula in terms of the density, conditional on y > 0:

$$T_{\mid y>0}={\int }_0^{\infty }\frac{y}{E[y]}log\frac{y}{E[y]}{f}_{\mid y>0}(y)dy$$

Generalizing this measure to the case where there can be probability mass at 0 gives the following:

$$T=(1-Pr(y=0)){\int }_0^{\infty }\frac{y}{E[y]}log\frac{y}{E[y]}{f}_{\mid y>0}(y)dy$$

Below, we report how the program affects each of these alternative measures of poverty.

2.4. Applying the simulation method to evaluation of Oportunidades

We next describe how the nonparametric simulation method is applied in the context of evaluating Oportunidades. y represents labor earnings, and is modeled as a function of three covariates: e denotes years of schooling attainment, h denotes height in centimeters (a measure of long-term nutritional status), and x denotes years of potential labor market experience⁵. The conditional density of labor market earnings is

$$f(y\mid e,h,x)$$

The overall income distribution integrates over the observed schooling attainment, height and experience distribution in the population:

$$f(y)={\int }_{(e,h,x)\in A}f(y\mid e,h,x){dF}_{e,h,x}(e,h,x).$$

The Oportunidades program is known to impact schooling attainment levels (e) and height (h) and we want to assess how these impacts translate into changes in the earnings distribution. If participation in the program was universal, we could nonparametrically simulate the effect of the program on the income distribution simply by augmenting schooling attainment and height values by the expected program impacts. Let Δ_e denote the expected impact on schooling attainment and Δ_h the impact on height.

$$\stackrel{\sim }{f}(y)={\int }_{(e,h,x)\in A}f(y\mid e,h,x){dF}_{e,h,x}(e+{\mathrm{\Delta }}_e,h+{\mathrm{\Delta }}_h,x\mid (e,h,x)\in S).$$

Because nonparametric estimation methods do not extrapolate beyond the observed support (A), this simulation can only be performed for the subset of people for whom (e + Δ_e, h + Δ_h, x) ∈ A, which we denote by S.

The above equation assumes that everyone experiences a program effect of the magnitude (Δ_e, Δ_h), but Oportunidades was targeted to a subset of the population based on poverty-related criteria that are discussed in detail below. Let D = 1 for the subset of individuals targeted by the program and D = 0 for those not targeted. The overall income distribution that results, g(y), reflects that of the combined targeted and nontargeted subgroups:

$$g(y)=Pr(D=0)f(y\mid D=0)+Pr(D=1)\stackrel{\sim }{f}(y\mid D=1)$$

Suppose the nontargeted subgroup experiences no effect of the program⁶. The larger the subgroup targeted by the program (Pr(D = 1)), the larger will be the potential effect on the overall earnings distribution.

Using this methodology, we can explore the relative contribution of impacts on schooling attainment and height in changing the overall income distribution, by considering the case where (i) we set Δ_e = 0 and the only effect is through Δ_h, and (ii) where Δ_h = 0 and the only effect comes through Δ_e. Implementing the simulation estimator of the previous section requires nonparametrically estimating the conditional density f(y | e,h, x) and the unconditional density f_{e, h,x}(e, h, x). We estimate the latter using a three dimensional kernel density estimator:

$$f_{e,h,x}(e_0,h_0,x_0)=\frac{1}{{na}_e{a}_h{a}_x}\sum _{i=1}^{n}K\left(\frac{e_i-e_0}{a_e}\right)K\left(\frac{h_i-h_0}{a_h}\right)K\left(\frac{x_i-x_0}{a_x}\right),$$

where a_e, a_h and a_x are the bandwidth choices. In our analysis below, we use a Gaussian kernel and apply Silverman’s rule for univariate distributions to each dimension of the data (Silverman, 1986). We also experimented with other bandwidth choices and found our main results were quite robust. To estimate the conditional density f(y | e,h, x), observe that the conditional density can be expressed as the ratio of two joint unconditional densities:

$$f(y\mid e,h,x)=\frac{f(y,e,h,x)}{f(e,h,x)},$$

each of which can be nonparametrically estimated by standard kernel density estimators.

The convergence rate of pointwise nonparametric density estimators slows down as the dimensionality increases, a problem known as the curse of dimensionality. However, the proposed estimators average over the nonparametric estimates and therefore converge at a faster rate.

3. Description of the Analysis Subsamples

We analyze data from the Mexican Family Life Survey (MxFLS-1), which conducted interviews with 8,440 households in 150 communities in 2002. Every household member age 15 or older was interviewed, yielding about 38,000 individual interviews. 16 of Mexico’s 32 states/districts are represented (roughly 70% of the population resides in these states). Weights are provided to make the sample nationally representative. The survey includes comprehensive information on employment and income for both primary and secondary jobs in the formal and informal sectors. The survey also includes information on household structure, education, and health. The key variables used in simulating counterfactual outcomes are income, employment, education level, height and labor market experience. Appendix A describes in more detail how we construct each of these variables from the data.

Table 1 presents descriptive statistics for our two main analysis samples: Adult men and women age 25 to 40. About 10% of men and 64% of women report zero labor income. Mean monthly earnings for males are 3,945 pesos and for women 1,140 pesos, where the means include zeros for nonworkers⁷. The average education level for men is 8.8 years, which is about one year higher than the average for women of 7.7 years. Men are on average 166 centimeters tall, and women are on average 153 centimeters tall. The Gini coefficient for earnings of men is 0.483 and for earnings of women is 0.819. The higher coefficient for women reflects the fact that a large fraction of women in Mexico do not work, so the earnings distribution for women is more unequal than that for men⁸.

TABLE 1.

DESCRIPTIVE STATISTICS

Men and Women, age 25–40

	Men	Women
Proportion with zero earnings	0.099	0.638
Mean monthly earnings (1000’s pesos)	3.945 (0.187)	1.140 (0.127)
Median earnings	3.000	0.000
Interquartile range of earnings	3.300	3.600
Coefficient of Variation	1.123	2.276
Gini Coefficient	0.483	0.819
Theil Index	0.443	1.459
Headcount Ratio (FGT, α = 0)*	0.227	0.763
Average Poverty Gap Ratio (FGT, α = 1)*	0.148	0.702
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.126	0.681
Mean schooling level (last grade completed)	8.8 (0.27)	7.7 (0.20)
Mean height (cms)	166 (0.52)	153 (0.41)
Mean potential labor market experience	17.3 (0.36)	18.5 (0.26)
Sample Size	1950	3221

^*The three poverty measures are computed using poverty line of 1,452 pesos/mth (= 5 USD/day).

4. Empirical Results

We use the methods described in section two to simulate the effect of the Oportunidades program on the earnings distribution as it operates through changing education and height levels of the younger generation. We infer the relationship between earnings, education, height and labor market experience from information on adults who are age 25 to 40 population and then use that estimated relationship to draw inferences about how increases in schooling and height would affect earnings distributions. Experimental evaluations of the Oportunidades program (as well as of its predecessor, the PROGRESA program) have found that the program increases schooling attainment levels by 0.6 years on average and adds about one cm to height for both men and women⁹. We consider the following hypothetical combinations of impacts and their effect on the earnings outcome distribution: (a) an increase in schooling attainment of 0.6 years, (b) an increase in height of one cm, (c) a combined increase in schooling attainment and height in the magnitudes specified in (a) and (b), (d) an increase in schooling attainment by three years, and (e) an increase in height of three centimeters. An increase of three years of education or an increase in height of three centimeters is a very large impact that is much greater than what was observed under the program, but we include these hypothetical impacts simply for purposes of comparison.

4.1. Program targeting

Our goal is to simulate the longer-term effects of Oportunidades on earnings inequality and poverty. Ideally, we would compare two groups: The “treatment” group would be the population targeted as children by the program observed 20 years later and the “control” group would be the same people in a world where the program did not exist. Unfortunately, we cannot currently observe either group. The program was implemented relatively recently (in the late 1990’s), so many of the children who participated are still too young to observe their longer-term labor market outcomes. Additionally, although we can observe which families are currently participating in the program, it is likely that children from today’s Oportunidades households may not themselves meet the program eligibility criteria as adults. In fact, one of the primary goals of the program is to reduce the intergenerational transmission of poverty.

Our simulation is therefore based on a synthetic cohort approach that assumes stability in earnings relationships for neighboring cohorts. In particular, it assumes that individuals age 25 to 40 can be used to represent the future earnings of children in families currently participating in the program. We simulate the effects of Oportunidades by identifying the 40% of current 25–40 year-olds that would have been most likely to be targeted when young had the program been available, making use of the observed family background characteristics. We analyze the effects of the program by changing this group’s observed characteristics (education, height, and potential experience) in a way that is consistent with the impacts that have been measured in recent program evaluation studies.

The MxFLS-1 dataset does not contain information on all the criteria used to determine eligibility for Oportunidades, and in fact the exact eligibility criteria are not public. However, from program officials we have learned the approximate criteria and use the most closely related variables from the MxFLS-1 dataset to approximate eligibility. Specifically, we estimate a probit model for program participation using data on children (age 9 to 12) who are currently participating in Oportunidades as a nonlinear function of several variables: mother’s education, father’s education, whether the household has indoor plumbing, and the number of children age 0–10 residing in the household.

Table 2 presents descriptive statistics for these variables. In the sample, 37% of children participate in Oportunidades. The program is most active in the poorer southern states (Chiapas, Oaxaca, Guerrero, Michoacan, and Puebla), where 31% of the children live. On average, the children in the sample have mothers with 4.7 years of schooling attained and fathers with 5.2 years. Only 46% of these children live in households with indoor plumbing. Table 3 shows the estimated coefficients from the probit model for program participation¹⁰. As expected, parental education, indoor plumbing, and the presence of young children in the household are highly significant predictors of program participation.

TABLE 2.

DESCRIPTIVE STATISTICS FOR VARIABLES USED IN TARGETING ANALYSIS

Children Age 9–12

	Children age 9–12
Participates in Oportunidades	0.37 (0.05)
Mother’s schooling	4.7 (0.28)
Father’s schooling	5.2 (0.21)
Maximum of parents’ schooling	6.1 (0.22)
Household has indoor plumbing	0.46 (0.05)
Number of children age 0–10 in household	2.1 (0.08)
Lives in Poor Southern State‡	0.31 (0.07)
Sample Size	1699

^‡ Chiapas, Oaxaca, Guerrero, Michoacan, or Puebla.

TABLE 3.

ESTIMATED PROBIT MODEL FOR PROBABILITY OF PARTICIPATING IN OPORTUNIDADES

Variable	Coefficient	p-value
Mother’s schooling less than 6 grades (omitted)
Mother’s schooling 6 grades	−0.624	0.000
Mother’s schooling 7 to 9 grades	−0.914	0.001
Mother’s schooling 10 to 12 grades	−1.286	0.006
Mother’s schooling 13 or more grades	−0.652	0.264
Father’s schooling less than 6 grades (omitted)
Father’s schooling 6 grades	−0.592	0.000
Father’s schooling 7 to 9 grades	−0.836	0.000
Father’s schooling 10 to 12 grades	−1.284	0.015
Father’s schooling 13 or more grades	0.317	0.453
Max parent’s schooling less than 6 grades (omitted)
Max parent’s schooling 6 grades	0.750	0.000
Max parent’s schooling 7 to 9 grades	0.916	0.000
Max parent’s schooling 10 to 12 grades	1.211	0.034
Max parent’s schooling 13 or more grades	−0.370	0.551
Indoor plumbing	−0.291	0.029
0 or 1 young children in household (omitted)
2 to 4 young children in household	0.139	0.160
5 young children in household	0.466	0.037
6 or more young children in household	1.159	0.023
Living in poor southern state‡	0.257	0.201
Constant term	−0.214	0.302
	1699
Sample Size
Pseudo R-squared	0.11

^‡Chiapas, Oaxaca, Guerrero, Michoacan, or Puebla.

Next, we compute a propensity score (the predicted probability of being eligible and participating in the program) for each adult age 25 to 40 using the estimated probit model coefficients and measures of their family background (parental education, characteristics of the household when they were age 12, and an approximation of the number of children age 0 to 10 in the household at that time). Although the actual targeting of Oportunidades is based on several additional variables, we have to restrict the analysis to the subset available in the dataset for both children and adults, which fortunately includes the major determinants of program eligibility. We classify the 40% with the highest predicted probabilities of participation as the “target group” and the remaining 60% as the “non-target group”.

Table 4 compares the characteristics of the target and non-target groups, separately for men and women. For both men and women, the target group has much lower maternal and paternal education levels. Individuals in the target groups also grew up with more young children in households that were much less likely to have indoor plumbing. For both men and women, there is a two year schooling attainment gap between the target and non-target groups as well as a two cm difference in height. The labor market experience measure we use is Mincer potential experience, which equals age minus years of education minus six. The target group has more experience under this measure, mainly because of having lower schooling attainment¹¹.

TABLE 4.

DESCRIPTIVE STATISTICS FOR MEN AND WOMEN, AGE 25–40, BY PROJECTED OPORTUNIDADES PARTICIPATION

	Men		Women
	40% Target	60% Non-target	40% Target	60% Non-target
Mother’s schooling	1.9 (0.14)	4.4 (0.22)	1.9 (0.12)	4.1 (0.21)
Father’s schooling	2.7 (0.17)	5.1 (0.26)	2.6 (0.13)	4.6 (0.25)
Max Parental education	3.2 (0.19)	5.7 (0.24)	3.2 (0.14)	5.3 (0.24)
Indoor plumbing	0.18 (0.03)	0.85 (0.03)	0.18 (0.03)	0.80 (0.03)
# children age 0–10 in household	2.5 (0.12)	1.1 (0.07)	2.5 (0.10)	1.2 (0.06)
Living in poor southern state	0.34 (0.06)	0.11 (0.05)	0.35 (0.06)	0.11 (0.04)
Mean monthy earnings (in 1000s of pesos)	3.3 (0.28)	4.3 (0.25)	0.7 (0.07)	1.5 (0.20)
Schooling	7.4 (0.25)	9.6 (0.30)	6.3 (0.20)	8.7 (0.22)
Height	164.4 (0.56)	166.9 (0.55)	152.1 (0.50)	154.3 (0.43)
Experience	19.5 (0.40)	16.1 (0.42)	20.7 (0.26)	16.9 (0.33)
Sample Size	867	1083	1629	1592

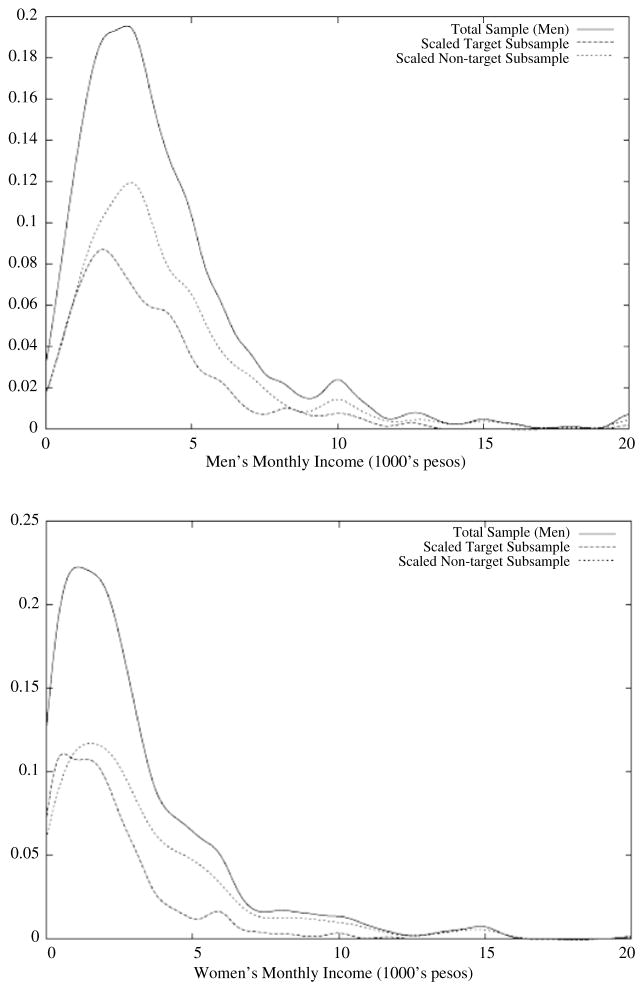
The mean levels in Table 4 shows that the target group is less advantaged than the non-target group. In particular, mean monthly earnings are 3,300 pesos per month for targeted men and 4,300 pesos per month for non-targeted men. Targeted women can expect about half (700 pesos per month) the labor income of non-targeted women (1,500 pesos per month). But there is still substantial overlap in the two earnings distributions, as shown in Figure 1. The top panel describes men’s labor income while the bottom panel describes women’s. The solid line in each panel is a nonparametric estimate of the density of positive earnings, while the two dashed lines correspond to the densities of positive earnings in the target and nontarget groups¹². Again, the mean of the the target subsample is clearly lower than that of the nontarget, but a substantial proportion of the target group can expect to receive earnings above the population mean and a large proportion of the nontarget group receives very little income¹³.

FIGURE 1.

DENSITIES OF INCOME FOR MEN AND WOMEN

Source: MxFLS 2002.

All densities are nonparametrically estimated using non-zero values of income.

4.2. Simulating counterfactual distributions

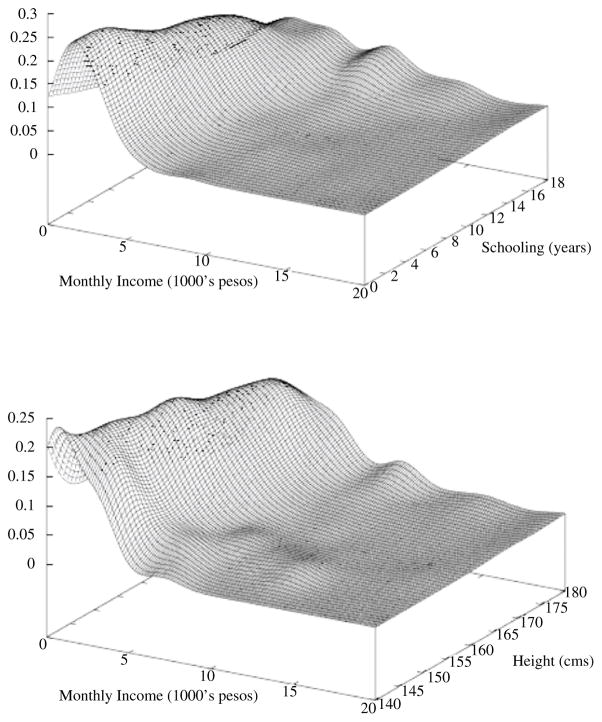
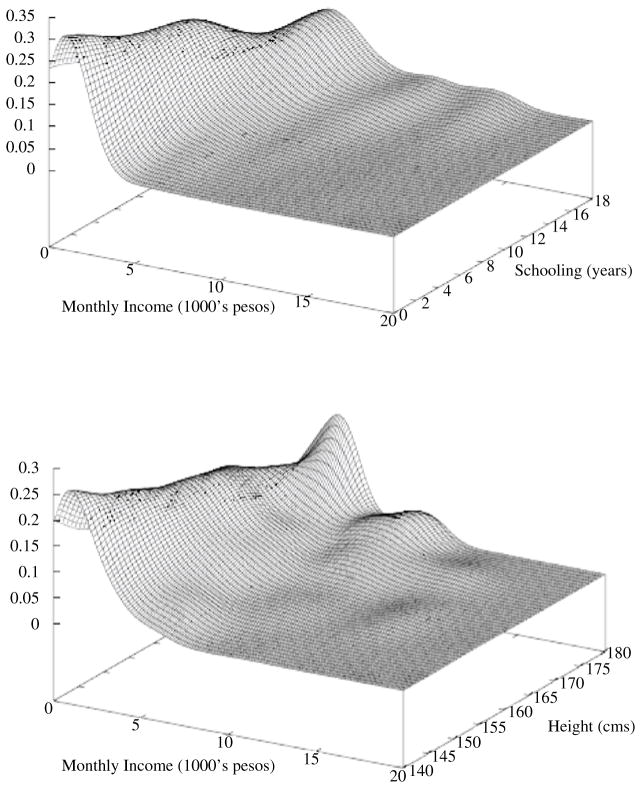
We next use the estimated earnings-schooling-height relationships to simulate the longer-term effects of the Oportunidades program on labor income. Figures 2 and 3 illustrate the nonlinearities in the density of non-zero labor income, conditional on schooling attainment and height; Figure 2 graphs the conditional density for men and Figure 3 for women. It is evident from the figures that higher levels of schooling attainment are associated with relatively larger increases in marginal earnings. The marginal earnings benefit is more homogeneous with respect to increases in height, but there also appears to be some nonlinearity near the upper end of the height distribution.

FIGURE 2.

DENSITY OF MEN’S INCOME CONDITIONAL ON SCHOOLING AND HEIGHT

Source: MxFLS 2002

All densities are nonparametrically estimated using non-zero values of income.

FIGURE 3.

DENSITY OF WOMEN’S INCOME CONDITIONAL ON SCHOOLING AND HEIGHT

Source: MxFLS 2002

All densities are nonparametrically estimated using non-zero values of income.

Tables 5a and 5b show the results of our main simulation experiments for men and women. The first column displays characteristics of the income distribution without any program impacts. This income distribution is equal to the original income distribution with the addition of a small amount of error introduced by the nonparametric smoothing. The other columns of Table 5a and 5b each represent a different set of hypothetical program impacts, given by (a)–(e), where we give the stated program impact to each individual in the target group and calculate the implied income distribution for the combined target and non-target groups. For example, case (a) augments each individual’s education level by 0.6 years. We use the nonparametric simulation method described above to simulate a counterfactual earnings distribution whose features can be compared to the original no-program earnings distribution. As previously noted, we simulate changes in employment along with changes in the distribution of positive earnings. That is, the earnings distribution includes a mass point at zero for nonworkers and the fraction of nonworkers can be affected by the program. Monthly earnings are measured in thousands of pesos.

TABLE 5A.

SIMULATED EFFECTS OF OPORTUNIDADES IMPACTS ON INCOME DISTRIBUTION BASED ON NONPARAMETRIC EARNINGS DENSITY ESTIMATIONS

Men, Age 25–40

	Original	Schooling (+0.6 yrs)	Height (+1 cm)	Schooling (+0.6 yrs) Height (+1 cm)	Schooling (+3 yrs)	Height (+3 cm)
		(a)	(b)	(c)	(d)	(e)
Proportion with zero earnings	0.098	0.099	0.099	0.099	0.097	0.101
Mean earnings	3.931	3.944	3.961	3.974	4.255	4.037
Std. Dev. earnings	4.382	4.382	4.455	4.456	4.857	4.631
Median earnings	3.003	3.013	3.012	3.021	3.180	3.030
Interquartile Range	3.331	3.337	3.338	3.339	3.443	3.371
Coefficient of Variation	1.115	1.111	1.125	1.121	1.142	1.147
Gini Coefficient	0.485	0.485	0.487	0.487	0.491	0.493
Theil Index	0.446	0.445	0.451	0.450	0.458	0.462
Headcount Ratio (FGT, α = 0)*	0.237	0.236	0.235	0.235	0.219	0.233
Average Poverty Gap Ratio (FGT, α = 1) *	0.158	0.158	0.158	0.157	0.149	0.158
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.126	0.126	0.126	0.126	0.121	0.127

Sample size is 1950.

TABLE 5B.

SIMULATED EFFECTS OF OPORTUNIDADES IMPACTS ON INCOME DISTRIBUTION BASED ON NONPARAMETRIC EARNINGS DENSITY ESTIMATIONS

Women, Age 25–40

	Original	Schooling (+0.6 yrs)	Height (+1 cm)	Schooling (+0.6 yrs) Height (+1 cm)	Schooling (+3 yrs)	Height (+3 cm)
		(a)	(b)	(c)	(d)	(e)
Proportion with zero earnings	0.637	0.632	0.639	0.633	0.589	0.640
Mean earnings	1.147	1.173	1.149	1.177	1.448	1.155
Std. Dev. earnings	2.618	2.644	2.618	2.650	2.954	2.626
Median earnings	0.000	0.000	0.000	0.000	0.000	0.000
Interquartile Range	1.335	1.394	1.337	1.399	1.909	1.335
Coefficient of Variation	2.283	2.254	2.228	2.251	2.040	2.274
Gini Coefficient	0.819	0.816	0.819	0.816	0.791	0.819
Theil Index	1.478	1.460	1.479	1.460	1.325	1.480
Headcount Ratio (FGT, α = 0)*	0.759	0.755	0.759	0.754	0.713	0.759
Average Poverty Gap Ratio (FGT, α = 1) *	0.706	0.701	0.707	0.702	0.658	0.708
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.675	0.670	0.676	0.671	0.627	0.678

Sample size is 3221.

Table 5a indicates that the program would not significantly affect the fraction of men participating in the labor market, which remains around 90% across all the simulations. Also, impacts (a)–(c) have modest effects on mean earnings for men and almost no effect on earnings inequality, regardless of the measure. The effect of a 0.6 year impact on schooling attainment (in columns (b) and (c)) is larger for women than it is for men; however, the changes in income inequality are relatively minor for both men and women. The hypothetical three year increase in schooling attainment, shown in column (d), leads to substantially higher mean earnings and a reduction in poverty as measured by the Headcount ratio and the average poverty gap. While income inequality actually increases slightly for men, it declines somewhat for women due to the large induced increase in female employment. A one cm increase in height leads to about a 30 peso increase in mean monthly earnings for men but no substantial difference for women. The height impact has almost no influence on earnings inequality, but a large hypothetical increase in height of three centimeters slightly increases mean earnings and inequality, without having much effect on poverty.

Even though Oportunidades significantly increased the human capital of children from disadvantaged families and substantially raised mean earnings, we have found its effects on earnings inequality to be minimal for two main reasons. First, returns to schooling in this environment are highly non-linear and in particular, we observe increasing returns at higher schooling levels. Those individuals in the target group that would have higher educational attainment in the absence of the program experience relatively larger increases in income as a result of the program, so it is not the case that the poorest of the target group experience the largest benefit. The second factor that dampens the program’s effect on inequality is that targeting children from poor backgrounds only imperfectly targets future low-earning adults, because of substantial inter-generational mobility.

We measure the influence of the nonlinearity in returns to schooling by estimating and simulating parametric models of the employment and earnings processes and comparing these results to those found in our nonparametric simulations. Tables 6a and 6b present estimated coefficients for a probit model of employment and a linear regression model of log earnings. Each model contains a linear term for years of schooling and quadratics for height and potential experience. To simulate the employment process, we augment schooling attainment, height, and/or experience under the same program scenarios evaluated above and predict employment using draws from the probit error distribution that are consistent with the observed choices. To simulate earnings, we make the same augmentations to the human capital variables and for each worker incorporate the original earnings residual if it was observed and draw from the earnings residual distribution for those who were not working in the original sample. These simulation results are shown in Tables 7a and 7b.

TABLE 6A.

ESTIMATED PARAMETRIC PROBIT MODELS FOR EMPLOYMENT

Variables	Men	Women
Schooling (years)	0.009 (0.022)	0.107 (0.013)
Height	0.141 (0.212)	0.070 (0.145)
Height2	−0.000 (0.001)	−0.000 (0.0005)
Experience	0.067 (0.038)	0.000 (0.029)
Experience2	−0.002 (0.001)	0.000 (0.0007)
Constant	−9.914 (17.628)	−6.030 (11.178)
Sample Size	1950	3221
Pseudo R-squared	0.0145	0.0513

Standard errors are in parentheses.

TABLE 6B.

ESTIMATED PARAMETRIC REGRESSION MODELS FOR LOG INCOME

Variables	Men	Women
Schooling (years)	0.087 (0.011)	0.154 (0.015)
Height	−0.073 (0.085)	0.090 (0.139)
Height2	0.000 (0.0002)	−0.000 (0.0004)
Experience	0.040 (0.019)	−0.002 (0.037)
Experience2	−0.001 (0.001)	0.001 (0.001)
Constant	4.298 (7.300)	−9.251 (10.768)
Sample Size	1720	1044
R-squared	0.1966	0.2712

Standard errors are in parentheses.

TABLE 7A.

SIMULATED EFFECTS OF OPORTUNIDADES IMPACTS ON INCOME DISTRIBUTION BASED ON PARAMETRIC EARNINGS MODELS

Men, Age 25–40

	Original	Schooling (+0.6 yrs)	Height (+1 cm)	Schooling (+0.6 yrs) Height (+1 cm)	Schooling (+3 yrs)	Height (+3 cm)
		(a)	(b)	(c)	(d)	(e)
Proportion with zero earnings	0.099	0.098	0.099	0.100	0.096	0.102
Mean earnings	3.945	4.006	3.968	4.023	4.247	4.015
Std. Dev. earnings	4.432	4.472	4.451	4.497	4.691	4.497
Median earnings	3.000	3.000	3.000	3.000	3.200	3.000
Interquartile Range	3.300	3.417	3.364	3.406	3.454	3.440
Coefficient of Variation	1.123	1.116	1.122	1.117	1.104	1.120
Gini Coefficient	0.483	0.481	0.483	0.482	0.479	0.483
Theil Index	0.443	0.439	0.443	0.441	0.433	0.444
Headcount Ratio (FGT, α = 0)*	0.227	0.220	0.225	0.222	0.206	0.222
Average Poverty Gap Ratio (FGT, α = 1) *	0.148	0.145	0.148	0.147	0.139	0.149
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.126	0.124	0.126	0.126	0.121	0.128

Sample size is 1950.

TABLE 7B.

SIMULATED EFFECTS OF OPORTUNIDADES IMPACTS ON INCOME DISTRIBUTION BASED ON PARAMETRIC EARNINGS MODEL

Women, Age 25–40

	Original	Schooling (+0.6 yrs)	Height (+1 cm)	Schooling (+0.6 yrs) Height (+1 cm)	Schooling (+3 yrs)	Height (+3 cm)
		(a)	(b)	(c)	(d)	(e)
Proportion with zero earnings	0.638	0.627	0.640	0.629	0.596	0.644
Mean earnings	1.140	1.196	1.132	1.199	1.438	1.133
Std. Dev. earnings	2.595	2.662	2.569	2.673	3.108	2.583
Median earnings	0.000	0.000	0.000	0.000	0.000	0.000
Interquartile Range	1.200	1.400	1.228	1.400	2.000	1.265
Coefficient of Variation	2.276	2.225	2.269	2.230	2.160	2.279
Gini Coefficient	0.819	0.813	0.819	0.813	0.796	0.821
Theil Index	1.459	1.423	1.458	1.428	1.344	1.467
Headcount Ratio (FGT, α = 0)*	0.763	0.753	0.764	0.754	0.715	0.764
Average Poverty Gap Ratio (FGT, α = 1) *	0.702	0.691	0.703	0.692	0.656	0.706
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.681	0.670	0.682	0.671	0.636	0.686

Sample size is 3221.

Because there is near universal employment of men across the human capital distribution we find little effect of schooling and height on employment with a small positive effect of experience. The story is quite different for women where a year of schooling has a strong and significant positive effect on the probability of employment. When schooling is constrained to have a linear effect on log earnings, a year of schooling increases earnings by 8.7% for men and 15.4% for women. The linear and quadratic terms for height are jointly significant (α < 0.05 for both men and women while the experience terms are only jointly significant for women.

A comparison of Table 7a with Table 5a shows that for men, the parametric simulation approach tends to predict small reductions in inequality relative to the small increases in inequality predicted by the nonparametric approach. These differences are almost entirely due to the fact that the parametric model constrains log earnings to be a linear function of schooling and does not capture the fact that schooling has increasing returns. For women (Tables 5b and 7b) the parametric model predicts a smaller reduction in inequality because of the differences in how schooling affects employment. In particular, the nonparametric model predicts that targeted increases in schooling will increase women’s employment more than a parametric model that includes schooling as a linear term. This difference in the effect on employment overpowers the impact of imposing constant returns to schooling in the earnings process.

The second major factor explaining Oportunidades’ modest effect on inequality is that it targets children from poor families and these children are not necessarily the future poor adults. That is, the program increases the completed schooling of some children from an already high level to an even higher level. To explore the importance of targeting, we performed another set of simulations using our nonparametric earnings model where we target the same fraction of individuals with the program but choose them on the basis of low adult education levels. Specifically, we give the program to those who would otherwise form the bottom of the education distribution. This targeting is of course not feasible in practice, because it is impossible to know which children would eventually complete the least amount of schooling. Nevertheless, the simulation results reported in Tables 8a and 8b give an upper bound for improving earnings and inequality through more precise targeting. A comparison with Tables 5a and 5b shows that targeting individuals at the bottom of the education distribution would be more effective in reducing inequality than the current targeting mechanism, but at the cost of lower mean earnings, because it does not take advantage of the larger program impacts at higher schooling levels.

TABLE 8A.

SIMULATED EFFECTS OF OPORTUNIDADES IMPACTS ON INCOME DISTRIBUTION BASED ON NONPARAMETRIC EARNINGS DENSITY ESTIMATIONS PERFECT TARGETING

Men, Age 25–40

	Original	Schooling (+0.6 yrs)	Height (+1 cm)	Schooling (+0.6 yrs) Height (+1 cm)	Schooling (+3 yrs)	Height (+3 cm)
		(a)	(b)	(c)	(d)	(e)
Proportion with zero earnings	0.098	0.097	0.098	0.097	0.090	0.101
Mean earnings	3.931	3.945	3.950	3.960	4.084	3.958
Std. Dev. earnings	4.382	4.381	4.409	4.402	4.405	4.451
Median earnings	3.003	3.015	3.018	3.030	3.214	3.031
Interquartile Range	3.331	3.344	3.324	3.333	3.289	3.308
Coefficient of Variation	1.115	1.111	1.116	1.111	1.079	1.124
Gini Coefficient	0.485	0.485	0.485	0.484	0.467	0.486
Theil Index	0.446	0.444	0.446	0.443	0.417	0.451
Headcount Ratio (FGT, α = 0)*	0.237	0.236	0.234	0.233	0.211	0.234
Average Poverty Gap Ratio (FGT, α = 1) *	0.158	0.157	0.157	0.156	0.141	0.159
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.126	0.125	0.126	0.124	0.113	0.128

Sample size is 1950.

TABLE 8B.

SIMULATED EFFECTS OF OPORTUNIDADES IMPACTS ON INCOME DISTRIBUTION BASED ON NONPARAMETRIC EARNINGS DENSITY ESTIMATIONS PERFECT TARGETING

Women, Age 25–40

	Original	Schooling (+0.6 yrs)	Height (+1 cm)	Schooling (+0.6 yrs) Height (+1 cm)	Schooling (+3 yrs)	Height (+3 cm)
		(a)	(b)	(c)	(d)	(e)
Proportion with zero earnings	0.637	0.635	0.637	0.635	0.606	0.640
Mean earnings	1.147	1.157	1.149	1.161	1.287	1.152
Std. Dev. earnings	2.618	2.624	2.623	2.630	2.740	2.638
Median earnings	0.000	0.000	0.000	0.000	0.000	0.000
Interquartile Range	1.335	1.366	1.336	1.372	1.713	1.332
Coefficient of Variation	2.283	2.267	2.283	2.264	2.129	2.290
Gini Coefficient	0.819	0.817	0.819	0.817	0.797	0.820
Theil Index	1.478	1.468	1.479	1.467	1.367	1.484
Headcount Ratio (FGT, α = 0)*	0.759	0.757	0.759	0.756	0.728	0.759
Average Poverty Gap Ratio (FGT, α = 1) *	0.706	0.704	0.706	0.704	0.673	0.708
Foster-Greer-Thorbecke Index (FGT, α = 2)*	0.675	0.673	0.676	0.673	0.643	0.678

Sample size is 3221.

In addition to the simulations we report, which assume constant treatment effects, we also carried out all the simulations under alternative scenarios of heterogeneous program effects. For example, we assigned half the target population impacts that were twice as high and half zero impact, keeping the average treatment effect the same. The half of the target group that received the double impact was alternatively chosen to be the less or more advantaged subgroup. Our findings with regard to effects on mean earnings and earnings inequality under the heterogeneous treatment impact simulations were very similar to those discussed previously, so we omit them for the sake of brevity¹⁴.

5. Conclusions

The Oportunidades program aims to reduce poverty of the current generation through transfers and to alleviate poverty of the next generation through human capital investment. A number of experimental and nonexperimental evaluation studies have documented that the program significantly improves schooling attainment, health and nutrition over the short-term. This paper develops and applies a nonparametric simulation method for the purpose of studying how increases in schooling attainment and in height, as a measure of long-term nutritional status, will affect the distribution of earnings in the next generation.

Our empirical findings suggest that the human capital investment in today’s youth will increase their mean earnings levels, but will have only a modest effect on earnings inequality. Behrman (2006) comes to a similar conclusion in a survey of human capital policies and from an empirical study of how increasing education affects earnings inequality in Chile. The key factors underlying the modest effects on inequality that we observe are the difficulty in predicting which children will become future low earning adults and nonlinearities in how health and education are priced in the labor market. With regard to the first factor, childhood poverty is a strong predictor of future low earnings, but there is also substantial intergenerational mobility that makes it difficult to target low adult earners on the basis of childhood characteristics. With regard to the second factor, we found evidence of important nonlinearities in how height and education influence earnings. Most notably, an additional year of secondary school has a higher monetary return than an additional year of primary school. Because of these nonlinearities, people at the upper deciles of the targeted population tend to benefit more from the program intervention.

We conclude by considering some limitations of the simulation method studied in this paper. First, the method assumes that the observed relationship between earnings and the covariates of education, height, and work experience is causal. This raises concern about potential bias due to unobserved ability, which is the subject of a large labor economics literature. Previous attempts to control for ability bias have relied mainly on instrumental variables or natural experiments (e.g. twins with different levels of schooling).¹⁵ Although there is variation in reported estimates, most estimates of the rate of return to schooling that purport to control for ability bias through the use of instrumental variables exceed those obtained by ordinary least squares. The variation in estimates is partly accounted for by heterogeneity in returns to education on earnings that requires a LATE (local average treatment effect) interpretation of the instrumental variables estimates.¹⁶ Estimates that account for ability bias using variation in twin pairs, on the other hand, tend to be somewhat lower than cross-sectional OLS estimates. Because the literature finds that OLS estimates do not necessarily overstate the causal effect, we have no reason to believe that our nonparametric procedure necessarily overstates the true return to schooling attainment. Also, much of the instrumental variables literature operates within a parametric framework and does not easily allow for the nonlinearities in the earnings-schooling-height-experience relationship that we find to be quantitatively important. Nevertheless, further exploration of how the simulation method could be modified to account for unobserved ability and endogenous covariates would be useful.

A second critical assumption of the simulation method is the usual synthetic cohort assumption, namely that the characteristics of today’s 25 to 40 year olds, observed in 2002, are representative of the future adulthood of today’s children. Extrapolating from current trends, children today would likely attain more education than current 25 to 40 year olds in the absence of the program intervention. Our estimates indicate that the marginal effect of education on earnings is increasing in years of education, so overall rising education levels could lead the simulation to understate somewhat the impact of Oportunidades on earnings. Third, the simulation method does not account for the general equilibrium effects of increasing the education levels of a large segment of the future labor force, which would tend to decrease returns to education. Any decline, though, is at least partially mitigated by the fact that Mexico is an open economy. Fourth, this study focused on individual level earnings for men and women, although household-level earnings inequality may be more relevant to policy makers. It is also not clear how to interpret high income inequality in a group (like women) where a large proportion choose not to work, because they have a partner who provides enough money for the household. The simulation method could be extended to model household formation by incorporating a marriage outcome, where marriage opportunities and outcomes potentially also depend on variables influenced by the program. Our method could similarly be extended to account for the influence of improving human capital on internal and external migration.

Lastly, improvements in future earnings are only one of the long-term benefits expected from the program. For example, there is a substantial literature documenting how upgrading mother’s education increases child test scores (e.g., Rosenzweig and Wolpin, 1994). Female program beneficiaries who choose not to work may be more effective mothers and may choose to have fewer children and to invest more in them. The simulation methodology in this paper could conceivably be extended to examine changes in fertility.

APPENDIX A

Construction of Samples and Variables

This appendix describes how each of the variables for the empirical analysis was constructed. The data analysis has three parts. First, we estimate a probability of participating in the Oportunidades program and use the estimated model to simulate program targeting for men and women between age 25 and 40. Second, we estimate nonparametrically the relationship between income, education, height, and work experience for men and women between age 25 and 40. Third, we compute the counterfactual income distribution under assumptions of how the program affects education, height, and work experience that are consistent with recent evaluations of short-term program impacts.

Sample Construction

The initial sample of MxFLS respondents between age 25 and 40 contains 6,564 observations. When we drop the individuals who worked but did not report their income, the number goes down to 5,871. It drops further to 5,180 (79% of the original sample) when we drop those individuals who did not report their education or whose height was not measured. Finally, we drop an additional 9 outlier observations for individuals who report receiving more than 40,000 pesos in the previous month. This leaves a final sample size of 5,171.

Construction of Variables

Income

Income is measured as total labor income earned (including net profits for the self-employed) in the previous month. It includes zeros for those individuals who don’t work. About 6% of individuals who reported working in the previous week are recorded as being “peasants on their plot”. 40% of these individuals report zero income in the last month. This seems plausible for subsistence farmers. Only 2% of other individuals who report working report zero income. Income is measured in thousands of pesos and in 2002 the average daily exchange rate was 1 USD = 9.68 pesos.

We do not use proxy reports on income, because it is not clear how to combine this data with the first-person reports and weight the data correctly. The proxy reports also have more missing data.

Schooling

The MxFLS collects the type of the last school attended and, for most individuals, the number of years that the individual completed at that level. We do not include years of “technical education” in our measure, because wage returns to technical education (based on our own linear regressions) are much lower than the returns of conventional schooling.

Height

Height is not self-reported but instead is measured by trained survey personnel.

Experience

MxFLS did not collect information on actual labor force experience, so we use the standard Mincer measure of potential experience equal to age minus years of schooling minus six.