The role of judgment frames and task precision in object attention: reduced template sharpness limits dual-object performance

Abstract

Multiple attributes of a single object are often processed more easily than attributes of different objects–a phenomenon associated with object attention. Here we investigate the influence of two factors, judgment frames and judgment precision, on dual-object report deficits as an index of object attention. Han, Dosher, & Lu (2003) predicted that consistency of the frame for judgments about two separate objects could reduce or eliminate the expression of object attention limitations. The current studies examine the effects of judgment frames and of task precision in orientation identification and find that dual-object report deficits within one feature are indeed affected modestly by the congruency of the judgments and more substantially by the required precision of judgments. The observed dual-object deficits affected contrast thresholds for incongruent frame conditions and for high precision judgments and reduce psychometric asymptotes. These dual-object deficits reflect a combined effect of multiplicative noise and external noise exclusion in dual-object conditions, both related to the effects of attention on the tuning of perceptual templates. These results have implications for modification of object attention theory, for understanding limitations on concurrent tasks.

1. Introduction

Object attention has evolved as a major explanatory principle for understanding cortical mechanisms of visual attention (Desimone, 1998). Complex visual scenes often involve many objects. Local detailed analyses carried out in early visual cortex (V1, V2) are further processed and transformed into object-based representations in cerebral cortex (Olson, 2001), and object characteristics may in some cases influence responses in early areas (Olson, 2001; Lee & Nguyen, 2001; Sugita, 1999; Zhou, Friedman, von der Heydt, 2000). Competition between objects for neural processing and the consequent modification of neural responses by voluntary attention (Olson, 2001; Reynolds, Chelazzi & Desimone, 1999; Missal, Vogels, Chao-Yi, & Obran, 1999; Reynolds, Pasternak, & Desimone, 2000) is an important principle of cortical processing (Kastner & Ungerleider, 2000; Olson, 2001).

These physiological observations have historically been associated with behavioral phenomena of object attention, where the primary findings focused on reduced effectiveness of reporting attributes from distinct objects. However, recent behavioral evidence suggests that dual-object attention deficits may reflect interactions of object limitations and processing limitations associated with judgment frames, and perhaps with other task demands. This paper further examines the evidence for exceptions to competitive dual-object report phenomena, and tests specific predictions about the role of judgment incongruence and task precision in creating the limiting processes often observed in object-attention. The results are related to the phenomena of feature attention and criterion setting as well as object attention, and capacity limits in concurrent tasks.

1.1 Object attention: dual object report deficits

Behaviorally, the concept of object attention traces its beginnings to the early investigation by Duncan (1984) of the limitations in report of several attributes of distinct objects, while report of those same attributes of the same object do not show the same limitations. To quote:

“If subjects must report two aspects of a brief visual display, performance should depend on whether these aspects concern the same or different objects. Reporting two aspects of one object should be no more difficult than reporting only one because focal attention is paid to the object as a whole. In contrast, reporting aspects of two different objects should be less successful, reflecting competition between these objects for focal attention”. (Duncan, 1984, p. 501).

The claim of object attention is that report deficits will occur whenever the to-be-reported attributes in a briefly presented (and masked) visual display (e.g., color and orientation), are divided over two objects (Duncan, 1984; see also Isenberg, Nissen, & Marchak, 1990; Vincent & Regan, 1995) compared to single-object, single-report controls. The dual-object deficit has been demonstrated for a wide range of features, including orientation and brightness (Duncan, 1984); orientation and displacement (Duncan, 1993b); surface properties such as brightness, color, and texture; and boundary properties such as location and length (Duncan & Nimmo-Smith, 1996), and “where” and “what” (Duncan, 1993a). A series of studies explicitly argued that object attention limitations occurred regardless of the nature of the attributes or features (Duncan, 1984, 1993a, 1993b, 1998; Duncan & Nimmo-Smith, 1996).

1.2 Limitations on object attention

The dual-object report deficit was seen as the behavioral marker of the foundational limitations of attending to multiple objects (Duncan, 1984; Desimone & Duncan, 1995). This classical view of object attention was challenged by the results of Han, Dosher & Lu (2003), who studied dual-object report deficits as exhibited in the psychometric functions (accuracy as a function of target contrast) of basic visual judgments. They showed that the classical dual-object report deficits were observed when different judgments were required for two spatially separated objects (i.e., orientation of one object and phase of the other object). In contrast with the classic claims of object attention, however, dual-object report deficits were not observed when the same judgments were required for the two objects (i.e., orientation of both objects or phase of both objects). Figure 1 shows a subset of the data from that experiment, for orientation judgments; the pattern was equivalent for judgments of phase. Dual-response conditions in which the same features of two objects were reported (i.e, two orientations or two phases) yielded performance essentially equivalent to the single-object single-report condition, in which only a single response was required.

Figure 1.

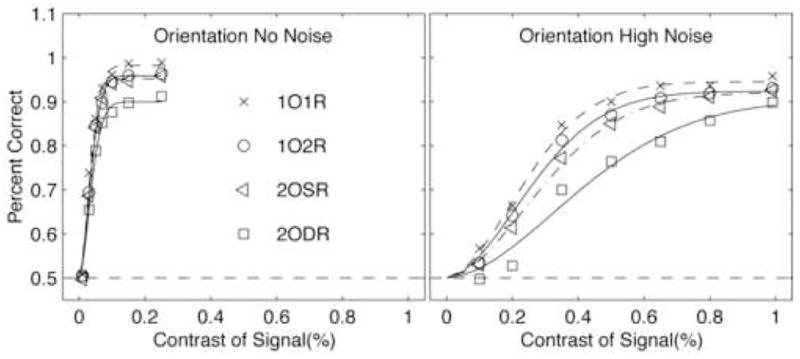
Percent correct as a function of signal contrast with and without external noise for single and dual-object report, orientation judgments in Han, Dosher, & Lu (2003). Only the psychometric function for dual-object different reported attributes (2ODR) showed significant dual-object report deficits in individual observers compared with single object control conditions. 1O1R = single object, single response; 1O2R = single object, dual report (orientation and phase); 20SR = dual-object with the same attribute reported (both orientation or both phase); 2ODR = dual-object report with different reported attributes (orientation and phase). (Data from Han, et al., 2003, Figure 2, top).

Han et al. (2003) suggested that dual-object report deficits were maximized when the task required two different (‘incongruent’) criteria or judgment frames and minimized or eliminated when the task required the report of two attributes using the same (‘congruent’) criteria or judgment frames. These findings and theoretical predictions stand in opposition to the classic report of dual-object report deficits, which contrasted object attention with various feature-dependent theories of attention (Treue & Martinez Trujillo, 1999), explicitly arguing that the nature of the judgments was irrelevant to the object effect. An analysis of the exact stimulus arrangements in these prior studies, however, supported the possible role of incongruent judgment frames. Studies claiming that ‘same judgments’ and ‘different judgments’ (Duncan, 1993a, 1993b; Duncan & Nimmo-Smith, 1996) are both equally affected by object attention limits had arranged for ‘same judgments’ to differ in detail. For example, the two location judgments were for right-vs-left in a bounding box on one object and up-vs-down in a bounding box on the other while the two orientation judgments were for clockwise-counterclockwise of a horizontal axis in one case and a vertical axis in another (Duncan 1993a). This analysis of the prior literature is suggestive. It is important to directly assess the new interpretation that dual-object report deficits may reflect incongruence of judgment frames, and that is a major goal of this study.

Other forms of object attention have been investigated by assessing the relationship between attention and the locations and attributes that are parts of hierarchically defined perceptual objects (Egly, Driver, & Rafal, 1994; Moore, Yantis, & Vaughan, 1998) or object part (Vecera, Behrmann, & Filapek, 2001; Vecera, Behrmann, & McGoldrick, 2000). Often, these experiments focus on the time to detect an onset or find an attribute after a cue to a location within an extended object. The response time differences may reflect an unknown mixture of increased processing efficiency or speed and response biases (Ratcliff, 1978). We have elected instead to study attention effects for basic intrinsic objects rather than for the more complex outline-delimited regions of space (Egly, Driver & Rafal, 1994) or pictures of complex objects. Understanding the function of object attention on such basic objects is the first step. Once the phenomena are better understood for the simple visual object patterns, the approach may be extended to more complex spatial objects.

1.3 Mechanisms of attention

Recently, we (Dosher & Lu, 2000a, 2000b; Lu & Dosher, 1998, 2000; see Lu & Dosher, 2008 for a review) developed a theoretical framework to identify separable mechanisms of attention through external noise tests and corresponding observer models. The model relates perceptual discriminability to the fundamental signal to noise properties of the perceptual processing systems, where the limiting noises reflect both external noise (masks) and internal noises (additive and multiplicative). This framework distinguishes three primary mechanisms of attention: external noise exclusion, stimulus enhancement, and multiplicative noise/gain control change. We evaluate the dual-object attention deficits to suggest the nature of the attention mechanisms underlying the phenomenon.

The perceptual template model predicts discriminability, d′(c,N_ext) as a function of stimulus contrast c and external noise contrast N_ext, a response β to the signal stimulus, an internal additive noise N_a, internal multiplicative noise N_m, nonlinear transduction parameter γ, and attention modulations of the noise sources:¹:

$$d(c)=\frac{{\beta }^{\gamma }{c}^{\gamma }}{\sqrt{A_f^2{N}_{\mathit{ext}}^{2\gamma }+A_m^2{N}_{\mathit{mul}}^2[A_f^2{N}_{\mathit{ext}}^{2\gamma }+{\beta }^{2\gamma }{c}^{2\gamma }]+A_a^2{N}_{\mathit{add}}^2}}$$

These three mechanisms have distinct signature patterns of contrast threshold versus external noise contrast (TvC) functions (Dosher & Lu, 1999; Lu & Dosher, 1998, 2008). There are corresponding effects on the psychometric functions in zero and high external noise. The TvC signatures (Figure 2a) and the psychometric function signatures (Figure 2b) are shown in zero and high external noise for three distinct attention modulations. As seen in Figure 2b, stimulus enhancement A_a affects the rising portion but not the asymptote of the psychometric functions in no noise (top left) and has essentially no effect in high noise (top right), where external noise is the limiting factor on performance. External noise exclusion A_f affects the rising portion but not the asymptote of the psychometric functions in high noise (middle right) but not in no noise (middle left) where there is no external noise to filter out. Changes in multiplicative noise A_m have effects across the psychometric functions, but focused especially at the asymptote (max) of the psychometric functions in both noises (lower panels); this is because multiplicative noise increases with increased stimulus contrast. These d′ and psychometric function predictions are directly related through the signal detection model.

Figure 2.

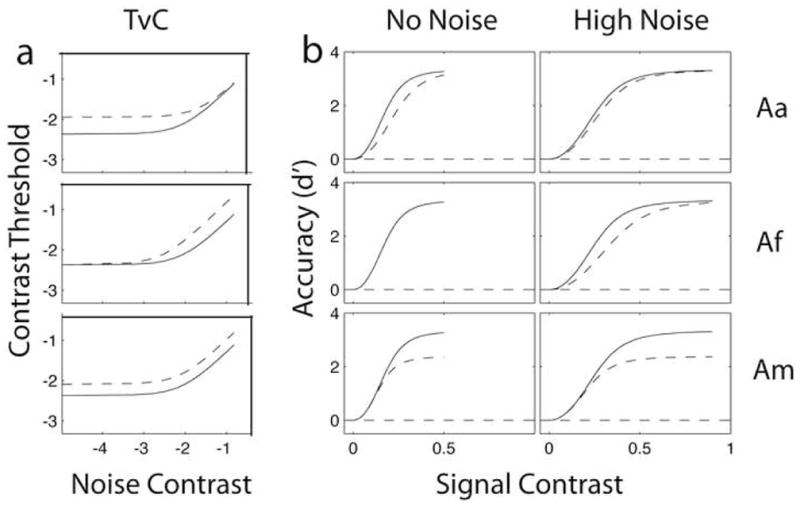
Performance signatures of the perceptual template model for stimulus enhancement (A_a, top), external noise reductions (A_f, middle), and multiplicative noise reduction (A_m, bottom) for dual-object dual-response (dashed line) and single-object single-response (solid line) conditions. (a) The signature differences in threshold versus external noise contrast (TvC) functions, which graph the contrast threshold (log₂(C_T)) against the external noise contrast (log₂(N_ext)). (b) Psychometric functions showing accuracy (d′) versus stimulus contrast in no external noise (left) and high external noise (right). Stimulus enhancement shows an effect at lower contrasts in no noise; external noise exclusion shows an effect at lower contrasts in high noise; and multiplicative noise reduction shows an effect in both noises, focused at high contrasts in the psychometric functions. The perceptual template parameters used to generate these functions were: N_m= 0.3, N_a =0.06, β = 2, γ = 2, A_m = 1.4, A_a = 1.8, and A_f = 1.4.

The basic perceptual template model (PTM) equation (above) treats the discrimination of orthogonal targets. An extension to non-orthogonal targets² replaces β^γ c^γ in the numerator (signal) with β^γ c^γ –β′^γ c^γ, where β′ is the response of the template to a distractor and replaces β^2γ c^2γ in the multiplicative noise term (denominator) with (β^2γ + β′^2γ)c^2γ (Jeon, Lu, & Dosher, 2008). Increasing β′ > 0 effectively reduces the signal and increases multiplicative noise, both leading to reductions in the asymptote of the psychometric function. Changes in β′, or coupled changes in A_f and β′ are similar to altered multiplicative noise signatures. Distinguishing these latter two possibilities is challenging, requiring elaborated experiments.

The first two of the three attention mechanisms – external noise exclusion and stimulus enhancement – have so far been observed empirically in spatially cued attention (see below). External noise exclusion reduces the impact of irrelevant external noise and corresponds to filtering in signal processing. Stimulus enhancement increases the relative strength of the stimulus compared to additive internal noise and corresponds to amplification in signal processing. Both yield increases in the net signal to noise ratio, or improvements in performance accuracy, over and above whatever changes in performance may result from attention changes in bias or decision. External noise exclusion is manifested in high external noise conditions, while stimulus enhancement is manifested in low or zero noise conditions.

Mechanisms of attention have now been extensively studied for spatially cued attention in which one attribute of a single object is reported (Dosher & Lu, 2000a, 2000b; Lu & Dosher, 2000; Carrasco, Williams, & Yeshurun, 2002). External noise exclusion – corresponding to an attention effect in noisy or masked situations – is the primary mechanism of spatially cued attention in these studies. Spatially cued attention improves the ability to process stimuli in the presence of external noise, with a prominent role whenever there are a sufficiently large number (usually 4 or more) potential objects (or locations) (Dosher & Lu, 2000b; Lu, Lesmes, & Dosher, 2002). Spatially cued attention, under certain circumstances, also improves performance in the absence of external noise (Lu & Dosher, 2000; Lu, Tse, Dosher, Lesmes, Posner, & Chu, in press). Those cases that reported effects in both zero and high external noise (i.e., peripheral precuing, Lu & Dosher, 2000) have been consistent with mixtures of external noise exclusion and stimulus enhancement, both cases in which accuracy converges at high contrasts of the psychometric functions of these tasks with relatively distinct targets.

Han, Dosher & Lu (2003) found that the object attention effect, as seen in the dual-object report deficit for two different feature reports, had its largest effect in the presence of external noise, although some effect of object attention also occurred in the absence of external noise. Subsequent unpublished experiments suggest that object attention effects may systematically occur in noiseless conditions under some conditions. However, a reexamination of the Han et al. (2003) data suggests a possible role for a mechanism that impacts the asymptotic portion of the psychometric function as well as the external noise exclusion that was the focus of the original interpretation. In this study, we interpret the psychometric functions through direct application of the perceptual template model and suggest a unique role of either multiplicative noise and/or changed β′ in object attention that has not observed in the simpler cases of spatially cued attention and orthogonal targets.

1.3 Task alternatives to object attention

As described above, the dual-object report deficit in brief displays was the foundational phenomenon upon which the concept of object attention was developed (Duncan, 1984; Desimone & Duncan, 1995). However, other processes may provide alternative explanations or make contributions, including concurrent task effects and memory demands. Many concurrent paradigms use quite dissimilar tasks or stimuli and responses in distinct modalities (Broadbent, 1982; Kahneman, 1973; Pashler, 1990). In the case of object attention, the stimuli, tasks, and reports are identical or nearly identical. The processing system may include serial bottlenecks in perception or response (Meyer & Kieras, 1997; Pashler, 1994; Pashler & Johnston, 1998), or shared capacity (Kahneman, 1973; Wickens, 1991; Bonnel, Stein, & Bertucci, 1992) or shared sampling (Hafter, Bonnel, Gallum, & Cohen, 1998) between tasks. These possible alternative or augmented interpretations are considered in the discussion.

1.4 Overview

This paper seeks to test the proposal (Han, Dosher, & Lu, 2003) that object attention effects – in this case dual-object report deficits – are increased with the demands of multiple reference frames for judgment and reduced or eliminated when judgments involve the same reference frame. The proposal stands in opposition to the classic claims (Duncan, 1984, 1993a, b), which dismissed a significant influence of the features being judged. These results by themselves might have been attributed to a match in dimension of judgment, but the pattern in the literature as a whole suggested that the explanation might reside in the judgment frame as well as dimension.

The current paper examines the conditions under which dual-object report deficits occur in same-dimension judgments. Previous experiments (e.g., Han et al, 2003) contrasted single-object single report (i.e., either phase or orientation) and single-object dual-report conditions (i.e., phase and orientation for a single object) with dual-object dual-response conditions (i.e., phase for one object and orientation for another). Single-dimension manipulations of judgment frame must involve the comparison of single-responses to dual-object dual-response conditions (i.e., reporting a single orientation of one object to reporting the orientations of both). This comparison should provide a good estimate of the dual-object report deficit, since previous experiments consistently showed that single-object single-responses and single-object dual-responses were nearly equivalent (Duncan, 1984, 1993a, Han et al., 2003). In any event, this is the only available within-dimension measure of object attention. The alternative requires the construction of complex, composite stimuli with two independently varying components of orientation that are known to be subject to configuration effects.

Experiment 1 repeated the two-object, same response (orientation, orientation) condition of Han et al. (2003) for orientation judgments with a vertical or horizontal judgment base angle for the two Gabor objects. Experiment 2 directly manipulated the consistency of judgment frames for orientation judgments for two diagonal Gabor objects. The dual-object effect was evaluated in zero and high external noise for matching or “congruent” frames: two right or two left diagonal base angles (/ / or \ \), or in mismatching or “incongruent” frames: one of each diagonal base angle (\ / or / \). Finally, Experiment 3 changed task demands by requiring more precise discriminations for the diagonal angles. These studies collectively replicate and extend the reduction of the dual-object report deficit through the use of congruent judgment frames, and of larger dual-object report deficits for incongruent frames. Introducing high precision demands for judgment can also re-engage a dual-object deficit, even when the judgment frames are congruent. The results are related to the three signature performance patterns of the perceptual template model (Dosher & Lu, 2000a, b; Lu & Dosher, 1998, 2008).

2. Materials and Methods

2.1 Subjects

A total of 17 observers, naïve to the purpose of the experiments, were recruited and paid for their participation (4 in Experiment 1-A; 4 in Experiment 1-B; 5 in Experiment 2, 4 in Experiment 3). All observers had normal or corrected-to-normal vision. Written informed consent was obtained from each of the observers under a protocol approved by the UC Irvine Institutional Review Board. Sufficient data were collected to support individual observer analysis as well as aggregate analyses.

2.2 Stimuli and Displays

Each display contained 2 oriented Gabor patches, one on each side of fixation. Observers were asked to make an orientation judgment about the target cued by a small central arrow in the single-report condition or give the first response to the cued target and the second response to the other target in dual-report condition.

The locations of the Gabor (signal) and external noise stimuli were marked by two framed circles with a diameter of 2°, centered at 5° eccentricity from fixation. Black cardboard with a circular aperture was used to mask edges of the monitor. The target Gabors were tilted θ degrees clockwise or counter-clockwise of a specified base angle, or judgment frame, ω. In different experiments or conditions, ω was set either to be vertical (ω=0°) or horizontal (ω=90°), or the left (ω=−45°), or the right diagonal (ω=45°). For horizontal and vertical judgment frames, θ=±8°; for the diagonal judgment frames of Experiment 2, θ=±18°. Experiment 3 used the θ=±8° orientation judgments, which were quite demanding in reference to diagonal judgment frames. Sample stimuli and the procedure are illustrated in Figure 3.

Figure 3.

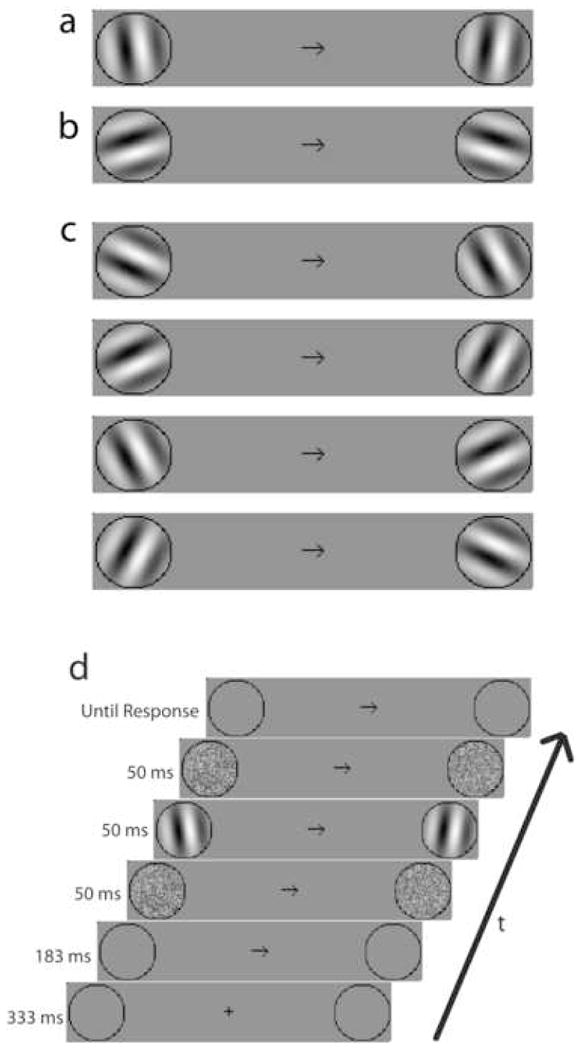
Examples of oriented Gabors used in different experiments, with a sample response cue. Observers reported the orientation (tilted θ degrees clockwise or counter-clockwise of a specified base angle, or judgment frame, ω) for the cued object (single-object) or for the cued object first (dual-object report condition). (a) Sample Gabors tilted clockwise (right) or counterclockwise (left) of vertical, from Experiment 1A. (b) Sample Gabors tilted clockwise (right) or counterclockwise (left) of horizontal, from Experiment 1B. (c) Sample Gabors tilted clockwise (left) and counterclockwise (right) of left diagonal (top), of the right diagonal (top-middle), or of the left-right diagonals (bottom-middle), or the right-left diagonals (bottom), from Experiments 2 and 3. (d) A sample trial sequence with high external noise, beginning with a fixation cross, a cue for first response, a sequence of noise-Gabor-noise frames, and finally a response cue. For zero noise conditions, the noise frames are replaced with neutral gray frames. For the object on the left of the display, subjects pressed the ‘f’ (clockwise) or ‘d’ (counterclockwise) key with the left hand; for the object on the right of the display, subjects pressed the ‘k’ (clockwise) or ‘j’ (counterclockwise) key with the right hand.

Each oriented Gabor was rendered on a 48 × 48-pixel grid:

$$\ell (\text{x},\text{y})={\ell }_0\{\{1.0+\text{c}·sin\{2\pi \text{f}[(\text{x}cos(\omega \pm \theta )+\text{y}sin(\omega \pm \theta )\}exp(-\frac{{\text{x}}^2+y^2}{2{\sigma }^2})\}\}$$

where x and y reference spatial positions within the 48 × 48-pixel grid, f=0.96 - 14 - cycles/degree (1/20 pixels) is the center frequency of the sine wave, which is spatially windowed by a Gaussian with standard deviation of σ = 0.542° (13 pixels), c is the maximum contrast of the sine wave, and ℓ₀ is the mid-gray contrast level. The diameter of 48 pixels corresponds to 2° of visual angle when viewed at ≈70 cm from the screen.

In the high external noise conditions, one signal frame was sandwiched between two noise frames and combined via temporal integration (Dosher & Lu, 2000a, b). The external-noise frames were composed of 2 × 2 pixel noise elements whose contrasts were drawn at random with a mean of 0 and a standard deviation of 0.333 of the highest contrast level – an approximation to Gaussian ‘white noise’. Noise frames were the same size as the signal Gabor frames. Both signal and external noise frames were circularly windowed at a diameter of 48 pixels. The fixation mark was a cross with arm-lengths of 0.125° and the report cue was an arrow originating at the center of fixation and extending 0.25° pointing towards one of the two object locations.

2.2 Apparatus

The experimental displays were controlled with a Macintosh G4 computer by Matlab programs with PsychToolbox (2.53) real-time control subroutines (Brainard, 1997; Pelli, 1997). The stimuli were presented on an HP 91 color monitor set to a spatial resolution of 640 × 480 with a refresh rate of 120Hz. A special circuit (Li, Lu, Xu, Jin, & Zhou, 2003) combined the outputs of two 8-bit graphic channels to produce 14 bits pseudo-gray-level resolution. The luminance levels of the display were gamma-corrected using a psychophysical procedure. The mean luminance l₀ was 44.7 cd/m², with the minimum luminance of 0 cd/m² and the maximum luminance of 89.4 cd/m². All displays were viewed binocularly with natural pupil at a viewing distance of approximately 70 cm in a dimly lighted room.

2.3 Experimental Design

These experiments measured full psychometric functions for two report conditions, single-report and dual-report. Each display consisted of two objects (Gabor patches), one to the left and one to the right of fixation. For single-report conditions, a central arrow cue indicated the target for report; for the dual-report condition, the arrow cue indicated the first one of two targets to report. The experiments tested two external noise conditions, no noise and high noise. Psychometric functions were estimated from seven signal contrast levels, separately chosen for no and high external noise based on pilot data to measure performance accuracy from chance level to asymptotic levels. Gabor contrasts ranged from 0.02 to 0.21 in no external noise and from 0.04 to 0.95 in high external noise.

Experiment 1A and 1B tested horizontal and vertical judgment frame displays, and used discrimination angles of θ=±8°. In these experiments, each session consisted of 2 sub-sessions, counterbalanced, one for the single report and the other for the dual-report conditions. Each dual-report sub-session had 504 trials, 3 blocks of 168 trials. Each block was composed of 2 noise conditions, 2 location cue conditions, 7 signal contrast levels, and 6 repetitions. Each single-report sub-session had 1008 trials, 3 blocks of 336 trials. Each block was composed of 2 noise conditions, 2 location cue conditions, 7 signal contrast levels, and 12 repetitions. Each observer participated in one practice session, followed by four experimental sessions, yielding a sample size of 144 trials per point on each psychometric function for each observer.

Experiments 2 and 3 tested four conditions of diagonal reference frames (congruent: / / or \ \, or incongruent: \ /, or / \) tested in separate blocks, and either θ=±18° (Experiment 2) or θ=±8° (Experiment 3, which used square location marks to achieve measurable thresholds.) Each session had two sub-sessions, one for single-report and one for dual-report, counter-balanced over days. In each sub-session, there are four blocks of judgment-frame combinations displayed randomly. Five practice trials were given at the beginning of each different judgment-frame block. In single-report condition, there were 336 trials in one block. Dual-report blocks had 168 trials. The whole session took 75 minutes approximately. Each observer in Experiment 2 completed one practice and eight experimental sessions, yielding a sample size of 96 trials per point on each psychometric function for each observer, derived from 96 trials in single-report and 48 trials (96 responses) in dual-report per external noise, signal contrast and cued location conditions. Each observer in Experiment 3 completed 1 practice and six experimental sessions, yielding sample sizes of 72 per point on each psychometric function for each observer. Experiments 2 and 3 combined two congruent (e.g., \ \ and / /) and two incongruent (e.g., \ / and / \) frame conditions, after finding no differences between them, so the effective sample sizes for each point on the psychometric functions for each observer were twice those listed here, or 192 and 144, respectively.

2.4 Procedure

Each block began with an instruction screen indicating the judgment frame and report condition and a sample stimulus layout. The trial display sequence (Figure 2d) included: a 333 ms display with a central fixation cross and two outline circles indicating the stimulus locations; an 183 ms pre-cue display with an arrow cue pointing to the left or right; a first 50 ms noise (or blank) display; a 50 ms signal display with two tilted Gabor patches within the circles; a second 50 ms noise (or blank) display; and a post-stimulus report cue that was identical to the pre-cue remaining on the screen until the first response. If the target was on left side of fixation, observer pressed “d” for the orientation tilted counterclockwise and “f” for clockwise with the left hand; the corresponding responses to the right target, made with the right hand, were “j” and “k”.

2.5 Statistical Analysis and Model Fit

Each experimental condition measured two seven-point psychometric functions for each observer: a single-object single-response condition and a dual-object two-response condition. The dual-object report deficit occurs when the psychometric function of the dual-object condition yields significantly worse performance, corresponding to higher contrast thresholds. The two psychometric functions were fit with two Weibull functions:

$$p=min+(max-min)\times \left(1-2^{-{(x/\alpha )}^{\rho }}\right)$$

In this function, p is the correct percentage, x is the signal contrast level, min is the accuracy at chance level (0.5 in these experiments), max is the asymptotic level of accuracy at high contrasts, α is a location (shift) parameter, and ρ is a slope parameter. The Weibull function provides an excellent empirical description of the psychometric functions, and is the basis of estimating contrast thresholds, e.g., at the 79% accuracy level, from interpolation. Two Weibull functions differing in location and maximum³ (with 2 α, 1 ρ, and 2 max) form a fuller model of a pair of single-report and dual-report conditions. Statistically equivalent pairs can be well described by a single Weibull (1 α, 1 ρ, and 1 max) for both report conditions, which is the reduced model in a nested model test. We fit the percent correct data using both least squares and maximum likelihood methods, as described in Appendix A. The results were essentially identical.

The perceptual template model provided a quantitative model for the data. It was fit to the percent correct data in all four conditions simultaneously (zero and high external noise and single and dual report) using either least squares or maximum likelihood. There were common parameters (β, N_m, N_m, and γ, respectively, the match to the signal stimulus, internal multiplicative noise, internal additive noise, and nonlinearity factor) that applied to all conditions, and weighting parameters A_m or A_a or A_f for the dual-object reports in congruent and incongruent frame conditions. The same nested-model logic is used to test different variants of the perceptual template model.

3. Results

3.1 Experiment 1A-B

Experiment 1 replicated and extended the finding of small to negligible dual-object effects for conditions with matching judgment frames in Han, Dosher, & Lu (2003). It tests moderately precise orientation discriminations, θ±8° about the horizontal or vertical axis (with circular location markers) in zero and high external noise.

Figure 4 shows the psychometric functions, averaged over observers, for single-object single-report and dual-object dual-report conditions in high and no external noise for vertical (Experiment 1A, top panels) and horizontal (Experiment 1B, bottom panels) reference frames. The error bars show 85% confidence intervals based on binomial variability of each observed probability. Consistent with the previous findings, the dual-object deficit for these congruent judgment conditions is small and generally non-significant in individual data, although small differences emerge as significant in the aggregate data. Nested Weibull tests were used to determine whether each pair of psychometric function curves in Figure 4 was statistically different or the same. The dual-object report deficits were statistically non-significant (p > .2) for all but one individual observer in zero noise and for all observers in high noise. The very small differences primarily at asymptote became significant in aggregate data in both zero and high noise. The threshold estimates at 79% are correspondingly essentially equivalent in single-object and dual-object conditions. Overall, these results extend those of Han et al. (2003) for same dimension judgments.

Figure 4.

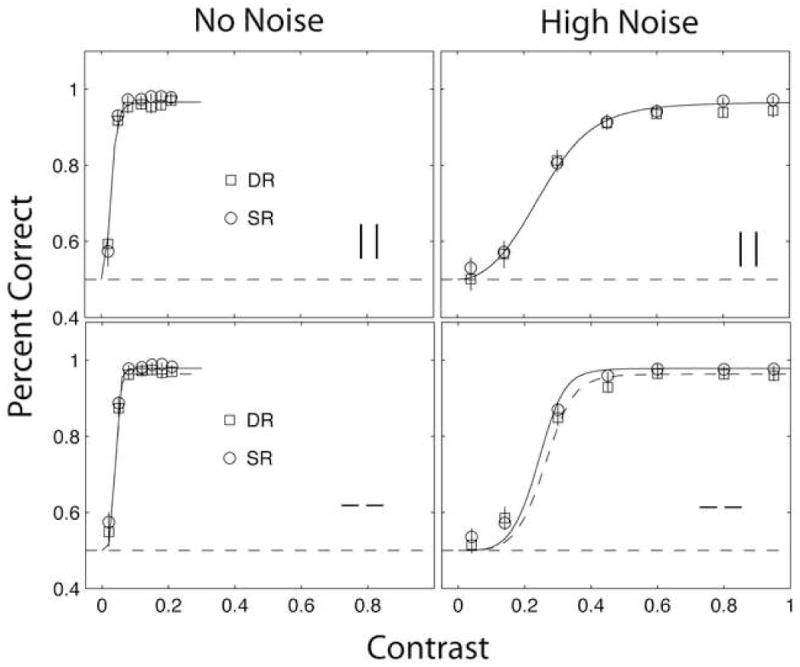
Average psychometric functions for single-object and dual-object report for congruent judgment frames, from Experiments 1A and 1B. (top panels) Psychometric functions for Experiment 1A using vertical base angles in zero (left) and high (right) external noise. (bottom panels) The same psychometric functions for Experiment 1B using horizontal base angles for judgment. Note the different scale of the contrast threshold axis in zero noise (0 to 0.4) and high external noise (0 to 1.0). Error bars (some smaller than the symbols) correspond to the 85% confidence intervals based on binomial variability. The dual-object report deficit was not significant for individual observers by Weibull tests. Smooth curves show the fits of a perceptual template model (see text).

The smooth curves in Figure 4 show best fits of a perceptual template model. The best-fitting perceptual template models for individual data (Dosher & Lu, 1999; Lu & Dosher, 1998, 2008) were either a no-difference model, or one with small asymptotic effects of dual-report on the psychometric function. These asymptotic effects were fit with a multiplicative noise factor, A_m for dual-object conditions. The best fitting perceptual template model parameters included the gain for the signal stimulus β, an internal additive noise factor N_a, an internal multiplicative noise factor N_m, and a nonlinear transduction parameter γ. This model fits the data for single-object and dual-object performance in both zero and high external noise all together. Even in a fully saturated model {N_m, N_a, β, γ, A_mC, A_aC, A_fC}, where the C subscripts indicate that these are congruent frame conditions, the attention modulations of stimulus enhancement (internal additive noise), A_a and external noise exclusion, A_f, were often estimated to be 1, for no effect. The best-fitting {N_m, N_a, β, γ, A_mC} model had estimated parameters of 0.235, 0.001, 1.642, 2.328, and 1.150 with an r² of 0.9897 for the average horizontal data and had estimated parameters of 0.254, 0.001, 1.482, 2.114, and 1.141 with an r² of 0.9874 for the average vertical data. Several, but not all, individual observers show a small but significant effect of multiplicative noise increase for dual-object conditions, while others show no significant effect. The estimated parameter values for the 5-parameter model and significance values are shown in Tables 1 and 2⁴. The extended perceptual template model for non-orthogonal targets provided an essentially equivalent fit with slight variations in β′-values in dual-report conditions. This alternative interpretation is considered in the discussion.

Table 1.

The Perceptual Template Model Fits to Experiment 1A-Vertical.

Parameter	Observers
	AW	KF	KN	SS	AV
Nm	0.295	0.224	0.246	0.224	0.254
AmC	1.166	1.191**	1.178	1.118	1.141**
Na	0.001	0.001	0.001	0.002	0.001
β	1.485	1.795	1.170	1.673	1.482
γ	1.221	2.171	1.985	1.823	2.114
R2fuller	.9744	0.9878**	0.9679	0.9913	0.9934**
R2reduced	.9703	0.9573	0.9666	0.9911	0.9915

Table 2.

The Perceptual Template Model Fits to Experiment 1B-Horizontal.

Parameter	Observers
	CW	GA	SJ	SP	AV
Nm	0.232	0.256	0.234	0.278	0.235
AmC	1.103	1.036*	1.095**	1.151**	1.150*
Na	0.001	0.001	0.001	0.001	0.001
β	1.738	1.639	2.648	2.412	1.642
γ	2.148	2.398	2.237	2.366	2.328
R2fuller	.9946	0.9858	0.9917**	0.9836**	0.9969*
R2reduced	.9942	0.9853	0.9887	0.9787	0.9950

Note:

R^{2 fuller} is for a 5-parameter (full) model:{N_m, N_a, β, γ, A_mC}, corresponding to the listed parameters. This model is statistically equivalent to an even fuller 7-parameter model N_m, N_a, β, γ, A_mC, A_aC, A_fC in most cases, except those marked by ^ζ.

R^{2 reduced} is for a 4-parameter reduced (no difference) model: {N_m, N_a, β, γ, A_mC}. The significance is determined through nested model tests.

To summarize: the dual-object report deficits for these conditions in which observer are making the same judgments – with congruent judgment frames – in the two objects were small and only sometimes significant in an empirical Weibull analysis of the psychometric functions. The perceptual template model attributed any small significant dual-object report deficits to increases in the multiplicative internal noise (or increases in β′) in dual-object conditions at high signal contrasts. Overall, these results are consistent with the claim that shared reference frames for attribute judgment reduce or eliminate dual-object report deficits. In the discussion, we show that the effects are sufficiently small that we can rule out alternative sample size sharing or switching models to account for the data.

3.2 Experiment 2

Experiment 2 manipulated the congruency of the reference frames for the orientation judgments of the two objects with diagonal reference angles. A lower precision discrimination angle about the diagonal, θ=±18° was chosen based on pilot data to allow measurable thresholds for these more difficult diagonal judgments. Figure 5 shows the psychometric functions for congruent frames (/ / or \ \) and incongruent frames (\ / or / \) in zero or high external noise, averaged over four of five observers. Each panel shows the dual-object report deficit by comparing the two single-object and dual-object conditions. The fifth observer (AA) was a clear outlier, and that individual’s results are discussed separately.

Figure 5.

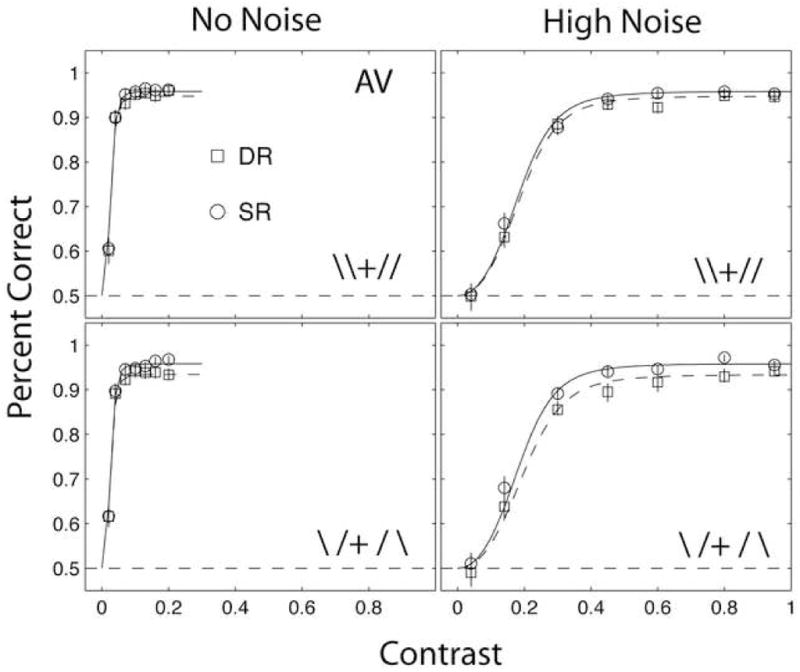
Average psychometric functions for single-object and dual-object report for congruent and incongruent judgment frames, from Experiment 2. Congruent (top panels) and incongruent (bottom panels) judgment frame conditions are shown for zero (left) and high (right) external noise conditions. Note the different scale of the contrast threshold axis in zero noise (0 to 0.4) and high external noise (0 to 1.0). Error bars correspond to the 85% confidence intervals based on binomial variability. Incongruent judgment frame conditions show significant dual-object report deficits, especially in high external noise in Weibull tests. Dual-object report deficits are reduced in congruent judgment frame conditions. Effects are largest in high external noise. Smooth curves show the fits of a perceptual template model (see text).

The data of observer AA are shown in Figure 6. This observer showed unusually large dual-object report deficits that were somewhat larger for incongruent frames, but were substantial and significant in all conditions. We have no explanation for the enormous dual-object report deficits exhibited by this observer.

Figure 6.

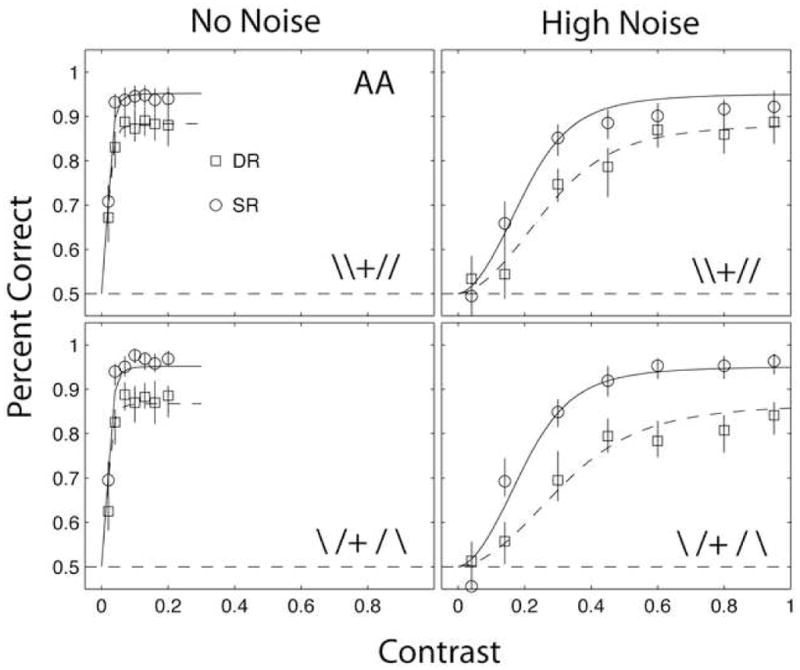
Result for an unusual individual observer in Experiment 2. Observer AA exhibited unusually large dual-object effects in all conditions. The scale of the contrast threshold axis is different in zero noise (0 to 0.4) and high external noise (0 to 1.0). Error bars correspond to the 85% confidence intervals based on binomial variability. Smooth curves show the fits of a perceptual template model (see text).

Dual-object report deficits were significant primarily for the inconsistent frames in high external noise in nested Weibull tests. In the congruent frame conditions, neither the aggregate data nor any of the four individual observers showed a significant difference (all p > .2) in either zero or high external noise. In contrast, in the incongruent frame conditions, both the aggregate data and all observers showed significant (or marginal) differences between single and dual-object reports (all p < .05 except for observer TS, where p < .10). The asymptotic accuracy (max) and location (α) of the Weibull - 22 - functions⁵ and the 79% contrast thresholds estimated for each condition are shown in Figure 7. The dual response versus single response measures of threshold, location, and max, are graphed for zero noise and high noise conditions, for congruent frames and incongruent frames. The error bars are derived with Monte Carlo methods based on simulated binomial variance of each observed probability in the psychometric functions (see Appendix A).

Figure 7.

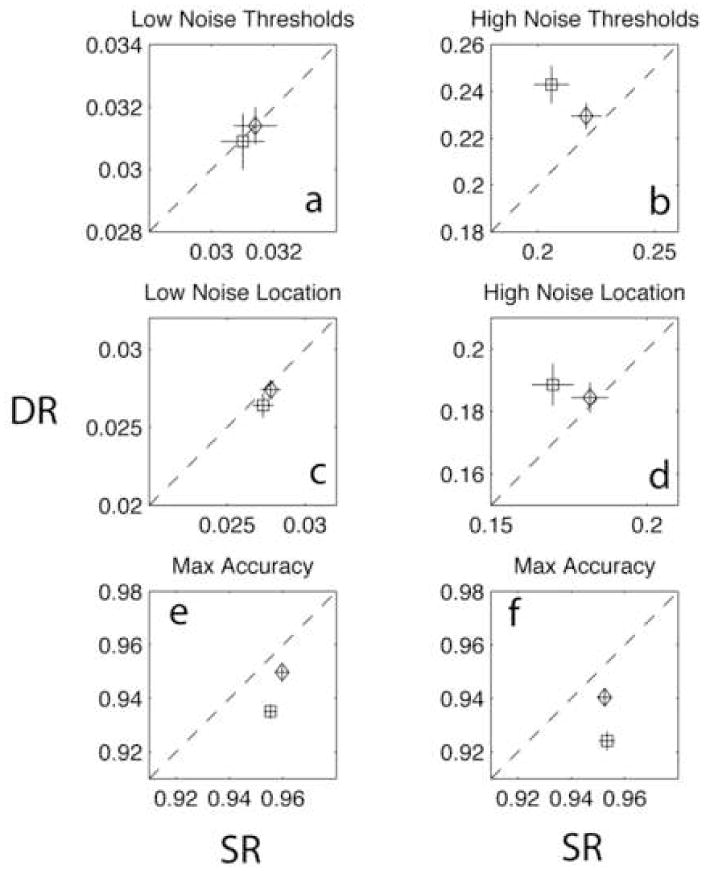
Contrast thresholds at 79% correct (panels a-b) and Weibull location (α_i) (c–d) and maximum accuracy (e–f) parameter estimates (see text) for the average psychometric functions, Experiment 2 (Figure 5), for low (left) and high (right) noise. Dual-object (DR) performance is plotted against single object (SR) performance, with triangles for congruent frames (/ / or \ \) and squares for incongruent frames (/ \ or \ /) data. Error bars show ±1σ estimated from Monte Carlo methods.

Empirical contrast thresholds showed consistent dual-object dual-report deficits only for incongruent frames in high external noise, although small effects in the asymptote of the psychometric functions were observed in all conditions. The average 79% thresholds in zero noise were 0.031 and 0.031 for congruent frame single- and dual-reports, respectively, and were 0.031 and 0.031 for incongruent single- and dual-reports, respectively (errors about ±0.002 in each case). The average thresholds in high noise were 0.221 and 0.229 for congruent frame single- and dual-reports, respectively, and were 0.206 and 0.243 for incongruent single- and dual-object reports, respectively (±0.006). Excluding AA⁶, the dual-object attention yielded about a 20% increase in threshold for incongruent frames in high external noise. These empirical threshold elevations combine the effects of asymptotic differences in max (Figure 6e–f) and ‘location’ (threshold relative to max) in the Weibull (Figure 6c–d). Excluding AA, the Weibull model tests indicated a dual-object effect for incongruent, but not congruent frames in both zero and high external noise

The perceptual template model fits initially considered three possible attention mechanisms: stimulus enhancement in low noise, external noise exclusion in high noise, and multiplicative noise alteration in both low and high noise at high stimulus contrasts. Attention factors A_a, A_f, and A_m greater than one indicate higher noise limiting performance in dual-response conditions relative to single-report conditions (set to 1.0), separately estimated for congruent and incongruent frame conditions. The smooth curves in Figures 5 and 6 show the fits of the perceptual template model. The best-fitting perceptual template model parameter values for the average data were: N_m= 0.285, N_a = 0.002, β = 2.107, and γ = 1.98. Two attention mechanisms were significant: the multiplicative noise factors A_m were estimated as 1.07 and 1.15 for congruent and incongruent frames and external noise exclusion factors A_f were estimated as 1.04 (ns) and 1.127 for congruent and incongruent frames. Stimulus enhancement had no significant effects (all A_a ≈ 1.0). This model yielded an r² of .9843 for the average data. The estimates for individual observers and the average for this model are listed in Table 3. An alternative model of psychometric asymptote holds A_m=1 and introduces β′ > 0 for non-orthogonal targets and larger β’s, or loss of template precision, in dual-object conditions. Since the θ=±18° stimuli are relatively dissimilar, single-object β’s were approximated as 0, and β’s for dual-object dual-responses were estimated as 0.009 and 0.021, respectively, along with A_fs of 1.086 and 1.239 for congruent and incongruent judgments. The estimates of β (2.149) and other parameters were similar in the two models. This alternate (non-nested) model had an r² of .9872. These two model interpretations are treated in the discussion (section 4.4).

Table 3.

The Perceptual Template Model Fits to Experiment 2.

Parameter	Observers
	AA	PM	JP	TS	JC	AV
Nm	0.301	0.320	0.294	0.238	0.278	0.286
AmC	1.394**	1.001	1.076◊	1.106◊	1.151*	1.068*
AmI	1.490**	1.168	1.142*	1.105◊	1.228*	1.152**
Na	0.004	0.002	0.005	0.001	0.001	0.002
β	1.983	1.645	1.664	2.648	2.412	2.032
γ	1.692	1.905	2.531	2.354	2.366	2.099
AfC	1.440*	1.032	1.085	1.010	1.010	1.023
AfI	1.730**	1.015**	1.250*	1.150◊	1.061	1.110**
R2fuller	0.9504	.9603	0.9819	0.9521	0.9653	0.9843
R2reduced	0.9402	.9602ns	0.9818 ns	0.9520ns	0.9653ns	0.9843ns

Note:

The average data AV excludes outlier observer AA. R²_fuller is for a 10-parameter (full) model:{N_m, N_a, β, γ, A_mC, A_mI, A_aC, A_aI, A_fC, A_fI}. R²_reduced is for a 7-parameter reduced model: {N_m, N_a, β, γ, A_mC, A_mI, A_fI}. The reduced model, for which parameter estimates are shown, provided an excellent account of the data, resulting in a non-significant reduction from R²_fuller to R²_reduced (indicated by the ^ns for the R²_reduced), except for observer AA. Other forms of reduced models tested for individual significance of A_mC, A_mI, A_fC, or A_fI through nested F-tests. Any attention parameter (A_mC, A_mI, A_fC, A_fI) significantly greater than 1.0 is marked with ^◊ <.10, *<.05, or **< .01. The fuller model fit marginally better for observer AA, with A_aC estimated as 1.424, and A_aI estimated as 1.619 in the full model and otherwise nearly equivalent parameter estimates.

In summary: For these low-precision orientation judgments, modest dual-object report deficits occurred for incongruent judgment frames in high external noise, and incongruent conditions showed small asymptotic deficits in the psychometric functions. In contrast, dual-object report deficits were (except for AA) very small or non-significant for congruent judgment frames. There was larger than typical individual observer variation, including one observer (AA) who showed comparatively very large dual-object report deficit in all conditions but slightly larger in the incongruent conditions. These effects were estimated as a combination of small increases in multiplicative internal noise or, alternatively, template broadening that is coupled with an effect of reduced external noise exclusion seen in incongruent frame conditions.

3.3 Experiment 3

Experiment 3, like Experiment 2, directly tested the influence of judgment congruency on the dual-object report effect, and tested higher precision orientation judgments for diagonal orientations θ=±8°. It is possible that dual-object deficits occur in a wider range of circumstances in very challenging tasks. Square, rather than circular, noise frames and location markers were used. While the change in location frames introduces a change in addition to that of task precision from Experiment 2, pilot data collected with circular frames and various degrees of higher precision orientation judgments led to quite poor performance, and difficulty achieving threshold levels even at the highest contrasts. We felt that the effects of judgment congruency would be difficult to assess under these conditions.

Figure 8 shows the psychometric functions for congruent (\ \ or / /, top) and incongruent (\ / or / \, bottom) diagonal reference frames in zero or high external noise, averaged over observers for Experiment 3. Dual-object report deficits occurred for both congruent and incongruent judgment frames, although the size of the deficit is slightly larger for the incongruent frames. Almost all subjects individually and the aggregate data showed a significant difference between single-object reports and dual-object reports in both zero and high external noise and for both congruent and incongruent judgment frames (all p < .05, some p < .01 except for HT for congruent, zero noise, ns, and p < .10 for LH for congruent, high noise) in nested Weibull tests. The average 79% thresholds in zero noise were 0.037 and 0.042 for congruent frame single- and dual-reports, respectively, and were 0.037 and 0.041 for incongruent single- and dual-reports, respectively (±0.003). The average thresholds in high noise were 0.294 and 0.375 for congruent frame single- and dual-reports, respectively, and were 0.300 and 0.380 for incongruent single- and dual-object reports, respectively (±0.01). All cases showed dual-object reductions in asymptote. The estimated thresholds, location and max parameters from the Weibulls are shown in Figure 9. In low external noise, the dual-object contrast thresholds were about 10% higher for both congruent and incongruent conditions. In high external noise, the contrast thresholds increased an average of 20% for congruent frames and by an average of about 30% for incongruent frames. As in Experiment 2, these effects reflected differences in asymptotic accuracy (max) and/or location (α).

Figure 8.

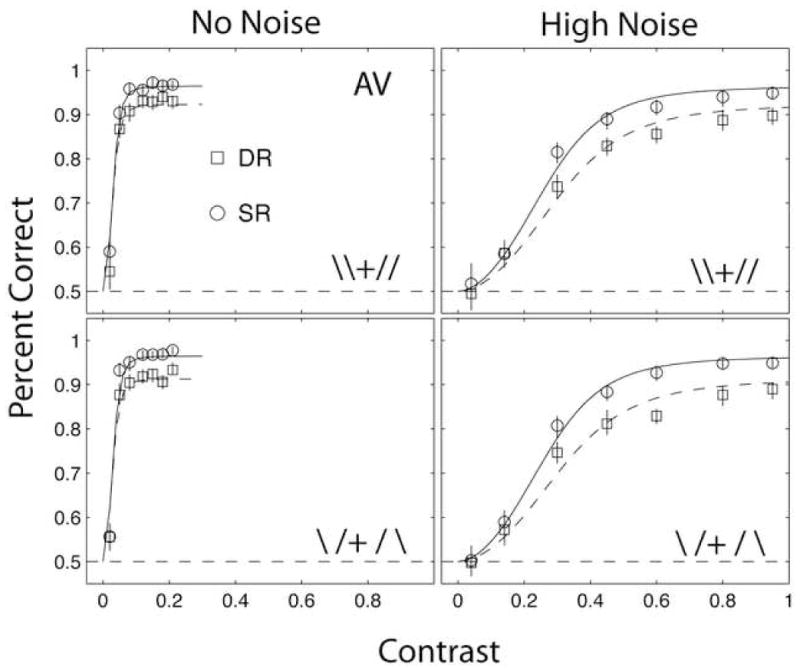
Average psychometric functions for single-object and dual-object report for congruent and incongruent judgment frames, from Experiment 3, which used very demanding orientation judgments. Congruent (top panels) and incongruent (bottom panels) judgment frame conditions are shown for zero (left) and high (right) external noise conditions. Dual-object report deficits occur for both incongruent and congruent frames and are largest in high external noise. Error bars correspond to the 85% confidence intervals based on binomial variability. Smooth curves show the fits of a perceptual template model (see text).

Figure 9.

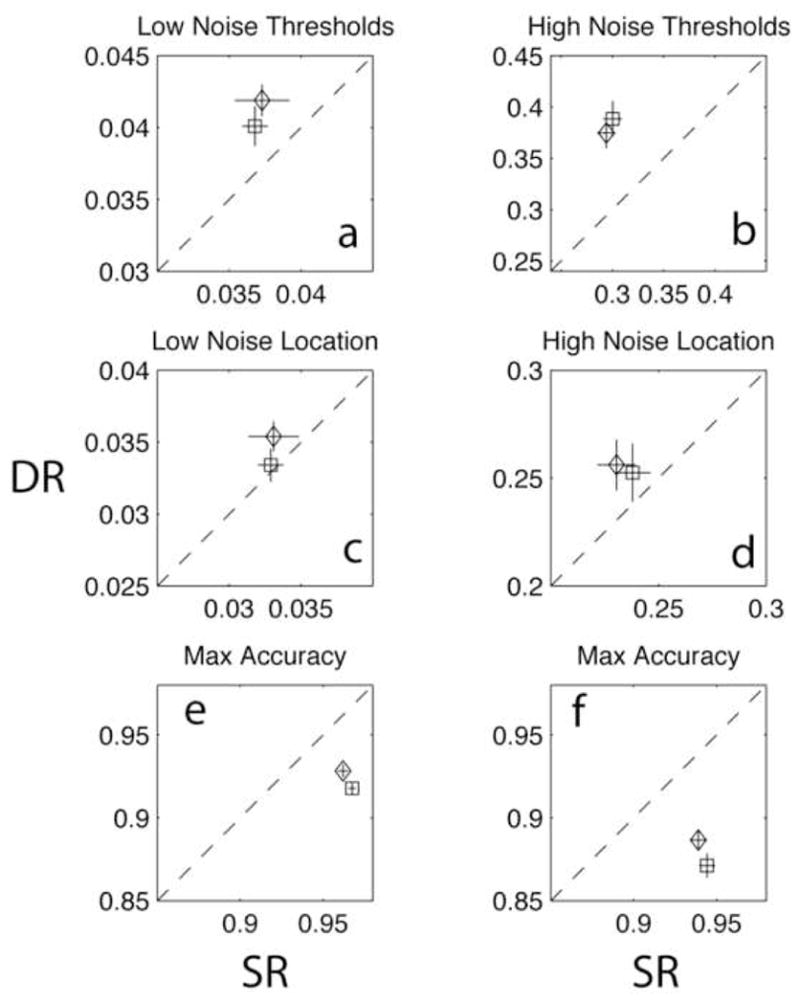
Contrast thresholds at 79% correct (panels a–b) and Weibull location (α_i) (c–d) and maximum accuracy (e–f) parameter estimates for the average psychometric functions, Experiment 3 (Figure 7), for low (left) and high (right) noise. Dual-object (DR) performance is plotted against single object (SR) performance, with triangles for congruent frames (/ / or \ \) and squares for incongruent frames (/ \ or \ /) data. Error bars show ±1σ estimated from Monte Carlo methods (see text).

The smooth curves in Figure 8 show the best fitting perceptual template model to the psychometric functions. The estimated parameters for the average data were: N_m= − 26 - 0.277, N_a = 0.003, β = 1.502, and γ = 1.827. For the aggregate data, the estimated multiplicative noise factors A_m were 1.264 and 1.327 for congruent and incongruent frames, and external noise exclusion factors A_f were 1.198 and 1.236 for congruent and incongruent frames. Stimulus enhancement had no significant effects (all A_a ≈ 1.0). The r² was 0.9775 for the average data, with estimates for individuals and the average listed in Table 4. The perceptual template model for non-orthogonal targets is more compelling here given the very similar (θ=±8°) targets for which a single-response conditionβ′ >0 must be estimated. By setting the starting parameter values based on the A_m model, we found a competitive fit (r² =0.9779 for the average data) of the elaborated model with β =1.544, and β′ =0.257 for single responses and β’s of 0.661 and 0.707, respectively, and A_f of 1.092 and 1.116 for congruent and incongruent dual-object reports. This identifies considerably less precise templates in dual-object dual-report conditions ⁷.

Table 4.

The Perceptual Template Model Fits to Experiment 3.

Paramters	Observers
	HT	JK	LH	XW	AV
Nm	0.318	0.317	0.215	0.244	0.277
AmC	1.059*	1.262**	1.296*	1.538**	1.260**
AmI	1.031*	1.383**	1.265*	1.812**	1.327**
Na	0.002	0.002	0.005	0.002	0.003
β	1.460	1.456	1.876	1.263	1.502
γ	1.976	2.040	1.657	1.830	1.830
AfC	1.289*	1.250*	1.000	1.310*	1.198◊ζ
AfI	1.270*	1.251*	1.202◊ζ	1.267*	1.235*
R2fuller	.9695	0.9583	0.9770	0.9635	0.9782
R2reduced	.9694ns	0.9562ns	0.9766ns	0.9653ns	0.9775ns

Note:

The average data AV excludes outlier observer AA.

R²_fuller is for a 10-parameter (full) model:{N_m, N_a, β, γ, A_mC, A_mI, A_aC, A_aI, A_fC, A_fI}.

R²_reduced is for a 7-parameter reduced model: {N_m, N_a, β, γ, A_mC, A_mI, A_fI}. The reduced model, for which parameter estimates are listed, provided an excellent account of the data, with non-significant reductions from R²_fuller to R²_reduced. Other forms of reduced models tested for individual significance of A_mC, A_mI, A_fC, or A_fI through nested F-tests. Attention parameters (A_mC, A_mI, A_fC, A_fI) significantly greater than 1.0 is marked with ^◊ <.10, *<.05, or **< .01. In several cases marked with ^ζ there was a tradeoff between the values of A_m’s and A_f’s, however eliminating A_f resulted in systematic misfits to the data.

In summary: both congruent and incongruent judgments show significant dual-object report deficits in this higher precision discrimination, as indicated in Weibull tests. The perceptual template model reveals increases in multiplicative noise or, alternatively, reductions in template precision as well as less efficient external noise exclusion in dual-object conditions. The estimated attention factors are slightly higher in incongruent than in congruent conditions, corresponding to average increases in thresholds in high external noise of about 20% and 30% for congruent and incongruent frames, respectively.

4. Discussion

4.1 Summary

Object attention is widely considered one of the most important phenomena in attention, with consequences measured in behavior and in neuroscience. Han, et al. (2003), in a behavioral analysis of object attention in a dual-object report paradigm, found a ‘same response’ condition (either two orientation judgments relative to the vertical or two phase judgments) that substantially reduced or eliminated the predicted dual-object limitations. The goal of the current project was to directly test whether object attention deficits were modulated by the congruency of judgment frame applied to the two objects within a particular feature or dimension, in this case orientation. We also evaluated whether the object attention effects depend upon the required precision of discrimination.

Experiment 1 extended the previous finding of Han et al. for same-frame orientation judgments for vertical and horizontal base angles. In both of these congruent-frame cases, the dual report effects were extremely small and generally not significant for individual observers. The estimated thresholds were essentially identical in single object single report and dual-object dual report conditions.

Experiment 2 explicitly manipulated the congruency of the judgment frames for the two objects and required a relatively low precision discrimination (θ=±18°) about diagonal angles. Dual-object report deficits were consistently observed for the incongruent report conditions, but – consistent with the prediction – were either quite small or non-significant in individual observers for the congruent report conditions. The dual-object report deficits were largest in high external noise, where they increased the contrast thresholds by about 20%. One unusual observer showed enormous dual-object report deficits in all conditions even for this low-precision task. We have no specific explanation for the difficulties of this observer, although there is some indication that dual-object effects exhibit larger individual variation in magnitude than do similar measurements of spatial cuing effects. The mechanisms of the dual-object attention loss identified by the perceptual template model are discussed in section 4.4.

Experiment 3 evaluated the dual-object deficit for congruent and incongruent frames in a high precision task (θ=±8°), compared to the relatively lower precision demands (θ=±18°) of Experiment 2, both about diagonal frames. The matched filters for the ±8° judgments have significant overlap (correlation) while the matched filters for the ±18° judgments of Experiment 2 have very little. Contrast thresholds were correspondingly higher and robust dual-object report deficits appeared in both congruent and incongruent frame conditions for this high precision task. The dual-object limitations increased thresholds by about 30% for incongruent conditions and by about 20% in congruent conditions in the average data. Again, see section 4.4 on the perceptual template model for a discussion of the attention mechanisms.

The effects for incongruent orientation-orientation judgments reported in Experiment 2 generally appear smaller than the incongruent cross-dimension orientation-phase judgments of Han, et al. (2003), which are as large or larger than those for the high precision task in Experiment 3.

Our experiments investigated the roles of judgment congruency and task precision in dual-object report deficits. We show effects of both. The studies are methodologically direct analogs of the seminal studies of Duncan (1984, 1993a, b), the inspiration for the theory of object attention – except that multiple contrast levels (full psychometric functions) were measured rather than a single contrast measurement. Alternative explanations of the dual-object report deficits in these studies would also imply alternative explanations for those classic studies of object attention.

The perceptual template model provides a strong framework for understanding these object attention phenomena, as described in 4.4. But first, we consider (and reject) several alternative explanations and comment on some possibly related phenomena.

4.2 Lapses, capacity-limited sample-size sharing, and switching

Any simple limitation on remembering and executing two responses such as a constant ‘lapse rate’ can be ruled out since the size of the dual-report effects depends on task precision and on the congruency of judgment frames. Futher, the observed dual-report deficits are in most cases not compatible with a fixed-capacity model of dual-task processing. A fixed-capacity model divides the total number of independent samples from two stimuli (Luce, 1977, see Hafter, Bonnel, Gallun & Cohen, 1998, for a discussion and an auditory example). If samples are divided between the two objects with probabilities (relative efforts) of p and (1-p), the signal detection limits are:

$${\left[d_{pM}^{\prime }\right]}^2+{\left[d_{(1-p)M}^{\prime }\right]}^2={\left[d_M^{\prime }\right]}^2\text{or}{d}_{DR}^{\prime }=\left(\sqrt{p}{d}_{SR}^{\prime }+\sqrt{1-p}{d}_{SR}^{\prime }\right)/2.$$

To test this model, the relationship between single and dual response max (asymptotic percent correct) was estimated from the empirical Weibull fits to the psychometric functions. Figure 10 shows the dual-object dual-response (DR) asymptotic accuracy graphed against the single-object asymptotic accuracies for individual observers (smaller symbols) and the average (larger symbols). The equal performance (no loss) line is the diagonal. Critically, the curved line demarks the maximum possible accuracies under the model of fixed-capacity loss, which occurs when capacity is shared equally between the two objects (in percent correct equivalents to the d′ relationship above). The model specifies a region of observable relationships with sharing, with much lower minimum accuracies (not shown on the graph) that correspond to pure switching.

Figure 10.

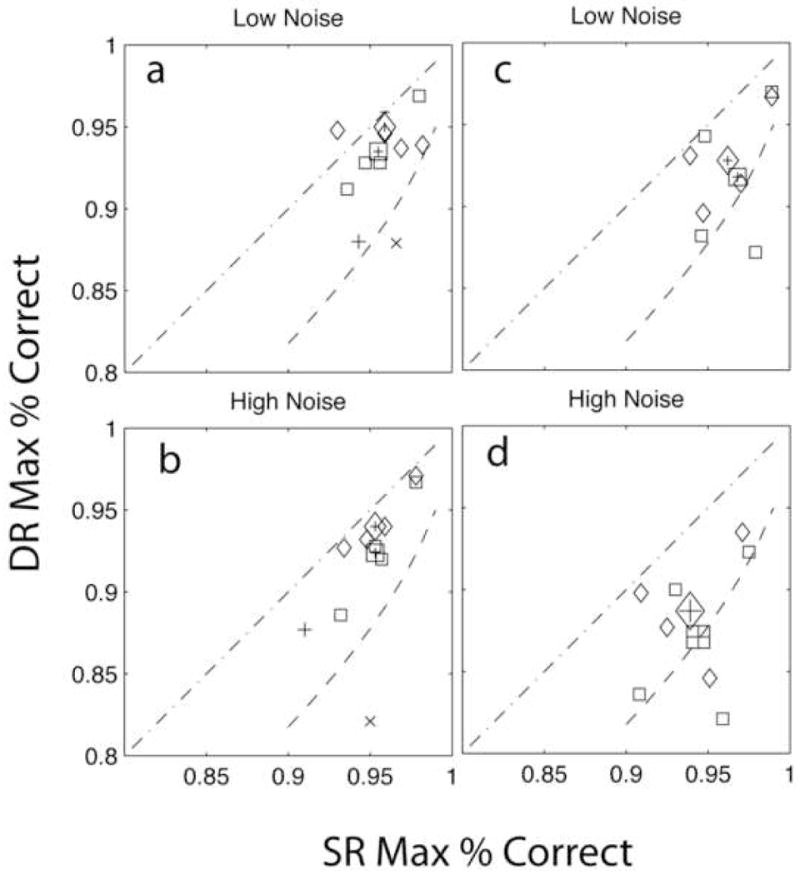
The relationship between the dual-object dual-response (DR) and the single-object single-response (SR) asymptotic accuracies (Weibull max) for congruent frames (diamonds) and incongruent frames (squares) in no noise (a) and high noise (b) for Experiment 2 and in no noise (c) and high noise (d) for Experiment 3. The small symbols are for individual observers, the larger symbols with error bars are for the average. The equal-performance diagonal indicates no loss for the DR condition. The curved line is the maximum performance of the fixed sample-sharing model (Bonnel & Hafter, 1998); the minimum performance range for the fixed sample-sharing model falls below the bottom of the figure.

Figure 10 shows individual and average data for Experiments 2 and 3, which showed the largest dual-object report deficits, in relation to the no-loss diagonal and the sample size sharing model’s maximum performance (curved line). The points for the Experiment 2 (panels a–b) lie well above the fixed-capacity performance region, with the congruent frame data (⋄) closer to the equal performance, no loss, line and incongruent frame data (□) closer – but still not consistent with – the fixed capacity model. In contrast, the outlier observer AA (+ and × symbols) does have performance which is consistent with the fixed-capacity model. The data for the high-precision task of Experiment 3 (panels c–d) still lie well above the fixed-capacity region, although the incongruent frame conditions in high noise approach the upper boundary of the sample-size sharing model. In general, then, all but the few conditions showing the largest dual-object effects exhibit dual-object performance losses that are clearly less than those predicted by the fixed-capacity sample size model. Only the most demanding task condition approaches the best fixed-sample size capacity performance that has been used to explain difficult auditory discriminations (Bonnel & Hafter, 1998; Hafter et al., 1998). These authors, who reported reductions in performance for two judgments consistent with fixed-capacity sample size in some conditions, have attributed these limits to the necessity to maintain multiple memory standards for judgments (Bonnel & Hafter, 1998; Palmer, 1990), a concept quite similar to the idea of a judgment frame.

4.3 Relation to ‘criterion attraction’?

Incongruent judgment frame effects on dual-object dual-responses are distinct from, although perhaps thematically related to, recent reports of constraints on the independent setting of criteria for two simultaneous perceptual decisions (e.g., Gorea & Sagi, 2000, 2005; Gorea, Caetta, & Sagi, 2005), or ‘criterion attraction’. Both have to do with limitations to process two independent stimuli according to different rules. Criterion attraction in detection refers to an inability to hold distinct optimal criteria such that criteria for two judgments converge. The interactions between strong and weak stimuli have especially high impact. Concretely, however, the measured effects are distinct. Criterion attraction is measured in yes/no detection procedures for two objects. Our procedures, in contrast, require identification judgments with different reference frames and few – or at least more subtle – criterion effects. Criterion attraction for two different dimensions (e.g., contrast and orientation) seems to occur within an object, whereas two judgments about the same object (e.g., orientation and phase) were made with little loss in Han et al. (2003). Finally, non-optimal criteria do not necessarily impact the underlying discriminability. So, these thematically related limitations of criterion attraction and limitations of incongruent judgment frame in object attention differ in the nature of the judgments and also have distinct empirical properties.

4.4 Perceptual template model

The perceptual template model provides a framework to interpret and test the underlying attention mechanisms for these dual-object attention phenomena. Perceptual template models were fit to the percent correct data, directly related to d′, to identify the attention mechanisms implicated in object attention. The dual-object report deficits consistently show reductions in psychometric asymptotes. In contrast, the published cases of spatially cued attention have shown an external noise exclusion pattern with converging psychometric asymptotes (center-right, Figure 2) (but see the discussion in section 4.5 below for boundary conditions).

Perceptual template models, originally developed for orthogonal or dissimilar targets (Lu & Dosher, 1998, 2008; Dosher & Lu, 2000a), provided an excellent fit to the data. The perceptual template analysis indicated that dual-object dual-report deficits are mediated by a combination of increases in multiplicative internal noise and reduced external noise exclusion in dual-object conditions relative to single-object reports. The elaborated perceptual template model, which extends predictions to potentially non-orthogonal or similar targets (Jeon, Lu & Dosher, 2008), provided equally good or slightly better accounts of the data, and are more appropriate for precise target discriminations:

$$d^{\prime }\left(c,N_{\mathit{ext}}^2\right)=\frac{S}{N}=\frac{({\beta }^{\gamma }-{{\beta }^{\prime }}^{\gamma })c^{\gamma }}{\sqrt{A_f^2{N}_{\mathit{ext}}^{2\gamma }+A_m^2{N}_m^2[({\beta }^{2\gamma }+{{\beta }^{\prime }}^{2\gamma })c^{2\gamma }+A_f^2{N}_{\mathit{ext}}^{2\gamma }]+A_a^2{N}_a^2}}.$$

Within the elaborated model, dual-object attention is associated with less-sharp target templates. Broadening the template in dual-object conditions causes the β′ to increase, reducing the net signal (β^γ –β′^γ)c^γ and increasing multiplicative noise by the factor $N_m^2{{\beta }^{\prime }}^{2\gamma }{c}^{2\gamma }$ (even while A_m=1) – both causing reductions in the asymptotic levels of the psychometric function. Finally, less sharp templates are conceptually associated with increases in the impact of external noise (A_m > 1). The estimated parameter values for the perceptual template models are quite consistent, estimating higher β′ (and lower β) for high precision than for low precision tasks. Overall, then, the perceptual template model provides a consistent account of these observed effects.

The current pattern of differences in the psychometric function asymptotes in dual-object conditions is an important new finding, especially within the context of the perceptual template model. The proposal that dual-object attention deficits reflect increases in multiplicative noise, either as an independent mechanism of attention, or as a result of template tuning, should be tested further. It would appear that template tuning, in which the broadness of tuning should have related effects on internal multiplicative noise, external noise exclusion, and the net signal strength, could offer a parsimonious account of object attention effects, especially for high precision judgments. The claims of the perceptual template model should be further validated and tested through the constraints from large inter-related data conditions of parametric variations such as those provided by full threshold versus external noise contrast (TVC) measurements at multiple criterion levels, manipulations of target similarity, and a variety of other manipulations (e.g., Lu & Dosher, 2008, for a discussion).

4.5 Relationship to spatial attention phenomena

There are distinct differences between the object attention effects seen in dual-object report deficits reported here and previous similar studies of spatially cued attention. Although the effects on empirical contrast thresholds are similar in magnitude in the two domains, the phenomena clearly differ in that these dual-object report deficits reflect higher demands on performance than spatially cued attention, which has no measurable effect in similar two-object displays except possibly for peripheral cuing (Dosher & Lu, 2000b, Lu & Dosher, 1998). Robust spatially cued attention effects on identification emerge for dissimilar targets when there are at least four potential locations (Dosher & Lu, 2000b; Lu, Lesmes, & Dosher, 2002).

Secondly, for centrally cued spatial attention in single judgments, the primary documented function of attention is to exclude external noise (Dosher & Lu, 2000a, 2000b; Lu & Dosher, 2000). Spatial-cued attention improves the thresholds of attended stimuli by shifting the location parameter of the psychometric function left to smaller contrasts relative to the unattended stimuli, but consistently converges at a single asymptotic accuracy level (Dosher & Lu, 2000a, b; Lu & Dosher, 2000; Lu, et al., 2002), at least in these published cases. Surprisingly, the asymptotic equivalence occurs even when attended conditions are compared to a neutral condition in the absence of report cues that equate structural uncertainty (Cameron, Leslie, Tai & Carrasco, 2002; Ling & Carrasco, 2006). In contrast, the dual-object report deficits, when they occur, show clear differences at high contrasts in the psychometric functions both here and in the data of Han et.al. (2003). The primary difference seems provisionally to reflect dual-object reports, although the contrast psychometric functions in spatial attention have generally not been measured for high precision discriminations and is another possible factor.

Combining all of these findings, external noise exclusion in high external noise is a core feature of all the attention phenomena. External noise exclusion occurs in isolation in endogenous (centrally-cued) spatial attention. External noise exclusion occurs in exogenous (peripherally-cued) spatial attention, together with stimulus enhancement in low external noise. External noise exclusion occurs in the incongruent conditions in object attention in the current experiments, but either multiplicative noise increases and/or corresponding template broadening are also features of incongruent frame conditions and in high precision tasks.

As we have noted previously (Han et al., 2003), some theorists might prefer to reframe the dual-response object attention results in terms of dual-task limitations in sharing attention across distal region of space. It has been shown, however, that object attention effects are similar when the objects occupy overlapping regions of space and distal regions of space (e.e., Baylis & Driver, 1993, Vecera & Farah, 1994). Taking one view or the other would alter the label from object attention to one of dual-task (spatially) divided attention, but would otherwise lead to the same sets of conclusions and the same set of contrasts with the spatial cuing of a single location or feature for attention and report.

4.6 Relationship to response and contrast gain

Previous researchers have evaluated psychometric functions and interpreted these in the context of the physiological constructs of contrast gain and response gain (Cameron, et al., 2002; Ling & Carrasco, 2006; Huang & Dobkins, 2005). Attention manipulations resulting in a change in the asymptotic or maximum level of the psychometric function have sometimes been associated with ‘response gain’, by analogy to the physiology (i.e., McAdams & Maunsell, 1999; Reynolds, et al., 2000). This issue has emerged as one of increasing relevance to the problem of relating models of attention based in the response properties of individual neurons to psychophysical evaluation of behavior.

The previous studies have provided insights into these processes. However, the analogy between physiological response gain and behavioral response gain is a complex one. Psychometric functions of contrast that measure accuracy (or discriminability d′) as a function of contrast are in many cases not directly analogous to contrast response functions of physiology that measure physiological response rates as a function of contrast. Increases in neural response may or may not correspond to changes in discriminability, depending on the associated effects on variability or noise (although see Huang & Dobkins, 2005, which measured contrast increment thresholds). Definitive conclusions require the application of a full signal detection model, and would also require the theoretical development of new psychophysical tests. However, in the current data, relative changes in signal and noise must underlie the observed changes in discrimination accuracy. Consideration of these patterns within the perceptual template model associates the pattern of differences at psychometric asymptote, commonly associated in the literature with response gain, with a reduction in template sharpness and a concomitant increase in internal multiplicative noise and possible reduction in net signal.

4.7 Implications for physiological claims of object attention

What implications do our findings have for theories of object attention? First, the simple concepts of object attention from the original behavioral analyses by Duncan (1984) and others explicitly claimed that object attention effects on dual-object report deficits should occur independent of the features being judged. The original object attention framework and the biased competition model (Desimone & Duncan, 1995) do not, by themselves, have additional explanatory mechanisms that would account for the mitigating influence of judgment frame consistency or for the large impact of judgment precision on presence and magnitude of dual-object response deficits.

Alternatively, the elimination of dual-object report deficits with congruent judgment frames might relate to feature attention. Several studies have reported that attending to a feature in one location activates that feature even far across the visual field (Treue & Martinez Trujillo, 1999; Martinez Tujilo & Treue, 2004; Melcher, Papathomas, & Vidnyánszky, 2005; Serences & Boynton, 2007). At a purely intuitive level, one can speculate that feature similarity engages a cooperative network that improves the saliency of the second object in the congruent frame conditions, thus partially or entirely defeating the biased competition between objects. However, specifying the appropriate interaction of feature attention with the object competition framework (Desimone & Duncan, 1995) so as to account for the complex pattern of results is a challenge. Spatial attention and feature attention are thought by some researchers to combine additively (McAdams, & Maunsell, 2000) or in any event to combine (Logan, 1996). A simple elaboration of the biased competition model with the addition of common-feature cooperation seems insufficient to account for the complex pattern of results in the current studies. Furthermore, the increased activation of the feature similarity gain model (Treue & Martinez Trujillo, 1999) seems to more naturally predict changes in baseline or perhaps improvements in detection, but how this would improve discrimination remains unclear.

Finally, the precision of judgment had a major influence on the magnitude and pattern of object attention effects. Precision of judgment has a fundamental impact on the accuracy of identification for a given contrast, and on properties of other domains such as perceptual learning and transfer (Ahissar & Hochstein, 1997). Manipulations of precision can contribute to judgment difficulty, but difficulty and precision are not one and the same (Jeter, Dosher, Lu, & Petrov, 2008). Difficulty more generically is related to performance accuracy – a more difficult task limits the accuracy of performance. There are many factors that determine difficulty, such as contrast, external noise, etc., of which judgment precision is only one. Here we show that precision has an effect on dual-object report deficits along the entire range of accuracies across the psychometric function. Highly precise judgments requiring the use of overlapping or close templates may engage distinct decision structures (Graham, 1989). However, at an intuitive level, demands for high precision may interact with object competition so as to re-engage dual-object report deficits with congruent stimuli because more narrow scrutiny might require stronger selection of each object by itself for processing. For this important phenomenon, too, existing ideas about object attention and feature attention should be augmented to incorporate the important effects of judgment precision on object attention limitations.

5. Conclusions

The current set of studies show an effect of object attention on report accuracy that may be distinct from that of spatially cued attention. It documents the important influence on object attention effects by judgment frame or feature matches and, importantly, by task precision. Individual observer differences in object attention seem to be significant, which may have concrete and practical relevance to an individual’s ability to perform in complex operator environments. Yet the complex effects of object attention have been comparatively little studied in psychophysics in relation to the many studies of spatially cued attention, where impacts of spatial attention on a range of perceptual factors have been examined. The current analysis sets the stage for further empirical investigation of behavioral accuracy and the influence of hierarchically defined objects and regions. It also calls for the development of a unified theoretical account of the many factors that influence this important aspect of human attention.

Appendix A

Appendix A describes the methods of model fitting and analysis. Sets of psychometric functions (percent correct or average percent correct versus Gabor signal contrast) were fit with sets of Weibull models (see Equation 1). The Weibull models range from separate parameters, for each psychometric function (n × {α, β, max}) to a single function all (1×{α, β, max}) were fit using both least-squares and maximum likelihood methods using fminsearch in Matlab 7.0 (Mathworks, 2004) to search for the best-fitting parameters for each model. See Wichmann and Hill (2001) for a discussion of the fitting of psychometric functions.

The least-squares method minimized the sum of squared errors between predicted and observed data across all of the psychometric functions within a model set. The proportion of variance accounted for by the model form was calculated using the r² statistic:

$$r^2=1.0-\frac{\sum {\left[x^{\mathit{theory}}-x^{\mathit{observed}})\right]}^2}{\sum {\left[x^{\mathit{observed}}-\overline{x}\right]}^2},$$ (A1)

where Σ is over all N observations and x̄ is the mean of the observed values. Statistical tests compared nested fuller models (with more parameters) with reduced models that were equivalent to the fullest with a reduced number of parameters. F-tests for nested models were used:

$$F({df}_1,{df}_2)=\frac{(r_{\mathit{full}}^2-r_{\mathit{reduced}}^2)/{df}_1}{(1-r_{\mathit{full}}^2)/{df}_2},$$ (A3)

where df₁ = k_full – k_reduced, and df₂ = N – k_full. The k’s are the number of parameters in each model, and N is the number of predicted data points.

The maximum likelihood method maximizes the likelihood of the observed data across the entire set of psychometric functions given the model predictions:

$$L=\prod _{i=1}^N\frac{n_i!}{c_i!(n_i-c_i)!}{p}_i^{c_i}{(1-p_i)}^{n_i-c_i},$$ (A1)

where ${\displaystyle \prod _{i=1}^N}$ is the product over the N observed points across the set of psychometric functions, p_i is the predicted percent correct, n_i is the number of trial per point, c_i is the number of correct trials and so n_i – c_i is the number of incorrect trials. Here nested models are statistically compared by the χ² statistic:

$${\chi }^2(df)=2.0xlog\left(\frac{max{\mathit{likelihood}}_{\mathit{fuller}}}{max{\mathit{likelihood}}_{\mathit{reduced}}}\right),$$ (A3)

where df = k_full – k_reduced.

The least-squared methods and the maximum likelihood methods resulted in almost the identical fitted functions and pattern of significance and estimated quantities in the least squares and maximum likelihood fits of the Weibull to the psychometric functions.. In addition, the perceptual template model equations (see text) were fitted to both to the psychometric functions via maximum likelihood methods and to equivalent d′ psychometric functions using least squared errors, also leading to very similar or equivalent results. The maximum likelihood fits of the perceptual template model to the psychometric function probabilities are reported in the paper.

Monte Carlo re-sampling for both least-squared and maximum likelihood methods derived standard deviations of model parameters and thresholds. Each data point on each psychometric function was re-sampled from a binomial distribution using Matlab function binornd based on the observed number of trials and observed probability. Each of these new simulated data sets (usually 100) was then re-fit for each model, yielding a mean and standard deviation for each model threshold and each model parameter. These standard deviation estimates fully reflect all of the binomial variability in the data.