Structure and Properties of Dense Silica Glass

Abstract

The O K-edge x-ray Raman scattering (XRS), Brillouin scattering and diffraction studies on silica glass at high pressure have been elucidated in a unified manner using model structures obtained from First-Principles molecular dynamics calculations. This study provides a comprehensive understanding on how the structure is related to the physical and electronic properties. The origin of the “two peak” pattern in the XRS is found to be the result of increased packing of oxygen near the Si and is not a specific sign for sixfold coordination. The compression mechanism involving the presence of 5- and 6-fold coordinated silicon is confirmed. A slight increase in the silicon-oxygen coordination higher than six was found to accompany the increase in the acoustic wave velocity near 140 GPa.

Silica (SiO₂) is one of the most important and abundant materials. In the crystalline state, it exists in several polymorphic forms. It is the fundamental building block of three-dimensional framework structure found in minerals¹,². In the amorphous form, silica glass has become a prototype system for understanding the disordered state. The study of silica glass under high pressure is particularly important and challenging as it has been used as a zeroth order model of silicate magma in the earth's interior. Numerous theoretical and a variety of experimental techniques have been employed to characterize the complex and sometimes anomalous behaviour of silica glass. The status of the research on high pressure amorphous silica has been reviewed recently². Since then many new results reaching 100 GPa or above have become available. In spite of these efforts, there is still no consensus on a number of outstanding issues such as the onset for the transformation from 4-fold coordinated quartz-like structure to 6-fold stishovite-like structure, the pressure for the completed transformation, intermediate structures, particularly the possible existence of 5-coordinated Si, and mechanisms for densification and the existence of “post-stishovite” polymorphic phase³,⁴. In recent years, conflicting conclusions drawn from different experiments concerning the threshold pressure for the formation of 6-fold coordinated Si have emerged. From the comparison the O K-edge x-ray Raman scattering spectra (XRS) of silica glass with crystalline quartz and stishovite, it was suggested that a change in the Si environment from 4-fold to 6-fold coordination occurred between 10 to 22 GPa⁵. The acoustic velocity data obtained from Brilluion scattering, however, suggested the onset should started at 30 GPa and the 6-fold coordination is sustained up to 140 GPa⁶. The results further hinted that there may be a denser phase with higher coordination number (CN) above 140 GPa. Diffraction results obtained from two groups⁷,⁸,⁹ agree that the change in CN should start around 20 GPa and completed at 45–50 GPa. In one of the studies, the existence of an intermediate 5-fold coordinated structure was proposed⁴,⁹. In contrast, a study on the Si–L edge x-ray Raman scattering spectra at high momentum transfer found no significant change in the spectral features and concluded that the 4-fold coordination environment of Si remains up to 74 GPa¹⁰. This is surprising that very different interpretation of the experimental results can be derived from an apparently identical material! The objective of this contribution is to provide a coherent explanation on the observed results based on a common structure model obtained from First-Principles molecular dynamic calculations. The structures obtained here will be compared against experimental structure factor at different pressures. O K-edge x–ray absorption spectra computed on the theoretical silica glass structures are compared to XRS measurements at small momentum transfer. The average acoustic velocities were evaluated from the knowledge of the theoretical densities and bulk moduli. As will be described below, the present results provide a coherent description of the experimental data. The major findings are summarized succinctly as follows. The appearance of the second band in the O-K spectra is due to the opening of an excitation channel as the result of new bonds form from the O lone pair and Si 3d-orbitals due to increased number of oxygen around the Si and need not signifies the presence of 6-fold coordination. The transformation from 4- to 6-fold coordination is not direct. The change in the Si environment commences at 12 GPa via the formation of substantial 5-fold coordinated local structures and largely completed at 60 GPa. The abrupt increase of acoustic velocity around 120 GPa was reproduced and related to a slight increase in coordination number higher than 6.

Results

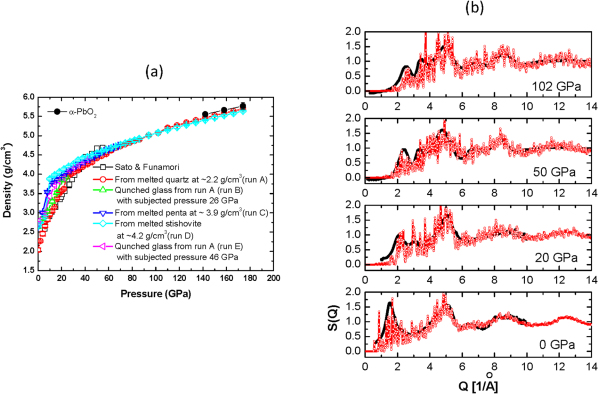
A common problem encountered in the study of disordered systems is the lack of precise knowledge on the short range and intermediate structures¹¹. Theoretical glass structures are often generated from quenching from the melts. The resulting structures, however, may subject to errors from various sources. To choose the most appropriate model, one needs to minimize the discrepancy between theoretical and experimental densities over the pressure range studied. For this purpose, silica structures were generated from five different methods (run A – E, Fig. 1a). In each case, using ab initio molecular dynamics (MD) method, the model was first melted at high temperature and then cooled to the desirable temperature-pressure conditions. As it can be seen from Fig. 1a, with the exception for run D where the glass structure was obtained from melting stishovite, the other glass models reproduced fairly well the recent experimental density measured by Sato and Funamori⁸. In particular, the model obtained from the melting of quartz (run A) gave the most consistent agreement with experiment over a wide pressure range from 0 to 60 GPa. At higher pressure where experimental data is not available, there is no discernible difference between model A and D. The experimental structure factor S(Q) and those calculated from model A at four selected pressure points over a broad pressure range from 0 to 10 GPa are compared in Fig. 1b. Although the calculated S(Q) are a bit noisy due to the small system size, they are in good accord with experiment⁸,⁹. All the major features are correctly reproduced. For example, the appearance of a new “peak” at ca. 3.3 Å⁻¹ at 20 GPa¹² and the three “peak” pattern from 0–6 Å-⁻¹ at 102 GPa⁹ observed in the experimental patterns are predicted by the model. The consistent agreement in both the density and structure factor gives credence to the reliability of model A and this model was used in in the ensuing study. Before embarking on the detail analysis of the structure of high pressure silica glass, the O K-edge x-ray absorption spectra (XAS) will be discussed.

Figure 1.

(a) Comparison of calculated densities as a function of pressure using different models (run A-E, see supplementary material) with experimental data. (b) Comparison of experimental⁸,⁹ and theoretical structure factors (red) of silica glass (black) at selected pressures. Note that the “spikes” in the calculated structure factor are due to the limited size of the simulation cell.

It is perhaps surprising that the O K-edge⁵ and not the Si L-edge¹⁰ XRS spectra are more sensitive to the Si environment as the oxygen atom is not expected be the most affected from increase coordination. Experimental O K-edge x-ray absorption spectra of quartz and stishovite are well-known¹³. The most distinctive difference separating them is the appearance of a second band in the stishovite spectrum. This feature has been used as the finger-print for the existence of 6-fold coordination in silicates even though the cause of this extra peak is unknown.

This is our intention to uncover the origin of this peak. Calculations of the core level absorption spectra must be exercised with care since a correct treatment of the core hole effect is essential¹⁴. At low momentum transfer, XRS is equivalent to dipolar x-ray absorption and techniques developed for the calculation of the x-ray near edge spectrum (XANES)¹⁵ can be used. To assess the appropriate level of approximation required, the O-K XANES of quartz and stishovite were computed by solving the all electron Bethe-Salpeter equation (BSE)¹⁶, which took into account explicitly the electron-hole correlation, and with the one-electron method adopting the full core-hole approximation¹⁷. In the latter method, the excited oxygen is replaced by core hole pseudopotential with the associated excited electron introduced as impurity in the glass mode. The absorption spectrum is the sum of all possible excitations from the core to the conduction band. Comparison of the XANES spectra of quartz and stishovite computed by the two methods (not shown, see supplementary material) revealed no significant difference⁵. Therefore, the more economical one-electron method was adopted here. For silica glass, XANES spectra were computed as the sum of the excitation spectra of all the oxygen atoms in the model.

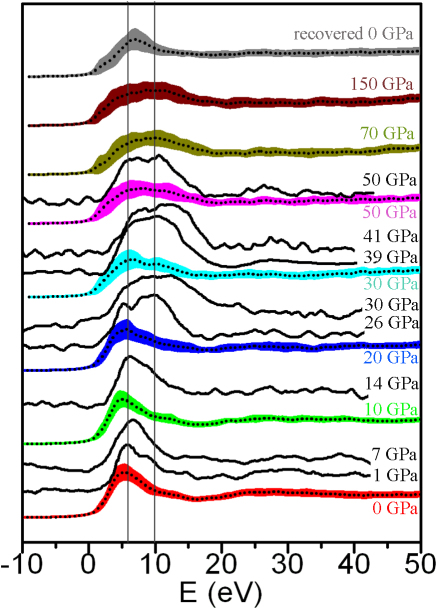
In addition, more than one snapshot were taken from the MD trajectory to ensure there is no significant change in the spectrum due to different structural configurations. As expected for a non-diffusive solid, no substantial difference was found. The theoretical spectra are compared with experiment in Fig. 2a. The agreement is very good. At 0 GPa, only one broad asymmetric band is predicted and observed. At 20 GPa, the asymmetry on the high energy side starts to develop into a separate peak separated by 5 eV from the first. This feature is fully formed at 30 GPa. The second peak is found to persist to the highest pressure (150 GPa) studied here.

Figure 2. Comparison of calculated (color) and experimental (black) x-ray absorption spectra at selected pressure.

Discussion

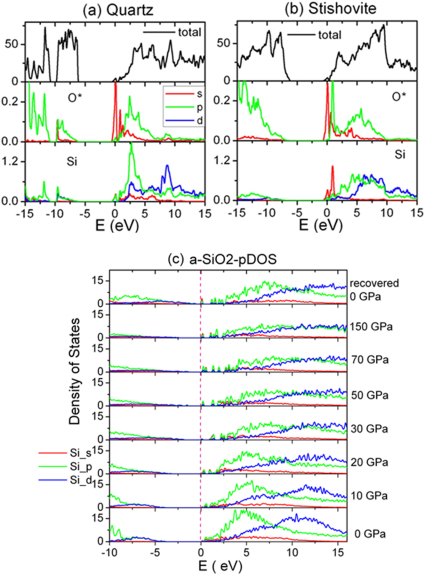
Is the second peak indicative of 6-fold coordination? The O-K absorption spectrum is a probe of the O 2p projected density of states (PDOS) in the conduction band¹⁵. In quartz, the Si is 4-fold coordinated. The change in chemical bonding from quartz to stishovite has been well characterized¹⁸. The top valence band is dominated by O 2p lone pair orbitals and separated from the Si-O (2p) band by a small gap (Fig. 3a). This distinction is lost in stishovite (Fig. 3b). When amorphous silica is compressed, O atoms outside the first coordination shell are pushed closer to the Si. Since the only available electrons are those from the O lone pairs and the Si valence octet is already filled it has to utilize the empty 3d orbitals to accommodate these electrons. Interactions between the oxygen lone pair orbitals with the vacant Si 3d orbitals lead to increase Si-O coordination and stabilization of the dense structure. The same effect is clearly seen in the comparison of the Si p- DOS of the valence and conduction band of compressed amorphous silica with quartz and stishovite in Fig. 3 where the lone pair band at the top of the valence level acquires more Si 3d character at higher pressure. Correspondingly, as in the case of stishovite, in the conduction band the Si 3d at around 5 eV above the bottom above the conduction band (see Fig. 3b) hybridized with the O 2p orbital and opening up new excitation channels. This is exactly at the same energy where the second peak is observed. The hybridization between Si 3d with the O 2p levels occurs whenever an O atom is pushed into the coordination shell of Si. Therefore, the emergence of a second peak in the XRS is an indication of increase coordination number and not necessary signal the presence of 6-fold coordination. The absence of significant spectral variation under high pressure in the Si L-edge XRS¹⁰ is puzzling. It is possible that the low experimental resolution (ca. 2.0 eV)¹⁰ may masks finer features in the spectra. The method employed here is not amendable to XRS spectrum measured at high momentum (q) transfer where non-dipolar excitations will become important. To a first approximation, these excitations are related to the p PDOS. The Si p-DOS of silica at high pressure are shown in Fig. 3c. The DOS profiles are rather monotonous and did not change appreciably with pressure. This helps to rationalize the lack of spectral variation in the Si L-XRS.

Figure 3.

Calculated (a) projected density of states of Si and O for α-quartz and (b) stishovite with a O 1s core hole. (c) Projected density of states for Si in amorphous silica at high pressure. The zero energy is reference to the minimum of the conduction band.

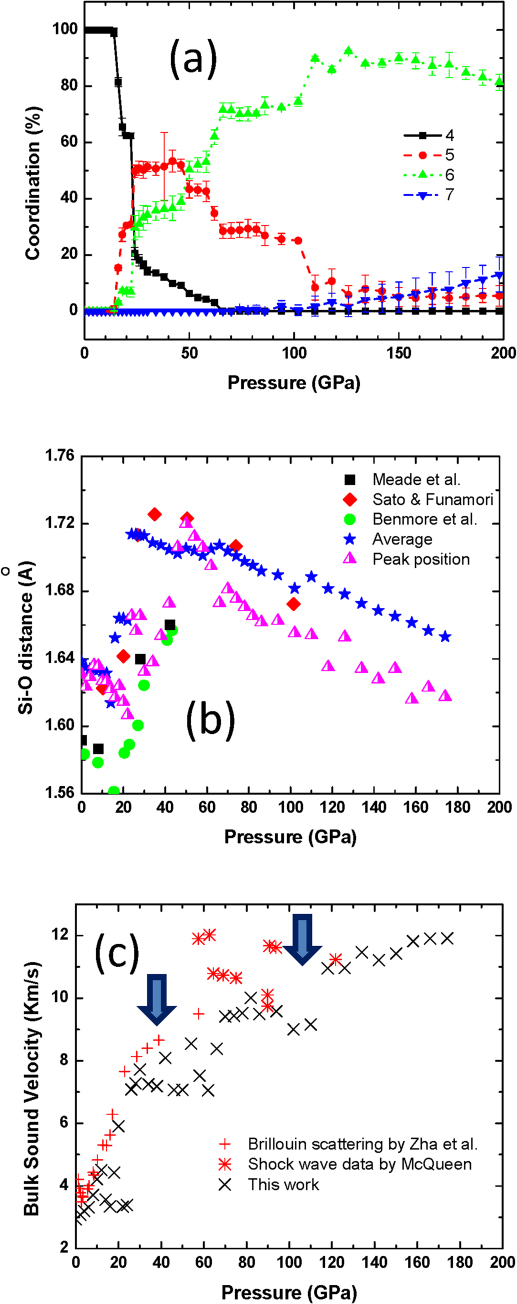
Calculations predicted the coordination starts to increase at 12 GPa (Fig. 4a). Between 12 and 22 GPa silica glass is consisted of mixed 4-, 5- and 6-fold coordination. However, the contribution of 6-fold within this pressure range is small (<10%). From 22 to 55 GPa both the 5- and 6-fold coordination increases at the expense of a rapid decrease in 4-fold coordination. At 22 GPa, the percentage of 4-fold coordination in the structure is 20% and decreases to almost zero at 64 GPa. Above 50 GPa 6-fold coordination starts to dominant and transformation is completed at 110 GPa. The observed trend in XRS spectra are in full accord with the calculated change in Si coordination number. The appearance of the second peak from 10–22 GPa is primarily due to an increase in 5-fold coordination. Above 22 GPa, the concentration of the 4-fold coordination is much less as compare to the 5- and 6-fold. The existence of 5-fold coordination has been a subject of much discussion². The present theoretical results are broadly similar to a previous MD study using empirical potentials²⁰ up to 20 GPa. It was shown that there was no change in the Si CN up to 3 GPa. Beyond this pressure, a continuous increase in the CN with concomitant decrease in the fraction of 4-coordinated Si was reported.

Figure 4. Calculated (a) distribution of Si coordination number; (b) nearest neighbor Si-O distance and (c) average velocity of sound for silica glass as a function of pressure.

The calculated average Si-O nearest distances as a function of pressure is shown in Fig. 4b. In agreement with experiment⁷,⁸,⁹,²⁰, as a result of elastic compression there is an initial shortening of the Si-O distance from 1.64 to 1.61 Å. The average Si-O distance increased abruptly to 1.72 Å above 12 GPa and reaches a maximum at ca. 30 GPa. A lengthening of the Si-O distance is expected since to accommodate extra oxygen into the first Si coordination shell (vide supra), the Si-O distances must elongate. The theoretical results are in good agreement with the diffraction results of Sato and Funamori⁹ showing the Si-O distance started to increase above 10 GPa and reached a maximum at 30 GPa. It is also consistent with the work of Meade¹⁸ and Benmore⁷ which also show the elongation of the Si-O distance commenced at ca. 15 GPa. However, their measurements were not extended beyond ca. 40 GPa. Conscious on the experimental difficulties in extracting accurate CN, nonetheless, no significant increase from the 4-fold coordination was observed below 10 GPa. The CN increases quickly from 4 to 6 between 22 to 40 GPa and plateau up to at less 100 GPa⁹. The theoretical glass structure in the pressure range from 60 – 100 GPa is a 75:25 mixture of 5- and 6-fold coordination. The average CN of 5.8 is within the experimental limits of accuracy. The presence of 5-fold coordination up to 100 GPa has been suggested recently⁹ and the present calculations support this postulate.

The average (longitudinal and transverse) sound velocity of silica glass at high pressure can be estimated from the theoretical bulk modulus and density determined from the calculated equation of states (Fig. 1). The results are compared with experimental data⁶,¹⁹,²⁰ in Fig. 4c. Calculations show a progressive increase in the bulk sound velocity with pressure but there are noticeable “breaks” in the slope at 40 and 120 GPa (Fig. 4a). The estimated sound velocities are in surprisingly good agreement with Brilluion scattering⁶,²¹ and shock wave²² data. Recently, the transverse acoustic wave velocities of silica glass as a function of pressure have been measured up to 207 GPa⁶. Clear changes in the slope in the plot of acoustic velocity against pressure are observed at ca. 30–40 and at 130–150 GPa. These changes have been attributed to the change in CN from 4→6 and 6→6+, respectively. The theoretical results support this interpretation. It is noteworthy that the emergence of 6+ coordination has been predicted in a MD calculations using empirical potentials²³ albeit at a much lower pressure of 80 −100 GPa. At 40 GPa the 4-fold coordination has started to diminish rapidly and full 6-fold coordination is established at 120 GPa. Above 120 GPa, 7-fold coordination is found in the glass structure and the concentration increases with pressure at the expense of decreasing 6-fold coordination (Fig. 4a). The extension of diffraction experiments to this pressure range is needed to confirm this finding.

A unified explanation of the electronic, acoustic and structure of silica glass based on the structure of silica glass obtained from First-Principles molecular dynamics calculations was presented. Apart from reproducing the experimental results connections between the electronic and acoustic properties and the structure have been established. The theoretical results provide a clear picture on the compression mechanism of silica glass and emphasize on the existence of 5- fold coordination of Si in silica glass. The appearance of a second band in the XRS may not be used as the indication of the occurrence of 6-fold coordination. A dense polymorph with higher than 6-fold coordination may exist above 140 GPa in silica glass.

Methods

All calculations were performed with First-Principles Car- Parrinello method²⁴,²⁵ on models containing 72 atoms (24 SiO2 units). Only the Γ point was used in the Brillouin zone sampling. Ultrasoft pseudopotentials²⁶ were used to describe valence electron-nuclei interactions. Electron orbitals were expanded in a plane wave basis set using an electron density cutoff of 240 Ry. The Perdew-Burke-Enzerhof functional (PBE)²⁷ and the Generalized Gradient Approximations (GGA) was used as it has been shown to reproduce the α-quartz-coesite and coesite-stishovite transition pressure very well²⁸. Variable cell Parrinello-Rahman molecular dynamics²⁹ in the isobaric-isothermal ensemble (NPT) were performed to determine the equation of state of the glass under compression. The FPMD program in the Quantum Espresso package (http://www.quantum-espresso.org/) was used for the calculations. The pressure and temperature are controlled by Nose-Hoover baths²⁹. An integration time step of 6 a.u. and a fictitious electron mass 200 a.u. were used. Detail description on the preparation of the different silica glasses is provided in the supplementary materials.

Author Contributions

JT planned the research. YL and WM performed all the calculations. JT and JJ wrote the manuscript.

Supplementary Material

Supplementary Information

Generation of glass models