Summary
A recently funded study of the impact of oral contraceptive use on the risk of bone fracture employed the randomized recruitment scheme of Weinberg and Wacholder (1990, Biometrics 46, 963–975). One potential complication in the bone fracture study is the potential for differential response rates between cases and controls; participation rates in previous, related studies have been around 70%. Although data from randomized recruitment schemes may be analyzed within the two-phase study framework, ignoring potential differential participation may lead to biased estimates of association. To overcome this, we build on the two-phase framework and propose an extension by introducing an additional stage of data collection aimed specifically at addressing potential differential participation. Four estimators that correct for both sampling and participation bias are proposed; two are general purpose and two are for the special case where covariates underlying the participation mechanism are discrete. Because the fracture study is ongoing, we illustrate the methods using infant mortality data from North Carolina.
Keywords: Logistic regression, Multiphase study, Nonresponse bias, Participation bias, Two-phase study
1. Introduction
A recently funded study of the impact of oral contraceptive use on the risk of bone fracture employed the randomized recruitment scheme of Weinberg and Wacholder (1990). Such schemes are essentially matched case–control designs, where the recruitment of study participants is governed, in part, by Bernoulli sampling with probabilities determined by the investigator in advance. Data arising from such schemes may be analyzed within the broader two-phase study framework (e.g., Breslow and Chatterjee, 1999). The latter are characterized at phase I with an initial (large) sample, cross-classified according to the outcome and some stratification variable. At phase II, individuals are sampled (according to their phase I classification) and additional exposure/confounder information is obtained. Beyond the basic two-phase design, numerous extensions have been proposed (Lawless, Kalbfleisch, and Wild, 1999; Chatterjee, Chen, and Breslow, 2003; Chatterjee, 2004; Chen and Breslow, 2004; Pfeiffer and Chatterjee, 2005).
A complication that arose during the design phase of the bone fracture study was that experience from previous, related studies indicated the potential for differential participation, or nonresponse, among invited cases and controls. In settings where the mechanism driving participation can be shown to be jointly driven by (i) the outcome of interest (or a cause of the outcome), and (ii) the exposure of interest (or a cause of the exposure), estimation of association parameters may be subject to bias (Austin et al., 1981; Hernán, Hernández-Diaz, and Robins, 2004). In broader epidemiological applications, a common approach used to assess the potential impact of differential participation is to perform post hoc comparisons between participants and nonparticipants (Rothman and Greenland, 1998). More formally, Lin and Paik (2001) proposed a conditional likelihood approach for matched case–control studies, although their development was restricted to settings where controls are subject to selection but cases are not. In more general settings, the problem of identifying and adjusting potential participation bias can usefully be cast as a missing data problem, for which there is a well-developed literature (e.g., Robins, Rotnitzky, and Zhao, 1994; Little and Rubin, 2002). A key assumption required for valid estimation/inference in missing data problems is that the mechanism driving the missingness (i.e., participation) depends solely on observable quantities; the so-called missing-at-random assumption (Little and Rubin, 2002). However, in observational studies, although emphasis is generally placed on ensuring adequate collection of variables that may confound relationships of interest, less emphasis is placed on ensuring collection of variables that may drive differential participation.
Motivated by this, we propose an extension of the two-phase design by introducing an intermediate phase, between the traditional phase I and phase II, where additional data aimed specifically at characterizing participation into the study are obtained. Building on the work of Breslow and Cain (1988) and Robins et al. (1994), we propose four estimators that account for both the sampling bias (inherent in the two-phase design), as well as potential participation bias. The remainder of this article is as follows. In the next section, we introduce notation and outline the proposed multiphase design. Section 3 presents the development of our proposed estimators. As the motivating bone fracture study is ongoing, Section 4 investigates operating characteristics of the proposed design/estimators with a simulation based on infant mortality data from the state of North Carolina. Finally, Section 5 concludes with a discussion.
2. Multiphase Design for Participation Bias
Suppose interest lies in estimating the association between some binary outcome Y and a vector of explanatory variables X; the vector X will generally include the exposure of interest as well as confounders and, potentially, interaction terms. Further, suppose the relationship between Y and X is summarized via the logistic regression model
| (1) |
so that the vector β is the target of estimation/inference.
In settings where Y is rare, researchers have a variety of designs at their disposal with which to collect data and estimate β. Here we present an extension of the two-phase design; the proposed phases I and III correspond to the traditional first and second phases of the two-phase design; the proposed phase II is introduced to collect additional information on the participation mechanism.
2.1 Phase I
Initially, assume a (large) sample of size N is drawn from the population of interest and cross-classified by the binary outcome and some stratification variable, denoted by S. The latter is assumed to be observable on all members of the sample and to take on one of K levels. The cross-classification of the initial sample, referred to as the phase I data, yields N0k controls and N1k cases in the kth stratum of S, k = 1, …, K; Table 1 summarizes the notation.
Table 1.
Notation summarizing phase I information
| S = 1 | S = 2 | … | S = K | |
|---|---|---|---|---|
| Y = 0 | N01 | N02 | … | N0K |
| Y = 1 | N11 | N12 | … | N1K |
Whereas S may involve components of X, it is assumed that Pr(Y = 1 | X, S) = Pr(Y = 1 | X).
2.2 Phase II
In the standard two-phase design the next step would be to sample a subset from each of the 2K phase I strata and (retrospectively) ascertain components of X not observed at phase I. Practically, this requires inviting individuals to join the study although some may not agree to participate.
Let I be a binary indicator for invitation and R be a binary indicator for participation. In a standard two-phase study, the mechanism driving I for any given member of the population is under the direct control of the researcher and, in particular, is dictated by phase I stratum-specific sampling probabilities. However, given that an individual has been invited, the participation mechanism driving R will not be under the direct control of the researcher. Suppose participation depends on a set of covariates Z, which may include Y, components of X, and variables unrelated to Y. Further, suppose the relationship between Z and R is characterized via some model for Pr(R = 1 | Z), indexed by the finite vector α.
If Z is observable on all individuals at phase I then we can proceed directly to the next phase (i.e., collection of X), with analyses based on existing methods. If Z is not (fully) observable at phase I, then we are required to collect additional information with which the participation mechanism can be characterized (i.e., α can be estimated). Towards this, suppose individuals are invited from the [y, k]th phase I stratum; at phase II of the proposed design, for each of the
| (2) |
individuals invited to participate in the study, collect information relevant to participation into the next phase. Specifically collect components of Z not available at phase I, to give zy k i for y = 0, 1, k = 1, …, K, and i = 1, …, . In the proposed design, these data are referred to as the phase II data.
2.3 Phase III
The final stage of the proposed design consists of collecting detailed exposure/confounder information on individuals who agree to participate from each of the 2K phase I strata. Hence the phase III data consist of covariate vectors xy k i, for i = 1, …, ny k.
3. Analytic Methods
In the absence of participation bias, various analytic approaches have been proposed to account for biased sampling in the two-phase study design (Breslow and Cain, 1988; Flanders and Greenland, 1991; Schill et al., 1993; Breslow and Holubkov, 1997; Scott and Wild, 1997). In the following we distinguish two settings; the first accommodates arbitrary Z, whereas the second is the special case where all components of Z are discrete.
3.1 Arbitrary Z
Here we present two general-purpose estimators for the setting where the components of Z are an arbitrary mixture of discrete and continuous variables.
3.1.1 Full weighted likelihood
Let U(β; y, x) denote the usual likelihood-based score function based on model (1):
| (3) |
In settings where participation is complete (i.e., N* = n), the weighted likelihood (WL) estimator for two-phase studies is obtained as the solution to the estimating equation
| (4) |
where are the observed phase II stratum-specific sampling fractions (Flanders and Greenland, 1991). Assuming random sampling, the latter are the nonparametric maximum likelihood (ML) estimators for the underlying selection probabilities, fy k = Pr(I = 1 ∣ Y = y, S = k).
In settings where participation is not guaranteed (i.e., N* > n), suppose participation depends on Z via the logistic model
| (5) |
Using information obtained on Z at phase II of the proposed design, estimate α and denote the fitted values for Pr(R = 1 ∣ Z = z) as
| (6) |
When estimating the components of α, an implicit assumption is that Pr(R = 1 ∣ I = 1, Z) = Pr(R = 1 Z). The latter can heuristically be interpreted as assuming that characterization and estimation of the underlying mechanism by which individuals decide to participate is independent of the fact that they were invited.
Finally, based on information obtained from the phase III participants, define a full weighted likelihood (FWL) estimator of β as the solution to the estimating equation
| (7) |
Given sufficient regularity conditions on the disease and participation models, asymptotic results for the FWL estimator follow from standard estimating equation theory (see the Appendix). Practically, obtaining estimates is straightforward in any statistical package/function with the capacity to incorporate weights into the estimating equation.
3.1.2 Weighted pseudolikelihood
In the standard two-phase design, where participation is taken to be complete, the WL estimator obtained by solving (4) is well known to be inefficient. An alternative is the profile- or pseudolikelihood (PL) estimator (Breslow and Cain, 1988; Schill et al., 1993), obtained by fitting a modified logistic model
| (8) |
to the observed data (i.e., the phase II data in a traditional two-phase design), where the δk = log(n1k/N1k) − log(n0k /N0k) are fixed offsets in the linear predictor. Model (8) corresponds to the phase I stratum-specific disease probability, with the δk providing an adjustment for the biased sampling scheme.
Under the proposed design of Section 2, where participation is not guaranteed, let denote the phase I stratum-specific disease probabilities but with modified offsets given by . That is, let
| (9) |
A weighted pseudolikelihood (WPL) estimator is obtained by maximizing
| (10) |
with respect to β where, as in (7), the are obtained from a fit based on the phase II data. As with the FWL estimate, obtaining the WPL estimate is straightforward in most statistical packages with the capacity to add offsets into the regression specification and weights into the estimating procedure.
3.2 Discrete Z
Although the FWL and WPL estimators are applicable in general settings, when Z consists purely of discrete covariates efficiency gains may be obtained by exploiting this knowledge. Specifically, suppose Z takes on one of J levels. Then each of the 2K [Y, S] phase I strata in Table 1 can be further stratified to give the array of strata given by Table 2.
Table 2.
Adjusted stratification based on discrete Z
| Z = z1 | Z = z2 | … | Z = zJ | ||
|---|---|---|---|---|---|
| Phase II totals | … | ||||
| Phase III totals | ny k1 | ny k2 | … | ny kJ | ny k |
3.2.1 Multiple outputation (MO)
In the context of analyzing complex clustered data, Follmann, Proschan, and Leifer (2003) introduced a MO procedure for settings where accounting for correlation is challenging, although methods exist for independent data. The approach works by throwing out “excess” data, so that methods for independent data are directly applicable. In the context of participation bias, the technique can similarly be used by throwing out data such that participation is independent of Z as follows.
From Table 2, the observed participation probabilities are
| (11) |
Let and re-sample
| (12) |
at random, from each of the phase III [Y, S, Z] strata. The new phase III data consist of
| (13) |
individuals for whom X is “observed.” In this new dataset, participation is (approximately) independent of Z because the participation probabilities for those individuals included at phase III have been artificially forced to be constant across the levels of Z. Using this new dataset, the usual PL approach is directly applicable with offsets . Denoting the resulting estimate β, estimation proceeds by repeating the procedure M times and taking the average, to give the MO estimator:
| (14) |
Asymptotic results for the MO estimator follow directly from Follmann et al. (2003), with a straightforward estimate of the asymptotic variance given by
| (15) |
where V[] is the asymptotic variance for the PL estimator of Breslow and Cain (1988).
3.2.2 Extended pseudolikelihood
The MO estimator, together with its corresponding variance estimator, has the advantage of being straightforward to calculate, using existing software for two-phase methods. One potential drawback of the estimator, however, is the trade-off between inducing independence of participation with Z and the corresponding loss of information (i.e., only analyzing ñ individuals at phase III). Following the work of Chen et al. (2008), consider the phase I/II stratum-specific disease probability
| (16) |
where δk is the same as in expression (8) and . An extended pseudolikelihood (EPL) estimator is obtained by maximizing
| (17) |
with respect to β. Via a derivation similar to that in Breslow and Cain (1988), the variance can be consistently estimated as that from the PL estimator software that ignores the fact that the additional offset in the EPL estimator is estimated.
4. Simulation Study
Because the motivating study concerning bone fracture is ongoing, we illustrate the methods and assess their small-sample properties with a simulation study. In particular we consider a hypothetical study examining the association between birth weight and infant mortality (death within the first year of life), using data from the Odum Institute for Research in Social Science at the University of North Carolina at Chapel Hill (http://www.odum.unc.edu). Restricting to the year 2004, there were N = 121, 348 births in North Carolina; of these 1031 passed away within the first year of life.
4.1 Simulation Setup
In the hypothetical study, the focus of scientific interest is taken to be the association between birth weight and infant mortality, adjusting for gender and time of gestation as potential confounders. As we expand upon below, participation (given invitation) is assumed to be jointly determined by the outcome and gestation period. Figure 1 provides a directed acyclic graph that summarizes the interplay between the outcome and participation models.
Figure 1.
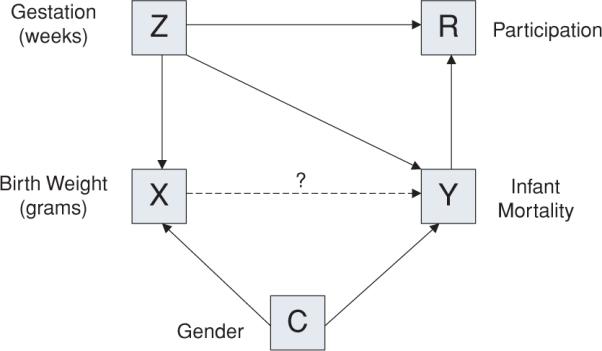
Directed acyclic graph summarizing the interplay between the outcome and participation models. This figure appears in color in the electronic version of this article.
4.1.1 Participation model
To illustrate the various estimators we present two sets of simulations; in the first participation is driven by gestation as a continuous term; in the second participation is driven by gestation as a discrete covariate.
Figure 2 illustrates two schemes for the participation model in the first set of simulations. Under both schemes, controls are assumed to have a constant underlying probability of participation of 0.7. Further, under both schemes, participation probabilities for cases are high for births with short gestation periods, decreasing over time. Under scheme 1, the decrease is fairly dramatic over (gestation) time, reflecting the situation from the motivating oral contraceptive/fracture study (where cases and controls had similar marginal rates of participation). Under scheme 2, the decrease is less dramatic, with the participation probability always greater than that for a control with the same gestation period. Following the criteria set out by Hernán et al. (2004) we see that, under both structures, there is potential for selection bias in the estimation of the effect of birth weight on infant mortality.
Figure 2.
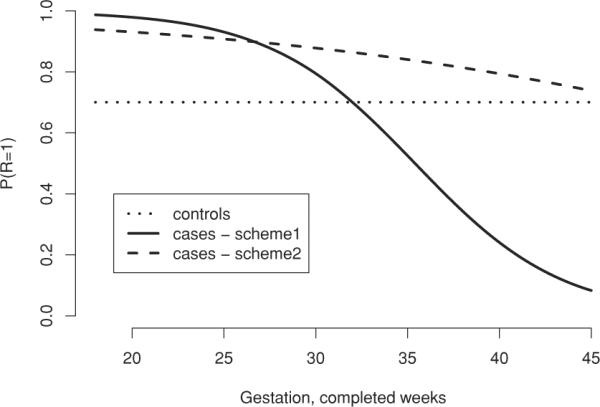
Participation models for the simulation study of Section 4.
For the second set of simulations, although gestation is included in the outcome model via a continuous term (see below), it is assumed that the impact of gestation on participation is via a threshold effect. We consider a single participation scheme where participation for cases depends on whether or not gestation was less than 36 weeks. Specifically, we take the probability of participation to equal 0.864 if gestation is less than 36 weeks and 0.587 otherwise. For controls, the participation probability is taken to be 0.701 regardless of gestation period.
4.1.2 Data generating mechanism
The hypothetical study we consider mimics a common setting where limited information is available on all individuals (in this case, births), whereas additional data collection is required to obtain detailed information. Specifically, we assume information on gender is readily available for all births and information on birth weight and gestation require additional data collection efforts.
For each scheme we generated 20,000 datasets. Each dataset retained the same joint gender/weight/gestation distribution and overall sample size as the original data (N = 121, 348). Outcome vectors were generated using a logistic outcome model with coefficient vector β = (−5.58, 0.29, −0.14, −0.63) corresponding to the intercept, gender (0 = male versus 1 = female), weight (a 100mg contrast), and gestation (a 4-week contrast). The latter were obtained from a fit of the complete data.
The resulting simulated dataset was then stratified according to the outcome and gender (thus yielding the phase I data). Using a balanced design, n individuals were “collected” from the four phase I strata as follows. An initial random draw was taken from a given phase I strata, and evaluated (according to the assumed participation model) as to whether or not they participated. If they did participate, their covariate information was recorded. The process was repeated until n/4 samples were obtained from each phase I strata. For the first set of simulations (with Z a mixture of discrete and continuous) we considered n = 200 and 1000; for the second set of simulations we considered n = 400 and 1000.
4.1.3 Analyses
For each dataset in the first set of simulations, we evaluated the FWL and WPL estimators of Section 3.1 using the true weights, estimated weights using the underlying participation model, and estimated weights using an overspecified model. For the latter, in addition to the structure provided in Figure 2 we (erroneously) assumed a gender main effect and gender interaction with weight in the participation model. For the second set of simulations we also evaluated the MO and EPL estimators of Section 3.2; for the former, we considered M = 5 and M = 10.
Throughout we also evaluated the näive WL and PL estimators that ignore participation bias. Finally, although the traditional WL and PL estimators are known to be consistent under full participation, given a finite sample size, there is the potential for small-sample bias. To evaluate this, and ground the investigation of participation bias, we also repeated the simulation assuming full participation. Throughout, data were generated and analyses performed in R v2.9.0 (R Development Core Team, 2009).
4.2 Results for Arbitrary Z
Tables 3 and 4 summarize the operating characteristics of the FWL and WPL estimators in the setting where Z is arbitrary. From Table 3, under full participation the traditional WL estimator exhibits substantial positive small-sample bias of 61.0% for the gestation effect when the phase II sample size is n = 200; for the other parameters there is little to moderate bias ranging from 4.1% to 22.1%. In contrast, the PL estimator exhibits far less small-sample bias with the gestation and weight effects only suffering 7.1% and 5.1% bias, respectively. As one would expect, the bias is substantially reduced for both the WL and PL estimators as the phase II sample size is increased to n = 1000.
Table 3.
Percent bias, by the phase II sample size, of the standard and modified WPL and PL estimators, based on a series of simulations each consisting of 20,000 repetitions
|
n = 200 |
n = 1000 |
|||||||
|---|---|---|---|---|---|---|---|---|
| Intercept | Gender | Weight | Gestation | Intercept | Gender | Weight | Gestation | |
| Full participation | ||||||||
| WL | 4.1 | 22.1 | 18.1 | 61.0 | 1.0 | 4.6 | 1.4 | 13.9 |
| PL | 0.3 | 1.7 | 5.1 | 7.1 | 0.1 | 0.2 | 1.0 | 1.1 |
| Participation scheme 1 | ||||||||
| WL | ||||||||
| Näive | 19.6 | 24.6 | 30.1 | 150.2 | 11.7 | 8.5 | 9.5 | 56.2 |
| FWL—true weights | 4.6 | 12.6 | 16.6 | 72.0 | 1.1 | 2.9 | 1.3 | 16.1 |
| FWL—estimated | 4.3 | 12.9 | 16.2 | 69.6 | 1.1 | 2.9 | 1.2 | 15.5 |
| FWL—overspecified | 4.2 | 13.3 | 16.0 | 69.2 | 1.0 | 3.0 | 1.1 | 15.4 |
| PL | ||||||||
| Näive | 10.0 | 2.0 | 5.7 | 86.2 | 9.1 | 0.4 | −0.5 | 73.8 |
| WPL—true weights | 1.0 | 0.5 | 6.2 | 20.2 | 0.2 | −0.4 | 0.8 | 4.5 |
| WPL—estimated | 0.8 | 0.3 | 6.0 | 17.3 | 0.1 | −0.4 | 0.8 | 3.6 |
| WPL—overspecified | 0.8 | 0.7 | 6.0 | 16.3 | 0.1 | −0.3 | 0.8 | 3.3 |
| Participation scheme 2 | ||||||||
| WL | ||||||||
| Näive | 1.1 | 18.6 | 17.6 | 66.4 | −2.0 | 1.7 | 2.0 | 18.3 |
| FWL—true weights | 4.2 | 19.6 | 17.9 | 63.9 | 1.0 | 1.9 | 1.5 | 14.9 |
| FWL—estimated | 4.2 | 19.6 | 18.0 | 62.8 | 1.0 | 1.9 | 1.5 | 14.3 |
| FWL—overspecified | 4.2 | 19.6 | 17.9 | 62.5 | 1.0 | 2.0 | 1.5 | 14.3 |
| PL | ||||||||
| Näive | −2.6 | 2.5 | 5.2 | 14.1 | −3.0 | −0.2 | 0.8 | 8.0 |
| WPL—true weights | 0.4 | 2.5 | 5.3 | 7.9 | 0.1 | −0.3 | 1.0 | 1.6 |
| WPL—estimated | 0.4 | 2.4 | 5.2 | 5.9 | 0.1 | −0.2 | 0.9 | 1.1 |
| WPL—overspecified | 0.4 | 2.6 | 5.2 | 5.3 | 0.1 | −0.2 | 0.9 | 0.9 |
Table 4.
Relative efficiency, by the phase II sample size, of the standard and modified WPL and PL estimators, based on a series of simulations each consisting of 20,000 repetitions
|
n = 200 |
n = 1000 |
|||||||
|---|---|---|---|---|---|---|---|---|
| Intercept | Gender | Weight | Gestation | Intercept | Gender | Weight | Gestation | |
| Full participation | ||||||||
| WL | 249 | 313 | 212 | 203 | 249 | 316 | 218 | 227 |
| PL | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Participation scheme 1 | ||||||||
| WL | ||||||||
| Näive | 363 | 463 | 293 | 293 | 362 | 443 | 299 | 311 |
| FWL—true weights | 268 | 331 | 224 | 218 | 263 | 324 | 223 | 231 |
| FWL—estimated | 258 | 331 | 224 | 212 | 256 | 327 | 224 | 230 |
| FWL—overspecified | 258 | 330 | 224 | 212 | 256 | 326 | 224 | 230 |
| PL | ||||||||
| Näive | 149 | 157 | 131 | 139 | 140 | 146 | 125 | 132 |
| WPL—true weights | 158 | 172 | 141 | 145 | 148 | 160 | 138 | 142 |
| WPL—estimated | 147 | 176 | 144 | 140 | 136 | 160 | 138 | 142 |
| WPL—overspecified | 147 | 175 | 145 | 141 | 135 | 158 | 139 | 137 |
| Participation scheme 2 | ||||||||
| WL | ||||||||
| Näive | 249 | 311 | 209 | 201 | 245 | 311 | 215 | 224 |
| FWL—true weights | 253 | 316 | 212 | 202 | 250 | 319 | 218 | 228 |
| FWL—estimated | 252 | 320 | 213 | 201 | 251 | 323 | 219 | 228 |
| FWL—overspecified | 251 | 319 | 313 | 201 | 250 | 322 | 219 | 228 |
| PL | ||||||||
| Näive | 109 | 110 | 102 | 103 | 108 | 111 | 102 | 101 |
| WPL—true weights | 109 | 110 | 102 | 103 | 108 | 111 | 102 | 101 |
| WPL—estimated | 103 | 111 | 103 | 100 | 103 | 111 | 102 | 98 |
| WPL—overspecified | 103 | 110 | 103 | 100 | 102 | 110 | 102 | 98 |
Under participation scheme 1, the näive WL and PL estimators for the gestation effect exhibit substantial bias, beyond ordinary small-sample bias. Specifically, when n = 200, the bias for the two estimators of the gestation effect increase to 150.2% and 86.2% for the WL and PL estimators, respectively; when n = 1000 the corresponding biases are reduced but still significant at 56.2% and 73.8%. Applying the methods of Section 3.1 results in much reduced small-sample bias across all estimators and both sample sizes. For both the FWL and WPL estimators, the use of true weights results in slightly greater bias, compared to the use of estimated weights; estimation based on an overspecified model does not appear to result in meaningful changes in bias. Under participation scheme 2, bias associated with ignoring the participation mechanism is lower than that under participation scheme 1. The näive WL estimator exhibits bias comparable to that of the WL estimator under full participation. With the exception of the gestation effect, the naïve PL estimator has similar bias to that under full participation; for the gestation effect the bias is increased from 7.1% to 14.1% and 1.1% to 8.0% for n = 200 and n = 1000, respectively. Each of the FWL and WPL exhibit reduced bias, with the results again not depending greatly on whether or not one uses the true or estimated weights.
Table 4 presents results for relative efficiency, defined here as the standard error of each estimator to that of the PL estimator under full participation. Note, each standard error was calculated as the empirical standard deviation of the 20,000 estimates. Under full participation, the WL estimator is substantially less efficient than the PL estimator, as has been noted by others (e.g. Breslow and Chatterjee, 1999). Overall the results suggest a decrease in efficiency associated with having to account for selective participation. Focusing on the gestation effect, under participation scheme 1, the relative efficiency for the FWL estimator based on estimated weights is 212% when n = 200, compared to 203% under full participation. For the WPL estimator, the relative efficiency is 140% suggesting a greater loss in the presence of participation bias. Under participation scheme 2, there is virtually no loss of efficiency for either the FWL or WPL estimators. Increasing the phase II sample size to n = 1000 does not appear to substantially impact relative efficiency, under either participation scheme.
Finally, under participation scheme 1, when n = 200 each of the FWL and PWL estimators exhibit a slight loss of efficiency associated with the use of the true weights (145%, compared to 140% when the weights are estimated), consistent with the results of Robins et al. (1994). However, the gains associated with estimation of the weights diminished under the increased phase II sample size and under the weaker participation scheme. Comparing the relative efficiencies for both the FWL and WPL estimators when the participation weights are based on an overspecified model to those based on weights estimated from the correct participation model indicates little impact.
4.3 Results for Discrete Z
Table 5 summarizes the operating characteristics of the proposed estimators in the setting where Z is discrete. As with the results from Table 3, both the ordinary WL and PL estimators exhibit some small-sample bias under full participation with the WL estimator suffering from greater bias (36.0% when n = 400, compared to 3.9% for the PL estimator). In addition the PL estimator is substantially more efficient (at least twice as efficient) than the WL estimator, with little dependence of relative efficiency on the phase II sample size.
Table 5.
Operating characteristics, by the phase II sample size, of four proposed estimators in the setting where Z is discrete. Results are based on a series of simulations each consisting of 20,000 repetitions.
| Phase II sample size | Scheme/Estimator | Percent bias |
Relative efficiency |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Intercept | Gender | Weight | Gestation | Intercept | Gender | Weight | Gestation | ||
| 400 | Full participation | ||||||||
| WL | 2.4 | 7.7 | 6.3 | 36.0 | 257 | 332 | 216 | 218 | |
| PL | 0.1 | 0.1 | 2.1 | 3.9 | 100 | 100 | 100 | 100 | |
| Selective participation | |||||||||
| WL | |||||||||
| Näive | 5.1 | 13.4 | 11.8 | 51.3 | 295 | 375 | 242 | 248 | |
| FWL—estimated | 2.4 | 8.8 | 6.2 | 36.5 | 258 | 335 | 220 | 221 | |
| PL | |||||||||
| Näive | 1.6 | 0.8 | 3.6 | 35.3 | 118 | 122 | 109 | 116 | |
| WPL—estimated | 0.2 | −0.4 | 2.6 | 3.7 | 111 | 126 | 111 | 106 | |
| EPL | 0.2 | 0.7 | 2.5 | 3.3 | 101 | 96 | 109 | 104 | |
| MO | |||||||||
| M = 5 | 0.2 | 0.6 | 2.9 | 3.0 | 103 | 96 | 112 | 106 | |
| M = 10 | 0.2 | 0.6 | 2.9 | 3.0 | 102 | 95 | 111 | 106 | |
| 1000 | Full participation | ||||||||
| WL | 1.0 | 4.4 | 1.5 | 15.1 | 250 | 319 | 216 | 228 | |
| PL | 0.1 | 0.5 | 1.0 | 1.3 | 100 | 100 | 100 | 100 | |
| Selective participation | |||||||||
| WL | |||||||||
| Näive | 3.0 | 4.8 | 6.5 | 24.8 | 282 | 354 | 238 | 253 | |
| FWL—estimated | 1.0 | 1.8 | 1.3 | 15.0 | 251 | 321 | 216 | 229 | |
| PL | |||||||||
| Näive | 1.6 | 1.3 | 2.1 | 31.8 | 116 | 120 | 107 | 114 | |
| WPL—estimated | 0.1 | 0.5 | 1.1 | 1.1 | 110 | 123 | 108 | 105 | |
| EPL | 0.1 | 0.4 | 1.1 | 0.9 | 100 | 95 | 107 | 103 | |
| MO | |||||||||
| M = 5 | 0.1 | 0.4 | 1.2 | 0.8 | 101 | 95 | 109 | 105 | |
| M = 10 | 0.1 | 0.4 | 1.2 | 0.8 | 101 | 95 | 108 | 105 | |
Given selective participation the naïve WL and PL have substantially increased bias; when n = 200 the bias for the gestation effect increases to 51.3% and 35.3% for the WL and PL estimators, respectively. Applying the general-purpose methods of Section 3.1 improves estimation considerable, with bias decreasing to 36.5% and 3.7% (approximately the small-sample bias levels under full participation) for the FWL and WPL estimators based on estimated weights from a correctly specified participation model. Examination of the relative efficiency estimates indicate a small loss of efficiency for the WPL estimator (compared to the PL estimator under full participation), with the greatest loss occurring for the gender effect (a 26% increase in the standard error). Across the board, the WPL estimator outperforms the FWL estimator. Consistent with Tables 3 and 4, using the true weights for the FWL and WPL estimators resulted in a small decrease in efficiency. Using estimated weights based on an overspecified participation resulted in little to no change in operating characteristics.
For both the MO and EPL estimators, we find that the primary gain is in efficiency of estimation for the gender effect, in contrast to the FWL and WPL estimators where there appears to be no loss in efficiency relative to estimates obtained full participation. For the settings considered here, no additional benefit was observed by increasing M from 5 to 10 for the MO estimator. Overall, the same patterns concerning both operating characteristics were observed when the phase II sample size was increased from n = 200 to n = 1000.
5. Discussion
We have proposed a simple extension of the traditional two-phase design aimed at addressing potential nonresponse or participation bias in observational studies. In contrast to consideration of potential confounding bias, potential participation bias is seldom considered when designing a study. Indeed, a typical strategy for evaluating the latter is to perform a post hoc comparison of participants and nonparticipants (e.g. Rothman and Greenland, 1998). However, given differences, there is often little one can do to adjust for participation bias once data collection efforts have been halted. Sensitivity analyses may often be the only recourse, although even this strategy will be inadequate if insufficient information is obtained on the participation mechanism. Here, we have adopted a design-based philosophy, emphasizing consideration of potential participation bias prior to data collection. In particular, taking advantage of well-established methods for two-phase designs and missing data, we have proposed a novel design/analytic framework that formalizes and facilitates consideration of participation bias.
At the time of submission, as the methodological development outlined here was not complete, the motivating bone fracture did not employ our multiphase approach. It may be instructive, however, to consider how the design could have been implemented. Briefly, the study was conducted at the Group Health Cooperative, a nonprofit health maintenance organization in the U.S. state of Washington. Initially, an extensive electronic medical record system was used to identify women aged 45–59 years with no prior fracture after age 45, no current/recent hormone therapy use, and no hysterectomy. Further, the electronic medical record system permitted the identification of outcome information (via ICD-9 codes for various fracture types) as well as demographic information, co-morbid conditions, and crude exposure data (via an electronic pharmacy database). Based on its potential strength as a confounder and the size of the study, the specific choice for the phase I stratification variable, S, was age categorized into 2-year age bands. Individual women were then sent letters of invitation and followed up with a telephone call. Had the multiphase approach been adopted, women who declined to participate in the main study could be asked during the telephone call to answer a brief survey aimed at completing ascertainment of Z at phase II. Based on previous studies, specific additional information not available at phase I would have been collected on race and family history of fracture. Women that participated would also be asked to provide this information as well as complete a detailed study questionnaire, primarily on prior oral contraceptive use, yielding complete X at phase III.
Under the usual assumption of full participation, ML methods have been proposed for analyzing data arising from the two-phase design (Breslow and Holubkov, 1997; Scott and Wild, 1997). Although the ML estimator has been shown to be asymptotically equivalent to the semiparametric efficient estimator (Breslow, Robins, and Wellner, 2000), numerous investigations have suggested that the PL estimator is largely comparable in terms of efficiency (e.g., Breslow and Chatterjee, 1999). Beyond comparisons with ML, additional work is needed to better characterize the operating characteristics of the proposed estimators. One key area is that of robustness to misspecification of either the outcome or participation models. In the absence of differential participation, WL is known to be robust to misspecification of the outcome model in the sense that the estimator is consistent for the value one would obtain by fitting the misspecified model to the entire population (Breslow and Chatterjee, 1999). This property is not shared by either the PL or ML estimators, and the extent to which the resulting bias–variance trade-off translates in the presence of participation bias would be of interest.
Similar to well-known methods for characterizing confounding bias (e.g., Pearl, 1995; Greenland, Pearl, and Robins, 1999), the work of Hernán et al. (2004) provides a directed acyclic graph framework for engaging subject-matter experts on determinants of participation into a study. Generally, establishing general rules on the consequences of under-specification is challenging because they will depend on the nature of the misspecification. In such settings, sensitivity analyses (within the scope of the available data) are the only recourse. Somewhat encouraging are the results of Tables 3 and 4 that indicate little loss when one overspecifies the participation model, suggesting a liberal strategy for characterizing participation and designing data collection efforts. In some settings, however, particularly when dealing with small sample sizes, there may be a decrease in efficiency associated with this strategy. Investigating this trade-off will also provide useful guidance for researchers as they design their studies.
Appendix
We present asymptotic properties of the FWL and WPL estimators proposed in Section 3.1. The derivations basically follow those presented in Robins et al. (1994). Specifically, following arguments of Foutz (1977), and assuming similar regularity conditions therein, we can conclude that there exist unique solutions to the two estimating equations, and that these solutions are consistent estimates of the odds ratio parameters. We mainly focus on showing asymptotic normality of the two estimators and deriving their asymptotic variances.
A.1 Full Weighted Likelihood Estimator
From Section 3.1, can be seen as fitted values from a saturated model for fy k = Pr(I = 1 | Y = y, S = k). Thus, we can write . Let ξ indicate whether a subject is invited to participate in the study, and let Zξ = (1, Y, S). Equation (14) can also be written as
Then based on simple Taylor series' expansion, we obtain
| (A1) |
where is between the true value (β; γ, α) and the estimates . Let Iββ = −lim ∂U(β; γ, α)/∂β, Iβγ = −lim ∂U(β; γ, α)/∂γ, and Iβα = −lim ∂U(β; γ, α)/∂α. By the law of large numbers, equation (A1) becomes
| (A2) |
Furthermore, we can easily obtain the following:
and
where Iγγ = E[Zξ (Zξ)T f(Zξ; γ){1 − f(Zξ; γ)}], Iαα = E[ξZZT π(Z; α){1 − π(Z; α)}], and ρ = limN →∞ N*/N. Plugging these two equations into (A2), we obtain the influence function for β, which is written as
Thus, the asymptotic variance of can be estimated .
A.2 Weighted Pseudolikelihood Estimator
Define and δy k = log ρy k where , y = 0, 1. Let and .
δy and δ are similarly defined. Breslow and Cain (1988) showed that is asymptotically normal with zero and covariance matrix , where Dqy is a K × K diagonal matrix with diagonal elements p(S = k|Y = y) and M denotes a K × K matrix whose entries are all 1. The WPL score function ∂ log PL(β)/∂β can then be written as
The WPL estimator is the unique consistent solution to the equation , so that . Performing Taylor's series expansion on , we obtain
| (A3) |
where is between the true value (β, δ, α) and . Let , , and . Equation (A3) can then be written as
The first two terms on the right-hand side are independent (Breslow and Cain, 1988), and their joint distribution is the same as that in Proposition 1 of Breslow and Cain (1988). But we obtain the influence function of β for easier calculation of the asymptotic variance. As above,
where Iαα = E[ξZZT π(Z; α){1 − π(Z; α)}]. Furthermore,
Putting all above together, we obtain the influence function for , so that its asymptotic variance can be obtained accordingly.
References
- Austin M, Criqui M, Barrett-Connor E, Holdbrook M. The effect of response bias on the odds ratio. American Journal of Epidemiology. 1981;114:137–143. doi: 10.1093/oxfordjournals.aje.a113160. [DOI] [PubMed] [Google Scholar]
- Breslow NE, Cain KC. Logistic regression for two-stage case-control data. Biometrika. 1988;75:11–20. [Google Scholar]
- Breslow N, Chatterjee N. Design and analysis of two-phase studies with binary outcomes applied to Wilms' tumor prognosis. Applied Statistics. 1999;48:457–468. [Google Scholar]
- Breslow N, Holubkov R. Maximum likelihood estimation of logistic regression parameters under two-phase, outcome-dependent sampling. Journal of the Royal Statistical Society, Series B, Methodological. 1997;59:447–461. [Google Scholar]
- Breslow N, Robins J, Wellner J. On the semiparametric efficiency of logistic regression under case-control sampling. Bernoulli. 2000;6:447–455. [Google Scholar]
- Chatterjee N. A two-stage regression model for epidemiological studies with multivariate disease classification data. Journal of the American Statistical Association. 2004;99:127–137. [Google Scholar]
- Chatterjee N, Chen Y, Breslow N. A pseudoscore estimator for regression problems with two-phase sampling. Journal of the American Statistical Association. 2003;98:158–168. [Google Scholar]
- Chen J, Breslow N. Semiparametric efficient estimation for the auxiliary outcome problem with the conditional mean model. The Canadian Journal of Statistics. 2004;32:359–372. [Google Scholar]
- Chen J, Ayyagari R, Chatterjee N, Pee D, Schaireer C, Byrne C, Benichou J, Gail M. Breast cancer relative hazard estimates from case-control and cohort designs with missing data on mammographic density. Journal of the American Statistical Association. 2008;103:976–988. [Google Scholar]
- Flanders WD, Greenland S. Analytic methods for two-stage case-control studies and other stratified designs. Statistics in Medicine. 1991;10:739–747. doi: 10.1002/sim.4780100509. [DOI] [PubMed] [Google Scholar]
- Follmann D, Proschan M, Leifer E. Multiple outputation: Inference for complex clustered data by averaging analyses from independent data. Biometrics. 2003;59:420–429. doi: 10.1111/1541-0420.00049. [DOI] [PubMed] [Google Scholar]
- Foutz R. On the unique consistent solution to likelihood equations. Journal of the American Statistical Association. 1977;72:147–148. [Google Scholar]
- Greenland S, Pearl J, Robins J. Causal diagrams for epidemiologic research. Epidemiology. 1999;10:37–48. [PubMed] [Google Scholar]
- Hernán M, Hernández-Diaz S, Robins J. A structural approach to selection bias. Epidemiology. 2004;15:615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- Lawless J, Kalbfleisch J, Wild C. Semiparametric methods for response-selective and missing data problems in regression. Journal of the Royal Statistical Society, Series B. 1999;21:413–438. [Google Scholar]
- Lin I, Paik M. Matched case-control data analysis with selection bias. Biometrics. 2001;57:1245–1250. doi: 10.1111/j.0006-341x.2001.01106.x. [DOI] [PubMed] [Google Scholar]
- Little R, Rubin D. Statistical Analysis of Missing Data. 2nd edition John Wiley and Sons; Hoboken, New Jersey: 2002. [Google Scholar]
- Pearl J. Causal diagrams for empirical research. Biometrika. 1995;82:669–710. [Google Scholar]
- Pfeiffer R, Chatterjee N. On a supplemeted case-control design. Biometrics. 2005;61:584–590. doi: 10.1111/j.1541-0420.2005.00319.x. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2009. [Google Scholar]
- Robins J, Rotnitzky A, Zhao L. Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association. 1994;89:846–866. [Google Scholar]
- Rothman K, Greenland S. Modern Epidemiology. 2nd edition Lippincott, Williams, and Wilkins; Philadelphia, Pennsylvania: 1998. [Google Scholar]
- Schill J, Jockel JH, Drescher K, Timm J. Logistic analysis in case-control studies under validation sampling. Biometrika. 1993;84:57–71. [Google Scholar]
- Scott AJ, Wild CJ. Fitting regression models to case-control data by maximum likelihood. Biometrika. 1997;84:57–71. [Google Scholar]
- Weinberg C, Wacholder S. The design and analysis of case-control studies with biased sampling. Biometrics. 1990;46:963–975. [PubMed] [Google Scholar]


