Abstract
Behavior in social dilemmas is often inconsistent with the predictions of classical game theory: people (and a wide variety of other organisms) are more cooperative than might be expected. Here we consider behavior in one such social dilemma, the Traveler's Dilemma, that has received considerable attention in the economics literature but is little known among theoretical biologists. The rules of the game are as follows. Two players each choose a value between R and M, where 0 < R < M. If the players choose the same value, both receive that amount. If the players choose different values v1 and v2, where v1 < v2, then the player choosing v1 earns v1 + R and the player choosing v2 earns v1 − R. While the players would maximize their payoffs by both declaring the largest possible value, M, the Nash equilibrium is to declare the smallest possible value, R. In behavioral experiments, however, people generally declare values much larger than the minimum and the deviation from the expected equilibrium decreases with R. In this paper, we show that the cooperative behavior observed in the Traveler's Dilemma can be explained in an evolutionary framework. We study stochastic evolutionary dynamics in finite populations with varying intensity of selection and varying mutation rate. We derive analytic results showing that strategies declaring high values can be favored when selection is weak. More generally, selection favors strategies that declare high values if R is small (relative to M) and strategies that declare low values if R is large. Finally, we show that a two-parameter model involving the intensity of selection and the mutation rate can quantitatively reproduce data that from a Traveler's Dilemma experiment. These results demonstrate the power of evolutionary game theory for explaining human behavior in contexts that are challenging for standard economic game theory.
1 Introduction
The evolution of cooperation is a central topic of interest in the biological and social sciences (Trivers, 1971; Axelrod and Hamilton, 1981; Levin, 2000; Boyd et al., 2003; Panchanathan and Boyd, 2004; Nowak and Sigmund, 2005; Fowler, 2005; Janssen and Bushman, 2008; Helbing and Yu, 2009; Levin, 2009; Wang et al., 2009; Sigmund et al., 2010). Cooperation is found at all levels of the natural world and lies at the heart of modern human societies. Yet cooperation is often costly, creating a social dilemma: cooperating maximizes the group payoff, but individuals do best by being selfish. In the context of evolutionary game theory, the Prisoner's Dilemma (Trivers, 1971; Axelrod and Hamilton, 1981; Milinski, 1987; Kraines and Kraines, 1989; Fudenberg and Maskin, 1990; Nowak and Sigmund, 1992, 1993, 2005; Lotem et al., 1999; Wedekind and Milinski, 2000; Ohtsuki and Iwasa, 2004, 2006; Brandt et al., 2005; Imhof et al., 2005, 2007; Pacheco et al., 2006; Fu et al., 2007; Worden and Levin, 2007; Helbing and Yu, 2009; Rand et al., 2009) and the public goods game (Levin, 2000; Hauert et al., 2002; Boyd et al., 2003; Panchanathan and Boyd, 2004; Fowler, 2005; Hauert et al., 2007; Janssen and Bushman, 2008; Levin, 2009; Ohtsuki et al., 2009; Wang et al., 2009; Sigmund et al., 2010; Rand and Nowak, 2011) are the standard paradigms for exploring social dilemmas. However, other interesting social dilemmas also exist. In this paper, we study the evolution of strategies in the Traveler's Dilemma (Basu, 1994), a game that has received little attention in the evolution literature (an exception is Smead (2008), a paper from the philosophy literature that used evolutionary computer simulations to study a version of the Centipede Game that is similar to the Traveler's Dilemma).
Just as the Prisoner's Dilemma is often characterized by a standard narrative (involving two prisoners charged with a crime), so too is the Traveler's Dilemma. Imagine that two travelers have purchased identical souvenirs while visiting a remote island. Their airline loses both souvenirs as the two travel home and asks each (separately and in private) to declare the value of the souvenir to the nearest dollar. If both travelers declare the same value, then the airline will compensate both with that amount. But if the travelers declare different values, the airline will pay both the smaller of the two. Furthermore, it will reward the traveler claiming the smaller value with a bonus of R and penalize the traveler claiming the larger value the same amount R. For instance, if one traveler claims the souvenir was worth 50 while the other claims it was worth 80, and if R = 2, then the first will receive 52 and the second 48.
For simplicity, we assume that R is an integer, and to make the game a social dilemma we assume that R ≥ 2. Furthermore, the game is typically structured so that players' payoffs cannot drop below zero (the airline cannot impose fines), so the players cannot declare values less than R. Figure 1 shows a (partial) payoff matrix for the game: each player's strategy is the value he or she claims for the item.
Figure 1.
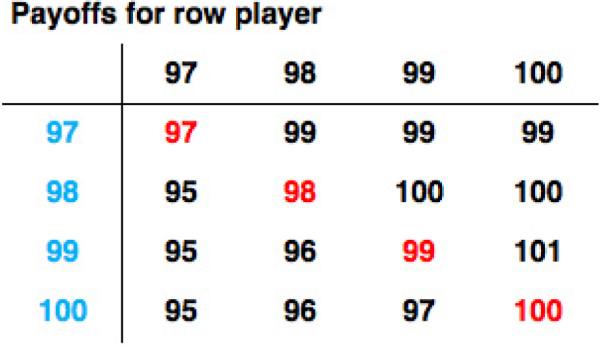
A partial payoff matrix for the Traveler's Dilemma when R = 2 and the maximum claim M = 100. Payoffs are shown for the row player (blue). When the travelers claim the same value, they are both awarded that amount (red). But if one traveler claims a value L and the other a value H > L, then the former receives L + R and the latter receives L – R. For example, if the row player claims 98 and the column player 99, the row player gets 98 + R = 100 and the column player 98 – R = 96.
What should the travelers do? It might seem natural for both to declare a value of M. However, this is not rational (assuming that both players seek to maximize their monetary payoffs). One player could switch his claim to M−1 and thereby earn a payoff of M−1+R > M (while reducing the other player's payoff to M −1−R). Continuing this iterative deletion of dominated strategies, one finds that the Nash equilibrium is to choose the minimum value, claiming the souvenir was worth just R. As in the Prisoner's Dilemma, “defection” (declaring a low value) dominates “cooperation” (declaring a high value) even though the travelers would be better off if both claimed high values. Thus, the Traveler's Dilemma presents a social dilemma involving coordination coupled with the temptation to exploit the other party.
The Traveler's Dilemma can be used to model situations not only among humans but also among other organisms. For example, competitive egg ejection in the Greater Ani, a communally nesting bird species, can be modeled by the Traveler's Dilemma (Riehl and Jara, 2009; Riehl, 2011). In a nest with two females, each female chooses a time to switch from ejecting eggs out of the nest to laying eggs. If both chose an early date (i.e., a large claim), then both successfully lay a large number of eggs and earn a large (fitness) payoff. But if one chooses to wait, she will eject the other's already-laid eggs and achieve an even higher payoff while inflicting a loss on the earlier-laying female.
Human behavior is the main focus of the current paper. When people are asked to play the Traveler's Dilemma in the laboratory, their behavior deviates significantly from the predictions of classical game theory. For example, Capra et al. (1999) conducted a repeated Traveler's Dilemma in which the value of R varied across treatments. Although the Nash equilibrium is to declare the minimum value regardless of R, Capra et al. (1999) found a significant inverse relationship between R and the average claim. This relationship held both in early rounds before any in-game learning occurred and in later rounds after subjects gained experience.
Capra et al. (1999) and Goeree and Holt (1999) proposed learning models based on the logit probabilistic decision rule to explain the development of the inverse relationship between R and the average claim over the course of the experimental session. Goeree and Holt (1999) adapted this rule to model the “introspection” that occurs before the game begins to explain behavior in initial rounds before in-game learning becomes a factor. They found that if the cognitive “noise” (defined in a suitably precise way) increases with each successive round of introspection, they could reproduce (qualitatively) the inverse relationship between R and the average claim.
In this paper, we instead propose an evolutionary model to explain people's behavior in the Traveler's Dilemma. We study stochastic population dynamics in finite populations with varying intensity of selection and varying mutation rate (Nowak et al., 2004). Critically—and unlike logic learning models or “introspection”—our model does not require any notion of cognition or rationality. We show that stochastic evolutionary models can explain the observed behavior in early rounds, reflecting the (genetically or culturally) evolved intuitions subjects bring with them into the laboratory. We also derive analytic results showing how the evolutionarily favored strategies vary as a function of R and the maximum claim M. In our model, higher payoff strategies are more likely to reproduce on average, but random chance also plays an important role. Sometimes lower payoff strategies reproduce, and sometimes higher payoff strategies die out. When the intensity of selection is low, people are uncertain when evaluating their own payoffs and the payoffs of others.
We also consider the role of mutation: sometimes offspring do not inherent their parent's strategy but instead assume a random new strategy. In the context of imitation dynamics, this means that players sometimes get confused when trying to imitate a higher payoff individual and adopt the wrong strategy. The higher the mutation rate, the greater the uncertainty about the strategies of others.
When selection is weak, the dynamics depend greatly on the mutation rate μ. In the high mutation limit, μ → 1, all strategies are present at approximately equal abundances at the same time (Antal et al., 2009; Traulsen et al., 2009). Thus, success is determined not by one's ability to resist invasion but rather by one's performance against a uniform population of all strategies. Put another way, the optimal strategy is the one that maximizes its expected payoff against a uniform distribution of opposing strategies.
In the low mutation limit, μ → 0, novel mutants will either die out or completely take over the population before a new mutant arises (Nowak et al., 2004; Fudenberg and Imhof, 2006; Hauert et al., 2007, 2008). The population makes transitions between homogeneous states in which all agents in the population play the same strategy. Hence, although all strategies are still present at equal frequency in the steady state distribution, at most two strategies are present in the population at the same time. Therefore, success in the low mutation limit is determined by one's ability to resist invasion by a single (randomly chosen) opponent. It is not expected payoff against a uniform distribution of strategies that determines success but rather expected relative payoff in pairwise competitions with a single random opposing strategy (Antal et al., 2009).
We can summarize the observations above as follows. Consider two strategies, one claiming a and one claiming b, b < a. Call the former strategy A and the latter strategy B. In A–A interactions, A receives a payoff of a. In A–B interactions, A receives a payoff of b − R. In B–B interactions, B receives a payoff of b. And in A–B interactions, B receives a payoff of b + R.
In the high mutation, weak selection limit, A and B are equally abundant in the population. A's average payoff is thus a + b − R and B's average payoff is b + b − R. When R is small, a + b − R > b + b + R, so the more “cooperative” strategy A is favored over the less cooperative B. When R is large, on the other hand, the opposite is true and B is favored over A.
In the low mutation, weak selection limit, A can be favored over B even though B beats A in pairwise interactions (b − R < b + R) since A does better against itself than B does against itself. When R is small, a population of A-players can be resistant to invasion by B-players, and A can in fact have a larger basin of attraction than B (when a + b − R > b + b + R).
In both cases, strategies that are not Nash equilibria can be favored by selection. Because the population is far from equilibrium, traditional game-theoretic solution concepts have little relevance. Instead, we ask what strategy is the most common in the stationary distribution of our stochastic model (see Section 2). The inclusion of the learning errors represented by weakening selection and increasing mutation are relevant and realistic: many real-world processes are in fact far from equilibrium and learning is rarely perfect. Importantly, our non-equilibrium calculations can explain laboratory behavior that traditional equilibrium approaches have had little success in explaining.
This paper is organized as follows. In Section 2, we introduce the model and describe the evolutionary process we are studying. In Sections 3 to 5, we derive analytic results showing how the favored and most frequent strategies vary as R changes in the limit of weak selection. In Section 6, we describe how earlier results can be used to determine the optimal choice of R from the perspective of the airline. Given that selection in the real world can be weak (but is short of the limit of weak selection), we examine the model via computer simulations in the case of arbitrary selection strength and mutation rates in Section 7. In Section 8, we find the values of the selection strength and mutation rate that best fit the data observed by Capra et al. (1999). In Section 9, we discuss our models in relation to other standard ones. Finally, we conclude in Section 10
2 Evolutionary Process
We examine the Traveler's Dilemma from the perspective of evolutionary game theory (Maynard Smith, 1982; Hofbauer and Sigmund, 1988, 1998; Weibull, 1997; Samuelson, 1998; Cressman, 2003; Nowak and Sigmund, 2004; Imhof and Nowak, 2006; Gintis, 2009; Sigmund, 2010) in finite populations (Nowak et al., 2004; Taylor et al., 2004; Nowak, 2006).
Each player chooses a strategy from a discrete space consisting of n = M −R+1 strategies (the value he or she is declaring between R and M). We index these strategies R, …,M. The payoff matrix A = (aij), R ≤ i, j ≤ M, where the entry aij is the payoff of a traveler declaring a value i when the other traveler declares a value j, is given by
| (1) |
Suppose there are N individuals in the population and Nk of them are playing strategy k (N = NR + … + NM). We assume that the population is well-mixed and that players interact randomly. Then the expected payoff (up to a constant factor) of an individual playing strategy i is
| (2) |
The fitness fi of an individual with strategy i is given by fi = exp(δπi) (Traulsen et al., 2008). While the payoff πi measures how well an individual is performing in the game, one's reproductive fitness may depend on factors other than πi. One could be engaged in multiple distinct games, for example, with the game in question only making a small contribution to the one's fecundity. The parameter δ, which we call the selection intensity, determines the nature of the payoff-to-fitness mapping. In the limit δ → 0, all individuals have roughly the same reproductive success. In the limit δ → ∞, even small payoff differences lead to large differences in reproductive success: a small payoff advantage results in a disproportionately large reproductive advantage.
Evolution occurs via the frequency-dependent Moran process. In each time step, an individual is chosen at random to be a “child” (or “learner”). That individual copies, with probability 1 − μ, the strategy of a “parent” (or “teacher”) chosen from the population with probability proportional to its fitness. With probability μ, the learner adopts one of the n strategies at random. Because mutation is possible from any one strategy to any other strategy, the random process describing the state of the population is ergodic. In particular, this means that it has a unique stationary distribution.
3 Low mutation, weak selection limit
In the absence of any payoff differences (or when δ = 0), each of the n strategies has frequency 1/n in the stationary distribution. Thus, when payoffs are different and individuals are subject to selection, we say that selection favors a strategy if its frequency in the stationary distribution is > 1/n. We say that selection opposes a strategy if its frequency in the stationary distribution is < 1/n.
When selection is weak, each strategy's frequency in the stationary distribution is still close to 1/n—there is just a small perturbation from the neutral value. Antal et al. (2009) showed that when δ → 0 and μ ≪ 1/N, the perturbation for strategy k is proportional to
| (3) |
Hence, strategy k is favored by selection when Lk > 0. We can interpret this condition as follows. When akk +aki > aii+aik, a k-mutant in a population of i-players has a higher probability of taking over the population than does an i-mutant in a population of k-players. The condition (3) thus says that strategy k on average can invade and take over uniform populations of other strategies. Conversely, a uniform population of k-players is on average resistant to invasion by other strategies.
Using the payoff matrix (1), we find that
| (4) |
Lk is an increasing function of k when R <(M + 1)/5 and a decreasing function of k when R > (M + 1)/5. Thus,
| (5) |
When R is large, strategies claiming larger values are favored. When R is small, strategies claiming smaller values are favored. When R = (M + 1)/5, then (weak) selection has no effect and each strategy has the same frequency 1/n.
The strategy k that maximizes Lk is the one that is most frequent in the stationary distribution. Since Lk is either monotonically increasing or decreasing, it follows that
| (6) |
When R is large relative to the maximum claim M, there is a strong incentive for individuals to declare low values as the reward for declaring the lower of the two values is large. Thus, the most successful strategy makes the minimum claim R. When the reward is small relative to M, on the other hand, the high payoffs obtained when both players claim large values trump the reward to be had by declaring a low value. Thus, the most successful strategy makes the maximum claim M.
For M = 100 and R = 2, Lk is maximized for k = 100. The strategy making the highest possible claim is thus chosen when the selection intensity and mutation rate are both small.
4 High mutation
In the high mutation case, μ ≫ 1/N, strategy k is favored by selection if
| (7) |
(Antal et al., 2009). To understand this condition, first observe that when mutation is high, all strategies are (roughly) equally abundant. Recall that since δ is small, fi = exp(δπ) ≈ 1 + δπ. Hence, the fitness of strategy k is . By comparing this to the average fitness , we obtain (7).
Using the payoff matrix (1), we find that
| (8) |
In the extreme cases when k = R (the lowest possible valuation) or k = M (the highest), we have
| (9) |
and
| (10) |
Thus, the lowest claim (the Nash equilibrium) is favored when R > (2M + 1)/8 and the largest claim is favored when R < (M + 2)/7. Note that we cannot have both HR > 0 and HM > 0 since (2M + 1)/8 > (M + 2)/7 for M ≥ 2. It now follows easily that
| (11) |
The endpoints of the second interval in (11) are precisely the roots of the quadratic (in k) Hk.
The most frequent strategy when mutation is high is k = (2M − 4R − 1)/2. This is the k that maximizes Hk. To see this directly, we argue as follows. When selection is weak and mutation is high, all strategies are (about) equally abundant. The average payoff of strategy k is
| (12) |
We have
| (13) |
so when k = M − 2R + 1/2. Since strategies are restricted to lie in the interval R ≤ k ≤ M and R > 1, we find that
| (14) |
In the first case, Hk increases when k < (2M − 4R + 1)/2 and decreases afterwards. In the second case, Hk is a decreasing function of k. As in the low mutation case, the size of the reward R is the determining factor. For M = 100 and R = 2, Hk is maximized for k = 96, 97 (since we require strategies to be integer-valued). A strategy is favored by selection, Hk > 0, when k ≥ 43.
5 Any mutation rate, weak selection limit
For an arbitrary mutation rate μ, selection favors strategy k if
| (15) |
(Antal et al., 2009). We can determine which strategy is most abundant in the stationary distribution by using the fact that strategy k is more abundant than strategy j if
| (16) |
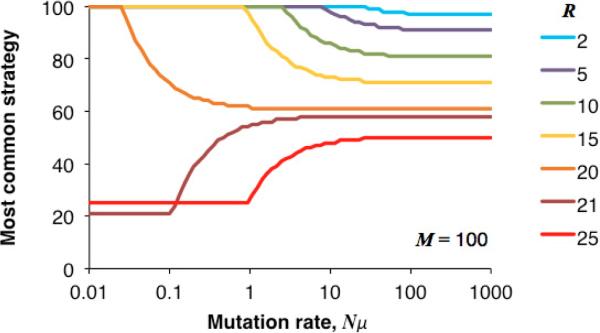
Figure 2 shows which strategy is most abundant as R and Nμ vary. For R equal to 2, 5, or 10, Lk increases with k. When Nμ is small, Lk dominates NμHk and so k = 100 is most frequent. When Nμ is large, on the other hand, NμHk dominates Lk and so k = [(2M − 4R + 1)/2] is most frequent. This means that high mutation results in a smaller k being the most frequent strategy. In contrast, for R equal to 25, Lk decreases with k. Thus, Lk is maximized for k = R whereas Hk is still maximized for k = [(2M − 4R + 1)/2]. As Nμ increases, the most frequent strategy claims a larger and larger value.
Figure 2.
The most common strategy versus the mutation rate (in terms of the expected number of mutants per generation, Nμ). N is the total population size and μ is the mutation rate. The most common strategy is the one that maximizes the quantity (16). Values must be between R and M. When R is small, “cooperative” strategies are most common. When R is large, the opposite is true.
6 Reward size and strategy selection
Now we consider the effect that R has on the average claim. When there is no selection, each of the n = M − R + 1 strategies has frequency 1/n. In the limit of weak selection, the frequency of strategy k is 1/n + δk, where δk is a small perturbation (positive or negative) from neutrality. Antal et al. (2009) showed that δk is proportional to Lk in the low mutation case, Hk in the high mutation case, and Lk + NμHk generally, where N is the population size and μ the mutation rate.
When there is no selection, the average claim is . We would like to know the minimum value of R such that the average claim becomes more “cooperative” when passing from the neutral case to the weak selection case. In such a situation, selection can be said to favor higher claims as adding selection to the neutral process increases the average offer.
For this to happen, we must have
| (17) |
or
| (18) |
We determine when this inequality holds in the low mutation case. Since Lk is proportional to δk, this condition can be written as
| (19) |
Since M > R, this condition is equivalent to
| (20) |
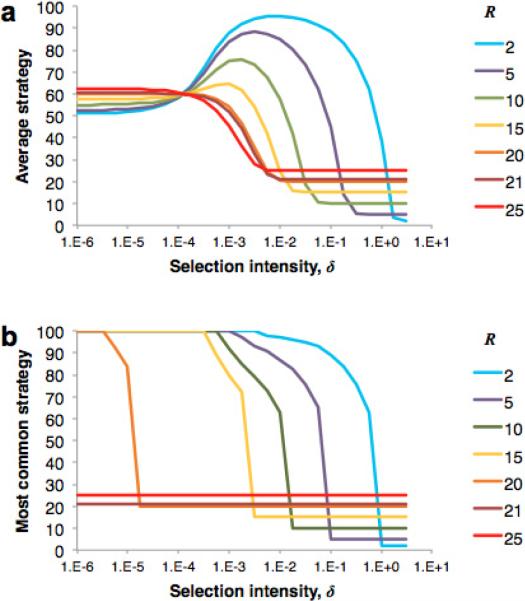
the same condition for Lk to be an increasing function of k. When M = 100, (M + 1)/5 = 20.2. Thus, when M = 100 and R ≤ 20, the average strategy becomes more “cooperative” when we pass from neutrality to weak selection. When R ≥ 21, the average strategy becomes less “cooperative.” Figure 3(a) shows the average strategy as R and the selection strength vary. The population size is 200. Consistent with the calculated threshold, the average strategy increases with the selection strength for R = 2, 5, and 10 whereas the average strategy decreases with selection strength for R = 25. Thus, if the airline wants to minimize its payments, it should choose an R that is at least 21. However, because the minimum claim increases with R, it is in the interest of the airline to choose an R that is not too much larger than the critical value of (M + 1)/5.
Figure 3.
The average strategy (a) and the most common strategy (b) in the low mutation case as the selection strength and R vary, determined numerically (Nowak, 2006) with a population size of 200. (a) When R < (M + 1)/5 = 20.2, the average strategy initially becomes more cooperative as the selection strength δ increases. As δ gets larger and larger, however, the average strategy approaches the Nash equilibrium of R. When R > (M + 1)/5 = 20.2, the average strategy decreases monotonically with R. (b) For small values of R, the most common strategy when selection is weak is the cooperative one of claiming the largest possible value, here M = 100. As δ increases, playing the Nash equilibrium eventually becomes most common. For large values of R, the Nash equilibrium is the most common strategy regardless of selection strength.
Figure 3(b) is the analogous plot for the most frequent strategy. When δ → 0 and R = 2, 5, 10, k = 100 = M is most frequent. But as the selection strength increases, the most common claims get smaller and smaller, ultimately reaching the Nash equilibrium k = R in the limit δ → ∞. On the other hand, when R = 25, there is a strong-enough incentive to make low claims, so k = R is most frequent regardless of selection strength.
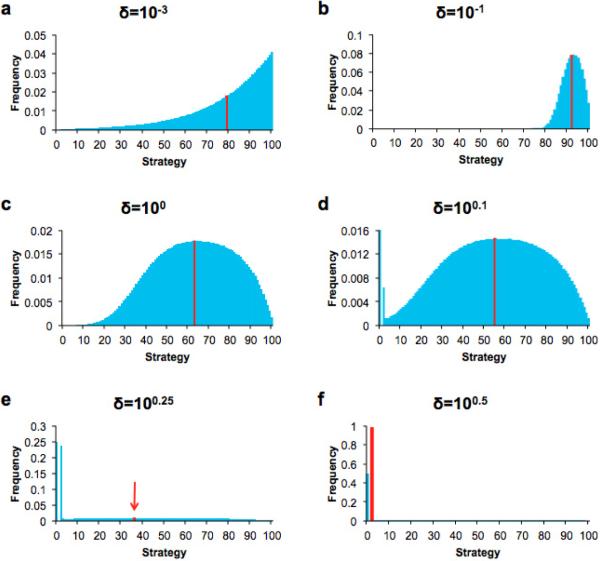
Figure 4 shows the distribution of strategy frequencies when R = 2 and M = 100 as the selection intensity varies. The population size is 200. Here we can compute the steady-state distribution numerically without resorting to simulations. We find that when selection is weak, the distribution is concentrated around k = M = 100. As the selection strength increases, the distribution moves to the left. Players are making smaller claims. Eventually, when selection is very strong, everyone is essentially playing the Nash equilibrium k = R = 2.
Figure 4.
The strategy distributions in the low mutation case as the selection strength varies, determined numerically with a population size of 200 (Nowak, 2006). Here R = 2 and M = 100. As the selection strength δ increases, the distribution moves from one with the weight around the “cooperative” strategies to one with the weight around the “selfish” ones. The average strategy for each distribution is marked by a red line.
These results have interesting implications for economic mechanism design. As we saw earlier, when selection is weak, the average strategy varies inversely with R. The larger R is, the smaller the typical claims. When selection is strong, on the other hand, everyone claims R (the equilibrium strategy), so the larger R is, the larger the typical claims. If we interpret the selection strength as a measure of how precise people's reasoning is, then this shows that the choice of the airline's mechanism (i.e., its choice of R) for reducing the amount it pays in compensation depends critically on assumptions about people's ability to reason. Indeed, past experimental work on the Traveler's Dilemma suggests that people do not behave rationally: their claims decrease as R increases, consistent with our theory in the weak selection case (Capra et al., 1999).
7 Any mutation rate and selection intensity
We have seen above that we can find the stationary distribution analytically when (1) selection is weak and mutation is low, or (2) mutation is high. We can calculate the distribution numerically in the low mutation case for arbitrary selection intensities. But when we would like to determine the stationary distribution for selection intensity δ and mutation rate μ outside these ranges, we must resort to agent-based simulations.
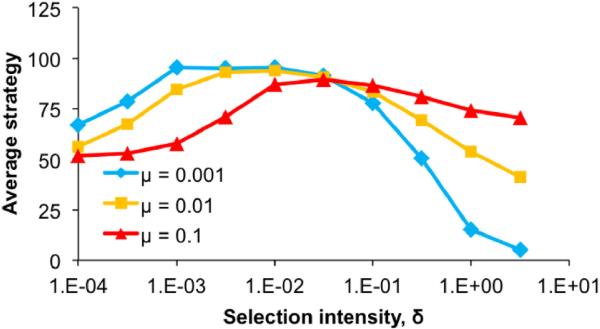
We performed agent-based simulations to determine how the average strategy varies as the mutation rate μ and the selection intensity δ range over arbitrary intervals. In Figure 5, R = 2, M = 100, and the population size N = 200. When δ is small, the average strategy is close to 1/2, its neutral value. As δ increases, the average strategy increases, similar to the behavior observed in Figure 3. When R is small, as it is here, the average strategy becomes more cooperative when selection is weak. Finally, as δ gets large, the average strategy declines towards the Nash equilibrium k = 2.
Figure 5.
The average strategy as the selection strength and the mutation rate vary, as determined by agent-based simulations. The population size N = 200. Results are averaged over 20 simulation runs, each run consisting of 10 million generations (with the stationary values calculated over the last 50% of generations).
8 Comparison with experimental data
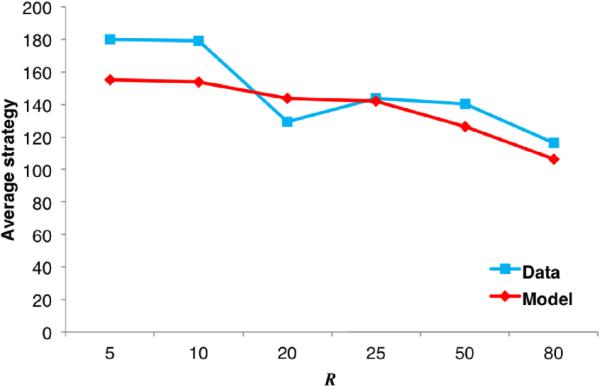
Figure 6 shows the average strategy as a function of R over the first two rounds in Capra et al. (1999)'s experiment. Players were required to make a claim between 80 and 200 (cents) so that the range of possible claims was the same over different treatments (as R varied). Clearly the average strategy decreases as R increases. This is intuitive as there is more incentive for players to reduce their claims (and approach the Nash equilibrium of 80) when R is large, but it is not consistent with the predictions of classical game theory.
Figure 6.
Data from the first two rounds of a repeated traveler's dilemma experiment (Capra et al., 1999) and the model of best fit (in the least-squares sense), obtained with agent-based simulations with a selection strength δ = 10−4 and a mutation rate μ = 10−2.75.
To determine if an evolutionary model could produce the observed behavior, we ran agent based simulations with a population size of N = 200, varying mutation rates μ (between 10−4 and 10−1), and varying intensities of selection δ (between 10−5 and 10−2). For each choice of μ and δ, twenty simulations were run, each simulation consisting of 10 million rounds. The stationary distribution was computed by averaging the frequency of each strategy over the last 5 million rounds. Finally, we obtained average distributions by averaging over all twenty simulations. We then asked which set of parameters minimized the sum of squared differences between the strategy frequencies in the simulation average distribution and those observed in the experimental data. We found that a selection strength of δ = 10−4 and a mutation rate of μ = 10−2.75 resulted in the best fit, parameters that are in the weak selection, low mutation regime. Note that here we are modeling the evolved intuitions that people bring into the lab—and that determine how they play in early rounds—and not the in-game learning that occurs.
The notion of the model-predicted average claim requires some elucidation. It is not necessarily the case that the distribution of strategies in the population eventually becomes fixed. It is possible, for example, that the population continually cycles through various states. What we compute above, both analytically and through agent-based simulations, are the averages in the stationary distribution, which roughly correspond to averages both over the population and over time. In an experiment with 10 subjects, for example, the ten observed claims can be viewed as the results of independent two-step processes: first, the choice of a population, and second, a choice from the stationary distribution of that population. The claims obtained from these choices are independent and identically distributed, the distribution being the stationary one we computed both analytically and through simulations.
9 Discussion
To illustrate the differences between our stochastic evolutionary model and other models, in this section we consider an instance of the Traveler's Dilemma with a limited strategy space: we take R = 2 and M = 10, so there are nine possible strategies (or valuations), k = 2, …, 10. We can summarize the conclusions of various models as follows.
Classical Nash equilibrium
The Nash equilibrium calls for individuals to make the smallest claim possible, k = 2.
Deterministic evolutionary dynamics the replicator equation
The replicator equation (Hofbauer and Sigmund, 1998) can be used to model evolutionary dynamics in the limit of infinite population size (and no mutation). The frequency xk of strategy k evolves according to the differential equation
| (21) |
where fk is the fitness of strategy k,
| (22) |
(akj an entry of the payoff matrix (1)), and ϕ is the average fitness,
| (23) |
We computed trajectories numerically for each of the nine strategies and found that strategies other than k = 2 die out while k = 2 eventually comes to dominate the population. This is not surprising as the equilibrium of replicator dynamics is generally a Nash equilibrium. Indeed, over a wide variety of choices for R and M, it was always the case that the replicator dynamics converged to the k = 2 corner of the (M − R)-simplex.
Stochastic evolutionary dynamics: low mutation, weak selection
We use the results of Section 3. Since
| (24) |
Lk is maximized when k = 10. Furthermore, the strategies favored by selection—those with Lk > 0—are k = 7, …, 10. In contrast to replicator dynamics, the most frequent strategy in this case is k = 10—the most “cooperative” —not k = 2, the least “cooperative.”
Stochastic evolutionary dynamics: high mutation
We use the results of Section 4. Since
| (25) |
Hk is maximized for
| (26) |
i.e., k = 6 and k = 7 are the most abundant strategies in the stationary distribution. This differs from both the low mutation case and the deterministic evolutionary dynamics case.
Logit learning
Capra et al. (1999) conducted a multi-round Traveler's Dilemma experiment and observed that the average claim decreased as the experiment progressed. They used a logit learning model to explain this decrease and to justify the inverse relationship between R and the average claim at equilibrium.
The logit learning model works as follows. At time t, player p has a set of beliefs about the strategies of other players. These are most easily represented as “counts”: wp(j, t) represents p's belief about the likelihood that someone else is playing a strategy j at time t. A uniform prior is assumed, so wp(j, 0) = α for all j and some fixed α. If player p observes someone playing strategy k at time t, he updates his beliefs by setting wp(k, t+1) = wp(k, t)+ρ, where the larger ρ is, the more weight p places on recent observations; wp(j, t + 1) = wp(j, t) for all j ≠ k.
At time t, p believes that the probability another individual will play strategy i is
| (27) |
Given this probability distribution, p can then compute the expected payoff πp(j, t) for each strategy j that he might play. The choice of which strategy to play is then made probabilistically, with the probability that p plays j given by
| (28) |
The parameter μ (distinct from our mutation rate μ) represents “cognitive noise.” The smaller it is, the more likely p is to play the strategy with the highest expected payoff. In the limit μ → ∞, on the other hand, p picks a strategy to play uniformly at random. As players “learn” according to this rule, an inverse relationship between R and the average strategy develops. To see why this is the case, note that when μ > 0, players make errors in implementing their strategies (they sometimes fail to choose the strategy with the highest expected payoff). When R is small, the penalty for the error is not very large, and the average claim can creep upward. When R is large, on the other hand, errors are penalized severely, and the average strategy remains low.
Capra et al. (1999) fit their experimental data to the logit learning model by finding the ρ and μ that best matched players' behavior over time. Their goal was to explain the in-game learning that occurs and the inverse relationship between R and the average claim in later rounds. While the logit rule is somewhat similar to an evolutionary process (with exponential fitnesses), it does not explain behavior in early rounds before any in-game learning has occurred. The stochastic evolutionary model we present in this paper, on the other hand, is concerned with explaining the evolved intuitions humans take with them into the lab. Our model justifies the inverse relationship between R and the average claim that Capra et al. (1999) observed in early rounds (Figure 6) without requiring the abilities of observation (needed in the logit model as players must update their beliefs) or reason.
10 Conclusion
The Nash equilibrium, and generalizations of it, have been the foremost solution concepts in game theory for almost the entire history of the field. However, deviation from equilibrium play has been observed in countless human subjects and in a multitude of games. In the Traveler's Dilemma, individuals usually make large claims and rarely play the Nash equilibrium of claiming the smallest possible value, R, at least before any in-game learning has occurred. This “irrational” behavior is observed even amongst economists (Becker et al., 2005), the individuals one would think are most likely to analyze the game and play the Nash equilibrium.
Here we have shown how a stochastic evolutionary model can explain why human intuition has evolved to favor such play. There is a population of individuals playing the game, and the evolution of this population is described by a frequency-dependent Moran process. When selection is weak, stochasticity results in higher claims being favored by selection. These results demonstrate the power of stochastic evolutionary game theory for explaining cooperative behavior in contexts outside of the Prisoner's Dilemma (see also (Rand and Nowak, 2012)). In a world in which both genetic inheritance and social learning are imperfect, then, “irrational” play can be evolutionarily advantageous, explaining the “anomalous behavior” so often observed by humans playing the Traveler's Dilemma.
Highlights
-
>
We study the “Traveler's Dilemma,” a game in which two players do best by both declaring large “values” but are incentivized by a reward/penalty to unilaterally declare small ones.
-
>
Actual human behavior in the laboratory is inconsistent with the predictions of classical game theory.
-
>
We use stochastic evolutionary dynamics with varying mutation rates and varying intensity of selection to show how evolution favors certain strategies when selection is weak.
-
>
We show how the evolutionarily-favored strategy depends on the relative sizes of the reward and the maximum allowable “value.”
-
>
We exhibit a stochastic evolutionary model that quantitatively reproduces the behavior observed in a past experiment.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Antal T, Traulsen A, Ohtsuki H, Tarnita CE, Nowak MA. Mutation-selection equilibrium in games with multiple strategies. J. Theor. Biol. 2009;258:614–622. doi: 10.1016/j.jtbi.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- Basu K. The traveler's dilemma: Paradoxes of rationality in game theory. Am. Econ. Rev. 1994;84:391–395. [Google Scholar]
- Becker T, Carter M, Naeve J. Experts playing the traveler's dilemma. Hohenheimer Diskussionbeiträge. 2005;252 [Google Scholar]
- Boyd R, Gintis H, Bowles S, Richerson PJ. The evolution of altruistic punishment. Proc. Nat. Acad. Sci. USA. 2003;100:3531–3535. doi: 10.1073/pnas.0630443100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandt H, Hauert C, Sigmund K. Punishing and abstaining for public goods. Proc. Nat. Acad. Sci. USA. 2005;103:495–497. doi: 10.1073/pnas.0507229103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capra CM, Goeree JK, Gomez R, Holt CA. Anomalous behavior in a traveler's dilemma? Am. Econ. Rev. 1999;89:678–690. [Google Scholar]
- Cressman R. Evolutionary Dynamics and Extensive Form Games. The MIT Press; 2003. [Google Scholar]
- Fowler JH. Altruistic punishment and the origin of cooperation. Proc. Nat. Acad. Sci. USA. 2005;102:7047–7049. doi: 10.1073/pnas.0500938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu F, Chen X, Liu L, Wang L. Social dilemmas in an online social network: The structure and evolution of cooperation. Phys. Lett. A. 2007;371:58–64. [Google Scholar]
- Fudenberg D, Imhof L. Imitation processes with small mutations. J. Econ. Theory. 2006;131:251–262. [Google Scholar]
- Fudenberg D, Maskin E. Evolution and cooperation in noisy repeated games. Am. Econ. Rev. 1990;80:274–279. [Google Scholar]
- Gintis H. Game Theory Evolving. Princeton University Press; 2009. [Google Scholar]
- Goeree JK, Holt Stochastic game theory: For playing games, not just for doing theory. Proc. Nat. Acad. Sci. USA. 1999;96:10564–10567. doi: 10.1073/pnas.96.19.10564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as red queen mechanism for cooperation in public goods games. Science. 2002;296:1129–1132. doi: 10.1126/science.1070582. [DOI] [PubMed] [Google Scholar]
- Hauert C, Traulsen A, Brandt H, Nowak MA, Sigmund K. Via freedom to coercion: the emergence of costly punishment. Science. 2007;316:1905–1907. doi: 10.1126/science.1141588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauert C, Traulsen A, de Silva H, Nowak MA, Sigmund K. Public goods with punishment and abstaining in finite and infinite populations. Biological Theory. 2008;3:114–122. doi: 10.1162/biot.2008.3.2.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helbing D, Yu W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc. Nat. Acad. Sci. USA. 2009;106:3680–3685. doi: 10.1073/pnas.0811503106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofbauer J, Sigmund K. The Theory of Evolution and Dynamical Systems: Mathematical Aspects of Selection. Cambridge University Press; 1988. [Google Scholar]
- Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge University Press; Cambridge: 1998. [Google Scholar]
- Imhof LA, Fudenberg D, Nowak MA. Evolutionary cycles of cooperation and defection. Proc. Nat. Acad. Sci. USA. 2005;102:10797–10800. doi: 10.1073/pnas.0502589102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imhof LA, Fudenberg D, Nowak MA. Tit-for-tat or win-stay, lose-shift? J. Theor. Biol. 2007;247:574–580. doi: 10.1016/j.jtbi.2007.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imhof LA, Nowak MA. Evolutionary game dynamics in a wright-fisher process. J. Math. Biol. 2006;52:667–681. doi: 10.1007/s00285-005-0369-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen MA, Bushman C. Evolution of cooperation and altruistic punishment when retaliation is possible. J. Theor. Biol. 2008;254:541–545. doi: 10.1016/j.jtbi.2008.06.017. [DOI] [PubMed] [Google Scholar]
- Kraines D, Kraines V. Pavlov and the prisoner's dilemma. Theory Decis. 1989;26:47–79. [Google Scholar]
- Levin S. Fragile Dominion. Basic Books; 2000. [Google Scholar]
- Levin SA, editor. Games, Groups, and the Global Good. Springer; 2009. [Google Scholar]
- Lotem A, Fishman MA, Stone L. Evolution of cooperation between individuals. Nature. 1999;400:226–227. doi: 10.1038/22247. [DOI] [PubMed] [Google Scholar]
- Maynard Smith J. Evolution and the Theory of Games. Cambridge University Press; Cambridge: 1982. [Google Scholar]
- Milinski M. Tit for tat in sticklebacks and the evolution of cooperation. Nature. 1987;325:433–435. doi: 10.1038/325433a0. [DOI] [PubMed] [Google Scholar]
- Nowak M, Sigmund K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the prisoner's dilemma game. Nature. 1993;364:56–58. doi: 10.1038/364056a0. [DOI] [PubMed] [Google Scholar]
- Nowak MA. Evolutionary Dynamics. Harvard University Press; Cambridge: 2006. [Google Scholar]
- Nowak MA, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature. 2004;428:646–650. doi: 10.1038/nature02414. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. Tit for tat in heterogeneous populations. Nature. 1992;355:250–253. [Google Scholar]
- Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303:793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature. 2005;437:1291–1298. doi: 10.1038/nature04131. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Iwasa Y. How should we define goodness?—reputation dynamics in indirect reciprocity. J. Theor. Biol. 2004;231:107–120. doi: 10.1016/j.jtbi.2004.06.005. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Iwasa Y. The leading eight: Social norms that can maintain cooperation by indirect reciprocity. J. Theor. Biol. 2006;239:435–444. doi: 10.1016/j.jtbi.2005.08.008. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Iwasa Y, Nowak MA. Indirect reciprocity provides only a narrow margin of efficency for costly punishment. Nature. 2009;457:79–82. doi: 10.1038/nature07601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pacheco JM, Santos FC, Chalub FACC. Stern-judgning: A simple, successful norm which promotes cooperation under indirect reciprocity. PLoS Comp. Biol. 2006;2:e178. doi: 10.1371/journal.pcbi.0020178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panchanathan K, Boyd R. Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature. 2004;432:499–502. doi: 10.1038/nature02978. [DOI] [PubMed] [Google Scholar]
- Rand DG, Nowak MA. The evolution of antisocial punishment in optional public goods games. Nat. Commun. 2011;2:434. doi: 10.1038/ncomms1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rand DG, Nowak MA. Evolutionary dynamics in finite populations can explain the full range of cooperative behaviors observed in the centipede game. J. Theor. Biol. 2012;300:212–221. doi: 10.1016/j.jtbi.2012.01.011. [DOI] [PubMed] [Google Scholar]
- Rand DG, Ohtsuki H, Nowak MA. Direct reciprocity with costly punishment: Generous tit-for-tat prevails. J. Theor. Biol. 2009;256:45–57. doi: 10.1016/j.jtbi.2008.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riehl C. Living with strangers: direct benefits favour non-kin cooperation in a communally nesting bird. Proc. R. Soc. B. 2011;278:1728–1735. doi: 10.1098/rspb.2010.1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riehl C, Jara L. Natural history and reproductive biology of the communally breeding Greater Ani (Crotophaga major) at gatún lake, panama. Wilson J. Ornithol. 2009;121:679–687. [Google Scholar]
- Samuelson L. Evolutionary Games and Equilibrium Selection. The MIT Press; 1998. [Google Scholar]
- Sigmund K. The Calculus of Selfishness. Princeton University Press; 2010. [Google Scholar]
- Sigmund K, De Silva H, Traulsen A, Hauert C. Social learning promotes institutions for governing the commons. Nature. 2010;466:861–863. doi: 10.1038/nature09203. [DOI] [PubMed] [Google Scholar]
- Smead R. The evolution of cooperation in the centipede game with finite populations. Philos. Sci. 2008;75:157–177. [Google Scholar]
- Taylor C, Fudenberg D, Sasaki A, Nowak MA. Evolutionary game dynamics in finite populations. B. Math. Biol. 2004;66:1621–1644. doi: 10.1016/j.bulm.2004.03.004. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Hauert C, de Silva H, Nowak MA, Sigmund K. Exploration dynamics in evolutionary games. Proc. Nat. Acad. Sci. USA. 2009;106:709–712. doi: 10.1073/pnas.0808450106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traulsen A, Shoresh N, Nowak MA. Analytic results for individual and group selection of any intensity. B. Math. Biol. 2008;70:1410–1424. doi: 10.1007/s11538-008-9305-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivers RL. The evolution of reciprocal altruism. Q. Rev. Biol. 1971;46:35–57. [Google Scholar]
- Wang J, Fu F, Wang L. Emergence of social cooperation in threshold public goods games with collective risk. Phys. Rev. E. 2009;80:036101. doi: 10.1103/PhysRevE.80.016101. [DOI] [PubMed] [Google Scholar]
- Wedekind C, Milinski M. Cooperation through image scoring in humans. Science. 2000;288:850–852. doi: 10.1126/science.288.5467.850. [DOI] [PubMed] [Google Scholar]
- Weibull JW. Evolutionary Game Theory. The MIT Press; 1997. [Google Scholar]
- Worden L, Levin SA. Evolutionary escape from the prisoner's dilemma. J. Theor. Biol. 2007;245:411–422. doi: 10.1016/j.jtbi.2006.10.011. [DOI] [PubMed] [Google Scholar]