Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2012 Apr 6;28(10):1353–1358. doi: 10.1093/bioinformatics/bts163

Matrix eQTL: ultra fast eQTL analysis via large matrix operations

Andrey A Shabalin 1
PMCID: PMC3348564  PMID: 22492648

Abstract

Motivation: Expression quantitative trait loci (eQTL) analysis links variations in gene expression levels to genotypes. For modern datasets, eQTL analysis is a computationally intensive task as it involves testing for association of billions of transcript-SNP (single-nucleotide polymorphism) pair. The heavy computational burden makes eQTL analysis less popular and sometimes forces analysts to restrict their attention to just a small subset of transcript-SNP pairs. As more transcripts and SNPs get interrogated over a growing number of samples, the demand for faster tools for eQTL analysis grows stronger.

Results: We have developed a new software for computationally efficient eQTL analysis called Matrix eQTL. In tests on large datasets, it was 2–3 orders of magnitude faster than existing popular tools for QTL/eQTL analysis, while finding the same eQTLs. The fast performance is achieved by special preprocessing and expressing the most computationally intensive part of the algorithm in terms of large matrix operations. Matrix eQTL supports additive linear and ANOVA models with covariates, including models with correlated and heteroskedastic errors. The issue of multiple testing is addressed by calculating false discovery rate; this can be done separately for cis- and trans-eQTLs.

Availability: Matlab and R implementations are available for free at http://www.bios.unc.edu/research/genomic_software/Matrix_eQTL

Contact: shabalin@email.unc.edu

1 INTRODUCTION

The goal of expression quantitative trait loci (eQTL) analysis is to identify single-nucleotide polymorphisms (SNPs) which are significantly associated with expression of known genes. These associations can help reveal biochemical processes underlying living systems, discover the genetic factors causing certain diseases and determine pathways that are affected by them. Expression QTL analysis is used to determine hotspots [DNA regions affecting multiple transcripts, Breitling et al. (2008)], construct causal networks, discover subclasses of clinical phenotypes, and select genes for clinical trials (see reviews of Gilad et al. 2008; Kendziorski and Wang, 2006; Zhang and Liu, 2010).

There are various approaches to eQTL analysis. Most eQTL studies perform separate testing for each transcript-SNP pair. The association between expression and genotype can be tested for using linear regression and ANOVA models, as well as non-linear techniques including generalized linear and mixed models, Bayessian regression (Servin and Stephens, 2007), and models accounting for pedigree (Abecasis et al., 2001) and latent variables (Leek and Storey, 2007). Several methods has been developed to find groups of SNPs associated with expression of a single gene (Hoggart et al., 2008; Kao et al., 1999; Lee et al., 2008; Zeng, 1993).

Expression QTL analysis is known to be computationally intensive. The issue is most pronounced for modern eQTL datasets, which have genotype measured over millions of SNPs and gene expression over tens of thousands of transcripts. For such data, the eQTL analysis involves over ten billion tests. The following three studies, analyzing relatively small datasets, indicate that non-linear methods can be prohibitively slow for large data. Degnan et al. (2008) applied family-based association tests to a dataset with 142 samples. They tested only 40 227 transcript-SNP pairs and report the total computation time to be ‘under 24 h on 20 processors in parallel on a Linux cluster’. Ghazalpour et al. (2008) were running efficient mixed-model association (EMMA), which is said to be computationally efficient. They analyzed a dataset with 110 samples, 1813 SNPs, and 10 013 transcripts. They tested all transcript-SNP pairs and report the computation time of ‘a few hours using a cluster of 50 processors’. Listgarten et al. (2010) tested their method on a dataset measuring 40 639 transcripts and 48 186 SNPs in 188 samples. They report that estimation took 10 h when parallelized across 1100 processors (this is more than a processor-year). Note that the dimensions of a modern eQTL dataset can greatly exceed those in the examples above.

In this article, we present a new tool, Matrix eQTL, for fast eQTL analysis of large datasets. Our tests show that Matrix eQTL is 2–3 orders of magnitude faster than existing popular QTL/eQTL software. Moreover, the computation time of Matrix eQTL stays practically unchanged when covariates are added to the model. Such performance is achieved, in particular, by expressing the most computationally intensive part of the algorithm in terms of large matrix operations. This allowed to implement the algorithm using high-level programming languages, R and Matlab, relying on their efficient implementation of matrix operations.

Matrix eQTL tests for association between each SNP and each transcript by modeling the effect of genotype as either additive linear (least squares model) or categorical (ANOVA model). Optionally, Matrix eQTL can test for the significance of genotype-covariate interaction. Matrix eQTL does not require genotypes to be discrete unless ANOVA model is chosen. The models can include covariates to account for such factors as gender, clinical variables, population structure and surrogate variables. Matrix eQTL also supports heteroscedastic and correlated errors to account for relatedness of the samples. Matrix eQTL performs a separate test for each gene-SNP pair and corrects for multiple comparisons by calculating false discovery rate (FDR, Benjamini and Hochberg, 1995). It is known that the SNPs located near a gene are more likely to affect its expression. To account for this fact, Matrix eQTL supports separate p-value thresholds and FDR calculation for local (cis-) and distant (trans-) eQTLs.

It can often be helpful to make a Q–Q plot or a histogram of all p-values, including those that did not pass the significance threshold. These plots can be used to assess the quality of data preprocessing and model selection. Matrix eQTL can record the distribution of all p-values by counting the number of p-values that fall in user-supplied histogram bins. These counts are then used to create Q–Q plots or histograms of the p-values.

2 RESULTS

We measured the performance of Matrix eQTL and six programs for QTL and eQTL analysis: Plink (Purcell et al., 2007), Merlin (Abecasis et al., 2001), R/qtl (Broman et al., 2003), snpMatrix (Leung, 2007), eMap (Sun, 2009) and FastMap (Gatti et al., 2009). Plink is a command line toolset for whole genome association analysis. It is a general purpose tool written in C/C++ not particularly optimized for eQTL analysis. Merlin is a command line tool for fast pedigree analysis written in C/C++. It is designed for analysis in pedigree, but has an option for analysis of unrelated samples. R/qtl, snpMatrix and eMap are R packages for QTL/eQTL analysis. Part of eMap is coded in C and requires GSL library (GNU Scientific Library). FastMap is a fast association mapping tool written in Java. It uses the discrete nature of genotype data to speed up calculations. FastMap is optimized for permutation-based testing. Among selected tools, only FastMap and eMap do not handle covariates. Note that FastMap is the only tool out of seven that has a graphical user interface.

All methods except R/qtl were set to use the simple linear model to test for association between levels of gene expression and frequencies of the minor allele of the genotype. R/qtl does not support the simple linear model and was set to estimate the ANOVA model (Haley–Knott method).

We estimated the time that Matrix eQTL and other eQTL tools require to analyze a typical modern eQTL dataset. As the model dataset we chose cystic fibrosis (CF) dataset from Wright et al. (2011). The dataset contains genotype information for 573 337 SNPs and the gene expression measurements for 22 011 transcripts for 840 patients.

We applied eQTL methods to a randomly generated dataset containing 2201 genes and 57 333 genes across 840 samples, which is ~10% of the number of genes and SNPs in the CF dataset. The performance of all eQTL tools depends dominantly on the dimensions of the dataset, and the computation time is approximately linear with respect to the number of genes and the number of SNPs. We used this observation to estimate the time required for the analysis of the full dataset. The performance of each method is reported in Table 1. Matrix eQTL requires only 9–12 s to analyze the test dataset. This did not allow us to make precise estimates of its performance, so we applied Matrix eQTL to the whole dataset and reported the performance in Table 1.

Table 1.

Estimated performance of various eQTL software on the CF dataset

Method\No. of covariates Zero Ten
Plink 9.4 583.3 days
Merlin 19.6 20.0 days
R/qtl (Revolution R) 1.0 4.7 days
snpMatrix 3.2 5.1 days
eMap 17.8 N/A days
FastMap 10.3 N/A hours
Matrix eQTL (Matlab) 11.8 11.8 minutes
Matrix eQTL (Revolution R) 14.6 14.6 minutes
Matrix eQTL (R, Goto BLAS) 19.4 19.4 minutes
Open in a new tab

The time for all methods is projected from tests on a dataset with 2201 genes and 57 333 SNPs. The timings projections for Matrix eQTL implementations were refined by applying them to the complete dataset.

To reduce the output we set the p-value threshold at 10−5 level for each method with such option. The specifications of the machine used to run the tests (except eMap, which does not run on Windows) are provided at the end of Section 3. All methods that support covariates were additionally tested with 10 covariates set to the first 10 eigenvectors of the genotype sample covariance matrix.

Two methods, Matrix eQTL (for R) and R/qtl were sensitive to the version of basic linear algebra subroutine (BLAS) installed in R (see Section 3.7 for more about BLAS). We ran both methods in three different settings: standard R installation, R with GOTO BLAS (Goto and Geijn, 2008) by Ei-Ji Nakama, and Revolution R. We observed that the methods demonstrated better performance in Revolution R, so we report only corresponding times for R/qtl in Table 1. The code for generating the test dataset and running the tests is available at Matrix eQTL website. We note that the methods that use linear regression models in the analysis (Plink, snpMatrix and FastMap) report the same test statistics and p-values as Matrix eQTL.

Matrix eQTL was the fastest tool among tested, with <1 s difference between runs with and without covariates. It is followed by FastMap which was 50 times slower than Matrix eQTL. Note that the good performance of FastMap comes at the expense of a limited set of supported models (no covariates, only discrete genotypes). Third was R/qtl, which was 122 times slower Matrix eQTL when tested without covariates and 574 times otherwise. SnpMatrix was 384 times slower Matrix eQTL without covariates in the model and 618 times with them. Plink, Merlin and eMap were at least 1145 times slower than Matrix eQTL.

The timing in Table 1 does not include the time required to load the data. Each method loaded the test dataset in just few minutes. We also tested the ability of each method to load the full CF dataset. We observed that R packages that use standard R functions to load the data, R/qtl and eMap, were the slowest. They required excessive amounts of RAM (>24 GB) and took hours to load the data. The remaining tools have demonstrated a good performance loading the data: FastMap — 18.4 min, Merlin — 12.3 min, Plink — 9.0 min, Matrix eQTL — 5.7 min and snpMatrix — 3.3 min. SnpMatrix was incredibly fast loading the genotype data (only 22 s), but it still relied on standard R functions to load the expression matrix.

The performance of Martix eQTL depends on the choice of the model and other parameters. Table 1 shows that for the simple linear regression model Matrix eQTL (Rev R) performs the analysis in 14.6 min. The analysis using ANOVA model takes twice as long (29.1 min). Testing for significance of genotype-covariate interaction takes slightly longer than ANOVA model (32.7 min). Testing additive linear model with correlated errors takes 15.4 min. Addition of covariates has almost no effect on the performance of Matrix eQTL regardless of the model. Recording the distribution of all 12 billion p-values adds 11 min to the running time. Cis-only analysis, which tests only gene-SNP pairs within 1 million base pairs of each other, takes only 3.6 min. Combined cis and trans eQTL analysis with separate p-value thresholds (10−3 and 10−5) and FDR calculation takes 16.6 min.

2.1 Computational efficiency

It is widely believed that the performance of most programs implemented in R and Matlab can be greatly improved if they are rewritten using a low-level programming language such as C/C++. Using simple calculations, presented below, we argue that this is not the case for both implementations of Matrix eQTL.

The most computationally intensive part of the Matrix eQTL algorithm is the calculation of correlations using large matrix multiplications. As we point out in Section 3, the complexity of this part of the algorithm is equal to twice the product of the number of transcripts, the number of SNPs, and the number of samples. Thus, for the CF dataset the complexity of the Matrix eQTL algorithm is bounded from below by

graphic file with name bts163um1.jpg

According to the specifications of the processor of the test machine, it is theoretically capable of performing 38.4 billion floating point operations per second. The ratio of these numbers gives us the best theoretically possible time for a Matrix eQTL implementation of 9.2 min. Dividing the best theoretically possible time by the time observed in practice, we get the lower bound on the efficiency of Matrix eQTL implementations: 63% for R and 78% for Matlab.

3 METHODS

The Matrix eQTL algorithm employs multiple optimizations. In what follows we first describe the algorithm for the simple linear regression model, which does not include covariates and assumes uncorrelated homoskedastic errors. Then, we extend the algorithm to handle ANOVA model, additive covariates, and heteroskedastic and correlated errors.

3.1 Simple linear regression

The simple linear regression is one of the most commonly used models for eQTL analysis. For each gene-SNP pair, with the SNP encoded by 0,1 and 2 according to the frequency of the minor allele, the association between gene expression g and genotype s is assumed to be linear:

graphic file with name bts163m1.jpg (1)

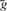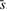The conventional algorithm for the analysis of the simple linear regression model involves calculation of a number of variables including: the sample means Inline graphic and Inline graphic, the slope coefficient 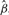Inline graphic, the intercept 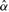Inline graphic, the residuals ei, the total sum of squares SST and the residual sum of squares SSE. This is followed by calculation of a test statistic, which can be t-statistic, F-test or likelihood ratio (LR) test. Finally, the p-value is calculated for the test statistic; this step can also be computationally intensive as it involves calculation of incomplete beta or gamma functions.

For better performance, Matrix eQTL does not calculate p-value for every transcript-SNP pair. Instead, for the test statistic of choice, we find the threshold, such that test statistics exceeding the threshold are significant at the required significance level. The test statistics for every transcript-SNP pair are then compared with the threshold, and the p-values are calculated only for those exceeding it. The number of significant transcript-SNP pairs is usually much smaller than the number of tests, so the p-values and other statistics of interest can be calculated for them in a much shorter time than is required to find them.

The choice of the test statistic is important for the performance of the method. It is natural to choose the test statistic that can be calculated faster, among statistics of equal power. Observe that for the simple linear regression (1), the common test statistics: t, F, R2 and LR, are equivalent and can be expressed as functions of the sample correlation r = cor(g, s)

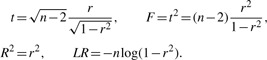graphic file with name bts163um2.jpg

We choose the absolute value of the sample correlation |r| as the test statistic for the simple linear regression and threshold it in search for significant gene-SNP associations. Note that the correlation does not change if we standardize the genotype and gene expression variables to have zero mean and unit sum of squares

graphic file with name bts163um3.jpg

The standardization does not add complexity to the calculations as it has to be performed only once for each transcript and once for each SNP, and it greatly simplifies the calculation of the sample correlation

graphic file with name bts163um4.jpg

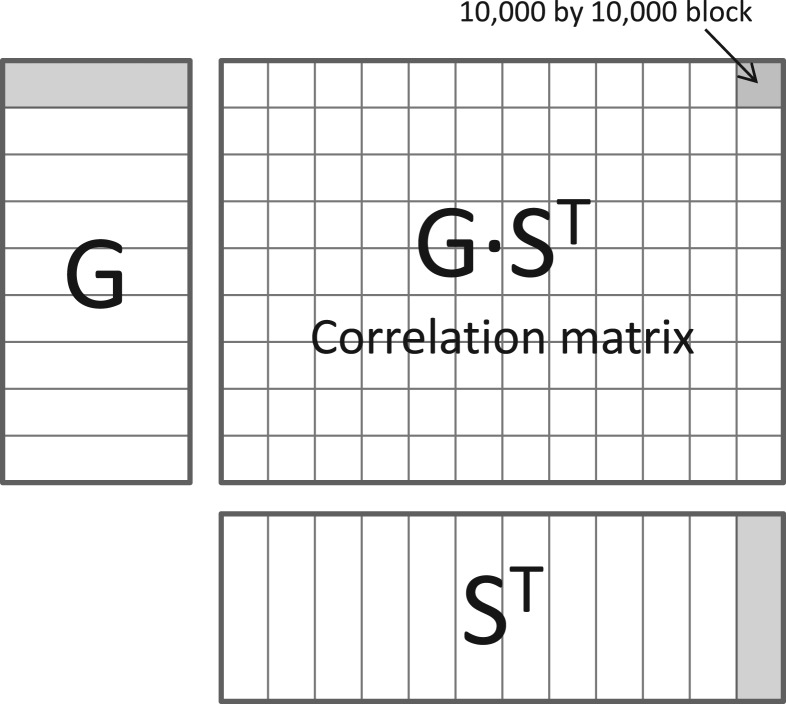
where 〈 s, g 〉 denotes the inner product between vectors s and g. Now, let S be the genotype matrix, with each row containing measurements for a single SNP across samples. Let G be the gene expression matrix, with each row containing measurements for a single gene across samples and let the columns (samples) of matrices S and G match. Then the matrix of all gene-SNP correlations can be calculated in one large matrix multiplication GST as illustrated in Figure 1.

Fig. 1.

Fig. 1.

Open in a new tab

Matrix of correlations can be calculated using multiplication of large matrices. Due to the large number of tests the analysis performed in 10 000× 10 000 blocks.

The number of tests in a modern eQTL study may exceed tens of billions and the full correlation matrix GST would require hundreds of gigabytes of RAM. To avoid excessive memory requirements we slice the data matrices in blocks of up to 10 000 variables and perform the analysis separately for each pair of blocks. Figure 1 illustrates the slicing and the calculation of the correlation matrix.

The algorithm of Matrix eQTL for the simple linear regression is then:

  1. Split input matrices into blocks of up to 10 000 variables.

  2. Standardize variables of both gene expression and genotype matrices.

  3. For each pair of blocks:
    1. Calculate the corresponding block of the correlation matrix in one matrix multiplication.
    2. Find correlations which have absolute value that exceeds a predefined threshold.
    3. For the selected correlations, calculate and report the corresponding test statistic, p-value, FDR and other variables of interest.

3.2 Model with covariates

It is common to include covariates in an eQTL model to account for such effects as population stratification, gender, age, white blood count and other clinical variables. For simplicity, let us consider the model with one extra covariate x,

graphic file with name bts163m2.jpg (2)

As for the simple linear regression, various test statistics measuring the significance of s, namely LR, F-test, and t-statistic, are equivalent. For fast computations, the testing of model (2) can be reduced to testing of the simple linear regression model (1) by orthogonalizing g and s with respect to x. The algorithm for the analysis is then:

  1. Center variables g, x, and s to remove constant α from the model.

  2. Orthogonalize g and s with respect to x:
    graphic file with name bts163um5.jpg

  3. Perform the analysis for the simple linear regression 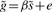Inline graphic using one less degree of freedom for the test statistic to account for the removed covariate.

3.3 ANOVA model

Another common approach to eQTL analysis is to include both additive and dominant effect of the genotype. This is equivalent to treating each genotype variable as categorical and modeling its effect on gene expression with ANOVA model. ANOVA model can be viewed as a linear regression

graphic file with name bts163m3.jpg (3)

where s1=I(s=1) and s2=I(s=2) are dummy variables constructed for the SNP s. For this model, F-test and LR statistics for testing joint significance of s1 and s2 are equivalent. Moreover, F and LR are monotone functions of R2 for this model, and thus we use R2 as the test statistic. The test statistic can be calculated efficiently if we orthogonalize the regressors. The algorithm for the analysis is then:

  1. Center variables g, s1 and s2 to remove the constant α from the model.

  2. Orthogonalize s2 with respect to s1 for every marker
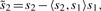
    graphic file with name bts163um6.jpg

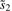  3. Standardize s1 and Inline graphic.

  4. Calculate test statistic: 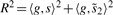Inline graphic via large matrix operations.

  5. The threshold for R2 and p-values can be derived from the formula for F-test
    graphic file with name bts163um7.jpg
    where k=2 is the number of regressors (s1 and s2).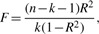

The same algorithm can be used to estimate the model with two marker-by-marker variables, such as genotype and copy number variations. It can also be generalized to test for joint significance of any subset of regressors.

3.4 Heteroskedastic and/or correlated errors

The previously described models assume the noise to be independent and identically distributed across samples. However, the errors can be heteroskedastic if the quality of the measurements differs across samples. The errors may also be correlated if the samples are taken from related individuals. To account for both possibilities, let us consider the model:

graphic file with name bts163m4.jpg (4)

and K is a known positive-definite covariance matrix. To apply the previously described methods to this problem we transform the input variables to make the errors independent and identically distributed:

graphic file with name bts163um8.jpg

where 1n is a vector of length n with unit elements. The new model equation is homoskedastic, has independent errors, but does not include a constant.

graphic file with name bts163m5.jpg (5)

The model is tested using the algorithm for the linear model with covariates with Step 1 (centering) omitted.

3.5 Q–Q plots and histograms of all p-values

Matrix eQTL has an option to record the distribution of all p-values. This is done by counting the number of p-values that fall in user-defined histogram bins. For better efficiency, Matrix eQTL collects this information without calculation of the actual p-values. Instead, the histogram bins for p-values are transformed into corresponding bins for the test statistic (which depends on the model). Then, the number of test statistics that fall in each bin is counted as part of eQTL analysis.

3.6 False discovery rate

Matrix eQTL calculates FDR only for the gene-SNP pairs that passed user-defined significance threshold. The calculations follow Benjamini and Hochberg (1995) procedure, adapted for the situation when not all p-values are recorded.

Let p(1)<p(2)<…<p(K) be the p-values that passed the significance threshold and let N be the total number of tests performed. Then the FDR for the corresponding gene-SNP pairs is calculated as follows

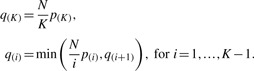graphic file with name bts163um9.jpg

3.7 Matrix multiplication algorithms

Matrix eQTL gains its efficiency by expressing the most computationally intensive part of the algorithm in terms of operations with large matrices. The most time consuming operation is matrix multiplication. Naturally, the performance of Matrix eQTL dependents strongly on the performance of the employed BLAS. In Table 2, we compare the performance of matrix multiplication for Matlab and different versions of R for Windows. For the comparison we measured the time required to multiply two 4096 × 4096 matrices with elements set to random values uniformly distributed on [0, 1]. To test the performance, the matrix multiplication was performed 10 times and the best time is recorded. The test code is available at Matrix eQTL website.

Table 2.

Speed of various software multiplying 4096 × 4096 matrices

Package BLAS Time (s) Comment
R x32 2.14.1 Build-in 98.1
R x64 2.14.1 Build-in 77.0
R x32 2.14.1 Atlas C2D 16.5
R x64 2.14.1 Goto 5.5
Revolution R 4.3 Intel KML 3.8
Matlab R2010b Intel KML 3.8
Matlab R2010b Intel KML 1.8 Single precision
Matlab R2010b GPU CUDA 0.8 GTX 480, double
Matlab R2010b GPU CUDA 0.2 GTX 480, single
Open in a new tab

The standard installation of R for Windows (R Development Core Team, 2010) includes a generic BLAS, not optimized for any particular central processing unit (CPU). The test finished in 98 and 77 s for 32 and 64 bit versions of R, respectively. There are faster versions of BLAS available for R called ATLAS (32 bit only) by (Whaley and Petitet, 2005) and GOTO (64 bit only) by (Goto and Geijn, 2008) adapted for R by Ei-Ji Nakama [http://prs.ism.ac.jp/~nakama/SurviveGotoBLAS2/binary/windows/x64/]. The matrix multiplication test on R with ATLAS BLAS finished in just 16.5 s. Next we tested Matlab and Revolution R, a commercial version of R available free of charge for academic purposes. They both employ Intel Kernel Math Library (KML), which is optimized for Intel CPUs (used in the test machine). Both Intel KML and GOTO BLAS are able to use multiple CPU cores and show 3–4 times better performance than ATLAS BLAS in R. About twice better performance can be achieved by switching from double to single precision calculations; we did not use this option in Matrix eQTL to avoid loss of accuracy. Single precision calculations are available only in Matlab. The last lines in the table show performance of Nvidia GeForce GTX 480 GPU (graphics processing unit). It offers ten times better performance than the best algorithm for the CPU for single precision calculations. Matlab 2010b has a limited build-in support for GPU-based calculations.

The complexity of the direct matrix multiplication algorithm for square n×n matrices is O(n3). More asymptotically efficient methods have been developed with complexity O(nlog2 7)≈O(n2.81) (Strassen, 1969) and even O(n2.376) (Coppersmith and Winograd, 1990). However, in practice, the new methods do not outperform the direct one even for relatively large matrices (n≈2000), and in certain circumstances they may experience numerical instability.

Specifications of the computer and software used for testing: CPU: Intel Xeon X3430 (2.4 GHz, 4 cores, 38.4 Gflop); RAM: 16 GB DDR3; OS: Windows 7 (64 bit); Matlab R2010b (64 bit); R 2.14.1; Revoluton R Enterprise 4.3 (64 bit).

4 DISCUSSION AND CONCLUSION

Matrix eQTL can perform analyses that previously required days or weeks in several minutes. QTL modelers who have only a handful of phenotypes understand the importance of testing several different models with covariates and interaction terms. Until now, this has not been feasible with eQTL analyses due to the computational burden. Matrix eQTL allows analysts to fit a variety of models with different mixes of covariates in <1 h and compare the results. Likewise, it allows analysts to compare different preprocessing and quality control procedures. Furthermore, once an appropriate model has been selected, Matrix eQTL can be used to determine permutation-based significance thresholds in less time than most packages take to generate nominal p-values. Matrix eQTL will greatly improve the ability of analysts to find true eQTLs by fitting the right model and choosing the best preprocessing and quality control procedures.

The utility of Matrix eQTL is not limited to association testing between microarray and genotype data. Matrix eQTL was used by Xia et al. (2012) to analyze RNA-seq data. RNA-seq data was preprocessed by applying variance stabilizing transformation for the Poisson counts and correcting for the differences in total read counts across samples. Matrix eQTL can be used for the analysis pairs of genetic/genomic datasets of various types, including measurements of allele specific gene expression, genotype, methylation and copy number variations. It can also be applied to find strongly dependent variables within a single dataset (e.g. gene–gene interactions).

For the future versions of Matrix eQTL we plan to consider several extensions and modification. First, we consider performing calculation on GPUs, instead of the CPU. The tests in Section 3.7 suggest that use of GPU in Matrix eQTL may provide 10-fold increase in the performance. We will also consider using Matrix eQTL optimization techniques for fast estimation of more complex models, such as multi-SNP models and generalized linear model (via efficient score statistic).

Funding: National Institutes of Health (R01-MH090936 and R01-ES015241), US Environmental Protection Agency (STAR RD83382501 and RD83272001), National Cancer Institute (R01-CA138255), National Science Foundation grant (DMS-0907177), National Institute of Mental Health (R01-MH090936) and the Gillings Innovation Laboratory in Statistical Genomics.

Conflict of Interest: none declared.

REFERENCES

  1. Abecasis G., et al. Merlin–rapid analysis of dense genetic maps using sparse gene flow trees. Nat. Genet. 2001;30:97–101. doi: 10.1038/ng786. [DOI] [PubMed] [Google Scholar]
  2. Benjamini Y., Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. Roy. Stat. Soc. B Meth. 1995;57:289–300. [Google Scholar]
  3. Breitling R., et al. Genetical genomics: spotlight on QTL hotspots. PLoS Genet. 2008;4:e1000232. doi: 10.1371/journal.pgen.1000232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Broman K., et al. R/qtl: QTL mapping in experimental crosses. Bioinformatics. 2003;19:889. doi: 10.1093/bioinformatics/btg112. [DOI] [PubMed] [Google Scholar]
  5. Coppersmith D., Winograd S. Matrix multiplication via arithmetic progressions. J. Symb. Comput. 1990;9:251–280. [Google Scholar]
  6. Degnan J., et al. Genomics and genome-wide association studies: an integrative approach to expression QTL mapping. Genomics. 2008;92:129–133. doi: 10.1016/j.ygeno.2008.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gatti D., et al. FastMap: fast eQTL mapping in homozygous populations. Bioinformatics. 2009;25:482. doi: 10.1093/bioinformatics/btn648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ghazalpour A., et al. High-resolution mapping of gene expression using association in an outbred mouse stock. PLoS Genet. 2008;4:e1000149. doi: 10.1371/journal.pgen.1000149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gilad Y., et al. Revealing the architecture of gene regulation: the promise of eQTL studies. Trends Genet. 2008;24:408–415. doi: 10.1016/j.tig.2008.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Goto K., Geijn R. Anatomy of high-performance matrix multiplication. ACM Trans. Math. Softw. 2008;34:12. [Google Scholar]
  11. Hoggart C., et al. Simultaneous analysis of all SNPs in genome-wide and re-sequencing association studies. PLoS Genet. 2008;4:e1000130. doi: 10.1371/journal.pgen.1000130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kao C., et al. Multiple interval mapping for quantitative trait loci. Genetics. 1999;152:1203. doi: 10.1093/genetics/152.3.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kendziorski C., Wang P. A review of statistical methods for expression quantitative trait loci mapping. Mamm. Genome. 2006;17:509–517. doi: 10.1007/s00335-005-0189-6. [DOI] [PubMed] [Google Scholar]
  14. Leek J., Storey J. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 2007;3:e161. doi: 10.1371/journal.pgen.0030161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lee S., et al. Predicting unobserved phenotypes for complex traits from whole-genome SNP data. PLoS Genet. 2008;4:e1000231. doi: 10.1371/journal.pgen.1000231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Leung D. An R package for analysis of whole-genome association studies. Hum. Hered. 2007;64:45–51. doi: 10.1159/000101422. [DOI] [PubMed] [Google Scholar]
  17. Listgarten J., et al. Correction for hidden confounders in the genetic analysis of gene expression. Proc. Natl Acad. Sci. 2010;107:16465. doi: 10.1073/pnas.1002425107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Purcell S., et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2010. ISBN 3-900051-07-0. [Google Scholar]
  20. Servin B., Stephens M. Imputation-based analysis of association studies: candidate regions and quantitative traits. PLoS Genet. 2007;3:e114. doi: 10.1371/journal.pgen.0030114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Strassen V. Gaussian elimination is not optimal. Numer. Math. 1969;13:354–356. [Google Scholar]
  22. Sun W. eQTL Analysis by Linear Model. 2009. Available at: http://www.bios.unc.edu/~wsun/software/eMap.pdf. [Google Scholar]
  23. Whaley R., Petitet A. Minimizing development and maintenance costs in supporting persistently optimized BLAS. Softw. Pract. Exp. 2005;35:101–121. [Google Scholar]
  24. Wright F., et al. Genome-wide association and linkage identify modifier loci of lung disease severity in cystic fibrosis at 11p13 and 20q13.2. Nat. Genet. 2011;43:539–546. doi: 10.1038/ng.838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Xia K., et al. seeQTL: a searchable database for human eQTLs. Bioinformatics. 2012;28:451–452. doi: 10.1093/bioinformatics/btr678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Zeng Z. Theoretical basis for separation of multiple linked gene effects in mapping quantitative trait loci. Proc. Natl Acad. Sci. 1993;90:10972. doi: 10.1073/pnas.90.23.10972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhang W., Liu J. From QTL Mapping to eQTL Analysis. In: Jianfeng F., Wenjiang F, Sun F., editors. Frontiers in Computational and Systems Biology. Vol. 15. 2010. pp. 301–329. [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES