The Structure, Thermodynamics and Solubility of Organic Crystals from Simulation with a Polarizable Force Field

Abstract

An important unsolved problem in materials science is prediction of the thermodynamic stability of organic crystals and their solubility from first principles. Solubility can be defined as the saturating concentration of a molecule within a liquid solvent, where the physical picture is of solvated molecules in equilibrium with their solid phase. Despite the importance of solubility in determining the oral bioavailability of pharmaceuticals, prediction tools are currently limited to quantitative structure–property relationships that are fit to experimental solubility measurements. For the first time, we describe a consistent procedure for the prediction of the structure, thermodynamic stability and solubility of organic crystals from molecular dynamics simulations using the polarizable multipole AMOEBA force field. Our approach is based on a thermodynamic cycle that decomposes standard state solubility into the sum of solid-vapor sublimation and vapor-liquid solvation free energies $\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}=\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}+\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$, which are computed via the orthogonal space random walk (OSRW) sampling strategy. Application to the n-alkylamides series from aeetamide through octanamide was selected due to the dependence of their solubility on both amide hydrogen bonding and the hydrophobic effect, which are each fundamental to protein structure and solubility. On average, the calculated absolute standard state solubility free energies are accurate to within 1.1 kcal/mol. The experimental trend of decreasing solubility as a function of n-alkylamide chain length is recapitulated by the increasing stability of the crystalline state and to a lesser degree by decreasing favorability of solvation (i.e. the hydrophobic effect). Our results suggest that coupling the polarizable AMOEBA force field with an orthogonal space based free energy algorithm, as implemented in the program Force Field X, is a consistent procedure for predicting the structure, thermodynamic stability and solubility of organic crystals.

INTRODUCTION

Organic crystals are a critical class of materials for the pharmaceutical industry¹ and represent an emerging approach for the low-pressure storage of gases within crystalline metal-organic frameworks (MOFs).^2,3 Specific examples of organic crystals include the polymorphs of ice⁴, pharmaceutical tablets such as paracetamol^5,6 (acetaminophen) and acetylsalicylic acid^7,8 (aspirin), and those responsible for diseases such as gout⁹ (monosodium urate monohydrate) and kidney stones¹⁰ (calcium oxalate). Key properties of organic crystals that are valuable to predict computationally include their atomic structure, thermodynamic stability and their solubility (i.e. pharmaceutical tablets within the digestive tract). Although significant progress has been made toward in silico crystal structure prediction (CSP),^11–14 computational prediction of the thermodynamic stability and solubility of organic crystals from first principles has remained a challenging unsolved problem.^11,15

For CSP, the underlying algorithms are characterized by application of a search protocol over space groups, unit cell dimensions and atomic coordinates using intermolecular potentials defined by fixed partial charge ^16–20 or fixed atomic multipole force fields.^21–24 Although a set of fixed atomic multipoles can model the quantum mechanical electrostatic potential outside the molecular surface of a polar organic molecule in vacuum to high accuracy, changes in electron distribution due to alternate conformations or transfer into a condensed phase environment are neglected unless polarization is accounted for.^25,26 Therefore, candidate low energy crystal structures are usually rescored using electronic structure calculations based on density functional theory (DFT) with dispersion corrections.^27,28 When these algorithms were applied during the 4^th blind test of CSP organized by the Cambridge Crystallographic Data Center (CCDC) in 2007, which featured 4 target organic crystals, 7 of 14 participating groups predicted at least one structure correctly and 4 groups had multiple successful predictions.¹² Moreover, in the 5^th blind test of CSP in 2010, each of the 6 target organic crystals was predicted correctly by at least one of the 14 participating groups.²⁸

However, despite its importance to the rational design of bioavailable pharmaceutical tablets, quantitative prediction of the thermodynamic stability and solubility of organic crystals from first principles has lagged behind both CSP and advancements in the computation of liquid state thermodynamics.^11,15,28 In the context of predicting solubility, the solvation free energy^15,29 and stability of amorphous solids³⁰ have been computed using Monte Carlo statistical mechanics simulations with the OPLS-AA force field,¹⁸ however, a procedure to predict the thermodynamic stability of crystalline solutes has not been presented. An alternative to predicting solubility from first principles (i.e. from an atomic resolution model of molecular energetics) is the revised General Solubility Equation^31,32 (GSE), which predicts the molar aqueous solubility S (i.e. the saturating concentration of the solute within solvent in mol/L) based on knowledge of the Celsius melting point (MP) of the crystal and the octonal-water partition coefficient (K_ow) of the molecule

$$logS=0.5-(MP-25)/10+log{K}_{\text{ow}}$$ Equation 1

The usefulness of the revised GSE in drug design settings where MP, K_ow or both are unknown is reduced. Therefore, practical tools for solubility prediction are currently limited to quantitative structure–property relationships (QSPR) and trained on experimental data^33–45 as discussed in recent reviews.^15,46–48

To address the challenge of computing the structure, thermodynamics and solubility of organic crystals from first principles, this work brings together recent advances from three complementary fields including polarizable atomic multipole force field development, free energy simulation methods and algorithms for efficient treatment of long-range electrostatics inherent to lattice summation. First, the importance of a polarizable atomic multipole force field to accurate modeling of crystal energy landscapes¹¹ arises from aspherical features of the electron density inherent to lone pairs and π-electrons,²⁵ and from perturbations such as conformational flexibility (i.e. intra-molecular polarization)²⁶ or transfer between vapor, liquid and crystalline environments (i.e. inter-molecular polarization). These critical features of the crystal energy landscape are neglected by fixed atomic charge force fields such as Amber⁴⁹, CHARMM⁵⁰ or OPLS-AA.¹⁸ In this work, the AMOEBA force field captures aspherical atomic electron density using permanent atomic multipoles through quadrupole order and transferability between confirmations and phases using explicit treatment of electronic polarization via induced dipoles.^51–53 Second, large energy barriers¹¹ that necessitate advanced statistical mechanics theories to efficiently converge sampling of molecular configurations characterize crystal potential energy surfaces.^54–56 Here we overcome these large energy barriers using the orthogonal space random walk (OSRW) strategy.^56–58 On the other hand, traditional methods such as free energy perturbation⁵⁹ or thermodynamic integration⁶⁰ require knowledge of the crystal structure coordinates, while use of OSRW allows coordinate prediction. Finally, algorithms for long-range van der Waals and electrostatics forces such as particle-mesh Ewald (PME) summation^61–63 must leverage the space group symmetry of crystalline solids to achieve computational efficiently, which has recently been implemented within the program Force Field X⁶⁴ On the other hand, widely used molecular dynamics programs such as Amber⁶⁵, CHARMM⁶⁶ and TINKER⁶⁷ require explicit sampling of the entire unit cell, which both increases the cost per energy evaluation while also slowing the kinetics of crystal nucleation.

In the next section, background on the polarizable AMOEBA force field, solubility thermodynamic cycle and space group symmetry extension of PME are presented. This is followed by theory describing the OSRW free energy algorithm, including details of the derivatives of the AMOEBA potential required by OSRW and are a superset of the derivatives required for thermodynamic integration, which are presented here for the first time. The overall implementation of AMOEBA and OSRW in Force Field X is validated by comparison to monovalent ion solvation free energies computed using standard free energy perturbation. Prediction of the structure, thermodynamics and solubility of the n-alkylamides from acetamide to octanamide is then presented. The n-alkylamides series was chosen due to the dependence of its solubility trend on both amide hydrogen bonding and the hydrophobic effect, which are both of broad importance to biomolecular structure and function.

BACKGROUND

A. The Potential Energy Surface of Organic Crystals

The non-covalent interactions between molecules of an organic crystal can be decomposed into van der Waals and electrostatic forces. Until recently, the atomic resolution force fields used to study crystal energetics and liquid state properties were based on the approximation that the electrostatic charge of each atom is invariant, or fixed, with respect to its local environment.⁶⁸ In reality, the electron density deforms in response to the electric field of its environment. For example, negatively charged electron density moves toward the positive potential of a cation such as Na+ or K+ and away from the negative potential of an anion such as Cl−. The average electric field within a crystal is different from that experienced by a molecule when solvated or in vapor. In the past, this necessitated choosing between fixed atomic charges that were optimal for either the crystalline phase or the liquid phase, but not both. Fortunately, increasing computational power has facilitated explicit inclusion of electronic polarization into force fields for organic molecules and thereby improved their transferability between vacuum, liquid and crystalline phases.^52,69–75 In this work, the crystal potential energy landscape is defined by the polarizable Atomic Mulitpole Optimized Energetics for Biomolecular Applications (AMOEBA) force field⁵² for organic molecules.^53,76 The AMOEBA potential is then sampled using the OSRW algorithm described below in order to compute the thermodynamic stability of crystals while also predicting their atomic coordinates.

B. Solubility Thermodynamic Cycle for Organic Crystals

Solubility defines the equilibrium concentration of a solute in contact with an excess of its solid state. The physical process reaches equilibrium when the rate of molecules joining the solid state (assumed to be crystalline in this work) from solution equals the rate of molecules leaving the solid to be solvated. Although the required system size and time scale for explicit atomic resolution simulation of the crystalline-solution phase equilibrium is prohibitive, the standard state solubility free energy ( $\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}$) can be decomposed into the sum of standard state sublimation ( $\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}$) and solvation ( $\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$) free energy steps

$$\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}=\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}+\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$$ Equation 2

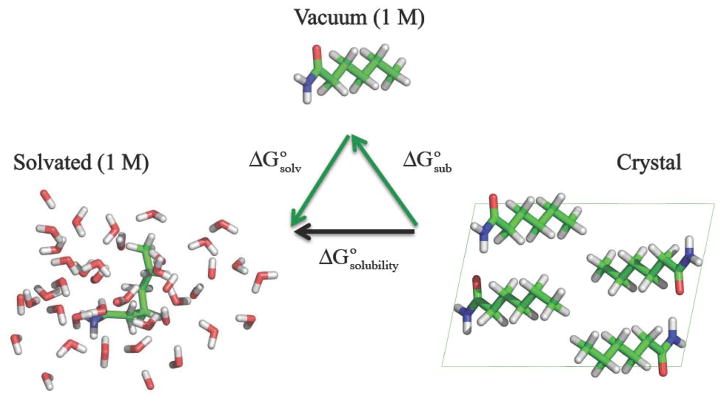
as shown in the thermodynamic cycle of Figure 1. Although solvation free energies are routinely computed to high precision,^77,78 calculation of the sublimation free energy by annihilation of the entire crystalline solid is novel to this work and is depicted in Figure 2. A correction is applied to the simulation result to account for the change in volume between a crystalline solid containing 1 mole of molecules and the standard state concentration of 1 M chosen for both the vapor and solvated states.

Figure 1.

This hexanamide thermodynamic cycle demonstrates that standard state solubility free energy ( $\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}$) can be decomposed into the sum of standard state sublimation ( $\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}$) and solvation ( $\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$) free energy steps.

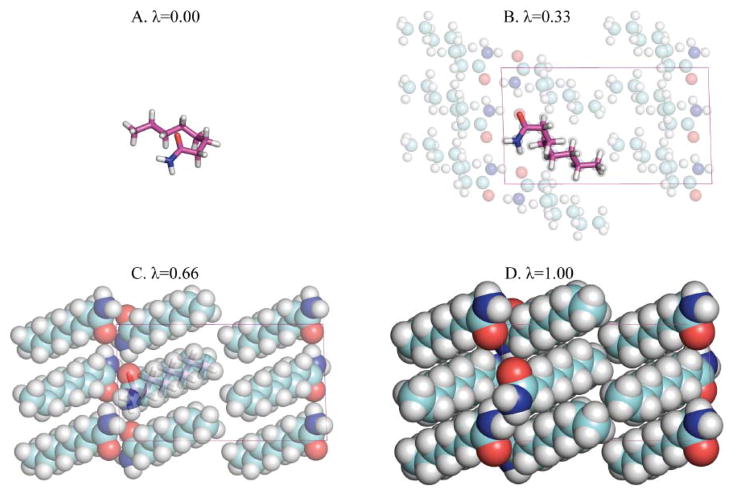
Figure 2.

An alchemical path for the calculation of the sublimation free energy change of octanamide is depicted. The infinite crystalline material (λ=1) is annihilated to leave a single molecule of octanamide in an infinite vacuum (λ=0). As the λ state variable is reduced, softcore descriptions of both van der Waals and multipolar electrostatics smoothly eliminate interactions between the asymmetric unit copy of octanamide (magenta) and its symmetry mates (cyan). The molecule is fully flexible for all λ values during the length of a simulation. No constraint on either molecular conformation or orientation is applied.

C. Long-Range Forces in Organic Crystals

Evaluation of the polarizable AMOEBA electrostatic energy for a crystalline lattice builds on the theory for lattice summation proposed by Ewald.⁷⁹ The real space portion of the theory was described by Ren and Ponder in the context of the AMOEBA water model⁸⁰ and was based on earlier work by Smith.⁸¹ The reciprocal space portion is accelerated by fast Fourier transforms (FFT) as described by Darden and colleagues for fixed charge^61,62 and multipolar⁶³ atomic electrostatics. Further acceleration of PME for crystals has been achieved via explicit support for space group symmetry,⁶⁴ which has been applied to biomolecular X-ray refinement.^64,82 Without explicit support for space group symmetry, the alchemical transformation shown in Figure 2 would need to consider n_symm molecules, where n_symm is the number of symmetry operators of the space group. For an acetamide crystal, which has 18 molecules in its unit cell (n_symm=18), the kinetics of nucleation for the alchemical transformation may be computationally prohibitive. In particular, the approximate 18x increase in the cost per energy evaluation is exacerbated by the need to convergence an 18x larger free energy change, which is accompanied by crystal nucleation kinetics.

METHODS

A. Orthogonal Space Random Walk

In order to effectively overcome large barriers in the crystalline free energy landscape, a second-order generalized ensemble method called the orthogonal-space random walk (OSRW) is applied.^56,57 The central idea of generalized ensemble (GE) free energy simulation methods is to employ a modified ensemble, which allows free energy barriers in the target ensemble to be crossed more frequently in order to efficiently sample the distributions required for free energy estimations. A first-order GE modification is based on the order parameter λ and the biasing energy term f_m(λ) in the following target potential:

$${\text{U}}_{\text{m}}={\text{U}}_{\text{AMOEBA}}(\lambda )+{\text{f}}_{\text{m}}(\lambda )$$ Equation 3

where λ=1 corresponds to the solute interacting with the condensed phase environment and λ=0 to the solute uncoupled from the condensed phase environment. In the first-order GE regime, the biasing term f_m(λ) is commonly updated to approach − G_AMOEBA(λ), which is the negative of the λ-dependent free energy profile corresponding to the canonical ensemble with the AMOEBA potential energy function. In this way, an order parameter space random walk can be achieved to uniformly sample all the target states. To adaptively estimate G_AMOEBA(λ), three major recursion schemes have been developed. The first is adaptive umbrella sampling,⁸³ in which free energy estimations are based on order parameter probability distributions. The second is the adaptive biasing force (ABF) method,^84–86 in which free energy estimations are based on the thermodynamic integration (TI) formula.^60,87 Finally, multiplicative approaches, such as the metadynamics method for molecular dynamics simulations⁵⁵ and the Wang-Landau method for Monte-Carlo simulations,⁸⁸ are realized through dynamic force-balancing.

In first-order GE simulations the free energy surface along λ is flattened, however, “hidden” free energy barriers may exist in the space perpendicular to λ. These “hidden” free energy barriers create a sampling challenge due to slow environmental relaxation. To address this, the second-order GE simulation method, the orthogonal space random walk (OSRW) algorithm, was introduced based on the following modified energy function:

$${\text{U}}_{\text{m}}={\text{U}}_{\text{AMOEBA}}(\lambda )+{\text{f}}_{\text{m}}(\lambda )+{\text{g}}_{\text{m}}(\lambda ,F_{\lambda })$$ Equation 4

where g_m(λ, F_λ) is targeted towards −G_AMOEBA(λ, F_λ) the negative of the free energy profile along (λ, F_λ) in the ensemble corresponding to the energy function U_AMOEBA(λ) − G_AMOEBA(λ), and F_λ = ∂U_AMOEBA(λ) ∂λ In contrast to first-order GE methods, OSRW requires two recursion components to be adaptively updated. The recursion component responsible for g_m(λ, F_λ) is called the “recursion kernel” and the recursion component responsible for f_m(λ) is called the “recursion slave” because its target − G_AMOEBA(λ) can be determined by the target of g_m(λ, F_λ). In our implementation, the recursion slave is determined using the TI relationship and metadynamics is used for the recursion kernel. However, the recursion kernel can be based on any of the three recursion methods discussed above.

The free energy biasing potential g_m(λ, F_λ) can be obtained by repetitively adding a relatively small Gaussian-shaped repulsive potential:

$$h{e}^{\left(-\frac{{\mid \lambda -\lambda (t_i)\mid }^2}{2w_1^2}\right)}{e}^{\left(-\frac{{\mid F_{\lambda }-F_{\lambda }(t_i)\mid }^2}{2w_2^2}\right)}$$ Equation 5

that is centered at the state [λ(t_i), F_λ(t_i)] being visited at time t_i and thereby discourages the system from often visited configurations. Repeating this procedure builds up the biasing potential

$${\text{g}}_{\text{m}}(\lambda ,F_{\lambda })=\sum _{t_i}h{e}^{\left(-\frac{{\mid \lambda -\lambda (t_i)\mid }^2}{2w_1^2}\right)}{e}^{\left(-\frac{{\mid F_{\lambda }-F_{\lambda }(t_i)\mid }^2}{2w_2^2}\right)}$$ Equation 6

and eventually flattens the underlying curvature of the free energy surface along the (λ, F_λ) space. Then, as in traditional metadynamics simulations, the free energy profile along the reaction coordinate (λ, F_λ) will eventually converge to −G_AMOEBA(λ, F_λ) and is estimated as −g_m(λ, F_λ). For any state λ́, the generalized force distribution should be proportional to e^{{βg_m[λ́F_λ(λ́)]}} and the free energy derivative at each state is

$${\frac{\text{dG}}{\text{d}\lambda }|}_{\acute{\lambda }}=\langle F_{\lambda }(\acute{\lambda })\rangle =\frac{{\int }_{F_{\lambda }}{F}_{\lambda }{\text{e}}^{[\beta {\text{g}}_{\text{m}}(\lambda ,F_{\lambda })]}\delta (\lambda -\acute{\lambda })}{{\int }_{F_{\lambda }}{\text{e}}^{[\beta g_{\text{m}}(\lambda ,F_{\lambda })]}\delta (\lambda -\acute{\lambda })}$$ Equation 7

Following the thermodynamic integration formula, the free energy change between the initial state λ_i (for example λ_i=0) and the target state λ (for example λ=1) is given by

$${\text{G}}_{\text{AMOEBA}}(\lambda )={\int }_{{\lambda }_i}^{\lambda }{\frac{\text{dG}}{\text{d}\lambda }|}_{\acute{\lambda }}\text{d}\acute{\lambda }$$ Equation 8

In our OSRW implementation, the metadynamics strategy described in Eq. 6 serves as the recursion kernel and the TI based formula (Eqs. 7 and 8) serves as the recursion slave with f_m(λ) set recursively as the instantaneous estimation of − G_AMOEBA(λ)

Our first goal was to derive, implement and parallelize derivatives with respect to λ of the polarizable AMOEBA potential energy function U(λ, X) where λ defines a continuous, softcore transition between the asymmetric unit (solute) fully interacting with its symmetry mates (condensed phase environment) to decoupled in order to compute the sublimation free energy. Analogous decoupling schemes are used for computing solvation free energy (i.e. a solute decoupled from solvent) and binding free energy (i.e. ligand decoupled from the binding pocket of a solvated protein). The terms needed for the various λ-based sampling methods may include ∂U(λ, X)/∂λ, ∂²U(λ, X)/∂λ² and/or ∂²U(λ, X)/∂X ∂λ. We briefly present key aspects of these derivatives with special emphasis on unique advancements required for the AMOEBA buffered 14-7 van der Waals softcore term, the permanent multipole softcore term and the polarization energy. Parallelization depends on Parallel Java, which is a unified API for shared memory and cluster parallel programming.⁸⁹

B. AMOEBA Intermolecular Interactions and Their λ Derivatives

1. Softcore Buffered 14-7 van der Waals

The AMOEBA model for water,^80,90 ions,⁹¹ organic molecules⁵³ and proteins^52,92 uses a buffered 14-7 van der Waals term proposed by Halgren.⁹³ A softcore form that allows the potential to smoothly disappear as λ goes to zero has been described previously⁹² and is given by

$${\text{U}}_{\text{vdW}}(\lambda ,r)={\lambda }^{\beta }{\epsilon }_{ij}{t}_1{t}_2$$ Equation 9

where for convenience the expression has been factored into the following two terms

$$t_1=\frac{{(1+\delta )}^{n-m}}{\alpha {(1-\lambda )}^2+{(\rho +\delta )}^{n-m}}$$ Equation 10

$$t_2=\frac{1+\gamma }{\alpha {(1-\lambda )}^2+{\rho }^m+\gamma }-2$$ Equation 11

where ε_ij is the well-depth, ρ = r/ŕ is the atomic separation distance r normalized by the minimum energy distance ŕ, the parameters (n=14, m=7, δ=0.07, γ=0.12) specify a buffered 14-7 form (a 6-12 Lennard-Jones potential is recovered by n=12, m=6, δ=0 and γ=0) and the parameters α and β tune the softcore transition.⁹² In the original work, the buffered 14-7 potential was completely turned on before polarizable atomic multipole electrostatics was considered,⁹² however, it is more convenient to modify both the van der Waals and electrostatics potentials concomitantly over the λ path. Adoption of the latter approach necessitated different α and β parameters, which are discussed further in the Results section below.

The various derivatives of the softcore buffered 14-7 interaction required for OSRW are now described. First, the partial derivative of U_vdw with respect to an atomic coordinate is given by

$$\frac{\partial {\text{U}}_{\text{vdW}}(\lambda ,r)}{\partial r_{i,\gamma }}={\epsilon }_{ij}{\lambda }^{\beta }\left(\frac{\partial t_1}{\partial r_{i,\gamma }}{t}_2+t_1\frac{\partial t_2}{\partial r_{i,\gamma }}\right)$$ Equation 12

where

$$\frac{\partial t_1}{\partial r_{i,\gamma }}=\frac{(n-m){(1+\delta )}^{n-m}{(\rho +\delta )}^{n-m-1}}{\acute{r}{[\alpha {(1-\lambda )}^2+{(\rho +\delta )}^{n-m}]}^2}\frac{r_{\gamma }}{r}$$ Equation 13

and

$$\frac{\partial t_2}{\partial r_{i,\gamma }}=\frac{m(1+\gamma ){\rho }^{m-1}}{{\acute{r}}^m{[\alpha {(1-\lambda )}^2+{\rho }^m+\gamma ]}^2}\frac{r_{\gamma }}{r}$$ Equation 14

Next, the partial derivative of U_vdw with respect to λ is shown

$$\frac{\partial {\text{U}}_{\text{vdW}}(\lambda ,r)}{\partial \lambda }={\epsilon }_{ij}\left[\beta {\lambda }^{\beta -1}{t}_1{t}_2+{\lambda }^{\beta }\left(\frac{\partial t_1}{\partial \lambda }{t}_2+t_1\frac{\partial t_2}{\partial \lambda }\right)\right]$$ Equation 15

where

$$\frac{\partial t_1}{\partial \lambda }=\frac{2\alpha (1-\lambda ){(1+\delta )}^{n-m}}{{[\alpha {(1-\lambda )}^2+{(\rho +\delta )}^{n-m}]}^2}$$ Equation 16

and

$$\frac{\partial t_2}{\partial \lambda }=\frac{2\alpha (1-\lambda )(1+\gamma )}{{[\alpha {(1-\lambda )}^2+{\rho }^m+\gamma ]}^2}$$ Equation 17

For the 2^nd derivative of the U_vdw with respect to λ it is convenient to separate the previous first derivative of Equation 15 into a sum of three terms as

$$\frac{\partial {\text{U}}_{\text{vdW}}(\lambda ,r)}{\partial \lambda }={\epsilon }_{ij}(f_1+f_2+f_3)$$ Equation 18

such that ∂²U_vdW(λ, r)/∂λ² is then given by

$$\frac{{\partial }^2{\text{U}}_{\text{vdW}}(\lambda ,r)}{\partial {\lambda }^2}={\epsilon }_{ij}\left(\frac{\partial f_1}{\partial \lambda }+\frac{\partial f_2}{\partial \lambda }+\frac{\partial f_3}{\partial \lambda }\right)$$ Equation 19

where

$$\frac{\partial f_1}{\partial \lambda }=\beta (\beta -1){\lambda }^{\beta -2}{t}_1{t}_2+\beta {\lambda }^{\beta -1}\left(\frac{\partial t_1}{\partial \lambda }{t}_2+t_1\frac{\partial t_2}{\partial \lambda }\right)$$ Equation 20

$$\frac{\partial f_2}{\partial \lambda }=\beta {\lambda }^{\beta -1}\frac{\partial t_1}{\partial \lambda }{t}_2+{\lambda }^{\beta }\left(\frac{{\partial }^2{t}_1}{\partial {\lambda }^2}{t}_2+\frac{\partial t_1}{\partial \lambda }\frac{\partial t_2}{\partial \lambda }\right)$$ Equation 21

and

$$\frac{\partial f_3}{\partial \lambda }=\beta {\lambda }^{\beta -1}{t}_1\frac{\partial t_2}{\partial \lambda }+{\lambda }^{\beta }\left(\frac{\partial t_1}{\partial \lambda }\frac{\partial t_2}{\partial \lambda }+t_1\frac{{\partial }^2{t}_2}{\partial {\lambda }^2}\right)$$ Equation 22

In the above expressions, only ∂²t₁/∂λ² and ∂²t₂/∂λ² remain to be defined and are given by

$$\frac{{\partial }^2{t}_1}{\partial {\lambda }^2}=\frac{8{\alpha }^2{(1-\lambda )}^2{(1+\delta )}^{n-m}}{{[\alpha {(1-\lambda )}^2+{(\rho +\delta )}^{n-m}]}^3}-\frac{2\alpha {(1+\delta )}^{n-m}}{{[\alpha {(1-\lambda )}^2+{(\rho +\delta )}^{n-m}]}^2}$$ Equation 23

and

$$\frac{{\partial }^{2}t}{\partial {\lambda }^2}=\frac{8{\alpha }^2{(1-\lambda )}^2(1+\gamma )}{{[\alpha {(1-\lambda )}^2+{\rho }^m+\gamma ]}^3}-\frac{2\alpha (1+\gamma )}{{[\alpha {(1-\lambda )}^2+{\rho }^m+\gamma ]}^2}$$ Equation 24

Finally, the 2^nd partial derivative with respect to both an atomic coordinate and λ is given by

$$\frac{{\partial }^2{\text{U}}_{\text{vdW}}(\lambda ,r)}{\partial \lambda \partial r_{i,\gamma }}={\epsilon }_{ij}\left(\frac{\partial f_1}{\partial r_{i,\gamma }}+\frac{\partial f_2}{\partial r_{i,\gamma }}+\frac{\partial f_3}{\partial r_{i,\gamma }}\right)$$ Equation 25

where

$$\frac{\partial f_1}{\partial r_{i,\gamma }}=\beta {\lambda }^{\beta -1}\left(\frac{\partial t_1}{\partial r_{i,\gamma }}{t}_2+t_1\frac{\partial t_2}{\partial r_{i,\gamma }}\right)$$ Equation 26

$$\frac{\partial f_2}{\partial r_{i,\gamma }}={\lambda }^{\beta }\left(\frac{{\partial }^2{t}_1}{\partial \lambda \partial r_{i,\gamma }}{t}_2+\frac{\partial t_1}{\partial \lambda }\frac{t_2}{\partial r_{i,\gamma }}\right)$$ Equation 27

and

$$\frac{\partial f_3}{\partial r_{i,\gamma }}={\lambda }^{\beta }\left(\frac{t_1}{\partial r_{i,\gamma }}\frac{\partial t_2}{\partial \lambda }+t_1\frac{{\partial }^2{t}_2}{\partial \lambda \partial r_{i,\gamma }}\right)$$ Equation 28

Only the terms ∂²t₁/∂λ∂r_i,γ and ∂²t₂/∂λ∂r_i,γ remain to be defined and are given by

$$\frac{{\partial }^2{t}_1}{\partial \lambda \partial r_{i,\gamma }}=\frac{4\alpha (1-\lambda )(n-m){(1+\delta )}^{n-m}{(\rho +\delta )}^{n-m-1}}{\acute{r}{[\alpha {(1-\lambda )}^2+{(\rho +\delta )}^{n-m}]}^3}\frac{r_{\gamma }}{r}$$ Equation 29

and

$$\frac{{\partial }^2{t}_2}{\partial \lambda \partial r_{i,\gamma }}=\frac{4\alpha (1-\lambda )m{(1+\gamma )}^{m-1}}{{\acute{r}}^m{[\alpha {(1-\lambda )}^2+{\rho }^m+\gamma ]}^3}\frac{r_{\gamma }}{r}$$ Equation 30

2. Softcore for Multipolar Real Space Ewald Summation

For real space Ewald electrostatic interactions between permanent multipoles, it is essential to formulate inclusion of softcore behavior in a manner that facilitates concise higher order tensors and partial derivatives. Our approach replaces the atomic separation distance r = |r_j − r_i| by $f=\sqrt{r^2+\alpha {(1-\lambda )}^2}$ and the parameter α tunes the softcore transition. The softcore electrostatic interaction energy between permanent multipoles through quadrupole order at sites i and j is given by

$${\text{U}}_{\text{real}}(\lambda ,r)={\lambda }^{\beta }\sum _{l=0}^4{G}_{ij}^l(r){\text{B}}_l(f)$$ Equation 31

where the coefficients $G_{ij}^l(r)$ for each order l depend on the multipole coefficients of each site and were given by Smith.⁸¹ The function B_l(u) is defined by

$${\text{B}}_0(u)=\text{erfc}(\xi u)/u$$ Equation 32

for the 0^th order term based on the complementary error function

$$\text{erfc}(\xi u)=\frac{2}{\sqrt{\pi }}{\int }_{\xi u}^{\infty }exp(-s^2)\text{d}s$$ Equation 33

and higher order B_l(u) terms are obtained from the recursion relationship

$${\text{B}}_l(u)=\frac{1}{u^2}\left[(2l-1){\text{B}}_{l-1}(u)+\frac{{(2{\xi }^2)}^l}{\xi \sqrt{\pi }}exp(-{\xi }^2{u}^2)\right]$$ Equation 34

The derivative of the permanent real space electrostatic energy with respect to an atomic coordinate r_i,_γ of atom i is given by

$$\frac{\partial {\text{U}}_{\text{real}}(\lambda ,r)}{\partial r_{i,\gamma }}={\lambda }^{\beta }\sum _{l=0}^4\frac{\partial G_{ij}^l(r)}{\partial r_{i,\gamma }}{\text{B}}_l(f)+{\text{G}}_{ij}^l(r)\frac{\partial {\text{B}}_l(f)}{\partial r_{i,\gamma }}$$ Equation 35

where the partial derivatives for $\partial G_{ij}^l(r)/\partial r_{i,\gamma }$ were given by Smith⁸¹ and

$$\frac{\partial {\text{B}}_l(f)}{\partial r_{i,\gamma }}=r_{\gamma }{\text{B}}_{l+1}(f)$$ Equation 36

The 1^st derivative with respect to λ is

$$\frac{\partial {\text{U}}_{\text{real}}(\lambda ,r)}{\partial \lambda }=\sum _{l=0}^4\text{G}{(r)}_{ij}^l\left[\beta {\lambda }^{\beta -1}{\text{B}}_l(f)+{\lambda }^{\beta }\frac{\partial {\text{B}}_l(f)}{\partial \lambda }\right]$$ Equation 37

where it can be shown that

$$\frac{\partial {\text{B}}_l(f)}{\partial \lambda }=\alpha (1-\lambda ){\text{B}}_{l+1}(f)$$ Equation 38

and the 2^nd derivative is given by

$${\partial }^2{\text{U}}_{\text{real}}(\lambda ,r)/\partial {\lambda }^2=\sum _{l=0}^4{G}_{ij}^l(r)\left[\beta (\beta -1){\lambda }^{\beta -2}{\text{B}}_l(f)+2\beta {\lambda }^{\beta -1}\frac{\partial {\text{B}}_l(f)}{\partial \lambda }+{\lambda }^{\beta }\frac{{\partial }^2{\text{B}}_l(f)}{\partial {\lambda }^2}\right]$$ Equation 39

where

$$\frac{{\partial }^2{\text{B}}_l(f)}{\partial {\lambda }^2}={\alpha }^2{(1-\lambda )}^2{\text{B}}_{l+2}(f)-\alpha {\text{B}}_{l+1}(f)$$ Equation 40

Finally, the 2^nd derivative of the softcore permanent multipole real space electrostatic energy with respect to an atomic coordinate r_i,γ of atom i and λ is given by

$$\frac{{\partial }^2{\text{U}}_{\text{real}}(\lambda ,r)}{\partial \lambda \partial r_{i,\gamma }}=\beta {\lambda }^{\beta -1}\sum _{l=0}^4\frac{\partial {\text{G}}_{ij}^l(r)}{\partial r_{i,\gamma }}{\text{B}}_l(f)+{\text{G}}_{ij}^l(r)\frac{\partial {\text{B}}_l(f)}{\partial r_{i,\gamma }}+{\lambda }^{\beta }\sum _{l=0}^4\frac{\partial {\text{G}}_{ij}^l(r)}{\partial r_{i,\gamma }}\frac{\partial {\text{B}}_l(f)}{\partial \lambda }+{\text{G}}_{ij}^l(r)\frac{{\partial }^2{\text{B}}_l(f)}{\partial \lambda \partial r_{i,\gamma }}$$ Equation 41

where

$$\frac{{\partial }^2{\text{B}}_l(f)}{\partial \lambda \partial r_{i,\gamma }}=\alpha (1-\lambda )r_{\gamma }{\text{B}}_{l+2}(f)$$ Equation 42

3. Permanent Reciprocal Space Ewald Summation

The reciprocal space portion of particle-mesh Ewald summation due to permanent multipoles is not pairwise and is therefore calculated by interpolating between the potential due to the total system ${\phi }_{\text{recip}}^{\text{total}}$ (i.e. infinite crystal, solute plus solvent, or ligand plus protein/solvent) and that due to only the solute ${\phi }_{\text{recip}}^{\text{solute}}$ (i.e. asymmetric unit, solute or ligand). The latter calculation is significantly faster than the computation of the reciprocal potential due to the entire condensed phase system minus the solute ${\phi }_{\text{recip}}^{\text{condensed}}$ (i.e. symmetry mates without the asymmetric unit, solvent without the solute or protein/solvent without the ligand), which can be determined from the relationship

$${\phi }_{\text{recip}}^{\text{condensed}}={\phi }_{\text{recip}}^{\text{total}}-{\phi }_{\text{recip}}^{\text{solute}}$$ Equation 43

The permanent reciprocal space potential is then given by

$${\phi }_{\text{recip}}(\lambda )=(1-\lambda ){\phi }_{\text{recip}}^{\text{condensed}}+\lambda {\phi }_{\text{recip}}^{\text{total}}={\phi }_{\text{recip}}^{\text{total}}+(\lambda -1){\phi }_{\text{recip}}^{\text{solute}}$$ Equation 44

and its 1^st derivative with respect to λ is

$$\frac{\partial {\phi }_{\text{recip}}(\lambda )}{\partial \lambda }={\phi }_{\text{recip}}^{\text{total}}-{\phi }_{\text{recip}}^{\text{condensed}}={\phi }_{\text{recip}}^{\text{solute}}$$ Equation 45

while the 2^nd derivative vanishes. The dependence of the permanent multipole reciprocal space energy U_recip(λ) on λ can be formulated as a function of the reciprocal space electrostatic potential φ_recip(λ) to give U_recip (φ_recip(λ)), which makes it clear that the energy and coordinate gradient can be computed as usual. The first derivative of the permanent multipole reciprocal space energy with respect to λ is given by $\partial {\text{U}}_{\text{recip}}\left({\phi }_{\text{recip}}(\lambda )\right)/\partial \lambda ={\text{U}}_{\text{recip}}\left({\phi }_{\text{recip}}^{\text{solute}}\right)$, the 2^nd derivative with respect to λ is zero and terms of the form ∂²U_recip(φ_recip(λ))/∂λ∂r_i,γ are analogous to the atomic coordinate gradient.

4. Polarization Energy

The AMOEBA polarization model is based on induced dipoles at each atomic center, which are polarized by the field of the permanent multipoles as well as the field of the induced dipoles themselves.⁵³ Pauli repulsion balances favorable deformation of the electron cloud, which is captured by smearing the induced dipole as described by Thole⁹⁴ via

$$\rho =\frac{3a}{4\pi }{\text{e}}^{-a{u}^3}$$ Equation 46

where a is a dimensionless constant that controls the degree of smearing and u = r_ij/(α_iα_j)^(1/6) is an effective distance that depends on the polarizability α of each atom.

Calculation of the induction energy along the alchemical path is similar to the calculation of the reciprocal space potential due to permanent multipoles because it is not pairwise and interpolation is used. For small values of λ, solute (i.e. asymmetric unit) atoms frequently overlap with solvent (i.e. symmetry mate) atoms because of the softcore modification to solute-solvent van der Waals interactions smoothly and completely eliminates Pauli repulsion by λ = 0. Although the Thole model damps polarization at short range, the self-consistent field (SCF) calculation can require a larger number of iterations than is usual at unphysical, small atomic separations. Therefore, the contribution of the solute to condensed phase polarization is not considered until λ achieves a value greater than ${\lambda }_{\text{pol}}^{\text{start}}=~0.7$. An additional benefit of this approach is that approximately ¾ of the alchemical path requires a single condensed phase SCF calculation, rather than two. As the SCF is the most computationally expensive aspect of evaluating the AMOEBA potential energy and its derivatives, this saves approximately a factor of 2 with regards to the overall efficiency of the OSRW algorithm.

For the interval $\lambda =0\dots {\lambda }_{\text{pol}}^{\text{start}}$, the vapor polarization energy for the solute ${\text{U}}_{\text{pol}\text{(}v\text{)}}^{\text{solute}}$ is calculated and summed with the condensed phase energy in the absence of the solute ${\text{U}}_{\text{pol}}^{\text{condensed}}$. Over the interval ${\lambda }_{\text{pol}}^{\text{start}}\le \lambda \le 1$, this sum is smoothly turned off based on shifting and scaling λ to give a state variable for polarization ${\lambda }_{\text{pol}}=\frac{\lambda -{\lambda }_{\text{pol}}^{\text{start}}}{1-{\lambda }_{\text{pol}}^{\text{start}}}$. Concomitantly, the total polarization energy of the condensed phase system is turned on

$${\text{U}}_{\text{pol}}(\lambda )=\{\begin{array}{cc}{\text{U}}_{\text{pol}(v)}^{\text{solute}}+{\text{U}}_{\text{pol}}^{\text{condensed}}& 0\le \lambda \le {\lambda }_{\text{pol}}^{\text{start}}\\ {\lambda }_{\text{pol}}^3{\text{U}}_{\text{pol}}^{\text{Total}}+(1-{\lambda }_{\text{pol}}^3)({\text{U}}_{\text{pol}(v)}^{\text{solute}}+{\text{U}}_{\text{pol}}^{\text{condensed}})& {\lambda }_{\text{pol}}^{\text{start}}\le \lambda \le 1\end{array}$$ Equation 47

The cubic dependence on λ ensures that the 1^st derivative of U_pol(λ) with respect to λ is zero at ${\lambda }_{\text{pol}}^{\text{start}}$

$$\frac{\partial {\text{U}}_{\text{pol}}(\lambda )}{\partial \lambda }=\{\begin{array}{cc}0& 0\le \lambda \le {\lambda }_{\text{pol}}^{\text{start}}\\ 3{\lambda }_{\text{pol}}^2({\text{U}}_{\text{pol}}^{\text{total}}-{\text{U}}_{\text{pol}(v)}^{\text{solute}}-{\text{U}}_{\text{pol}}^{\text{condensed}})& {\lambda }_{\text{pol}}^{\text{start}}\le \lambda \le 1\end{array}$$ Equation 48

as are the 2^nd derivatives

$$\frac{{\partial }^2{\text{U}}_{\text{pol}}(\lambda )}{\partial {\lambda }^2}=\{\begin{array}{cc}0& 0\le \lambda \le {\lambda }_{\text{pol}}^{\text{start}}\\ 6{\lambda }_{\text{pol}}({\text{U}}_{\text{pol}}^{\text{total}}-{\text{U}}_{\text{pol}(v)}^{\text{solute}}-{\text{U}}_{\text{pol}}^{\text{condensed}})& {\lambda }_{\text{pol}}^{\text{start}}\le \lambda \le 1\end{array}$$ Equation 49

and

$$\frac{{\partial }^2{\text{U}}_{\text{pol}}(\lambda )}{\partial \lambda \partial r_{i,\gamma }}=\{\begin{array}{cc}0& 0\le \lambda \le {\lambda }_{\text{pol}}^{\text{start}}\\ 3{\lambda }_{\text{pol}}^2\left(\frac{\partial {\text{U}}_{\text{pol}}^{\text{total}}}{\partial r_{i,\gamma }}-\frac{\partial {\text{U}}_{\text{pol}(v)}^{\text{solute}}}{\partial r_{i,\gamma }}-\frac{\partial {\text{U}}_{\text{pol}}^{\text{condensed}}}{\partial r_{i,\gamma }}\right)& {\lambda }_{\text{pol}}^{\text{start}}\le \lambda \le 1\end{array}$$ Equation 50

C. Parameterization of Amide Functional Groups for AMOEBA

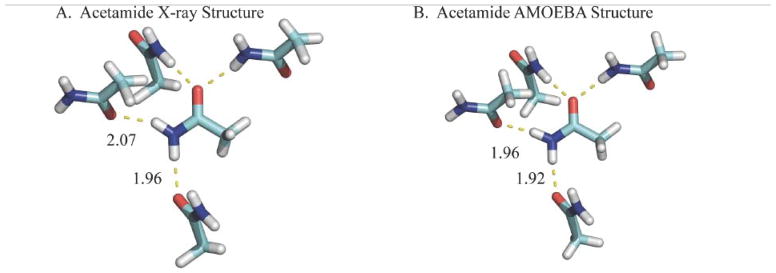
A 1981 study of acetamide structures from a neutron diffraction experiment at 23 K and ab initio molecular orbital studies in vacuum demonstrated that there are significant equilibrium bond length differences for both C=O and C-N as a function of environment due to hydrogen bonding.⁹⁵ One consequence is that the total dipole moment in vacuum of the equilibrium vacuum and crystalline structures differ by approximately 10%, as shown in Table 1. This difference is large enough that the solvation free energy for members of the n-alkylamide series is sensitive to the bond lengths used during parameterization of AMOEBA electrostatics. The sensitivity can be rationalized from the quadratic dependence of the solvation free energy on the total molecular dipole moment. For AMOEBA parameterization, the C-N and C=O bond lengths of the n-alkylamides were fixed at 1.34 Å and 1.23 Å, respectively. This protocol yielded a dipole moment for acetamide of 3.98 Debye, which is intermediate between that of unrestrained vacuum optimization (3.69 Debye) and that from fixing the C=O and C-N bond lengths at condensed phase values (4.07 to 4.17 Debye).

Table 1.

Shown are C-N and C=O bond lengths for acetamide from various sources including vacuum and crystalline experiments, as well as vacuum and crystalline QM optimizations. The experimental vacuum C-N bond length of 1.38 Å is reduced to 1.33–1.34 Å in condensed phase based on experimental crystal structures. Conversely, the experimental vacuum C=O bond length of 1.22 Å increases to 1.24–1.26 Å in condensed phase. These modest changes in equilibrium geometry have a significant effect on the molecular electron distribution, as demonstrated by the increase in the total dipole moment from a vacuum value of ~3.7 Debye to the condensed phase geometry value of ~4.1 Debye. Optimization of all atomic coordinates (ALL) or only carbon and hydrogen coordinates (C, H) was performed at the 6–31G* level in the environment listed, except for two cases optimized at the B3LYP/6311++G** and B3LYP/6311G** levels. The B3LYP/6311G** geometry optimization was performed using periodic boundary conditions^96,97 with cell parameters fixed and with inclusion of a dispersion correction.²⁷ The total dipole moment of each conformation was then calculated in vacuum at the MP2/6-311++G(2d,2p) level.

Source	Environment	Opt.	Temp. (K)	C-N	C=O	Dipole
6-31G*	Vacuum	All		1.359	1.197	3.69
Electron Diffraction98	Vacuum	C, H		1.380	1.220	3.71
B3LYP/6311++G**	Vacuum	All		1.369	1.215	3.78
AMOEBA Parameterization	Vacuum	C, H		1.340	1.230	3.98
X-ray (ACEMID02)99	R3c	C, H	108	1.336	1.243	4.07
Neutron (ACEMID03)95	R3c	C, H	23	1.337	1.250	4.10
X-ray (ACEMID05)100	R3c	C, H	23	1.335	1.252	4.12
X-ray (ACEMID01)101	R3c	C, H	283–303	1.338	1.258	4.14
X-ray (ACEMID)102	Pccn	C, H	283–303	1.334	1.260	4.17
B3LYP/6311G**	R3c	ALL		1.336	1.249	4.17

The lattice energy (E_lattice) for the AMOEBA acetamide model will be compared to periodic solid-state ab initio calculations based on the program suite CRYSTAL’09,^96,97 which uses functions localized at atoms as the basis for expansion of the crystalline orbitals via a linear combination of atomic orbitals (LCAO) technique. All-electron Gaussian type basis sets and the hybrid B3LYP^103,104 Hamiltonian was used. The DFT exchange–correlation contribution is evaluated by numerical integration over the unit cell volume. Radial and angular points of the grid were generated through Gauss–Legendre radial quadrature and Lebedev two-dimensional angular point distributions with a pruned grid of 75 radial and 974 angular points. The level of accuracy in evaluating the Coulomb and Hartree–Fock exchange series was controlled by five parameters,⁹⁷ and values of 7, 7, 7, 7, 16 were used. The reciprocal space integration was performed by sampling the Brillouin zone with the 6 × 6 × 6 Pack-Monkhorst net.¹⁰⁵ Structure optimizations were performed using analytical energy gradients with respect to atomic coordinates with cell parameters fixed,^106–108 within a quasi-Newton scheme combined with the Broyden–Fletcher–Goldfarb–Shanno scheme for Hessian updating.^109–112 Convergence was checked on both gradient components and nuclear displacements and was signaled when the RMS gradient was 0.00015 Hartree/Bohr and RMS displacement was 0.0006 Bohr. The 6-31G*^113,114 and 6-311G**¹¹⁵ basis sets were used and condensed phase energies were corrected for BSSE via the counterpoise method.¹¹⁶

The lattice energy was computed as

$$E_{\text{lattice}}=\frac{E_{\text{unit}}}{Z}-E_{\text{mol}}$$ Equation 51

where E_unit is the total energy of the unit cell, Z is the number of the molecules in the unit cell and E_mol is the total energy of acetamide optimized in vacuum. Observing the results in Table 2, the AMOEBA lattice energy for acetamide compares well to the ab initio values before the zero point energy (ZPE) was applied. After the ZPE is taken into account, AMOEBA overestimates the lattice energy by a little more than 2 kcal/mol at 0°K compared to DFT. The effect of this limitation on crystal thermodynamics near room temperature is difficult to project.

Table 2.

Shown is the lattice energy for acetamide using the AMOEBA potential in comparison to ab initio results with and without ZPE correction. Energy values correspond to structural minima of their respective potentials.

Potential	Elattice	Elattice with ZPE
AMOEBA	−20.78
B3LYP/6-31G*	−20.54	−18.28
B3LYP/6-311G**	−20.06	−17.84

D. Previous AMOEBA Free Energy Perturbation Protocol

The first applications of the AMOEBA force field to the computation of free energy were limited to procedures that did not require the derivative of the potential energy with respect to λ, such as thermodynamic integration, which was not been completed until the present work. The original protocol, based on free energy perturbation (FEP), is described here for ion solvation and will be compared to OSRW in the Results section that follows.⁹¹ For FEP, particle growth was completed with the charge and polarizability of each ion set to zero. During particle growth, the van der Waals radius (r) and well depth (ε) parameters were defined by

$$\text{r}(\lambda )=1+\lambda (r_{\text{final}}-1)$$ Equation 52

and

$$\epsilon (\lambda )=\lambda {\epsilon }_{\text{final}}$$ Equation 53

respectively, for λ = (0.01,0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0). During the subsequent charging stage, the charge (q) and polarizability (α) of each ion were defined by

$$\text{q}(\lambda )=\lambda q_{\text{final}}$$ Equation 54

and

$$\alpha (\lambda )=\lambda {\alpha }_{\text{final}}$$ Equation 55

respectively, for λ = (0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0) where the first charging trajectory is equivalent to the last growth trajectory. For each λ value, 200 psec of constant volume molecular dynamics was performed using an 18.643 Å cubic box containing 216 AMOEBA water molecules. The Helmholtz free energy between adjacent λ values ΔA(λ_i → λ_i+1) was calculated via half-steps as

$$\mathrm{\Delta }\text{A}\left(i\to i+\frac{1}{2}\right)=-{\text{k}}_{\text{B}}Tln\langle exp\left(\frac{E_{{\lambda }_i}-E_{{\lambda }_{i+1/2}}}{{\text{k}}_{\text{B}}T}\right)\rangle {\lambda }_i$$ Equation 56

plus

$$\mathrm{\Delta }\text{A}\left(i+\frac{1}{2}\to i+1\right)={\text{k}}_{\text{B}}Tln\langle exp\left(\frac{E_{{\lambda }_{i+1}}-E_{{\lambda }_{i+1/2}}}{{\text{k}}_{\text{B}}T}\right)\rangle {\lambda }_{i+1}$$ Equation 57

using the last 150 psec of each trajectory.⁹¹

The standard state solvation free energy $\mathrm{\Delta }{G}_{\text{solv}}^{\text{o}}$ (a relative free energy due to transferring the solute from vapor to solution phase) is independent of the solution concentration (C_s) as long as the standard state of the vapor phase is chosen to be the same as that of solution (e.g. 1 M), and the solution is dilute enough that solute molecules do not interact (no excess free energy of solvation). The standard state concentration C° then cancels as shown below

$$\mathrm{\Delta }{G}_{\text{solv}}^{\text{o}}=-\mathit{RT}ln\left(\frac{C_s/C^{\text{o}}}{C_v/C^{\text{o}}}\right)=-\mathit{RT}ln\left(\frac{C_s}{C_v}\right)$$ Equation 58

In this case, solvation free energy simulation results are essentially independent of the number of water molecules beyond a lower threshold. For example, the volume per molecule at 1M is 1660 ų, while for the ion solvation simulations the volume per molecule was approximately 6500 ų and for the n-alkylamides discussed below it was 15000 ų. In both cases, there are negligible interactions between solute periodic images.

RESULTS

A. Validation on Ion Solvation Free Energy

The first free energy calculations using the AMOEBA water model^80,90 focused on the solvation free energy of K+, Na+ and CI− ions and demonstrated very good agreement with experimental results for the solvation energy of KCl and NaCl salts.⁹¹ Here we compare the free energy methodology used in the initial ion solvation work, described above, with our OSRW approach in terms of accuracy and efficiency. The current OSRW protocol follows Grossfield et al. in terms of simulation box size (18.643 Å), number of water molecules (216), temperature (300 K), use of a Berendsen weak coupling thermostat (0.1 psec time constant),¹¹⁷ time step (1.0 fsec), SCF convergence criteria (0.01 RMS Debye), van der Waals cutoff (12 Å) and ensemble (NVT), but differs in a few notable ways that are now described.⁹¹ First, the current work uses of a softcore version of the buffered 14-7 van der Waals potential⁹² as described above, which avoids the difficulties encountered in the original particle growth protocol as λ → 0. Secondly, the original work used conventional Ewald summation⁸⁰ whereas the more efficient PME approach is used for the current AMOEBA/OSRW protocol as implemented in Force Field X^63,64 The PME parameters used throughout this work include a real space cutoff of 7.0 Å, an Ewald convergence parameter of 0.545, 5^th order B-spline interpolation and a reciprocal grid spacing of 1.2 per Å. Finally, whereas the original protocol divided particle growth and charging into separate steps, our approach simultaneously performs 1.) growth of the van der Waals potential, 2.) charging of the condensed phase permanent electrostatic interactions and 3.) interpolation between vapor and condensed phase ligand polarization. Coupling ligand van der Waals growth with scaling up of electrostatic interactions between the ligand and condensed phase environment may be more efficient than separation into two stages. In addition, the latter approach does not require a vapor-discharging step for polyatomic ligands because intramolecular solute electrostatics are used throughout the protocol.

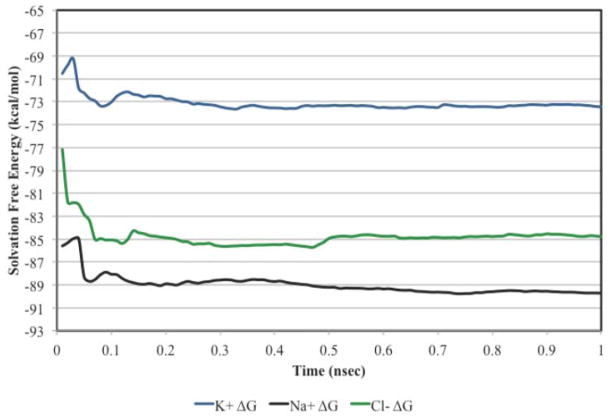
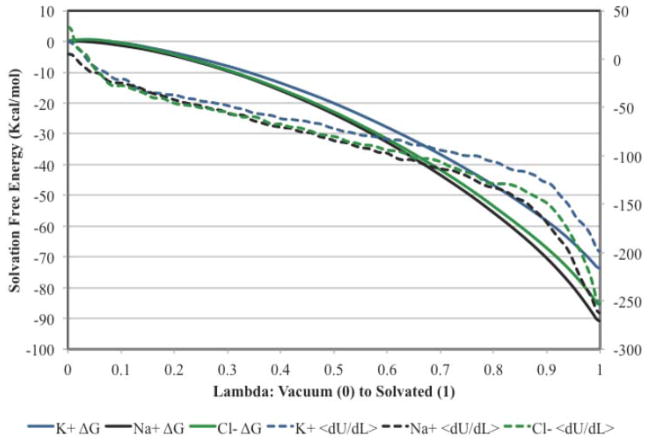
The ion solvation free energies under the AMOEBA/OSRW protocol are converged after only 0.5 nsec as shown in Figure 3. Furthermore, a plot of the cumulative free energy as a function of λ demonstrates smooth behavior, although small fluctuations in the ensemble average of ∂U/∂λ remain as shown in Figure 4. The original results of Grossfield et al were referenced to a vapor standard state of 1 atm. Therefore, the AMOEBA/OSRW single ion solvation results were corrected to account for the cost to compress an ideal gas to 1M, which is given by

Figure 3.

Convergence of the AMOEBA/OSRW ion solvation free energy simulations as a function of time.

Figure 4.

Ion solvation free energy as a function of the state variable.

$$T\mathrm{\Delta }S=-k_{\text{B}}Tln\left(\frac{V_{1\text{M}}}{V_{1\text{atm}}}\right)=-k_{B}Tln\left(\frac{1}{24.46}\right)=3.197\cdot k_{B}T$$ Equation 59

where k_B is the Boltzmann constant, T is absolute temperature and the resulting correction is 1.9 kcal/mol.

In Table 3, we compare the AMOEBA/OSRW ion solvation energies for K+, Na+ and Cl− to the original values for AMOEBA, OPLS-AA and CHARMM27 that were computed using FEP by Grossfield et al.⁹¹ In each case, the AMOEBA/OSRW result is approximately 1 kcal/mol more positive than the original calculation using FEP. This is partially explained by the lack of a softcore definition of ion-solvent van der Waals interactions in the original work, which is consistent with underestimating the cost to form a cavity. This effect cancels for the relative solvation free energy between K+ and Na+ such that OSRW and FEP agree to within 0.1 kcal/mol. For the whole salts, the original FEP solvation energies were too negative by approximately 0.5 kcal/mol, while our results with OSRW are too positive by 1.2–1.5 kcal/mol. However, the original conclusions of Grossfield et al are unchanged.

Table 3.

A comparison of AMOEBA ion solvation free energies using both FEP and OSRW protocols is presented. The AMOEBA/FEP, OPLS-AA and CHARMM27 results are taken from Grossfield et al.⁹¹ All values are in units of kcal/mol.

Method	Potassium	Sodium	K+ -> Na+	Chloride	KCl Salt	NaCl Salt
AMOEBA/OSRW	−71.7	−88.9	−17.2	−83.5	−155.3	−172.4
AMOEBA/FEP	−72.6	−89.9	−17.3	−84.6	−157.2	−174.5
OPLS-AA	−65.7	−83.9	−18.2	−85.3	−151.0	−169.2
CHARMM27	−70.3	−91.0	−20.7	−91.2	−161.5	−182.2
Schmid118	−69.3	−86.8	−17.5	−87.2	−156.5	−174.0
Friedman119	−80.8	−98.3	−17.5	−75.8	−156.6	−174.1
Tissandier120	−84.1	−101.3	−17.2	−72.7	−156.8	−174.0

B. Structure, Thermodynamics and Solubility of n-Alkylamides

1. Experimental n-Alkylamide Unit Cell Parameters, Solvation Free Energy and Standard State Solubility

In this work we limit ourselves to canonical ensemble crystal thermodynamics based on the experimentally determined space group and unit cell parameters for the n-alkylamides as shown in Table 4.^101,12–24 The space group for each n-alkylamide is P2₁/c,¹²¹ except for the rhombohedral structure of acetamide.¹⁰¹ For propanamide through octanamide, the length of a increases monotonically with chain length, while b and c are nearly constant.¹²¹ Atomic coordinates for acetamide,¹⁰¹ propanamide,¹²² butanamide,¹²⁴ and pentanamide¹²³ have been solved and deposited in the Cambridge Crystallography Database permitting comparisons with the lowest energy structures found during this work. Although experimental structures for hexanamide, heptanamide and octanamide are currently unknown, we present predictions below as an illustration that the current approach yields structural information in addition to thermodynamics.

Table 4.

Shown are the temperature (K), space group (SG), lattice lengths (Å) and angles (degrees), volume (ų), number of molecules per unit cell (Z) and volume per molecule (ų) for the n-alkylamide series. Although Turner and Lingafelter reported lattice lengths and angles for propanamide through octanamide at room temperature¹²¹, atomic coordinates were not determined. Later work by separate groups led to experimental structures for propanamide¹²², butanamide¹²⁴ and pentanamide.¹²³

n-alkylamide	Temp.	SG	a	b	C	α	β	γ	Vol.	Z	Vol./Z
Acetamide	298a	R3c	11.53	11.53	13.59	90	90.0	120	1563.4	18	86.9
Propanamide	298b	P21/c	8.97	5.78	9.76	90	113.5	90	464.1	4	116.0
	203c	P21/c	8.67	5.76	9.81	90	113.8	90	448.2	4	112.1
Butanamide	298b	P21/c	10.02	5.79	9.94	90	100.9	90	566.3	4	141.6
	150d	P21/c	9.81	5.92	9.70	90	112.1	90	522.6	4	130.7
Pentanamide	298b	P21/c	11.08	6.13	9.84	90	100.7	90	656.7	4	164.2
	150e	P21/c	11.06	5.83	9.79	90	103.5	90	613.8	4	153.5
Hexanamide	298b	P21/c	14.11	5.65	9.78	90	101.6	90	763.8	4	190.9
Heptanamide	298b	P21/c	15.29	5.65	9.90	90	105.0	90	826.1	4	206.5
Octanamide	298b	P21/c	17.39	5.69	9.78	90	91.9	90	967.2	4	241.8

^aDenne and Small¹⁰¹

^bTurner and Lingafelter¹²¹

^cUsanmaz and Alder¹²²

^dLewis and Tocher¹²⁴

^ePombeiro et al.¹²³

In addition to structural information, experimental values for the melting point¹²¹ and solubility¹²⁵ for n-alkylamides have been reported and are summarized in Table 5. Furthermore, the solvation free energy of acetamide (−9.68 kcal/mol) and propanamide (−9.38 kcal/mol) have been determined in the context of studying amino acid side-chain analogues.¹²⁶ We note that the melting points of acetamide and propanamide are lower by 20°K than those for the longer chain length n-alkylamides. Experimental solubility values for acetamide, butanamide, pentanamide and hexanamide are available from the Handbook of Aqueous Solubility Data,¹²⁵ although uncertainty estimates were not provided. Discrepancies between the saturating concentrations of acetamide from three sources suggest errors on the order of ~0.5 kcal/mol.¹²⁵

Table 5.

The experimental melting point,¹²¹ solubility,¹²⁵ volume entropy (ΔG_vol) for moving from a saturated concentration to a 1 M standard state concentration, experimental estimate for the excess free energy lost (ΔG_excess) moving from a saturated concentration to the 1 M standard state^127,128 and finally, the absolute standard state solubility free energy ( $\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}$) for the n-alkylamides through octanamide are given. The absolute standard state solubility is the sum of ΔG_vol and ΔG_excess. All free energy values are in units of kcal/mol. The experimental solubilities for propanamide, heptanamide and octanamide are currently not available.

n-Alkylamide	Melting Point (K)	Solubility (mg/ml)	ΔGvol	ΔGexcessa	$\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}$
Acetamide	352–354	705, 2000	−1.46, −2.08	1.9	0.44, −0.18
Propanamide	350–351
Butanamide	386–388	230	−0.57	0.3	−0.27
Pentanamide	378–379	80	0.14		0.14
Hexanamide	372–374	30	0.80		0.80
Heptanamide	368–369
Octanamide	378–379

^aExcess free energy values were estimated via multiplication of experimental molal saturating concentrations¹²⁸ by experimental pairwise free energy interaction coefficients (g_xx).¹²⁷ Higher order coefficients g_xxx and g_xxxx were neglected due to their uncertainty.¹²⁷

2. n-Alkylamide Solubility from Sublimation and Solvation Free Energies

The sublimation free energy for each n-alkylamide was calculated based on sampling the AMOEBA potential for organic molecules⁵³ using OSRW^56–58 by alchemically transforming a single molecule in vapor (λ = 0) into an infinite, perfectly symmetric crystal (λ = 1) via strict enforcement of space group symmetry⁶⁴ within the Force Field X program.^64,82,129 Each n-alkylamide molecule repeatedly sampled the minimum crystalline free energy basin (λ = 1) over the course of the simulation, as well as alternative conformations relatively higher in free energy. Each initial n-alkylamide conformation was a vacuum minima used for parameterization of the AMOEBA model in combination with an initial λ value of 0. Any reasonable starting confirmation produces identical thermodynamics once convergence has been reached. The sublimation simulations employed the parameters described above for ion solvation, with one notable difference. Unlike the ion and n-alkylamide solvation free energy calculations that used molecular dynamics, sublimation simulations used stochastic dynamics due to the small number of atoms being simulated.

Each n-alkylamide was fully flexible at all points in the simulation such that conformations or orientations that were not appropriate for the crystalline phase create a large force on the metadynamics particle favoring a return to vapor. Once in vapor, the molecule can easily change conformation and/or orientation. When a conformation is sampled in vapor that is consistent with the crystalline phase, a term in the force applied to the metadynamics particle (−∂U/∂λ) favors changing into condensed phase. Once in an energetically favorable crystalline state, the time dependent biasing potential builds up to allow the simulation to return to the vapor state. Before convergence is reached, each n-alkylamide sampled the correct crystalline conformation tens of times, in addition to exhaustively sampling torsional and rigid body degrees of freedom in vapor.

Based on the results shown in Table 6, the standard deviation for the sublimation free energy of each n-alkylamide averages only 0.25 kcal/mol after 100 nsec simulations for acetamide through hexanamide and 200 nsec simulations for heptanamide and octanamide. The sublimation free energies increase monotonically for propanamide through octanamide, which each share the P 2₁/c space group. The rhombohedral acetamide crystal is not expected to follow the trend of the larger n-alkylamides, since its crystal packing is substantially different from the others.

Table 6.

Shown are the n-alkylamide standard state sublimation free energy values $\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}$ (kcal/mol) based on the mean of 5 independent simulations along with their standard deviations (σ). A standard state volume correction ΔG_vol is added to the simulation result ΔG_sim to account for the increase in entropy due to moving from the volume occupied by the crystalline solid (see Table 4) into 1 M vapor concentration.

n-Alkylamide	Simulation					ΔGsim	ΔGvol	$\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}$	σ
	1	2	3	4	5
Acetamide	12.7	12.8	12.7	12.6	12.5	12.7	−1.8	10.9	0.1
Propanamide	10.1	10.1	10.0	9.8	10.2	10.1	−1.6	8.5	0.2
Butanamide	11.8	12.2	11.8	12.1	11.9	12.0	−1.5	10.5	0.2
Pentanamide	12.5	12.6	12.8	12.3	12.8	12.6	−1.4	11.2	0.2
Hexanamide	13.5	13.1	13.1	13.4	13.4	13.3	−1.3	12.0	0.2
Heptanamide	14.9	13.6	14.6	14.5	13.6	14.2	−1.3	13.0	0.6
Octanamide	15.3	15.5	16.1	15.4	15.2	15.5	−1.2	14.4	0.4

The standard state solvation free energies for each n-alkylamides are given in Table 7 and were calculated based on 5 nsec simulations with the AMOEBA model for water^80,90 and organic molecules.⁵³ The OSRW^56–58 sampling method was used to alchemically solvate a single molecule in vapor (λ = 0) into a cubic box of water (λ = 1) using the Force Field X program. The simulation system was equilibrated with 500 waters within a cubic box of 24.662 Å. All other simulation parameters were changed from those reported for ion solvation. As for the sublimation free energy simulations, the initial conformation of each n-alkylamides was a vacuum energy minimum used for parameterization in tandem with an initial λ value of 0. The calculated standard state solvation free energies of acetamide and propanamide of −10.3 and −8.3 kcal/mol, respectively, agree with experiment to within 0.8 kcal/mol on average. We note that mean standard deviation for the solvation free energies of 0.3 kcal/mol is comparable to that for the sublimation free energies.

Table 7.

Shown are the n-alkylamide standard state solvation free energies $\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$ (kcal/mol) based on the mean of 5 independent simulations, along with their standard deviations (σ).

n-Alkylamide	Simulation					$\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$	σ
	1	2	3	4	5
Acetamide	−10.2	−10.2	−10.5	−10.4	−10.3	−10.3	0.1
Propanamide	−8.6	−8.4	−8.2	−8.0	−8.4	−8.3	0.2
Butanamide	−10.8	−10.9	−10.1	−10.3	−10.4	−10.5	0.3
Pentanamide	−9.8	−9.6	−9.3	−9.9	−9.9	−9.7	0.2
Hexanamide	−9.4	−9.1	−9.4	−9.6	−9.5	−9.4	0.2
Heptanamide	−9.6	−9.3	−9.6	−10.2	−8.9	−9.5	0.5
Octanamide	−10.1	−8.7	−9.4	−9.2	−9.6	−9.4	0.5

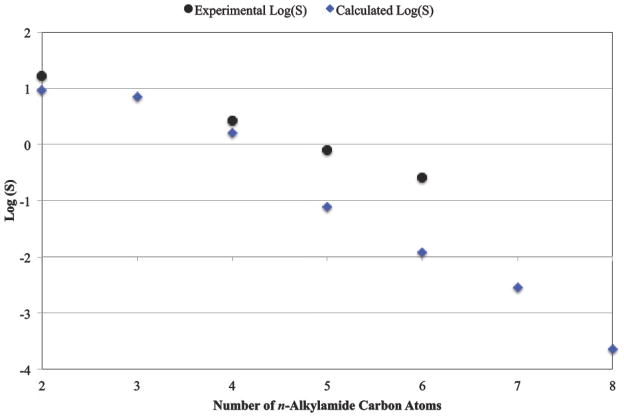
From the thermodynamic cycle depicted in Figure 1, summing the sublimation free energies given in Table 6 with the solvation free energies given in Table 7 yields the standard state solubility free energies as reported in Table 8. For acetamide through butanamide, the standard state sublimation and solvation free energy values nearly cancel, which yields absolute standard state solubility free energy values near zero. For the n-alkylamides from pentanamide through octanamide, the combined trends of increasingly stable crystals coupled with decreasingly favorable solvation due to the hydrophobic effect leads to increasingly lower solubility, as shown in Figure 5. The reason for the relatively lower solubility predicted for hexanamide by our method remains unclear. Until further studies can be completed, possible explanations include experimental uncertainty, force field accuracy or undetected sampling difficulties for the larger molecules.

Table 8.

Shown are the calculated and experimental absolute standard state solubility free energies $\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}$ for the n-alkylamides from acetamide to octanamide (kcal/mol) based on summing $\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}$ and $\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$. The

n-Alkylamide	$\mathrm{\Delta }{\text{G}}_{\text{sub}}^{\text{o}}$	$\mathrm{\Delta }{\text{G}}_{\text{solv}}^{\text{o}}$	$\mathrm{\Delta }{\text{G}}_{\text{solubility}}^{\text{o}}$			Log (S)a
			Calc.	Expt.	Error	Calc.	Expt.	Error
Acetamide	10.9	−10.3	0.6	−0.18	0.8	1.0	1.2	0.3
Propanamide	8.5	−8.3	0.1			0.9
Butanamide	10.5	−10.5	0.0	−0.27	0.3	0.2	0.4	0.2
Pentanamide	11.2	−9.7	1.5	0.14	1.4	−1.1	−0.1	1.0
Hexanamide	12.0	−9.4	2.6	0.80	1.8	−1.9	−0.6	1.3
Heptanamide	13.0	−9.5	3.5			−2.6
Octanamide	14.4	−9.4	5.0			−3.6
Mean					1.1			0.7

^aSolubility (S) in units of mol/L is calculated from $S=exp[(-\mathrm{\Delta }{G}_{\text{solubility}}^{\text{o}}+\mathrm{\Delta }{\text{G}}_{\text{excess}})/{\text{k}}_{\text{B}}T]$ where ΔG_excess was given in Table 5, k_B is the Boltzmann constant and T is temperature (298°K).

Figure 5.

Shown are experimental and calculated Log(S) values for the n-alkylamides (S has units of mol/L) from acetamide to octanamide. There is a monotonic trend in both the experimental and calculated values toward lower solubility with each additional CH₂ group due to increasingly favorable deposition and to a lesser extent from unfavorable solvation.

3. n-Alkylamide Crystal Structures

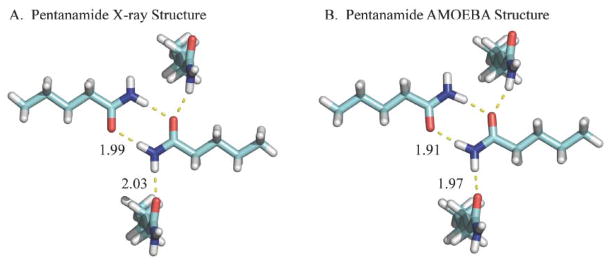
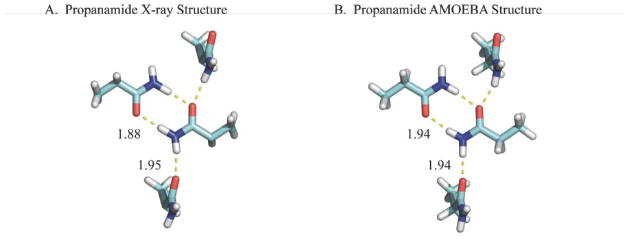
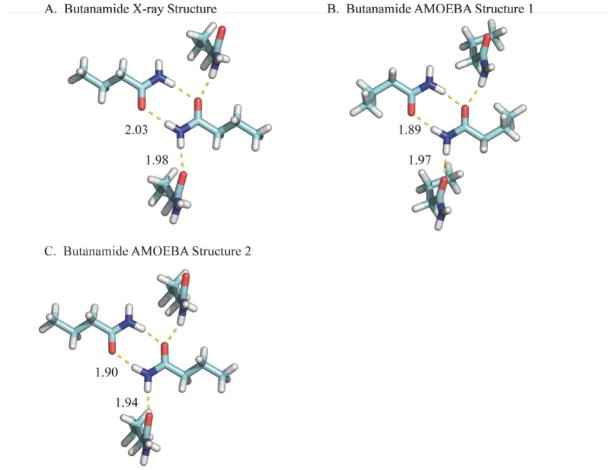
As the OSRW procedure initially approaches the crystalline state (i.e. as λ approaches 1), conformations that are sampled will likely be in the free energy minimum region. However, there may exist hidden free energy barriers that promote sampling of conformations whose ∂U/∂λ values are inconsistent with the free energy minimum. In either case, the OSRW procedure will build up repulsive Gaussian potentials that drive ∂U/∂λ toward a random walk and thereby accelerate convergence of crystalline conformations. As a validation of the OSRW sampling procedure and the AMOEBA force field, samples were saved every 0.1 nsec that were subsequently completely optimized. The lowest potential energy structures for acetamide through pentanamide are shown in Figures 6–9, respectively. Except in the case of butanamide, the structure of the AMOEBA potential energy minimum agrees with the experimental X-ray structure. However, the AMOEBA models are more accurate with regards to the placement of hydrogen atoms, which results from limitations in the isolated atom scattering model (IAM) used in many X-ray structure refinement programs.¹³⁰

Figure 6.

The conformations of the acetamide X-ray structure (ACEMID01¹⁰¹) and lowest potential energy structure sampled by AMOEBA/OSRW agree.

Figure 9.

The conformations of the pentanamide X-ray structure (ZZZKJQ01¹²³) and the lowest potential energy structure sampled by AMOEBA/OSRW agree.

DISCUSSION

A. AMOEBA Transferability Between Vacuum, Liquid and Solid Phases

An important motivation for developing polarizable force fields is to improve transferability between vacuum, liquid and solid phases and between environments with vastly different dielectric constants. ^52,68,72 The inherent dependence of solubility on the equilibrium between a molecule in a solid crystalline phase and solvated in a liquid phase provides a test of the transferability of the AMOEBA force field.^53,80 The mean signed error between the experimental and calculated absolute standard state solubility values for the n-alkylamides of 1.1 kcal/mol (Table 8) is a promising first step toward the prediction of solubility from first principles to chemical accuracy.

B. Efficient Computation of Free Energies via OSRW

Advancements in potential energy functions require further work to integrate them with existing alchemical free energy methods such as thermodynamic integration, meta-dynamics^55,131 and OSRW.^56–58 In this work, we have presented derivatives of the AMOEBA potential that are required for OSRW, which include ∂U(λ, X)/∂λ, ∂U²(λ, X)/∂λ² and ∂U²(λ, X)/∂X∂λ. In particular, our approach includes softcore modifications to the buffered 14-7 van der Waals term and to the real space portion of Ewald summation in order to facilitate a smooth transition between full strength intermolecular interactions and non-interacting. As demonstrated, an approach that allows simultaneous sampling of the λ and ∂U(λ, X)/∂λ spaces is very effective for sampling the rough free energy landscape of the deposition/sublimation phase transition.

C. Deposition/Sublimation Phase Transitions in Force Field X

To the best of our knowledge, Force Field X^64,82,129 is the first and only implementation of an algorithm that permits calculation of the free energy of the deposition/sublimation phase transition from first principles. This requires two layers of complexity beyond the implementation of AMOEBA in other widely used computer codes such as TINKER,⁶⁷ OpenMM¹³² and Amber.⁶⁵ First, explicit support for space group symmetry and replicates of the unit cell is necessary,⁶⁴ otherwise the complete annihilation of the crystalline phase becomes untenable. Consider the case of acetamide, which includes 18 copies of the molecule (i.e. the asymmetric unit) within the unit cell and 144 copies within a replicated super cell large enough to allow application of the minimum image convention. The 1 or 2 orders of magnitude increase in the degrees of freedom not only increases the cost of a single energy and gradient evaluation, but also exponentially increases the complexity of the crystalline free energy surface. Second, the crystalline annihilation algorithm in Force Field X depends on a meta-dynamics sampling algorithm in order to escape the large crystalline free energy barriers. Therefore, derivatives of the polarizable multipole AMOEBA potential energy function such as ∂U(λ, X)/∂λ, ∂²U(λ, X)/∂λ² and ∂²U(λ, X)/∂X∂λ have been implemented not only for P1 unit cells, but also for the asymmetric unit of each of the 230 space groups.

Figure 7.

The heavy atom positions of the propanamide X-ray structure (ZZZKAY01¹²²) and lowest potential energy structure sampled by AMOEBA/OSRW agree, although a hydrogen from the central carbon atom was not included in the experimental model.

Figure 8.

The conformations of the butanamide X-ray structure (ZZZKDQ01¹²⁴) and the 2^nd lowest potential energy structure sampled by AMOEBA/OSRW agree (Structure 2). The lowest AMOEBA potential energy structure (Structure 1) exhibits a gauche conformation across the penultimate C-C bond and is lower in energy than the all trans conformation by ~0.4 kcal/mol.

Figure 10.

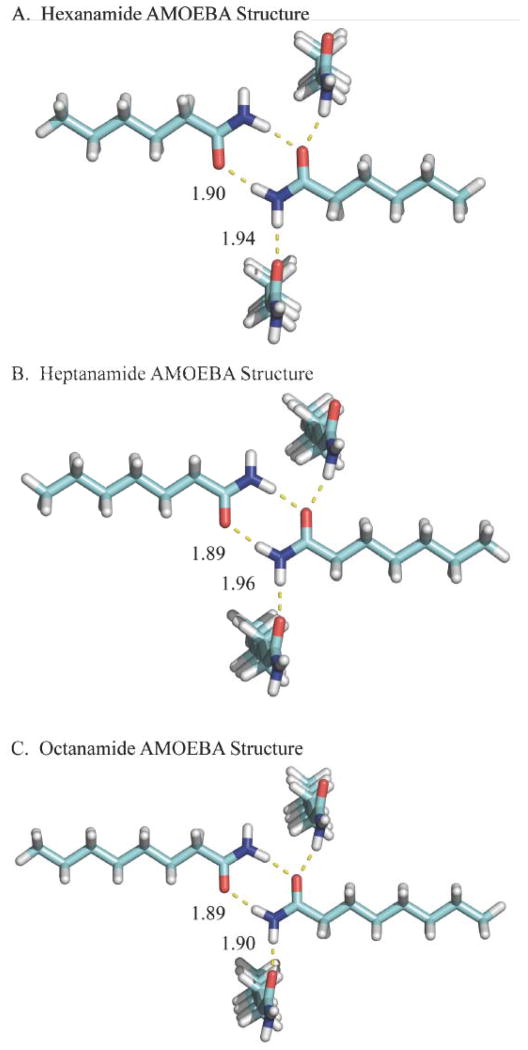
Shown are the lowest potential energy structures for hexanamide, heptanamide and octanamide that were determined via AMOEBA/OSRW sampling, although experimental structures are not yet available for comparison. The two hydrogen-bonds between a single pair of amides is consistent with the shorter chain experimental structures. In addition, all C-C bonds are in a trans conformation.