A Three-Dimensional Computational Fluid Dynamics Model of Regurgitant Mitral Valve Flow: Validation Against in vitro Standards and 3D Color Doppler Methods

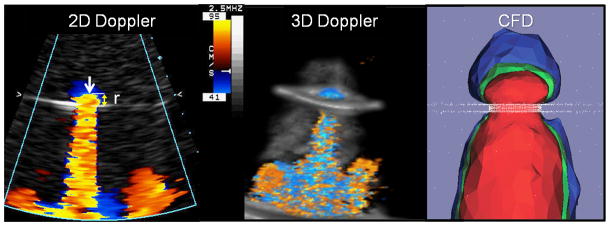
Introduction

Mitral valve regurgitation (MR) can lead to atrial arrhythmias, pulmonary artery hypertension, congestive heart failure and death. The decision to proceed with surgical valve repair or replacement is based on an assessment of symptoms and valve regurgitation severity. The primary tool to assess the severity of MR is echocardiography. The accurate and reproducible assessment of regurgitant volume using echocardiography is an ongoing challenge. [1–6]

The proximal isovelocity surface area (PISA) of a regurgitant color Doppler jet has been a useful tool in the estimation of valvular insufficiency. PISA is based on the hemodynamic principle that flow accelerates as it approaches the regurgitant orifice. If the orifice is circular, the approaching isovelocity surfaces are assumed to be hemispheres whose radius becomes smaller as the flow approaches the orifice. For an incompressible fluid, the flow through each isovelocity surface is equal to the outflow through the orifice. The 2D PISA method is used to measure regurgitant volume (RV) in the following way;

$$RV\approx \mathit{EROA}\underset{T_i^r}{\overset{T_f^r}{\int }}{V}_{CW}dt=\mathit{EROA}·\mathit{TVI}$$ (Eqn 1)

where TVI is the total velocity integral (i.e., the time integral of the component of the velocity aligned with the Continuous Wave Doppler transducer beam V_CW over the interval [ $T_i^r,T_f^r$] in which regurgitation is observed), and EROA is the effective regurgitant orifice area. The effective regurgitant orifice area approximates the actual orifice area via a calculation which is based on the conservation of mass principle coupled with the assumption that the isovelocity surfaces in the flow convergence zone form hemispheres. More precisely,

$$\mathit{EROA}=\frac{2\pi r^2{\text{V}}_{\text{a}}}{{\text{V}}_{\text{MR}}}$$ (Eqn 2)

where r is the radius of the isovelocity surface corresponding to the Nyquist aliasing velocity V_a while V_MR is the peak mitral regurgitation velocity through the orifice. [3] Thus, the main feature of 2D color Doppler single-radius hemispherical formula is the assumption that the isovelocity surfaces form a hemisphere where only one radius, r, is necessary for the calculation of the surface area, as shown in equation (2). However when applied in patients, the regurgitant mitral orifice is often not circular and the approaching isovelocities not hemispheric. Thus the assumption of this single-radius hemispherical formula has been shown to under-estimate regurgitant volume and EROA when this simplified formula is applied clinically for the evaluation of MR severity. [7–12] Recently developed 3D color Doppler imaging methods can be used to directly visualize the PISA shape and may obviate the need for some of these geometric assumptions. Using a 3D color Doppler data set, radial planes of the largest PISA zone can be traced and the total isovelocity surface area reconstructed. [9] As such, 3D color Doppler methods can be used to directly measure an isovelocity surface area without an erroneous assumption of the isovelocity shape. In vitro and clinical studies have demonstrated that estimates of the regurgitant volume from such a 3D color Doppler approach may be more accurate than the 2D PISA method. [9]

Another recently proposed method to quantify MR is based on measurement of the diameter or area of the regurgitant jet at its narrowest point just distal to the regurgitant orifice. Clinically this narrow jet region, known as the vena contracta (VC), is relatively independent of the regurgitant flow rate and largely dependent on the size of the regurgitant valve orifice. [5;13–15] The severity of MR can be estimated using 2D color Doppler to evaluate VC diameter [15] or 3D color Doppler to evaluate VC area. [5;16] Again, recent studies have demonstrated the advantage of the 3D method when flow conditions are complex and the regurgitant orifice shape irregular. [5;17;18]

As the clinical application of these 3D color Doppler techniques continue to evolve, it is important to develop complementary models to help better understand these complex intra-cardiac flow events. The objectives of this investigation were to: (1) Simulate simple pulsatile flow conditions of MR and validate a CFD model against in vitro measurements of transvalvular pressure and flow; (2) compare this model against 2D color Doppler estimates of regurgitant flow, and; (3) demonstrate how a CFD model can be used to support the use of novel imaging tools such as the 3D PISA and the 3D VC area methods for the quantification of MR severity.

Methods

Flow Loop

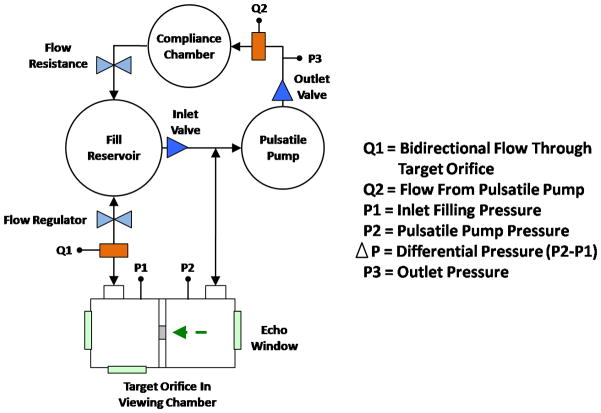
We developed a CFD model to simulate hemodynamics conditions in patients with MR. To validate this model we employed a circulatory flow loop and imaging chamber developed at the Methodist DeBakey Heart & Vascular Center. [19] In brief, the pulsatile flow loop was designed to achieve up to 7 L/min forward flow. To mimic blood viscosity (4 cP) the circulatory fluid was 30% glycerin, 70% water, with 1% corn starch added as ultrasound scattering particles. Total flow rate was assessed using an ultrasonic flow meter (Transonic Systems, Ithaca, NY, USA). Using constant pump volume displacement and frequency, flow volume tailored to experimental need was directed into the regurgitant limb by increasing downstream resistance within the circulatory loop. Regurgitant volume per cardiac cycle was estimated by dividing the flow rate reading from the flow meter (ml/min) by the stroke frequency per minute. The regurgitant loop incorporated an imaging chamber composed of two acrylic cylinders partitioned by a divider plate containing a geometric orifice (Figure 1). High fidelity pressure transducers (Merit Medical, South Jordan, UT, USA) were positioned on either side of the divider plate to record peak chamber pressure and the transorifice pressure difference. Inflow and outflow pressure, were measured for two orifices differing in size and shape: 0.4 cm² circle and 0.35 cm² rectangle (2.2 cm × 0.16 cm). Each orifice was evaluated at a flow rate consistent with moderate MR (30ml/beat) and severe MR (70ml/beat).

Figure 1.

Flow loop schematic. Broken arrow indicates primary flow direction as well as the Doppler imaging perspective.

Imaging

Incorporated into the imaging chamber were ultrasound windows at standard cardiac anatomic position and distance to the flow orifice, mimicking the apical and parasternal clinical imaging windows. A 2D spectral Doppler transducer (2 to 4 MHz,) and hand-held 3D-Color Doppler transducer (X4, Sonos 7500, Philips Medical Systems, Andover, MA) were used to assess trans-orifice flow from an apical equivalent view parallel to regurgitant flow and from a parasternal equivalent view perpendicular to flow. A 3D color Doppler data set was created by rapidly stitching together sub-volumes acquired over 7 sequential beats. Color Doppler scan depth, beam focus, and gain settings were optimized to distinguish the proximal flow convergence zone, the vena contracta and a rapidly expanding jet. Doppler and CFD measures were taken at the midpoint of the ejection phase (mid-systole). The 3D color Doppler method for the calculation of PISA requires manual tracing of equidistant radial planes (of equal velocity) through the flow convergence zone. [9] A computer program specifically developed for 3D-PISA reconstruction and surface area determination (TomTec Imaging, Germany) was employed to calculate the isovelocity surface areas as previously reported. [9] Hemodynamics conditions in the imaging chamber were simulated using our CFD model.

CFD Model

The CFD model was based on solving the Navier-Stokes equations for an incompressible, viscous fluid using a Finite Element Method approach developed at CIMNE UPC-Barcelona, and implemented in a multiphysics software ZEPHYR. ZEPHYR was developed for academic use: the source code can be accessed and modified for a particular application under consideration. Versions of this software have been used and validated in several engineering applications ranging from foam casting [20] to the simulation of flow in rotary pumps [21]. In this manuscript, for the first time, this software has been customized for a biomedical application. In the present work, the Navier-Stokes equations were solved on a fixed computational domain shown in Figure 2. Space discretization of the computational domain in this work was achieved using a mesh of tetrahedra. We implemented unstructured (non-uniform) meshes in order to capture the fine flow structures in different parts of the domain. Meshes with different level of refinement were tested. In particular, the following three sets of meshes showed the relative L¹-error to be within the 2% range:

Figure 2.

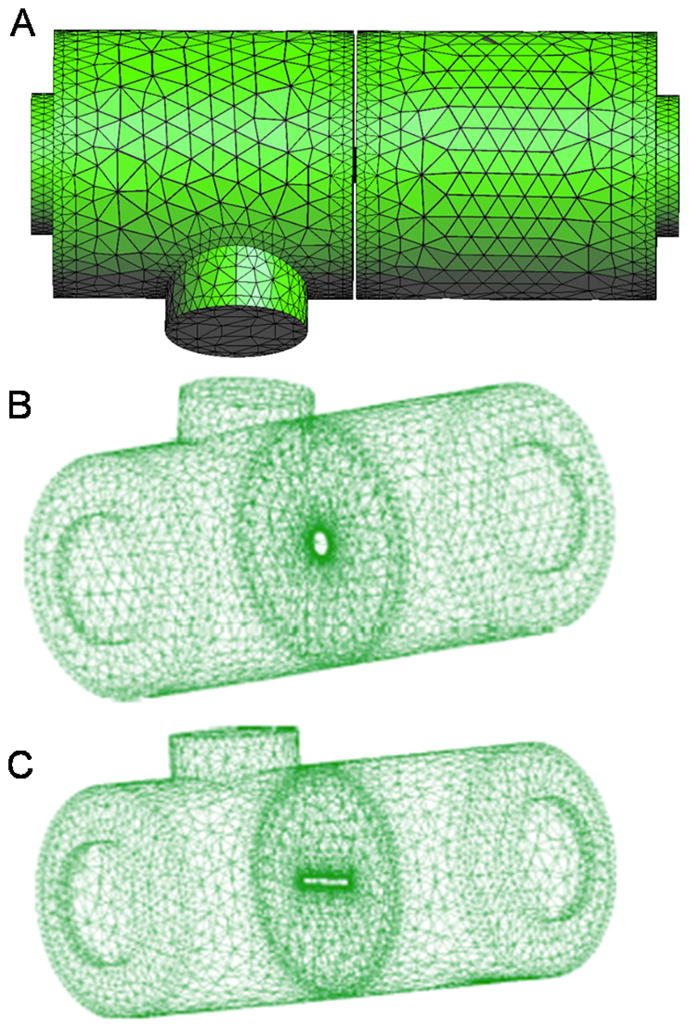
Computational geometry for the CFD simulations. A) A coarse version of actual meshes is shown. B) Geometry with circular orifice. C) Geometry with rectangular orifice. Unstructured (non-uniform) meshes were used in all the simulations to capture the fine flow structures of flow in complex geometries.

1. 46116 tetrahedra with 10325 nodes (corresponding to the mesh diameter h = 0.6 cm away from the orifice, and h = 0.03 cm near the orifice)

2. 63967 tetrahedra with 16074 nodes (corresponding to the mesh diameter h = 0.3 cm away from the orifice, and h = 0.03 cm near the orifice)

3. 67728 tetrahedra with 16978 nodes (corresponding to the mesh diameter h = 0.3 cm away from the orifice, and h = 0.015 cm near the orifice).

The results presented in this manuscript correspond to those obtained using the most refined mesh, namely that one described in (3) above. The corresponding time step (which was also tested for different values until the difference in the relative L¹ norm was within 2%) is equal to 10⁻³. Both global and local L¹ errors were tested for velocity and pressure. Figure 2 shows examples of boundary meshes used in the simulation. To approximate the Navier-Stokes equations for an incompressible viscous fluid we chose stabilized P1–P1 finite elements. Convergence and accuracy of the method were previously tested [22], [23] providing a stable and convergent method which is 1st-order accurate in time and 1st-order accurate in space with respect to the H¹-norm, but 2nd-order accurate in space with respect to the L²-norm. The values of the density and viscosity parameters in the Navier-Stokes equations were determined from the measurements mentioned above. To simulate the flow conditions in the chamber, we imposed the time-dependent normal stress inlet and outlet boundary conditions. The values of the time-dependent normal stress data were chosen in such a way as to recover (within some reasonable accuracy) the measured pressure at two points inside the inlet and outlet chamber (as a function of time), the variations of the pressure gradient at the orifice as a function of time, and the peak velocity at the orifice as a function of time. This is in line of other works currently available in the literature where physiologically reasonable (but not physiological) boundary conditions were prescribed (e.g., pulsatile pressure was prescribed in [24] to recover Re=900 and St=0.3; sinusoidal in time stress condition was used in [25]; steady parabolic velocity profile in [26]; sinusoidal in time velocity [27–30]; non-pulsatile characteristic based boundary conditions in [31]; steady fully developed turbulent velocity in pipe flow [32–35]; and piecewise constant in time pressure [36]). The Reynolds number based on the velocity at the orifice at peak systole (i.e., the highest velocity over one cycle) was around Re = 5000 for the circular orifice and around Re = 2400 for the rectangular orifice, while the Reynolds number based on the root mean square of the velocity at the orifice was around Re = 3100 for the circular orifice and around Re = 1800 for the rectangular orifice. These Reynolds numbers were computed based on the (local) flow conditions at the orifice; more precisely, Re = RV/ν where R is the characteristic dimension of the orifice (i.e., the hydraulic diameter), V is the magnitude of the fluid velocity at the orifice and ν is the kinematic viscosity of the fluid. This flow regime has been studied in literature by direct simulations (see e.g., [24;30;36–39]), and by turbulence models (see e.g., [32;33;35;40]. During the experiments, no chaotic behavior in the pressure or the velocity was observed to obligate the use of turbulence models. The CDF method developed in the present work uses direct simulations, which have been validated on the classical benchmark problem of Lid-Driven Cavity Flow [41–44], for which Hopf bifuraction was recovered for a Reynolds number between 8000 and 8100 [45].

Results

CFD Simulations of Pressure, Velocity and Flow rate

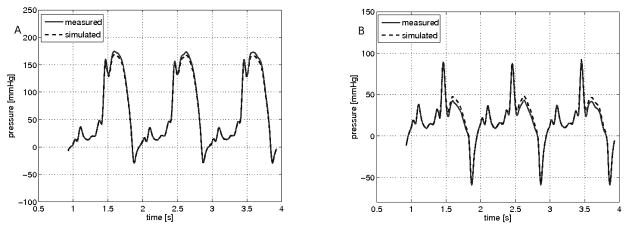
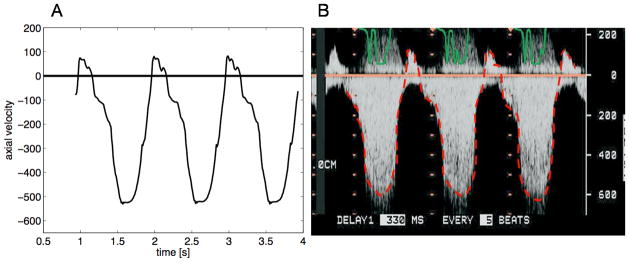
Initial assessment of the CFD simulation was focused on an accurate evaluation the “hemodynamic” conditions typical of clinical MR including pressure gradient, flow velocity and flow rate. Figure 3 shows a comparison between measured and CFD simulated pressures for both the inflow and outflow chambers. Of note, the pressure manometers were each located at mid-chamber, approximately 3cm away from the location of the fluid inlet and outlet where the normal stress data were prescribed. The comparative results for each orifice and flow rate are summarized in Table 1. Overall the value for the peak transorifice pressure gradient compared favorably between the mean measured value (90 mmHg) and the mean modeled value (85 mmHg); difference 10.4%. Measurement of the velocity across the circular orifice was also compared to the velocity calculated using CFD simulations. Velocity (in cm/s) was measured using continuous wave spectral Doppler. Figure 4(b) shows the results of the measurements, while Figure 4(a) shows the CFD modeled velocity. The graph in Figure 4(a) was flipped across the horizontal axis to capture the velocity direction with respect to the position of the ultrasonic probe. Figure 5 shows the CFD calculated flow rate resembling the velocity waveform shown in Figure 4b.

Figure 3.

Simulated and measured hemodynamic conditions through a circular orifice: A) depicts the pressure at the inlet chamber. B) depicts the pressure at the outlet chamber. The measured pressure (solid red line) and CFD simulated pressure (dashed blue line) are shown over three cycles.

Table 1.

Comparison between measured and CFD simulated peak pressure gradient and peak velocity at the orifice for two orifice shapes (circular and rectangular) and for two flow conditions.

	Peak Δp			Peak Velocity
	Measured (mmHg)	CFD Simulated (mmHg)	% Difference	Measured (cm/s)	CFD Simulated (cm/s)	% Difference
Circular Orifice
30 ml	40	43.8	9.5	317	332	4.7
70 ml	129	123	4.6	567	539	4.9
Rectangular Orifice
30 ml	52	43.8	15.7	359	332	7.5
70 ml	140	128	8.6	591	562	4.9
Combined Mean	90	85	10.4	459	442	5.7

Figure 4.

Comparison of trans-orifice velocity predicted by the computational model and recorded by continuous wave spectral Doppler. CFD model (A) shows the a very similar velocity profile to the Doppler recording (B) across a circular orifice at 70ml/beat. Positive velocity is shown as a negative deflection due to the typical top-to-bottom scan orientation of the ultrasound probe.

Figure 5.

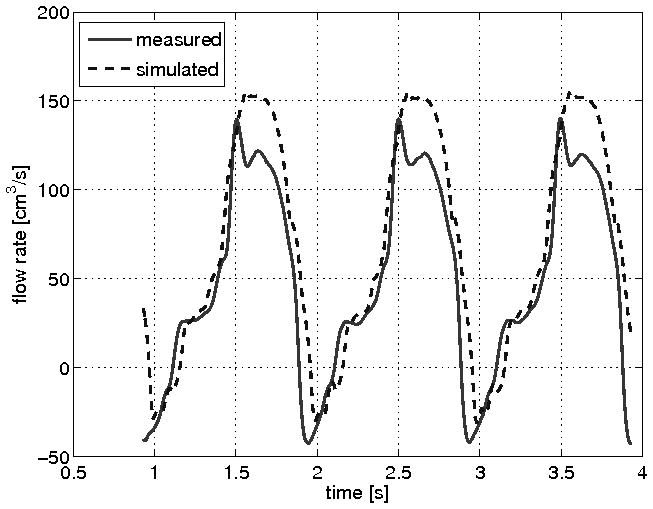
Comparison of flow rate across a circular orifice. CFD simulation of flow (dashed blue line) compares well with flow measured immediately downstream from the imaging chamber (solid red line).

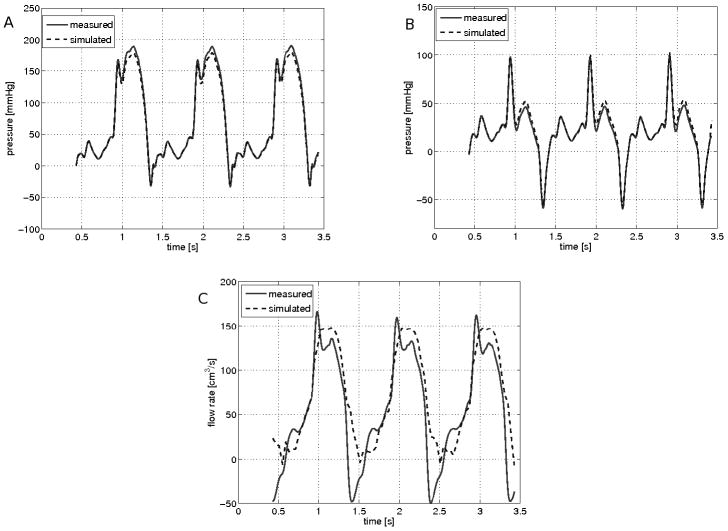
These comparisons were repeated using a rectangular flow orifice (Table 1). Figure 6 shows the corresponding comparisons. As shown in table 1, the % difference between measured and modeled peak velocity was small irrespective of the flow rate, or orifice geometry or size. Overall the mean measured trans-orifice velocity of 459 cm/s compared favorably to the modeled velocity of 441 cm/s; mean difference 5.7%.

Figure 6.

Simulated and measured hemodynamic conditions through a rectangular orifice: A) depicts the pressure at the inlet chamber. B) depicts the pressure at the outlet chamber. The measured pressure (solid red line) and CFD simulated pressure (dashed blue line) are shown over three cycles. C) Comparison of measured and simulated flow rate.

CFD Simulations of Proximal Flow Events

In addition to assessing the CFD simulation of MR hemodynamics, the ability of the model to simulate the proximal MR flow events was also tested. Specifically, the classical 2D PISA method, and 3D PISA surface reconstruction and area calculation, and 3D color Doppler measure of vena contracta area were compared to CFD simulations of these events.

A display of the computed velocity within the imaging chamber is shown in figure 7. In this 2D projection of the 3D CFD simulation, the pulsatile flow moves from left to right (as from ventricle to atria) across a central circular orifice representing a regurgitant mitral valve. The colors indicate the magnitude of the axial component of the velocity in cm/s. In figure 8, streamlines were used to depict the converging flow. On the left of the orifice the flow convergence zone is shown where blue streamlines transition into green (faster flow) as the flow velocity increases approaching the orifice. Downstream from the orifice one can observe the symmetric jet with a high velocity core depicted in red. The streamlines are colored based on the magnitude of the velocity with the same coloring scale as that in Figure 7. A slight convergence of the streamlines can be observed just downstream from the orifice. The point at which the diameter of the convergence of the streamlines is smallest, corresponding to the vena contracta, is depicted with a dark line. The corresponding 3D color Doppler view of flow demonstrating a discrete converging isovelocity hemisphere and vena contracta is shown in Figure 8(b). A study of the in vitro and clinical application of 3D vena contracta area has recently been reported by our group. [5]

Figure 7.

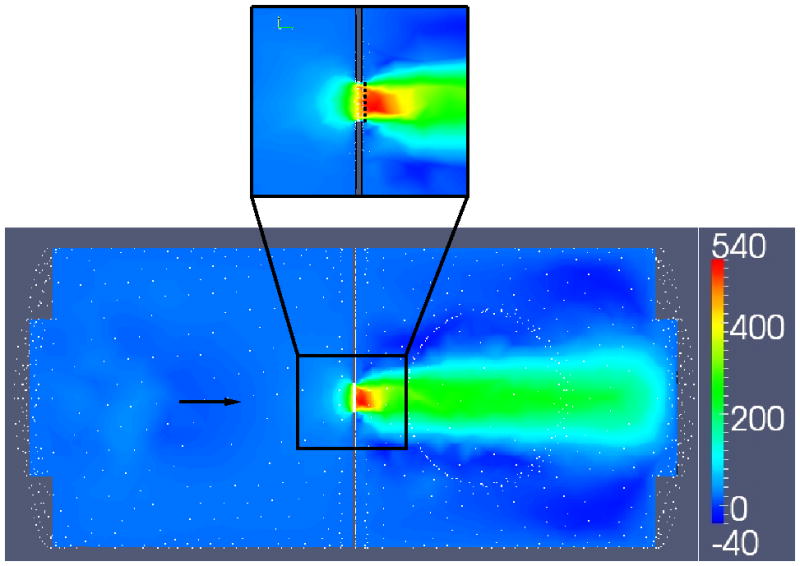
Display of computational flow velocities within the imaging chamber. Colors indicate the magnitude of the axial component of the velocity in cm/s. A) depicts the entire flow chamber. B) Shows a magnified view near the orifice with a dotted white line indicating the vena contracta. The black arrows indicates flow direction, from left to right.

Figure 8.

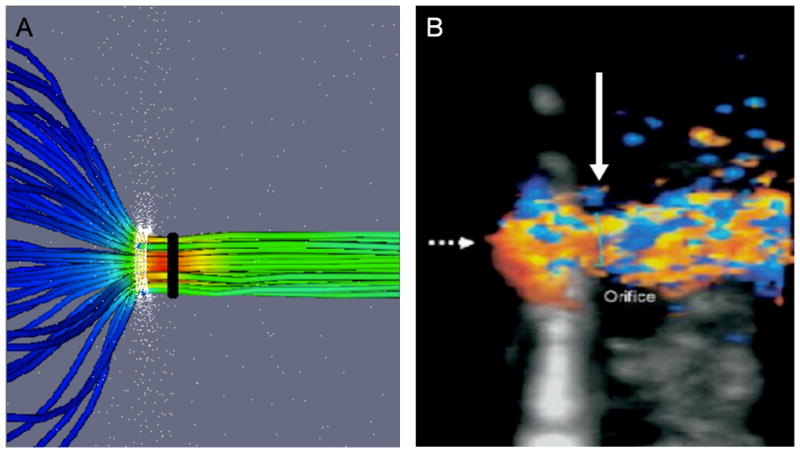
A comparison of flow convergence and vena contracta, as depicted by CFD modeling and 3D color Doppler. A) CFD depicts converging upstream streamlines and the distal vena contracta region. The orifice is circular (white band) and the vena contracta diameter (black) is shown. B) 3D Color Doppler (orthogonal long-axis view with US probe at top) demonstrating a converging isovelocity “hemisphere” (broken arrow) and vena contracta (solid white arrow). This standard clinical view is optimal for VC imaging (maximal axial resolution) but suboptimal for flow convergence imaging (large Doppler angle, ~ 90°).

The vena contracta area obtained using our CFD simulations and was compared to the actual orifice area (OA) and the VC area by 3D color Doppler. The comparisons were performed for two orifice shapes (circular orifice area=0.39 cm²; and rectangular orifice area 0.35cm²) and for two flow conditions (RV=30ml/beat and RV=70ml/beat). The results are presented in Table 2. For all conditions tested the 3D color Doppler VC measure slightly over-estimates the orifice area (3–14% relative difference), while the CFD VC measure slightly underestimates the orifice area (8–9% relative difference). Both CFD and 3D CD VC area measures demonstrated larger % difference for the rectangular orifice.

Table 2.

Comparison of computational and Doppler assessment of the proximal flow events. Simulation and measurement of the 3D PISA and VC area for a circular (0.39cm²) and rectangular (0.35cm²) orifice under different flow conditions. CFD PISA is compared to direct measurement of 3D color Doppler surface area at defined aliasing velocities. CFD simulated and 3D color Doppler VC area were compared to the actual orifice area (OA), since known. Vena Contracta, VC. Proximal Isovelocity Surface Area, PISA. Aliasing velocity, V_a (cm/s)

	PISA			VC AREA
	3D color Doppler	CFD Simulation	Relative Difference	3D color Doppler	rel. diff. with OA	CFD Simulation	rel. diff. with OA
Circular Orifice
30 ml	2.0cm2(Va=36)	2.4cm2(Va=36)	20%	0.40cm2	3%	0.36cm2	8%
70 ml	3.0cm2(Va=41)	3.7cm2(Va=41)	23%	0.40cm2	3%	0.36cm2	8%
Rectangular Orifice
30 ml	2.7cm2(Va=36)	2.9cm2(Va=36)	7%	0.40cm2	14%	0.32cm2	9%
70 ml	3.7cm2(Va=36)	4.1cm2(Va=36)	11%	0.40cm2	14%	0.32cm2	9%
Combined Mean			15.3%				8.5%

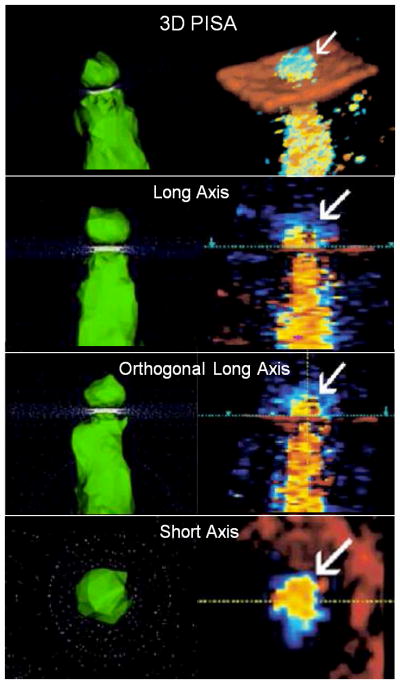
CFD simulations of the proximal isovelocity surfaces were compared to 2D color Doppler and 3D color Doppler measurements of the same event. An example of what is typically seen by an echocardiographic observer is shown in Figure 9. In this figure, a 2D color Doppler recording of flow through a circular orifice is shown, with flow direction from top to bottom. The curve determined by the color change between orange and dark blue corresponds to the location of the proximal isovelocity surface for a chosen Nyquist aliasing velocity (41 cm/s in this figure). This curve is denoted by the white arrow showing the PISA surface. The PISA surface radius is then determined manually. The PISA radius, corresponding to the radius r in equation (2), is shown. Also shown is a 3D Color Doppler acquisition under the same flow conditions and 3D CFD simulations of a long axis slice through the 3D proximal isovelocity surfaces corresponding to V_a = 20 cm/s (blue), V_a = 40 cm/s (green), and V_a = 60 cm/s (red), is shown for circular orifice. These 3D CFD simulations of the proximal isovelocity surfaces were compared to 3D color Doppler recording of the same flow conditions (figure 10).

Figure 9.

Doppler and Simulated Proximal Isovelocity Surface Area (PISA). Images from the in vitro flow loop simulating regurgitation from top to bottom through a circular orifice. The 2D color Doppler in the first panel shows a hemispheric isovelocity at 41cm/s with a defined radius (r). Middle panel shows a 3D color Doppler acquisition of the same flow condition. The last panel depicts the 3D computational domain showing 3 isovelocity surfaces near a circular orifice for V_a = 20 cm/s (blue), V_a = 40 cm/s (green) and V_a = 60 cm/s (red).

Figure 10.

A comparison of computational and Doppler 3D PISA images. Computational images (left) and 3D color Doppler images (right) of pulsatile flow through a simple circular orifice. The hemispheric geometry of the converging isovelocity is demonstrated by both methods. Flow direction is top to bottom. Each method is depicted in long axis, orthogonal long-axis (90° rotation) and short-axis views.

To quantitatively assess the 3D CFD simulation of the PISA surface we calculated the proximal isovelocity surface areas for circular and rectangular orifice shapes and for the flow conditions corresponding to the regurgitation of 30 ml/beat and 70 ml/beat, and compared those values with the 3D color Doppler-based calculation of proximal isovelocity surface area (Table 2). Regurgitant volume or the derived effective orifice area was not compared between CFD and 3D color Doppler methods since these were input functions for the CFD model. We report a comparison of the isovelocity surface area at a given aliasing velocity since that was an uncontrolled parameter for both methods. The resulting area measures were compared with the numerically calculate PISA of the 3D CFD model. The results are presented in Table 2 show the difference between the two ranging between 7% and 23%.

The 3D CFD model of the PISA surfaces for two orifice shapes (circular and rectangular) and two regurgitant volumes were then compared against the 2D color Doppler PISA method which requires an assumption of hemispheric PISA shape. Figure 11 shows superimposed PISA hemispheres (shown in white) over the proximal isovelocity surfaces (shown in green) obtained using CFD simulations. For the rectangular orifice, there is a large discrepancy in surface area between methods but that the difference diminishes as greater flow volume (70ml/beat) is modeled.

Figure 11.

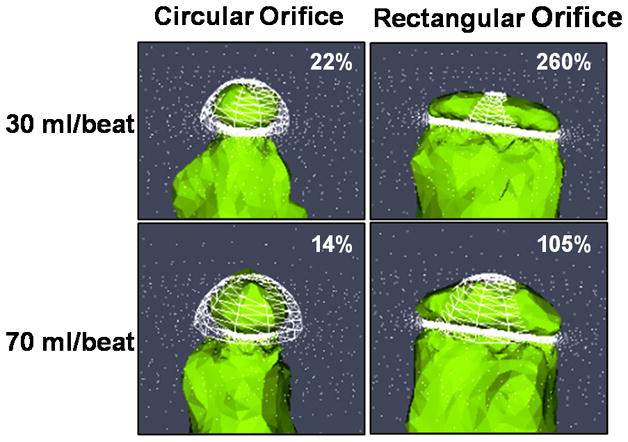
Comparison of 2D Doppler and 3D CFD Proximal Isovelocity Surface Area. Simulated PISA for two orifice shapes under moderate (30ml/beat) and severe (70ml/beat) flow conditions. Compared the 3D CFD model (green), the 2D Doppler method (white mesh) relies upon a single radius measurement and appears to overestimate PISA for the circular office and underestimate PISA for the rectangular orifice. The percent relative difference between 2D PISA and 3D CFD PISA is given for each flow condition. In each image the flow direction is top to bottom and the plane of the orifice is indicated by the white bar at the bottom of the mesh.

Discussion

In this manuscript, our CFD model simulating the clinically relevant flow conditions associated with MR was validated using an in vitro pulsatile flow loop containing an imaging chamber with a centrally located orifice. Two orifice shapes (circular and rectangular) and two regurgitant volumes (clinically moderate and severe) were considered. A comparison between the CFD simulations and measurements of the chamber pressure and velocity at the orifice showed good agreement. CFD calculated flow conditions near the orifice were compared with the 3D color Doppler depiction of the corresponding flow conditions represented by the convergence and vena contracta. This comparison of discrete flow events demonstrated that the CFD model is accurate and may provide important insight into the limitations and future development of 3D color Doppler tools.

Modeling Pressure, Velocity and Flow

For the prediction of pressure, velocity and flow rate, the proposed CFD model performed well. As shown in Figure 3, the modeled pressure gradient and waveform were nearly super imposable for the simulation of moderate (30 ml/beat) MR through a circular orifice. When compared to the spectral Doppler standard measure of peak trans-orifice velocity (as in Figure 4), the CFD model again performed well. For the estimate of flow rate across either a circular orifice (Figure 5) or a rectangular orifice (Figure 6C) we see a small discrepancy between CFD modeling and flow rate as measured by ultrasonic flowmeter standard. This discrepancy between the simulated and measured waveforms can likely be attributed to the location of the flow meter being attached to silicon rubber tubing several centimeters distal to the imaging chamber. In addition, other factors affecting calibration such as acoustic coupling through the tubing wall or the use of water with 30% glycerin may have contributed. Since the flow obtained using our CFD simulation resembles closely that expected in clinical MR [3] we suggest that the small flow rate discrepancy is a feature of the flow model design rather than the CFD model performance.

Modeling the Vena Contracta

Clinically, the vena contracta zone of a regurgitant jet is a potentially very useful target for efforts aiming to better quantify MR severity. It has been well demonstrated that the VC zone is proportional to the effective regurgitant orifice area (EROA). [46;47] A larger valve defect creates a larger VC zone. When the flow orifice is circular, the VC diameter represents well the flow orifice area. However when the flow orifice is non-circular (rectangular in our model), or commonly arc-shaped in clinical MR, then the VC area better represents the effective flow (regurgitation) area. In this study we demonstrated that the 3D CFD model clearly created the expected VC zone. As previously reported [13;15] and as shown in Table 2, both the 3D color Doppler and 3D CFD methods demonstrated that the VC area is independent of flow rate.

In addition the CFD model revealed a central core of even higher velocity flow through the middle of the VC zone (Figure 7 and 8). This high velocity core is usually not appreciated, even by 3D color Doppler methods. So for this simple model of MR, the 3D CFD model has provided novel insight about these dynamic flow events. When compared to the known area of the flow orifice we see that the VC area from the 3D CFD model is a little smaller than the actual orifice area (e.g. 0.32 cm² vs 0.35cm², respectively), whereas the 3C color Doppler VC area is larger (0.40cm²). This finding of a smaller CFD VC area suggests that the model is robust and highly sensitive since fluid dynamics would predict a slight reduction in flow area just distal to the fixed anatomic orifice. This effect is evident for the CFD model but not for the 3D color Doppler imaging. Findings such as these highlight how CFD modeling could support the development of 3D color Doppler imaging methods. When applied clinically, the accuracy of 3D Doppler measures such as VC area can be affected by several user and machine settings such as color Doppler gain, and the tissue-priority algorithm [an adjustable algorithm to stipulate whether a volume of 3D data at the interface of tissue and blood is displayed as either tissue (B-mode image) or flowing blood (color Doppler)]. By comparing to CFD derived measures under controlled flow conditions, these sorts of Doppler variables can be prescribed to ensure maximal agreement with both known orifice area and CFD modeled flow area.

Modeling Flow Convergence

If a comprehensive computational model of MR is the goal, then the proximal flow convergence must be accurately characterized. In this study we report both qualitative and quantitative comparison of the proximal isovelocity surface area from the CFD model and from 2D and 3D Doppler methods. Figures 9 and 10 demonstrate that the converging roughly hemispheric isovelocities are well represented by the 3D CFD model and that both area and shape of each converging flow surface is highly influenced by the isovelocity modeled (Doppler aliasing velocity). The CFD panel in Figure 9 clearly demonstrates that the largest and slowest PISA (blue) has a “mushroom” non-hemispheric geometry. The next PISA contour (green) is closest in shape to a hemisphere. The smallest and fastest PISA (red) has a flattened appearance. Clinically the radius of this roughly hemispheric green PISA contour would be measured to derive the surface area of the isovelocity shell converging at 40 cm/s towards the flow orifice. This CFD model correlates well with the 2D Doppler image and with clinical experience. [3] Figure 10 shows the computationally calculated isovelocity surfaces (left panels) depicting the flow conditions near a circular orifice, and the isovelocity surfaces recorded using 3D Doppler measurements (right panels). Here again, the change in the color between red and blue corresponds to the Nyquist aliasing isovelocity surface. The white arrow in the subfigures shows the location of the corresponding proximal isovelocity surface. Flow direction is from top to bottom. The location of the orifice plate is clearly seen. These images demonstrate that the CFD simulation accurately depicts the complex 3D geometry of the flow convergence zone created by pulsatile flow through a simple circular orifice.

The depictions of the 3D CFD isovelocities for the circular and rectangular orifice (Figure 11) are important. Here we see that the classic 2D Doppler PISA method (based on a single radius measurement) would overestimate PISA (and necessarily the regurgitant volume and effective orifice area derived from that PISA value) for the circular orifice. In contrast, the 2D PISA method would underestimate the isovelocity area (depicted by the CFD model) for the non-circular orifice. Recall that when applied clinically the regurgitant orifice is often non-circular, and the 2D PISA method has been reported to underestimate the MR regurgitant volume and EROA.

For a quantitative evaluation we compared 3D isovelocity area measures by CFD and 3D color Doppler techniques. EROA and regurgitant volumes could not be analyzed as they were input functions for the CFD model. As shown in table 2, for circular and rectangular orifices, each at 2 flow rates, the CFD model predicted slightly larger isovelocity surface areas than measured by 3D Color Doppler method. One explanation for this discrepancy may be the Doppler angle dependency of the 3D color Doppler technique as depicted in Figure 12. Since the lateral margins of the PISA zone are almost perpendicular to the central Doppler beam, it follows that the true isovelocity surface area will be under-measured by a factor related to the Doppler beam angle. This discrepancy between the Doppler defined converging isovelocity and the true isovelocity is an example of how 3D CFD modeling may help refine the development and future application of 3D color Doppler flow quantification methods. Only through robust CFD modeling can we begin to evaluate the importance of these Doppler-angle limitations for the accurate assessment of clinical MR severity.

Figure 12.

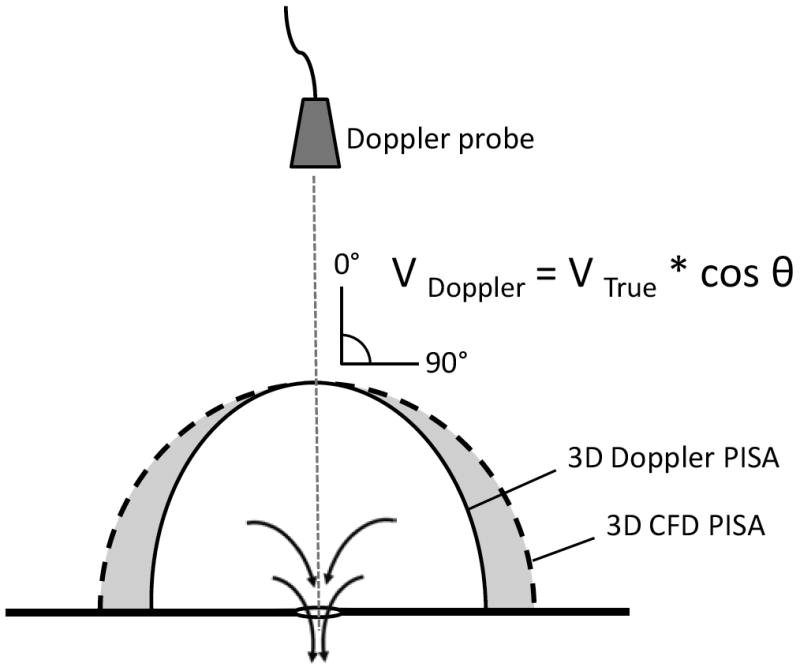
Underestimation of the true isovelocity is caused by the Doppler angle effect. Moving away from the mid-line, the Doppler angle increases and creates a progressive underestimation of the true isovelocity. The CFD model approximates the true isovelocity (V _True) rather than the Doppler velocity (V _Doppler). Proximal Isovelocity Surface Area, PISA.

As clinical imaging tasks become increasingly complex the need for well validated CFD modeling will increase. On the near horizon is the clinical challenge of evaluating outcomes of percutaneous valve interventions such as mitral valve clips and stent-mounted valves. [48] Soon clinicians will be asked to evaluate the severity of increasingly complex flow conditions with eccentric regurgitant jets, multiple jets and foreshortened or mechanically obstructed regurgitant valve jets. To further refine our imaging tools and to resolve these emerging challenges, robust computational modeling will likely play an important role.

Limitations

For this initial validation study we assessed the performance of the 3D CFD method in a simple model of mitral regurgitation quantification. By design, we compared the CFD model to pressure measures, flow measures, and Doppler measures of pulsatile flow through a rigid, non-deformable orifice. Further development of the CFD model includes a study of fluid-structure interaction between blood flow and cardiovascular tissue in the context of compliant tissue models. Preliminary results based on the FSI solver developed in [22] indicate that this approach promises to uncover a wide variety of computational “signatures” of clinical events observed in echocardiographic assessment of mitral regurgitation including the Coanda effect associated with eccentric, “wall-hugging” jets, multiple MR, and periprosthetic valve flow. In addition to modeling more complex fluid-structure interaction at the regurgitant orifice, we also intend to further improve the physical model of MR by incorporating non-rigid upstream (left ventricle) and downstream (left atrium) compartments into the imaging chamber. Thus improving the “anatomic” model will permit CFD model analysis of flow events both proximal and distal to the regurgitant orifice.

Conclusion

The examples presented in this manuscript show that CFD simulations provide a powerful tool to study various aspects of MR. The in vitro validation of the CFD model presented in this manuscript is an important first step. The in vivo echocardiographic assessment of complex intracardiac flow events has long been a challenge; however, rapid improvements in imaging technology (including single beat 3D color Doppler imaging) are providing new tools. Robust CFD models of these current imaging challenges (including eccentric MR, multiple MR jets, and periprosthetic valve flow) are being developed and are expected to refine and reinforce emerging 3D echocardiographic applications.