A model of high-frequency oscillatory potentials in retinal ganglion cells

Abstract

High-frequency oscillatory potentials (HFOPs) have been recorded from ganglion cells in cat, rabbit, frog, and mudpuppy retina and in electroretinograms (ERGs) from humans and other primates. However, the origin of HFOPs is unknown. Based on patterns of tracer coupling, we hypothesized that HFOPs could be generated, in part, by negative feedback from axon-bearing amacrine cells excited via electrical synapses with neighboring ganglion cells. Computer simulations were used to determine whether such axon-mediated feedback was consistent with the experimentally observed properties of HFOPs. (1) Periodic signals are typically absent from ganglion cell PSTHs, in part because the phases of retinal HFOPs vary randomly over time and are only weakly stimulus locked. In the retinal model, this phase variability resulted from the nonlinear properties of axon-mediated feedback in combination with synaptic noise. (2) HFOPs increase as a function of stimulus size up to several times the receptive-field center diameter. In the model, axon-mediated feedback pooled signals over a large retinal area, producing HFOPs that were similarly size dependent. (3) HFOPs are stimulus specific. In the model, gap junctions between neighboring neurons caused contiguous regions to become phase locked, but did not synchronize separate regions. Model-generated HFOPs were consistent with the receptive-field center dynamics and spatial organization of cat alpha cells. HFOPs did not depend qualitatively on the exact value of any model parameter or on the numerical precision of the integration method. We conclude that HFOPs could be mediated, in part, by circuitry consistent with known retinal anatomy.

Introduction

A number of studies, going back many decades, report that large or diffuse stimuli evoke synchronous high-frequency oscillatory potentials (HFOPs) in the vertebrate retina (Steinberg, 1966; Laufer & Verzeano, 1967; Wachtmeister & Dowling, 1978; Ariel et al., 1983; Neuenschwander & Singer, 1996; Ishikane et al., 1999; Neuenschwander et al., 1999; Frishman et al., 2000; De Carli et al., 2001). Such HFOPs reflect coherent oscillations across many cells and should not be confused with “oscillatory” activity in single spike trains resulting from regular firing. Diffuse stimuli evoke HFOPs at frequencies around 100 Hz in cat optic nerve activity and in local retinal field potentials (Steinberg, 1966; Laufer & Verzeano, 1967). More recently, auto- and cross-correlation measures of brisk ganglion cell responses indicate that HFOPs in the cat retina are stimulus specific and increase markedly with stimulus size (Neuenschwander & Singer, 1996; Neuenschwander et al., 1999). When stimulated with low spatial-frequency gratings, these same brisk cell types exhibit a corresponding high-frequency resonance in their temporal modulation transfer functions (tMTFs) that is consistent with HFOPs (Frishman et al., 1987). In the rabbit retina, large—but not small—stimuli elicit HFOPs in a variety of ganglion cell types (Ariel et al., 1983). HFOPs with similar characteristics to those reported in mammals have been recorded from frog (Ishikane et al., 1999) and mudpuppy (Wachtmeister & Dowling, 1978) ganglion cells, but at lower frequencies, around 30 Hz, as expected for cold-blooded vertebrates. HFOPs are also present in electroretinograms (ERGs) of humans (Wachtmeister, 1998; De Carli et al., 2001) and other primates (Frishman et al., 2000; Rangaswamy et al., 2003). The conservation of retinal HFOPs across such a broad range of vertebrate species suggests they may be important for visual function.

Despite numerous reports of HFOPs in various species, there is typically no high-frequency periodic structure in peristimulus-time histograms (PSTHs) recorded from retinal ganglion cells (however, see Steinberg, 1966; Ariel et al., 1983; Reich et al., 1997; Neuenschwander et al., 1999). There are several factors that may account for this ubiquitous negative finding. Because HFOPs are proportional to stimulus size (Wachtmeister & Dowling, 1978; Ariel et al., 1983; Ishikane et al., 1999; Neuenschwander et al., 1999), and as a result are not evoked by small spots or random checkerboard patterns (Meister et al., 1994), periodic responses are not elicited by many commonly used stimuli. Even when large spots or gratings are employed, the phases of the evoked HFOPs can vary randomly over time and may therefore be suppressed in stimulus-locked averages such as the PSTH (Neuenschwander et al., 1999). Although HFOPs can be partially stimulus locked at high contrasts (Steinberg, 1966; Ariel et al., 1983; Neuenschwander et al., 1999), they still cannot be resolved by standard PSTH bin widths, typically 10–20 ms, and thus may often be obscured in published data.

HFOPs in cats occur above the resonance frequencies of horizontal cells (Foerster et al., 1977; Smith et al., 2001), are abolished by bicuculline in frogs (Ishikane et al., 1999), by gamma-amino butyric acid (GABA) in mudpuppy (Wachtmeister & Dowling, 1978), and require wide-field stimulation in both frog (Ishikane et al., 1999), cat (Neuenschwander et al., 1999), rabbit (Ariel et al., 1983), and mudpuppy (Wachtmeister & Dowling, 1978) retinas. Taken together, these experimental results indicate that the generation of HFOPs is likely to involve wide-field, spiking amacrine cells. In previous work using a linear model of the inner retina, we proposed that HFOPs could be produced, in part, by negative feedback from axon-bearing amacrine cells onto ganglion cells (Kenyon & Marshak, 1998). According to this hypothesis, the dendrites of axon-bearing amacrine cells are excited by neighboring ganglion cells via gap junctions while their axons provided feedback inhibition to more distant ganglion cells (Dacey & Brace, 1992; Vaney, 1994; Jacoby et al., 1996).

Here, we used a more realistic model of the inner retina to determine whether the proposed circuitry could account for the following experimentally observed properties of HFOPs: (1) HFOPs increase with stimulus size, growing approximately linearly with spot diameter over a range that exceeds the width of the receptive-field center by several times (Ariel et al., 1983; Ishikane et al., 1999; Neuenschwander et al., 1999). (2) The phases of evoked HFOPs vary randomly and become less stimulus locked over time (Neuenschwander et al., 1999). (3) HFOPs are stimulus specific—only cells responding to contiguous regions are phase locked, or synchronized (Ishikane et al., 1999; Neuenschwander et al., 1999). Other mechanisms may contribute to retinal HFOPs as well, such as negative feedback from amacrine cells onto bipolar cells (Euler & Wassle, 1998; Euler & Masland, 2000; Shields & Lukasiewicz, 2003). Here, however, we focus on the possible contribution of axon-mediated feedback onto ganglion cells. Additional experiments were conducted to ensure that model parameters which produced realistic HFOPs were consistent with other aspects of alpha ganglion cell physiology, particularly their responses to small spots of varying intensity (Creutzfeldt et al., 1970), their known center/surround organization (Troy et al., 1993), and their spontaneous correlations during background firing (Mastronarde, 1983). Preliminary versions of our results have been reported previously (Kenyon et al., 1999; Kenyon & Marshak, 2000, 2001).

Materials and methods

Model overview

Bipolar cells and ganglion cells

Input to the model retina was conveyed by ON bipolar cells, which were driven by external currents representing light-modulated synaptic input from cone photoreceptors (Fig. 1). These external currents were processed through a temporal low-pass filter with a time constant of 10 ms, but were not spatially filtered. The model bipolar cells produced excitatory postsynaptic potentials (EPSPs) in both ganglion cells and amacrine cells according to a random process (Freed, 2000). Ganglion cells were modeled as cat alpha (Y) ganglion cells, based on physiological evidence that alpha ganglion cells fire synchronously (Mastronarde, 1989; Castelo-Branco et al., 1998). The radius of influence of the model ganglion cells, defined as the radius over which they could make and receive synapses, was twice as large as that for the bipolar cells, consistent with fact that alpha ganglion cells are larger than bipolar cells. The actual convergence of bipolar cells to alpha ganglion cells is much higher (Freed & Sterling, 1988), but due to computational constraints it was necessary to limit the number of bipolar cells in the model. This approximation is reasonable for stimuli that were equal in size to, or larger than, the ganglion cell receptive-field center diameter.

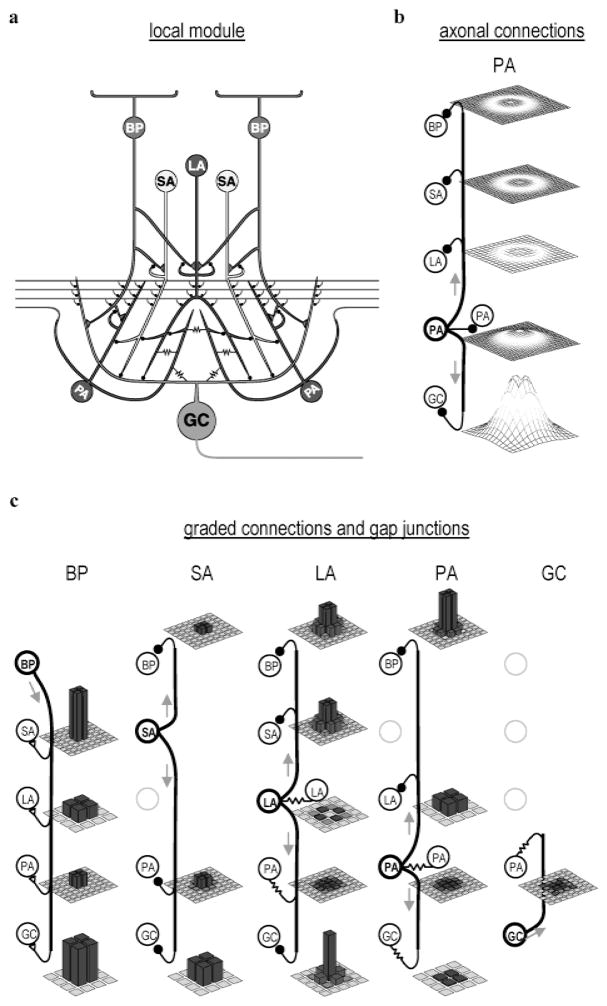
Fig. 1.

Model used for simulating synaptic interactions in the inner retina. (a) Schematic of single processing unit, one of 32 × 32 identical processing units in the model. Input conveyed by a 2 × 2 array of bipolar cells (BPs; only 2 shown). Output conveyed by single ganglion cell (GC) axon. Each processing unit contained three different inhibitory interneuron types, implemented as local arrays containing 2 × 2 small (SA), 1 × 1 large (LA), and 2 × 2 polyaxonal (PA) amacrine cells (ACs) (not all cells are shown). All cells consisted of a single compartment, but are drawn with complex morphologies to better illustrate their synaptic interactions. Filled black circles are inhibitory synapses, triangular contacts excitatory synapses, and resistors gap junctions. (b) Spatial distribution and relative strength of PA axon mediated inhibition. Heights of mesh surfaces show spatial distribution of total synaptic input from the 2 × 2 array of PA axons arising from a single local processing module. Mesh spacing indicates density of corresponding postsynaptic cells. Same vertical scale, in arbitrary units, used in all mesh plots. (c) Spatial distribution and relative strength of short-range connections. Bar height indicates relative strength of the maximum synaptic input from the indicated presynaptic cell types, arising from a single local processing module, to the indicated postsynaptic cells types. Each bar corresponds to a single postsynaptic cell. Grid density reflects density of the postsynaptic cell population. Same vertical scale used in all bar graphs.

Amacrine cells

The model amacrine cells made both local and long-range inhibitory connections that gave rise to inhibitory surrounds, modulated the time course of ganglion cell light responses, and were essential for the generation of HFOPs. Local amacrine cell connections consisted of feed forward synapses onto ganglion cells, feedback synapses onto bipolar cells, and serial synapses among themselves (Marc & Liu, 2000; Roska et al., 2000). Long-range connections were made exclusive by the axon-bearing amacrine cells. Consistent with the three amacrine cell types included in the model, the amacrine cells presynaptic to cat alpha ganglion cells include small types, possibly the A2, A3, A8, and AII amacrine cells, larger types, possibly the A13 and starburst amacrine cells, and axon-bearing types, probably the A19-22 amacrine cells (Kolb & Nelson, 1985, 1993; Vardi et al., 1989; Freed et al., 1996; Owczarzak & Pourcho, 1999). In the cat retina, approximately 80% of all synapses onto alpha ganglion cells are from amacrine cells (Freed & Sterling, 1988; Owczarzak & Pourcho, 1999), consistent with the major contribution made by the model amacrine cells to ganglion cell light responses. The serial interactions between the model amacrine cells are consistent with known patterns of retinal connectivity (Dubin, 1970; Marc & Liu, 2000). The projections of the axon-bearing amacrine cells, which contacted all five cell types in the model, were consistent with reports that the processes of A19-22 amacrine cells in the cat retina make synaptic contacts onto bipolar, amacrine, and ganglion cells, including alpha ganglion cells (Kolb & Nelson, 1993; Freed et al., 1996).

Electrical coupling

When cat alpha ganglion cells are filled with Neurobiotin, at least two distinct amacrine cell types are labeled, one that gives rise to long axons as well as one or more conventional cell types (Vaney, 1994). Axon-bearing amacrine cells are more densely labeled than the conventional amacrine cells, suggesting that ganglion cells are directly coupled only to the axon-bearing amacrine cells. The axon-bearing amacrine cells that are tracer coupled to the alpha ganglion cells are also tracer coupled to each other (Vaney, 1994). Consistent with the above studies, the axon-bearing amacrine cells in the model were electrically coupled to the alpha cells, to nonspiking amacrine cells and to each other (Vaney, 1994). Like the A19-22 amacrine cells, the axon-bearing amacrine cells in the model received only a small percentage of their input from bipolar cells (Freed et al., 1996), a finding consistent with our assumption that their major excitatory input was from electrical synapses.

Model parameters

Ganglion cell time constants and coverage factors were consistent with published physiological data (Vaney, 1990, 1994; O’Brien et al., 2002). Where experimental values were unavailable, model parameters were determined by trial-and-error until the simulated light responses qualitatively matched the corresponding electrophysiological data. Physiologically reasonable bounds were used to constrain parameter values as much as possible. This approach was validated by control experiments showing that the qualitative behavior of the model was not dependent on the precise value of any single parameter. No systematic attempt was made to optimize parameter values, as the phenomena reported here were quite robust and required no fine-tuning of the model. While we were able to identify a robust set of model parameters that reproduced the main features of experimentally measured HFOPs, it is possible that other parameter sets would have predicted quite different functions for the same patterns of connectivity. As in any modeling study, we do not attempt to prove that a particular pattern of connectivity mediates a particular function, only that such connectivity could, in principle, do so in a robust manner. Final parameters, which were the same for all experiments unless otherwise noted, are listed in Tables 1 and 2.

Table 1.

Cellular parameters^a

	τ	b	n × n	d	σ
BP	10.0	−0.0	64×64	0.25	0.25
SA	25.0	−0.5	64×64	0.25	0.25
LA	20.0	−0.25	32×32	1.0	0.5
PA	5.0	−0.025	64×64	0.2509.0b	0.2503.0b
GC	5.0	−0.025	32×32	1.0	0.5

^aExplanation of symbols: τ: time constant (ms); b: bias; n × n: array size; d: cutoff radius, σ: Gaussian radius [see eqn. (5)].

^bInner radius/outer radius.

Table 2.

Synaptic weights^a

	BP	SA	LA	PA	GC
BP	*	−0.375c	−3.0c	−3.0c/−15.0d	*
SA	3.0c	*	−3.0c	0.0b/−15.0d	*
LA	3.0c	*	0.25b	−3.0b/−15.0d	*
PA	0.75b	−0.75c	0.25b	0.25b/−45.0d	0.25b.e
GC	9.0c	−4.5c	−4.5c	0.25b/−270.0d	*

^aEach term represents the total integrated weight from all synapses arising from the corresponding presynaptic type (columns) to each cell of the corresponding postsynaptic type (rows) [the quantity W ^{(k, k′)} in eqn. (5)]. Asterisk (*) indicates absence of corresponding connection. Synapse type indicated by superscript:

^bgap junction,

^cgraded synapse,

^dconventional synapse.

^eMaximum coupling efficiency (ratio of postsynaptic to presynaptic depolarization) for this gap junction synapse: DC = 11.3%, action potential = 2.7%.

Simulation

There were five distinct cell types in the retinal model: Bipolar cells (BP), small amacrine cells (SA), large amacrine cells (LA), poly-axonal amacrine cells (PA), and alpha ganglion cells (GC). The entire model consisted of five parallel, interconnected, two-dimensional (2-D) grids, one for each cell type. All cell types were modeled as single compartment, RC circuit elements obeying a first-order differential equation of the following form:

$${\stackrel{.}{\overleftrightarrow{V}}}^{(k)}=-\frac{1}{{\tau }^{(k)}}\left({\overleftrightarrow{V}}^{(k)}-\sum _{k^{\prime }}{\overleftrightarrow{W}}^{(k,k^{\prime })}·f^{(k,k^{\prime })}({\overleftrightarrow{V}}^{(k^{\prime })})·{\overleftrightarrow{W}}^{{(k,k^{\prime })}^T}-b^{(k)}-{\overleftrightarrow{L}}^{(k)}\right),$$ (1)

where V↔^(k) is a 2-D array denoting the membrane potentials of all cells of type k, (1 ≤ k ≤ 5), τ^(k) is the time constant, b^(k) is a bias current for setting the resting potential, L↔^(k) is an external input representing light stimulation, which was nonzero only for bipolar cells (k = 1 only), W↔^{(k, k′)} gives the connection strengths between presynaptic {k′} and postsynaptic {k} cell types as a function of their vertical (row) separation, W↔^{(k, k′)T} gives the same information as a function of horizontal (column) separation, and the functions f ^{(k, k′)} give the associated input–output relations for each matrix element, detailed below. The form of the matrix multiplications in eqn. (1), equivalent to a 2-D spatial convolution, assumes that all synaptic interactions are separable, which requires that the row and column separations contribute independently to the total synaptic weight. The connections of the axon-bearing amacrine cells, which made synapses within an annular region that excluded the local processing unit, are not separable but could be described by a sum of three such separable interaction terms. The output of the axon-mediated inhibition was delayed by 2 ms, except for the axonal connections onto the axon-bearing amacrine cells, which was delayed for 1 ms. All other synaptic interactions were delayed by 1 ms. To represent the finite reversal potential of inhibitory channels, a minimum membrane potential equal to −1.5 was imposed for all cell types.

The input–output function for gap junctions was given by the identity,

$$f^{(k,k^{\prime })}({\overleftrightarrow{V}}^{(k^{\prime })})={\overleftrightarrow{V}}^{(k^{\prime })},$$ (2)

where the dependence on the presynaptic potential has been absorbed into the definition of τ^(k). This is possible because both the decay term in eqn. (1) and the omitted dependence on the presynaptic potential in eqn. (2) depend linearly on V↔^(k), allowing the coefficients to be combined.

The input–output function for graded synapses driven by a stochastic release process was constructed by comparing, on each time step, a random number with a Fermi function:

$$f^{(k,k^{\prime })}({\overleftrightarrow{V}}^{(k^{\prime })})=\theta \left(\left[\frac{1}{1+exp(-\alpha {\overleftrightarrow{V}}^{(k^{\prime })})}\right]-r\right),$$ (3)

where α sets the gain (equal to 4 for all graded synapses); r is a uniform random deviate equally likely to take any real value between 0 and 1, and θ is a step function, θ(x) = 1, x ≥ 0; θ(x) = 0, x < 0. In accord with published observations (Freed, 2000), graded synapses produced postsynaptic currents according to a rate-modulated binomial process, which reduces to a Poison process at low quantal release rates. The release probability was set proportional to the width of the time step, so that a given presynaptic membrane potential would produce, on average, the same number of postsynaptic impulses per unit time regardless of the integration step size. The postsynaptic current from each impulse was distributed uniformly over a 1-ms interval and scaled so that the total integrated current was independent of the integration step size.

The input–output relation used for conventional synapses was

$$f^{(k,k^{\prime })}({\overleftrightarrow{V}}^{(k^{\prime })})=\theta ({\overleftrightarrow{V}}^{(k^{\prime })}).$$ (4)

The kinetics of the postsynaptic current resulting from each pre-synaptic impulse was the same as for the graded stochastic synapses described above.

Spike generation

A standard integrate-and-fire mechanism was used to describe spike generation with the added modification that action potentials were modeled explicitly to account for the resulting postsynaptic potentials in electrically coupled cells. A depolarizing current was delivered to the cell for 1 ms on the time step immediately following a threshold crossing, followed by an equal and opposite 1-ms hyperpolarizing current, producing an approximately rectangular action potential with a width of 1 ms. For the standard integration time step of 1 ms, the action potential amplitude equaled 10.0. For smaller step sizes, this amplitude was increased by a small amount in order to keep the total area independent of the integration time step despite the decay in the membrane potential during the 1-ms duration of the spike itself. An absolute refractory period prevented a second spike from being generated within 1 ms of a previous spike. A relative refractory period was implemented by incrementing the bias current, b, by −0.5, which then decayed back to the resting value with the time constant of the cell.

Synaptic weights

Along both the horizontal and vertical directions, synaptic strengths fell off as Gaussian functions of the distance between the presynaptic and postsynaptic cells. For a given column separation, the horizontal weight factor was determined by a Gaussian function of the following form:

$$W_{i^{(k)},j^{(k^{\prime })}}^{(k,k^{\prime })}=\alpha \sqrt{W^{(k,k^{\prime })}}exp\left[-\frac{{\left|\right|i^{(k)}-j^{(k^{\prime })}\left|\right|}^2}{2{\sigma }^2}\right],$$ (5)

where $W_{i^{(k)},j^{(k^{\prime })}}^{(k,k^{\prime })}$ is the horizontal weight factor for the set of presynaptic cells j^(k′) (located in the jth column in the array of cells of type k′) to the set of postsynaptic cells i ^(k) (located in the ith column in the array of cells of type k), α is a normalization factor which ensured that the total synaptic input integrated over all presynaptic cells of type k′ to every postsynaptic cell of type k equaled W ^{(k, k′)}, σ is the Gaussian radius of the interaction, and the quantity ||i ^(k) − j ^(k′)|| denotes the horizontal distance (number of columns) between the presynaptic and postsynaptic cells, taking into account the wrap-around boundary conditions employed to mitigate edge effects. An analogous weight factor describes the dependence on vertical (row) separation. Eqn. (5) was augmented by a cutoff condition that prevented synaptic interactions beyond a specified distance, determined by the radius of influence of the presynaptic outputs and the postsynaptic inputs, roughly corresponding to the axonal and dendritic field radii, respectively. A synaptic connection was only made if the output radius of the presynaptic cell overlapped the input radius of the postsynaptic cell. Except for axonal connections, the input and output radii were the same for all cell types. For the large amacrine cells and the ganglion cells, the radius of influence extended out to the centers of the nearest-neighboring cells of the same type. To reduce the effective size of the bipolar, small, and axon-bearing amacrine cells (non-axonal connections only), their radii extended only halfway to the nearest cell of the same type. The external input was multiplied by a gain factor of 3, which was found empirically to produce an approximately saturating response for a stimulus intensity of 1.

Numerical integration

To minimize the computational demands of the reported simulations, a simple Euler method was used to numerically integrate the dynamical equations. Control experiments indicated that the model produced qualitatively similar behavior across a wide range of integration step sizes. To reduce the computational demands of the simulations, we used a standard time step of 1 ms, which was adequate to test whether axon-mediated feedback could qualitatively account for the experimentally measured properties of HFOPs.

Data analysis

Unless otherwise noted, correlations due to stimulus coordination, estimated by the shift-predictor constructed from spike trains drawn from separate stimulus trials (Gerstein & Perkel, 1972), were always subtracted. Reported correlations were expressed as a fraction of the expected synchrony, given by the product of the two firing rates, computed either during baseline activity or during the plateau portion of the response (usually 200–600 ms). With this normalization, a correlation amplitude of one at zero delay corresponded to a doubling in the number of synchronous events over the expected rate due to chance. Correlations were plotted as a function of the time delay between the two spikes, with all events occurring during the plateau portion of the response contributing to the average. For each delay value, this average was compensated for edge effects arising from the finite length of the two spike trains (lag corrected). To better approximate multiunit experimental recordings, and to improve signal-to-noise, in some analyses the PSTHs or cross-correlation histograms (CCHs) were averaged over all cells, or all distinct cell pairs, responding to the same stimulus, producing a multiunit measure, denoted as mPSTH or mCCH, respectively. Auto-correlation functions were never included in the mCCH. Error bars were estimated by assuming Poisson statistics for the count in each histogram bin. All correlations, unless otherwise noted, were obtained by averaging over 200 stimulus trials, using a bin width of 1 ms. Distances within the model retina are reported in units of ganglion cell receptive-field diameters, equivalent to the center-to-center separation between nearest-neighbor pairs, roughly 0.5–2 deg in the cat retina depending on eccentricity (Peichl et al., 1987).

Results

Consistency with alpha ganglion cell receptive field center dynamics

Model parameters were qualitatively consistent with the dynamics of the alpha ganglion cell responses to stimulation of their receptive-field centers. A representative model ganglion cell was stimulated with small spots of increasing intensity (Fig. 2). The model PSTHs, if expressed as a fraction of baseline activity, were similar to the responses of cat ganglion cells to analogous stimuli (Creutzfeldt et al., 1970). We compared relative instead of absolute firing rates because the baseline firing rates of cat alpha cells vary widely (Troy & Robson, 1992). The responses of cat ganglion cells become more transient as the stimulus intensity increases, a phenomenon that has been attributed to a contrast gain control (Shapley & Victor, 1978). In the model, local amacrine cell interactions mediated a form of contrast gain control that caused the ganglion cell responses to small spots to become more transient with increasing stimulus intensity.

Fig. 2.

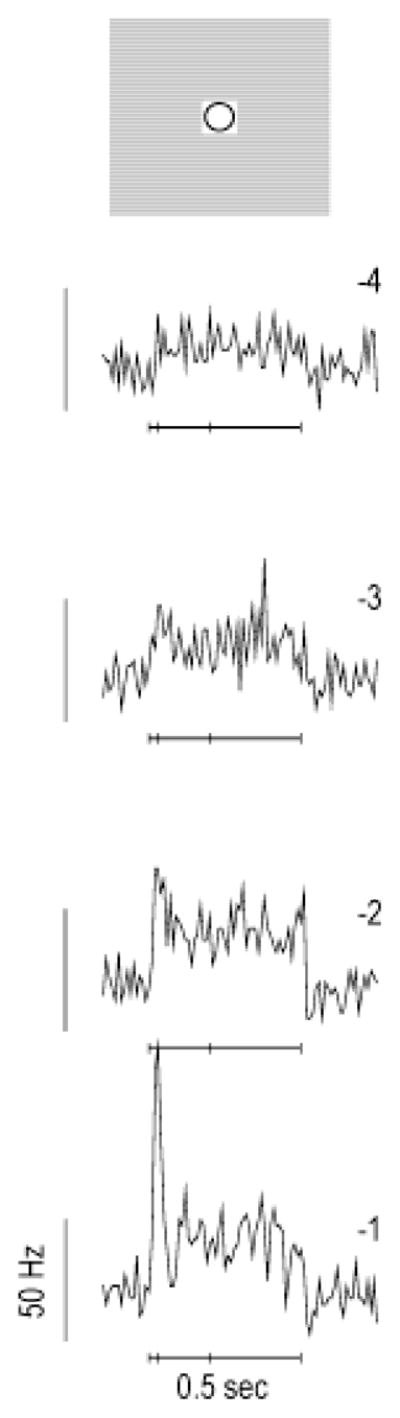
Consistency of retinal model with the receptive-field center dynamics of cat alpha ganglion cells. Illustration: A representative model ganglion cell was stimulated with a small square that activated the receptive field center out to a distance of one σ [Gaussian radius, see eqn. (5)]. Panels: Peristimulus-time histograms (PSTHs) recorded over a four-fold range of stimulus intensities ( $\frac{1}{16}-\frac{1}{2}$). The stimulus intensity (log₂ units) is indicated to the upper right of each PSTH. Local inhibition from nonspiking amacrine cells produced a form of contrast gain control that caused ganglion cell responses to become more transient as the stimulus intensity was increased (40 trials, 10-ms bin width). Model PSTHs were similar to those recorded from cat ganglion cells (Creutzfeldt et al., 1970).

The model did not include several physiological mechanisms known to the affect alpha ganglion cells responses to small, centered spots. Many sources of light adaptation, particularly in the outer retina, were not modeled, and thus the decline to a plateau response level was mediated entirely by local synaptic inhibition. While there is evidence for such inhibition during light responses (Cohen, 1998; Euler & Masland, 2000), the bipolar cell input to alpha cells is also likely to be intrinsically transient (Freed, 2000). To achieve an approximately correct ratio of peak to plateau activity in the absence of intrinsic adaptation in the bipolar cell terminal, the contribution from local inhibition in the model had to be correspondingly increased. As a consequence, at high stimulus intensities the model PSTHs developed a downward notch following the response peak that is not present in the physiological data. In addition, the model does not include slow GABA(C)-mediated inhibition, which is also likely to reduce ganglion cell responses to maintained stimuli (Euler & Masland, 2000; Matsui et al., 2001). However, it is unlikely that our conclusions were affected by the omission of such features, since HFOPs in the model depended primarily on widely distributed axon-mediated feedback rather than on the dynamics of the receptive field center.

Consistency with alpha cell center/surround organization

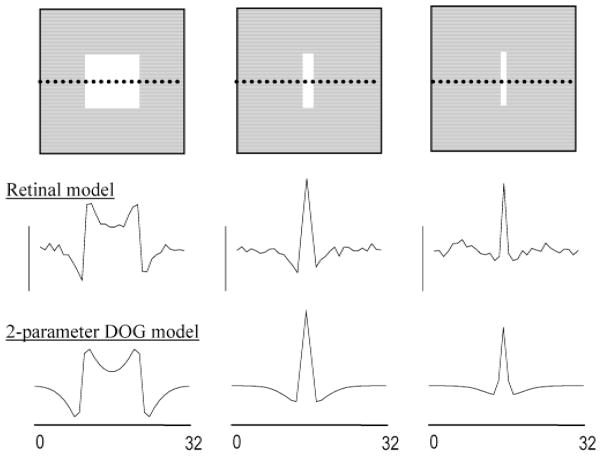
The retinal model was also qualitatively consistent with the measured spatial organization of cat alpha cells, which have been described quantitatively using a Difference-of-Gaussians (DOG) model employing four parameters to characterize the amplitude and radius of the receptive-field center and surround (Troy et al., 1993). At low stimulus intensities for which responses remained in the linear operating range, the center/surround organization of the model ganglion cells could similarly be described by concentric Gaussian receptive fields whose relative amplitudes and radii were fixed at their published values (Fig. 3). The restricted DOG model used to fit the simulation results therefore had two free parameters, corresponding to the overall response amplitude, which could be chosen arbitrarily due to the assumed linearity, and the absolute size of the model ganglion cell’s receptive-field center. The response profile obtained by plotting the plateau firing rates of the model ganglion cells along a cross section passing through spots of varying thickness (Figs. 3a–3c) was in reasonable agreement with the response profile generated by the two-parameter DOG model (Figs. 3d–3f). The center radius of the “best fit” two-parameter DOG model was determined by eye to be approximately $\sigma /\sqrt{2}$, where the parameter σ characterizes the Gaussian falloff with distance of the weighted bipolar cell input to the model ganglion cell [eqn. (5)]. Electrical coupling did not increase the effective size of the model ganglion cell’s receptive-field center because such expansion was directly opposed by lateral inhibition (Kenyon & Marshak, 1998). The fact that the spatial profile of simulated ganglion cell responses to stimuli of various widths could be fit with the two-parameter DOG model implies that the level of axon-mediated feedback in the model was consistent with the spatial organization of cat alpha cell receptive fields.

Fig. 3.

Consistency of the retinal model with the center/surround organization of cat alpha ganglion cells. Top row: The retinal model was stimulated with low intensity bars of varying thickness. Middle row: Plateau firing rates of the ganglion cells along a cross section passing through the center of each bar (dotted line in top panels). Bottom row: Firing rate profile predicted by a two-parameter Difference-of-Gaussians (DOG) model in which the ratio of center-to-surround strengths and radii were fixed at published values for cat alpha cells (Troy et al., 1993).

Model HFOPs are not stimulus locked

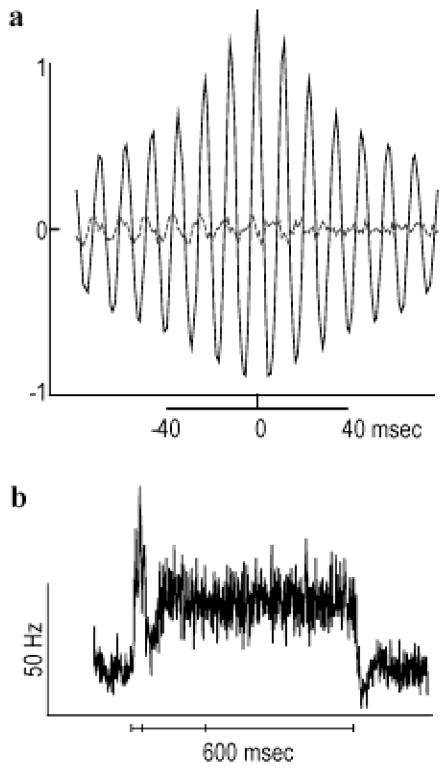
Large spots evoke HFOPs in cat retinal ganglion cells (Neuenschwander et al., 1999). In the retinal model, a spot stimulus (log₂ intensity = −2) covering a 6 × 6 array of ganglion cells evoked HFOPs of similar frequency and magnitude to those observed experimentally (Fig. 4a, solid line). To approximate the multiunit recordings used in the experimental analysis, cross-correlation histograms (CCHs) between six distinct pairs of ganglion cells occupying a 2 × 2 window at the center of the stimulus were combined into a multiunit correlogram (mCCH), and the result expressed as a fraction of the expected synchrony due to chance. The mCCH between spike trains drawn from separate stimulus trials, or shift predictor, indicated that correlations due to stimulus coordination were negligible during the plateau portion of the response (Fig. 4a, dashed line). The peak correlation amplitude corresponded to an approximate doubling in the number of synchronous events relative to the expected level, similar to levels of synchrony observed experimentally. Furthermore, the oscillatory side peaks in the mCCH fell off in amplitude as the magnitude of the delay increased. This decline in amplitude with increasing delay revealed that the phases of HFOPs in the retinal model varied randomly over time, a characteristic property of HFOPs measured experimentally.

Fig. 4.

HFOPs in the retinal model are not strongly stimulus locked. (a) A 6 × 6 array of model ganglion cells was stimulated by a square spot ( $\text{intensity}=\frac{1}{4}$). Solid black lines: Multiunit mCCHs, obtained by combining individual CCHs from all pairs of ganglion cells within a 2 × 2 window at the center of the stimulus. Correlations expressed as a fraction of the expected synchrony due to chance. Dashed gray lines: Shift predictors, obtained by recomputing the mCCHs using spike trains from different stimulus trials. Model mCCHs were similar to multiunit correlograms recorded from cat ganglion cells in response to analogous stimuli (Neuenschwander et al., 1999). (b) Multiunit mPSTH, obtained by averaging the individual PSTHs over all model ganglion cells within a 2 × 2 window at the center of the stimulus (bin width, 1 ms). The solid line at the bottom of the panel indicates the stimulus duration (600 ms). Periodic structure is mostly absent from the mPSTH since HFOPs in the retinal model were not strongly stimulus locked for spots of this size and intensity.

Although strong oscillations were clearly present in the responses of the model ganglion cells, periodic structure was not apparent in the mPSTH (Fig. 4b), constructed with 1-ms time bins to ensure that stimulus-locked HFOPs could be resolved if present. Oscillations produced by linear systems, such as a damped harmonic oscillator, are always phase locked to the driving stimulus. Furthermore, because linear systems obey superposition, multitrial averaging only eliminates the responses due to noise, but cannot eliminate a response to the driving term itself. The axon-mediated feedback loop contained fundamentally nonlinear components, particularly the threshold mechanism governing spike generation in both ganglion cells and axon-bearing amacrine cells. Such nonlinearities, along with the presence of synaptic noise, caused the phases of HFOPs in the model to drift randomly over time. The highly nonlinear nature of axon-mediated feedback in the model thus naturally accounted for the absence of strong stimulus locking in experimentally recorded HFOPs. Larger and/or brighter spots produced HFOPs that were less variable and more strongly stimulus locked (cf. Fig. 5). Our results do not imply that HFOPs are never present in the PSTHs of retinal ganglion cells, only that the periodic structure can be suppressed in multitrial measures that are time locked to the stimulus.

Fig. 5.

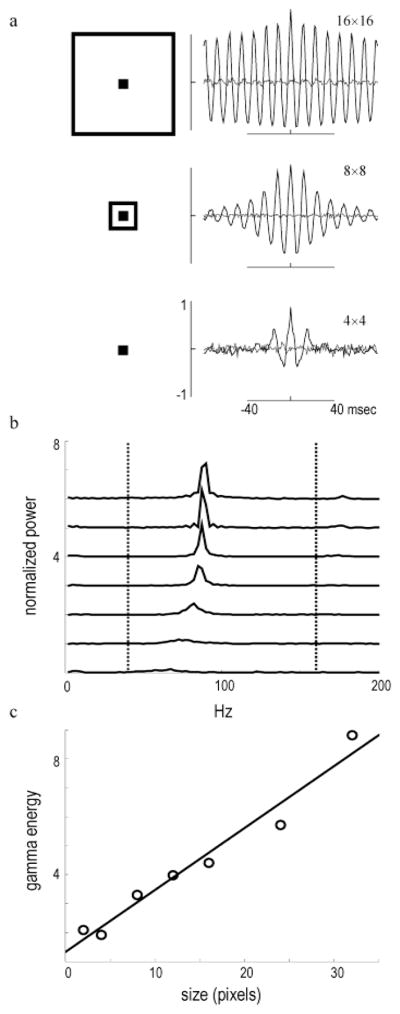
HFOPs in the retinal model are proportional to stimulus size. (a) mCCHs measured during the plateau response for a 2 × 2 array of ganglion cells centered within stimuli of increasing size (see illustrations). Stimulus size (in pixels) indicated to upper right of each mCCH. HFOPs increased sharply with stimulus size. Shift predictors were negligible. (b) Power spectra of model mCCHs for a range of spot sizes (2 × 2, 4 × 4, 6 × 6, 8 × 8, 12 × 12, 16 × 16, 24 × 24, and 32 × 32 pixels). (c) Total energy of the model HFOPs in the gamma-frequency band (40–160 Hz) increased approximately linearly with spot diameter (best fit regression line shown). Each pixel corresponded to approximately $\frac{1}{4}$ of a degree in the area centralis. A similar dependence on spot size is exhibited by HFOPs between cat ganglion cells (Neuenschwander et al., 1999).

HFOPs in the retinal model increase with stimulus size

In physiological recordings from cat retinal ganglion cells, HFOPs become larger in amplitude and the resulting correlations persist over more cycles as the stimulus becomes larger (Neuenschwander et al., 1999), a size dependence also observed in frog (Ishikane et al., 1999), rabbit (Ariel et al., 1983), and mudpuppy (Wachtmeister & Dowling, 1978) ganglion cells. A similar phenomenon was observed in the retinal model (Fig. 5). A relatively small spot (2 × 2 GCs, log₂ intensity = −2) evoked responses that were only weakly oscillatory, as assessed by the degree of periodicity in the mCCH. As the size of the spot was increased, oscillations among the same quartet of model ganglion cells, always positioned at the center of the stimulus, grew markedly in amplitude and persistence (Fig. 5a). Power spectra of the model mCCHs exhibited pronounced peaks between 60–100 Hz that increased in amplitude with stimulus diameter (Fig. 5b). To obtain a measure of oscillatory power, the individual spectra were integrated from 40 Hz to 160 Hz, representing the maximum range of the gamma frequency band. When the total energy in the gamma band was plotted as a function of stimulus size, a monotonic dependence similar to that seen in the cat retina was clearly evident (Fig. 5c).

Size-dependent HFOPs are a natural consequence of axon-mediated feedback. In the cat retina, one population of amacrine cells that are tracer coupled to alpha ganglion cells possess long axons that extend for several millimeters (Vaney, 1994) and a similar morphology is exhibited by the axon-bearing amacrine cells that are electrically coupled to primate M cells (Dacey & Brace, 1992; Jacoby et al., 1996). In the retinal model, axon-bearing amacrine cells gave rise to widely divergent output, so that each ganglion cell received axonal inputs arising from an area exceeding its receptive-field center by several factors. By activating a greater fraction of the axonal inputs to each ganglion cell, larger stimuli produced more prominent HFOPs.

In the area centralis, cat alpha ganglion cell dendritic fields are approximately 1 deg in diameter, and reach approximately 4 deg in the periphery (Peichl, 1991). The diameter of the model ganglion cells was 4 pixels, implying that each pixel spanned at least one-fourth of a degree. HFOPs in the retinal model increased with stimulus size for spots up to 32 pixels across (the largest size tested), which corresponds to at least 8 deg in the cat retina. The size dependence of HFOPs in the retinal model was therefore qualitatively consistent with the measured size dependence of HFOPs in the cat retina, which increase monotonically with stimulus size up to approximately 10 deg (Neuenschwander et al., 1999).

In the retinal model, the oscillation frequency also increased with stimulus diameter (Fig. 5b). During baseline activity, there was a small hump in gamma-band energy around 60 Hz, consistent with the spontaneous oscillations seen in electrophysiological data (Neuenschwander et al., 1999). As the size of the stimulus increased, the gamma-band peak grew in amplitude and shifted towards higher frequencies, reaching an asymptote at around 90 Hz. As the stimulus became larger, more long-range axons were recruited into the collective oscillation, thereby increasing the gain of the feedback circuit. This extra gain caused the axon-mediated feedback inhibition to rise more rapidly, which in turn caused the entire oscillatory cycle to speed up. In contrast, linear oscillators never exhibit such changes in frequency as a function of stimulus parameters.

HFOPs in the retinal model are stimulus specific

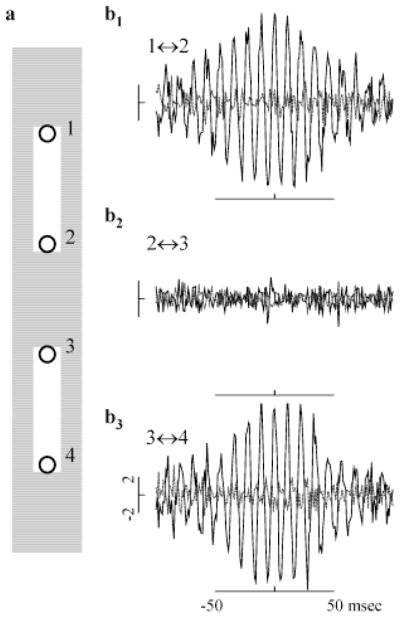
To investigate whether the oscillatory responses between model ganglion cells exhibited a stimulus specificity similar to that reported in both the cat (Neuenschwander & Singer, 1996) and frog (Ishikane et al., 1999) retina, we examined the firing correlations produced during the plateau responses to two identical bars that were turned on simultaneously (Fig. 6a). Synaptic interactions produced significant correlations between ganglion cells responding to the same bar, but not between ganglion cells responding to different bars. CCHs obtained during the plateau portion of the response were plotted for ganglion cell pairs at opposite ends of the same bar (Fig. 6b₁, upper bar; Fig. 6b₃, lower bar), or at the nearest opposing tips of the two separate bars (Fig. 6b₂). Even though the ganglion cells in each pair were separated by the same distance and were stimulated identically within their receptive-field centers, only those pairs responding to the same bar were strongly correlated. By suppressing the activity of ganglion cells in the gap between the two stimuli, lateral inhibition played a major role in ensuring that HFOPs within the two separate populations did not become phase locked to each other. Due to low-pass filtering, spikes, and to a lesser extent generator potentials, are strongly attenuated when passively conducted through a chain of electrical synapses (Kenyon & Marshak, 1998). Phase information was therefore effectively prevented from propagating between the two bars as a result of the strong lateral inhibition of cells in the unstimulated gap region.

Fig. 6.

HFOPs in the retinal model are stimulus specific. (a) Location of stimuli (white rectangles) relative to the receptive-field centers of recorded ganglion cells, labeled 1–4 (circles). (b₁–b₃) CCHs (solid black lines) and associated shift predictors (dashed gray lines) computed during the plateau portion of the response for pairs of ganglion cells at opposite ends of the same bar or at opposing tips of separate bars. Correlations expressed as a fraction of the baseline synchrony. All ganglion cell pairs were separated by seven GC receptive-field diameters. (b₁) pair 1 ↔ 2 from upper bar; (b₂) pair 2 ↔ 3 from separate bars; (b₃) pair 3 ↔ 4 from lower bar. Correlations were only significant between pairs from the same bar, as with HFOPs between cat ganglion cells (Neuenschwander et al., 1996).

Consistency with background correlations between cat alpha cells

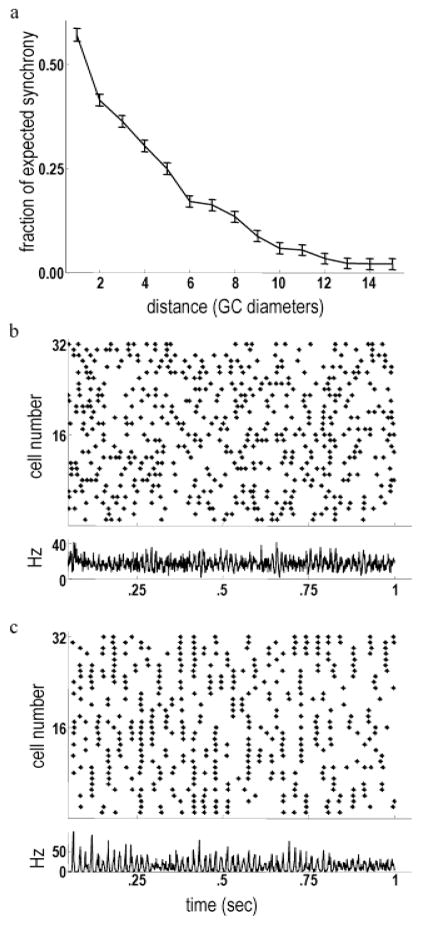
In physiological recordings of background firing activity under photopic illumination, the strength of the spontaneous correlations between pairs of cat alpha cells decreased rapidly as a function of their center-to-center distance (Mastronarde, 1983). A qualitatively similar decline in relative correlation strength as a function of distance was observed in the retinal model. Background correlations between model ganglion cells were measured as a fractional increase in the number of synchronous spikes relative to baseline. Background correlations between the model ganglion cells became half-maximal at a separation of approximately four times the diameter of the receptive-field center. Although correlations between cat alpha cells appear to fall off more rapidly, a precise comparison may be confounded by the irregular spacing of retinal neurons and the difficulty of detecting very small correlations in physiological data.

The absence of long-range synchrony during background activity resulted from the low baseline firing rates of the axon-bearing amacrine cells. Small-amplitude HFOPs were present during background activity in the retinal model, but these were too weak to promote strong synchrony between widely separated ganglion cells. Electrical coupling was similarly ineffective in mediating long-range synchrony during normal spontaneous activity. However, even weak indirect coupling could mediate long-range synchrony when the level of background synaptic noise in the model was reduced. During normal background activity, the model ganglion cells fired mostly independently (Fig. 7b). When the strengths of all nonelectrical synapses in the model were reduced by 95%, thereby eliminating most of the background synaptic noise, ganglion cells became synchronized over long distances due to their indirect electrical coupling via amacrine cells (Fig. 7c). Qualitatively similar increases in long-range synchrony have been observed after blocking synaptic transmission with Co²⁺ (Brivanlou et al., 1998).

Fig. 7.

Background firing correlations declined as a function of increasing center-to-center distance. (a) Synchrony (mCCH peak relative to baseline, averaged over all GC pairs) of model ganglion cells as a function of center-to-center distance. Synchrony declined rapidly with increasing separation. A similar decline with increasing center-to-center separation is exhibited by the background correlations between cat alpha cells (Mastronarde, 1983). (b) Top: Raster plot showing the spontaneous firing activity of a line of ganglion cells stretching across the model retina. Bottom: Instantaneous firing rate of all ganglion cells. Background gamma-band oscillations are evident, as in physiological data (Neuenschwander et al., 1999). (c) Top: Raster plot of ganglion cell activity after reducing synaptic weights by 95%. Long-range synchrony mediated by gap junctions is clearly apparent. Bottom: The instantaneous firing rate of all ganglion cells shows very strong synchronization. Blocking synaptic transmission produces qualitatively similar effects in salamander retina (Brivanlou et al., 1998).

HFOPs in the retinal model depend on feedback loop gain

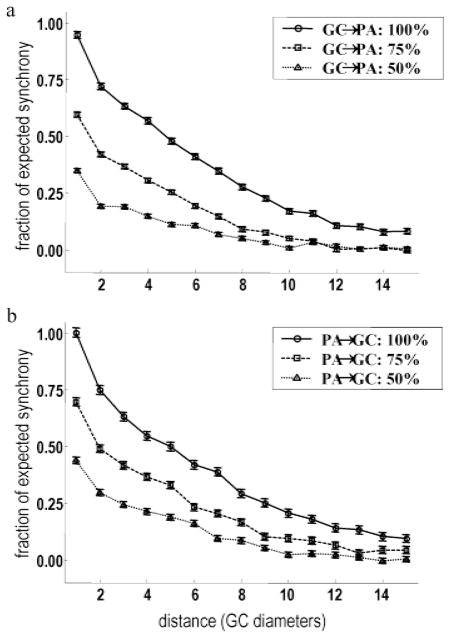
Having established consistency with experimental data, we now turn our attention to the robustness of the proposed model and its dependence on key parameters. HFOPs in the retinal model were expected to be strongly dependent on parameters affecting the overall gain of the axon-mediated feedback loop, particularly the strength of the electrical excitation from the alpha cells to the axon-bearing amacrine cells and the strength of the axon-mediated feedback inhibition. To test this conjecture, we first applied a low-intensity, full-field stimulus (intensity = 〈1/16〉) that roughly doubled the number of synchronous events, relative to the expected background rate, between ganglion cell pairs at all separations (Fig. 8a, solid line–circles). As expected, the increase in long-range synchrony produced by full-field stimulation could be reversed by reducing the coupling strength of the gap junctions from ganglion cells to axon-bearing amacrine cells by 25% (Fig. 8a, dashed line–squares). Reducing the strength of this coupling by 50% (Fig. 8a, dotted line–triangles) produced levels of long-range synchrony that were significantly below the background rate. These results show that electrical synapses from ganglion cells provided the major contribution to the gain of the axon-mediated feedback loop responsible for HFOPs.

Fig. 8.

HFOPs in the retinal model depend on gap junction-mediated excitation and axon-mediated inhibition. (a,b) Applying a weak full-field stimulus (intensity = 1/16) approximately doubled the level of synchrony between ganglion cell pairs at all separations relative to spontaneous levels (solid line, circles). (a) The increase in long-range synchrony produced by full-field stimulation could be reversed by reducing the coupling strength of the gap junctions from ganglion cells to axon-bearing amacrine cells by 25% (dashed line, squares). Reducing this coupling by 50% (dotted line, triangles) produced levels of long-range synchrony that were significantly below background. (b) Reducing axon-mediated inhibition of the ganglion cells by 25% (dashed line, squares) reduced the long-range synchrony evoked by full-field stimulation to near background levels. Reducing this axon-mediated inhibition by 50% (dotted line, triangles) reduced long-range synchrony to below background levels.

In the presence of synaptic noise, gap junction coupling between ganglion cells and amacrine cells was not sufficient to mediate long-range synchrony in the retinal model; axon-mediated inhibition was also necessary. Reducing the strength of the axon-mediated inhibition of the model ganglion cells by 25% (Fig. 8b, dashed line–squares) reduced the long-range synchrony evoked by full-field stimulation to near background levels and reducing the strength of this inhibition by 50% (Fig. 8b, dotted line–triangles) reduced long-range synchrony to below background levels. Similar results were obtained when the strengths of all axon-mediated inhibitory synapses, not just those onto ganglion cells, were reduced (not shown). These results demonstrate that axon-mediated inhibition was necessary for the long-range correlations between the model ganglion cells, both during background activity and under full-field stimulation.

HFOPs in the retinal model depend on conduction velocity

A second factor expected to strongly affect HFOPs was the time delay of the axon-mediated feedback. Using the total power in the gamma-frequency band as a measure of correlation strength, we investigated the effects of conduction velocity on both stimulus-evoked and background oscillations (Fig. 9). For these experiments, power spectra were computed from the multiunit membrane potentials obtained by combining the single-trial membrane potential traces of an 8 × 8 array of ganglion cells after clipping off action potential spikes and normalizing by the standard deviation to control for broad-band power increases due to noise. The total power in the gamma-frequency band, both during evoked and background activity, was inversely related to the axonal conduction velocity, since longer axonal delays made the retinal circuitry more prone to oscillate. For comparison, oscillation strength is also shown for the standard retinal model in which all axonal delays were set to fixed values regardless of the conduction distance. A fixed axonal delay of 1 ms produced oscillations that were relatively small, while a fixed delay of 2 ms produced oscillations that were unphysiologically large. For reasons related to the historical development of the simulation software, the standard retinal model used mixed values for the axonal delays corresponding to different connections. The axonal delay to all postsynaptic cell types was set equal to 2 ms, except for the axon-mediated interactions between axon-bearing amacrine cells, which used a delay of 1 ms. The oscillations resulting from this mixed delay strategy were similar to those produced by intermediate axonal conduction velocities, corresponding to approximately 6–8 ganglion cell receptive-field center diameters/ms. In the cat, alpha ganglion cell receptive-field diameters are between 100–500 μm, depending on eccentricity (Boycott & Wässle, 1974). Small, unmyelinated fibers between 0.25–0.5 μm in diameter conduct at speeds less than 1.0 mm/ms (Waxman & Bennett, 1972), implying that typical axon-mediated conduction delays in the cat retina, not including fixed synaptic delays, require on the order of 1 ms to traverse 5–10 alpha ganglion cells in the area centralis. Thus, the delays employed in the model, when compared with the total axonal, synaptic, and dendritic delays present in the retina, are within the physiological range.

Fig. 9.

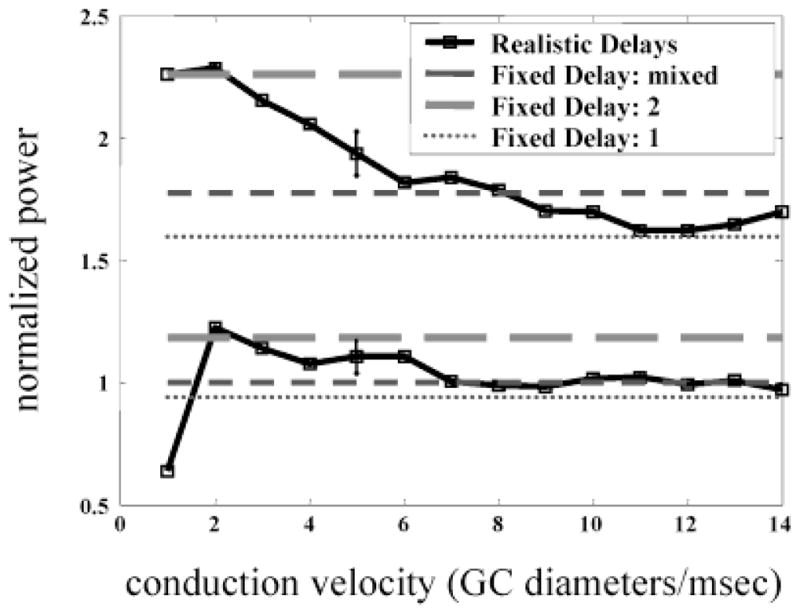
HFOPs in the retinal model increase with average axonal delay. Total energy in the gamma-frequency band (40–160 Hz) is plotted either as a function of axonal conduction velocity (solid lines), or for different values of a fixed axonal conduction delay (fixed delay = 1, thin line, short dashes; fixed delay = 2, intermediate thickness and dash length; mixed delay, fixed delay = 1 for PA ↔ PA connections, 2 for all other axonal connections, thickest line, longest dashes). Total gamma power expressed as a fraction of the baseline value obtained with the canonical model parameters (mixed delay). In response to a constant stimulus centered over the recorded ganglion cells (size = 8 × 8 GC diameters, $\text{intensity}=\frac{1}{2}$, solid lines), total power in the gamma-frequency band during the plateau portion of the response declined as the average conduction delay was reduced. A similar effect was seen during background activity (lower set of curves). All connections had a minimum fixed delay of 1 ms.

Nonspiking amacrine cells

The nonspiking amacrine cells were not essential for the production of HFOPs, but synaptic interactions among the three model amacrine cell types extended the dynamic range of ganglion cell responses to spots centered in their receptive fields. Serial inhibition between the three amacrine cell types was implemented as a negative feedback loop: {PA} → {LA} → {SA} → {PA}, where the arrows indicate inhibitory synapses (see Fig. 1 for abbreviations). The different amacrine cell types in the model thus regulated each other. To test whether serial connections among the different amacrine cell types extended the dynamic range of the ganglion cell receptive-field center, the synaptic strengths of all three serial connections in the feedback loop were reduced by a factor of four and a constant hyperpolarizing bias current was applied to each amacrine cell to compensate for the reduction in tonic inhibition. With the loop gain thus decreased, amacrine cell activity saturated more quickly as a function of stimulus intensity, thereby eliminating the plateau portion of the ganglion cell response at higher stimulus amplitudes (Fig. 10a). A second synaptic mechanism that increased the dynamic range of the model ganglion cells was negative feedback from all three amacrine cell types onto bipolar cells. When the strengths of these feedback connections were all reduced by a factor of 4, the plateau phase of the ganglion cell response to maintained center stimulation saturated at lower stimulus intensities (Fig. 10b), as reported for amacrine cell feedback onto mammalian bipolar cells (Euler & Masland, 2000).

Fig. 10.

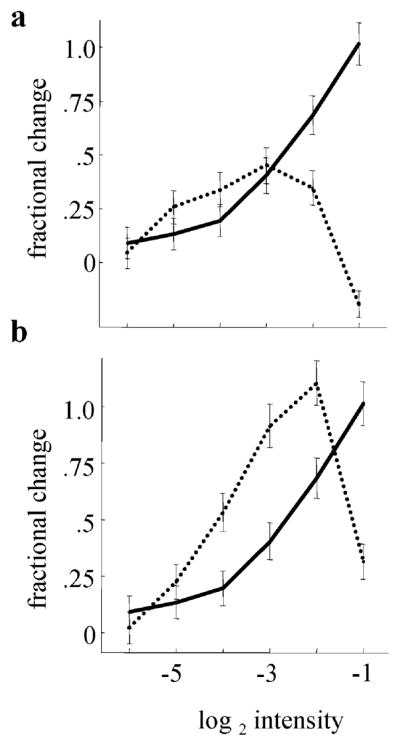
Synaptic interactions mediated by nonspiking amacrine cell increased the dynamic range of model ganglion cell responses. The fractional change in the firing rate of a representative ganglion cell during the plateau portion of the response, relative to baseline, is plotted as a function of stimulus intensity. Solid line: Standard parameters. (a) Dashed line: The gain of the negative feedback loop: PA → LA → SA → PA (see Fig. 1 for abbreviations), was reduced by decreasing the weight of each synapse by a factor of 4. At higher stimulus intensities, reduced serial inhibition between amacrine cells caused ganglion cell plateau responses to be suppressed. (b) Dashed line: Inhibitory feedback from amacrine cell dendrites onto bipolar cells was reduced by a factor of 4. Reduced feedback onto bipolar cells caused ganglion cell responses to saturate more quickly as a function of stimulus intensity. (40 trials, 10-ms bin width. Plateau period: 200–600 ms after onset.)

Robustness

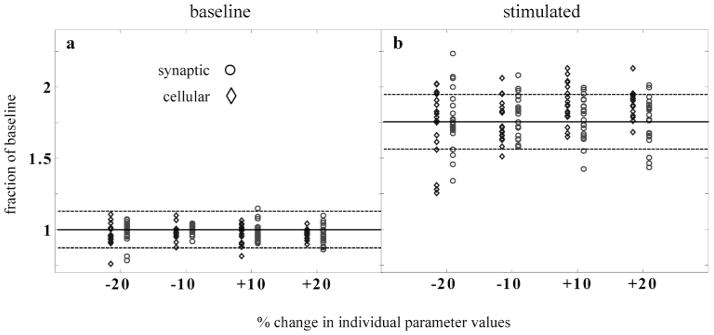
Biological parameters are typically distributed within broad physiological ranges. It would thus be highly unrealistic if the main dynamical properties of the retinal model depended critically on the precise value of any one parameter. To ensure that this was not the case, we assessed the total energy of high-frequency gamma oscillations, both stimulus-evoked and during baseline conditions, after varying every continuous parameter in the model by ±10% and ±20% (Fig. 11). To quantify the strength of the gamma oscillations, subthreshold membrane potentials from an 8 × 8 array of ganglion cells were added together and normalized by the standard deviation to ensure that changes in gamma energy did not simply reflect noisier membrane potentials. The result was Fourier analyzed to determine the total energy in the gamma-frequency band. To eliminate a possible source of confounding noise, the same random number seed was used for each trial, except for ten runs that were conducted with the standard parameter values in order to determine a mean (normalized to 1 in the absence of stimulation) and standard deviation. Model parameters were organized into two categories, depending on whether they specified cellular or synaptic quantities. Changing either category of parameter values by up to 20% did not strongly affect the total baseline energy in the gamma band, as only a few trials were more than three standard deviations from the mean baseline gamma energy obtained with the standard parameters. In no case did the total baseline gamma power deviate by more than ±25% from the standard baseline level.

Fig. 11.

HFOPs in the retinal model were robust to changes in individual model parameters. Each parameter in the model was separately modified by ±10% or ±20% and the strength of HFOPs assessed by measuring the total power in the gamma-frequency band. Results expressed as a fraction of the baseline energy in the gamma band obtained with the standard model parameters. Four modified values are plotted for each canonical parameter value. Cellular parameters (Table 1) indicated by diamonds, synaptic parameters (Table 2) by circles. (a) Robustness of baseline activity. In the absence of stimulation, changing individual parameter values by the amount indicated did not generally cause the total energy in the gamma-frequency band to change by more than three standard deviations from the baseline value obtained with the standard parameters (solid line, mean; dashed lines, 3 S.D.; 10 trials) and in all cases remained within 25% of the mean of the standard value. (b) Robustness of stimulated activity. During stimulation by a large spot (size = 8 × 8 GC diameters, $\text{intensity}=\frac{1}{2}$), in only a few cases did parameter changes of ±10% produce a decrease in total gamma band energy that was more than three standard deviations (dashed lines) below the mean obtained with the canonical parameter values (solid line). Reducing certain parameter values by −20% produced significant reductions in gamma activity, but in no case did total power fall within the range of baseline activity. These results show that HFOPs, while sensitive to certain model parameters, are not critically dependent on the precise value of any one parameter.

To examine the effects of parameter changes on stimulus-evoked activity, we used an 8 × 8 square spot centered over the recorded cells. In no case did changing any single parameter by up to ±20% cause the stimulated oscillatory activity fall within the range of the unstimulated baseline activity, indicating that the collective high-frequency oscillations exhibited by the retinal model were indeed robust. However, for a few parameters, a 20% change produced a significant reduction in oscillatory activity. Most of these “sensitive” parameter changes were clearly related to the generation of oscillatory responses.

Numerical precision

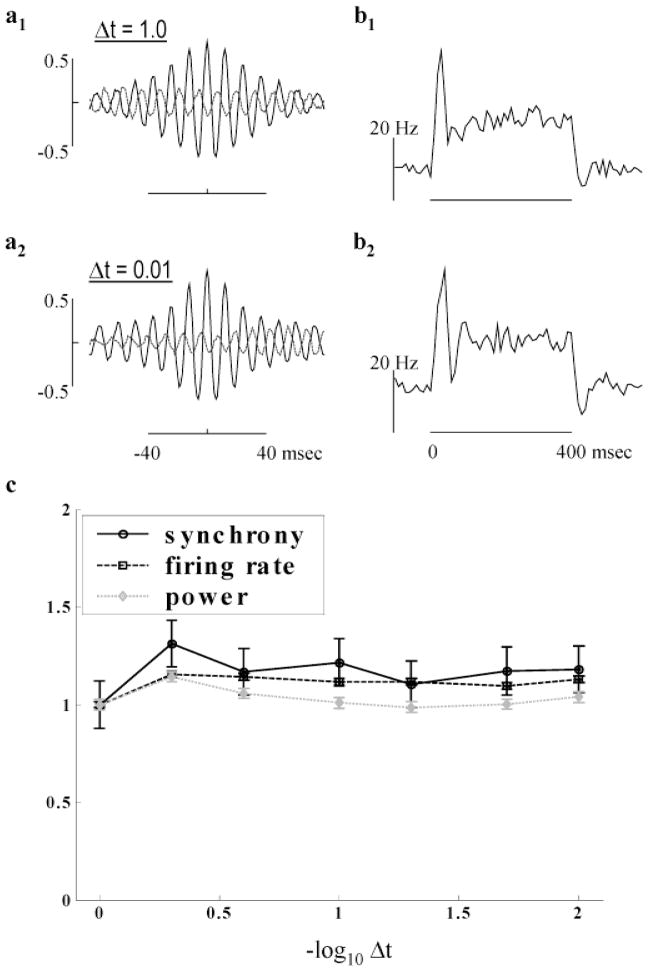
For computational necessity, our simulations employed a simple Euler method and a relatively coarse time step of 1 ms. In noiseless, fully interconnected networks of excitatory integrate-and-fire neurons, global synchronization can be very sensitive to the duration of the simulation time step (Hansel et al., 1998). To investigate the sensitivity of the retinal model to the numerical precision of the integration method, we examined the HFOPs produced by a square spot covering an 8 × 8 array of ganglion cells (intensity = 0.5) after re-running the simulation with a range of integration step sizes, from 1.0 (standard value) down to 0.01 ms, and after modifying the axonal conduction delays as described below (Fig. 12). Due to the additional computational burden of using smaller time steps, only ten stimulus trials were used for the following analysis.

Fig. 12.

Dependence of HFOPs on integration step size. (a_1–2) mCCHs, combining data from all distinct cell pairs stimulated by a square spot covering an 8 × 8 array of ganglion cells (intensity = 0.5, 10 trials). (a₁) Standard model and integration parameters. (a₂) The integration time step was reduced to 0.01 ms and all axonal delays set equal to 2.5 ms. HFOPs were very similar to those obtained with the standard time step and axonal delays, showing that model behavior is independent of step size to within a simple change of parameters. (b_1–2) mPSTHs, computed from the same data as the corresponding mCCH to the left, were mostly unaffected by step size. (c) Model behavior vs. step size. The plateau firing rate (squares), synchrony (circles), and total gamma power (diamonds) reach asymptote for step sizes below approximately 0.25 ms, consistent with the 1-ms rise time of both post-synaptic potentials and artificial spikes in the model.

To assess the amplitude, frequency, and persistence of model-generated HFOPs, mCCHs with high signal-to-noise were obtained by combining the individual CCHs from all stimulated cell pairs (Figs. 12a₁–a₂). Due to the small number of trials, the shift predictors (dashed gray lines) were not subtracted. As a control, the mPSTHs, representing the average response of all stimulated cells, were also calculated (Figs. 12b₁–b₂). When all axonal delays were increased to have the same value of 2.5 ms, HFOPs of similar strength and persistence as those exhibited by the standard model with a 1-ms time step were produced (Fig. 12a₂) while the mPSTH remained approximately constant (Fig. 12b₂). These results demonstrate that quantitatively similar HFOPs could be produced even when using very small step sizes after a relatively simple change in model parameters.

To further document the behavior of the model with respect to increasing numerical precision, the dependence of HFOPs on the integration time step was examined by plotting the synchrony, plateau firing rate, and total gamma power as a function of step size for the case where all axonal delays were equal to 2.5 ms (Fig. 12c). The first set of data points, at a time step of 1 ms, were obtained using the standard model parameters and all values for smaller time steps expressed relative to these. The synchrony, gamma power, and plateau firing rate were all approximately constant for step sizes less than approximately 0.25 ms, below which decreases in the integration time step had negligible effects.

Discussion

A model retinal circuit for generating physiologically realistic HFOPs

We used a computer model to test the hypothesis that physiologically realistic HFOPs could be generated by axon-mediated feedback onto ganglion cells. In support of this hypothesis, model HFOPs were of similar amplitude, frequency, and duration to those reported in the cat retina. Moreover, model HFOPs increased with stimulus size, were only weakly time locked to the stimulus onset, and exhibited an absence of phase locking between noncontiguously stimulated regions, all characteristic properties of retinal HFOPs. The model was generally consistent with other known physiological properties of cat alpha ganglion cells, particularly the dynamics of the receptive-field center, the center-surround organization, and spontaneous levels of correlated firing. The model was robust with respect to small changes in individual parameter values and to the numerical precision of the integration method. Our results demonstrate that there exists a robust set of parameters over which a model based on axon-mediated feedback and consistent with known anatomy can account for key features of retinal HFOPs.

The model consisted of five major cell types, bipolar cells, ganglion cells, and three different kinds of amacrine cells, labeled small, large, and polyaxonal, reflecting the three different spatial scales encompassed by their synaptic connections. Conceptually, the synaptic connections between the various cell types could be organized into four broad categories. (1) Excitation from bipolar cells. (2) Local feedforward and feedback inhibition from amacrine cells. (3) Local serial inhibition between amacrine cells. (4) Long-range axon-mediated feedback.

Connections falling within the first two categories had straightforward effects on the simulated light responses similar to those identified in previous models of retinal networks (Teeters et al., 1997). Excitation from the bipolar cells produced graded responses in both ganglion cells and in the small and large amacrine cells. The amacrine cells, in turn, provided reciprocal inhibition back onto the bipolar cells and forward inhibition of the ganglion cells. Reciprocal inhibition back onto the bipolar cells stabilized retinal activity and expanded the dynamic range over which ganglion cell output increased with stimulus intensity. Graded feedforward inhibition, on the other hand, made the ganglion cell responses more transient, so that the plateau portion of the response to a sustained stimulus was much smaller than the response peak. Inhibitory postsynaptic potentials (IPSPs) from the small and large amacrine cells, as well as EPSPs from the bipolar cells, were stochastically distributed, providing a source of noise that prevented long-range firing correlations between ganglion cells during background firing.

The third category of connections, represented by local serial inhibition between the three amacrine cell types, provided an additional source of negative feedback that allowed the different amacrine cell types to regulate each other. Serial inhibition between amacrine cell types was implemented as a closed loop. The polyaxonal amacrine cells inhibited the large amacrines, the large amacrines inhibited the small amacrines, and the small amacrines inhibited the polyaxonal amacrines. Increasing the excitation to a given amacrine cell type produced a corresponding increase in its inhibitory input, thereby driving the system back toward the resting equilibrium. Local feedforward, feedback, and serial interactions mediated by the model amacrine cells did not contribute directly to HFOPs, but rather played supporting roles that helped stabilize the dynamics of the circuit while increasing sensitivity to spatial and temporal contrast.

Synaptic connections falling in the fourth category, representing interactions that directly contributed to the axon-mediated feedback loop, were essential for the generation of HFOPs. When a group of neighboring ganglion cells was excited by a large, contiguous stimulus, they in turn activated the axon-bearing amacrine cells that were electrically coupled to them. The resulting wave of inhibition affected all cell types, but was most strongly directed to the ganglion cells and axon-bearing amacrine cells. If the stimulus was sustained, ganglion cell firing activity recovered after several milliseconds, thus initiating the next cycle of the oscillation.

Axon-mediated feedback naturally accounted for the main characteristics of HFOPs measured experimentally.

1. Retinal HFOPs are only weakly phase locked to the stimulus onset. The absence of strong stimulus locking indicates that HFOPs arise from a fundamentally nonlinear mechanism. Due to the threshold process for spike generation, axon-mediated feedback is intrinsically nonlinear. Oscillations produced by more linear feedback loops in the inner retina, as might be implemented by reciprocal graded synapses between nonspiking amacrine and bipolar cells, would necessarily be more strongly stimulus locked.

2. Retinal HFOPs are stimulus specific. In the model, gap junctions played a critical role in phase locking oscillations within contiguously stimulated regions. Gap junctions could not phase lock oscillations between separate stimuli, however, as gap junctions strongly attenuate time-varying signals in the absence of spiking (Kenyon & Marshak, 1998). By suppressing spiking activity along a border surrounding each stimulated region, lateral inhibition contributed to making retinal HFOPs stimulus specific.

3. Retinal HFOPs increase markedly with stimulus size. Model HFOPs were strongly size dependent due to the wide spatial divergence of the axon-mediated feedback. By activating a much greater fraction of the axonal inputs to a given ganglion cell, large spots produced much more prominent HFOPs than did small spots.

The above results suggest that with appropriate parameters, axon-mediated feedback is able to account for the main experimental characteristics of retinal HFOPs. This does not imply that the present model is complete, however, as other feedback loops in the inner retina, as well the intrinsic properties of wide-field amacrine cells (Solessio et al., 2002; Vigh et al., 2003), voltage-gated channels in ganglion cell dendrites (Miller et al., 2002) and anodal break excitation (Lipton & Tauck, 1987) might all contribute to HFOPs as well.

Retinal HFOPs in other species and cell types

Our model suggests an explanation for HFOPs measured in retinal cell types other that cat alpha ganglion cells. Beta, or X, ganglion cells in the cat retina also exhibit HFOPs (Neuenschwander et al., 1999), but unlike alpha cells are not tracer coupled to amacrine cells (Vaney, 1994) and thus are unlikely to actively participate in the oscillatory feedback loop. However, beta cells may still receive inhibitory synapses from axon-bearing amacrine cells and through this pathway may be modulated by HFOPs. In the primate retina, M ganglion cells are thought to be homologous to alpha cells in the cat retina (Peichl, 1991) and exhibit similar patterns of tracer coupling (Dacey & Brace, 1992; Vaney, 1994; Jacoby et al., 1996). This homology suggests that primate M cells may participate in the generation of HFOPs via axon-mediated feedback. HFOPs are evident in human (De Carli et al., 2001) and monkey ERG and impulse response functions recorded from primate M cells exhibit a damped, high-frequency oscillation in response to large-diameter spots (Lee et al., 1994). In addition, both alpha cells and M cells exhibit a high-frequency resonance in their temporal modulation transfer functions (Frishman et al., 1987; Solomon et al., 2002). HFOPs are also present in the rabbit retina (Ariel et al., 1983), where tracer coupling between ganglion cells and amacrine cells has also been described (Xin & Bloomfield, 1997).

Role of HFOPs in visual processing

We suggest that retinal HFOPs represent a novel form of contrast enhancement. Because retinal HFOPs are only evoked by large, contiguous stimuli, they allow neighboring ganglion cells to indicate when they are responding to a large contiguous object as opposed to a small isolated spot. The mean firing rate among neighboring ganglion cells is strongly modulated by local contrast (Troy & Enroth-Cugell, 1993) and thus cannot signal information about global size as well. HFOPs allow global topological information to be encoded in the local firing activity of neighboring ganglion cells independent of their mean firing rates. In principle, HFOPs could allow downstream neurons in the lateral geniculate nucleus (LGN) and primary visual cortex to respond more vigorously to inputs arising from large objects. Consistent with this hypothesis, simultaneous recordings in cat from the retina, the LGN, and from area 18 of the visual cortex indicate that phase-locked oscillations between retinal ganglion cells can propagate to higher levels in the visual system (Castelo-Branco et al., 1998), and both experimental and theoretical evidence suggests that synchronous inputs are particularly salient inputs to cortical neurons (Kenyon et al., 1990; Alonso et al., 1996; Usrey et al., 2000).

Predictions of the model

The model predicts that HFOPs among retinal ganglion cells depend critically on spiking amacrine cells and heterologous gap junctions, and it should be possible to test these predictions experimentally. There is evidence that the axon-bearing amacrine cells electrically coupled to ganglion cells contain cholecystokinin (Jacoby et al., 1996). It might therefore be possible to use immunotoxin-mediated cell-targeting techniques, such as have been used to eliminate cholinergic amacrine cells (Yoshida et al., 2001), or cell ablation methods tied to the expression of a particular peptide (Nirenberg & Meister, 1997), to directly investigate the contribution of axon-bearing amacrine cells to the generation of HFOPs. Knock-outs deficient in specific connexins have been used to assess the role of gap junctions in normal light responses (Guldenagel et al., 2001) and in the generation of gamma oscillations (Hormuzdi et al., 2001), raising the possibility that selective ablation of gap junctions between amacrine cells and ganglion cells may soon be experimentally feasible.