Shape-Based Classification of 3D Facial Data to Support 22q11.2DS Craniofacial Research

Abstract

3D imaging systems are used to construct high-resolution meshes of patient’s heads that can be analyzed by computer algorithms. Our work starts with such 3D head meshes and produces both global and local descriptors of 3D shape. Since these descriptors are numeric feature vectors, they can be used in both classification and quantification of various different abnormalities. In this paper, we define these descriptors, describe our methodology for constructing them from 3D head meshes, and show through a set of classification experiments involving cases and controls for a genetic disorder called 22q11.2 deletion syndrome that they are suitable for use in craniofacial research studies. The main contributions of this work include: automatic generation of novel global and local data representations, robust automatic placement of anthropometric landmarks, generation of local descriptors for nasal and oral facial features from landmarks, use of local descriptors for predicting various local facial features, and use of global features for 22q11.2DS classification, showing their potential use as descriptors in craniofacial research.

Introduction

Many genetic conditions are associated with characteristic facial features. A number of medical studies have sought both to quantify the facial features that are affected in these conditions and to help clinicians and researchers to better understand specific shape deformations. Examples of such conditions include: craniosynostosis, a condition caused by the premature fusion of cranial sutures due to biomechanical, environmental, hormonal or genetic factors [1, 2]; 22q11.2 deletion syndrome, a genetically caused condition with its widely variable and often subtle facial feature dysmorphology [3]; and cleft lip and/or palate, a condition that causes abnormal facial development and is the subject of a large NIH-funded research effort called the FaceBase Consortium [4]. This article presents computational methodologies to aid craniofacial research by developing automated and objective measurements of craniofacial dysmorphologies.

From a craniofacial research standpoint, such methods are needed for several reasons. Primarily, computational methodologies can be used to better understand the relationship between different features through associations. For example, the link between facial dysmorphology and brain problems has been shown in [5, 6]. Relationships between facial dysmorphology and cognitive disorders are also being studied [7]. Further, as a specialist's training may lead to subjective detection and grading of a specific feature, an objective mechanism to assess dysmorphology becomes necessary.

Imaging technology has reached a state in which large studies of thousands of individuals can be carried out. After this data is collected, each 3D digital image must be analyzed to produce features that can be used to describe its craniofacial shape. Manual landmarking, the most common form of feature extraction in the craniofacial research community, becomes extremely burdensome or even impossible for the highly trained specialists who would perform this task. Furthermore, a small number of craniofacial landmarks do not fully capture the dysmorphologies being studied. An automatic approach can alleviate this burden and the objective measures used can be leveraged to subdivide the population into feature specific subgroups for further study. Finally, using automatic and objective quantification of craniofacial features in combination with other symptoms, may 1 day aid in the diagnosis of difficult or uncommon syndromes.

In this article we present methods for quantifying 3D facial shape for any condition where the dysmorphology of the craniofacial features is of interest. The craniofacial data used in our studies are 3D meshes from the 3dMD imaging system, which obtains full head meshes using a 12-camera stereo vision data acquisition system. Our methodology includes image acquisition, image cleaning, pose normalization (so that all heads are in a neutral forward-facing position), extraction of descriptors, and representation as feature vectors for use in quantification and classification of the dysmorphologies being studied.

The literature related to 3D craniofacial analysis spans two different communities: computer vision and craniofacial research. In the area of computer vision, 3D facial data is defined as a wire mesh of the head that includes the face. It is of note that there are methods that use texture information for facial analysis [8, 9], but there will be little focus on them here as the data used in this research is textureless, due to human subjects requirements (IRB). Morphable model approaches [10–12] leverage databases of already enrolled 3D head meshes (often hand labeled with landmarks or features) for new image intake and recognition. To reduce the computational requirements, new data representation schemes have been used. Canonical face depth maps [13] create a smaller representation for 3D face data, while work like symbolic surface curvatures [14] concentrated on exactly describing a specific local facial feature. There is also a significant body of work on 3D landmarks and features ranging from landmark detection to appropriate analysis of facial features [15–18]. In each of these cases, landmarks are either hand-labeled or induced from previously labeled faces. Lastly, hybrid 2D–3D methods, where information from one-dimensional space is used to add detail to another dimensional space, are used in an effort to improve facial recognition results [19–22].

Our studies have focused on patients afflicted with 22q11.2 deletion syndrome. Studies investigating the craniofacial phenotype in 22q11.2DS have relied on clinical description and/or anthropometric measurements. Automated methods for 22q11.2DS analysis are limited to just two. Boehringer et al. [23] applied a Gabor wavelet transformation to ten different syndromes associated with facial dysmorphology. The generated data sets were then transformed using principal component analysis (PCA) and classified using linear discriminant analysis (LDA), support vector machines, and k-nearest neighbors. The best prediction accuracy for 22q11.2DS was found to be 96% using LDA, dropping to 77% when using a completely automated landmark-placement system.

The second automated method is the dense surface model approach [24], which aligns training samples according to point correspondences and is thus able to produce an “average” face for each population being studied. Once the average is computed, PCA is used to represent each face by a vector of coefficients. Multiple classifiers were tested, and the best sensitivity and specificity results for 22q11.2DS (0.83 and 0.92, respectively) were obtained using support vector machines [25]. Studying discrimination abilities of local features (face, eyes, nose, mouth) achieved a correct 22q11.2DS classification rate of 89% [26].

The results presented by Boehringer or the dense surface model approach cannot be repeated, as we have neither access to their data nor to the code used to calculate the specific craniofacial descriptors developed in the studies. Both methods require hand-placement of landmarks, exemplifying the lack of automation that makes craniofacial research of large populations so prohibitive. Our landmark-free methodology was designed to remove these limitations and provide both global and local shape descriptors that can advance the state of craniofacial research.

Methods

The methods used in our research are designed to be widely applicable to studying any craniofacial condition. In our work, we have focused on analyzing the shape features of 3D head meshes collected by the Craniofacial Center of Seattle Children's Hospital using the 3dMDcranial™ imaging system. The work was motivated by an ongoing research study of 22q11.2 deletion syndrome, a genetic disorder that affects facial appearance. The Seattle Children's Institutional Review Board approved the study procedures.

The 3dMD imaging system (see http://www.3dmd.com/) constructs 3D meshes from multiple-camera stereo. Our system has 12 cameras, three on each of four stands. The system takes 12 color images of the patient's head from multiple directions, all within a few milliseconds. 3D data is obtained by a technique called active stereo photogrammetry, which projects a unique light pattern on the subject while the images are taken. Using this light pattern, the system is able to identify the same unique point on the head from multiple images in which it appears. Since the cameras are pre-calibrated, the correspondences can then be used by a triangulation algorithm that produces a 3D point for each of the 2D point correspondences. From these 3D points, a 3D mesh is constructed in which each point is a vertex and neighboring points are connected by edges. The 3D mesh is the input to our algorithms.

An automated system to align the pose of each mesh to a forward-facing neutral position was developed and is described in [27]. In brief, the original 3D double precision mesh was interpolated to a 2.5D ordered grid. Symmetry was used to align the yaw and roll angles. The depth differential between the chin and forehead was used to align the pitch angle.

Global Data Representations

Since operations on 3D meshes can be computationally expensive, and 3D meshes do not provide any inherent ordering of the data, we chose to simplify the data through extraction of alternate representations. Three global representations were chosen based on desired face information: (1) frontal and side snapshots of the 3D meshes, (2) 2.5D depth images, and (3) 1D curved line segments. 2D snapshots of the 3D mesh images were used as a starting point, while interpolation to a 2.5D depth image was used as a means of retaining the 3D aspect of the original mesh while simplifying the representation. The 1D curved line segments were used to determine if there was any affected signal in the subsampled face profile. In each data representation, the information was normalized to the same width, while height and depth were scaled to maintain the original image aspect ratio.

2D Snapshots

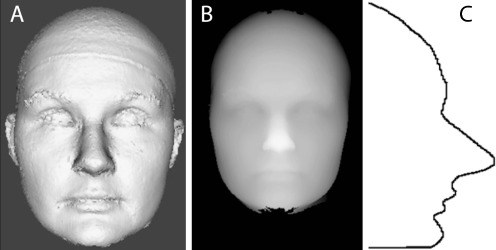
The motivation for using 2D snapshots of textureless 3D meshes came from the eigenfaces [28] approach in computer vision. After neutral pose alignment, a set of frontal photographs of the 3D meshes was generated (Fig. 1a) using the visualization library VTK [29]. Additionally, as these images are most like standard photographs, our automated results could be compared to those of humans in other published papers, or to ratings from dysmorphology experts.

Fig. 1.

Examples of data representations used in experiments. (A) is an example of a frontal snapshot of a 3D facial mesh, (B) is the same individual represented as a 2.5D depth image, and (C) is a 1D curved line segment through the midline of the face

2.5D Depth Images

2.5D images are represented as pixels (Fig. 1b), where the original mesh data is rasterized to an integer-precision structured grid with the highest Z value (the tip of the nose) placed at high illumination. The final width and height of each face is given by the X- and Y-axes, with final depth of the face given by Z. For the X-axis normalization, the face of each individual was scaled to be exactly 200 units wide; the Y- and Z-axes information were scaled to maintain the aspect ratio of the original image. To avoid depth of the face noise, all faces were cut off at the tragus landmarks, from now on referred to as earcut.

Curved Lines

As using full images of participants is always fraught with privacy concerns, we considered the possibility that a less identifiable subset of the data may be sufficient for detecting facial dysmorphology. Using the 2.5D images, curved lines can be extracted that can be used to describe faces. For example, a facial profile, which is a vertical line down the middle of the face (Fig. 1c), becomes a waveform (depth as a function of height) that can be analyzed.

Four versions for both vertical and horizontal lines were selected for signal testing. Odd numbers of lines were used to maintain symmetry in the data. Finally, a combination of the horizontal and vertical lines was used to create grids of sizes 1 × 1, 3 × 3, 5 × 5, and 7 × 7.

PCA Representations

2D snapshots, 2.5D depth images and curved line representations were converted using PCA. PCA is mathematically defined as an orthogonal linear transformation that transforms the data to a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on [30].

Although the genetic defect in a group of individuals may be the same, the expression of a specific clinical feature may be quite varied. For example, palatal abnormalities in 22q11.2DS can vary from dysfunction of an otherwise normal-appearing palate to an overt cleft of the palate [31]. In order to understand this range of feature phenotypes, we choose to develop local facial feature descriptors as described below.

Local Data Representation

Local facial features were developed based on the 2.5D depth images. The nose and mouth areas, with arguably the strongest signals for 22q11.2DS based on literature, were chosen as the first of local features to examine. As anthropometric studies are the current standard in craniofacial research, and since the positions of the nose and mouth were needed for shape-based analysis, an automatic landmark detection algorithm was developed.

A set of craniofacial anthropometric landmarks and inter-landmark distances to characterize the craniofacial features frequently affected in 22q11.2DS were initially selected [32]. Thirty-three of these measurements were identified based on demonstrated high inter- and intra-rater reliability, as well as high inter-method reliability when comparing measurements taken directly with calipers and those taken indirectly on the 3dMD imaging system [33]. Twelve of these landmarks were amenable to automatic detection, and were used to calculate ten inter-landmark distances (see Table 1) for subsequent inter-method comparisons between hand-labeled and automatically detected landmarks. The landmark detection was described with mathematical detail in [34].

Table 1.

Landmark distances obtained using automatically detected landmarks. Note that the landmark placement of ac is approximated to be in the same location as the landmark al

Symbol	Description	Landmarks involved
LA1	Nose width	right al, left al
LA2	Nose tip protrusion	sn, prn
LA3	Mouth width	right ch, left ch
LA4	Upper lip height	sn, sto
LA5	Upper lip vermillion height	ls, sto
LA6	Vermillion height of lower lip	sto, li
LA7	Right alar base length	right ac, sn
LA8	Right alar stretch length	right ac, prn
LA9	Left alar base length	left ac, sn
LA10	Left alar stretch length	left ac, prn

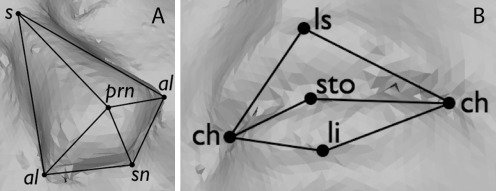
The nasal landmarks used are the sellion(s), pronasale (prn), subnasale (sn), and left and right alae (al). Additionally, a helper landmark mf′ was used that is similar to the maxillofrontale (mf): a landmark that is located by palpation of the anterior lacrimal crest of the maxilla at the frontomaxillary suture (Fig. 2a). The oral landmarks of interest are the labiale superius (ls), stomion (sto), labiale inferius (li) and left and right cheilion(ch) (Fig. 2b). Automatic detection of nasal landmarks was performed using methods described in [34], while oral landmarks were detected using new methods described below.

Fig. 2.

Landmarks of interest, where (A) shows nasal landmarks, while (B) shows oral landmarks

Using Besl-Jain peak curvature information, the prominent parts of the upper and lower lip area are found [35]. The labiale superius (ls) location is found where the lower edge of the upper lip area intersects with midline; while the labiale inferius (li) is found where the upper edge of the lower lip area intersects with midline, see Fig. 3. To detect the stomion (sto) the local z value minimum between ls and li is used.

Fig. 3.

Detecting landmarks of the mouth. (A) lips and corners of mouth show in dark and light gray. (B) ls and li landmarks shown in light gray. (C) mouth line shown in dark gray. (D) ch landmarks detected shown in light gray as ends of mouth line

The left and right cheilion (right ch and left ch) are detected using a combination of two methods. The first method builds on the local minimum search by detecting a mouth line as the trough between the upper and lower lip, ending once the trough disappears as the lips meet (Fig. 3c). Specifically, using sto as the starting point, the line is extended to the left by selecting the minimum of the closest three neighbor points. This process stops when no local minima can be found. The approach is then repeated for extending the mouth line to the right. The one drawback to this method is that it may fail to stop at the appropriate point.

The second approach used is based on the peak curvature values. As the corners of the mouth are natural peaks, this method searches along the horizontal for the two nearest peak areas (or dots) to sto, shown in light gray in Fig. 3a. Once each mouth corner dot is found, a bounding box is defined. The geometrical center of each bounding box is calculated, yielding the location of ch (Fig. 3d). The drawback of this method is that due to face shape the peak image may not contain the mouth corner dots or the dots may extended downward to the bottom of the chin. When the mouth line and dot approaches are used together, the drawbacks of each method are minimized.

We have found that anthropometric landmark distances are not very good predictors of 22q11.2DS. Therefore, we have developed landmark-based features that are better predictors. Landmark-based features go beyond the traditional anthropometric landmarks by providing normalized landmark distances and angles that allow us to compare diverse ages of individuals. Combinations of landmark measurements can be used to better describe the shape of a particular facial feature than standard anthropometric alone. Eight such descriptors were developed for the nose and six for the mouth.

The landmark-based descriptors for the nose and their symbolic representations are given in Table 2. Normalized nose depth landmark-based nasal descriptor (LN)1 is the ratio of nose depth to face depth. The normalized nose width LN2 is the ratio of the width of the nose to the width of the face. The normalized nasal root width LN3 is the ratio of the nasal root width to face width. The normalized nasal root depth LN4 is the ratio of the nasal root depth to face depth. Average nostril inclination LN5 is the average of the left and right angles created by the lines outlining the side of the nose and the base of the nose. Nasal tip angle LN6 is the angle on the midline M between the sellion and subnasale. Alar-slope angle LN7 is the 3D angle between the left and right alae passing through the pronasale. Finally, the nasal root-slope angle LN8 is calculated as the 3D angle through the sellion, stopping at the left and right mf′.

Table 2.

List of nasal landmark-based descriptors

Symbol	Description
LN1	Normalized nose depth
LN2	Normalized nose width
LN3	Normalized nasal root width
LN4	Normalized nasal root depth
LN5	Average nostril inclination anglea
LN6	Nasal tip anglea
LN7	Alar-slope anglea
LN8	Nasal root-slope anglea

^aDenotes a standard anthropometric distance measure not included in [33] subset

The landmark-based oral descriptors and their symbolic representations are listed in Table 3. The normalized mouth length landmark-based oral descriptor (LO)1 is the ratio of the mouth width to face width. LO2 is the ratio of the height of the vermilion (red pigmented portion of the lips) part of the upper lip to full mouth height. LO3 is calculated similarly to LO2, but for the vermilion portion of the lower lip. The inclination of the labial fissure LO4 calculates the angle between the line given by the location of the left and right cheilion and the horizontal line through the right cheilion. The upper vermilion angle LO5 is the angle between the corners of the mouth and the top of the vermilion part of the upper lip. The lower vermilion angle LO6 is calculated similarly to LO5, but for the vermilion portion of the lower lip.

Table 3.

List of oral landmark-based descriptors

Symbol	Description
LO1	Normalized mouth length
LO2	Normalized vermilion height of upper lip
LO3	Normalized vermilion height of lower lip
LO4	Inclination of labial fissurea
LO5	Upper vermilion anglea
LO6	Lower vermilion anglea

^aDenotes a standard anthropometric distance measure not included in [33] subset

Results

The data set used contained 53 affected individuals, who all had a genetic laboratory-confirmed 22q11.2 deletion, and 136 control individuals. The study participants were between the ages of 0.8 and 39 years (median 4.75 years), and 51% were female. As the facial features of 22q11.2DS affected individuals can be very subtle compared to the effects of race, gender, or age [27] and because we had very few non-Caucasian cases, we chose to restrict our dataset to a homogonous population of Caucasian only and matched controls and cases in age and gender when possible. This resulted in a subset with even distribution of 43 affected and 43 control individuals; this data set will be called W86. For participant privacy reasons, the data used in this research was restricted to 3D meshes without facial color and texture maps.

To develop ground truth for the local facial features, three dysmorphology experts were asked to predict 22q11.2DS status and to rate commonly known 22q11.2DS facial features as none, mild, or severe on the W86 dataset. When predicting disease status, the sensitivity of these experts was 0.76, 0.91, and 0.97, respectively, with specificity at 0.73, 0.64, and 0.84, and percent correct 74%, 71%, and 90%. We must note that expert 3 had previously met each participant in the study, which may have unconsciously biased her results. When assessing facial feature severity, the experts agreed with each other in 48.5% of the cases. Simplification of the ground truth to represent just the absence or presence of a specific feature only improved the expert agreement to 53%. Therefore, the ground truth was further simplified to represent a median agreement; if two experts agreed as to the presence of a facial feature in an individual, the ground truth was set to reflect this consensus. In this simplified case, the experts agreed with each other 82% on the presence or absence of a facial feature.

As mentioned earlier, global data representations were transformed using PCA. The attributes were assessed as to their ability to distinguish between affected and control individuals. Since 22q11.2DS is associated with a subtle facial appearance and the data is varied in age and sex, the simple solution of examining only the top ten principle components fails. This can be illustrated by using correlation-based feature selection [36] to find the attributes that best predict age, sex and affected in data set W86. Attributes used to best predict affected span the entire principle component list.

The WEKA suite of classifiers [37] was used for all classification experiments. Tenfold cross validation was used for all classifiers, an approach that subdivides the dataset into a 90% training set, and 10% testing set. This is done ten times (folds), each time with a different 90/10 split of the data. Each fold of this system is independently run, and then the results of all tenfolds are averaged. Of all classifiers used, the Naive Bayes classifier (henceforth referred to as Naive Bayes) was found to perform equally well or better than more complex classifiers, most likely due to the small data set and relatively large number of descriptors per individual [38].

The measures used to evaluate success in this research are sensitivity, specificity and percent correct. Sensitivity measures the proportion of actual affected that are correctly labeled as affected. Specificity measures the proportion of actual unaffected individuals correctly labeled as unaffected. Finally, percent correct (also known as accuracy) measures the portion of all decisions that were correct decisions. For all the measures listed here the results range from 0 to 1, with a score of 1 being the best.

Global Classification Experiments

Snapshots Versus 2.5D

The purpose of this experiment was to determine how much data loss would happen by moving from a 3D Snapshot representation to the 2.5D representation of the data. Additionally, since ears are known as a signal carrier for 22q11.2DS and the 2.5D data format is without ears, it was also necessary to test how much data was potentially lost by using the ear cutoff threshold. All images were 250 × 380 in size.

As seen in Table 4, the 2.5D data format was found to be better than the original 2D snapshot and earcut 2D snapshot at classifying 22q11.2DS disease status. This 2.5D will be used as a baseline for the following experiments.

Table 4.

Checking for data loss between data representations

Data Set	2D snapshot of 3D head	2D snapshot of 3D head earcut	2.5D earcut
Specificity	0.89	0.86	0.87
Sensitivity	0.63	0.60a	0.72
% Correct	76.13	72.93	79.90

All data shown here is from the W86 dataset classified using Naive Bayes

earcut refers to head data which was trimmed to show the face only from the tragus to the pronasale

^aStatistically significant degradation as compared to 2.5D is marked

Curved Lines

The purpose of this experiment was to discover if subsets of the data, such as curved lines, contain 22q11.2DS signal. The three and five vertical curved line representations performed the best (Table 5). Generally, horizontal lines performed poorly. Based on known 22q11.2DS signals such as a hooded appearance of the eyes, prominent forehead profile, relatively flat midface or general hypotonic facial appearance, there is promise in using sparse vertical lines to describe one or more of these anthropometric features.

Table 5.

Classification of vertical curved lines using Naive Bayes on the W86 data set compared to 2.5D depth image

Data Set	2.5D	1 line	3 line	5 lines	7 lines
Specificity	0.87	0.84	0.88	0.85	0.85
Sensitivity	0.72	0.66	0.69	0.72	0.65
% Correct	79.90	74.89	78.74	78.21	74.85

Landmark-Based Descriptor Experiments

Landmark-Based Nasal Descriptor Similarity to Expert Scores

The purpose of this experiment was to assess the ability of the LN to match the experts' median scores for these features. As seen in Table 6, the ability of LN to match the experts' median response for any nasal facial feature is relatively weak. While sensitivity is reasonable, specificity is low, and overall accuracy is, at best, about 60%.

Table 6.

Predicting expert-marked nasal features using landmark-based nasal descriptor (LN) dataset

Data set	Bulbous nasal tip	Prominent nasal root	Tubular appearance	Small nasal alae
Specificity	0.42	0.38	0.22	0.46
Sensitivity	0.65	0.69	0.76	0.71
% Correct	55.71	58.74	59.32	59.72

Landmark-Based Oral Descriptor Similarity to Expert Scores

The purpose of this experiment was to assess the ability of the LO to match the experts' median scores for oral facial features. As seen in Table 7, Open Mouth is well predicted, most likely due to LO2 and LO3, which are ratios of the upper and lower lips to the entire mouth height, and LO5 and LO6, whose angles would become steeper as the mouth is opened. In most cases, both sensitivity and specificity are higher for the oral descriptors than for the nasal descriptors.

Table 7.

Predicting expert-marked oral features using landmark-based oral descriptor (LO) dataset

Data set	Open mouth	Small mouth	Downturned corners of the mouth
Specificity	0.66	0.52	0.38
Sensitivity	0.90	0.68	0.86
% Correct	86.38	63.46	68.18

Landmark-Based Descriptor Classification of 22q11.2DS

The prediction of 22q11.2DS performance for the nasal, oral and combined landmark-based descriptors is compared to the 2.5D global approach. Although using the combination of both the nasal and oral landmark-based descriptors provides an improvement over using just one type of landmark-based descriptor, none of these outperform the 2.5D global descriptor (Table 8), whose performance is significantly higher.

Table 8.

Comparing the prediction of 22q11.2DS using 2.5D, landmark-based descriptors and a combination of all descriptor data

Data set	2.5D	Landmark-based nasal descriptors	Landmark-based oral descriptors	All landmark-based descriptors	2.5D and all landmark-based descriptors
Specificity	0.87	0.60a	0.73	0.68	0.86
Sensitivity	0.72	0.54	0.41a	0.54	0.73
% Accuracy	79.90	56.63a	57.29a	61.17a	79.22

^aStatistically significant degradation as compared to 2.5D

When the landmark-based local descriptors and the 2.5D approach were all used to predict 22q11.2DS, the performance was similar to that of using 2.5D alone. Since the number of descriptors in the 2.5D representation exceeded those of landmark-based and symmetry descriptors by more than a multiple of two an equally weighted combination of descriptors was defined. This was done by using the individual predictions from each of the three descriptor-sets and then using these values as features for a new classification. This weighted approach did not yield further improvement.

Discussion

The main contributions of this work are twofold. First there is automated generation of global data representations, including human-readable representations such as snapshots of 3D data and curved lines, and a computational representation that preserves 3D information: the 2.5D depth image. Second, a robust automated detection of landmarks was developed and used for the automated generation of local data descriptors for the nose and mouth. For each facial feature, landmark-based descriptors were developed. These global and local descriptors were then tested by performing experiments on classification of 22q11.2 deletion syndrome on clinical data. Although the most successful classification algorithm results are presented here (Naive Bayes), 12 other classifiers and boosting methods of variable complexity were explored.

The local descriptors were also used for shape quantification of nasal and oral facial features. Each landmark-based descriptor method was compared to the median of the experts' scores. The mismatches to the expert scores in both the nasal and oral features are not necessarily incorrect predictions, as selective screening of mismatches has suggested mislabeling of the facial feature by experts. Examples of such mislabeling include marking the presence of a bulbous nasal tip, when the small size of the nasal alae is the actual feature or marking the presence of a prominent nasal root, when the nose is tubular in appearance. This further substantiates the need for automated computer algorithms.

Although the focus of this work was on individuals with 22q11.2 deletion syndrome, the methods developed for this phenotype should be widely applicable to the shape-based quantification of any other craniofacial dysmorphology or towards biometric uses. The general methodology is applicable to other medical imaging domains, but the current algorithms are specifically designed to look for the face and its local features. In order to use the methodology to describe other biological shapes, such as feet or hands, the initial processing steps would need to be defined for the particular shape and the shape aspect of interest. Our methodology is not suitable for internal organs, because all our representations rely on there being an important part of the shape (i.e., the face) that can be reduced from 3D to our 2D and 1D representations that allow for very efficient computations compared to the full 3D mesh. Finally, the methodology can be applied to other imaging modalities, such as CT and MRI, as long as the original voxel image can be converted to a 3D mesh.

Conclusions

We have presented a successful methodology using a set of labeled 3D training meshes for discriminating between the craniofacial characteristics of individuals with 22q11.2DS and controls. The main contributions of this work include: an automated methodology for pose alignment, automatic generation of global and local data representations, robust automatic placement of landmarks, generation of local descriptors for nasal and oral facial features, and 22q11.2DS classification that has high correlation with clinical expert ratings.

Due to this promising classification performance, the best-performing descriptors are expected to be useful in craniofacial research studies that attempt to correlate both local and global facial shape with such factors as treatment outcomes, genetic conditions, and cognitive testing. To further prove the effectiveness of these contributions, studies with larger numbers of participants and with different racial and genetic makeup should be conducted. Ratings from a larger number of craniofacial experts should also be used to elucidate a more accurate ground truth for local facial features.