Strategic Insight and Age-Related Goal-Neglect Influence Risky Decision-Making

Abstract

Maximizing long-run gains often requires taking on some degree of risk, yet decision-makers often exhibit risk aversion (RA), rejecting risky prospects even when these have higher expected value (EV) than safer alternatives. We investigated whether explicit strategy instruction and practice can decrease prepotent RA, and whether aging impacts the efficacy of such an intervention. Participants performed a paired lottery task with options varying in risk and magnitude, both before and after practice with a similar task that encouraged maximization of EV and instruction to use this strategy in risky decisions. In both younger and older adults (OAs), strategy training reduced RA. Although RA was age-equivalent at baseline, larger training effects were observed in younger adults (YAs). These effects were not explained by risk-related (i.e., affective) interference effects or computation ability, but were consistent with a progressive, age-related neglect of the strategy across trials. Our findings suggest that strategy training can diminish RA, but that training efficacy is reduced among OAs, potentially due to goal neglect. We discuss implications for neural mechanisms that may distinguish older and YAs’ risky decision-making.

Introduction

Risk taking plays an essential role in the transactions, investments, and decisions that comprise daily life. Assuming a decision-maker wishes to maximize long-run gains, they should select according to expected value (EV): the product of probability and amount, in a given lottery. However, behavioral economists have demonstrated that choices during risky decision-making are best described by a non-linear transformation of both amount and probability values (Kahneman and Tversky, 1979). In particular, decision-makers act as if they find risk aversive by undervaluing risky gains relative to their EV. One operational definition (that we adopt in this paper) of risk aversion (RA) is when decision-makers select a more likely gain with lower EV over a less likely gain with higher EV, on forced-choice, paired lotteries.

Two psychological explanations for RA have different implications for potential interventions. One explanation involves a dual-process tug-of-war between slow deliberation on one side, and automatic, effortless processing on the other (Epstein, 1994; Loewenstein et al., 2001). Automatic, predominantly affective responses to risk (fear or anticipatory regret, for example) are prepotent in that they drive decisions toward safer options even when deliberative assessments warrant risk taking (Thaler et al., 1997; Loewenstein et al., 2001; Slovic et al., 2005). Thus deliberative decision-making may depend on cognitive control processes that facilitate emotion regulation and/or the inhibition of automatic affective responses to risk.

Another explanation is that the difference between RA and a balanced assumption of risk hinges on knowledge of, and experience utilizing, optimal decision-making strategies. Decision-makers may be risk-averse primarily because they do not realize that selecting on the basis of EV will yield higher long-run returns than minimizing risk on individual decisions. Instead, they rely on a sub-optimal strategy like deciding on the basis of probabilities alone. If RA stems primarily from a lack of knowledge and application of an EV-based decision-making strategy, then training to promote insight and experience with this strategy should reduce RA.

Strategy training has improved performance in a variety of cognitive domains (Hartley and Anderson, 1986; McNamara and Scott, 2001; Saczynski et al., 2002; Touron and Hertzog, 2004; Paxton et al., 2006; Dunlosky and Kane, 2007), and spontaneous adaptive strategy shifts have been observed in risky decision-making contexts (Mata et al., 2007, 2010). However, it has not been tested whether simply providing explicit instructions and practice with optimal decision-making strategies can reduce RA.

Even if strategy training reduces RA, cognitive resources may constrain the efficacy of the intervention. Computing and selecting on the basis of EV is more complicated than heuristics like probability maximization, thus placing greater demands on working memory. Decision-makers with diminished working memory may, therefore, make more mistakes when trying to implement the EV-selection strategy. Cognitive control may also be important for several reasons. According to the dual-process account, deliberative EV-based responding will conflict with automatic, risk-averse responding, and cognitive control processes may be required to resolve this response conflict (Botvinick et al., 2001). It is important to note that the lack-of-insight and dual-process explanations of RA are not mutually exclusive. A decision-maker might be less risk averse when they have insight about, and practice selecting based on EV, but only if they can also inhibit automatic response tendencies, for example, by down-regulating their initial affective response to risk. Cognitive control may also play an important role in boosting signals of goal-relevant stimulus features (e.g., EV) in valuation centers of the brain during decision-making (Hare et al., 2009). Hence, even if optimal strategy insight and training reduce RA, training might be less effective for decision-makers with either (or both) diminished working memory or cognitive control.

Older adults (OAs) represent one such population. It is well established that OAs exhibit declines in both working memory and cognitive control (Salthouse, 1990; Park and Reuter-Lorenz, 2009). Reduced working memory, along with reduced processing speed, has been shown to explain apparent RA among OAs across decision-making tasks (Henninger et al., 2010). Another potential handicap for OAs is an age-related impairment in the cognitive control function of goal maintenance (Braver and West, 2008). If overcoming RA depends on goal-directed, top-down biasing of EV-based selection over prepotent risk avoidance, then success with this decision-making strategy will critically depend on cognitive control. Yet, OAs frequently exhibit goal neglect: a progressive tendency to make prepotent, but goal-irrelevant responses over goal-appropriate ones (Duncan et al., 1996; De Jong, 2001; West, 2002; Butler and Zacks, 2006). Thus, OAs are a good population in which to test the limitations of strategy training for reducing RA.

In the current study, younger and OAs were assessed for evidence of RA, both before and after explicit strategy training in EV-based decision-making. The paradigm involved paired lotteries varying explicitly in reward magnitude and probability (cf. Holt and Laury, 2002). We operationalized RA in terms of the proportion of trials in which the lower-risk option was selected when the other (higher-risk) option had a higher EV. In training, participants were instructed to compute and maximize EV and were given practice and feedback explicitly informative of the EV associated with each choice. In the post-training phase, participants were encouraged to use this EV-based decision-making strategy and told it would maximize payoffs.

Our primary goal was to determine whether RA results from a lack of strategy insight and practice, independent of ability to inhibit affective responses to risk. We predicted that if insight matters, our strategy training should be effective in reducing RA, even without targeting affective control. Alternatively, if RA results solely from affective responses to risk, then our strategy training should be ineffective. A secondary goal was to test whether age-related cognitive decline would limit training efficacy among OAs. We further predicted that if implementation of an EV-based decision-strategy critically depends on working memory or cognitive control, reduced training effects should be observed in OAs.

Materials and Methods

Participants

Participants included 40 younger (M_age= 21.0, SD = 2.5, range = 18–33) and 46 OAs (M_age= 75.4, SD = 7.4, range = 65–95). Younger adults (YAs) were recruited from the Washington University in Saint Louis undergraduate community, while OAs were recruited from the Volunteers for Health community database. All participants self-reported no history of neurological or psychiatric disease, and provided informed consent approved by the Human Research Protection Office human subject committee at Washington University in Saint Louis.

Procedure

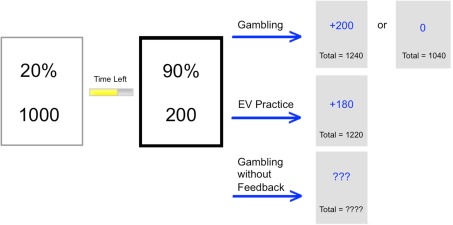
Participants performed a paired lottery task that was programmed and presented in E-Prime 2.0. At the beginning of the experiment, participants were instructed to make a series of choices between paired offers worth different point values. Participants were encouraged to earn as many points as possible since points would later be converted to real money (at an unspecified conversion rate). At the end of the experiment, participants were shown their total point earnings, told the conversion rate, and the amount of money they earned, based on their performance (Figure 1).

Figure 1.

During instructed and uninstructed gambling and EV training, participants choose between paired offers. In gambling conditions, outcomes are all-or-nothing, while in EV training, they are the product of percentages and points. In the follow-up study, older adults received no-feedback as to the outcome of their choices. The option on the right is highlighted to reflect that the participant has chosen that option and the consequences of that choice are shown to the right of each arrow.

Participants were given 7.5 s during each trial to select between the paired offers. A sliding bar indicated the time remaining on each trial. If participants did not make a selection in time, they received feedback indicating that their response was too slow and the next trial was presented. Though trials were time-limited, responses were practically self-paced since 7.5 s apparently provided ample time for most responses for both younger (M = 3.23 s, SD = 1.49 s) and OAs (M = 4.13 s, SD = 1.55 s). Likewise, speed of responding was de-emphasized with the fixed response window, in that faster responses did not increase the rate at which trials were completed.

Two decision-making blocks were performed in counterbalanced order, uninstructed gambling and EV training, followed by a last decision-making block: instructed gambling. During uninstructed gambling, participants were permitted to make their selections by any strategy they wanted in an attempt to maximize earnings. After participants chose an offer, they were informed about the outcome: all-or-none points earned in that trial, and a cumulative total of earnings throughout the experiment.

In the EV-training block, participants were instructed to practice computing and maximizing EV. Trial parameters in this block included reward points, and a percentage indicating the fraction of those points that they were guaranteed to receive. The instructions were to multiply the points and the percentages (i.e., to explicitly compute EV for each offer), decide which offer was larger, and then use this as the basis for their decision. Earnings were always the precise product (equivalent to EV in an all-or-nothing gamble) of their choice. After participants decided, they were informed of the outcome as before: earnings in that trial, and those earned throughout the experiment.

The last block, instructed gambling, was identical to uninstructed gambling but was preceded by explicit instructions that the EV-based selection strategy was in fact optimal and that it should be consistently applied during decision-making in order to maximize earnings.

Instructions prior to instructed gambling

Before starting the instructed gambling block, participants read the following instructions. Note that these referred to the uninstructed and instructed gambling blocks “Probabilistic” and “Deterministic,” respectively, reflecting the key distinction between blocks that outcome was either probabilistic or deterministic in relationship to choice.

• SCREEN 1:

  • Before we begin the next round, we would like to tell you one more thing. In previous versions of this study, we have found that people tend to use very different strategies in the Probabilistic and Deterministic conditions. You might have noticed yourself doing this too!

  • In the Probabilistic condition, we find that most people tend to choose the higher probability option because it feels “safer,” whereas in the Deterministic condition people tend to multiply the probability by the amount on each side and then to choose the larger.

• SCREEN 2:

  • In fact, people’s tendency to choose the higher probability reward in the Probabilistic condition usually results in them earning many fewer points than they could. Mathematically, it is far better to use the SAME strategy in both conditions. If you do this, you will tend to earn many more points.

  • Specifically, you will tend to make the most points if you treat the Probabilistic condition just like the Deterministic condition. In other words, instead of thinking only about the probability of winning, you should always multiply the probability by the amount on each side and choose the larger. Although this may result in smaller gains on some individual turns, over the course of the entire experiment, you will earn many more points.

• SCREEN 3:

  • Now, you will begin doing the PROBABILISTIC version of the task. However, we would like you to use the strategy we just told you about. You should now make all your choices the same way you would make them in the DETERMINISTIC condition: by multiplying the probability times the amount for each option, and choosing the larger. If you do this, you will earn more points (and hence, more money) than if you used a different strategy.

Trial parameters and implications for detecting RA

The same 96 different trials (orthogonal combinations of probabilities and amounts) were used in each of the three blocks described above, presented in pseudo-random order for each participant, and were generated using the following procedure. First, four levels of probability (expressed in percent likelihood) and four levels of amount (expressed as points) were selected for low-risk, low-reward (LL) and high-risk, high-reward (HH) sets of choice parameters (Table 1). Next, for each set, the probabilities and amounts were combined factorially, producing 16 different probability/amount trials for each set. The 16 trials of the LL set were then crossed with the 16 trials of the HH set, producing 256 possible trials.

Table 1.

Probability and amount parameters used to generate the list of 96 trials experienced by every participant.

Probabilities (%)	Magnitudes
LOW-RISK/LOW-REWARD (LL)
50	100
70	200
90	300
100	400
HIGH-RISK/HIGH-REWARD (HH)
10	250
20	500
40	750
60	1000

Because practical constraints precluded presentation of all 256 trials in each experimental condition, a subset of 96 trials were selected according to the following criteria. First, the 256 trials were sorted based on the absolute difference in EVs between the two decks. Values ranged from 0 (identical EVs for both decks) to 550 (one deck had an EV 550 points greater than the other). A majority of the 100 trials with the lowest absolute difference (range = 0–110 points) were selected for inclusion in the final set of 96 trials. These trials represented relatively “difficult” choices, i.e., trials on which the EV of one option was not substantially larger than the other (though there was still substantial variability across trials). The rest of the 96 trials were deliberately selected to (a) have a relatively large difference in EVs between the two sets and (b) roughly equate the number of trials in which each parameter level was presented (e.g., roughly the same number of offers involving probabilities of 10, 20, 40%, etc.). By this method, all 96 trials involved a pairing from a distribution of LL (high probability, Hi Prob) values (point range = 100–400, M = 237.5; probability range = 50–100%, M = 78.5%), while the other involved a pairing from a set of HH (lower-probability) values (point range = 250–1000, M = 622.4; probability range = 10–60%, M = 31.4%). Care was also taken to ensure that the two sets (LL and HH) were closely matched in mean EV (M_LL = 187, M_HH = 183).

In a critical subset of trials (38 of 96), which we refer to as conflict (CF) trials, EV was higher in one option while probability was higher in the other option (e.g., 90% chance of winning 200 points vs. 20% chance of winning 1000). Thus, choosing the Hi Prob option on these trials represents a clear case of RA. In the remainder of the trials, the low-risk option had either equal (EQ) or higher EV than the high-risk option (thus termed non-conflict; NC). Consequently, these trials are non-diagnostic of the particular decision-strategy employed by participants. However, they were included as buffer trials, to make the conflict present in conflict trials less obvious to participants, and to increase the variation of probabilities, rewards, and EVs present across trials. The analyses reported below focused on performance within the conflict trials, except where otherwise noted.

Results

All 96 trials, the average rate of RA on each trial in uninstructed gambling, and the average RA rate in instructed gambling (after the training) are given in the Table A1 in Appendix.

Basic training effects

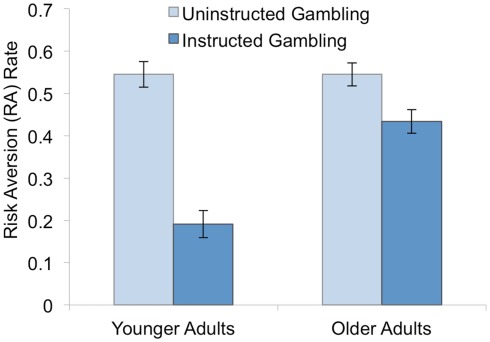
To determine whether strategy training was effective at reducing RA, we performed a 2 × 2 × 2 Block (instructed vs. uninstructed gambling) × Order (uninstructed gambling before EV training or vice versa) × Age (OAs vs. YAs) ANOVA. The dependent measure was the RA rate (i.e., proportion of conflict trials in which the low-risk option was chosen instead of the high-EV option). Results revealed a main effect of instruction block [F(2, 86) = 90.34, p < 0.01] (Figure 2). RA rate was lower in instructed gambling (0.31) than uninstructed gambling (0.55). Thus, training was successful in reducing RA by promoting EV-based decision-making. Moreover, the effect was significant in each group separately [YA: F(1, 38) = 100.39, p < 0.01, OA: F(1, 44) = 10.95, p < 0.01], indicating its robustness. Block order did not interact with the block effect [F(1, 82) = 2.37, p = 0.13], nor was the three-way interaction (Age × Order × Block) significant [F(1, 82) = 0.11, p = 0.74]. Importantly, strategic insight generated a significant reduction in RA from uninstructed to instructed gambling (the main effect of Block) even for the subset of participants who practiced EV-based selection before baseline uninstructed gambling [i.e., for those participants who first gambled after practicing EV-based selection, but before being told EV-based selection could be used to maximize outcomes in gambling; F(1, 42) = 28.96, p < 0.01]. Comparing means in each Order group, uninstructed gambling RA was not significantly lower after EV training rather than before it [uninstructed gambling before EV training: RA = 0.58; uninstructed gambling after EV training: RA = 0.51; t(84) = 1.62, p = 0.11]. These results suggest that practice computing EV has little effect on RA, and that the critical factor in optimizing decision-making is the qualitative insight provided by the explicit instructional manipulation.

Figure 2.

Influence of age and EV-strategy training and instruction on average rate of RA. Strategy practice and instruction reduces RA but less so among older adults.

Although the training effect was significant in both age groups, there was also a significant main effect of Age [F(1, 82) = 13.28, p < 0.01], and an Age × Block interaction [F(1, 82) = 24.33, p < 0.01] revealing that strategy training was less effective in OAs compared to YAs. Average RA in the instructed gambling block was higher for OAs (0.44) than YAs [0.19; t(85) = −6.11, p < 0.01], despite the fact that RA was identical in the two groups during uninstructed gambling (OA: RA = 0.55, YA:RA = 0.55; t < 1). Based on these results, we conducted a series of analyses to better understand both why training reduced RA in both groups, and also why EV training was less effective for OAs.

Potential explanations of training effects

Training was successful in reducing RA, but this could have resulted from some combination of increased reliance on EV, as the training was designed to promote, or increased ability to inhibit the automatic affective response to risk. In the former case, EV-related trial parameters should become more important predictors of choice after training. In the latter case, choice probabilities should become less important predictors of choice after training since choice probabilities presumably drive the automatic affective response.

A multiple regression was conducted to test the influence of trial-by-trial parameters on choice. Specifically, we tested the extent to which EV-related or RA-related predictor variables could predict the pattern of choice on each trial out of the full set of 96 decision trials (indexed by t) performed by participants (Eq. 1). For this analysis, the dependent measure was the proportion of participants (indexed by i) choosing the Hi Prob option. Because each participant received the exact same 96 trials but in permuted order, it is possible to treat the choice pattern across the 96 trials, averaged across participants, as an independent random effect. Two trial-level predictors were selected as independent variables: the probability value of the Hi Prob option, and the difference in EV between the Hi Prob and low probability options (i.e., ΔEV = EV Hi Prob option − EV low probability option; −/+ for conflict/non-conflict trials). These two predictor variables were chosen out of a set of three potential RA-related variables and three potential EV-related variables on the basis of relative reliability. Prior to inclusion the two trial-level predictors were z-scored, while the dependent variable was logit-transformed and then z-scored. Note that for the purpose of transforming proportions of 1 (e.g., where all participants selected the Hi Prob option on a non-conflict trial), a small constant, equal to the smallest, non-zero proportion value across all trials (0.025) was added to the numerator and denominator of the logit function. This ad hoc solution is recommended for logit transformations while introducing minimal bias (Warton and Hui, 2011).

$$\begin{array}{llll}& \text{logit}\left(\frac{{\sum }_{i=1}^{k_{j,m,t}}\text{RA}\text{response}{\text{s}}_{i,j,m,t}}{k_{j,m,t}}\right)& & \\ & ={\beta }_0+{\beta }_1\text{Hi}\text{Pro}{\text{b}}_{j,m,t}+{\beta }_2\Delta \text{E}{\text{V}}_{j,m,t}+{\beta }_3\text{Bloc}{\text{k}}_{j,m,t}& & \\ & +{\beta }_4\Delta \text{E}{\text{V}}_{j,m,t}\times \text{Bloc}{\text{k}}_{j,m,t}+{\beta }_4\text{Hi}\text{Pro}{\text{b}}_{j,m,t}& & \\ & \times \text{Bloc}{\text{k}}_{j,m,t}+{\epsilon }_{j,m,t}& & \text{(1)}\end{array}$$

The first analysis focused on YAs (age-group indexed by m; here m = younger adults), since this was the group showing the largest effects of strategy training in the instructed relative to uninstructed gambling block. To determine the source of this effect, we compared performance on both blocks of the task (indexed by j), examining block-related effects by including a dummy-coded block predictor variable in the analysis (Block_j,m,t = −1/1 for uninstructed/instructed gambling, respectively), with additional predictor variables coding for the interaction of block with the Hi Prob and ΔEV trial-level variables. The results of this multiple regression analysis are presented in Table 2. Both the RA and EV-related parameters were found to be significant predictors of choice. Critically, however, training increased the influence of the EV-related predictor (as evidenced by the significant ΔEV × Block interaction), but had no effect on the influence of the RA-related variable (the Hi Prob × Block interaction). This finding is consistent with the hypothesis that strategy training was effective because it promoted a goal of EV-based selection rather than promoting general affective control.

Table 2.

Multiple regression of standardized, logit-transformed proportion of high probability choices among k_j,young,t ≤40 younger adults on 96 independent trials with one RA-related predictor (the probability of the high probability option, Hi Prob), one EV-related predictor (the difference in EVs: ΔEV), and a dummy variable for block.

Term	β	SE	t	p
Hi Prob	0.20	0.04	4.68	<0.01
ΔEV	0.69	0.04	15.96	<0.01
Block	−0.26	0.04	−6.22	<0.01
ΔEV × block	0.21	0.04	4.97	<0.01
Hi Prob × block	−0.01	0.04	−0.20	0.84

Trial-level predictors were z-scored. N = 2 × 96 = 192 (blocks × trials per block).

Potential explanations of aging effects

A second multiple regression analysis (Eq. 2) was conducted to examine the source of age differences (age indexed by m) that were observed in the instructed gambling block (block indexed by j; here j = instructed gambling), which indicated increased RA among OAs (participant indexed by i) on all 96 trials (trial indexed by t). We tested whether this apparent increased RA in OAs might be due relative inability to control the affective response to risk, which should be reflected in a relatively greater influence of Hi Prob, the RA-related predictor variable. Specifically, a plausible hypothesis is that relatively greater sensitivity to the affective consequences of risk among OAs interfered with their attempts to select based on EV in instructed gambling. To examine this hypothesis we compared performance of the OAs and YAs in the instructed gambling condition, examining age effects by including a dummy-coded age-group predictor variable in the analysis (Age_j,m,t = −1/1 for YA/OAs, respectively), with additional predictor variables coding for the interaction of age group with the Hi Prob and ΔEV trial-level variables. The results of this regression analysis are presented in Table 3.

Table 3.

Multiple regression of the standardized, logit-transformed proportion of high probability choices on 96 independent trials in the instructed gambling block by k younger or older adults, with one RA-related predictor (Hi Prob), one EV-related predictor (ΔEV), and a dummy-coded age variable.

Term	β	SE	t	p
Hi Prob	0.17	0.05	3.69	<0.01
ΔEV	0.70	0.05	14.46	<0.01
Age	0.15	0.05	3.31	<0.01
ΔEV × age	−0.30	0.05	−6.47	<0.01
Hi Prob × age	−0.04	0.05	−0.80	0.43

Trial-level parameters were z-scored. k_j,m,t ≤40/46 for younger/older adults. N = 2 × 96 = 192 (age groups × trials per group).

$$\begin{array}{llll}& \text{logit}\left(\frac{{\sum }_{i=1}^{k_{j,m,t}}\text{RA}\text{response}{\text{s}}_{i,j,m,t}}{k_{j,m,t}}\right)& & \\ & ={\beta }_0+{\beta }_1\text{Hi}\text{Pro}{\text{b}}_{j,m,t}+{\beta }_2\Delta \text{E}{\text{V}}_{j,m,t}+{\beta }_3\text{Ag}{\text{e}}_{j,m,t}& & \\ & +{\beta }_4\Delta \text{E}{\text{V}}_{j,m,t}\times \text{Ag}{\text{e}}_{j,m,t}+{\beta }_4\text{Hi}\text{Pro}{\text{b}}_{j,m,t}& & \\ & \times \text{Ag}{\text{e}}_{j,m,t}+{\epsilon }_{j,m,t}& & \text{(2)}\end{array}$$

This analysis provided no support for the affective response to risk hypothesis of aging effects. Although Hi Prob, the RA-related predictor, remained significant in the instructed gambling block, there was no interaction of this variable with age group. This suggests that the Hi Prob had no greater influence over choice in OAs. In contrast, a significant interaction of ΔEV and age was observed, the sign of which reflected reduced EV influence on choice among OAs. Thus, the results suggest that the apparent age-related increase in RA during the instructed gambling block was not due to a greater influence of probability on choice, but instead to the reduced influence of EV-related information in this age group, after explicit strategy training and instruction.

Another key prediction of the affective interference account is that more frequent (negative) feedback promotes risk-averse behavior (cf. Thaler et al., 1997). Thus, OAs might have shown reduced training effects because these were counteracted by experiences with negative feedback when selecting high-risk options. We tested for feedback effects by conducting a follow-up study with a second group of OAs (N = 40; M_age = 74.0, SD = 6.1, range = 66–88) who experienced the exact same paradigm and procedure but without trial-by-trial feedback regarding decision outcome eliminated in the last, post-training block (i.e., instructed gambling). Comparing the effect of training on RA in the two older adult groups in a 2 × 2 Training (uninstructed gambling vs. instructed gambling) × Feedback Group (present vs. absent) ANOVA, demonstrated that the main effect of training was still present [F(1, 84) = 29.25, p < 0.01, RA: M_uninstructed = 0.54, M_instructed = 0.39], but there was neither a significant main effect of Feedback [F(1, 84) = 2.18, p = 0.14, RA: M_no-feedback = 0.43, M_feedback = 0.49] nor Block × Feedback interaction [F(1, 84) = 2.14, p = 0.15]. Likewise, when comparing the no-feedback older adult group with the YAs, we replicated the Block × Age interaction observed in the original analysis [F(1, 78) = 8.02, p < 0.01].

Alternative explanations for OAs’ relatively higher RA after training include: an age-related impairment in the ability to compute and compare EVs, and an age-related bias toward a probability (as opposed to amount) maximization heuristic, independent of EV. Because the training block explicitly required participants to compute and select on the basis of EV, we used participants’ average performance in this block as a measure of their EV-computation ability in a hierarchical regression analysis of individual RA in instructed gambling (Table 4). We also included their frequency of selecting the Hi Prob option on EQ trials as yet another predictor, reasoning that it represents a measure of how much participants’ decisions are biased by probability (as opposed to amount) when their preference regarding EV is neutralized. This predictor was added after the EV-selection ability measure since a decision-maker would have to compute EV correctly to know that that choice dimension was irrelevant on a given equivalence trial.

Table 4.

Hierarchical regression analysis of alternative explanations of relatively higher RA among older adults in instructed gambling including EV-selection ability and probability-based selection bias.

	β	SE	t	adj R2	ΔR2
STEP 1
Baseline (uninstructed) RA	0.26	0.11	2.46*	0.07	–
STEP 2
EV-computation ability (EV-training block accuracy)	0.53	0.09	5.82**	0.32	0.25**
STEP 3
Probability-based selection bias (EQ high-probability choice)	0.35	0.08	4.11**	0.43	0.11**
STEP 4
Age	0.86	0.15	5.73**	0.59	0.16**

*p < 0.05; **p < 0.01.

The dependent variable is the proportion of RA choices on conflict trials in instructed gambling across both age groups. All proportion data is logit-transformed then standardized. Age is dummy coded (−1/1 for younger/older adults).

As expected, EV-computation ability explained a significant component of between-participants variance in average (averaged across an individual’s choices) instructed gambling RA when controlling for baseline RA (in uninstructed gambling). Also, the bias to select based on probability (as measured by the tendency to select the Hi Prob option on EQ trials) in instructed gambling explained a significant amount of variance when controlling for baseline RA and EV-computation ability. Importantly, however, age was still a significant predictor of RA during instructed gambling even after controlling for uninstructed gambling RA, EV-selection ability, and probability-based selection bias. This implies that even though EV-selection ability and probability-based selection bias constrained training efficacy, they do not fully explain the age differences in training effects.

Aging and goal neglect

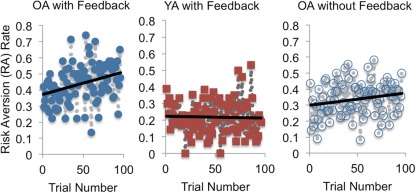
Our preferred interpretation of OAs’ increased propensity to revert to RA after training is that it reflects goal neglect, rather than affective interference, impaired EV-selection abilities, or some other bias to select on the single dimension of probability. The goal-neglect account suggests that even in the absence of active interference, OAs are more likely to commit goal-inconsistent behavior because their goal representations are particularly prone to progressive, but passive decay, when not supported by their environment (Duncan et al., 1996). A key prediction of this account is a decreasing tendency to select on the basis of EV, and a corresponding increase in RA, throughout the instructed gambling block. We tested this by computing the correlation between trial number and RA (Figure 3). Among OAs, a significant positive correlation was observed (r = 0.33, p < 0.01), while in YAs no such correlation was present (r = −0.03, p = 0.77). That is, selectively for OAs, there was a greater tendency to exhibit RA on conflict trials encountered later rather than earlier in the block (i.e., farther removed from training and instructions). The positive correlation was also obtained in the second, independent, sample of OAs who received no-feedback (r = 0.20, p = 0.049), providing further evidence that OAs’ relative failure to maintain the goal of EV-based selection results from passive decay, rather than active feedback-related interference.

Figure 3.

Correlation of average RA rate and trial number for conflict trials in instructed gambling. Significant positive correlations obtain for older adults (OA) but not younger adults (YA), suggesting a goal-neglect effect among OA only. That the positive correlation obtains for OA under both feedback and no-feedback conditions implies that a passive process like goal neglect is a better explanation of the correlations than active interference by affective responses to negative feedback.

An alternative explanation for the steady rise in RA rates among OAs in the instructed gambling block, and one that we believe is incorrect, is that OAs were selectively fatigued by 96 consecutive decisions and thus were simply making more errors as each block progressed. We do not believe this to be the correct explanation for multiple reasons. First, if OAs are prone to fatigue across 96 consecutive trials, we would expect to observe an increasing error rate across the 96 trials of the EV-training block, since in this participants are also explicitly instructed to engage in effortful EV computation. Instead of increasing errors, however, the error rate gradually decreased among OAs during EV training (r = −0.35, p < 0.01). Thus, rather than fatigue effects, OAs showed evidence of improvement, reflective of practice effects across the block.

An analysis of response times (RTs) also provides evidence against a fatigue account. Instead, it supports the goal-neglect consistent explanation that OAs attempted to implement the EV-selection strategy throughout the block, even though their resulting decisions were progressively less biased by their goal to select on the basis of EV. RT analyses are complicated by the fact that participants were not encouraged to respond rapidly, but instead given ample time to respond. However, it is still possible to make predictions regarding the RTs trends expected if participants were becoming fatigued. The average RT to conflict trials among OAs was slower in instructed (4489 ms) compared to uninstructed gambling [4101 ms; t(189) = −8.21, p < 0.01], implying that, as expected, the more complicated EV-selection strategy took longer to implement. If OAs suffered fatigue, their RTs should have either progressively increased, as they took still longer to implement the strategy, or progressively decreased, if they instead relinquished the more taxing strategy and utilized the simpler probability maximization heuristic. However, we observed neither of these trends. Instead, RTs on conflict trials were uncorrelated with trial number among OAs (r = −0.05, p = 0.701). Importantly, this stands in contrast to RT trends on the other two trial types, NC (r = −0.19, p = 0.06) and EQ (r = −0.28, p < 0.01), both of which showed a progressive drop in RTs, reflective of practice effects. Taken together, these two findings are inconsistent with a fatigue account: (a) OAs slowed down after EV instruction and then maintained this slowing on conflict trials, while (b) showing a progressive speeding on non-conflict and equivalence trials, demonstrating that RTs are sensitive to practice effects occurring on some trials. The RT results are most consistent with the interpretation that OAs continued to treat conflict trials as a special case, despite the fact that they were increasingly likely to make the RA choice as the trials progressed. In other words, we suggest that OAs attempted utilize the EV-computation strategy throughout the instructed gambling block; however, as predicted by goal neglect, their behavior became progressively less biased by the goal to actually make selections on the basis of EV.

Discussion

Our results have two important implications for understanding RA. First, we show that RA can be explained in terms of a lack-of-insight regarding which decision-making strategy to employ to maximize returns. Simply orienting participants to the optimal EV-based strategy substantially reduced RA, without any effort to down-regulate automatic, affective biases. Conversely, mere practice at mental computation and selection of EV was not sufficient to reduce RA, demonstrating that the root problem was not an inability or unwillingness to mentally compute EV, but a failure to apply this as an optimal strategy. If practice was sufficient, then a significant reduction in RA should have occurred after the EV-training block, even before receiving explicit instructions. However, we found that the block order of EV training did not significantly affect the amount of benefit obtained by explicit instruction. Conscious insight obtained by explicit instruction was necessary to enable robust implementation of the newly practiced strategy. By suggesting that practice is insufficient to ameliorate RA, we leave open the possibility that spontaneous insight into the nature of the task acquired in the course of practice might indeed exert such a shift in strategy. In an independent set of data (Yarkoni, T., and Braver, T. S., in preparation), we have in fact observed an effect of block order that appears to be attributable to some participants spontaneously realizing that they can apply a maximizing strategy across multiple conditions. The critical point is that it is the strategic insight and not the practice at computing EV that is the essential element.

Second, the gradual return to risk-averse decision-making among OAs appeared to reflect passive decay of goal representations rather than the biasing effects of feedback toward affective responding. The complete removal of feedback did not have a significant effect on the amount of RA (though there was a slight numerical reduction) observed among a second group of OAs in a follow-up study. On the other hand, OAs displayed increasing RA for decisions farther removed from training, suggesting passive decay of representations of the goal to select on the basis of EV. The progressive rise occurred independent of feedback, demonstrating that cumulative feedback effects did not cause it. The progressive rise in RA was also specific to OAs; YAs showed no gradual decay in performance, consistent with the idea that OAs are particularly susceptible to goal neglect and the broader context of age-related decline in cognitive control (Duncan et al., 1996; De Jong, 2001; West, 2002; Nieuwenhuis et al., 2004; Braver and West, 2008).

Our study also adds to the growing literature examining the role of cognitive factors in older adult decision-making. Prior work has suggested that OAs tend to adopt simpler, less-demanding decision-making strategies (Kim et al., 2005; Rafaely et al., 2006; Peters et al., 2007), and that this might be explained in terms of age-related declines in fluid intelligence (Mata et al., 2007). Concomitantly, the mixed findings regarding whether aging is associated with increased RA per se (Dror et al., 1998; Bellante and Green, 2004; Deakin et al., 2004; Denburg et al., 2005; see Mather, 2006) have led some to argue that RA depends more on decision-makers’ cognitive capacities and the nature of the decision-making task, than on inherent effects of age. For example, a recent meta-analysis (Mata et al., 2011), found that age-related differences in risk preference tend to disappear when decision-makers are provided with explicit probability information as opposed to when they must learn about probabilities through experience. Our finding of equivalent baseline RA across age groups is consistent with this literature, since our task involves explicit probability information. Another recent study emphasized the role of the decision-makers’ cognitive capacities rather than age by demonstrating that OAs can evince both relatively elevated risk seeking and elevated RA across tasks with different demands, and that outcomes are mediated by processing speed and working memory (Henninger et al., 2010). Our results agree in that under naïve conditions that are likely promote low-demand, heuristic decision strategies, OAs exhibit equivalent levels of RA to YAs. It was only when the task emphasized the cognitively demanding EV-selection strategy that age-related differences in RA emerged. Nevertheless, even though reduced cognitive capacities, such as working memory, may have limited the effectiveness of EV-strategy training in OAs, the data suggest it is not a full account of age differences, since these were present even after controlling for EV-selection ability.

These findings have important implications for both the theoretical understanding and practical remediation of decision-making deficits in OAs. If, as we have argued, such deficits result in part from passive decay of goal representations, efforts to improve older adult decision-making should focus on developing interventions that emphasize environmental support and contextual information, and not affect regulation. Evidence for the potentially important role of environmental support can be found in a recent study of risky decision-making (Samanez-Larkin et al., 2011). In this study, one condition provided a visual representation of the running EV of options, thereby furnishing continuous, if implicit, environmental support for an EV-selection strategy. Under this condition, performance improved for both older and YAs, with the older group matching YAs’ baseline performance. Unlike our study, however, they did not instruct participants which strategy to use. Instead, participants came to utilize EV signals through reinforcement learning, an approach taken throughout much of the risky decision-making literature. The advantage of explicit insight is that decision-makers in the real world are more commonly presented with single, one-off decisions for which the application of decontextualized, abstract decision strategies may be crucial. If individuals can be given insight, and supported by their environment to apply EV-selection strategies whenever they encounter a risky decision, they might make better choices even in entirely novel decisions.

Our account of the strategy training effects and putative goal neglect among OAs during instructed gambling implies specific predictions regarding neural mechanisms that could be tested in future imaging studies. One prediction that follows from our interpretation is that cognitive control processes related to task-set (goal) maintenance will be engaged preferentially in the instructed gambling block in order to implement the EV-selection strategy. Thus, we would expect to see a neural signature of this strategy in frontoparietal cognitive control networks. Indeed, in preliminary data from YAs, increased frontoparietal activity was observed when comparing the EV-training condition to uninstructed gambling (Yarkoni, 2010). We would further expect this pattern when comparing instructed to uninstructed gambling. A particular region of interest might be the anterior prefrontal cortex (aPFC). Sustained activity in this region has been thought to reflect abstract (or higher-order) task-set maintenance (Braver and Bongiolatti, 2002; Braver et al., 2003; Sakai, 2008). In the context of decision-making, increased sustained activity in aPFC has been observed when decision strategies needed to be maintained across a temporally extended interval (Yarkoni et al., 2005). Thus, we predict increased sustained activity in aPFC in instructed compared to uninstructed gambling, but similar activity in EV practice and instructed gambling. Further, the degree of similarity between EV practice and instructed gambling should predict behavioral findings of greater EV maximization during instructed gambling.

Brain activity dynamics can also provide a convergent test of our account of the age-related findings observed here. As the behavioral signature of goal neglect was a progressive rise in RA, the neural signature of goal neglect would be a progressive decay in sustained aPFC activity, reflecting the loss of task-set. Such a finding would be consistent with prior work, which demonstrated a reduction in sustained aPFC activity among OAs during task-switching, a pattern that was also interpreted as impaired task-set maintenance (Jimura and Braver, 2010). Finally, it would be useful to examine activity dynamics in brain regions responsive to risk and negative feedback (e.g., insula, amygdala, anterior cingulate cortex; Kahn et al., 2002; Kuhnen and Knutson, 2005; Brown and Braver, 2007). Our interpretation of the results is that training and age effects are not due to an altered response to risk and/or negative feedback; thus, we predict that these regions would be active during the gambling conditions (but not EV training, which eliminates the risk component of decision-making), and would show equivalent activity in younger and OAs, along with no decrease in activity among these regions when comparing in instructed to uninstructed gambling. Together, this pattern of imaging results would provide strong support that an interaction of insight and age-related cognitive control processes, such as task-set maintenance, are what differentiate age groups, but not necessarily the affective response to risk.

Our preferred interpretation of the steady return to RA among OAs is age-related goal neglect. Other interpretations are possible, however. OAs may have evinced increasing RA because they progressively abandoned the EV-selection strategy for other unknown reasons. For example, it may have been an intentional decision (instead of an implicit one, based on goal maintenance difficulties), made because of progressive discomfort with utilizing the novel instructed strategy, relative to their greater familiarity and experience in using more heuristic, risk-based decision-making strategies. OAs may have experienced this familiarity asymmetry between experienced-based and the instructed strategy more acutely than YAs, given their longer life-time of experience. However, we did assess compliance with the instructions in a post-experiment debriefing questionnaire, and there was no indication of any participant intentionally switching strategies during the instructed gambling block. Indeed, most participants explicitly reported utilizing the instructed strategy throughout the whole block (in a few cases the question was either not answered, the answer was ambiguous, or, in the case of one participant, the instructions were misunderstood). Nevertheless, in future studies, it may be useful to examine this issue more systematically.

A related account, and one that was not considered in our original design, relates to the age-dependent experience of arousal and emotion regulation. OAs tend to experience arousing stimuli as more aversive than YAs (Keil and Freund, 2009). Despite their relatively enhanced emotion regulation strategies, sustained durations of emotional distress may be more difficult for OAs to overcome (for a review, see Charles, 2010). If selecting the riskier (low probability) option on conflict trials causes arousal in a way that OAs find increasingly aversive and difficult to cope with, they may have found the instructed strategy more discomforting to implement, and instead would develop an accumulating bias against the high-EV option, as it acquires a punishing character. This would be true even for the group of OAs who received no-feedback (and therefore no error signals), because the arousal associated with greater risk taking itself is aversive. However, if OAs are sensitive to the negative valence of arousal associated with risk taking in this paradigm, it is unclear why they would not also be sensitive to the valence consequences of feedback. The fact that feedback did not influence OAs’ RA therefore implies that affective consequences of arousal were not the primary driver of RA among OAs. Nevertheless, more rigorously determining whether the age-related experience of arousal influenced decision-making for OAs would require independent measures of arousal, which were not collected. Hence we cannot rule out that arousal-related aversion to risk taking contributed to what we believe to be age-related goal neglect. The mechanisms that contribute to goal neglect are themselves not fully understood. It is thus possible that goal neglect could be influenced by reinforcement learning (as from punishing arousal) about co-existing, competing goals. Future study is required to understand how aversive arousal may contribute to goal neglect among OAs.

Finally, while we have explained the efficacy of our insight manipulation in terms of task-sets and the proper weighting of choice dimensions (probability and amount in EV), we note that our results could also be accounted for by the behavioral economic theory of “narrow framing” (Barberis et al., 2006; Barberis and Huang, 2009). Narrow framing means that the consequences of a gamble are considered in isolation rather than in the context of the decision-maker’s overall risk profile (including, for example, their income and housing risks). According to the theory, a decision-maker may avoid an independent, actuarially favorable gamble because they do not weigh the benefit of diversifying their risk portfolio, focusing instead on the potential regret associated with losing the gamble. While our results are consistent with helping participants overcome narrow framing, our manipulation was directed at changing participants’ task construal such that they select on the basis of EV. We did not explicitly manipulate whether participants were instructed to select choices in the context of their overall risk profile. Other studies that have done so have found significant changes in individuals’ risk preference parameters. For example, van der Heijden et al. (2011) incited decision-makers to consider multiple gambles at once and found a reduction in RA relative to when they considered single gambles in isolation, consistent with the narrow framing theory. Similarly, Guiso (2009) saw a reduction in RA when participants were asked to consider their future income probability distribution prior to considering a gamble. Future work may consider whether our manipulation promoting a strategy of EV-based selection is convergent with the economic concept of narrow framing.

The primary conclusion of our study is that insight and strategy training can yield better decision-making, but the benefits may be constrained by age-related factors that impact the decision-maker’s ability or willingness to implement the trained strategy. We hypothesize that one important factor to consider is cognitive control and goal maintenance ability. If correct, this hypothesis suggests that apparent RA might manifest under situations in which cognitive control demands drive decision-making. In contrast, under naïve situations, RA may reflect most prominently a lack of knowledge about which strategies are optimal and a lack of practice in implementing them. The benefits of insight were not trivial in our paradigm. Knowing about EV-selection prompted many more decision-makers to take calculated risks. To illustrate, consider a decision between a 90% chance of 200 points and a 20% chance of 1000 points. Prior to training, 56 out of 86 (65%) decision-makers chose the 200-point “safe-bet.” After training, that number reduced to 23, with 73% of participants (63 out of 86) instead preferring the riskier (but higher EV) 1000-point option. Our findings suggest that the role of strategy and insight in decision-making under risk have been underappreciated, and could lead to the development of new intervention programs designed to remediate decision-making deficits in both younger and older adults.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Table A1.

Parameters for each of the 96 trials as well as average rate of risk aversion on each trial both in uninstructed gambling (UG) and instructed gambling (IG), after the training; Trial types include conflict (CF), Non-conflict (NC), for which the high expected value option also has the higher probability, and Equivalence (EQ) trials for which the expected value of the two options is equivalent.

Trial type	Low-risk		High-risk		Older adults			Younger adults
	Prob.	Amt.	Prob.	Amt.	UG	IG	Change in RA*	UG	IG	Change in RA*
CF	1	100	0.2	750	0.54	0.49	−0.05	0.85	0.23	−0.63
CF	0.7	100	0.2	500	0.65	0.41	−0.24	0.73	0.15	−0.58
CF	0.7	300	0.4	750	0.68	0.47	−0.21	0.73	0.18	−0.55
CF	0.7	100	0.4	250	0.57	0.50	−0.07	0.75	0.20	−0.55
CF	1	100	0.6	250	0.57	0.55	−0.03	0.75	0.21	−0.54
CF	0.7	100	0.1	750	0.51	0.49	−0.02	0.78	0.23	−0.54
CF	0.7	100	0.2	750	0.57	0.36	−0.20	0.65	0.13	−0.53
CF	0.9	200	0.4	500	0.57	0.41	−0.17	0.68	0.15	−0.53
CF	0.9	200	0.2	1000	0.60	0.34	−0.26	0.70	0.18	−0.53
CF	0.9	100	0.4	250	0.53	0.51	−0.02	0.85	0.35	−0.50
CF	0.9	100	0.2	500	0.64	0.53	−0.11	0.70	0.20	−0.50
CF	0.7	400	0.4	750	0.68	0.70	0.01	0.78	0.31	−0.47
CF	0.7	100	0.1	1000	0.46	0.28	−0.18	0.55	0.10	−0.45
CF	0.9	400	0.4	1000	0.53	0.38	−0.15	0.50	0.08	−0.43
CF	0.9	100	0.2	1000	0.40	0.41	0.01	0.48	0.05	−0.43
CF	0.7	200	0.2	750	0.72	0.47	−0.26	0.78	0.38	−0.40
CF	1	300	0.4	1000	0.50	0.67	0.17	0.55	0.15	−0.40
CF	0.9	300	0.4	1000	0.49	0.30	−0.19	0.45	0.08	−0.38
CF	0.9	100	0.1	1000	0.59	0.48	−0.11	0.50	0.13	−0.38
CF	0.7	200	0.2	1000	0.55	0.37	−0.18	0.43	0.08	−0.35
CF	0.5	100	0.2	750	0.44	0.65	0.21	0.45	0.10	−0.35
CF	0.9	300	0.6	500	0.68	0.49	−0.19	0.68	0.40	−0.28
CF	0.5	200	0.2	1000	0.50	0.33	−0.17	0.38	0.10	−0.28
CF	0.5	100	0.2	500	0.45	0.36	−0.09	0.38	0.10	−0.28
CF	0.5	300	0.2	1000	0.50	0.46	−0.04	0.35	0.08	−0.28
CF	0.9	300	0.4	750	0.72	0.64	−0.09	0.83	0.55	−0.28
CF	0.9	400	0.6	750	0.61	0.62	0.01	0.73	0.46	−0.26
CF	0.7	200	0.6	250	0.72	0.68	−0.04	0.68	0.43	−0.25
CF	0.7	200	0.4	1000	0.43	0.24	−0.19	0.28	0.03	−0.25
CF	0.7	400	0.4	1000	0.49	0.43	−0.06	0.30	0.05	−0.25
CF	0.5	300	0.4	500	0.40	0.28	−0.12	0.28	0.08	−0.20
EQ	1	200	0.4	500	0.76	0.72	−0.03	0.88	0.68	−0.20
CF	0.7	400	0.6	500	0.45	0.30	−0.14	0.58	0.38	−0.19
EQ	1	300	0.6	500	0.83	0.81	−0.02	0.93	0.75	−0.18
EQ	1	100	0.2	500	0.76	0.77	0.01	0.88	0.70	−0.18
CF	0.6	250	0.5	400	0.49	0.16	−0.33	0.23	0.05	−0.18
EQ	0.5	200	0.1	1000	0.74	0.60	−0.14	0.63	0.45	−0.18
EQ	0.5	200	0.2	500	0.68	0.81	0.13	0.85	0.68	−0.17
EQ	0.6	250	0.5	300	0.47	0.43	−0.03	0.60	0.44	−0.16
CF	0.9	100	0.4	1000	0.48	0.38	−0.10	0.18	0.03	−0.15
EQ	0.5	300	0.2	750	0.68	0.76	0.08	0.75	0.62	−0.13
EQ	1	300	0.4	750	0.78	0.85	0.07	0.90	0.77	−0.13
CF	0.7	300	0.6	500	0.34	0.22	−0.12	0.23	0.10	−0.13
NC	0.9	100	0.2	250	0.87	0.79	−0.09	0.98	0.85	−0.13
EQ	1	100	0.4	250	0.79	0.77	−0.02	0.95	0.83	−0.13
CF	0.5	100	0.4	250	0.47	0.34	−0.13	0.23	0.13	−0.10
EQ	0.5	100	0.2	250	0.83	0.77	−0.06	0.78	0.68	−0.10
CF	1	400	0.6	750	0.79	0.83	0.04	0.78	0.68	−0.10
EQ	1	400	0.4	1000	0.66	0.79	0.13	0.73	0.63	−0.10
EQ	0.5	400	0.2	1000	0.70	0.64	−0.06	0.65	0.58	−0.08
EQ	1	200	0.2	1000	0.66	0.61	−0.05	0.75	0.68	−0.08
NC	1	300	0.4	500	0.91	0.89	−0.03	0.98	0.90	−0.08
EQ	0.5	200	0.4	250	0.74	0.73	−0.01	0.75	0.68	−0.08
NC	0.9	300	0.2	1000	0.85	0.81	−0.04	0.85	0.79	−0.06
NC	1	400	0.4	500	0.87	0.83	−0.04	1.00	0.95	−0.05
NC	1	200	0.2	250	0.89	0.89	0.00	1.00	0.95	−0.05
NC	1	200	0.6	250	0.89	0.89	0.00	1.00	0.95	−0.05
NC	0.6	500	0.5	100	0.87	0.91	0.04	1.00	0.95	−0.05
NC	1	100	0.1	500	0.83	0.91	0.09	0.98	0.93	−0.05
NC	0.6	750	0.5	400	0.82	0.76	−0.07	0.98	0.95	−0.03
NC	0.9	200	0.4	250	0.87	0.85	−0.02	0.98	0.95	−0.03
NC	0.7	300	0.2	500	0.89	0.89	0.00	0.98	0.95	−0.03
NC	0.7	100	0.2	250	0.74	0.76	0.02	0.98	0.95	−0.03
NC	1	100	0.1	250	0.87	0.91	0.04	1.00	0.98	−0.03
NC	1	300	0.2	750	0.81	0.87	0.06	1.00	0.98	−0.03
NC	1	400	0.6	500	0.87	0.96	0.09	0.98	0.95	−0.03
EQ	1	100	0.1	1000	0.70	0.81	0.11	0.75	0.73	−0.03
CF	0.5	200	0.4	1000	0.37	0.11	−0.26	0.05	0.03	−0.03
NC	1	200	0.2	750	0.79	0.76	−0.03	0.95	0.93	−0.02
NC	0.9	400	0.4	750	0.85	0.89	0.04	0.93	0.92	0.00
NC	0.9	200	0.2	750	0.85	0.83	−0.02	0.93	0.93	0.00
NC	0.9	400	0.2	500	0.83	0.85	0.02	1.00	1.00	0.00
NC	1	400	0.1	1000	0.85	0.87	0.02	0.95	0.95	0.00
NC	0.7	400	0.1	250	0.93	0.96	0.02	1.00	1.00	0.00
NC	1	400	0.4	750	0.85	0.89	0.04	0.93	0.93	0.00
NC	1	300	0.2	250	0.91	0.96	0.04	0.98	0.98	0.00
NC	1	300	0.1	750	0.78	0.89	0.12	1.00	1.00	0.00
NC	0.7	300	0.4	500	0.82	0.83	0.01	0.80	0.83	0.02
NC	0.9	300	0.4	500	0.89	0.77	−0.13	0.90	0.93	0.03
NC	0.9	400	0.6	500	0.89	0.81	−0.09	0.95	0.98	0.03
NC	0.5	400	0.1	250	0.87	0.79	−0.09	0.98	1.00	0.03
NC	0.7	200	0.1	1000	0.87	0.83	−0.04	0.83	0.85	0.03
NC	0.9	300	0.6	250	0.81	0.83	0.02	0.98	1.00	0.03
NC	0.7	300	0.6	250	0.79	0.81	0.02	0.95	0.98	0.03
NC	0.7	400	0.1	500	0.77	0.79	0.02	0.98	1.00	0.03
NC	0.9	200	0.6	250	0.77	0.83	0.06	0.95	0.98	0.03
NC	0.6	1000	0.5	100	0.85	0.96	0.11	0.98	1.00	0.03
NC	0.9	200	0.1	500	0.81	0.74	−0.07	0.95	1.00	0.05
NC	0.9	200	0.1	750	0.85	0.83	−0.02	0.95	1.00	0.05
NC	0.5	400	0.2	750	0.83	0.82	−0.01	0.88	0.93	0.05
NC	0.5	300	0.1	250	0.89	0.93	0.04	0.95	1.00	0.05
NC	1	100	0.1	750	0.87	0.96	0.09	0.85	0.95	0.10
NC	0.9	100	0.1	750	0.78	0.89	0.11	0.88	0.98	0.10
EQ	0.5	100	0.1	500	0.64	0.71	0.07	0.55	0.68	0.13
NC	0.5	200	0.1	750	0.79	0.89	0.11	0.75	0.95	0.20
NC	0.7	100	0.1	500	0.87	0.85	−0.02	0.78	1.00	0.23

*Change in RA refers to the change in the frequency of selecting the high probability option, which, during conflict trials, was the operational measure of RA in our study.