Abstract
For the past five decades there has been wide acceptance of a relationship between the firing rate of motor units and the afterhyperpolarization of motoneurons. It has been promulgated that the higher-threshold, larger-soma, motoneurons fire faster than the lower-threshold, smaller-soma, motor units. This relationship was based on studies on anesthetized cats with electrically stimulated motoneurons. We questioned its applicability to motor unit control during voluntary contractions in humans. We found that during linearly force-increasing contractions, firing rates increased as exponential functions. At any time and force level, including at recruitment, the firing rate values were inversely related to the recruitment threshold of the motor unit. The time constants of the exponential functions were directly related to the recruitment threshold. From the Henneman size principle it follows that the characteristics of the firing rates are also related to the size of the soma. The “firing rate spectrum” presents a beautifully simple control scheme in which, at any given time or force, the firing rate value of earlier-recruited motor units is greater than that of later-recruited motor units. This hierarchical control scheme describes a mechanism that provides an effective economy of force generation for the earlier-recruited lower force-twitch motor units, and reduces the fatigue of later-recruited higher force-twitch motor units—both characteristics being well suited for generating and sustaining force during the fight-or-flight response.
Keywords: motoneuron, firing rate, recruitment threshold, voluntary control
the mechanism that regulates the firing behavior of motor units as a function of the excitation to the motoneuron pool during voluntary contractions has been a subject of study and speculation for nearly a century. Early studies on voluntary contractions in humans from Adrian and Bronk (1929) and Seyffarth (1940) found that, as the level of force increases, additional motor units are recruited and the firing rates of motor units increase. Later Henneman (1957), working with anesthetized cats, showed that in response to increasing (physiological) excitation motoneurons are recruited in order of increasing size. This fundamentally important finding was verified by Milner-Brown et al. (1973a) to hold in humans performing voluntary contractions. The recruitment mechanism is now generally accepted. However, the mechanism controlling the firing rates during voluntary contractions remains a subject of controversy.
Over five decades ago, Eccles et al. (1958) reported that, when electrically stimulated, phasic (higher threshold, larger diameter) motoneurons exhibited a shorter afterhyperpolarization and greater firing rates than the tonic (lower threshold, smaller diameter) motoneurons. They postulated that the duration of the afterhyperpolarization is a dominant factor in determining the firing rate of motoneurons. On the basis of these observations they posited that earlier-recruited motoneurons would fire with lower firing rates than later-recruited ones. They also indicated that such a mechanism would provide a fused tetanus of “optimal” size to the low-threshold motor units, which have longer-duration force twitches. This hypothesis was later supported by Kernell (1965c, 2003), who like Eccles performed experiments on anesthetized cats.
In contrast, numerous investigators studying the behavior of the firing rate during voluntary isometric contractions in humans (De Luca et al. 1982a; De Luca and Hostage 2010; Freund et al. 1975; Holobar et al. 2009; Kamen et al. 1995; Kanosue et al. 1979; Masakado 1991, 1994; Masakado et al. 1995; McGill et al. 2005; Monster and Chan 1977; Person and Kudina 1972; Seyffarth 1940; Stashuk and De Bruin 1988; Tanji and Kato 1973 among others) have reported an opposite behavior. That is, higher-threshold motor units, activated at greater levels of excitation, have lower firing rates than lower-threshold motor units.
This study was undertaken to reconcile the disparity in these sets of observations and to propose a model that describes the behavior of motoneuron firing rates. The intent is to formulate a model that provides a general description of the firing behavior of a set of motoneurons in a pool regulating voluntary isometric contractions where the force varies linearly with time. Finer details such as the irregularities of the instantaneous firing rates due to synaptic noise are not considered in this study. They can be included if a more detailed model is necessary, but the version developed in this study provides considerable insight into the manner in which motoneurons are controlled during a voluntary isometric contraction.
METHODS
Subjects.
Eight healthy subjects, five men and three women, reporting no known neurological disorder participated in the study. The average age of the subjects was 24.38 ± 5.21 yr (range 19–35 yr). An informed consent form, approved by the Institutional Review Board at Boston University, was read, understood, and signed by all subjects before participation in the study.
Muscles.
Two muscles were studied: the vastus lateralis (VL) and the first dorsal interosseous (FDI). These muscles were chosen because they are known to have different firing rate properties. The VL muscle recruits motor units to almost maximum voluntary contraction (MVC) force and exhibits firing rates up to a range between 37 and 50 pulses per second (pps) (De Luca and Hostage 2010; Jakobi and Cafarelli 1998; Woods et al. 1987). The FDI muscle has a smaller range of recruitment (up to 67% MVC) and firing rates up to 47–92 pps (De Luca and Hostage 2010; Duchateau and Hainaut 1990; Seki et al. 2007).
Force measurements.
Subjects were seated in a chair that restrained hip movement, immobilized the leg at a knee angle of 60° flexion, immobilized the forearm, and restrained the wrist and fingers. Isometric force during leg extension and index finger abduction was measured via load cells attached to the lever arms of each restraint. The force was band-pass filtered from DC to 450 Hz and digitized at 20 kHz. Visual feedback of the contraction force was displayed on a computer screen.
EMG recording.
Surface EMG (sEMG) signals were recorded from the two muscles by a surface sensor that contained five cylindrical probes (0.5 mm in diameter) with blunted ends that protruded from the housing. The probes were located at the corners and in the middle of a 5 × 5-mm square. The sensor was sized so as to ensure proper electrical contact without piercing the skin when pressed forcefully. For additional details, refer to De Luca et al. (2006) and Nawab et al. (2010). The output of the sensor was connected to an EMG amplifier (a modified Bagnoli 16-channel system developed by Delsys). The subject's skin was prepared by removal of superficial dead skin with adhesive tape and sterilized with an alcohol swab. The surface sensor was placed on a location near the center of the belly of the muscle. The signals from four pairs of the sensor electrodes were differentially amplified and filtered with a bandwidth of 20 Hz to 1,750 Hz. The signals were sampled at 20 kHz and stored in computer memory for off-line data analysis.
Protocol.
The subjects were familiarized with the protocol and practiced the force tracking procedure and the MVC generation task prior to their formal participation in the experiment. At the beginning of the experimental session, we measured the MVC force. Three brief maximal contractions of ∼3-s duration were performed with a rest period of 3 min between trials. The greatest value of the three trials was chosen as the MVC force and was used to normalize the force level among subjects for later comparison. The subjects were then asked to track a series of trapezoidal trajectories displayed on a computer screen, with the output of the force transducers. The trajectories increased at a rate of 10%, 4%, and 2% MVC/s and were sustained at 100%, 80%, and 50% MVC, respectively, for approximately 5, 8, and 10 s. A rest period of at least 10 min was given between trials. The fastest and slowest force rates were the limits of contractions whose EMG signals could be decomposed with the current decomposition technology. The procedure was repeated for both muscles. Most subjects were not able to reach the premeasured 100% MVC level when tracking the prescribed force rates. Those subjects were asked to follow the trajectory up to the highest force level they could achieve.
EMG signal decomposition.
The raw EMG signals from the four channels of the sensor were decomposed into their constituent motor unit action potential trains (MUAPTs) with the sEMG signal decomposition algorithms first described by De Luca et al. (2006) and substantially improved by Nawab et al. (2010). The algorithms use artificial intelligence techniques to separate superimposed action potentials in the sEMG signal, identifying the presence of action potentials and allocating them to individual trains belonging to specific motor units. Note that not all the trains embedded in the sEMG signal are identifiable throughout the signal; hence they are not presented in the output of the decomposition. However, all the sporadic activity of any event above the set threshold throughout the signal is used by the algorithm to make decisions that lead to identifications of firing times and shapes. The technique generally extracts the firings of 30–40 MUAPTs per contraction, and in rare cases reaches 60.
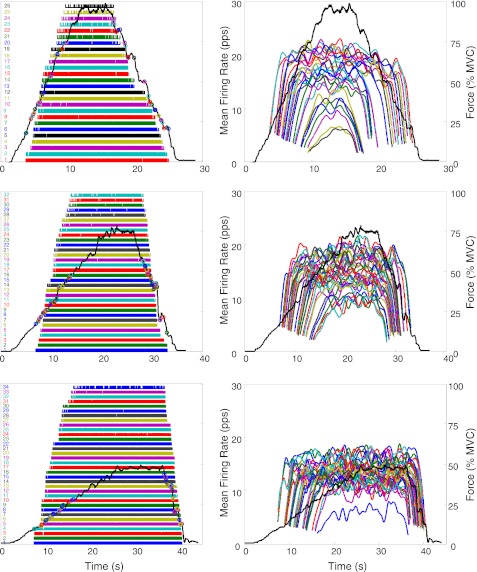
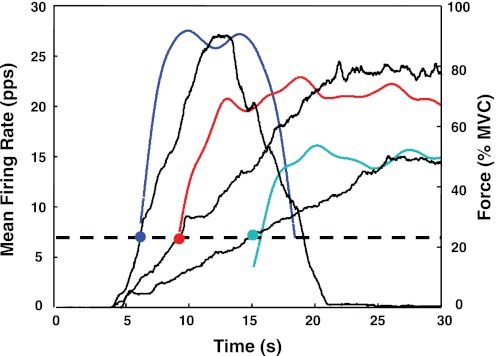
The algorithm produces a file containing the number of motor units observed and the instances of their firings. An example may be seen in Fig. 1, left, which shows the individual firings of the motor units detected during the three force paradigms performed by one subject with the VL. The force trajectories traced by the subject are shown as a dark continuous line. Firing instances (the locations of the action potentials) are plotted as bars (impulses) at the time of occurrence. Figure 1, right, shows a plot of the mean firing rates of these motor units over time. In this figure, the mean firing rate trajectory of each motor unit was computed by low-pass filtering the impulse train with a unit-area Hanning window of 2-s duration. For additional details on the filtering procedure refer to De Luca et al. (1982a).
Fig. 1.
An example of the results of the decomposition of surface EMG (sEMG) signals detected during 3 isometric constant-force contractions of the vastus lateralis (VL) muscle: up to 100% maximum voluntary contraction (MVC) at 10% MVC/s (top), up to 80% MVC at 4% MVC/s (middle), and up to 50% MVC at 2% MVC/s (bottom). The dark solid line represents the force output scaled in % of MVC. Left: firing instances of the decomposed motor units are represented with vertical bars. Circles represent the location of the motor unit recruitment and derecruitment. Right: time-varying mean firing rates. Firing rates were filtered with a unit-area Hanning window of 2 s. pps, Pulses per second.
Accuracy and bias of decomposition algorithm.
Two critical questions arise when a sophisticated algorithm is used to identify, with high accuracy, the individual firings of a large number, commonly 30–50, of motor units from the sEMG signal. One is the accuracy of the algorithm. The other is whether the algorithm introduces a bias that disposes the firing instances to have a structured behavior such as the inverse relationship between the recruitment threshold and the firing rate values of the motor units reported by De Luca and Hostage (2010).
The procedure for measuring the accuracy of the decomposed firing instances is discussed by Nawab et al. (2010). Briefly, the sEMG signal is decomposed to obtain the firing instances of the action potential of each identified MUAPT and the waveform of the action potential. The MUAPTs are summed to form a synthesized signal to which is added a Gaussian noise with a root-mean-squared value equivalent to that of the residual of the decomposed signal. [As discussed in De Luca and Nawab (2011), the advantage of generating a synthesized signal in this manner is that the action potential shapes are real waveforms that contain all the characteristics of a real sEMG signal.] The synthesized signal is decomposed, and all the firing instances are identified and compared with those obtained from the decomposition of the real signal. This operation is referred to as the Decompose-Synthesize-Decompose-Compare (DSDC) test, first introduced in Nawab et al. (2010), improved in the Appendix of De Luca and Hostage (2010), and further improved in appendix 1 of this report.
A measurement of the degree of accuracy of the firings for each MUAPT is obtained according to
where Nerror represents the total number of unmatched events and Ntruth represents the total number of true events found when comparing the firing instances of the real decomposed EMG (dEMG) signal and the decomposed synthesized signal. This calculation was performed for every MUAPT. The accuracy of the decomposition was obtained by averaging the individual accuracies for each train.
The average accuracy of the firing instances tested on a set of 22 isometric contractions from different muscles and at various levels of MVC, including 100% MVC, was 95.2% on average (De Luca and Nawab 2011). Occasionally, the accuracy reached 100% for individual motor units.
To investigate the question of bias, we performed a test that is described in detail in appendix 1 and is summarized here. We decomposed a real sEMG signal to obtain the original decomposed MUAPTs (dMUAPTs) identified in the sEMG signal. We then randomized the firing instances of the MUAPTs, superimposed them, and added Gaussian noise to reconstruct a synthesized signal of randomized MUAPTs. This signal was not imbued with any structured pattern of firing rates. The synthesized signal of randomized MUAPTs was then decomposed. The decomposition yielded the same number of MUAPTs, with similar shapes, and similar time instances to those of the randomized MUAPTs. There was no evident tendency for the algorithm to alter the firing characteristics of the motor units. Therefore, the patterns and trends of the firing rates from the real dEMG can be considered to describe the actual behavior of the motor unit firing properties.
The bias assessment procedure also provided another means for measuring the accuracy of the algorithm. When the accuracy measurement described above was performed by comparing the firing instances of the decomposition of the synthesized signal consisting of a superposition of randomized MUAPTs to the firing instances of the randomized MUAPTs, it was found to be 95.4 ± 1.2%. This value is similar to the 95.6 ± 0.8% obtained when measuring the accuracy by comparing the firing instances of the MUAPTs from the decomposition of the real sEMG signal to those from the synthesized signal consisting of a superposition of the original MUAPTs. These procedures are explained in greater detail in appendix 1.
Data analysis.
The firing rate trajectory of each motor unit was computed by low-pass filtering the impulse train with a unit-area Hanning window of 1-s duration. For each motor unit i, three parameters were extracted from the mean firing rate data: the recruitment threshold (τi), the firing rate at recruitment (λri), and the peak firing rate at the targeted contraction level (λpi). The recruitment threshold was calculated as the force level at which the motor unit began to fire. The firing rate at recruitment was estimated from the inverse of the average of the first three interpulse intervals; the peak firing rate was computed as the average value of the mean firing rate trajectory during the duration of the constant force. If no constant mean firing rate region could be identified in the higher-level contractions at 10% MVC/s, the maximum value of the mean firing rate trajectory was taken as the peak firing rate. Linear regressions were performed on the firing rates at recruitment and peak firing rates versus the recruitment threshold.
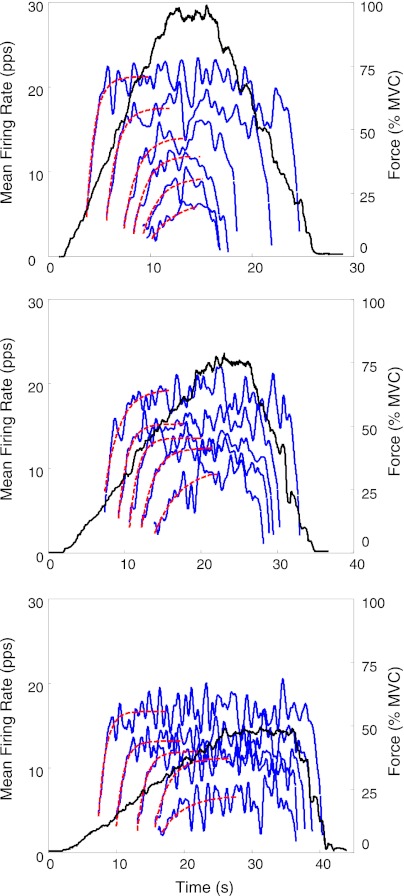
Our data showed a nonlinear increase in the firing rate with respect to the force, with the “velocity” of the firing rate decreasing as the force reaches the highest value. For examples, see Figs. 1 and 2. We fitted an exponential equation to the firing rate trajectory of each motor unit in each contraction to analyze their behavior as a function of time, using the above estimated values for τi, λri, and λpi as starting values for the fit:
| (1) |
for t > tri, where λ̂i is the mean firing rate as a function of time and recruitment threshold; τi is the recruitment threshold as a function of normalized MVC (0 < τi < 1); θ̂i is the time constant of the fitted curve; tri is the recruitment time; λ̂ri is the estimated value of the firing rate at recruitment obtained from the fitted curve; and λ̂pi is the estimated value of the peak firing rate obtained from the fitted curve. See Fig. 2, where the fit is shown superimposed on the actual firing rates of several motor units in three contractions of the VL muscle. Other contractions in the FDI and VL muscles provided equivalently good fits (R2 values between 0.51 and 0.97 for both the FDI and the VL muscles). The estimated value for θi from the fit was obtained for each motor unit. A linear regression was performed on the time constant θi versus the recruitment threshold.
Fig. 2.
Examples of the fit of an exponential function to the mean firing rates in 3 contractions performed with the VL muscle at different rates: 10% MVC/s up to 100% MVC (top), 4% MVC/s up to 80% MVC (middle), and 2% MVC/s up to 50% MVC (bottom). Blue lines represent the mean firing rates of the motor units, which were low-pass filtered with a 1-s unit-area Hanning window. Red dashed lines represent the exponential functions obtained from fitting Eq. 1 by optimizing the firing rate at recruitment, the maximal firing rate, and the time constant of the exponential increase. Note that firing rates of motor units recruited at progressively higher thresholds have a progressively more sluggish rise time, which suggests greater time constants.
The slope and the intercept of the regression lines of each analyzed parameter (λri, λpi, θi) against the recruitment threshold (τi) obtained from the contractions increasing up to 50%, 80%, and 100% MVC at respectively faster force rates were compared. An unpaired t-test was used to determine whether the regressions changed significantly as a function of the force rate by using a threshold α = 0.05.
RESULTS
There are three main observations from our data. The first is that the firing rate of a motor unit increases as a negative exponential function as the excitation (force) increases. See Fig. 2, where the mathematically generated dashed lines are superimposed on the actual firing rates of several motor units in three contractions. The second observation is that the parameters of the firing rates may be expressed as a function of the recruitment threshold (see Figs. 3 and 4) The third observation is that the trajectory of the firing rate is only weakly influenced by the force rate of the contraction within the range of 2% to 10% MVC/s. See Fig. 5, where the firing rate trajectories of three different motor units recruited at approximately the same force level in contractions performed at three different force rates are presented.
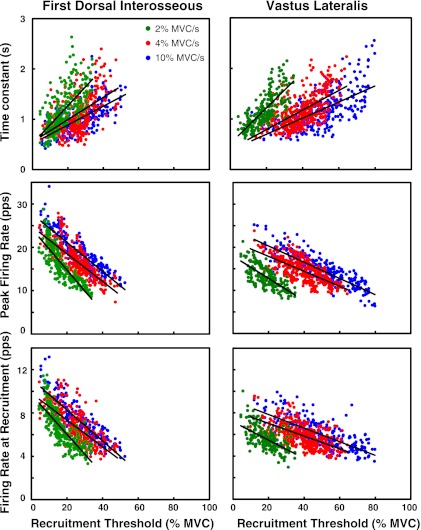
Fig. 3.
Grouped values from all 8 subjects for the firing rates at recruitment (λr), the peak firing rates (λp), and the time constant (θ) vs. the recruitment threshold (τ) for the first dorsal interosseus (FDI) and VL muscles. Results from the contractions performed at 10%, 4%, and 2% MVC/s up to 100%, 80%, and 50% MVC are presented in blue, red, and green, respectively.
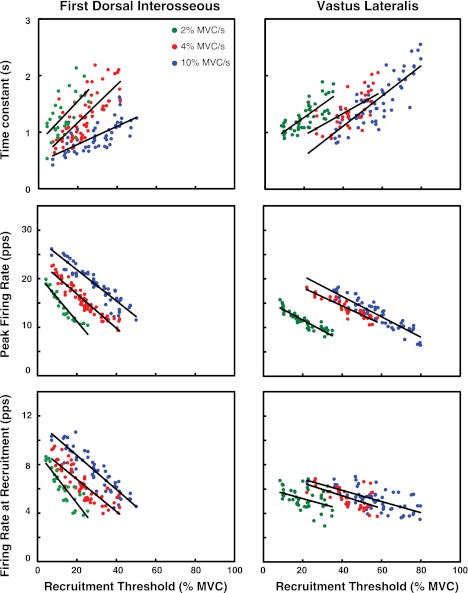
Fig. 4.
Values for the firing rates at recruitment (λr), the peak firing rates (λp), and the time constant (θ) of the firing rate vs. the recruitment threshold (τ) for the FDI and VL muscles of 1 individual subject. Results from the contractions performed at 10%, 4%, and 2% MVC/s up to 100%, 80%, and 50% MVC are presented in blue, red, and green, respectively.
Fig. 5.
The mean firing rate behavior of 3 different motor units recruited at approximately the same force level is shown as the force of the contraction increases at different rates (10%, 4%, and 2% MVC/s). Note how the rate of rise of the mean firing rate trajectories is similar regardless of the different rate of rise of the force.
The number of motor units analyzed in the 10% MVC/s was 224 for the FDI and 289 for the VL; in the 4% MVC/s it was 323 for the FDI and 375 for the VL; and for the 2% MVC/s it was 272 for the FDI and 222 for the VL (see Table 1). Note that, in the regression analysis, the intersubject variability (measured with the R2 value) in the grouped data was generally greater than the intrasubject variability in the individual subjects (see Table 2). Figure 3 and Table 1 contain details on the grouped data and the regression lines for each target force level analyzed. Data from an individual subject are presented in Fig. 4. This observation indicates that trends are more likely to be noticed in data sets obtained within each subject than in data sets formed by grouping subjects.
Table 1.
Statistics, grouped data
| FDI |
VL |
|||||
|---|---|---|---|---|---|---|
| λr(τ) | λp(τ) | θ(τ) | λr(τ) | λp(τ) | θ(τ) | |
| 10% MVC/s | ||||||
| Slope | −14.29 | −33.53 | 1.86 | −6.31 | −18.84 | 1.59 |
| Intercept | 11.14 | 27.85 | 0.51 | 9.11 | 24.05 | 0.38 |
| R2 value | 0.72 | 0.77 | 0.42 | 0.53 | 0.70 | 0.44 |
| No. motor units | 224 | 224 | 224 | 289 | 289 | 289 |
| 4% MVC/s | ||||||
| Slope | −12.35 | −31.93 | 2.21 | −5.91 | −17.32 | 1.94 |
| Intercept | 9.48 | 24.91 | 0.55 | 8.21 | 21.34 | 0.40 |
| R2 value | 0.52 | 0.64 | 0.31 | 0.34 | 0.47 | 0.38 |
| No. motor units | 323 | 323 | 323 | 375 | 375 | 375 |
| 2% MVC/s | ||||||
| Slope | −18.38 | −48.22 | 3.78 | −8.52 | −25.92 | 3.53 |
| Intercept | 9.71 | 24.40 | 0.52 | 7.18 | 17.95 | 0.51 |
| R2 value | 0.62 | 0.72 | 0.45 | 0.34 | 0.51 | 0.56 |
| No. motor units | 272 | 272 | 272 | 222 | 222 | 222 |
Statistics from the regression analysis on the firing rates at recruitment (λr), the peak firing rates (λp), and the time constant of the firing rates (θ) vs. the recruitment thresholds (τ) of the motor units for the grouped data are shown. FDI, first dorsal interosseous; VL, vastus lateralis; MVC, maximum voluntary contraction.
Table 2.
Individual versus common regressions
| FDI |
VL |
|||||
|---|---|---|---|---|---|---|
| λr(τ) | λp(τ) | θ(τ) | λr(τ) | λp(τ) | θ(τ) | |
| 10% MVC/s | ||||||
| R2 value: individual subjects, averaged | 0.78 | 0.86 | 0.60 | 0.63 | 0.82 | 0.54 |
| R2 value: common regression | 0.72 | 0.77 | 0.42 | 0.53 | 0.70 | 0.44 |
| 4% MVC/s | ||||||
| R2 value: individual subjects, averaged | 0.68 | 0.85 | 0.43 | 0.59 | 0.90 | 0.43 |
| R2 value: common regression | 0.52 | 0.64 | 0.31 | 0.34 | 0.47 | 0.38 |
| 2% MVC/s | ||||||
| R2 value: individual subjects, averaged | 0.71 | 0.87 | 0.50 | 0.44 | 0.79 | 0.47 |
| R2 value: common regression | 0.62 | 0.72 | 0.45 | 0.34 | 0.51 | 0.56 |
Comparison of average R2 values of the individual subjects to R2 values of the common regressions (grouped subjects) for the regression analysis on the firing rates at recruitment (λr), the peak firing rates (λp), and the time constant of the firing rates (θ) vs. the recruitment thresholds (τ) of the motor units.
Recruitment threshold.
The VL muscle and the FDI muscle were characterized by different recruitment ranges: Motor units were recruited up to 53% MVC in the FDI muscle and up to 80% MVC in the VL muscle. The values for the FDI are consistent with those reported by De Luca et al. (1982a) (52% MVC), Thomas et al. (1986) (54% MVC), and Kamen et al. (1995) (60% MVC). It should be noted that the maximal recruitment threshold seen in this and other studies does not define the maximal recruitment range in the muscles. For example, De Luca and Hostage (2010) used the same technology employed in this study and reported a maximal recruitment threshold of 67% MVC for the FDI and 95% MVC for the VL muscles. The maximal recruitment threshold identified by our decomposition algorithm in any individual contraction depends on the characteristics of the sEMG signal, the signal-to-noise ratio of the collected signals, and the shapes of the action potentials.
Time constant of firing rate.
The time constant of the firing rate (θ) was computed by fitting the mean firing rate trajectories with Eq. 1. The mean firing trajectories were computed by filtering the trains of impulses of each motor unit with a 1-s Hanning window. This window length was chosen because it provided a smoothed version of the firing rate trajectories without excessively biasing the estimate of the time constant. This choice is discussed further in appendix 2.
Equation 1 provided a good fit to the firing rate trajectories (R2 values are between 0.51 and 0.97 for both FDI and VL muscles). The values of the time constants ranged from 0.42 to 2.64 s for the FDI and from 0.58 to 2.55 s for the VL muscle. When regressed against the recruitment threshold (τ), a positive linear relation was found between θ and τ for all three target force levels analyzed (see Fig. 3 and Table 1). There was a trend for the slope and the intercept of the regression lines to decrease with increasing force rate. The change in the slope was significant only when comparing the contractions at 2% and 4% MVC/s (P < 0.001) and the contractions at 2% and 10% MVC/s (P < 0.001). The change was negligible when comparing the contractions at 4% and 10% MVC/s (P = 0.14) in the FDI muscle and barely significant (P = 0.04) in the VL muscle. The change was negligible also when comparing the intercept (see Table 3 for the complete set of values). The next section will show that a time-dependent excitation function does influence the firing rate trajectory, but the influence is minor for the force rates considered in this study. Thus in our data the time constant is not systematically influenced by the force rate in the force rate range tested.
Table 3.
Comparison between regression lines
| FDI |
VL |
|||||
|---|---|---|---|---|---|---|
| λr(τ) | λp(τ) | θ(τ) | λr(τ) | λp(τ) | θ(τ) | |
| 2%–4% MVC/s | ||||||
| Slope | <0.001* | <0.001* | <0.001* | 0.004* | <0.001* | <0.001* |
| Intercept | 0.64 | 0.30 | 0.59 | <0.001* | <0.001* | 0.10 |
| 2%–10% MVC/s | ||||||
| Slope | <0.001* | <0.001* | <0.001* | 0.012* | <0.001* | <0.001* |
| Intercept | <0.001* | <0.001* | 0.99 | <0.001* | <0.001* | 0.06 |
| 4%–10% MVC/s | ||||||
| Slope | 0.03* | 0.38 | 0.14 | 0.46 | 0.21 | 0.04* |
| Intercept | <0.001* | <0.001* | 0.58 | <0.001* | <0.001* | 0.76 |
P values of the unpaired t-test when comparing the slope and intercept of the regression lines (the relation between λr, λp, and θ vs. τ) for the contractions at different force rates are shown.
Statistical significance of P < 0.05.
The values of the time constant estimated from the fastest contractions (10% MVC/s) are the best representatives of the actual values that can be obtained from our data. Their intrinsic values would be available from contractions where the excitation (force) is provided as a step function, but the sEMG signal from such contractions cannot be decomposed with the present technology.
The regression equation of the data from the fastest (10% MVC/s) contractions was
and
Firing rate at recruitment.
Firing rates at recruitment ranged from 3 to 13 pps in the FDI muscle and from 3 to 10 pps in the VL muscle. These values are consistent with those previously reported by Milner-Brown et al. (1973b), De Luca et al. (1982a), and Duchateau and Hainaut (1990). When regressed against the recruitment threshold (τ), a negative linear relation was found for all three target force levels analyzed (see Fig. 3 and Table 1) The slopes of the regression lines were significantly (P < 0.05) different among all contractions, except for 4% versus 10% MVC/s in the VL muscle (P = 0.46). The intercepts of the regression lines increased significantly (P < 0.001) with force rate in both muscles, with the singular exception between 2% and 4% MVC/s in the FDI muscle (P = 0.64) (see Table 3 for the complete set of values). The increase is likely an artifact of the computational procedure used to estimate the value of the firing rate at recruitment as the excitation increases: The value of the first three interpulse intervals decreases to a greater degree during faster force rates, and the decrease will also be more pronounced for earlier-recruited faster time-constant motor units. This bias has also been noted by Tanji and Kato (1973), who found greater firing rates at recruitment during contractions performed at greater speeds.
The regression equation for the data from the contractions at 10% MVC/s was
and
Peak firing rate.
In the FDI muscle, the peak firing rates observed in this study ranged from 7 to 34 pps. This range is consistent with that found in previous work by De Luca and Hostage (2010) and that reported by Duchateau and Hainaut (1990). In the VL muscle, the peak firing rate range was from 6 to 25 pps. These values are consistent with those found by De Luca and Hostage (2010) and slightly lower (12–40 pps) than those reported by Woods et al. (1987). When regressed against the recruitment threshold (τ), a negative linear relation was found for all three target force levels analyzed (see Fig. 3 and Table 1). The slopes of the regression lines were significantly (P < 0.001) different among all contractions, except for 4% versus 10% MVC/s in the FDI (P = 0.38) and in the VL muscle (P = 0.21). The intercepts of the regression lines increased significantly (P < 0.001) with force rate in both muscles, with the singular exception between 2% and 4% MVC/s in the FDI muscle (P = 0.30) (see Table 3 for the complete set of values). This result is expected given that the target force level of the contractions at faster rates was also increasing. See De Luca and Hostage (2010) for additional details.
A MODEL FOR THE FIRING RATES OF MOTONEURONS
Firing rate spectrum.
We now proceed to deriving an expression for the firing rate of the motoneurons in a pool that activates a muscle during linearly varying force contractions. For each motoneuron i in the pool, the time course of the exponential equation that describes the firing rate may be defined by the time constant θi, the firing rate at recruitment λri, the peak firing rate reached at a target force level λpi, and the recruitment threshold τi. As discussed previously, our data show that in the range of 10% to 2% MVC/s the force rate does not influence the firing rate significantly. Therefore, it can be reduced to a function of time and recruitment threshold approximated by the following equation:
| (2) |
For t ≥ tri, λr, λp, and θ are all linearly related to the recruitment threshold τ of the motor units and may be expressed by the following equations:
| (3) |
| (4) |
| (5) |
Substituting Eqs. 3, 4, and 5 into Eq. 2, we obtain
| (6) |
In an earlier study by De Luca and Hostage (2010), we investigated the relationship of the firing rate with force at target levels of 20%, 50%, 80%, and 100% MVC. We obtained the following relations for the slope mp and the intercept bp of the peak firing rate as a function of force:
| (7) |
| (8) |
The two equations can be incorporated to provide a complete description of the mean firing rate behavior of a specific motor unit i recruited at the threshold force τi, increasing over time as the force φ of the contraction varies:
| (9) |
for t ≥ tri and 0 < τi < 1 and τi+1 > τi. This general equation describes the family of firing rates of the motor units in a muscle during an isometric contraction as it progresses from 0 to maximal force level.
To customize the equation to a specific muscle, the specific parameter values are required. For both the FDI and the VL, parameters mθ, bθ, mr, and br have been previously defined for the greatest force rate contraction (10% MVC/s) since they are the best representatives of the actual values, which would be available from contractions where the excitation (force) is provided as a step function, as previously discussed (see results and Table 1). The values reported for the parameters A, B, C, D, and E are 85, 0.32, −23, 6.93, and 20.9 for the FDI muscle and 116, 0.15, −21, 8.03, and 19.0 for the VL muscle (De Luca and Hostage 2010). Hence, we obtain the following equations for the FDI muscle:
| (10A) |
and for the VL muscle:
| (10B) |
Two other factors are required: the number of motor units in the muscle and the distribution of the recruitment threshold. For the FDI muscle, the number of motor units (n) is ∼120 (Feinstein et al. 1955), the range of recruitment (RR) is 0 to 0.67 (De Luca and Hostage 2010), and, according to Fuglevand et al. (1993), the recruitment threshold distribution is exponential, as shown in Fig. 6, bottom, and may be expressed as:
| (11) |
with
For the VL muscle, the number of units is ∼600. This number is based on a comparison to the rectus femoris muscle reported by Christensen (1959). The range of recruitment threshold is 0 to 0.95 (De Luca and Hostage 2010). We are not aware of any data in the literature reporting the distribution of recruitment threshold for the VL muscle or for other muscles of the quadriceps group. However, Kukulka and Clamann (1981) have provided evidence that the distribution of recruitment threshold for larger more proximal muscles, such as the biceps brachii, is less skewed compared with the exponential distribution of the FDI muscle. Therefore, for the purpose of demonstration, we used the following exponential distribution with a more gradual slope to represent the distribution for the VL muscle:
| (12) |
with
Fig. 6.
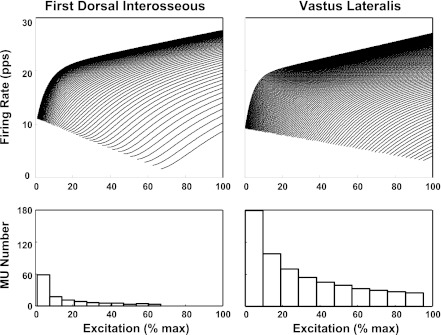
Top: the firing rate spectrum calculated from Eq. 10A for the FDI and Eq. 10B for the VL for some selected motoneurons in the pool of the respective muscles. Note that the firing rate at recruitment is inversely proportional to the recruitment threshold for both muscles and the pattern of the spectra are largely similar, with mild difference between the 2 muscles. For purpose of clarity 1 of every 2 motor units and 1 of every 6 motor units are shown for the FDI and VL muscles, respectively. Bottom: the distribution of recruitment thresholds as a function of excitation for the FDI and VL muscles. The distribution for the FDI is obtained from Eq. 11 (Fuglevand et al. 1993); the similar but less skewed distribution for the VL muscle is obtained from a slightly different equation (Eq. 12) (see text for details). Note that the FDI muscle has a lower number of motor units whose recruitment threshold distribution is skewed to the lower end of the firing rate spectrum compared with that of the VL muscle. Also, the maximal recruitment threshold is greater for the VL than for the FDI muscle.
It is now possible to solve the function λi (t, φ, τi) for all the motor units in a muscle as a function of time, recruitment threshold and excitation (force) level. The resulting spectra of the two muscles for the contraction increasing up to 100% MVC (maximal excitation) are shown in Fig. 6, top, for the FDI and the VL muscles. The two spectra have the appearance of the onion skin property reported by De Luca et al. (1982a), De Luca and Erim (1994), and De Luca and Hostage (2010). The firing rate at recruitment is inversely proportional to the recruitment threshold, and the time constant of the firing rate increase, as evidenced by the sluggishness of the rise of the trajectory, is directly proportional to the recruitment threshold. Overall, the appearance of the trajectories is consistent with the data collected in this study, which are presented in Figs. 1 and 2.
The firing rate spectrum describes the behavior of the firing rate of each motor unit in a muscle when the motoneuron pool is excited to a specific level. Consider the diagrams in Fig. 7. The horizontal axis represents the force produced by the muscle or the excitation received by the motoneuron pool in order to exert a given force output (in %MVC). These two variables are likely nonlinearly related, but they are both monotonic functions of time. The excitation is received by all the motoneurons in a pool, via their interconnections in the pool, and each motoneuron responds according to Eq. 9. The excitation represented here is the net excitation to the motoneuron pool, consisting of the sum of all excitatory and inhibitory inputs. There is evidence for this “common drive” to the pool in our earlier work (De Luca et al. 1982b; De Luca and Erim 1994), which showed that the firing rates of concurrently active motor units have common oscillations that fluctuate in unison at or near zero time delay among the firing rates.
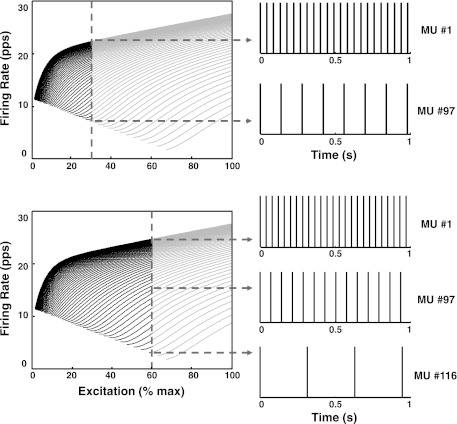
Fig. 7.
A schematic displaying the interpretation of the firing rate spectrum described in Fig. 6. Top: the vertical line indicates the excitation required to produce a constant-force isometric contraction at 30% MVC. This is the common drive to the motoneuron pool. The motoneurons to the left of the excitation line respond to the excitation. The intersection of the vertical line with each of the firing rates corresponds to the value of the firing rate of each motoneuron at the 30% excitation level. Note that earlier-recruited motoneurons have progressively greater firing rates. This is made clear on the right of the panel, which presents the firing impulses of the first recruited motoneuron (1) and the last recruited motoneuron (97) in the distribution. Bottom: the excitation is moved to 60% MVC. Additional motoneurons are recruited, and the excitation line now intersects the firing rates at greater values. This behavior is shown on the firing trains on right of the spectra: the shorter firing intervals indicate that the firing rates of all the motoneurons increase, and the additional train at bottom indicates that new motoneurons (up to 116) have been recruited.
Consider the common drive to a motoneuron pool to be fixed at the equivalent of 30% MVC (φ = 0.3) as in Fig. 7, top. The dashed vertical line traverses the values of the mean firing rates of all the recruited motor units at this excitation level at the left portion of the excitation line. The first motor unit to be recruited has the greatest average firing rate, as shown by the trajectory at the top of the firing rate spectrum. The last motor unit to be recruited at the designated excitation (force) level has the lowest average firing rate. The firing trains of the two motor units at the extremities of the activation range are shown on the right of the firing rate spectrum diagram. If the excitation is increased to the 60% MVC level (φ = 0.6) as shown in Fig. 7, bottom, additional motor units are recruited, each with increasingly lower firing rate at recruitment and increasingly lower average firing rate thereafter.
The firing rate spectrum provides a pragmatic understanding of the control to the motoneuron pool that regulates the firing of individual motor units. It describes the dominant characteristics of the firing rate behavior provided by investigating the behavior of the average firing rate values. It does not describe the realistic irregular interpulse intervals. Such a representation requires the synaptic noise to be added, but is beyond the scope of this work.
DISCUSSION
This study presents evidence that once a motoneuron is activated the firing rate increases as a negative exponential function having the form of Eq. 9. The parameters that define the exponential function (the time constant, the firing rate at recruitment, and the peak firing rate) can all be expressed as linear functions of the recruitment threshold, with the time constant being directly proportional and the firing rate at recruitment and the peak firing rate being inversely proportional. We found these relationships to hold for both the FDI and the VL muscles, which are known to have different numbers of motor units and are considerably different in size.
Firing rate at recruitment.
The firing rate values at recruitment decrease with increasing recruitment threshold according to Eq. 3. This finding is consistent with that of Tanji and Kato (1973). Although the results of some of our previous studies suggested a positive relation between initial firing rate and recruitment threshold (Adam et al. 1998; De Luca et al. 1982a; Erim et al. 1996), the previous work included observation of only a few motor units that could be tracked with our earlier and less sophisticated technology described by LeFever and De Luca (1982) and LeFever et al. (1982). The present technology described by De Luca et al. (2006) and Nawab et al. (2010) contains specialized algorithms for identifying the firings of motor unit near the point of recruitment. The present technology also enables the identification and classification of motor unit firings throughout the full range of force production, from very low to maximal levels, including MVC. The expanded force range provides a more complete assessment of the motor unit firing behavior within a muscle.
Our present findings counter those of Grimby et al. (1979), Moritz et al. (2005), Tracy et al. (2005), and Barry et al. (2007), who also investigated voluntary isometric contractions in humans but found a direct relationship between the firing rate at recruitment and the recruitment threshold. A direct relationship was also reported by Kernell (1965c, 1979), who investigated the firing behavior of severed motoneurons in decerebrated cats. This seeming disparity with our results can be explained by the methodology of the measurements used in all these works. In the work of Kernell (1965c, 1979), the firing rate at recruitment was elicited by providing a barely above-threshold current to trigger the motoneuron to fire. As the motoneuron began to fire, the current was held constant. In a similar way, in the work of Grimby et al. (1979), Moritz et al. (2005), Tracy et al. (2005), and Barry et al. (2007) the firing rate at recruitment was obtained by executing a graded increase or decrease in the force until a minimal and constant firing rate was achieved. This constant-excitation condition differs from that used in this study and is not consistent with the execution of a force-modulated voluntary contraction that is the ordinary modality of muscle use. In the varying-excitation case, after the first firing of the motoneuron, the excitation to the motoneuron increases prior to the subsequent firing. This increase in the excitation causes the motoneuron to fire sooner, decreasing the interpulse interval and resulting in a greater firing rate. According to Figs. 3 and 4, the earlier-recruited (smaller diameter) fibers have a smaller time constant; consequently, the exponential function that describes the firing rate increases faster as a function of time, rendering the earlier-recruited motoneurons more sensitive to the influence of the rising excitation. The inverse relationship follows. The important point is that experiments in which the excitation to the motoneurons is administered as a constant-level marginally suprathreshold current provide firing rate information that is not applicable to describing the firing rate behavior in force-modulated voluntary contractions.
Firing rate trajectory.
Once a motoneuron is recruited and the excitation increases, the firing rate increases as an exponential function according to Eq. 9. The velocity of the firing rate gradually decreases until the firing rate trajectory reaches a peak value that is inversely proportional to the recruitment threshold, as described by Eq. 4. A similar behavior in humans has been reported by Seyffarth (1940), Bracchi et al. (1966), Milner-Brown et al. (1973b), Monster and Chan (1977), Kiehn and Eken (1997), and Westgaard and De Luca (2001); in cats by Hoffer et al. (1987); and in turtles by Hornby et al. (2002). We also found that the firing rate trajectory appears to be essentially independent of the force rate in contractions ranging from 2% to 10% MVC/s.
An exponential equation was found to provide a good fit to all the firing rate trajectories from our data (R2 = 0.51–0.97). The rate of increase is determined by the time constant, which was found to increase as a function of recruitment threshold. Consequently the larger-diameter, later-recruited motoneurons have a progressively slower firing rate increase as has been reported by De Luca and Hostage (2010) and is plainly evident in Figs. 1 and 2. As a consequence, the firing rate value of the later-recruited, larger-diameter motoneurons will be lower at any time and force. This pattern is evident in Figs. 1 and 2, and in all our work over the past four decades (Adam et al. 1998; De Luca et al. 1982a, 1996; De Luca and Hostage 2010; Erim et al. 1996) as well as that of others who studied voluntary contractions in humans (Freund et al. 1975; Holobar et al. 2009; Kamen et al. 1995; Kanosue et al. 1979; Masakado 1991, 1994; Masakado et al. 1995; McGill et al. 2005; Monster and Chan 1977; Person and Kudina 1972; Seyffarth 1940; Stashuk and De Bruin 1988; Tanji and Kato 1973) and that of Hoffer et al. (1987), who studied voluntary contractions of cats.
There have been contrasting reports by Gydikov and Kosarov (1974), Grimby et al. (1979), Moritz et al. (2005), Tracy et al. (2005), and Barry et al. (2007), who found that during voluntary isometric contractions in humans later-recruited motor units have greater firing rates. These studies grouped firing rate data from different subjects, some from contractions performed on different days and also from contractions performed at different target force levels for the different motor units analyzed. As discussed by De Luca and Hostage (2010), this approach introduces errors due to intersubject variability and inconsistencies in the normalization across measurements made in different contractions and different subjects. The studies that agreed with our results all analyzed data that were collected either from individual contractions or at a common target force level. Figures 2 and 3 in Moritz et al. (2005) actually show the hierarchically decreasing firing rates with increasing recruitment threshold when the firing rates from different motor units are compared at the same force level. However, when data from motor units firing at different target force levels (higher for later-recruited motor units) are grouped together, the relationship appears to be inconsistent and even reversed. Our data show that the firing rate hierarchical progression remains unaltered in contractions ranging from 2% to 10% MVC/s. A similar firing rate behavior was seen in much faster contractions reported in Fig. 5 of Nawab et al. (2010), where the force rate was 120% MVC/s.
Studies performed on animals by electrical stimulation of severed motoneurons also contrast with our data. Granit et al. (1963), who worked with cats and rats, and Kernell (1965a, 1965b) who worked with cats, both reported that when an incrementally increased current was used to stimulate the motoneurons, a positive linear relation was found between the current amplitude and the firing rate. Kernell (1965b) referred to this response as the “primary range.” In this range the firing rate values reached 74 pps. Kernell (1965b), Granit et al. (1966), and Schwindt and Calvin (1972) also reported that some motoneurons are able to fire at greater rates when stimulated with higher-amplitude currents, and that the slope of the firing rate response is greater in this region, which was named the “secondary range,” where the firing rate values reached 195 pps (Kernell 1965b). Schwindt (1973) observed that at the highest firing rates the frequency-stimulating current curve tended to become less steep before a final stage of inactivation was reached, and he called these greater rates the “tertiary range.”
There are several reports indicating that the results of electrically elicited firing rates may not be applicable to describing the firing rate behavior during voluntary contractions. Experiments performed on decerebrated cats in which the excitation to the motoneuron pool was provided via a stretch reflex did not produce such levels of firing rates. Adrian and Bronk (1929) found that the greatest firing rates of reflexively activated lumbosacral motoneurons were in the range of 60–90 pps. Denny-Brown (1929) and Granit (1958) observed that during a stretch reflex in a decerebrated cat the firing rate initially increased with muscle length but remained constant or only increased slightly after reaching a low firing rate on the order of 10–30 pps. Comparable results were obtained by Hoffer et al. (1987), who monitored the firing rate in the cat quadriceps and sartorius motoneurons during walking at up to 1.3 m/s. Their highest observed firing rate was 45 pps. It was attained by the earlier-recruited motoneurons, which substantially decreased their firing rate velocity at this value, meaning that more strenuous contractions would not substantially extend the firing rate range of the earlier-recruited faster-firing motoneurons. Thus the secondary range reported by Kernell (1965b) and the tertiary range reported by Schwindt (1973) are likely responses that can be induced by electrical stimulation but do not occur during voluntary contractions or during a stretch reflex.
The works of Granit and that of Kernell teach us that the firing capacity of the motoneurons is intrinsically greater than that exercised during voluntary contractions, but they do not teach us that this capacity of the motoneuron is exploited during voluntary contractions.
If the intrinsic properties of motoneurons can produce greater firing rates than those produced during voluntary contractions, it follows that the excitation to the motoneuron pool is limited by some emergent properties of the motoneuron pool, such as the influence of spindle feedback or by some descending projections not yet identified.
The firing rate spectrum.
The firing rate spectrum of the motoneuron pool derived for linear force-varying contractions may be described by an equation (Eq. 9) that is expressed as a function of time, contraction force, and the recruitment threshold of the motoneurons. The recruitment threshold parameter can be replaced by the diameter of the motoneuron. It is more convenient to express it as a function of the recruitment threshold because this parameter is more readily available. The family of firing rates for the complete sets of motor units in the FDI and the VL muscles, or the motoneuron pool of these muscles, is presented in Fig. 6. In both muscles, firing rates are always inversely related to the recruitment threshold, including the firing rates at recruitment. They describe an exponential function whose time constant increases with recruitment threshold.
From a practical perspective, the value of the time constants might have been influenced by time-dependent factors in the different force paradigms presented, since the greater force level contractions were especially difficult for the subjects to track. However, we did not focus on the effect of time-dependent factors on the time constant for the purposes of our analysis; rather we were interested in the relation between the time constant and the recruitment threshold for a pool of motoneurons. Thus the firing rate spectrum presents a time-invariant view of the behavior of the firing rates of all the motoneurons that are present in a muscle. If the electrical characteristics of the motoneurons change as a function of time, then the characteristics of the firing rate spectrum may change.
The firing rate spectrum differs for the two muscles in this study, although the maximal firing rate value reached by the motor units is not as different as that reported in previous studies. For instance, for the FDI muscle maximal firing rate values are lower than those previously reported (Seki et al. 2007). This outcome is largely due to the manner in which the firing rate values are computed. In this study, the interpulse intervals of the motor unit trains are filtered with a 1-s Hanning window, and the firing rate estimate is obtained as the average over a time interval. As a result, the estimated firing rate has lower values than measurements taken over sporadic shorter intervals that capture brief but greater fluctuations in the firing rate commonly reported in the literature.
The firing rate spectrum reveals an interesting characteristic of the scheme that controls the firing of motoneurons. The hierarchical increase in the time constant with recruitment threshold determines the hierarchical increase (velocity) of the firing rates, so that earlier-recruited motor units present a greater velocity in their firing rates than later-recruited motor units [see De Luca and Hostage (2010) for additional details]. Note that, according to Eq. 9, the hierarchy in the velocity is maintained at all force levels, as the velocity of the firing rate depends on the value of both the time constant θ and the peak firing rate value λpi. The latter is dependent on the force level or the excitation to the motoneuron pool. Consequently, the hierarchical progression of the firing rates is evident at all force levels.
As the excitation increases, the firing rate of all the motor units increases and vice versa. The presence of this common excitation has been reported previously by De Luca et al. (1982b) and De Luca and Erim (1994) and has been termed the “common drive,” which represents a net excitation applied to all the motoneurons in the motoneuron pool. The hierarchical progression of the firing rate values and the inverse relation to the recruitment threshold present a pictorial image that resembles the layering of an onion and has been termed the “onion skin” property (De Luca et al. 1982a; De Luca and Erim 1994; De Luca and Hostage 2010).
The central nervous system does not control the firing behavior of each individual motor unit, but instead it modulates the behavior of the entire motoneuron pool of a muscle in the same way. This is an extremely simple and computationally efficient scheme for the brain. All the motoneurons in a pool are driven by the same excitation, and the resulting recruitment and firing characteristics are determined by the physical properties of the motoneurons.
Implications for motor unit control.
In addition to formulating the behavior of the firing rates of motoneurons during isometric voluntary contractions, the findings of this study support the previously reported observation that at any time or excitation (force) the firing rates of later-recruited motoneurons have lower values than those of earlier-recruited motoneurons or, stated differently, the firing rate of motoneurons is inversely proportional to their recruitment threshold.
This control strategy does not optimize the force output of the muscle. If it were so, the firing rate would be directly proportional to the recruitment threshold. Then, the higher-threshold motor units having higher-amplitude and shorter-duration force-twitches would fire faster to tetanize the force output of the motor unit. In contrast, the lower-threshold motor units having lower-amplitude and longer-duration force-twitches would not need to fire as fast to produce tetanic forces. In the control scheme reported here, the higher-threshold, higher-amplitude, shorter-duration force-twitch motor units do not tetanize. The lower-threshold motor units fire faster and are tetanized, but the firing rate trajectory decelerates more quickly to economize the energy used in generating more action potential pulses when the force output of the motor unit would not increase further.
The onion skin control scheme provides at least two favorable aspects that are expedient for daily activities. The first is that the scheme for motor unit control did not evolve to enhance force; instead it seems to have optimized some combination of force magnitude and time duration. High-threshold motor units generally fatigue at a faster rate. If they were to fire at relatively greater rates, they would fatigue more quickly and their force could not be maintained. An outcome of this control structure is that it produces greater variability in the force output of the muscle because the high-threshold motor units do not tetanize. When a high force output is required, force smoothness is sacrificed for force sustainability. The onion skin control scheme would seem to better serve the flight-and-fight response by providing the capacity to generate force and the capacity to sustain it. The second advantageous feature of the control scheme is that it provides a greater economy of force generation during most normal functional daily activities, such as normal walking, that require low force levels generated over short periods of time. In these cases, the lower time constant of the earlier-recruited motor units renders a faster-rising firing rate, which generates more force from the low-threshold motor units used for low-level contractions.
GRANTS
This work was supported in part by National Institute of Neurological Disorders and Stroke Grant NS-058250 to Altec Inc. for the development of the decomposition system; National Center for Medical Rehabilitation Research (NCMRR)/National Institute of Child Health and Human Development (NICHD) Grant HD-050111; a grant from the Italian Ministero dell'Università e della Ricerca; and a grant from Fondazione Ing. A. Gini.
DISCLOSURES
The first author is the President and CEO of Delsys Inc., the company that developed the sEMG decomposition technology.
AUTHOR CONTRIBUTIONS
Author contributions: C.J.D.L. conception and design of research; C.J.D.L. and P.C. interpreted results of experiments; C.J.D.L. and P.C. drafted manuscript; C.J.D.L. and P.C. edited and revised manuscript; C.J.D.L. approved final version of manuscript; P.C. performed experiments; P.C. analyzed data; P.C. prepared figures.
ACKNOWLEDGMENTS
We are grateful to Dr. S. H. Nawab for his contribution in improving the accuracy measurement and for his numerous comments that improved the manuscript; to D. Gilmore and Dr. S. Chang for assisting with the preparation of the manuscript; and to F. Zaheer and J. Kline for their assistance in performing the experiments. We thank the subjects who painstakingly participated in the experiments.
This work was done, in part, while P. Contessa was a doctoral candidate in the Bioengineering Curriculum at the School of Information Engineering at the University of Padova. We thank Dr. Claudio Cobelli for effectuating the collaboration.
APPENDIX 1
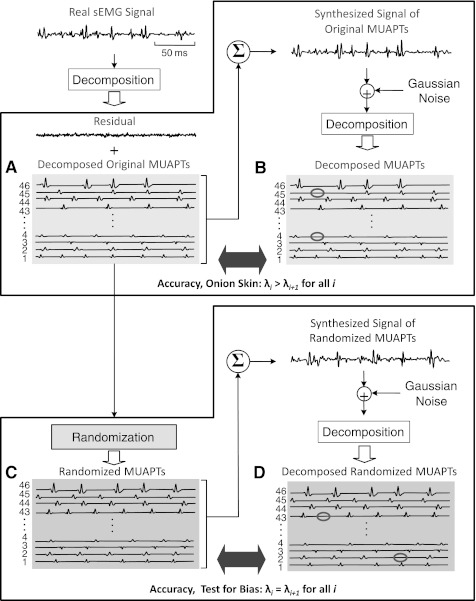
Here we address the performance of the sEMG signal decomposition in terms of its accuracy and potential bias for modifying the characteristics of the firing intervals. The test for accuracy is depicted in Fig. 8, A and B. Figure 8, C and D, represents the test for potential bias, as well as another test for accuracy.
Fig. 8.
Diagram of the procedure for measuring the accuracy of the algorithm and for testing the algorithm for the absence of a biased structured result. The test for accuracy involves steps A and B (top). The test for bias involves steps A, C, and D (bottom). Accuracy test: a real sEMG signal is decomposed to obtain all the firing instances and the action potential shapes of all the identifiable motor unit action potential trains (MUAPTs) in the signal [original decomposed MUAPTs (dMUAPTs) in A]. The firing instances and the action potential shapes are used to construct a synthesized signal of MUAPTs to which Gaussian noise is added. The synthesized signal of MUAPTs is then decomposed, and the results of the decomposition (dMUAPTs in B) are compared with the decomposition of the real sEMG signal (original dMUAPTs in A). Test for bias: the test for bias is similar to the test for accuracy with the only addition of a randomization process (C). The identified firing times of each motor unit obtained from the decomposition of a real sEMG signal undergo a stochastic process whereby firings are either randomly inserted or deleted until all motor unit trains have approximately the same number of firings (randomized MUAPTs in C). The randomized trains and action potential shapes are then used to construct a synthesized signal, which is comprised of randomized MUAPTs that do not present structured behavior. The synthesized signal of randomized MUAPTs is decomposed, and the output of the decomposition algorithm (randomized dMUAPTs in D) is compared with the input to the decomposition algorithm (randomized MUAPTs in C).
The accuracy of the algorithm is evaluated with the Decompose-Synthesize-Decompose-Compare (DSDC) test proposed by Nawab et al. (2010) and expanded in the Appendix of De Luca and Hostage (2010). A real sEMG signal is decomposed to obtain all the firing instances (original dMUAPTs in Fig. 8A) and the action potential shapes of all the identified motor units. The original dMUAPTs and the action potential shapes are used to synthesize a signal to which Gaussian noise is added with a root-mean-square value equivalent to that of the residual of the real dEMG. The synthesized signal of MUAPTs is then decomposed, and the result of the decomposition (dMUAPTs in Fig. 8B) is compared with the decomposition of the real sEMG signal (original dMUAPTs in Fig. 8A). We obtain the action potentials from a real sEMG signal because we wish to challenge the test with shapes that are realistic rather than well-behaved functions derived from mathematical models.
The accuracy of each MUAPT then is measured as follows:
where Ntruth represents the total number of true events identified in the decomposition of the real sEMG signal, including all firing occurrences [true positive (TP)] and all quiescent periods [true negative (TN)] between any two consecutive firings. Nerror represents the total number of unmatched events between the decomposition of the real sEMG signal and the decomposition of the synthesized signal [false positive (FP) and false negative (FN)].
This formula is an improvement over that presented in the Appendix of De Luca and Hostage (2010). Quiescent periods in the real sEMG signal are now considered as part of true events, ensuring that all true and false events are considered and are equally weighed in the accuracy evaluation. The modification results in only a few percent change in the degree of accuracy, but it is a more comprehensive evaluation approach.
Average accuracy values obtained from 55 contractions in 3 different muscles ranged between 91% and 94% in De Luca and Hostage (2010). Nawab et al. (2010) reported an average accuracy of 92.5% from 22 contractions from 5 muscles, which increased to >95.2% with recent improvements (De Luca and Nawab 2011).
Now we proceed to address any tendency of bias in the decomposition algorithm. This study provides evidence of a hierarchical organization in the behavior of motor units, whose firing rates present a layered structure with the earlier-recruited motor units achieving higher firing rates than the later-recruited motor units. An issue can be raised as to whether the algorithm itself biases the results and artificially produces a structured behavior. This issue can be addressed by testing the decomposition algorithm with a synthesized signal consisting of MUAPTs whose firing instances are randomized and do not possess a structured behavior. If the firing instances of the decomposition of such a randomized signal do not possess a structured behavior, then there is no bias. A procedure for this test is depicted in Fig. 8, A, C, and D: The structure of the test is similar to the accuracy test, with the singular addition of the process for the randomization of the firing instances in Fig. 8C prior to generating the synthesized signal.
The trains with randomized firing intervals are generated as follows.
1) A real sEMG signal is decomposed to obtain the firing instances of each identified MUAPT and the waveform of the action potential. These are the original dMUAPTs in Fig. 8A.
2) The mean firing rate of each MUAPT (MFRi, where i indicates the ith train) identified in the decomposition of the real sEMG signal is computed over the entire signal length, and the median value of all MFRi is taken as the firing rate value (MFRmed) for each motor unit.
3) For each MUAPT, firing instances are either randomly inserted or randomly removed until MFRi = MFRmed ± Δ. The permissible deviation Δ between the actual value MFRi and the desired median value MFRmed is set to Δ = 0.05 pps.
If MFRi < MFRmed ± Δ, firings are added. For each extra firing, a random location is chosen between the first and last firing instance, with the only constraint that the new generated interpulse interval be greater than the shortest observed interpulse interval.
If MFRi > MFRmed ± Δ, firings are deleted. A firing is randomly selected from the train and deleted, with the constraint that the new generated interpulse interval be less than the longest observed interpulse interval.
The stochastic process employs a uniform distribution to ensure that each firing is equally likely to be removed or that each interpulse interval is equally likely to be modified with an extra firing.
4) The firing instances of each MUAPT are then shuffled to ensure that no relation exists between each consecutive interpulse interval.
The process generates a set of MUAPTs with random firing interpulse intervals (Fig. 8C), all having the same mean firing rate, void of a structured hierarchical configuration. The randomized MUAPTs are used to create a synthesized signal of randomized MUAPTs, which is decomposed. The firing instances of the decomposition (randomized dMUAPTs in Fig. 8D) are compared with those of the randomized MUAPTs (Fig. 8C).
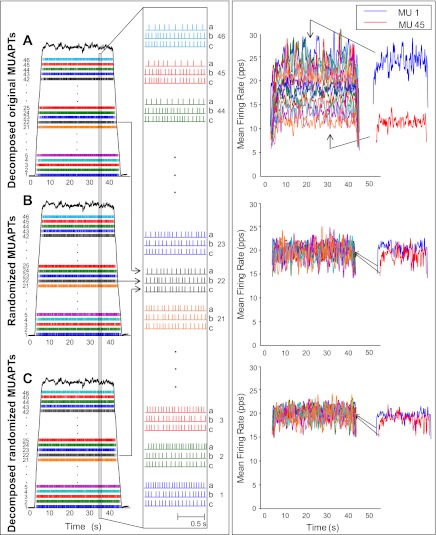
An example of this operation is presented in Fig. 9, left. Figure 9A shows the firing instances of 46 MUAPTs from the decomposition of the real sEMG signal obtained from the VL muscle during a 35% MVC. Figure 9B presents the same information from the randomized MUAPTs generated as described above, i.e., from the randomization process applied to the original dMUAPTs in Fig. 9A. Figure 9C presents the same information obtained from the decomposition of the synthesized signal of randomized MUAPTs generated using the randomized MUAPTs in Fig. 9B. For clarity, the firing instances of nine representative motor units are expanded over a 1-s interval on the right of the plots. Note that the expanded view on the right contains three trains for each motor unit. The top train (a) belongs to the original dMUAPTs in the top panel, the middle train (b) belongs to the randomized MUAPTs in the middle panel, and the bottom train (c) belongs to the randomized dMUAPTs in the bottom panel. This view facilitates comparison among the original firing train (a), the randomized train input to the decomposition algorithm (b), and the output of the decomposition algorithm (c) for each expanded motor unit. Note that the middle randomized train (b) of each motor unit differs from the original train (a) of the same motor unit. Also, the top trains display a gradually greater number of firings for earlier-recruited motor units, whereas the middle trains have a similar number of firings. Finally, the firing instances in the middle and bottom panels (randomized MUAPTs and randomized dMUAPTs) match closely, indicating that the synthesized signal of randomized MUAPTs was decomposed accurately.
Fig. 9.
Test for measuring the accuracy of the decomposition algorithm and for proving that the algorithm does not bias the behavior of the firing rates of the dMUAPTs. Left: A: firing instances of a set of 46 MUAPTs that were decomposed from a real sEMG signal obtained from a 35% MVC contraction from the VL muscle. The dark line represents the force output of the muscle. B: firing instances of each of the original MUAPTs (in A) that were randomized according to the description in the text. C: firing instances of the MUAPTs that were obtained by decomposing the synthesized signal of the randomized MUAPTs in B. Note that the MUAPTs identified by the decomposition were the same as the 46 that were used to construct the synthesized signal of randomized MUAPTs, as evidenced by the shapes of the action potentials presented in Fig. 10. The expansions on right show 1-s epoch of 9 selected MUAPTs in all 3 segments (A, B, and C). The MUAPTs are presented in groups of 3. The top one (a) contains those from the original dMUAPTs in the top section (A). The middle one (b) contains those with the randomized firing instances in the middle section (B). The bottom one (c) contains those from the decomposed signal constructed from the randomized MUAPTs in the bottom section (C). Note that the randomization effect is noticeable when comparing the middle train to the top train. The accuracy of the decomposition algorithm is noticeable when comparing the bottom train to the middle train. These latter 2 are nearly similar, as would be expected from the measured high (95.4 ± 1.2%) accuracy value of the decomposition of the synthesized signal of randomized MUAPTs. Note that this accuracy value is similar to that obtained by the decomposition of the synthesized, but not randomized, signal of MUAPTs (95.6 ± 0.8%). For details of the method used to calculate the accuracy, refer to appendix 1. Right: mean firing rates computed by low-pass filtering the 46 MUAPTs in the 3 segments shown on left with a Hanning window of 1-s duration. On right the mean firing rates of motor units 1 and 45 are provided for clarity. Note that the mean firing rates computed from the original dMUAPTs (top section) present a hierarchical sequence. The range of firing rates between the first and the last recruited motor unit is ∼18 pps, whereas the mean firing rates computed from the randomized MUAPTs (middle section) as well as those computed from the randomized dMUAPTs (bottom section) all present firing rates with similar values (∼20 pps). This is a proof that the algorithm does not bias the data to artificially introduce the structured behavior clearly observable in the real sEMG signal of the top section.
The mean firing rates of the three sets of MUAPTs, computed by applying a 1-s Hanning window to the interpulse intervals of each MUAPT are presented in Fig. 9, right. Note that the mean firing rates from the decomposition of the real sEMG signal (top panel) show the “onion skin” property in which the firing rate of the motor units are inversely proportional to the recruitment threshold. A range of ∼18 pps is observed between the first-recruited and the last-recruited motor units, a point more clearly observed in the extraction of the firing rates of motor units 1 and 45 on the right of the plot, whereas the mean firing rates of the randomized MUAPTs (middle panel) and those of the decomposition of the synthesized signal of randomized MUAPTs (bottom panel) show no such relationship. Thus no bias was introduced by the algorithm in the decomposition of the synthesized signal of randomized MUAPTs.
This test proves that the structured behavior observed in the decomposition of real sEMG signals does not derive from a model imbued in the algorithm; instead, it represents a physiological hierarchical organization of motor unit behavior.
The test for bias provides another measure of accuracy in addition to the DSDC test. These two tests are similar, with the sole exception that in the bias test the firing instances of the MUAPTs are randomized, whereas in the DSDC test the original dMUAPTs (no randomization) are used to synthesize a signal that is decomposed. In Fig. 8, the top panels (A and B) represent the DSDC test and the bottom panels (C and D) show the bias test structure.
The results of the accuracy evaluation from the comparison of the firing instances and shapes of the MUAPTs from the randomized set and the MUAPTs from the randomized dMUAPTs are presented in Fig. 10. In Fig. 10, top, the blue shapes represent the action potentials from the randomized MUAPTs (Fig. 9B) and the red represent those of the decomposed randomized MUAPTs (Fig. 9C). Note that the number of motor units is the same and the identified shapes of each motor unit are, in large part, similar. Figure 10, bottom, presents an epoch of the firings of the identified MUAPTs from the decomposition of the synthesized signal of randomized MUAPTs. The blue bars represent the firing instances of the randomized MUAPTs, and the black Xs indicate the identified firing instances in the decomposition of the synthesized signal of randomized MUAPTs. Thus the blue bars and blue quiescent periods between bars indicate true firing instances (TP) and quiescent periods (TN) in the synthesized signal of randomized MUAPTs. The red markers indicate errors. A red circle indicates a missed firing instance (FN), i.e., a firing that is present in the synthesized signal but was missed in the decomposition of the synthesized signal. A red cross indicates an additional firing (FP), that is, a firing instance that is detected in the decomposition of the synthesized signal but does not exist in the randomized MUAPTs. The accuracy and the number of errors per second for the selected 2-s interval are tabulated next to the comparison of firing instances in Fig. 10, bottom. For all 46 MUAPTs, the average accuracy is 95.4 ± 1.2%.
Fig. 10.
Here we show the action potentials of the 46 MUAPTs presented in Fig. 9 and a detailed comparison of the firing instances. Top: the blue action potential shapes belong to the MUAPTs that were identified in the decomposition of the real sEMG signal (top segment in Fig. 9) and were used to construct the signal with randomized firing instances. The red action potentials were obtained by the decomposition of the randomized signal constructed with the blue action potentials and with randomized firing instances. Note the similarity. Bottom: a short epoch of the firings of the first and last 10 MUAPTs. Bars and quiescent periods between bars represent the firing instances of the randomized MUAPTs in Fig. 9B [true positive (TP) and true negative (TN)]; Xs indicate those from the MUAPTs obtained from the decomposition of the synthesized signal in Fig. 9C constructed from the randomized MUAPTs. A red circle represents a missing firing [false negative (FN)] that is not recognized in the MUAPT from the decomposition of the synthesized signal. A red cross indicates an additional firing [false positive (FP)] in the MUAPT from the decomposition of the synthesized signal that is not present in the randomized MUAPT. The accuracy of the decomposition and the number of errors per second are listed at bottom left. In the presented MUAPTs the accuracy ranges from 95.1% to 100%. The average accuracy over all 46 MUAPTs is 95.4 ± 1.2%.
When the accuracy for the DSDC test performed by comparing the firing instances of the real dEMG signal to the synthesized signal is calculated, the average value over all 46 MUAPTs is 95.6 ± 0.8%. This degree of accuracy is similar to that obtained from the bias test, which required the randomization of the interpulse intervals. It is also similar to the values reported in previous studies (Nawab et al. 2010; De Luca and Hostage 2010; De Luca and Nawab 2011).
Hence, the DSDC test may be used to assess the accuracy of the decomposition algorithm of each MUAPT, without performing the randomization of the interpulse intervals.
APPENDIX 2
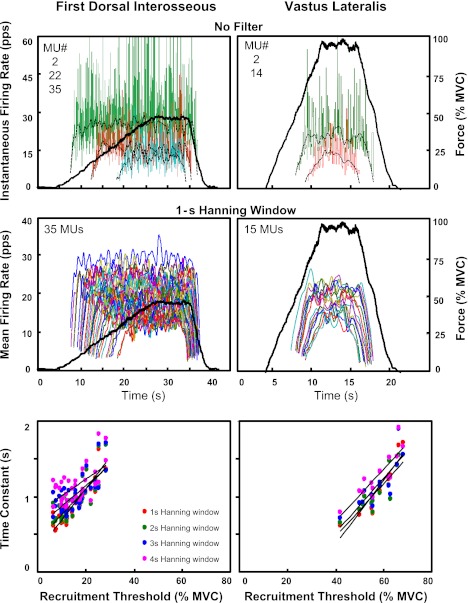
To determine a suitable length for the Hanning window used to filter the firing rates when estimating θ(τ), we tested window lengths of 1-, 2-, 3-, and 4-s duration. Figure 11, top and middle, shows the firing rates of motor units from a 50% MVC contraction of the FDI muscle (left) and a 100% MVC contraction of the VL muscle (right). The instantaneous firing rates are presented in Fig. 11, top, for three and two representative motor units identified in the FDI and VL muscles, respectively. The mean firing rates computed with a 1-s Hanning window for all the identified motor units in the two contractions are presented in Fig. 11, middle. Figure 11, bottom, displays the relation between the estimated time constant and the recruitment threshold for the motor units obtained in the two different contractions when the mean firing rates are computed with Hanning windows of 1-, 2-, 3-, and 4-s duration. It is evident that the estimate of the time constant is influenced by the filtering process. As the length of the Hanning window increases, values of θ also increase and the regression lines shift upward. The slope of the regression lines decreases with increasing window duration: from 4.13 to 3.39, 2.70, 2.19 in the FDI muscle and from 3.60 to 3.50, 3.62, and 3.44 in the VL muscle for windows of 1, 2, 3, and 4 s, respectively. The intercept of the regression lines increases with increasing window duration: from 0.28 to 0.43, 0.61, 0.80 in the FDI muscle and from −1.30 to −0.92, −0.92, and −0.69 in the VL muscle for windows of 1, 2, 3, and 4 s, respectively.
Fig. 11.
Influence of the filtering window on the estimate of the time constant of the firing rates. Top: instantaneous firing rates of some selected motor units and the superimposed mean firing rates, computed by filtering the motor unit impulse trains with a Hanning window of 1-s duration, are presented for 2 different contractions. A slow (2% MVC/s) contraction from the FDI muscle is shown on left, and a fast (10% MVC/s) contraction from the VL muscle is shown on right. For clarity, only 3 motor units (2, 22, 35) are shown for the FDI muscle and 2 motor units (2, 14) for the VL muscle. Note that the instantaneous firing rates are presented up to 60 pps. Middle: mean firing rates computed by filtering the motor unit trains with a 1-s Hanning window are presented for all motor units identified in the 2 contractions (35 motor units and 15 motor units in the FDI and VL muscle, respectively). Bottom: relation between the recruitment threshold and the time constant of the firing rate estimated by fitting the mean firing rate trajectories with Eq. 1 (see text). The individual regression lines are obtained as the firing rate trajectories are computed with length of the Hanning window ranging from 1 to 4 s.
A 1-s Hanning window was chosen, as it smoothes the firing rate trajectories while reducing the filtering bias.
REFERENCES
- Adam A, De Luca CJ, Erim Z. Hand dominance and motor unit firing behavior. J Neurophysiol 80: 1373–1382, 1998 [DOI] [PubMed] [Google Scholar]
- Adrian ED, Bronk DW. The discharge of impulses in motor nerve fibres. II. The frequency of discharge in reflex and voluntary contractions. J Physiol 67: i3–i51, 1929 [PMC free article] [PubMed] [Google Scholar]
- Barry BK, Pascoe MA, Jesunathadas M, Enoka RM. Rate coding is compressed but variability is unaltered for motor units in a hand muscle of old adults. J Neurophysiol 97: 3206–3218, 2007 [DOI] [PubMed] [Google Scholar]
- Bracchi F, Decandia M, Gualtierotti T. Frequency stabilization in the motor centers of spinal cord and caudal brain stem. Am J Physiol 210: 1170–1177, 1966 [DOI] [PubMed] [Google Scholar]
- Christensen E. Topography of terminal motor innervation in striated muscles from stillborn infants. Am J Phys Med 38: 65–78, 1959 [PubMed] [Google Scholar]
- De Luca CJ, Erim Z. Common drive of motor units in regulation of muscle force. Trends Neurosci 17: 299–305, 1994 [DOI] [PubMed] [Google Scholar]
- De Luca CJ, Hostage EC. Relationship between firing rate and recruitment threshold of motoneurons in voluntary isometric contractions. J Neurophysiol 104: 1034–1046, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luca CJ, Nawab SH. Reply to Farina and Enoka: the Reconstruct-and-Test approach is the most appropriate validation for surface EMG signal decomposition to date. J Neurophysiol 105: 983–984, 2011 [DOI] [PubMed] [Google Scholar]
- De Luca CJ, LeFever RS, McCue MP, Xenakis AP. Behavior of human motor units in different muscles during linearly varying contractions. J Physiol 329: 113–128, 1982a [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luca CJ, LeFever RS, McCue MP, Xenakis AP. Control scheme governing concurrently active human motor units during voluntary contractions. J Physiol 329: 129–142, 1982b [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luca CJ, Foley PJ, Erim Z. Motor unit control properties in constant-force isometric contractions. J Neurophysiol 76: 1503–1516, 1996 [DOI] [PubMed] [Google Scholar]
- De Luca CJ, Adam A, Wotiz R, Gilmore LD, Nawab SH. Decomposition of surface EMG signals. J Neurophysiol 96: 1646–1657, 2006 [DOI] [PubMed] [Google Scholar]
- Denny-Brown D. On the nature of postural reflexes. Proc R Soc Lond B 730: 252–301, 1929 [Google Scholar]
- Duchateau J, Hainaut K. Effects of immobilization on contractile properties, recruitment and firing rates of human motor units. J Physiol 422: 55–65, 1990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles JC, Eccles RM, Lundberg A. The action potentials of the alpha motoneurones supplying fast and slow muscles. J Physiol 142: 275–291, 1958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erim Z, De Luca CJ, Mineo K, Aki T. Rank-ordered regulation of motor units. Muscle Nerve 19: 563–573, 1996 [DOI] [PubMed] [Google Scholar]
- Feinstein B, Lindegard B, Nyman E, Wohlfart G. Morphologic studies of motor units in normal human muscles. Acta Anat (Basel) 23: 127–142, 1955 [DOI] [PubMed] [Google Scholar]
- Freund HJ, Büdingen HJ, Dietz V. Activity of single motor units from human forearm muscles during voluntary isometric contractions. J Neurophysiol 38: 933–946, 1975 [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. J Neurophysiol 70: 2470–2488, 1993 [DOI] [PubMed] [Google Scholar]
- Granit R. Neuromuscular interaction in postural tone of the cat's isometric soleus muscle. J Physiol 143: 387–402, 1958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granit R, Kernell D, Shortess GK. Quantitative aspects of repetitive firing of mammalian motoneurones, caused by injected currents. J Physiol 168: 911–931, 1963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granit R, Kernell D, Lamarre Y. Synaptic stimulation superimposed on motoneurones firing in the secondary range to injected current. J Physiol 187: 401–415, 1966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimby L, Hannerz J, Hedman B. Contraction time and voluntary discharge properties of individual short toe extensor motor units in man. J Physiol 289: 191–201, 1979 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gydikov A, Kosarov D. Some features of different motor units in human biceps brachii. Pflügers Arch 347: 75–88, 1974 [DOI] [PubMed] [Google Scholar]
- Henneman E. Relation between size of neurons and their susceptibility to discharge. Science 126: 1345–1347, 1957 [DOI] [PubMed] [Google Scholar]
- Hoffer JA, Sugano N, Loeb GE, Marks WB, O'Donovan MJ, Pratt CA. Cat hindlimb motoneurons during locomotion. II. Normal activity patterns. J Neurophysiol 57: 530–553, 1987 [DOI] [PubMed] [Google Scholar]
- Holobar A, Farina D, Gazzoni M, Merletti R, Zazula D. Estimating motor unit discharge patterns from high-density surface electromyogram. Clin Neurophysiol 120: 551–562, 2009 [DOI] [PubMed] [Google Scholar]
- Hornby TG, McDonagh JC, Reinking RM, Stuart DG. Motoneurons: a preferred firing range across vertebrate species? Muscle Nerve 25: 632–648, 2002 [DOI] [PubMed] [Google Scholar]
- Jakobi JM, Cafarelli E. Neuromuscular drive and force production are not altered during bilateral contractions. J Appl Physiol 84: 200–206, 1998 [DOI] [PubMed] [Google Scholar]
- Kamen G, Sison SV, Du CC, Patten C. Motor unit discharge behavior in older adults during maximal-effort contractions. J Appl Physiol 79: 1908–1913, 1995 [DOI] [PubMed] [Google Scholar]
- Kanosue K, Yoshida M, Akazawa K, Fuji K. The number of active motor units and their firing rates in voluntary contraction of human brachialis muscle. Jpn J Physiol 29: 427–443, 1979 [DOI] [PubMed] [Google Scholar]
- Kernell D. The adaptation and the relation between discharge frequency and current strength of cat lumbosacral motoneurones stimulated by long-lasting injected currents. Acta Physiol Scand 65: 65–73, 1965a [DOI] [PubMed] [Google Scholar]
- Kernell D. High-frequency repetitive firing of cat lumbosacral motoneurones stimulated by long-lasting injected currents. Acta Physiol Scand 65: 74–86, 1965b [DOI] [PubMed] [Google Scholar]
- Kernell D. The limits of firing frequency in cat lumbosacral motoneurones possessing different time course of afterhyperpolarization. Acta Physiol Scand 65: 87–100, 1965c [Google Scholar]
- Kernell D. Rhythmic properties of motoneurones innervating muscle fibres of different speed in m. gastrocnemius medialis of the cat. Brain Res 160: 159–162, 1979 [DOI] [PubMed] [Google Scholar]
- Kernell D. Principles of force gradation in skeletal muscles. Neural Plast 1–2: 69–76, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiehn O, Eken T. Prolonged firing in motor units: evidence of plateau potentials in human motoneurons? J Neurophysiol 78: 3061–3068, 1997 [DOI] [PubMed] [Google Scholar]
- Kukulka CG, Clamann HP. Comparison of the recruitment and discharge properties of motor units in human brachial biceps and adductor pollicis during isometric contractions. Brain Res 219: 45–55, 1981 [DOI] [PubMed] [Google Scholar]
- LeFever RS, De Luca CJ. A procedure for decomposing the myoelectric signal into its constituent action potentials. I. Technique, theory, and implementation. IEEE Trans Biomed Eng 29: 149–157, 1982 [DOI] [PubMed] [Google Scholar]
- LeFever RS, Xenakis AP, De Luca CJ. A procedure for decomposing the myoelectric signal into its constituent action potentials. II. Execution and test for accuracy. IEEE Trans Biomed Eng 29: 158–164, 1982 [DOI] [PubMed] [Google Scholar]
- Masakado Y. The firing pattern of motor units in the mono- and multidirectional muscle. Jpn Rehabil Med 28: 703–712, 1991 [Google Scholar]
- Masakado Y. Motor unit firing behavior in man. Keio J Med 43: 137–142, 1994 [DOI] [PubMed] [Google Scholar]
- Masakado Y, Akaboshi K, Nagata M, Kimura A, Chino N. Motor unit firing behavior in slow and fast contractions of the first dorsal interosseous muscle of healthy men. Electroencephalogr Clin Neurophysiol 97: 290–295, 1995 [DOI] [PubMed] [Google Scholar]
- McGill CK, Lateva ZC, Marateb HR. EMGLAB: an interactive EMG decomposition program. J Neurosci Methods 149: 121–133, 2005 [DOI] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB, Yemm R. The orderly recruitment of human motor units during voluntary isometric contractions. J Physiol 230: 359–370, 1973a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB, Yemm R. Changes in firing rates of human motor units during linearly changing voluntary contractions. J Physiol 230: 371–390, 1973b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monster W, Chan H. Isometric force production by motor units of extensor digitorum communis muscle in man. J Neurophysiol 40: 1432–1443, 1977 [DOI] [PubMed] [Google Scholar]
- Moritz CT, Barry BK, Pascoe MA, Enoka RM. Discharge rate variability influences the variation in force fluctuations across the working range of a hand muscle. J Neurophysiol 93: 2449–2459, 2005 [DOI] [PubMed] [Google Scholar]
- Nawab SH, Chang SS, De Luca CJ. High-yield decomposition of surface EMG signals. Clin Neurophysiol 121: 1602–1615, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Person RS, Kudina LP. Discharge frequency and discharge pattern of human motor units during voluntary contraction of muscle. Electroencephalogr Clin Neurophysiol 32: 471–483, 1972 [DOI] [PubMed] [Google Scholar]
- Schwindt PC. Membrane-potential trajectories underlying motoneuron rhythmic firing at high rates. J Neurophysiol 36: 434–439, 1973 [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Calvin WH. Membrane-potential trajectories between spikes underlying motoneuron firing rates. J Neurophysiol 35: 311–325, 1972 [DOI] [PubMed] [Google Scholar]
- Seki K, Kizuka T, Yamada H. Reduction in maximal firing rate of motoneurons after 1-week immobilization of finger muscle in human subjects. J Electromyogr Kinesiol 17: 113–120, 2007 [DOI] [PubMed] [Google Scholar]
- Seyffarth H. The Behavior of Motor-Units in Voluntary Contraction. University of Oslo; Jacob DybWads, Forlag Oslo, Norway, 1940 [Google Scholar]
- Stashuk D, De Bruin H. Automatic decomposition of selective needle-detected myoelectric signals. IEEE Trans Biomed Eng 35: 1–10, 1988 [DOI] [PubMed] [Google Scholar]
- Tanji J, Kato M. Firing rate of individual motor units in voluntary contraction of abductor digiti minimi muscle in man. Exp Neurol 40: 771–783, 1973 [DOI] [PubMed] [Google Scholar]
- Thomas CK, Ross BH, Stein RB. Motor-unit recruitment in human first dorsal interosseous muscle for static contractions in three different directions. J Neurophysiol 55: 1017–1029, 1986 [DOI] [PubMed] [Google Scholar]
- Tracy BL, Maluf KS, Stephenson JL, Hunter SK, Enoka RM. Variability of motor unit discharge and force fluctuations across a range of muscle forces in older adults. Muscle Nerve 32: 533–540, 2005 [DOI] [PubMed] [Google Scholar]
- Westgaard RH, De Luca CJ. Motor control of low-threshold motor units in the human trapezius muscle. J Neurophysiol 85: 1777–1781, 2001 [DOI] [PubMed] [Google Scholar]
- Woods JJ, Furbush F, Bigland-Ritchie B. Evidence for a fatigue-induced reflex inhibition of motoneuron firing rates. J Neurophysiol 58: 125–137, 1987 [DOI] [PubMed] [Google Scholar]