Slowing down DNA translocation through a nanopore in lithium chloride

Abstract

The charge of a DNA molecule is a crucial parameter in many DNA detection and manipulation schemes such as gel electrophoresis and lab-on-a-chip applications. Here, we study the partial reduction of the DNA charge due to counterion binding by means of nanopore translocation experiments and all-atom molecular dynamics (MD) simulations. Surprisingly, we find that the translocation time of a DNA molecule through a solid-state nanopore strongly increases as the counterions decrease in size from K⁺ to Na⁺ to Li⁺, both for double-stranded DNA (dsDNA) and single-stranded DNA (ssDNA). MD simulations elucidate the microscopic origin of this effect: Li⁺ and Na⁺ bind DNA stronger than K⁺. These fundamental insights into the counterion binding to DNA also provide a practical method for achieving at least ten-fold enhanced resolution in nanopore applications.

Introduction

It is well known that interactions between DNA and counterions can profoundly affect its physical properties (1, 2). Although valuable as first-order approximations, traditional models for polyelectrolyte-counterion interactions, i.e., Manning (1) and Poisson-Boltzmann (3) theory, ignore relevant details such as the discrete nature of charges on DNA, the type of cation, and ion-ion interactions. Here, we combine nanopore experiments with MD simulations to quantitatively reveal the effect of different counterions (K⁺, Na⁺, and Li⁺) on the charge reduction of a DNA molecule. Surprisingly, we find that the various monovalent ions can have very different effects.

Nanopores have emerged as a versatile tool for the detection and manipulation of charged biomolecules (4–9). In a typical setup, an external electric field drives a (bio)molecule through a nanometer-size pore in a thin synthetic membrane, producing a characteristic temporary change in the trans-pore ionic current. This can be used for sensitive single-molecule sensing platforms. A major difficulty in experiments to date, however, has been the speed of DNA translocation, which is very fast. The average translocation speed is set by the electrophoretic drive which in turn is determined by the charge on the DNA. A lower charge would result in lower translocation speed and therefore higher read-out accuracy in these types of experiments. In this paper, we use the nanopore as a tool to determine the effect of the electrolyte conditions on the charge of DNA.

Results

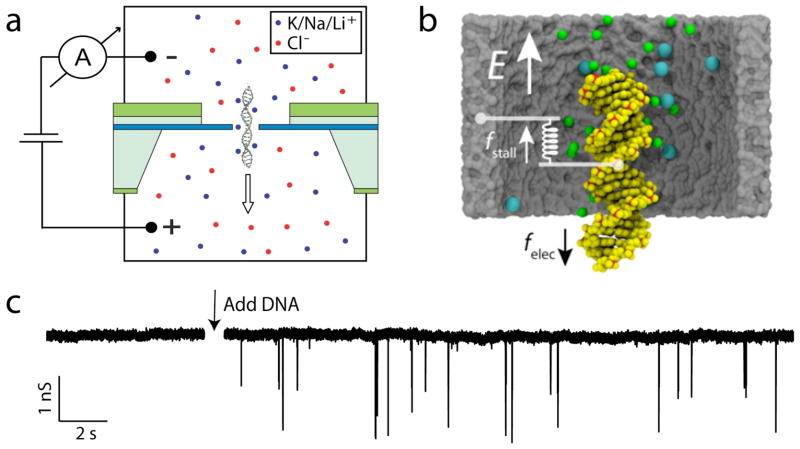
Figure 1a shows the layout of the nanopore experiments, depicting a double stranded (ds) DNA molecule in an ionic solution containing KCl, NaCl, or LiCl. Briefly, a single nanopore is fabricated using the focused electron beam of a transmission electron microscope (TEM) in a thin, low-stress silicon nitride (SiN) membrane (see inset of Figure S1). The membrane is placed between two compartments filled with a monovalent salt solution. Subsequent application of an electric voltage (~ 0.1 V) across the membrane results in an ionic current (~ 10 nA) through the pore, which is temporarily reduced upon passage of a molecule. For this study, we used nanopores of 15–20 nm in diameter, with linear I-V relations, and good noise characteristics (10). The open-pore conductance is approximately proportional to the cation mobility (I–V curves shown in Figure S1), as reported previously for slightly different (conical) pore geometries (11). All experiments were reproduced multiple times, with essentially the same results.

Figure 1.

(a) Side-view schematic of our device, consisting of a 20 nm thin free-standing silicon nitride window (blue layer) embedded in a silicon wafer. Upon application of an electric field across the nanopore, DNA translocates through the pore. (b) MD simulation system, showing a DNA molecule, a 0.1 M KCl solution and an 8 nm nanopore. Silica is shown as a gray surface, DNA is shown as yellow van der Waals spheres with the phosphates shown in red, chloride ions are shown in blue, and potassium ions are shown in green. Water is not shown. (c) Example of an experimental data trace. Spikes in the current can be seen to appear upon addition of DNA. Each spike represents a single DNA molecule passing through the pore. Data taken in 1 M KCl at 120 mV, and filtered at 1 kHz for display.

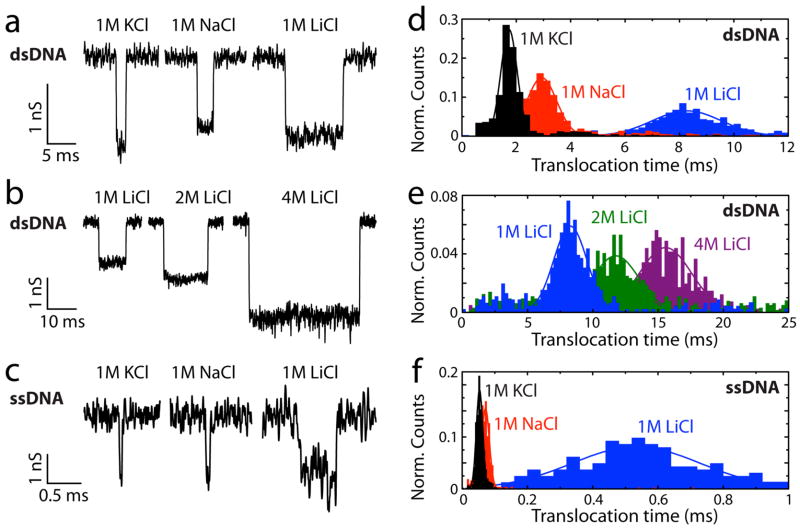
Figure 1c shows an example current trace. Spikes appear in the current upon addition of dsDNA. Each spike represents a single dsDNA molecule translocating through the pore. Figure 2a shows current traces for some typical events of 48.5 kbp dsDNA translocations in 1 M KCl, NaCl, and LiCl salt solution (from left to right). Interestingly, while the event amplitudes are similar (~ 1–1.5 nS; for scatter diagrams see Fig. S2), the translocation times increase greatly upon changing the solute from KCl to NaCl to LiCl. Figure 2d shows histograms of the translocation times (τ) for a large number of events. We find that for 1 M solutions, the ratios for the experimental translocation times of dsDNA are KCl:NaCl:LiCl = 1:1.7:4.8. This is a surprising observation since, a priori, one would expect that the monovalent K⁺, Na⁺, and Li⁺ ions would behave very similarly. Note that we limit our studies to monovalent ions. Experiments performed in the presence of divalent ions (MgCl₂) resulted in significant sticking of DNA to the membrane, which does not come as a surprise as divalent ions like Mg²⁺ are regularly used to adhere DNA to inorganic surfaces such as mica or SiO₂.

Figure 2.

Experiments showing the slowing down of DNA translocation in LiCl. (a) Example current recordings for 48.5 kbp λ-dsDNA filtered at 5 kHz in 1 M KCl (left), 1 M NaCl (middle) and 1 M LiCl (right). (b) Same for 1 M LiCl, 2 M LiCl and 4 M LiCl. (c) Same for heat-shocked M13mp18 ssDNA in an additional 8 M Urea, filtered at 30 kHz. (d-f) Translocation time histograms corresponding to (a–c). For the dsDNA we find translocation times of τ = 1.72 ± 0.29 ms, 2.94 ± 0.55 ms, 8.23 ± 1.43 ms, 12.1 ± 1.9 ms, and 16.5 ± 2.2 ms in 1 M KCl, 1 M NaCl, 1 M LiCl, 2 M LiCl, and 4 M LiCl respectively. For the ssDNA we find translocation times of τ = 52 ± 10 μs, 71 ± 13 μs, and 530 ± 190 μs in 1 M KCl, NaCl, and LiCl respectively.

Higher salt concentrations of LiCl result in even longer translocation times, with a ratio of 1:1.5:2 for 1M:2M:4M (see Fig. 2b for typical events and Fig. 2e for translocation time histograms). Also, larger current blockades are observed at higher salt concentrations. Note that changing the measurement buffer from that typically used in nanopore experiments (1 M KCl) to 4 M LiCl slows down the dsDNA in the nanopore by a factor of 10, which is very beneficial for read-out resolution. The number of events per second is found to scale inversely with the measured translocation times (see Fig. S3). This can be understood based on the reduced capture probability of a lower-charged object at fixed voltage (12). These results are qualitatively consistent with bulk measurements on the electrophoretic mobility of DNA (13). However, the ion-type dependence appears to be much stronger in the case of nanopores. The reason likely is that these bulk measurements were done at very low ionic strength (30 mM), whereas much higher ionic strengths can be applied in nanopore experiments, leading to stronger screening.

For ssDNA, we also find that the event amplitudes are similar between the different solutions (for scatter diagrams, see Fig. S2). To ensure the 7.2 kb long circular M13mp18 ssDNA is in a denatured state (no secondary structures), the ssDNA is heat-shock treated prior to experiments and measurements are done in 8 M Urea (see Materials and Methods). Event amplitudes of ~ 1.5–2 nS are measured (example events shown in Fig. 2c). Note that the ssDNA used is circular, resulting in the presence of two single strands of DNA at each point in time during translocation through the pore. The measured amplitude of about 1 nS per strand indicates that the ssDNA is indeed denatured (9), because non-denatured ssDNA under similar conditions gives much higher (~10 nS) event amplitudes due to the formation of large ssDNA blobs that stall at the pore entrance (14). Similar to dsDNA, but quantitatively even more pronounced, the ssDNA exhibits a slowing down upon changing the solute from KCl to NaCl to LiCl with translocation times of ssDNA for KCl:NaCl:LiCl = 1:1.4:10.2 (see Fig. 2f for translocation time histograms). Investigation at much higher salt concentrations is not possible for ssDNA because the 8 M Urea solution saturates at about 1.5 M salt concentration.

How can we understand this pronounced and unexpected slowing down of DNA translocation upon merely changing the buffer from KCl to LiCl? To elucidate the microscopic mechanism of the dependence of the DNA translocation velocity on the type and concentration of the electrolyte, we carried out all-atom MD simulations of several nanopore systems each containing a fragment of dsDNA, a circular nanopore and electrolyte, as depicted in Figure 1b. Each system was periodic in all three dimensions, and hence represented an infinite DNA molecule confined in an infinite nanochannel. In the radial direction, the DNA fragment was harmonically restrained to remain in proximity of the geometrical center of the pore. In the axial direction, an additional harmonic potential was enforced between the centers of mass of the DNA fragment and of the nanopore. Subject to an external electric field directed along the nanopore axis, the DNA fragment was observed to move in the direction opposite to the direction of the field until the force of the harmonic potential balanced the effective force exerted by the electric field on the DNA. A detailed description of the simulation methods and protocols is provided in Materials and Methods.

Using the setup described above, we simulated the dependence of the stall force on the type and concentration of the electrolyte and on the diameter of the nanopore. We chose to simulate the stall force rather than translocation velocity because, for the long DNA molecules used in experiment (λ-DNA), the translocation velocity is determined by the balance of the effective driving force of the electric field in the nanopore and the hydrodynamic drag on the DNA coil outside the nanopore. Assuming the hydrodynamic drag on the coil depends only on the viscosity of the electrolyte, the simulated dependence of the stall force should, ideally, match the measured dependence of the translocation velocity after scaling by the viscosity, even if the DNA translocation velocity varies (increases) as the translocation progresses (45).

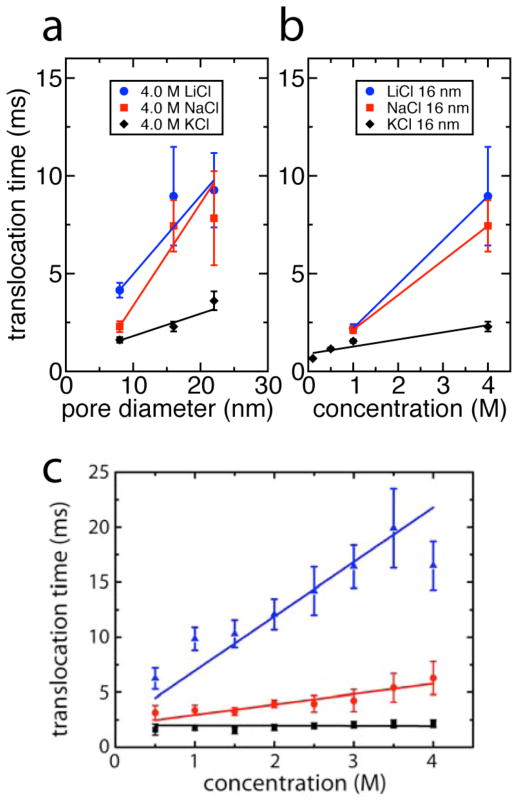
Figure 3a and b plots the simulated dependence of the stall force, expressed as translocation time for comparison to experiment. To convert forces to translocation times, we adopt the model of Storm et al. (16), in which the dominant force opposing translocation is the viscous drag of the coil of untranslocated DNA. The persistence length of DNA is independent of ion conditions at the ionic strengths examined here (42), and thus translocation times τ can be calculated as τ = αη/F_stall, where η is the solution viscosity (44), F_stall is the stall force determined in the MD simulations, and α = 62 μm² is a parameter chosen to fit the experimental 1.0 M KCl translocation time of 1.7 ms. The simulations were performed for KCl, NaCl, and LiCl at 0.1 M, 0.5 M, 1.0 M, and 4.0 M concentrations using nanopores of 8, 16, and 22 nm in diameter. The results of the simulations are in qualitative agreement with the experimentally observed dependence of the translocation speed on salt species and concentration, as presented in Fig. 3c. For all pores examined, the stall force in 4.0 M LiCl is lower than in 4.0 M NaCl, which is in turn is lower than in 4.0 M KCl. The simulations also correctly capture the decrease of the stall force as the pore diameter increases, as was measured before (46). The stall forces are shown in Fig. S5.

Figure 3.

Molecular dynamics simulations. (a) Translocation time as a function of pore size for 4.0 M ion concentration. LiCl is seen to result in the longest translocation time in all pore sizes, followed by NaCl, and finally by KCl. Lines are linear fits. (b) Translocation time as a function of ion concentration in the 16 nm diameter pore. Translocation times τ were calculated as τ = αη/F_stall, where η is the solution viscosity, F_stall is the stall force determined in the MD simulations, and α = 62 μm² is a parameter chosen to fit the experimental 1 M KCl translocation time of 1.7 ms. Lines are linear fits to the data. (c) Experimental translocation times for dsDNA as a function of ion species and concentration (same color coding as in panel b). Solid lines are linear fits to the data.

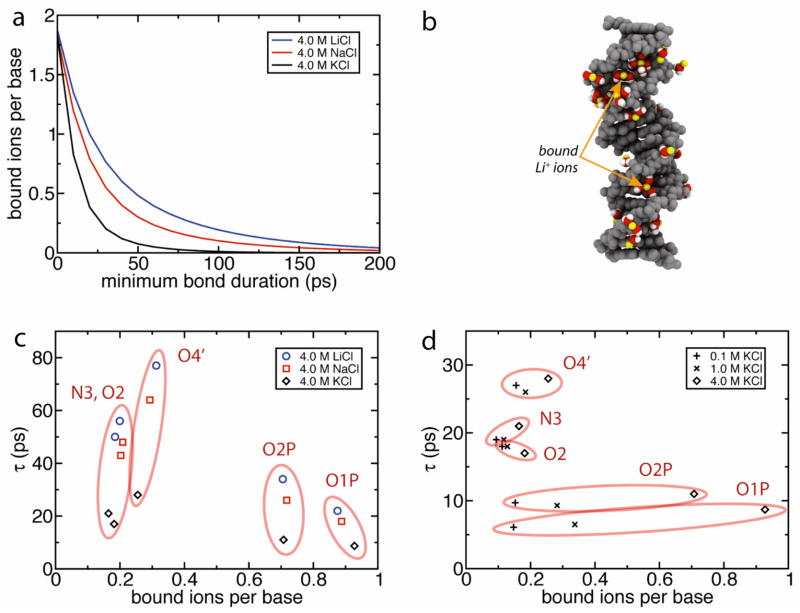
To investigate the microscopic mechanism responsible for the slow translocation of DNA in the presence of LiCl, we computed the average number of ions bound to the DNA surface in the MD trajectories. Direct ion binding to DNA was rarely observed in our MD simulation trajectories. Ion binding in the first solvation shell, however, was prevalent, see Figure 4b for illustration. In Figure 4a, we show the number of bound counterions per base N in the 8 nm pore at 4.0 M ion concentration. The number N is plotted as a function of minimum bond duration (see Materials and Methods). The plot shows that the instantaneous number of bound ions (minimum bond duration of 0 ps) is independent of ion type. Importantly, however, the bond strengths are not equal: Li⁺ bonds last longer, on average, than Na⁺ bonds, which in turn last longer than K⁺ bonds. For example, in the 4.0 M LiCl system, each base has on average 0.5 lithium ions which have been bound for at least 50 ps, while in the 4.0 M KCl system, each base has less than 0.1 potassium ions which have been bound that long. This difference in bond strength leads to a difference in net force, and thus velocity, for the different solutions. Note that taking into account chloride ions, the instantaneous total charge of bound ions per base approaches 1 as the minimum bond duration approaches 0, see Fig. S6a. Chloride ions were found to bind much more weakly to the DNA surface than the cations, Fig. S6b.

Figure 4.

(a) Number of bound counterions per base as a function of minimum bond duration in MD simulation with 4 M ion concentration and an 8 nm diameter pore. Ion binding to DNA takes place through an intermediate water molecule. The instantaneous number of bound ions (i.e. zero minimum bond duration) is seen to be independent of the ion type. However, at higher minimum bond durations, the number of bound lithium ions is seen to be higher than the number of bound sodium and potassium ions. (b) Lithium counterions bound to DNA in MD simulations. DNA is shown in gray, lithium is shown in yellow, and intermediate water is shown in red and white. Only water molecules involved in the bonds are shown. (c) Bond duration τ at 4 M concentration of LiCl (●), NaCl (■), and KCl (◆) versus number of bound ions per base n for MD simulations of an 8 nm diameter pore. Each data point represents binding to a single type of DNA atom; the five most popular binding sites are shown and labeled. Atom names are those used in the CHARMM force field. Each binding site is seen to exhibit essentially the same number of bound ions upon changing the ion type. However, the strength of the bonds is highly dependent on ion type, with the most durable bonds are seen in LiCl, followed by NaCl, and finally KCl. Note also that although the phosphate oxygens O1P and O2P exhibit the most bound ions (i.e., large n), those bonds are relatively weak (i.e., low τ). The longest-lasting bond type seen is to the O4’ oxygen atom in the minor groove. (d) Comparison of bond duration versus number of bound ions per base at different KCl concentrations: 0.1 M (+), 1 M (×), and 4 M (◆). Changing the ion concentration is seen to change the number of bound ions, but, as expected, not the strength of the bonds.

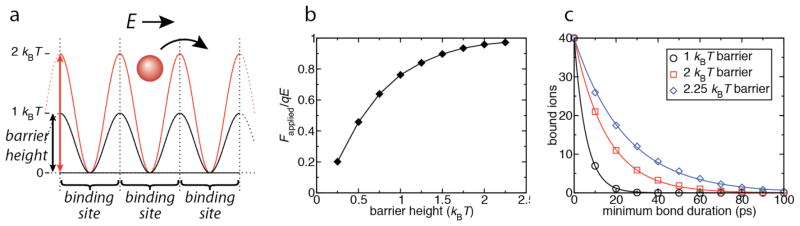
To demonstrate the effect of bond strength on the force transmitted to the DNA by the ions, we consider a system of electrically driven ions in a periodic potential, shown in Fig. 5a. The potential represents a simplified toy model of the charge distribution along the DNA molecule. MD simulations of this system performed for different barrier heights reveal the dependence of the effective force applied by ions to the potential representing the surface of a DNA molecule, as well as the dependence of ion residence time in individual binding sites. Thus, Fig. 5b shows F_applied/qE, where F_applied is the average magnitude of the force applied to each ion by the potential (and thus the average force applied by each ion to the potential), q is the charge of the ion, and E is the magnitude of the applied electric field. At a barrier height of 0.25 k_BT, the ions apply little force to the potential, because thermal and electrical energy dominates and the ions do not bind strongly to the binding sites. At a barrier height of 2.25 k_BT, on the other hand, the ions apply nearly the maximum possible force (qE), because the ions are strongly bound and spend a relatively long time in each binding site, and therefore transfer the force due to the electric field to the DNA rather than dissipate it to the solution. At intermediate barrier heights, the complete range of possible forces is seen, despite the fact that all ions are bound (i.e. occupy a binding site) at all times. In Fig. 5c, we characterize the number of ions that bind to the wells of the potential (compare with Fig. 4a) for several intermediate values of the barrier height, illustrating the dependence of bond duration on the latter. The results clearly show the effect of barrier height on the effective force applied by the ions on the DNA, and therefore on the effective charge of DNA in the electric field.

Figure 5.

The effect of barrier height on force transmission. (a) Model system, in which a sinusoidal potential, representing a toy model for the DNA charge along its length, is applied to ions. Barrier heights of 1 and 2 k_BT are shown. Each period of the potential represents a binding site. Three binding sites are shown; the model system contained 20 binding sites per 6.4 nm length, similar to DNA. (b) Average force per ion applied to the potential representing DNA as a function of barrier height, normalized by the applied electric force. (c) Binding curves similar to those plotted in Fig. 4a, shown for barrier heights of 1, 2, and 2.25 k_BT. Varying the barrier height is seen to affect both the bond lifetime and the effective force applied to the potential representing DNA. Solid lines are exponential fits to the data.

Counterion binding and the dependence on ion type are illuminated further by examining binding to individual sites on DNA. To this end, binding curves such as those shown in Figure 4a were calculated for every binding site seen in the simulations, then fit by an exponential of the form ne^−t/τ, where n and τ are fitting parameters. The five sites with the highest n for the 4.0 M LiCl 8 nm system are plotted in Figures 4c and d. We see in Figure 4c that the number of bound ions per site is largely independent of the ion type, but that the bond duration τ is highest for lithium, followed by sodium, and finally potassium. Figure 4d shows the dependence on ion concentration: as expected, the ion concentration only affects the number of bound ions, not the bond duration.

Discussion

Through a combination of MD simulations and nanopore translocation experiments, we have characterized the effective charge of a DNA molecule in monovalent electrolytes. While it has been known that the charge of a DNA molecule sensitively depends on the valence of counterions (21, 22), here we demonstrate that the size of counterions can considerably influence the effective DNA charge, and hence the average translocation speed through a nanopore.

One may ask whether interactions between DNA and the nanopore surface play a role in the reducing of the average translocation speed. In very small pores (well under 5 nm in diameter) DNA-pore wall interactions were reported to slow down DNA translocation (23, 24) as well as to lead to a considerable spread in event characteristics (25). In our case however, we used wide pores of ~ 20 nm in diameter where such effects have not been reported, and there are no obvious reasons to assume adsorption because of the negative charge of both the membrane surface and DNA. Indeed, we obtained similarly different translocation speeds for LiCl and KCl for graphene nanopore experiments (26), confirming that the slowing down is intrinsic to the Li-DNA interactions rather than due to extrinsic reasons such as sticking to the SiN surface.

At the molecular level, we found a partial neutralization of the DNA charge that originates from transient binding of counterions. Although we found the number of bound counterions to be the same for each ion type, the duration, and hence strength, of those bonds was not. Indeed, lithium bonds to DNA were found to be the longest lived, followed by sodium, and finally potassium. Using a simplified ion system, we demonstrated that such a change in bond strength does indeed affect the force transmitted from ion to DNA, and hence the velocity of the translocating DNA. If compared to direct experimental measurements, the simulations quantitatively underestimate the net force on DNA in the case of KCl. However, the qualitative agreement between simulation and experiment is satisfactory, given the relative simplicity of MD models, the known imperfections of the water model in classical MD simulation (for example, a 3-fold underestimation of its viscosity), and the sensitive dependence of the stall force on the ion-DNA interaction. From a practical perspective, our findings indicate that LiCl offers significant advantages compared to the traditionally used ionic solutions for nanopore applications.

Materials and Methods

1. MD Methods

All simulations were performed using the software package NAMD (28), 2–2–6-fs multiple timestepping, CHARMM27 parameters (29) with CMAP corrections (30), a 7–8 Å cutoff for van der Waals and short-range electrostatic forces, and the Particle Mesh Ewald (PME) method for long-range electrostatics computed over a 1.0 Å-spaced grid. The temperature was maintained at 295 K using the Lowe-Andersen thermostat. For NPT simulations, the Langevin piston method was used, with a period of 2000 fs and a decay of 200 fs. Ions were simulated with parameters produced by recent refinements to Beglov and Roux ion parameters (43). Trajectory frames were saved every 10 ps. Visualization and analysis were performed using VMD (33).

The simulation systems consisted of a 6.4 nm thick block of annealed SiO₂ (34) containing an 8 nm, 16 nm, or 22 nm diameter circular pore along the short axis of the block, DNA, and ionic solution of 0.1, 0.5, 1 M, or 4 M of LiCl, NaCl, or KCl. Simulations with larger systems, in which the pore was connected to a solution bath, verified that the ion concentrations quoted correspond to bulk concentrations. Systems contained 20 bp (two turns) of a random sequence. To avoid interaction of DNA with the silica surface, the center of mass of DNA phosphate atoms was radially restrained to the center of the pore, with a spring constant of 93.72 kcal mol⁻¹ Å⁻². Periodic boundary conditions were used, with DNA covalently bonded over the periodic boundaries, effectively making the simulation system an infinite nanopore containing infinite DNA. An electric field was applied parallel to the nanopore/DNA axis. Electric potential differences reported refer to the difference over a single 6.4 nm periodic image. No absolute restraints were applied along the dimension of the pore axis of the system, and the zero momentum feature of NAMD was used (47).

Ion binding in the second solvation shell of DNA was computed as follows. An ion was considered bound if it was within 0.34 nm of a water oxygen atom, which in turn was within 0.31 nm of a DNA heavy atom. These distances, which are measured between atom centers, correspond to minima in the applicable radial distribution functions. When calculating the number of bound ions as a function of minimum bond duration, a bond is considered to persist when the same three atoms (ion, water oxygen, and DNA heavy atom) form a bond in adjacent trajectory frames.

The model system measured 2 × 2 × 6.4 nm³. It contained 40 ions (q = +1) only; no water was present. Periodic boundary conditions were applied. The system was simulated using NAMD, with a dielectric constant of 80. A sinusoidal potential of the form (U₀/2) cos(2πmz/L) was applied to all ions using Tcl boundary forces (28), where the barrier height U₀ was a constant in the range of 0.25–2.25 k_BT, z is the position along the long axis of the system, and m = 20 is the number of binding sites. Simulations were run for 9.6 ns, and force was output for each ion every 48 fs. A Langevin thermostat was used to control temperature, with a temperature of 295 K and a damping constant of 5.0 ps⁻¹. An electric field corresponding to 500 mV was applied along the long axis of the system. Timestep, cutoff, and PME parameters were the same as those used in the all-atom simulations. During each simulation, we recorded the average force the potential applied to each ion. According to the Newton’s third law, the magnitude of this force equals the force exerted by each ion on the potential representing the surface of DNA.

2. Solid-state nanopores

Solid-state nanopore fabrication starts with the fabrication of 20 nm thin free-standing SiN membranes through the use of electron-beam lithography and wet etching. In each such membrane, we drill a nanopore of the desired size through the use of a highly focused electron beam in a transmission electron microscope (TEM). Details of the fabrication process are described elsewhere (37). The reported data on dsDNA was taken on a 15.3 nm pore, the data on ssDNA on a 19.8 nm pore. Nanopores are treated in an oxygen plasma for 30 s on both sides prior to use. Subsequently, the nanopores are mounted in a polyether ether ketone (PEEK) microfluidic flow cell and sealed to liquid compartments on either side of the sample. Measurements are performed in KCl/NaCl/LiCl salt solution of the stated molarity containing 10 mM Tris-HCl and 1mM EDTA at pH 8.0 at room temperature. The viscosities of these solutions (η = 0.99, 1.10, 1.15 × 10⁻³ Pa·s respectively) do not differ much. Experiments with divalent ions were performed in 1 M MgCl₂ containing 10 mM Tris-HCl and 1 mM EDTA at pH 8.0. Ag/AgCl electrodes are used to detect ionic currents and to apply electric fields. Current traces are measured at 100 kHz using a resistive feedback amplifier (Axopatch 200B, Axon Instruments) and digitized at 500 kHz. When necessary, further low-pass filtering is performed. Only pores with minimal low-frequency current noise (< 20 pA RMS) are used (10).

3. Preparation of single-stranded DNA

To ensure that no secondary structure is present in the ssDNA, M13mp18 circular ssDNA is heat-shock treated for 10 minutes at 90°C, which removes all secondary structure. The final DNA concentration used in the nanopore experiment was 2 ng/μl. Measurements are done in 1 M salt solutions with an additional 8 M Urea to prevent refolding of the ssDNA (39). This results in a reduction of ~ 40% of the open-pore pore conductance (see Fig. S7) as reported before (40), because of the increased viscosity (1.7 × 10⁻³ Pa·s for 8 M Urea) and the fact that the ionic electrophoretic mobility (and hence the total current) is proportional to the inverse of the viscosity (41).