On the genome-wide analysis of copy number variants in family-based designs: Methods for combining family-based and population based information for testing dichotomous or quantitative traits, or completely ascertained samples

Abstract

We propose a new approach for the analysis of copy number variants (CNVs)for genome-wide association studies in family-based designs. Our new overall association test combines the between-family component and the within-family component of the data so that the new test statistic is fully efficient and, at the same time, achieves the complete robustness against population-admixture and stratification, as classical family-based association tests that are based only on the between-family component. Although all data are incorporated into the test statistic, an adjustment for genetic confounding is not needed, not even for the between-family component. The new test statistic is valid for testing either quantitative or dichotomous phenotypes. If external CNV data are available, the approach can also be used in completely ascertained samples. Similar to the approach by Ionita-Laza et al.(1), the proposed test statistic does not required a CNV-calling algorithm and is based directly on the CNV probe intensity data. We show, via simulation studies, that our methodology increases the power of the FBAT statistic to levels comparable to those of population-based designs. The advantages of the approach in practice are demonstrated by an application to a genome-wide association study for body mass index (BMI).

1. Introduction

Recent studies (2; 3; 4; 5; 6) have highlighted the importance of copy number variation in modifying the risk of certain diseases. With the increasing interest in the study of copy number variants (CNVs), a number of methodologies for analyzing these data have been developed for both population-based and family-based analyses (1; 7; 8; 9; 10; 11). Recently, Ionita-Laza et al. (2008) (1) introduced a statistic for association testing of CNVs in family-based settings. Noting that, for SNP-chips, the calling of CNVs can be a difficult and error-prone process when standard calling algorithms are applied(12; 13; 14; 15), the test statistic is constructed using genetic information based on the probe intensity data rather than by the called CNVs. Since then, new, improved algorithms to call CNVs’ genotypes based on intensity data from SNP-chips(16; 17; 18) have been developed. While the algorithms are able to provide important genomic insights into the underlying genetic architecture, the advantages of using called CNVs over probe intensities in the association test statistic are not clear. In the best-case scenario for the calling-algorithms, (i.e. genotypes called based on intensities for SNPs), Ionita-Laza et al.(1) showed that there is virtually no difference in terms of statistical power between association tests that are based on genotype data and association tests that are based on intensity data. Furthermore, the advantage of using intensity data is that it avoids bias due to incorrectly called CNV genotypes. In family-based association tests, mis-called genotypes for SNPs or CNVs can introduce a systematic bias in terms of increased α-levels (19; 20; 21; 22; 23).

Currently, the methodology by Ionita-Laza et al. (2008) (1) for family-based association test in CNV analysis solely utilizes the within-family component. Similar to the standard FBAT-approach, the between-family component can only be incorporated into test-strategies and model building steps in which the between-family component is used to inform the “final” FBAT-testing step or to construct an FBAT-statistic with maximal statistical power(24; 25). In order to maintain complete robustness against confounding due to population admixture and stratification, the between-family component can not be included directly in the test statistic.

In this manuscript, we develop an overall family-based association test that simultaneously utilizes all information about the genetic association that is included in both components, i.e., the between-family component and the within-family component. However, by virtue of its design, the new overall association test for CNVs maintains the complete robustness of classical family-based association tests, e.g., TDT (26), FBAT(27; 28). The new FBAT-CNV test combines an association test for the population-based component, the between-family component, with a standard FBAT test that is based only on the within-family component, using Liptak’s method for combining p-values. Similar to the philosophy of genomic control(29), the significance of the association test for the between-family component is not assessed based on its asymptotic distribution, but relative to the other CNVs, using rank-based p-values. As will be shown, the use of rank-based p-values in the overall test statistic is sufficient to ensure that the approach is robust against population admixture and stratification.

The proposed overall CNV-FBAT statistic utilizes the standard FBAT-CNV statistic(1) and an association test for the between-family component that is constructed based on the conditional mean model or its non-parametric extensions (24; 25). It is therefore straight-forward to apply the new approach to any trait types which have been integrated into the FBAT-framework, e.g., binary traits, continuous traits, multivariate traits, time-to-onset, etc. (30; 31; 32; 33; 34; 35; 36). However, for simplicity, we will illustrate the new overall FBAT-CNV statistic for scenarios in which dichotomous or quantitative traits are analyzed and for samples that are either unascertained, i.e., total population samples, or completely ascertained, i.e., every subject is affected. Using simulation studies that are based on ~900,000 CNV probes, the performance of the overall FBAT-CNV statistic is assessed under the null-hypothesis and its power levels are estimated. The features of the new approach are demonstrated by an application to a genome-wide association study for BMI.

2. Methods

Prior to describing the joint test, we briefly review the FBAT-CNV statistic introduced by Ionita-Laza and colleagues(1). We assume that genotype intensity data have been collected for nuclear families (i.e., offspring and parents). Let x_ij denote the probe intensity for the j^th offspring in the i^th family. The recoded offspring phenotype is denoted by T_ij, which represents the offspring phenotype minus an offset value. For example, the phenotype is quantitative, T_ij might be residual from the regression of the offspring phenotype on important clinical predictors of the phenotype (e.g. BMI ~ SEX + AGE). The FBAT statistic for copy number variation, introduced by Ionita-Laza et al. (2008)(1) is given by:

$$Z_{\mathit{\text{FBAT}}-\mathit{\text{CNV}}}=\frac{{\mathrm{\Sigma }}_{\mathit{\text{ij}}}[T_{\mathit{\text{ij}}}(x_{\mathit{\text{ij}}}-E(X_i))]}{{\left[{\mathrm{\Sigma }}_{\mathit{\text{ij}}}{\mathrm{\Sigma }}_{\mathit{\text{ij}}\prime }{T}_{\mathit{\text{ij}}}{T}_{\mathit{\text{ij}}\prime }(x_{\mathit{\text{ij}}}-E(X_i))(x_{\mathit{\text{ij}}\prime }-E(X_i))\right]}^{0.5}}$$ (2.1)

where E(X_i) is the ’expected’ intensity score given the parental intensities. When parental intensities are available, E(X_i) is given by the mean of parental probe intensities. If parental data are missing, E(X_i) may be obtained by averaging the intensity data across all offspring within a family E(X_i) = Σ_j x_ij/n_j. This concept is similar to the sufficient statistic given by Rabinowitz and Laird (2000) (28). It should also be noted that the empirical variance as given by Lake et al. (2000) (37), rather than the theoretical variance, is used to standardize the test statistic, since Mendelian transmissions cannot be identified in the intensity data. For further details on the derivation of the test statistic, please see Ionita-Laza et al. (2008)(1).

2.1. Quantitative Traits

Next, we turn our attention to the joint test statistic, as originally developed by Won et al. (2009)(38). Won proposes an overall family-based association test statistic, Z_i, which is a weighted sum:

$$Z_i={\omega }_{\mathit{\text{FBAT}}}{Z}_{{\mathit{\text{FBAT}}}_i}+{\omega }_P{Z}_{P_i}$$ (2.2)

The parameters ω_FBAT and ω_P are specified a priori to the analysis, and are standardized so that ${\omega }_{\mathit{\text{FBAT}}}^2+{\omega }_P^2=1$. Z_FBATi is the Z-score corresponding to the p-value of the i^th FBAT statistic, and Z_Pi is the Z-score corresponding to a p-value that reflects the relative ranking of the i^th population-based test statistic. To preserve the type I error of the test in the presence of population stratification, the p-values obtained from Z_Pi are based on the relative ranking of the i^th test statistic, rather than its asymptotic value. For details, see Won et al.(38). This method of combining independent test statistics was originally conceived by Liptak(39), and henceforth, the joint test of family-based and population based information will be referred to as the FBAT-Liptak test.

2.1.1. Implementation of FBAT-CNV Liptak test for Quantitative or dichotomous traits

The extension of the method by Won et al. (2009)(38) to copy number variants is fairly straightforward, when using the statistic developed by Ionita-Laza et al. (2008)(1). In the joint test statistic, Z_i, the family component Z_FBATi is replaced by Z_FBAT–CNVi, as given in equation 2.1. The between-family component of the test statistic, Z_Pi is obtained from a Wald test of the genetic effect size from a regression of the offspring phenotype on the expected offspring probe intensity, E(X_i), using a generalization of the conditional mean model(24; 30). In the case of CNVs, this quantity is given by the mean of parental probe intensities (or in the event of missing parental data, E(X_i) = Σ_j x_ij/n_j), rather than by the expected transmissions based on parental genotypes, assuming Mendelian transmission, as is the case with SNP data. This concept is applicable to both quantitative or dichotomous (i.e., case-control) traits, using an identity or logit link, respectively, in a generalized linear model. As noted above, to protect against potential confounding such as by population stratification, the p-values from Z_Pi reflect the relative rank of the CNV rather than an asymptotic value obtained from standard normal or student’s t distribution. As with the standard method using SNP data, the joint test statistic reflects the summed weighted family-based and population-based components, and may be adjusted for multiple comparisons using standard approaches. It should be noted, however, that while the FBAT-CNV statistic may detect either de novo or germline mutations, the power to detect de novo mutations will be decreased using this method, as the between-family component solely is based on parental intensities.

2.1.2. Implementation of Liptak FBAT-CNV for fully ascertained family-based samples

Recently, Lasky-Su and colleagues (2009)(36) extended the idea proposed by Won et al.(38) to family-based studies in which all offspring in the study are affected with the disease or trait of interest. From equation 2.2, it is easy to see that a standard Transmission Disequilibrium Test (TDT)(26) could be used to calculate Z_FBATi . However, family-based designs where all offspring are affected pose a problem for calculating the effect size for the between-family component, as the conditional mean model(24; 30) requires variation in the offspring phenotype. Murphy et al.(40) propose using relative risk ratios based on the parental genotypes (which assume Hardy-Weinberg Equilibrium in the general population) for estimating the between-family effect size for SNP data, but this method is not applicable in the context of CNVs. Lasky-Su et al.(36) address the issue of generating between-family information by using control genotype data from either publicly available (e.g., dbGap) or commercial (e.g., Illumnina, Affymetrix, and Perlegen) sources. However, the method by Lasky-Su et al. requires called genotype data and thus is not applicable to CNV intensities. For CNV data, we will extend the concept of using freely available genetic data to devise a test for generating the statistic Z_Pi in 2.2.

We assume that CNV probe intensity values will be available for a population of control subjects from a publicly available source. Let Z_Pi be the Z-score corresponding to the rank of the p-value from a Wald test from a generalized linear model with a logit link:

$$Y_{\mathit{\text{ij}}}~I(G(X_{\mathit{\text{ij}}})),\text{where}:\{\begin{array}{c}I(G(X_{\mathit{\text{ij}}}))=E(X_i)\text{if the subject is a case}\hfill \\ I(G(X_{i}j))=X_{\mathit{\text{ij}}}\text{if the subject is a control}\end{array}$$ (2.3)

where Y_ij is the offspring or control phenotype (i.e., Y_ij=1 if an affected offspring, 0 if a control), E(X_i) is the expected offspring CNV probe intensity, and X_ij is observed CNV probe intensity in the control. As noted previously, E(X_i) is given by the mean of parental probe intensities, or in the event of missing parental data, E(X_i) = Σ_j x_ij/n_j. After obtaining the Wald test statistic rank-based p-value of the CNV genetic effect size for the population based component (Z_Pi), and the FBAT – CNV statistic asymptotic p-value for the family-based component (Z_FBATi), the method by Won et al. follows straightforwardly(38).

As shown in the next section, while this method has slightly less power than a standard case-control test (where the asymptotic p-value from the Wald test is used), its power loss is minimal while preserving the attractive feature of FBAT robustness against population structure.

3. Simulation Studies

3.1. Quantitative trait

Using simulation studies, we contrast the new testing strategy to a both a standard FBAT statistic, as well as a standard population-based analysis (i.e., a generalized linear model regressing the phenotype on the observed CNV intensity) of only the offspring. For the Liptak-CNV test, we varied the weights for the FBAT and Wald components of the of the statistic from 1:3 and 3:1 (i.e., the FBAT weight ranged from 1 to 3 times the weight of the Wald weight, and vice-versa), and set δ=0.5. For details on the weights and appropriate specifications for δ, see Won et al.(38). All three analytic approaches are compared under scenarios with varying sample and effect sizes. We simulated the trio data under the assumption that all of the offspring data are available and that the genotype probe intensity of the parents are known. Additionally, we assumed independence between the CNV loci. The parental CNV data were generated from a N(0,1) distribution. The offspring intensities were generated using a N(EX,1) distribution, where EX is the mean of the parental intensities.

In each simulation, one locus is assumed to be the DSL, while the other CNVs are considered null loci. For the null loci, the offspring phenotype was simulated using a N(0,1) distribution. For the DSL, the distribution was N(a * X), where X is the probe intensity of the CNV locus. In the simulations, the genetic effect size ranges between 0.1 and 0.2. The trio sample size varies between 500 – 2000 trios.

For each test, the p-value was adjusted using a standard Bonferroni correction. Thus, the power was defined as the proportion of replicates with an FBAT statistic p-value < 5.56×10⁻8 (i.e., 0.05/900,000), to reflect the current capacity of CNV typing technology. The power was based on 10,000 replicates. In table 1 below, the standard FBAT test is denoted as “FBAT,” the population-based test is denoted as “Wald”, and our new integrated approach using both the population and family based information is denoted as “FBAT-Liptak.”

Table 1.

Power for 500–2000 trios and 900,000 markers for a quantitative trait.

N	Effect			Equal weights	FBAT up-weighted		Wald up-weighted
trios	Size	FBAT	Wald	Liptak(1:1)	Liptak(2:1)	Liptak(3:1)	Liptak(1:2)	Liptak(1:3)
500	0.1	0.000	0.004	0.003	0.001	0.002	0.002	0.001
	0.125	0.000	0.026	0.016	0.013	0.012	0.011	0.009
	0.15	0.004	0.095	0.061	0.060	0.062	0.042	0.036
	0.175	0.024	0.259	0.176	0.182	0.183	0.133	0.108
	0.2	0.075	0.504	0.376	0.396	0.392	0.309	0.251
1000	0.1	0.008	0.058	0.041	0.054	0.049	0.033	0.024
	0.125	0.043	0.265	0.210	0.242	0.231	0.172	0.136
	0.15	0.172	0.637	0.547	0.587	0.577	0.467	0.402
	0.175	0.417	0.906	0.853	0.879	0.869	0.786	0.721
	0.2	0.712	0.987	0.972	0.983	0.980	0.948	0.917
2000	0.1	0.144	0.519	0.458	0.488	0.478	0.378	0.297
	0.125	0.511	0.922	0.891	0.907	0.895	0.823	0.753
	0.15	0.867	0.997	0.994	0.996	0.995	0.985	0.972
	0.175	0.987	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999
	0.2	0.999	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999

The standard FBAT test is denoted as “FBAT,” the population-based test is denoted as “Wald”, and our new integrated approach using both the population and family based information is denoted as “FBAT-Liptak. The numbers in parentheses, reflect the weighting of the FBAT component of the Liptak-CNV test relative to the Wald component of the Liptak-CNV, (e.g., (2:1) indicates that the FBAT component has twice the weight of the Wald component). The power reflects the proportion of replicates were the association p-value< 5.56×10⁻⁸.

Across all sample and effect size, the FBAT-Liptak test demonstrates considerable power gains over the standard FBAT test, and generally has less than a <10% power loss in comparison to the population-based Wald test. In the scenario with equal weighting, 1000 trios and an effect size of 0.175, the FBAT-Liptak test has a 200% power gain over the FBAT test, while the Wald test only has a 6% power gain over the FBAT-Liptak test. From the simulations, the optimal weighting scheme tends to range between weighting the FBAT component 2 to 3 times more heavily than the Wald component. In Won et al. (38), the optimal weights for the FBAT and Wald components are described as a ratio of their standardized effect sizes. Overall, the power estimates in the FBAT-Liptak test demonstrate modest power reductions in comparison to a population based test, while preserving one of the most desirable properties of the FBAT, robustness against population stratification.

3.2. Completely ascertained sample

In this section, we also compare the new testing strategy to a both the standard FBAT statistic and population-based test, except that a logit link was used in the generalized linear model for the population based analysis. The CNV intensities for the unrelated control population (i.e., to be obtained from a publicly available resource) were simulated using a N(0,1) distribution. The trio CNV intensities, were simulated using the methods described above, except that large trio (i.e., parents and offspring) population, from which “affected” offspring were sampled, using the following approach.

As above, we assumed that there was one locus contributing to disease risk and that there was no LD between the loci. We assumed that the baseline risk of the disease, K, was 5%. We used a logistic regression model to estimate the risk of disease for each offspring, where Pr(Affected) = e^α+βX/1 + e^α+βX, where α = log(K/1 − K), β is the log of the odds ratio, and X is the observed CNV intensity in the offspring. From the pool of trio CNV intensity data, we randomly selected a subset of affected offspring and their parents, to simulate a completely ascertained sample. The controls were all assigned an affection status of unaffected, regardless of their CNV intensity value, to reflect the fact that a proportion of subjects in the “control” dataset are likely to have the disease or trait of interest, at a rate roughly equivalent to the population prevalence of the disease. We denote these subjects as “unselected controls.”

The simulations included sample sizes of 250–500 trios, where the corresponding population-based test (i.e., denoted as “Wald”) comprises 250–500 pairs of unrelated individuals, the affected offspring from the trios and the unrelated control population. The effect size ranged from an odds ratio of 1.25 – 2. As above, the power was defined as the proportion of replicates with an FBAT statistic p-value < 5.56×10⁻8 (i.e., 0.05/900,000), applying standard Bonferonni correction for multiple comparisons. The power was based on 10,000 replicates. The results are displayed in table 2 below.

Table 2.

Power for 250–1000 trios/subjects and 900,000 markers in a completely ascertained sample

N trios/	Effect			Equal weights	FBAT up-weighted		Wald up-weighted
pairs	Size	FBAT	Wald	Liptak(1:1)	Liptak(2:1)	Liptak(3:1)	Liptak(1:2)	Liptak(1:3)
250	1.25	0.004	0.008	0.009	0.013	0.014	0.007	0.005
	1.375	0.104	0.116	0.121	0.177	0.196	0.075	0.050
	1.5	0.446	0.462	0.470	0.586	0.623	0.304	0.217
	1.625	0.804	0.796	0.803	0.889	0.910	0.623	0.486
	1.75	0.957	0.949	0.949	0.983	0.991	0.850	0.734
500	1.25	0.128	0.128	0.147	0.208	0.227	0.086	0.054
	1.375	0.749	0.705	0.756	0.851	0.875	0.570	0.431
	1.5	0.990	0.974	0.984	0.997	0.998	0.935	0.859
	1.625	>0.999	>0.999	>0.999	>0.999	>0.999	0.997	0.984
	1.75	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999	0.999
1000	1.25	0.776	0.696	0.773	0.869	0.891	0.594	0.450
	1.375	>0.999	0.997	0.999	1.000	>0.999	0.992	0.972
	1.5	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999
	1.625	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999
	1.75	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999	>0.999

The number of trios reflects the number of trios included in either the FBAT or in the family-based component of the FBAT-Liptak tests. The number of subjects reflects the total number of subjects used (including both the offspring from the trios and unselected controls) used in the Wald or in the population-based component of the Wald-Liptak test. The standard FBAT test is denoted as “FBAT,” the population-based test is denoted as “Wald”, and our new integrated approach using both the population and family based information is denoted as “FBAT-Liptak. The numbers in parentheses, reflect the weighting of the FBAT component of the Liptak-CNV test relative to the Wald component of the Liptak-CNV, (e.g., (2:1) indicates that the FBAT component has twice the weight of the Wald component). The power reflects the proportion of replicates were the association p-value< 5.56×10⁻⁸.

For completely ascertained samples, the power of both the FBAT and Liptak-CNV tests generally exceed the population-based Wald test. It should be noted that the simulations are designed such that the number of trios and number of case-control pairs (e.g. 250 trios/250 case-control pairs) are equivalent. With an equal weighting scheme, the power for the FBAT and Liptak tests are fairly comparable, although the Liptak-CNV test does give a power boost in lower power ranges. When the weights for the FBAT and Wald compon-ponents of the Liptak-CNV are varied, an up-weighting of the FBAT component boosts the power, with the 3:1 weighting of the FBAT to Wald component, respectively, consistently demonstrating the highest power.

4. Data Analysis

Asthma is a complex respiratory disorder, with both environmental and genetic components, which has been shown to have substantial heritability (41; 42; 43). We applied our methodology to a genome-wide association study of child asthmatics and their families. The families were identified through the Childhood Asthma Management Program (CAMP) (44) Genetics Ancillary Study. Increasing body mass index (BMI) and obesity has been previously linked to increasing asthma risk, and a recent study(45) found a gene associated with both BMI and asthma. In our analysis, we screened for potential copy number variants for associated with BMI.

In the CAMP study, SNP genotyping was performed using Illumina HumanHap 550v3 array. Of the 561,466 SNPs, 16,419 (2.9%) were removed during data cleaning due to the following reasons: 1) probe sequences did not map uniquely to hg18 genome build, 2) poor cluster separation as manually reviewed in Illumina BeadStudio software, 3) −log10(pval) for Hardy-Weinberg equilibrium >= 8, and/or 4) completion rate < 95%, 5) Mendelian error count >=5, or 6) minor allele frequency = 0. Overall, adequate DNA for genome-wide SNP genotyping was available for 1172 subjects in 403 families (43 subjects in 19 families were removed due to inadequate DNA samples)

To reduce the number of multiple comparisons (and false positive results), we applied a circular binary segmentation algorithm to identify the most likely CNV regions in our cohort. Circular binary segmentation (CBS) uses SNP intensity at sequential markers to call CNV regions(46). The goal of CBS is to parse the genome into segments of equal copy number, while accounting for the inherent noise in measuring array intensities. This is achieved by identifying change-points, locations at which the distribution preceding the change-point differs from the distribution proceeding the change-point. The change- or break- points may then be used to limit testing to regions where copy number gains or losses have occurred. Practically speaking, this algorithm allows us to restrict the testing of potential trait-associated CNVs to markers that fall within CNV regions, thus substantially reducing the number of association tests conducted. The CBS algorithm was applied to all autosomal SNP in the CAMP dataset using the Bioconductor package DNAcopy(47). In our analysis, a CNV was called in an individual when the (absolute) intensity value of a segment was greater than four standard deviations of the middle 50% quantile of all data(48). For inclusion in the analysis, we required CNV prevalence of at least 1% (i.e., present in 12 individuals). If called markers were within 50kb of one another, they were considered part of the same CNV region. Using this approach, 976 common CNVs (from 6,965 SNPs) were identified in the CAMP data set with frequency of at least 1%. For the analysis, we applied our joint test statistic to the probe intensities of all 6,965 (called CNV region) SNP, testing for potential association with BMI at baseline, adjusting for age and sex. Table 3 displays the results for the CAMP data analysis.

Table 3.

Top 10 Results for identified CNV regions, sorted by Liptak p-value, for the CAMP BMI analysis

SNP	Chr.	Position*	FBAT	Rank-based	Liptak	Liptak
		(bp)	p-value	Wald p-value	test	p-value
rs1758827	10	56295820	4.931E-03	7.128E-05	4.68	2.902E-06
rs1831078	9	25416556	2.411E-03	2.138E-04	4.64	3.547E-06
rs1886314	13	67392298	3.583E-04	1.019E-02	4.16	3.133E-05
rs9351261	6	65171419	1.999E-02	4.989E-04	3.97	7.118E-05
rs11758713	6	67036364	2.593E-04	3.899E-02	3.83	1.285E-04
rs7072438	10	59013036	2.775E-02	7.840E-04	3.79	1.495E-04
rs696279	7	16700798	3.811E-03	1.133E-02	3.66	2.547E-04
rs11004706	10	56813669	7.685E-02	3.564E-04	3.64	2.681E-04
rs7856324	9	28366643	1.814E-03	2.145E-02	3.64	2.756E-04

^*SNP positions are from NCBI build 37.1. The FBAT p-value is the asymptotic p-value obtained from the Ionita-Laza FBAT – CNV test statistic. The Observed Wald p-value is the asymptotic p-value from a Wald test regressing the BMI phenotype on the expected parental CNV intensities. The Rank-based Wald p-value reflects the p-value based on the rank of the Wald test. The Liptak test is the value of the test statistic given in equation 2.2, which combines the FBAT p-value and the Rank-based Wald p-value. The Liptak p-value is the asymptotic p-value from this combined test statistic. Results with a Liptak p-value< 7.18×10⁻⁶ are significant at the α=0.05 level after Bonferroni correction for multiple comparisons.

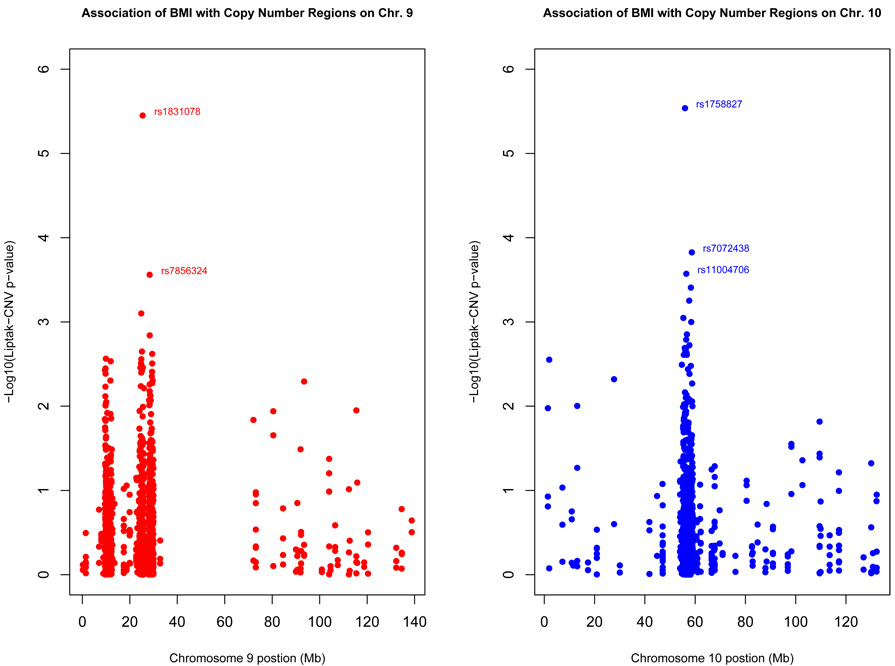
Interestingly, two of the top SNPs (rs1758827 and rs1886314) are in intronic regions of protocadherin genes (PCDH15 and PCDH9 on chromosomes 10 and 13, respectively), which are members of the cadherin superfamily. The top two results were significant (at α=0.05) after Bonferroni correction for multiple comparisons. As noted in Figure 1, there is significant enrichment in the regions surrounding the top SNP on chromosomes 9 and 10. Overall, among the top findings, there was consistency in the family-based and population-based association results.

Fig. 1. Association of BMI with Copy Number Regions on Chromosomes 9 and 10.

These figures plot the −Log10 Liptak-CNV p-values against the chromosomal position of SNP in identified copy number regions on chromosomes 9 and 10. There are areas of significant enrichment on both chromosomes, centered around two markers, rs1831078 and rs1758827, which met genome-wide significance criteria.

5. Discussion

In this manuscript, we present a new method for maximizing the available information in family-based genome-wide studies of copy number variants. Our new methodology combines the population level and family level data in family-based designs into a more powerful association test. This test can be applied to both quantitative and dichotomous traits. Additionally, although public repositories of CNV data are generally not currently available, it is not unreasonable to anticipate their availability in the near future, given the current initiatives to develop a public repository of both phenotype and genome-wide SNP data (e.g. dbGap, http://www.ncbi.nlm.nih.gov/sites/entrez?Db=gap). When control CNV data become available from a public repository, our methodology also can be applied to completely ascertained family-based samples. For continuous traits, our methodology approaches that of a strictly population-based test. For completely ascertained samples, we have shown that our method can be more powerful than a population based approach combining affected offspring with unrelated controls. And unlike a population-based approach, our method is robust against population admixture(38), like the standard FBAT statistic. The power of our methodology may be further increased by using alternative approaches for multiple comparisons adjustment. Although we have applied a very conservative Bonferroni correction to our combined test statistic, other methods, such as FDR(49) could be applied.