Adaptively deformed mesh based interface method for elliptic equations with discontinuous coefficients

Abstract

Mesh deformation methods are a versatile strategy for solving partial differential equations (PDEs) with a vast variety of practical applications. However, these methods break down for elliptic PDEs with discontinuous coefficients, namely, elliptic interface problems. For this class of problems, the additional interface jump conditions are required to maintain the well-posedness of the governing equation. Consequently, in order to achieve high accuracy and high order convergence, additional numerical algorithms are required to enforce the interface jump conditions in solving elliptic interface problems. The present work introduces an interface technique based adaptively deformed mesh strategy for resolving elliptic interface problems. We take the advantages of the high accuracy, flexibility and robustness of the matched interface and boundary (MIB) method to construct an adaptively deformed mesh based interface method for elliptic equations with discontinuous coefficients. The proposed method generates deformed meshes in the physical domain and solves the transformed governed equations in the computational domain, which maintains regular Cartesian meshes. The mesh deformation is realized by a mesh transformation PDE, which controls the mesh redistribution by a source term. The source term consists of a monitor function, which builds in mesh contraction rules. Both interface geometry based deformed meshes and solution gradient based deformed meshes are constructed to reduce the L_∞ and L₂ errors in solving elliptic interface problems. The proposed adaptively deformed mesh based interface method is extensively validated by many numerical experiments. Numerical results indicate that the adaptively deformed mesh based interface method outperforms the original MIB method for dealing with elliptic interface problems.

I Introduction

To solve partial differential equations (PDEs) in real world applications, adaptive strategy is often desirable. There are three main tactics, i.e., mesh subdivision (i.e., h-refinement), local high order schemes (i.e., p-refinement) and grid deformation method (i.e., r-method). Among them, the grid deformation strategy is an important approach. It has been applied to a variety of physical and engineering problems, such as combustion, shock waves, reaction diffusions, and two-phase flows.^{7,19,21,35,36,46} When the underlying problems are time-dependent, the deformed meshes change during the course of time evolution and the method is thus called moving mesh method. The essential idea of mesh deformation approaches can be dated back to 1974 by de Boor,³ who proposed the equi-distribution principle, which governs the selection of the spatial grid such that the solution error is equally distributed over all subintervals and the total error is minimized. This principle has been successfully employed to generate meshes in a one-dimensional (1D) setting with a number of elegant methods.

For mesh deformation methods in higher dimensions, a major advance was due to Winslow,⁴⁰ who used the solution of the Poisson equation to generate a mapping from a regular mesh in the computational domain to an irregular mesh in the physical domain. This method was further studied by Thompson, Thames and Mastin.^33,34,37 A body-fitted coordinate system was constructed for arbitrarily shaped geometries and a source term was introduced to control the spacing of coordinate lines. However, all these methods were mainly focused on the geometry of the physical domain. Little attention was paid to adaptive grid generations for singular solutions before Brackbill and Saltzman’s work in 1982.^4,5 These authors incorporated the adaptation of the solution into Winslow’s method. Based on the variational approach, they managed to improve the smoothness and orthogonality of their mesh by considering some controlling terms. In 1991, Dvinsky introduced a harmonic mapping to realize adaptive mesh generations.¹² In his work, a single energy functional is minimized by using the Euler-Lagrange equation. By using the equi-distribution principle, Huang, Cao and Russell^7,20,21 derived a series of moving mesh PDEs in a 1D setting, and then extends this method to a 2D domain based on a gradient flow. In 1992, Liao and Anderson²⁶ introduced a new mesh deformion method, in which grid nodes were moved according to the velocity field such that a specified cell volume distribution could be achieved.

In computational fluid dynamics, the mesh equation and the original equation are to be solved simultaneously. For problems with boundary layers or near-shock solutions, Miller and Miller²⁹ proposed a moving mesh finite element method, in which grid nodes concentrate automatically in critical regions and move along the velocity. Dorfi and Drury¹¹ proposed a moving mesh finite difference method in a 1D domain. They combined the adaptive grid with the implicit finite difference method to achieve high accuracy and allow relatively large time steps to be taken. Motivated by Dvinsky’s work, Li and Tang²⁴ proposed a moving mesh finite element method. In this approach, the change of meshes in the computational domain is used to guide the mesh redistribution in the physical domain at each time step. The solution is then updated through certain formula. Their method has been used in many applications.³²

In general, mesh deformation methods are only applicable to PDEs with near singular solutions, boundary layers or interior layers. In particular, these methods do not work for elliptic equations with discontinuous coefficients, also known as elliptic interface problems. Usually, due to the discontinuous coefficients, the solution of these problems is of low regularity. Typically the solution admits jumps. In case that the solution is continuous, the gradient of the solution is usually discontinuous. Consequently, for this class of problems, even if the meshlines are highly concentrated around the interface, the traditional mesh deformation solution can not maintain the desired order of convergence and may even diverge. In fact, the solution can be completely wrong as illustrated in our numerical test in Section III. This is due to the fact that the traditional mesh deformation does not automatically enforce interface jump conditions required at discontinuities. Whereas elliptic interface techniques can achieve high order convergence for this class of problems. Therefore, in order to make traditional mesh deformation strategy applicable to elliptic equations with discontinuous coefficients, one needs to incorporate elliptic interface techniques.

Elliptic equations with discontinuous coefficients and singular sources are of great importance in fluid dynamics, material science, and biological systems. Since Peskin’s pioneer work of immersed boundary method (IBM),³¹ many other methods have been proposed in the past few decades. Among them, immersed interface method (IIM) proposed by LeVeque and Li²³ is a remarkable scheme that achieves the second order accuracy and preserves the jump information at the interface. In their method, a local correction of the finite difference scheme is employed to incorporate the interface jump conditions.²⁵ The ghost fluid method (GFM) proposed by Fedkiw, Osher and coworkers¹³ is relatively simple and easy-to-use approach. Other methods such as finite element formulations,^1,6 finite volume based methods,³⁰ the piecewise-polynomial discretization,⁹ integral equation methods,²⁸ coupling interface method,¹⁰ and discontinuous Galerkin techniques¹⁸ have also generated much interest.

The matched interface boundary (MIB) method was initially introduced by Zhao and Wei for solving the Maxwell’s equation with material interfaces⁴⁸ and later generalized to the solution of elliptic equations with discontinuous coefficients and singular sources,^43,45,49,50 as well as the Helmholtz equation with material interfaces.⁴⁷ It is a systematic higher-order method for interface problems. The 16th order scheme is demonstrated with a simple geometry,⁵⁰ and 6th order MIB scheme has been constructed for irregular interfaces in 3D domains.⁴³ In the MIB method, the fictitious values are used on irregular points so that the standard finite difference scheme can be employed throughout the computational domain.⁴⁸ Similar ideas have been used in our discrete singular convolution algorithm for many years.^38,39 To further achieve flexibility, the enforcement of the jump condition is separated from the discretization of the original equation.⁵⁰ One important feature of the MIB method is that, in order to avoid the use of high order jump conditions, it iteratively enforces the lowest order jump conditions to achieve high order accuracy.^48,50 Another feature of the MIB method is that if possible, it splits a high-dimensional interface problem into multiple 1D ones.^39,48 As for geometric singularities, the disassociation technique and some schemes for handling singularities are invented.⁴⁵ Equipped with Krylov-subspace acceleration techniques, the state of the art MIB method is able to efficiently solve elliptic PDEs with arbitrarily complex interfaces, geometric singularities and singular sources in 3D settings.^8,43

Although there are many existing elegant methods for solving interface problems, simple regular Cartesian meshes are usually used in most approaches. Such meshes are certainly not optimal for problems with localized dramatically varying solutions. These problems differ from the normal high frequency ones, which can be dealt with high order interface schemes, such as the high order MIB method, with an optimal performance. One of optimal strategies for localized dramatic changes is the local mesh refinement. Finite element and finite volume based interface methods can build in locally adaptive grid generation algorithms.^22,41 However, it is very difficult to construct high-order convergent finite element or finite volume based interface methods for arbitrarily complex interfaces, particularly, interfaces with geometric singularities.^42,43 Consequently, it is extremely valuable to develop an adaptive mesh strategy for solving elliptic equations with discontinuous coefficients and locally fast varying solutions. To our knowledge, such a method does not yet exit at present.

The objective of the present work is to construct the first known adaptively deformed mesh based interface technique for solving elliptic equations with discontinuous coefficients and locally fast varying solutions. Our goal is to take the advantage of the mesh deformation strategy for elliptic interface problems. To this end, we generalize the MIB technique to mesh deformation settings. Two mesh deformation strategies, i.e., interface geometry based deformed meshes and solution gradient based deformed meshes are incorporated with our interface techniques in the present work. The resulting interface method is not only high accuracy but also high-order convergence. We believe that the proposed numerical algorithm is a significant advance of both traditional mesh deformation methods and elliptic interface schemes.

The rest of the paper is organized as follows. Section II is devoted to the theory and algorithm. To provide essential knowledge and establish notation, we provide a brief review of the mesh deformation method proposed by Liao and Anderson.^26,27 The construction of general monitor functions for location specific mesh mapping is described. The transformation of the governing equation from the physical domain to the logical domain (i.e., the computational domain) is discussed. In Section II.B, the essential techniques of the MIB method are presented. This discussion provides a basis for the development of an adaptively deformed mesh based elliptic equation solver. In Section II.C, we construct new interface techniques in the transformed domain, which are a reformulation of the original MIB method in the mesh deformation framework. In Section III, we carry out a large number of numerical experiments to validate the proposed new adaptively deformed mesh based interface method. In the first test case, we illustrate that the traditional mesh deformation methods do not converge for elliptic equations with discontinuous coefficients. Either the discontinuity in the solution or the discontinuity in the solution gradient will cause the failure of the traditional mesh deformation methods. The rest of the test examples are designed to demonstrate the performance of the proposed method. The effectiveness of two types of deformed meshes, namely, the interface geometry based ones and solution gradient based ones, is examined in the present work. Comparison is made to the original MIB method. We show the improvement of the proposed interface technique based deformed mesh strategy to the original MIB method for elliptic interface problems. This paper ends with some concluding remarks.

II Theory and algorithm

We define the elliptic interface problem in an open bounded domain Ω ∈ ℝ². The interface is usually originated from a physical setting. Let us consider a given interface Γ which divides Ω into two subdomains, Ω^a and Ω^b, such that Ω = Ω^a ∪ Ω^b and Γ = Ω^a ∩ Ω^b. In the present work, we limit our attention to the situation that the boundary ∂Ω and interfaces Γ are continuous, although more general nonsmooth cases often occur in applications.^42,43 We define a level-set function Φ on Ω̄, such that Γ = {x, y|Φ = 0; x, y ∈ Ω}, Ω^a = {x, y|Φ ≥ 0; x, y ∈ Ω}, Ω^b = {x, y|Φ ≤ 0; x, y ∈ Ω}. The two dimensional (2D) elliptic interface problem is given as

$${(\beta (x,y)u_x(x,y))}_x+{(\beta (x,y)u_y(x,y))}_y=g(x,y),$$ (1)

where the variable coefficient β(x, y) may have jumps at the interface Γ, at which two jump conditions can be prescribed to ensure the well posedness of the mathematical formulation

$$[u]=u^a-u^b={\mathrm{\Psi }}_1,$$ (2)

$$[\beta u_n]={\beta }^a{u}_n^a-{\beta }^b{u}_n^b={\mathrm{\Psi }}_2.$$ (3)

Here we denote u^a as the limiting value of function u from the Ω^a side of the interface, u^b the limiting value from Ω^b side of the interface, and u_n is the derivative along the norm direction. For simplicity, we assume that both Ψ₁(x, y) and Ψ₂(x, y) are C¹ continuous in the present work.

In the following subsections, we construct deformed mesh based interface technique for the solution of Eq. (1), subject to interface conditions (2) and (3). The boundary condition of Eq. (1) can be either Dirichlet, Neumann or Robin. To establish notation and introduce basic concepts, we first describe the mesh deformation method proposed by Liao and Anderson and our MIB method. Then the a new elliptic interface technique will be developed based these methods.

II.A Mesh deformation methods

Mesh deformation methods are designed to generate a mapping φ⃗: ℝⁿ → ℝⁿ which transforms a regular mesh in the logical domain to the physical domain based on certain rules. There are many kinds of mesh deformation methods or moving mesh methods as we have reviewed in the introduction. The most important ingredients shared by all mesh deformation methods are monitor functions, mesh equations, and the transformation of the governing equation.

Monitor functions are used to control the meshline distribution. They can be designed based on either the geometry, the solution, the gradient of solution, or the posterior errors. The selection of the monitor function has a major impact on the final mesh distribution and thus the accuracy of the solution. In practice, smoothness and regularity of the monitor function are usually needed. The mesh equation governs the mesh redistribution. A satisfactory mesh equation should concentrate sufficiently many grid nodes in local regions of interest. On the other hand, it should deliver the smoothness and orthogonality of the new mesh. The transformation of the governing equations may not be necessary for finite element methods as governing equation is directly solved on the irregular mesh or some iterative strategy may be used.²⁴ However, for finite difference methods, it is important to transform the governing equation from the physical domain to the computational domain. Otherwise, irregular grid finite difference schemes must be used, which may lead to accuracy reduction.

In the present work, we develop our mesh deformation method based interface technique by reformulating the mesh deformation algorithm proposed by Liao and Anderson.²⁶ In their work, the grid nodes are shifted according to a velocity field determined by a linear Poisson equation. The cell “volume” of the new mesh directly related to the transformation Jacobian is specified on the regular logical grid. After normalization, the monitor function is designed as a source term to control the contraction or expansion of the mesh at each node point.

The essential idea of Liao and Anderson’s mesh deformation method is equi-distribution.^2,34 In a 1D setting, it can be stated as,

$$\frac{d(\phi (\xi ))}{d\xi }f=\text{constant},$$ (4)

where φ is a transformation from the Cartesian grid ξ to the physical grid x, and f is the weight function, which is equi-distributed over the grid when Eq. (4) is satisfied. In a discrete representation, the equi-distribution takes the form

$$\mathrm{\Delta }{x}_i{f}_i=\text{constant},\mathrm{\Delta }{x}_i=x_{i+1}-x_i.$$ (5)

In higher dimensions, we assume that there is a smooth monitor function f(x⃗) defined on the physical domain Ω ⊂ ℝⁿ and satisfies two conditions

$$f(\overrightarrow{x})>0,\overrightarrow{x}\in \mathrm{\Omega },$$ (6)

$${\int }_{\mathrm{\Omega }}\frac{1}{f}d\overrightarrow{x}=A_{\mathrm{\Omega }},$$ (7)

where the A_Ω is the area of the physical domain. We construct certain transformation φ⃗: ℝⁿ → ℝⁿ satisfying the relation

$$\mid \nabla \overrightarrow{\phi }(\overrightarrow{\xi })\mid =f(\overrightarrow{\phi }(\overrightarrow{\xi })),\overrightarrow{\xi }\in \mathrm{\Omega },$$ (8)

$$\overrightarrow{\phi }(\overrightarrow{\xi })=\overrightarrow{\xi },\overrightarrow{\xi }\in \partial \mathrm{\Omega },$$ (9)

where ξ⃗ is the Cartesian grid in the computational domain, and φ⃗(ξ⃗) is the new grid in the physical domain. The “volume” element in the physical domain is given by |∇φ⃗(ξ⃗) |dξ⃗, and it is determined by the specified monitor function. On the other hand, function $\frac{1}{f}$ can be viewed as the weight function and satisfies the equi-distribution principle on the new mesh in the physical domain.

II.A.1 Algorithm for mesh deformation

Liao and Anderson provide a computational algorithm to carry out the above transformation.^16,17,26,36 Here, we outline a practical procedure for the mesh generation.

1. Design a temporal monitor function h(x⃗) > 0 according to a desirable role of choice. The performance of a mesh deformation method depends crucially on the appropriate choice of the monitor function. In the literature, monitor functions based on arc-length and/or error indicator are often used.

2. Normalize the monitor function according to (7) by finding a coefficient c_f such that

   $$c_f{\int }_{\mathrm{\Omega }}\frac{1}{h(\overrightarrow{x})}d\overrightarrow{x}=A_{\mathrm{\Omega }}.$$ (10)

   Then, we set the normalized monitor function as $f(\overrightarrow{x})=\frac{c_f}{h(\overrightarrow{x})}$.

3. Construct a Poisson equation with the zero flux boundary condition

   $$\nabla ·(c(\overrightarrow{x})\nabla w(\overrightarrow{x}))=f(\overrightarrow{x})-1,\overrightarrow{x}\in \mathrm{\Omega },$$ (11)

   $$\frac{\partial w(\overrightarrow{x})}{\partial \overrightarrow{n}}=0,\overrightarrow{x}\in \partial \mathrm{\Omega },$$ (12)

   where c is a continuous monitor function for mesh control²⁰ and w is a C² function for mesh generation. Obviously, the mesh can be adjusted by using either c or f, or the both. In the present work, we set c = 1 and control the mesh movement by appropriate f. Here n⃗ is the unit normal vector at the boundary. One needs to specify a value of w(x⃗) at a boundary point to make the final solution unique.

4. Define a velocity field vector v⃗: Ω → ℝⁿ by the gradient

   $$\overrightarrow{v}=\nabla w(\overrightarrow{x}).$$ (13)
5. Construct a deformation equation, i.e., a mesh equation, as

   $$\frac{d}{dt}\overrightarrow{\varphi }(\overrightarrow{x},t)=\frac{\overrightarrow{v}(\overrightarrow{\varphi }(\overrightarrow{x},t))}{(1-t)+tf(\overrightarrow{\varphi }(\overrightarrow{x},t))},0<t<1,$$ (14)

   $$\overrightarrow{\varphi }(\overrightarrow{x},0)=\overrightarrow{x},t=0.$$ (15)

   Obviously, this equation has to be solved iteratively.

6. Set the new mesh as

   $$\overrightarrow{\phi }(\overrightarrow{x})=\overrightarrow{\varphi }(\overrightarrow{x},1).$$ (16)

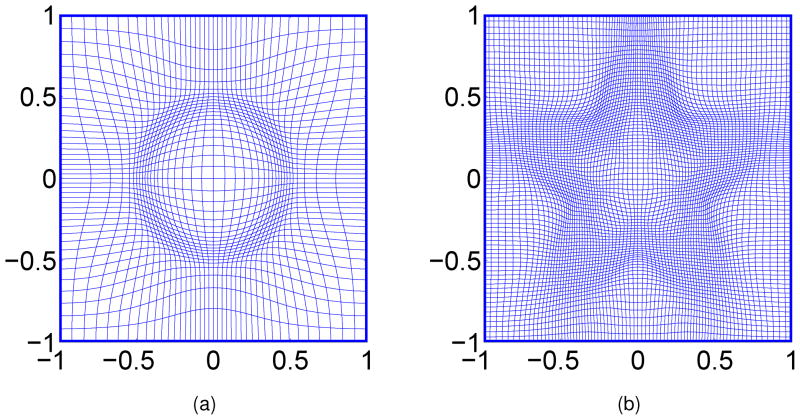
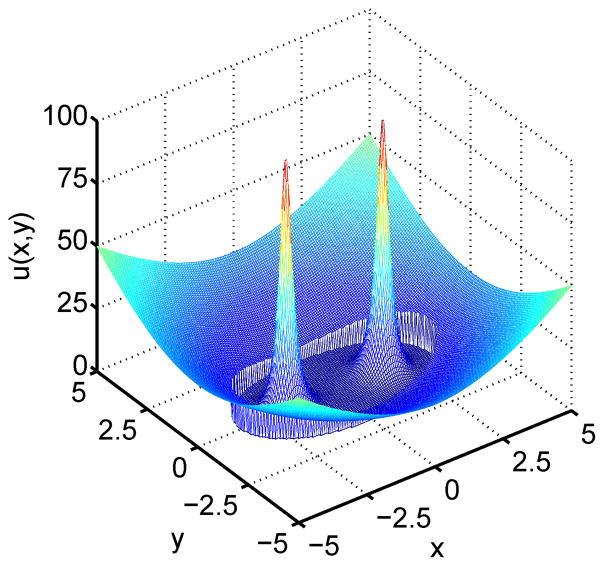
Liao and Anderson give a detailed description to show that the mesh generated by such an algorithm can satisfy Eq. (8). The cell volume here can be directly controlled by the monitor function according to one’s need. Normally, there are two ways to choose a suitable monitor function. The first way is based on the geometric characteristic. For example, if we want meshlines to concentrate in the region near the interface, we calculate the absolute distance from every point to the nearest interface, and this absolute distance is then treated as a variable in the monitor function. Figure 1 gives two examples of using geometry based monitor functions to control the mesh movement.

Figure 1.

The deformed mesh generated by two geometry based monitor functions. (a) The mesh used in Cases 1 and 2 of Section III; (b) The mesh used in Case 5 of Section III.

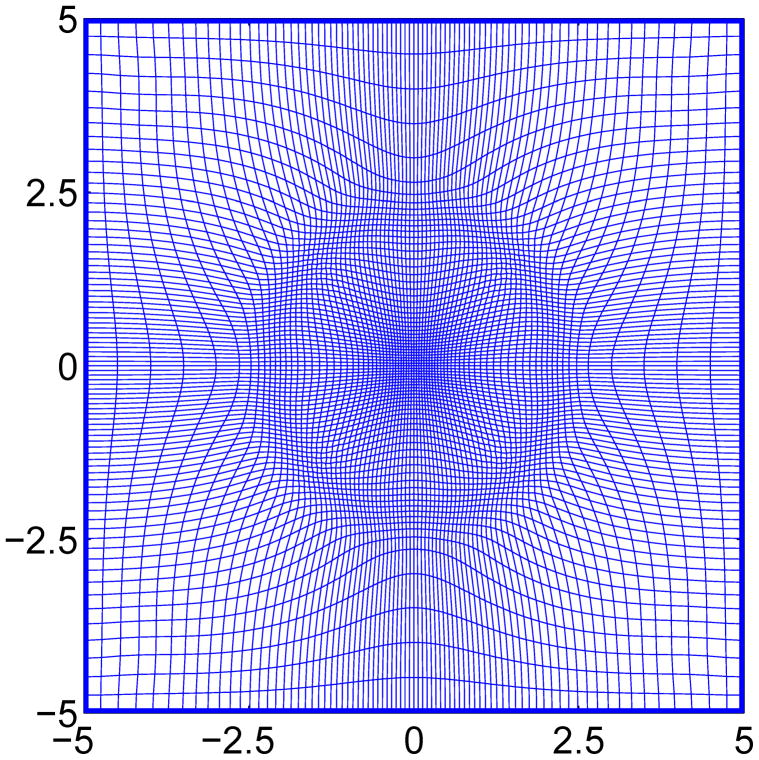
The second way is based on the solution characteristic. As such, the monitor function is incorporated with either the solution arclength, curvature, or posterior errors. Usually, if the solution is denoted as u, then this monitor function is of the form f(u, ∇u, Δu). Figure 2 depicts an example of a deformed mesh.

Figure 2.

The deformed mesh generated by a solution gradient based monitor function for Case 6 of Section III.

II.A.2 Transformation of governing equations

For finite difference methods, the governing equation can be solved either on a regular Cartesian mesh or on an irregular mesh. However, for a given number of finite difference nodes, the method on a regular Cartesian mesh has higher accuracy than that on an irregular mesh. Therefore, it is worthwhile to transform the governing equations defined in the irregular coordinate x⃗ in the physical domain back to the regular coordinate ξ⃗ in the logical or the computational domain. This transformation can be viewed as the inverse process of the mesh generation. For 2D problems, if we denote x⃗ = (x, y), and ξ⃗ = (ξ, η). We have the transformation relations

$$\left(\begin{array}{cc}{\xi }_x& {\xi }_y\\ {\eta }_x& {\eta }_y\end{array}\right)={\left(\begin{array}{cc}{x}_{\xi }& x_{\eta }\\ y_{\xi }& y_{\eta }\end{array}\right)}^{-1}=\frac{1}{J}\left(\begin{array}{cc}{y}_{\eta }& -x_{\eta }\\ -y_{\xi }& x_{\xi }\end{array}\right).$$ (17)

Here J is determination of the transformation matrix, J = x_ξy_η − x_ηy_ξ. Combined with the chain rules

$$\begin{array}{l}\frac{\partial }{\partial x}={\xi }_x\frac{\partial }{\partial \xi }+{\eta }_x\frac{\partial }{\partial \eta },\\ \frac{\partial }{\partial y}={\xi }_y\frac{\partial }{\partial \xi }+{\eta }_y\frac{\partial }{\partial \eta },\end{array}$$ (18)

one can transform u_x into the new coordinate,

$$u_x=(u_{\xi }{y}_{\eta }-u_{\eta }{y}_{\xi })/J.$$ (19)

In this way, the first and second derivatives of the solution can also be transformed into the new coordinate,

$$u_y=(-u_{\xi }{x}_{\eta }+u_{\eta }{x}_{\xi })/J,$$ (20)

$$u_{xx}=(y_{\eta }^2{u}_{\xi \xi }-2y_{\xi }{y}_{\eta }{u}_{\xi \eta }+y_{\xi }^2{u}_{\eta \eta }+a_1{u}_{\xi }+a_2{u}_{\eta })/J^2,$$ (21)

$$u_{yy}=(x_{\eta }^2{u}_{\xi \xi }-2x_{\xi }{x}_{\eta }{u}_{\xi \eta }+x_{\xi }^2{u}_{\eta \eta }+b_1{u}_{\xi }+b_2{u}_{\eta })/J^2,$$ (22)

$$u_{xy}=(x_{\xi }{y}_{\eta }+y_{\xi }{x}_{\eta })u_{\xi \eta }-x_{\xi }{y}_{\xi }{u}_{\eta \eta }-x_{\eta }{y}_{\eta }{u}_{\xi \xi }+c_1{u}_{\xi }+c_2{u}_{\eta }/J^2,$$ (23)

$${\nabla }^{2}u=(f_1{u}_{\xi \xi }+f_2{u}_{\xi \eta }+f_3{u}_{\eta \eta }+f_4{u}_{\xi }+f_5{u}_{\eta })/J^2.$$ (24)

Here the a₁,a₂, b₁,b₂ and f₁ to f₅ are some coefficients. They are determined when the mesh is generated. Their explicit expressions are given as

$$a_1=(y_{\eta }^2{y}_{\xi \xi }-2y_{\xi }{y}_{\eta }{y}_{\xi \eta }+y_{\xi }^2{y}_{\eta \eta })x_{\eta }-(y_{\eta }^2{x}_{\xi \xi }-2y_{\xi }{y}_{\eta }{x}_{\xi \eta }+y_{\xi }^2{x}_{\eta \eta })y_{\eta }/J,$$ (25)

$$a_2=(y_{\eta }^2{x}_{\xi \xi }-2y_{\xi }{y}_{\eta }{x}_{\xi \eta }+y_{\xi }^2{x}_{\eta \eta })y_{\xi }-(y_{\eta }^2{x}_{\xi \xi }-2y_{\xi }{y}_{\eta }{x}_{\xi \eta }+y_{\xi }^2{x}_{\eta \eta })x_{\xi }/J,$$ (26)

$$b_1=(x_{\eta }^2{y}_{\xi \xi }-2x_{\xi }{x}_{\eta }{y}_{\xi \eta }+x_{\xi }^2{y}_{\eta \eta })x_{\eta }-(x_{\eta }^2{x}_{\xi \xi }-2x_{\xi }{x}_{\eta }{x}_{\xi \eta }+x_{\xi }^2{x}_{\eta \eta })y_{\eta }/J,$$ (27)

$$b_2=(x_{\eta }^2{x}_{\xi \xi }-2x_{\xi }{x}_{\eta }{x}_{\xi \eta }+x_{\xi }^2{x}_{\eta \eta })y_{\xi }-(x_{\eta }^2{y}_{\xi \xi }-2x_{\xi }{x}_{\eta }{y}_{\xi \eta }+x_{\xi }^2{y}_{\eta \eta })x_{\xi }/J,$$ (28)

$$c_1=(x_{\xi }{y}_{\eta \eta }-x_{\eta }{y}_{\xi \eta })+(x_{\eta }{y}_{\eta }{J}_{\xi }-x_{\xi }{y}_{\eta }{J}_{\eta })/J,$$ (29)

$$c_2=(x_{\eta }{y}_{\xi \xi }-x_{\xi }{y}_{\xi \eta })+(x_{\xi }{y}_{\xi }{J}_{\eta }-x_{\eta }{y}_{\xi }{J}_{\xi })/J,$$ (30)

$$f_1=x_{\eta }^2+y_{\eta }^2,$$ (31)

$$f_2=-2(x_{\xi }{y}_{\eta }+x_{\eta }{y}_{\xi }),$$ (32)

$$f_3=x_{\xi }^2+y_{\xi }^2,$$ (33)

$$f_4=a_1+b_1,$$ (34)

$$f_5=a_2+b_2.$$ (35)

In mesh deformation methods, usually there is no explicit expression of x⃗ with ξ⃗ or the inverse. So all these coefficients should be evaluated on each grid point numerically. For example, if a grid node (i, j) is not on the boundary, one can have the approximation of x_ξ at (i, j) as

$$x_{\xi }{\mid }_{i,j}=\frac{x_{i+1,j}-x_{i-1,j}}{{\xi }_{i+1,j}-{\xi }_{i-1,j}}=\frac{x_{i+1,j}-x_{i-1,j}}{2h_{\overrightarrow{\xi }}}.$$ (36)

Here since coordinate system ξ⃗ is of Cartesian, the grid spacing is equal and one denotes it as h_ξ⃗. During the process of transformation of the governing equation, we implement the transformation relations (17) just for the purpose of avoiding the difficulty of approximation ξ_x, ξ_y, η_x, and η_y directly. Once the mesh generation is completed, all these coefficients can be calculated numerically.

II.B Matched interface and boundary method

The mesh deformation method obtained in Sections II.A.1 and II.A.2 can be used to solve the elliptic equation (1) directly for continuous coefficients or at the absence of interface conditions (2) and (3). However, mesh deformation methods can not achieve the designed order of convergence, accuracy and efficiency when the elliptic equation has discontinuous coefficients. In fact, the deformed mesh solution can be completely wrong when the solution admits jumps at the interface. To restore the power of mesh deformation methods, one needs to enforce interface conditions (2) and (3) in the mesh deformation framework. To this end, we consider the MIB method.

In the MIB method, irregular points are defined as the grid points which lie near the interface so that at least one of the required node points of a standard central finite difference scheme is located on the other side of the interface. In order to employ the central finite difference scheme for this kind of grid points. We introduce fictitious values, which can be viewed as a smooth extension of function values from the other side of the interface. Jump conditions are used to calculate the fictitious values, so that their implementation is disassociated with the discretization of the elliptic equation. As such, the same MIB scheme can be used for many different PDEs. We split a high dimensional problem to 1D problems. Therefore, the treatment of high dimensional problems is essentially the same as the treatment of 2D problems.

The MIB method enforces interface jump conditions at each intersecting point of the interface and meshlines. Let us consider a 2D problem. The first thing to do is to define a local coordinate system at an intersecting point of the interface and a meshline. To this end, we derive one more interface condition by differentiating Eq. (2) along the tangential direction of the interface when the interface is not aligned with the x- or the y- mesh line. This tangential direction jump condition can be expressed as $[u_{\tau }]=u_{\tau }^a-u_{\tau }^b$. Hence, if we define the norm direction n⃗ = (cos θ, sin θ) of the interface at the intersecting point, we can have three jump conditions

$$[u]=u^a-u^b,$$ (37)

$$[u_{\tau }]=(-u_x^{a}sin\theta +u_y^{a}cos\theta )-(-u_x^{b}sin\theta +u_y^{b}cos\theta ),$$ (38)

$$[\beta u_n]={\beta }^a(u_x^{a}cos\theta +u_y^{a}sin\theta )-{\beta }^b(u_x^{b}cos\theta +u_y^{b}sin\theta ),$$ (39)

where θ is defined with respect to the Cartesian meshline.

We discretize (βu_x)_x and (βu_y)_y separately using the second-order central finite difference scheme. For example, if the interface intersects the jth mesh line at a point between (i, j) and (i + 1, j), the function values u_i,j and u_i+1,j are located in different subdomains. Hence, (i, j) and (i + 1, j) are irregular points and fictitious values f_i,j and f_i+1,j are defined. The discretized form of (βu_x)_x at the irregular points (i, j) and (i + 1, j) can be given as,

$$\begin{array}{l}{(\beta u_x)}_x=\frac{1}{\mathrm{\Delta }{x}^2}\left({\beta }_{i-\frac{1}{2},j}^a,-{\beta }_{i-\frac{1}{2},j}^a-{\beta }_{i+\frac{1}{2},j}^a,{\beta }_{i+\frac{1}{2},j}^a\right){(u_{i-1,j},u_{i,j},f_{i+1,j})}^T\text{at}(i,j),\\ {(\beta u_x)}_x=\frac{1}{\mathrm{\Delta }{x}^2}\left({\beta }_{i+\frac{1}{2},j}^b,-{\beta }_{i+\frac{1}{2},j}^b-{\beta }_{i+\frac{3}{2},j}^b,{\beta }_{i+\frac{3}{2},j}^b\right){(f_{i,j},u_{i+1,j},u_{i+2,j})}^T\text{at}(i+1,j).\end{array}$$ (40)

Therefore, the direct evaluation of (βu_x)_x at point (i, j) involves grid points u_i−1,j, u_i,j and fictitious value f_i+1,j. The enforcement of the jump conditions in fact defines the fictitious values. This is done by discretizing some of terms u^a, u^b, $u_x^a,u_x^b,u_y^a$, and $u_y^b$ based on the geometry. Two linear equations involving two fictitious values can be constructed. This is always possible in practice. If $u_y^b$ is difficult to evaluate, one can eliminate it from Eqs. (38) and (39) to attain

$$[u]=u^a-u^b,\text{and}[\beta u_n]-{\beta }^{b}tan\theta [u_{\tau }]=C_x^a{u}_x^a-C_x^b{u}_x^b+C_y^a{u}_y^a,$$ (41)

where $C_x^a={\beta }^{a}cos\theta +{\beta }^{b}tan\theta sin\theta ,C_x^b={\beta }^{b}cos\theta +{\beta }^{b}tan\theta sin\theta$ and $C_y^a={\beta }^{a}sin\theta -{\beta }^{b}sin\theta$.

Based on the geometry, one can choose to eliminate one of $u_y^a,u_x^b$ and $u_x^a$ and attain two linear equations. Normally, one eliminates the derivative which is difficult to evaluate due to the constraint of the interface geometry. If one eliminates $u_y^a$, then

$$[u]=u^a-u^b,\text{and}[\beta u_n]-{\beta }^{a}tan\theta [u_{\tau }]=C_x^a{u}_x^a-C_x^b{u}_x^b-C_y^b{u}_y^b,$$ (42)

where $C_x^a={\beta }^{a}cos\theta +{\beta }^{a}tan\theta sin\theta ,C_x^b={\beta }^{b}cos\theta +{\beta }^{a}tan\theta sin\theta$ and $C_y^b={\beta }^{b}sin\theta -{\beta }^{a}sin\theta$. If one eliminates $u_x^b$, then

$$[u]=u^a-u^b,\text{and}[\beta u_n]+{\beta }^{b}cot\theta [u_{\tau }]=C_x^a{u}_x^a+C_y^a{u}_y^a-C_y^b{u}_y^b,$$ (43)

where $C_x^a=({\beta }^a-{\beta }^b)cos\theta ,C_y^a={\beta }^{b}cos\theta cot\theta +{\beta }^{a}sin\theta$ and $C_y^b={\beta }^b(cos\theta cot\theta +sin\theta )$. If one eliminates $u_x^a$, then

$$[u]=u^a-u^b,\text{and}[\beta u_n]+{\beta }^{a}cot\theta [u_{\tau }]=C_x^b{u}_x^b+C_y^a{u}_y^a-C_y^b{u}_y^b,$$ (44)

where $C_x^b=({\beta }^a-{\beta }^b)cos\theta ,C_y^b={\beta }^{a}cos\theta cot\theta +{\beta }^{b}sin\theta$ and $C_y^a={\beta }^a(cos\theta cot\theta +sin\theta )$.

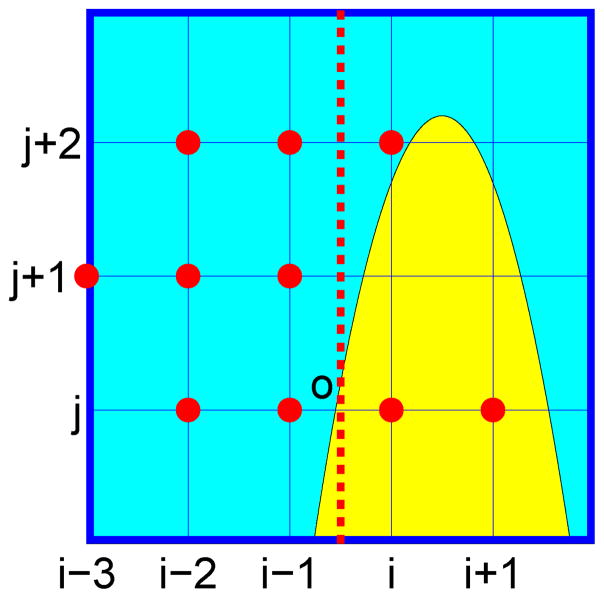
As depicted in Fig. 3, the interface divides the whole computational domain into two subdomains, denoted as Ω^a and Ω^b. Here Ω^a is marked with yellow color, while Ω^b is marked with green color. To make it more clear, we denote u^ao the limiting value of function u at point o from the Ω^a, and u^bo the limiting value at point o from Ω^b. The derivative of u with respect to x at point o from Ω^a is represented as $u_x^{ao}$, and that from domain b is represented as $u_x^{bo}$.

Figure 3.

Here domain Ω^a is marked with yellow color, while domain Ω^b is marked with green color.

Therefore, for point o, using u_i−2,j, u_i−1,j, u_i,j, u_i+1,j and the fictitious values f_i−1,j f_i,j, one can discretize u^ao, u^bo, $u_x^{ao},u_x^{bo}$ explicitly as

$$\begin{array}{l}{u}^{ao}=(w_{0,i-1}^{ao},w_{0,i}^{ao},w_{0,i+1}^{ao}){(f_{i-1,j},u_{i,j},u_{i+1,j})}^T,\\ u^{bo}=(w_{0,i-2}^{bo},w_{0,i-1}^{bo},w_{0,i}^{bo}){(u_{i-2,j},u_{i-1,j},f_{i,j})}^T,\\ u_x^{ao}=(w_{1,i-1}^{ao},w_{1,i}^{ao},w_{1,i+1}^{ao}){(f_{i-1,j},u_{i,j},u_{i+1,j})}^T,\\ u_x^{bo}=(w_{1,i-2}^{bo},w_{1,i-1}^{bo},w_{1,i}^{bo}){(u_{i-2,j},u_{i-1,j},f_{i,j})}^T,\end{array}$$ (45)

where $w_{n,m}^l$ is the standard finite difference weights computed from Lagrange polynomials. Subscript n = 0 represents the interpolation of the solution and subscript n = 1 represents the first order derivative of the solution. Here, subscript m is for the node index and superscript l indicates the position. For example, ao stands for the limiting value at the interface point o from domain Ω^a.

In Fig. 3, it is difficult for us to find suitable auxiliary points to discretize $u_y^{ao}$ as there are not enough grid points in Ω^a around point o. Thus, we choose to discretize $u_y^{bo}$. In order to do so, we need three u values along the y-direction in domain Ω^b. If we denote the coordinate of point o as (i_o, j), then these three values lie at points (i_o, j), (i_o, j + 1) and (i_o, j + 2). Since we have already had the expression for the value u^bo at point (i_o, j), the other two values can be approximated by auxiliary values u_i−3,j+1, u_i−2,j+1, u_i−1,j+1, u_i−2,j+2, u_i−1,j+2 and u_i,j+2. Here $u_y^{bo}$ can be computed as

$$\begin{array}{l}{u}_y^{bo}={\left[\begin{array}{c}{w}_{1,j}^{bo}\\ w_{1,j+1}^{bo}\\ w_{1,j+2}^{bo}\end{array}\right]}^T\left[\begin{array}{ccccccccc}{w}_{0,i-2}^{bo}& w_{0,i-1}^{bo}& w_{0,i}^{bo}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& w{1}_{0,i-3}^{bo}& w{1}_{0,i-2}^{bo}& w{1}_{0,i-1}^{bo}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& w{2}_{0,i-2}^{bo}& w{2}_{0,i-1}^{bo}& w{2}_{0,i}^{bo}\end{array}\right]\\ \times {[u_{i-2,j},u_{i-1,j},f_{i,j},u_{i-3,j+1},u_{i-2,j+1},u_{i-1,j+1},u_{i-2,j+2},u_{i-1,j+2},u_{i,j+2}]}^T,\end{array}$$ (46)

where, w1 and w2 are finite difference coefficients for the points at two auxiliary lines. Two equations can be attained by substituting Eqs. (45) and (46) into Eq. (42) to eliminate $u_y^{ao}$,

$${[u]}_o=(w_{0,i-1}^{ao},w_{0,i}^{ao},w_{0,i+1}^{ao})·{(f_{i-1,j},u_{i,j},u_{i+1,j})}^T-(w_{0,i-2}^{bo},w_{0,i-1}^{bo},w_{0,i}^{bo}){(u_{i-2,j},u_{i-1,j},f_{i,j})}^T,$$ (47)

$$\begin{array}{c}{[\beta u_n]}_o-{\beta }^{a}tan\theta {[u_{\tau }]}_o=C_x^a{\left[\begin{array}{c}{w}_{1,i-1}^{ao}\\ w_{1,i}^{ao}\\ w_{1,i+1}^{ao}\end{array}\right]}^T·\left[\begin{array}{c}{f}_{i-1,j}\\ u_{i,j}\\ u_{i+1,j}\end{array}\right]-C_x^b{\left[\begin{array}{c}{w}_{1,i-2}^{bo}\\ w_{1,i-1}^{bo}\\ w_{1,i}^{bo}\end{array}\right]}^T·\left[\begin{array}{c}{u}_{i-2,j}\\ u_{i-1,j}\\ f_{i,j}\end{array}\right]-C_y^b{\left[\begin{array}{c}{w}_{1,j}\\ w_{1,j+1}\\ w_{1,j+2}\end{array}\right]}^T\\ \left[\begin{array}{ccccccccc}{w}_{0,i-2}^{bo}& w_{0,i-1}^{bo}& w_{0,i}^{bo}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& w{1}_{0,i-3}^{bo}& w{1}_{0,i-2}^{bo}& w{1}_{0,i-1}^{bo}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& w{2}_{0,i-2}^{bo}& w{2}_{0,i-1}^{bo}& w{2}_{0,i}^{bo}\end{array}\right]\\ {[u_{i-2,j},u_{i-1,j},f_{i,j},u_{i-3,j+1},u_{i-2,j+1},u_{i-1,j+1},u_{i-2,j+2},u_{i-1,j+2},u_{i,j+2}]}^T.\end{array}$$ (48)

Here n⃗ = (cos θ, sin θ) is a unit normal vector, $C_x^a={\beta }^{a}cos\theta +{\beta }^{a}tan\theta sin\theta ,C_x^b={\beta }^{b}cos\theta +{\beta }^{a}tan\theta sin\theta$ and $C_y^b={\beta }^{b}sin\theta -{\beta }^{a}sin\theta$. Therefore, we obtain two equations from the interface information at point o.

To evaluate fictitious values, we solve Eqs. (47) and (48) together. The fictitious values can be represented by node values and jump conditions

$$\left[\begin{array}{c}{f}_{i-1,j}\\ f_{i,j}\end{array}\right]={\{C\}}_{2\times 13}·{\{U\}}_{13\times 1},$$ (49)

where vector {U}_13×1 consists of 10 function values and 3 jump conditions

$${\{U\}}_{13\times 1}={(u_{i-2,j},u_{i-1,j},u_{i,j},u_{i+1,j},u_{i-3,j+1},u_{i-2,j+1},u_{i-1,j+1},u_{i-2,j+2},u_{i-1,j+2},u_{i,j+2},{[u]}_o,{[\beta u_n]}_o,{[u_{\tau }]}_o)}^T.$$ (50)

Here, {C}_2×13 is a coefficient matrix and its components are the combination of weights and trigonometric functions of the normal direction at points o. Thus, once the locations of o is given, one can easily calculate the matrix and then the expression of fictitious values. Finally, one discretizes (βu_x)_x at irregular points (i − 1, j) and (i, j) as

$$\begin{array}{l}{(\beta u_x)}_x=\frac{1}{\mathrm{\Delta }{x}^2}\left({\beta }_{i-\frac{3}{2},j}^b,-{\beta }_{i-\frac{3}{2},j}^b-{\beta }_{i+\frac{1}{2},j}^b,{\beta }_{i+\frac{1}{2},j}^b\right){(u_{i-2,j},u_{i-1,j},f_{i,j})}^T\text{at}(i-1,j),\\ {(\beta u_x)}_x=\frac{1}{\mathrm{\Delta }{x}^2}\left({\beta }_{i-\frac{1}{2},j}^a,-{\beta }_{i-\frac{1}{2},j}^a-{\beta }_{i+\frac{1}{2},j}^a,{\beta }_{i+\frac{1}{2},j}^a\right){(f_{i-1,j},u_{i,j},u_{i+1,j})}^T\text{at}(i,j).\end{array}$$ (51)

Many other MIB schemes are created to handle geometric singularities (i.e., nonsmooth interfaces) and on-grid interface situations.^45,48,49 So far, many MIB techniques have been developed, such as dimension splitting, iteratively enforcement of the lowest order jump conditions, disassociation of equation discretization and fictitious value evaluation, simultaneously using two sets of interface conditions, etc. These techniques endow the MIB method the robustness, flexibility and accuracy in tackling arbitrarily complex interface geometries.

II.C Adaptively deformed mesh based interface methods

The MIB method is based on finite difference schemes. Both regular Cartesian grids and irregular grids⁴⁴ have been used in the MIB method. When an irregular mesh is generated by a mesh deformation method, we can either apply the MIB method directly on the irregular grids or implement the MIB method on the Cartesian mesh, which requires the transform of the governing equation. Since normal interface techniques may reduce their accuracy on irregular meshes, it it preferred to solve the transformed equation on the Cartesian mesh. For this purpose, the same kind of transformation as shown in Section II.A.2 should be employed. To make it clear, the transformation here is the inverse process of mesh transformation form curvilinear coordinate (x, y) to the regular coordinate (ξ, η). As the elliptic equation has discontinuous coefficient, which can be a function depending on the location. The transformation of the elliptic equation is given by

$$\begin{array}{l}{(\beta u_x)}_x+{(\beta u_y)}_y=\beta (u_{xx}+u_{yy})+{\beta }_x{u}_x+{\beta }_y{u}_y\\ =\beta (f_1{u}_{\xi \xi }+f_2{u}_{\xi \eta }+f_3{u}_{\eta \eta }+f_4{u}_{\xi }+f_5{u}_{\eta })+{\beta }_x({\xi }_x{u}_{\xi }+{\eta }_x{u}_{\eta })+{\beta }_y({\xi }_y{u}_{\xi }+{\eta }_y{u}_{\eta })\\ ={co}_1{u}_{\xi \xi }+{co}_2{u}_{\xi \eta }+{co}_3{u}_{\eta \eta }+{co}_4{u}_{\xi }+{co}_5{u}_{\eta },\end{array}$$ (52)

where coefficients f₁, ··· f₅ share the same form as those in Section II.A.2

$$\begin{array}{l}{co}_1=\beta f_1\\ {co}_2=\beta f_2\\ {co}_3=\beta f_3\\ {co}_4=\beta f_4+({\beta }_x{y}_{\eta }-{\beta }_y{x}_{\eta })/J\\ {co}_5=\beta f_5+(-{\beta }_x{y}_{\xi }+{\beta }_y{x}_{\xi })/J.\end{array}$$ (53)

Here coefficients co₁, ··· co₅ are similar to the coefficients f₁, ··· f₅ and can be evaluated numerically when the new mesh is generated. The discretization of terms u_ξξand u_ηη is the same as that in the MIB method. On regular point, the central finite difference scheme is implemented. For irregular points, we replace the gird values located at the other side of the interface with fictitious values. The first order derivatives are evaluated by the central finite difference scheme involving fictitious values at irregular points.

For the term u_ξη, at a point (i, j), the usual central difference scheme is,

$$u_{\xi \eta }{\mid }_{i,j}\approx \frac{1}{4}(u_{i+1,j+1}+u_{i-1,j-1}-u_{i+1,j-1}-u_{i-1,j+1}).$$

In order to approximate the term u_ξη, we divide all grid points into two kinds. For a point (i, j), if the four grid points needed for the central difference scheme of u_ξη are all in the same domain of (i, j), this point belongs to the first category. The rest belongs to the second kind. The discretization of the term u_ξη involves finding the suitable points in the same subdomain based on the geometry. The technique of finding points based on the geometry is discussed in detail in our earlier work.^44,45

During the transformation from curvilinear coordinate (x, y) to the regular coordinate (ξ, η), the relative location of the grid nodes and the topology of the interface do not change. That is to say, if a point (i, j) is located in certain subdomain in the physical domain, after transformation this point still lies in the same type of subdomain but in the logical domain. Although the shape and length of the interface may change during this process, the topological relation of the interface with respect to its surrounding grid nodes is kept unchanged.

The implement of jump conditions is of great importance. Assume there is an interface intersecting point o in the physical domain, the jump values at this point are denoted as [u]_o, [u_τ]_o and [βu_n]_o. There exists a corresponding interface intersecting point o′ in the computational domain with the same jump values

$$\begin{array}{c}{[u]}_o={[u]}_{o^{\prime }},\\ {[u_{\tau }]}_o={[u_{\tau }]}_{o^{\prime }},\\ {[\beta u_n]}_o={[\beta u_n]}_{o^{\prime }}.\end{array}$$ (54)

If we defined the normal direction at point o as n⃗ = (cos θ, sin θ). The tangential direction jump condition can be rewritten as

$$\begin{array}{l}{[u_{\tau }]}_{o^{\prime }}={[u_{\tau }]}_o\\ =(-u_x^{a}sin\theta +u_y^{a}cos\theta )-(-u_x^{b}sin\theta +u_y^{b}cos\theta )\\ =(-(u_{\xi }^a{\xi }_x+u_{\eta }^a{\eta }_x)sin\theta +(u_{\xi }^a{\xi }_y+u_{\eta }^a{\eta }_y)cos\theta )-(-(u_{\xi }^b{\xi }_x+u_{\eta }^b{\eta }_x)sin\theta +(u_{\xi }^b{\xi }_y+u_{\eta }^b{\eta }_y)cos\theta )\\ =C_{1\times 4}^1{(u_{\xi }^a,u_{\eta }^a,u_{\xi }^b,u_{\eta }^b)}^T.\end{array}$$ (55)

Here $C_{1\times 4}^1$ is a vector, and its expression is,

$$C_{1\times 4}^1=(-{\xi }_{x}sin\theta +{\xi }_{y}cos\theta ,-{\eta }_{x}sin\theta +{\eta }_{y}cos\theta ,{\xi }_{x}sin\theta -{\xi }_{y}cos\theta ,{\eta }_{x}sin\theta -{\eta }_{y}cos\theta ).$$

To make it clear, here the derivative $u_x^a$ is evaluated at point o in the physical domain. But $u_{\xi }^a{\xi }_x+u_{\eta }^a{\eta }_x$ is evaluated at point o′ in the computational domain. Their values are equal due to chain rules. The normal direction jump condition can be rewritten in the same way

$${[\beta u_n]}_{o^{\prime }}=C_{1\times 4}^2{(u_{\xi }^a,u_{\eta }^a,u_{\xi }^b,u_{\eta }^b)}^T,$$ (56)

and $C_{1\times 4}^2$ is a vector with expression

$$C_{1\times 4}^2=({\beta }_a({\xi }_{x}cos\theta +{\xi }_{y}sin\theta ),{\beta }_a({\eta }_{x}cos\theta +{\eta }_{y}sin\theta ),-{\beta }_b({\xi }_{x}cos\theta -{\xi }_{y}sin\theta ),-{\beta }_b({\eta }_{x}cos\theta -{\eta }_{y}sin\theta )).$$

Here $C_{1\times 4}^1$ and $C_{1\times 4}^2$ can be viewed as coefficient vectors. Their values are to be approximated at point o′ in the logical domain. To attain the discretized physical coordinate system {x_i,j, y_i,j}, one computes the relative location of interface point o and the value of the normal unit vector n⃗ = (cos θ, sin θ). Then the problem lies in how to evaluate coefficient ξ_x, ξ_y, η_x and η_y at point o′ or more specifically, the coordinate of point o′ in (ξ, η).

The approximation of these values is the key to the transformation of the jump conditions. We give a detailed description of the approximation. For example, if point o is located on the mesh line between irregular points (i, j) and irregular (i + 1, j) in coordinate system {x_i,j, y_i,j}. Point o′ should also be located on the mesh line between points (i, j) and (i + 1, j), but in different axis (ξ, η). We denote (x_i,j, y_i,j) as the coordinate for point (i, j) and (x_o, y_o) as the coordinate for point o in the coordinate system (x, y). The coordinate for o′ is denoted as (ξ_o′, η_o′) and point (i, j) as (ξ_i, η_j) in coordinate system (ξ, η). From Taylor expansion we obtain the relation,

$$x_o-x_{i,j}\approx x_{\xi }({\xi }_{o^{\prime }}-{\xi }_i)+x_{\eta }({\eta }_{o^{\prime }}-{\eta }_i),$$ (57)

$$y_o-y_{i,j}\approx y_{\xi }({\xi }_{o^{\prime }}-{\xi }_j)+y_{\eta }({\eta }_{o^{\prime }}-{\eta }_j).$$ (58)

As (ξ, η) is a Cartesian grid and o′ is a point in which the interface intersects with the mesh line. Therefore, either ξ_o′− ξ_i or η_o′− η_i is equal to zero. The distance from point o′ to point (i, j) can be approximated by one of two equations

$$\mid {\xi }_{o^{\prime }}-{\xi }_i\mid \approx \sqrt{\frac{{(x_o-x_{i,j})}^2+{(y_o-y_{i,j})}^2}{x_{\xi }^2+y_{\xi }^2}},$$ (59)

$$\mid {\eta }_{o^{\prime }}-{\eta }_i\mid \approx \sqrt{\frac{{(x_o-x_{i,j})}^2+{(y_o-y_{i,j})}^2}{x_{\eta }^2+y_{\eta }^2}}.$$ (60)

Coefficients ξ_x, ξ_y, η_x and η_y can be approximated numerically at each grid point by using the transformation relation Eq. (17). As the coordinate of point o′ is already known, the value of the coefficients at this point can be evaluated by interpolation. Therefore, we obtain a new set of jump conditions in the new coordinate system (ξ, η). The MIB scheme can then be directly employed to solve the problem as (ξ, η) is a Cartesian grid. The jump conditions can also be transformed from the physical domain to the computational domain in the same manner. Therefore, we can combine mesh deformation techniques with the MIB method to solve the elliptic interface problem in the computational domain. We call this approach an adaptively deformed mesh based interface method.

III Numerical studies

In this section, we carry out numerical experiments to validate the proposed the adaptively deformed mesh based interface technique. Section III.A is devoted to an illustration that traditional mesh deformation methods do not converge for elliptic equations with discontinuous coefficients. Therefore, they can not be applied directly to solve elliptic interface problems. Whereas, the MIB method works well for this class of problems. In Section III.B, we use three test examples to demonstrate the performance of the present adaptively deformed mesh based interface method which is also called “adaptively deformed mesh based MIB”, with interface geometry based monitor functions. Indeed, if the solution has largest changes near the interface, the geometry based monitor functions work well. Significant improvement on the original MIB method can be obtained. However, if the solution has dramatically changes away from the interface, interface geometry based monitor functions can not achieve better performance. Therefore, we design solution gradient based monitor functions in Section III.C. We show that this class of monitor functions has better performance than the original MIB method in terms of accuracy.

III.A Failure of traditional mesh deformation methods for equations with discontinuous coefficients

Case 1a

In this example, we solve the elliptic equation (1) with domain Ω = {(x, y)| |x| < 5, |y| < 5} by using the MIB method and a traditional mesh deformation method described in Sections II.A.1 and II.A.2. We design the level set function φ(x, y) as

$$\phi (x,y)=r_0^2-x^2-y^2,$$ (61)

where $r_0=2+\frac{1}{3}$ is the radius of the circle, Γ = {(x, y)|Φ = 0;x, y, ∈ Ω }, Ω^a = {(x, y)|Φ ≥ 0; x, y, ∈ Ω}, Ω^b = {(x, y)|Φ ≤ 0; x, y, ∈ Ω }. The coefficients are discontinuous and are given by

$${\beta }^a(x,y)=1,{\beta }^b(x,y)=4.$$ (62)

The solution at two different domains is

$$u^a(x,y)=sin(x^2+y^2),u^b(x,y)=x^2+y^2.$$ (63)

To focus the mesh in the physical domain around the interface, we design a monitor function based on the interface geometry

$$f(x,y)=min(1.0,max(\mid d-r_0\mid /r_0,0.3)),$$ (64)

with $d=\sqrt{x^2+y^2}$.

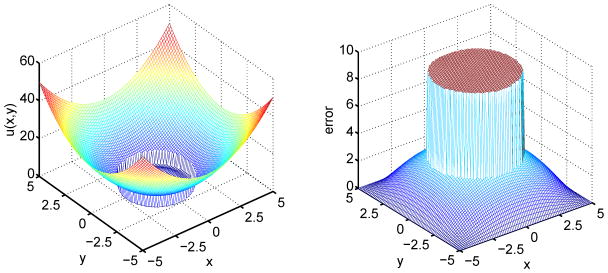
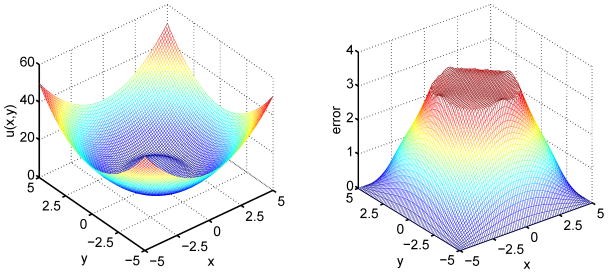
Figure 1 illustrates a deformed mesh for this problem. A much denser meshlines are attracted to the interface region. Figure 4 shows the solution calculated by using the original MIB method and the error computed from the traditional mesh deformation method with the grid size 80 × 80. Obviously, the errors are very large. Table 1 lists main results for both methods. It is seen that the original MIB method can achieve the second order convergence, while the solution of the mesh deformation method is completely wrong due to the large amplitude of errors on the interface and in the whole inner subdomain Ω^a. These errors persist when the mesh is refined, even though we test different monitor functions. The main reason is that the traditional mesh deformation method does not enforce the interface jump conditions. Which is equivalent to saying that the original problem is not well posed. Therefore, errors induced at the interface propagate to the whole inner subdomain. In order to employ the mesh deformation techniques for elliptic interface problems, one needs to combine the mesh deformation strategy with interface techniques.

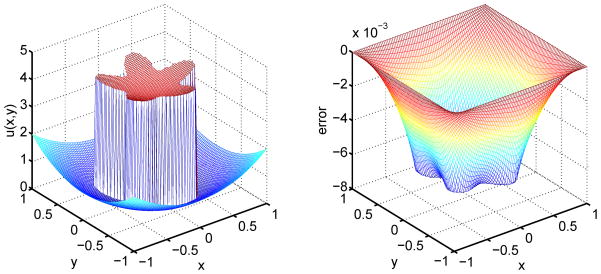
Figure 4.

The numerical solution (Left) and error (Right) of a mesh deformation method on a 80 × 80 grid for Case 1a.

Table 1.

Error and convergence order for Case 1a.

nx × ny	MIB			Mesh deformation
	L∞	Order	L2	Order	L∞	L2
40 × 40	9.009e-2		2.611e-2		9.096	4.614
80 × 80	2.680e-2	1.75	7.187e-3	1.86	9.189	4.786
160 × 160	8.652e-3	1.63	2.454e-3	1.55	9.236	4.847

Case 1b

In the last example, the discontinuity of the solution at the interface certainly has contributed to the failure of the traditional mesh deformation method. One may hope to understand what happens to the traditional mesh deformation method when the solution is continuous. To this end, we consider another test example. In the above case, we change the solution to C⁰

$$u^a(x,y)=sin(x^2+y^2)-sin\left(\frac{49}{9}\right)+\frac{49}{9},u^b(x,y)=x^2+y^2,$$ (65)

and we set the monitor function as

$$f(x,y)=min(1.0,max(\mid d-r_0\mid /r_0,0.5)),$$ (66)

with $d=\sqrt{x^2+y^2}$.

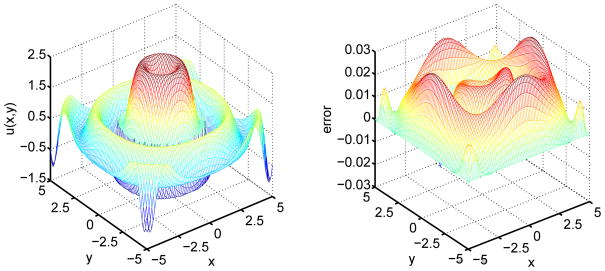
In this case, the solution is continuous at the interface. However, the first order derivatives still have jumps at the interface. Figure 5 shows the solution calculated by using the original MIB method and the error computed from the traditional mesh deformation method with the grid size of 80 × 80. Table 2 lists main results for both methods. Obviously, the original MIB method works well. Whereas, the errors of the traditional mesh deformation method do not decrease as the mesh is refined. Note that we have tested different monitor functions and find no obvious improvement. This again demonstrates the importance of the enforcement of interface conditions. It is clear that the mesh deformation strategy by itself does not work for elliptic equations with discontinuous coefficients.

Figure 5.

The numerical solution (Left) and error (Right) of a mesh deformation method on a 80 × 80 grid for Case 1b.

Table 2.

Error and convergence order for Case 1b.

nx × ny	MIB			Mesh deformation
	L∞	Order	L2	Order	L∞	L2
40 × 40	9.009e-2		2.611e-2		2.589	1.569
80 × 80	2.680e-2	1.75	7.187e-3	1.86	3.301	2.035
160 × 160	8.652e-3	1.63	2.454e-3	1.55	3.104	1.976

III.B Performance of interface geometry based deformed meshes

In this subsection we first demonstrate the performance of the adaptively deformed mesh based interface method with interface geometry based monitor functions in Cases 2, 3 and 4. We then illustrate the limitation of this approach in Case 5. The performance the proposed adaptively deformed mesh based interface method is compared with that of the original MIB method. We calculate relative ratios of L_∞ and L₂ errors obtained from the original MIB method and from the adaptively deformed mesh based interface method, and denote them as R_L∞ and R_L2, respectively

$$R_{L_{\infty }}=\frac{L_{\infty }\text{error}\text{of}\text{the}\text{original}\text{MIB}}{L_{\infty }\text{error}\text{of}\text{the}\text{adaptively}\text{deformed}\text{mesh}\text{based}\text{MIB}}$$ (67)

$$R_{L_2}=\frac{L_2\text{error}\text{of}\text{the}\text{original}\text{MIB}}{L_2\text{error}\text{of}\text{the}\text{adaptively}\text{deformed}\text{mesh}\text{based}\text{MIB}}.$$ (68)

For instance, if R_L∞= 3, then the L_∞ error of the original MIB method is 3 times as large as that of the adaptively deformed mesh based MIB method. Therefore R_L∞ and R_L2 ratios indicate the improvement of proposed adaptively deformed mesh based MIB upon the original MIB method when they are larger than one.

Case 2a

In this case, the elliptic equation (1) is solved in domain Ω = {(x, y)| |x| < 5, |y| < 5}. The interface is specified by the level set function φ(x, y)

$$\phi (x,y)=r_0^2-x^2-y^2,$$ (69)

where $r_0=2+\frac{1}{3}$ is the radius of the circle, Γ = {(x, y)|Φ = 0; x, y, ∈ Ω }, Ω^a = {(x, y)| Φ ≥ 0; x, y, ∈ Ω }, Ω^b = {(x, y)| Φ ≤ 0; x, y, ∈ Ω }. The discontinuous coefficients are given by

$${\beta }^a(x,y)=1,{\beta }^b(x,y)=3.$$ (70)

We design the solution at two different subdomains as

$$u^a(x,y)=sin(x^2+y^2)+1.5,u^b(x,y)=sin\left({\left(2r_0-\sqrt{x^2+y^2}\right)}^2\right).$$ (71)

To redistribute the mesh in the physical domain around the interface, we construct the mesh monitor function according to the interface geometry

$$f(x,y)=min(1.0,max(\mid d-r_0\mid /r_0,0.4)),$$ (72)

where $d=\sqrt{x^2+y^2}$. Here max(|d − r₀|/r₀, 0. 4) determines the maximal contraction rate and it is less than 0. 4.

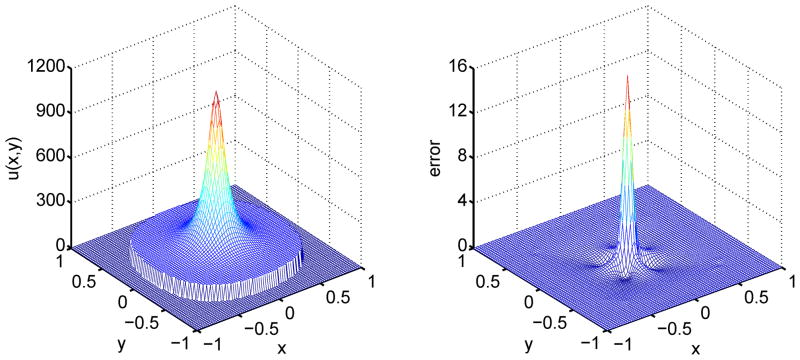
Figure 6 depicts the numerical solution and error. In Table 3, we list the main results of L_∞ and L₂ errors, the order of accuracy, and the ratios R_L∞ and R_L2. It can be seen from Table 3, compared with the original MIB method, the adaptively deformed mesh based MIB method can significantly reduce both the L_∞ and L₂ errors. It is worthwhile to mention that, the proposed new method also keeps the designed second order convergence.

Figure 6.

The numerical solution (Left) and error (Right) on a 80 × 80 grid (Right) for Case 2a.

Table 3.

Error and convergence order for Case 2a.

nx × ny	MIB				Adaptively deformed mesh based MIB				Ratios
	L∞	Order	L2	Order	L∞	Order	L2	Order	RL∞	RL2
80 × 80	1.088e-1		4.326e-2		3.281e-2		1.498e-2		3.3	2.9
160 × 160	3.549e-2	1.62	1.555e-2	1.48	1.292e-2	1.34	3.807e-3	1.98	2.7	4.1
320 × 320	1.090e-2	1.70	4.626e-3	1.75	4.613e-3	1.49	1.162e-3	1.71	2.4	4.0

Case 2b

In the above case, we change the solution to

$$u^a(x,y)=sin(2(x^2+y^2))+1.5,u^b(x,y)=sin\left(2{\left(2r_0-\sqrt{x^2+y^2}\right)}^2\right),$$ (73)

and we set the monitor function as

$$f(x,y)=min(1.0,max(\mid d-r_0\mid /r_0,0.3)),$$ (74)

where $d=\sqrt{x^2+y^2}$. The main results are listed in Table 4. It is seen that the present adaptively deformed mesh based MIB method significantly improves the L_∞ and L₂ accuracy of the original MIB method. The second order convergence is maintained for this problem.

Table 4.

Error and convergence order for Case 2b.

nx × ny	MIB				Adaptively deformed mesh based MIB				Ratios
	L∞	Order	L2	Order	L∞	Order	L2	Order	RL∞	RL2
80 × 80	1.560		7.221e-1		5.092e-1		2.178e-1		3.1	3.3
160 × 160	3.424e-1	2.19	1.680e-1	2.10	8.939e-2	2.51	3.910e-2	2.48	3.8	4.3
320 × 320	5.544e-2	2.63	2.628e-2	2.68	2.317e-2	1.95	4.343e-3	3.17	2.4	6.1

Case 3

We next consider the elliptic equation (1) in domain Ω = {(x, y)| |x| < 5, |y| < 5}. To characterize the interface, we design a level set function φ(x, y)

$$\phi (x,y)=1-\frac{x^2}{r_a^2}-\frac{y^2}{r_b^2},$$ (75)

where $r_a=3+\frac{2}{3}$ and $r_b=1+\frac{1}{3}$ Γ = {(x, y)| Φ = 0; x, y, ∈ Ω}, Ω^a = {(x, y)| Φ ≥ 0; x, y, ∈ Ω}, Ω^b = {(x, y)| Φ ≤ 0; x, y, ∈ Ω}. The coefficients are discontinuous and are given by

$${\beta }^a(x,y)=1,{\beta }^b(x,y)=3.$$ (76)

We design the analytical solution at two different subdomains as

$$u^a(x,y)=sin\left(\frac{1}{{\left(\frac{x^2}{r_a^2}+\frac{y^2}{r_b^2}-1\right)}^2+0.5}\right)+1.0,u^b(x,y)=sin\left(\frac{1}{{\left(\frac{x^2}{r_a^2}+\frac{y^2}{r_b^2}-1\right)}^2+0.5}\right).$$ (77)

For this problem, it is convenient to choose the monitor function according to the interface geometry

$$f(x,y)=min(1.0,max(\mid d-1.0\mid ,0.3)),$$ (78)

where $d=\sqrt{\frac{x^2}{r_a^2}+\frac{y^2}{r_b^2}}$.

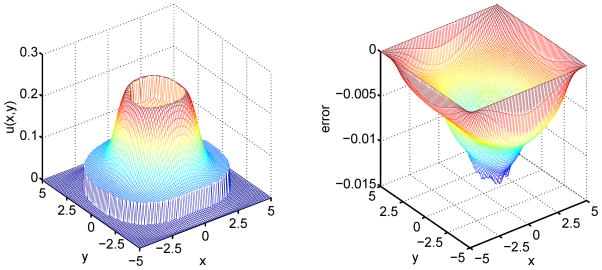
The numerical solution and error distribution are illustrated in Fig. 7. Detailed results are listed in Table 5. Compared with the original MIB method, the adaptively deformed mesh based MIB method achieves more than 5 times of improvement on L_∞ and L₂ accuracy. It also maintains the designed second order convergence.

Figure 7.

The numerical solution (Left) and error (Right) on a 80 × 80 grid for Case 3.

Table 5.

Error and convergence order for Case 3.

nx × ny	MIB				Adaptively deformed mesh based MIB				Ratios
	L∞	Order	L2	Order	L∞	Order	L2	Order	RL∞	RL2
40 × 40	1.480		6.276e-1		2.659e-1		1.045e-1		5.6	6.0
80 × 80	1.488e-1	3.31	6.468e-2	3.28	2.855e-2	3.22	1.212e-2	3.11	5.2	5.3
160 × 160	3.576e-2	2.06	1.577e-2	2.04	5.323e-3	2.42	2.829e-3	2.10	6.7	5.6

Case 4

In this case, the elliptic equation (1) is solved in domain Ω = {(x, y)| |x| < 5, |y| < 5}. We choose the level set function φ(x, y) as

$$\phi (x,y)=-(x^2+y^2-r_0^2)\left(\frac{x^2}{r_a^2}-\frac{y^2}{r_b^2}-1.0\right),$$ (79)

where $r_0=1+\frac{1}{3},r_a=2+\frac{2}{3}$ and $r_b=3+\frac{1}{3}$, Γ = {(x, y)}| Φ = 0; x, y, ∈ Ω}, Ω^a = {(x, y)| Φ ≥ 0; x, y, ∈ Ω}, Ω^b = {(x, y)| Φ ≤ 0; x, y, ∈ Ω}. The discontinuous coefficients are given by

$${\beta }^a(x,y)=1,{\beta }^b(x,y)=3.$$ (80)

The solution at two different subdomains is designed as

$$u^a(x,y)=\frac{1}{{\left(\frac{x^2}{r_a^2}+\frac{y^2}{r_b^2}-1\right)}^2+2.0}·\frac{1}{{(x^2+y^2-r_0^2)}^2+2.0}+0.05,$$ (81)

$$u^b(x,y)=\frac{1}{{\left(\frac{x^2}{r_a^2}+\frac{y^2}{r_b^2}-1\right)}^2+2.0}·\frac{1}{{(x^2+y^2-r_0^2)}^2+2.0}.$$ (82)

In this problem, one can simply design the monitor function according the geometric shape

$$f(x,y)=min(1.0,max(\mid d\mid ,0.1)),$$ (83)

where $d=\left(\sqrt{\frac{x^2}{r_a^2}+\frac{y^2}{r_b^2}}-1.0\right)\left(\sqrt{(x^2+y^2)}-r_0\right)/r_0$.

Figure 8 plots the numerical solution and error. Table 6 gives a summary of the accuracy and convergence. The L_∞ and L₂ errors of the proposed adaptively deformed mesh based MIB method are much smaller than those of the original MIB method. The second order accuracy is essentially achieved by both methods.

Figure 8.

The numerical solution (Left) and error (Right) on a 80 × 80 grid for Case 4.

Table 6.

Error and convergence order for Case 4.

nx × ny	MIB				Adaptively deformed mesh based MIB				Ratios
	L∞	Order	L2	Order	L∞	Order	L2	Order	RL∞	RL2
40 × 40	1.459e-1		5.738e-2		3.355e-2		1.426e-2		4.3	4.0
80 × 80	4.517e-2	1.69	1.870e-2	1.62	1.291e-2	1.38	5.746e-3	1.31	3.5	3.3
160 × 160	1.121e-2	2.01	4.653e-3	2.01	1.969e-3	2.71	7.419e-4	2.95	5.7	6.3

Case 5

The above four examples indicate that the proposed adaptively deformed mesh based MIB method work well for problems with relatively simple interfaces. In this test case, we consider a more complex interface geometry. We solve the elliptic equation (1) in the domain Ω = {(x, y)| |x| < 1, |y| < 1}. The interface is defined as

$$\phi (r,\theta )=r-\left(0.5+\frac{sin(5\theta )}{7}\right),$$ (84)

where Γ = {(r, θ)| Φ = 0; r, θ, ∈ Ω}, Ω^a = {(r, θ)| Φ ≥ 0; r, θ, ∈ Ω}, Ω^b = {(r, θ)| Φ ≤ 0; r, θ, ∈ Ω}. The discontinuous coefficients are given by

$${\beta }^a(x,y)=100,{\beta }^b(x,y)=1.$$ (85)

The solution at two different subdomains is designed as

$$u^a(x,y)=4.0+sin(x^2+y^2),u^b(x,y)=x^2+y^2.$$ (86)

We design a monitor function

$$f(x,y)=min\left(1.0,max\left(\frac{\mid d-r\mid }{r},0.9\right)\right),$$ (87)

where $d=\sqrt{x^2+y^2}$ and $r=0.5+\frac{sin(5\theta )}{7}$.

Figure 1 shows a deformed mesh for this problem. More meshlines are focused around the interface. The numerical solution and error are presented in Fig. 9. It is seen from Table 7 that the present adaptively deformed mesh based MIB method is essentially second order accurate, but it does not improve the original MIB method very much. This test case highlights the difficulty in the construction of appropriate monitor functions when there is an interface.

Figure 9.

The numerical solution (Left) and error (Right) on a 80 × 80 grid for Case 5.

Table 7.

Error and convergence order for Case 5.

nx × ny	MIB				Adaptively deformed mesh based MIB				Ratios
	L∞	Order	L2	Order	L∞	Order	L2	Order	RL∞	RL2
40 × 40	2.278e-2		1.349e-2		1.895e-2		1.135e-2		1.2	1.2
80 × 80	7.572e-3	1.59	4.620e-3	1.55	6.605e-3	1.52	4.082e-3	1.48	1.1	1.1
160 × 160	2.072e-3	1.87	1.287e-3	1.84	1.615e-3	2.03	1.017e-3	2.00	1.3	1.3

III.C Performance of solution gradient based deformed meshes

In Cases 2, 3 and 4, all the solutions are more oscillatory near the interface. Therefore, we just need to concentrate the mesh density around the interface so as to reduce both L_∞ and L₂ errors. However, the selection of the monitor function based on the geometry may not always work. In Case 5, the solution does not oscillate more intensively in the interface region. As such, distributing a denser mesh around the interface does not have a significant improvement to the final solution. Therefore, for general interface problems, one should make the monitor function adaptive to the gradient of the solution. As such, one concentrates more meshlines to the regions where the solution varies dramatically. We test this kind of deformed meshes in the next two examples.

Case 6a

We consider the elliptic equation (1) in domain Ω = {(x, y)||x| < 1, |y| < 1}. We specify the interface by using the level set function φ(x, y)

$$\phi (x,y)=r_0^2-x^2-y^2,$$ (88)

where $r_0=\frac{2}{3}$ is the radius of the circle, Γ = {(x, y)| Φ = 0; x, y, ∈ Ω}, Ω^a = {(x, y)| Φ ≥ 0; x, y, ∈ Ω}, Ω^b = {(x, y)| Φ ≤ 0; x, y, ∈ Ω}. We set discontinuous coefficients to

$${\beta }^a(x,y)=1,{\beta }^b(x,y)=5.$$ (89)

We design the solution at two different subdomains as

$$u^a(x,y)=100.0+\frac{1}{x^2+y^2+0.001},u^b(x,y)=x^2+y^2.$$ (90)

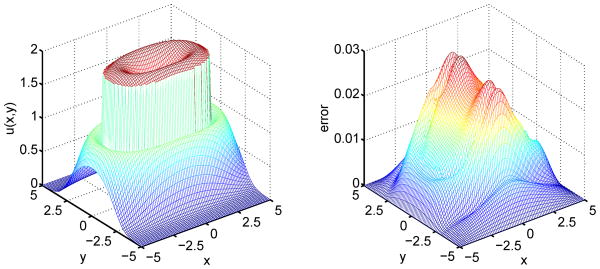
This solution has a large peak at the origin as shown in Fig. 10. Therefore, the previous geometry based monitor functions do not work well. Here we design a monitor function according to the gradient of the solution

Figure 10.

The numerical solution (Left) and error (Right) on a 80 × 80 grid for Case 6a.

$$f(x,y)=\sqrt{1.0+c_1{(u_x^2+u_y^2)}^{c_2}},$$ (91)

where c₁ and c₂ are two parameters controlling the shift of the mesh. The solution is first calculated by the original MIB method, and then the gradient of the solution is evaluated by the central difference scheme. If the computed monitor function is non-smooth, it may lead to an improper mesh, which may concentrate too many meshlines in certain regions and sometime may even cause mesh tangling at certain regions, as a result of insufficient accuracy in solving the mapping Poisson equation. A commonly used technique is to smooth the monitor function by a filter or an averaging algorithm. Here we use a simple algorithm to smooth f

$$f(x_i,y_j)=\frac{1}{4}(f(x_{i+1},y_j)+f(x_{i-1},y_j)+f(x_i,y_{j+1})+f(x_i,y_{j-1})).$$ (92)

Another important aspect is how to distribute meshlines near the interface. The mesh deformation strategy is usually designed for shock-wave type of problems with dramatic solution changes at the shock front. However, too much concentration of the meshlines in the areas with large gradient may jeopardize the accuracy of the solution in other areas and thus leads to the L₂ accuracy reduction. This is particularly true for elliptic interface problems, as the MIB schemes already take special treatment of points near interface. However, certain mild concentration of the meshlines around the interface region will yield better results.

In test Case 6a, the gradient of interface jumps is relatively large, so that one does not need to employ any additional mesh adjustment at the interface. When the mesh is 80 ×80, three sets of parameters are tested. Table 8 lists the main results. It can be seen from the table that compared with the original MIB method, the adaptively deformed mesh based MIB method can reduce L_∞ and L₂ errors dramatically when the mesh size is small. This result shows the main advantage of the mesh deformation strategy.

Table 8.

Error and convergence order for Case 6a.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
80 × 80	1.0	0.5	393.1	14.53	16.30	6.388e-1	24	23
80 × 80	1.0	0.6	393.1	14.53	10.05	9.249e-1	39	16
80 × 80	1.0	0.7	393.1	14.53	5.592	1.685	70	8.6

When the mesh sizes are 160 × 160 and 320 × 320, we test a set of monitor functions obtained by adjusting coefficients. The results are listed in Tables 9 and 10. The original MIB method demonstrates the designed second order convergence. Compared the original MIB method, the adaptively deformed mesh based MIB method can still significantly improve the L_∞ errors. However, as the number of grid points is increased, The L₂ accuracy does not improve much compared with the original MIB method, due to the fact that the solution is near singular at the origin. Additionally, although the adaptively deformed mesh based MIB method shows better accuracy, it does not maintain the designed second order convergence.

Table 9.

Error and convergence order for Case 6a.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
160 × 160	1.0	0.3	43.86	4.349e-1	5.588	1.734e-1	7.8	2.5
160 × 160	10.0	0.3	43.86	4.349e-1	4.760	1.672e-1	9.2	2.6
160 × 160	1.0	0.4	43.86	4.349e-1	2.376	3.296e-1	18	1.3

Table 10.

Error and convergence order for Case 6a.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
320 × 320	1.0	0.2	10.01	1.036e-1	2.306	6.872e-2	4.3	1.5
320 × 320	1.0	0.3	10.01	1.036e-1	1.042	6.177e-2	9.6	1.7
320 × 320	10.0	0.3	10.01	1.036e-1	8.068e-1	7.356e-2	12	1.4

Case 6b

In the above case, we make the solution C⁰ continuous across the domain

$$u^a(x,y)=\frac{1}{x^2+y^2+0.001}-\frac{1}{\frac{4}{9}+0.001}+\frac{4}{9},u^b(x,y)=x^2+y^2.$$ (93)

With this solution, we hope to understand the behavior the monitor function (91) for the discontinuous coefficients.

Results are presented in Fig. 11 and Tables 11, 12 and 13. When the results in three tables are compared, it is easy to see that the original MIB is still second order convergent. However, the adaptively deformed mesh based MIB method outperforms the original MIB method under all meshes. At a coarse mesh, the adaptively deformed mesh based MIB method is much more accurate than the original MIB method. In particular, the present monitor function works well. Therefore, the present adaptively deformed mesh based strategy is relatively robust and stable for elliptic interface problems.

Figure 11.

The numerical solution (Left) and error (Right) on a 80 × 80 grid for Case 6b.

Table 11.

Error and convergence order for Case 6b.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
80 × 80	1.0	0.5	393.1	14.53	13.20	5.783e-1	30	25
80 × 80	1.0	0.6	393.1	14.53	7.536	7.735e-1	52	19
80 × 80	1.0	0.7	393.1	14.53	4.025	1.326	98	11

Table 12.

Error and convergence order for Case 6b.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
160 × 160	1.0	0.3	43.86	4.349e-1	5.184	1.755e-1	8.5	2.5
160 × 160	1.0	0.4	43.86	4.349e-1	2.253	2.328e-1	19	1.9
160 × 160	10.0	0.3	43.86	4.349e-1	4.383	1.715e-1	10	2.5

Table 13.

Error and convergence order for Case 6b.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
320 × 320	1.0	0.2	10.01	1.036e-1	2.259	6.369e-2	4.4	1.6
320 × 320	1.0	0.3	10.01	1.036e-1	9.151e-1	7.642e-2	11	1.4
320 × 320	10.0	0.2	10.01	1.036e-1	1.821	6.547e-2	5.5	1.6

Case 7

We next consider a more difficult case that has two near singular peaks, in addition to the interface jump of the solution. The elliptic equation (1) is solved in domain Ω = {(x, y)| |x| < 5, |y| < 5}. To specify the interface, we construct the level set function φ(x, y) as

$$\phi (x,y)=1.0-\frac{x^2}{r_b}-\frac{y^2}{r_b},$$ (94)

where $r_a=3+\frac{2}{3},r_b=2+\frac{1}{3}$ is the radius of the ellipse, Γ = {(x, y)| Φ = 0; x, y, ∈ Ω}, Ω^a = {(x, y)| Φ ≥ 0; x, y, ∈ Ω}, Ω^b = {(x, y)| Φ ≤ 0; x, y, ∈ Ω}. The discontinuous coefficients are chosen as

$${\beta }^a(x,y)=2,{\beta }^b(x,y)=5.$$ (95)

The solution at two different subdomains is designed as

$$u^a(x,y)=\frac{1}{y^2+{(x-2.0)}^2+0.01}+\frac{1}{y^2+{(x+2.0)}^2+0.01},u^b(x,y)=x^2+y^2.$$ (96)

As shown in Fig. 12, the solution admits an interface jump and two near singular peaks. Obviously, we need to choose the monitor function based on the gradient of the solution

Figure 12.

The numerical solution on a 160 × 160 grid for Case 7.

$$f(x,y)=\sqrt{1.0+c_1{(u_x^2+u_y^2)}^{c_2}}.$$ (97)

In this test example, we test the deformed mesh strategy for a near singular solution. The results are listed in Tables 14 and 15. Here as the solution has relatively large jumps at the interface, we do not incorporate any additional special term in the monitor function to emphasize the interface. When the mesh size is 160 × 160, the adaptively deformed mesh based MIB method can dramatically reduce L_∞ and L₂ errors. As the mesh size is further increased, the adaptively deformed mesh based MIB method can improve the L_∞ accuracy to certain extend. However, the L₂ errors do not reduce much.

Table 14.

Error and convergence order for Case 7.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
160 × 160	1.0	0.4	16.97	7.560e-1	3.308	6.594e-2	5.1	11
160 × 160	1.0	0.5	16.97	7.560e-1	1.863	1.445e-1	9.1	5.2
160 × 160	1.0	0.6	16.97	7.560e-1	8.945e-1	2.620e-1	19	2.9

Table 15.

Error and convergence order for Case 7.

nx × ny	Parameter		MIB		Adaptively deformed mesh based MIB		Ratios
	c1	c2	L∞	L2	L∞	L2	RL∞	RL2
320 × 320	1.0	0.2	2.607	2.363e-2	1.356	2.094e-2	1.9	1.1
320 × 320	5.0	0.2	2.607	2.363e-2	1.182	2.060e-2	2.2	1.1

Similar to the behavior in the last case, the original MIB method show the second order convergence, while the adaptively deformed mesh based MIB method does not have the designed second order convergence, although it is more accurate.

A possible solution to this problem is to take into consideration the interface information as in the Section III when one designs the monitor functions. State differently, we may construct a mesh based on both the interface geometry and the solution gradient. There are many ways to do so. For example, one may add a special weight function to the monitor function to emphasize the interface

$$f(x,y)=w_1(x,y)\sqrt{1.0+c_1{(u_x^2+u_y^2)}^{c_2}}+w_2(x,y)g(x,y),$$ (98)

where w₁(x, y) and w₂(x, y) are two weight functions, and g(x, y) is a function related to the interface. However, the construction of multipurpose weight functions is by no means trivial. Therefore, more study is needed in order to reveal the full potential of the mesh deformation strategy for elliptic interface problems. A detailed exploration of this aspect is beyond the scope of the present work.

IV Concluding Remarks

Mesh deformation methods are an effective and mesh-adaptive strategy for the numerical solution of a wide class of physical models. They are particularly popular in computational fluid dynamics, material science and many other engineering problems. However, traditional mesh deformation methods break down when the governing partial differential equations (PDEs) admit discontinuous coefficients, especially when the solution has jumps at the interface. This class of problems, known as interface problems, requires the enforcement of interface jump conditions to maintain their well-posedness. As such, the corresponding numerical techniques, known as interface techniques, have to implement the interface jump conditions in their solution procedures. The present work develops the first known interface technique based adaptively deformed mesh method for solving elliptic PDEs with discontinuous coefficients.

In general, the mesh movement is often driven by an elliptic PDE. Essentially, there are two ways to formulate the elliptic mesh-movement PDE. One way is to incorporate the mesh movement information in the elliptic operator, while the other is to embed mesh movement as the source term of the mesh movement equation.²⁶ The latter is relatively simple and is adopted in the present work. The procedure of this mesh deformation method involves the mesh deformation and the transformation of the governing equation. The new mesh is generated by using a PDE with a source term to control the mesh redistribution in the physical domain. After the transformation of the governing equation, the new governing equation is solved on a Cartesian mesh.

There are a large number of elliptic interface techniques in the literature that can be equipped with the mesh deformation strategy. In the present work, we choose the matched interface and boundary (MIB) method which is a highly accurate, robust and flexible method for a wide range of interface problems. The combination of the mesh deformation strategy and the MIB technique results in a mesh adaptive interface algorithm, called adaptively deformed mesh based interface method or adaptively deformed mesh based MIB method. In this approach, the MIB method is used to solve the elliptic PDE in its transformed form on a Cartesian mesh, i.e., on the computational domain.

A large number of test cases are designed to demonstrate the usefulness, accuracy, convergence order, and flexibility of the proposed adaptively deformed mesh based interface method. Two types of deformed meshes, namely, the interface geometry based deformed meshes and solution gradient based deformed meshes are constructed in the present work to understand the performance of mesh deformation strategies. The original MIB method is used as a reference to assess the performance the proposed new interface method. Meanwhile, we also show that the traditional mesh deformation method does not work for elliptic PDEs with discontinuous coefficients. In contrast, the proposed adaptively deformed mesh based interface method significantly outperforms the original MIB method. Therefore, the present interface technique based adaptively deformed mesh method is a viable, effective and accurate strategy for solving elliptic PDEs with discontinuous coefficients.

However, there are still technical difficulties in maintaining the second order convergence as shown in the last two test cases. First, transformed governing equation (52) in the computational domain has a second order cross derivative u_ξ,η,. To maintain the second order accuracy, there must be certain grid points around the interface so that the cross derivative can be evaluated. When the solution admits singularities, it is difficult to find enough grid points to achieve the second order accuracy for evaluating the cross derivative term. Additionally, the solution gradient based monitor function should also incorporate the interface information. Unfortunately, it is not an easy task to optimize a multicomponent monitor function so as to achieve the second order accuracy when the solution is discontinuous and singular. Finally, the use of a low-pass filter in Eq. (92) for smoothing the monitor function may also contribute to the order reduction.

Technically, there is a long way to go before the proposed adaptively deformed mesh based interface method becomes as practical and robust as the original MIB method for solving real world elliptic interface problems.^8,14,15,42 First, for most realistic applications, it is a must to take care of geometric singularities, i.e., nonsmooth interfaces.^43,45 This class of interface problems are typically more challenging than those with smooth interfaces. Currently, it is unknown how a mesh deformation strategy works for nonsmooth interfaces because the low regularity of the original problem may reduce the accuracy of the mesh generation and hinder the transformation of the governing equation. Additionally, to deal with real-world problems, one needs to further develop three dimensional (3D) schemes. Although there is no conceptual difficulty in generalizing the present 2D method into a 3D one, the computational cost of a 3D mesh deformation method can be significantly large. Finally, the appropriate design of effective monitor functions is still an important issue in adaptively deformed mesh based interface methods. As discussed earlier, it is particularly difficult to construct efficient multipurpose monitor functions that can maintain the designed order of convergence for complex interface geometries and solution. These issues are beyond the scope of the present work and are under our consideration.