Abstract

Excitatory amino acid transporters (EAATs) are membrane proteins responsible for reuptake of glutamate from the synaptic cleft to terminate neurotransmission and help prevent neurotoxically high, extracellular glutamate concentrations. Important structural information about these proteins emerged from crystal structures of GltPh, a bacterial homologue of EAATs, in conformations facing outward and inward. These remarkably different conformations are considered to be end points of the substrate translocation path (STP), suggesting that the transport mechanism involves major conformational rearrangements that remain uncharted. To investigate possible steps in the structural transitions of the STP between the two end-point conformations, we applied a combination of computational modeling methods (motion planning, molecular dynamics simulations, and mixed elastic network models). We found that the conformational changes in the transition involve mainly the repositioning the “transport domain” and the “trimerization domain” identified previously in the crystal structures. The two domains move in opposite directions along the membrane normal, and the transport domain also tilts by ∼17° with respect to this axis. Moreover, the TM3–4 loop undergoes a flexible, “restraining bar”-like conformational change with respect to the transport domain. As a consequence of these conformational rearrangements along the transition path we calculated a significant decrease of nearly 20% in the area of the transport-to-trimerization domain interface (TTDI). Water penetrates parts of the TTDI in the modeled intermediates but very much less in the end-point conformations. We show that these characteristics of the modeled intermediate states agree with experimental results from residue-accessibility studies in individual monomers and identify specific residues that can be used to test the proposed STP. Moreover, MD simulations of complete GltPh trimers constructed from initially identical monomer intermediates suggest that asymmetry can appear in the trimer, consonant with available experimental data showing independent transport kinetics by individual monomers in the trimers.
1. Introduction
Excitatory amino acid transporters (EAATs) are membrane proteins that remove glutamate from the synaptic environment to terminate neurotransmission and help prevent neurotoxicity caused by high concentrations of the neurotransmitter. In the central nervous system, these proteins perform the glutamate reuptake into the presynaptic cells or astrocytes by coupling the transport of one glutamate substrate to the cotransport of three sodium ions1,2 and carry out antiport of one proton and one potassium ion while using this transport for a flux of chloride ions.3−5 EAATs are important drug targets because their dysfunction is related to a variety of neurological and other conditions, including depression, schizophrenia, stroke,6 Alzheimer’s disease,7 or human dicarboxylic aminoaciduria.8
A major breakthrough toward a molecular mechanistic understanding of substrate transport in EAATs has been the elucidation of crystal structures of GltPh, a bacterial homologue that shares about 37% sequence identity with EAATs.9−11 GltPh transports one aspartic acid substrate molecule in symport with three12 sodium ions while also enabling chloride conductance. Like the mammalian EAATs, the bacterial GltPh forms trimers,13,14 which in the crystals were shown to have a C3 symmetry that produces a bowl-shaped, membrane-traversing structure that presumably reaches deep into the lipid bilayer (Figure 1). This symmetry is remarkable given the fact that the monomers in GltPh and EAAT have been suggested to transport substrate independently15−17 and are expected to “move stochastically and independently”10 (see also ref (18)). Within each monomer, the neurotransmitter transport mechanism has long been considered to involve a sequential “opening” of the transporter molecule toward the extracellular environment (“outward”, to receive the substrate) and an opening toward the intracellular environment (“inward”, to release the substrate). The conformations of the GltPh observed in the two available crystal structures are considered to represent, respectively, an outward-facing closed conformation (OfCC)11 (Figure 1a and 1c) and an inward-facing closed conformation (IfCC)10 (Figure 1b and 1d). While the OfCC and IfCC structures present the substrate binding site in the respective directions, the site is occluded in both of them (hence “closed”) by two structural hairpin motifs that face the extracellular environment and intracellular cytoplasm, respectively. On the basis of these configurations, the structural information suggest that the outward- and inward-facing structures are the end-point conformations of GltPh’s substrate translocation path10 and thereby provide invaluable information about the structural relation between protein, substrate, and presumably sodium ions.
Figure 1.
Crystal structures of GltPh. Outward-facing closed conformation (OfCC)11 (a and c) and inward-facing closed conformation (IfCC)10 (b and d), viewed from the side, parallel to the membrane (top) and from the top (bottom). Transport domains are represented as orange ribbons; trimerization domains are green. Sequence stretches in the N- and C-terminal loops that were unresolved in the crystal structures have been modeled using the program FUGUE,33 and parts of the TM3–4 loop, unresolved in the OfCC, were modeled with ArchPRED,32 as described in Methods.
A comparison of the two crystal structures suggests that monomers undergo a rigid-body conformational rearrangement.10 However, the mechanism of substrate translocation across the membrane through the transporter molecule remains unknown despite the breakthrough crystallographic data and other observations from experimental and computational studies with regard to ion and substrate binding,19−22 extracellular capture,9,23 and intracellular release.24 To gain insight about the substrate translocation pathway (STP) at a detailed molecular level, we modeled structural intermediates along a putative transition path between the two crystal structures. These intermediates were constructed with the motion planning (MP)25 approach and analyzed with molecular dynamics (MD) simulations and mixed elastic network models (mENM).26 Together, they provide an all-atom model of the translocation path within each monomer in the context of the GltPh trimer and the surrounding lipid membrane. We find that the modeled translocation path involves both the transport domain and the trimerization domain that were identified earlier in the crystal structures,10 moving in opposite directions (and to different extents) along the membrane normal. We also observe a tilt of the transport domain with respect to the membrane normal axis, and a global conformational change of the TM3–4 loop with respect to the transport domain. The MD simulations of intermediate trimers constructed from initial identical monomers preserved their tertiary structure and the quaternary frame of the trimer, while one exhibited an asymmetric structure in which the monomers adopted different conformations. A striking change observed from the comparison of MD simulation results from all systems (including both the crystal structures and the modeled intermediates) is the change in character of the interfaces between the transport and the trimerization domains (transport–trimerization domain interface, TTDI) along the modeled STP. The pattern of changes in size and water accessibility of the TTDI indicates how the domain dynamics is facilitated along the translocation path and suggests the identity of specific residues that can be used to test experimentally the proposed STP modeled by the intermediates we calculated.
2. Methods
2.1. Motion Planning
To model conformations representing intermediates between the outward- and the inward-facing conformations observed crystallographically (PDB codes 2NWX and 3KBC, respectively, Figure 1), we first used the motion planning module “PathRover”,27 implemented in the Rosetta28 docking distribution. In PathRover, a protein structure is represented by the dihedral angles of its heavy-atom backbone and the Cβ atoms. Starting from this “source” representation, the conformational space of the protein is explored with a rapidly exploring random tree (RRT) algorithm,29 in our case using the “RMSD Minimize” predicate (which applies a transformation from dihedral to Cartesian coordinates) to bias the search toward a “target” conformation. Here, the “source” and “target” are the monomers from an averaged, MD-equilibrated state of the GltPh trimer obtained from either the OfCC or the IfCC (see molecular dynamics, “MD1”) and they serve alternately. The MP paths are produced for single monomers, based on the experimental evidence that (1) individual monomers do transport substrate independently,15−17 (2) the OfCC and IfCC crystal structures preserve the trimerization interfaces in GltPh, as indicated by superposition results (Cα-RMSD = 0.5 Å of residues 60–64, 139–161, 183–190 of all three monomers), and (3) residue pairs in these interfaces may be cross-linked without affecting substrate transport.30
The degrees of freedom for the conformational search included all the backbone dihedrals of residue i ∈ {13, ..., 414} with Δφi or Δψi ≥20°, where Δφi or Δψi are the two average backbone dihedral differences between the OfCC and the IfCC for any residue i. The complete set of PathRover parameters we used is presented in Table SI12, Supporting Information, and is default,27 except for “MAX_TREE_SIZE” and “EXTEND_MAX_STEP_SIZE”, which are, respectively, larger and smaller than in default,27 and “ENERGY_FUNCTION”, which is set to the centroid “score4” function.
The path-searching strategy was to use the path conformation with the lowest possible target RMSD from each run and to restart the search from this conformation. Twelve such subsequent replicated restarts were used to construct an ensemble of MP conformations. This strategy was more successful than using single PathRover “RMSD Minimize” predicate runs, which did not produce any paths with a target RMSD below 7.9 Å (from an initial 9.7 Å) for 25 initial replicated runs. To choose representative intermediates along this path ensemble, we grouped the MP conformations in ranges of 0.5 Å (RMSDIfCC.A) and identified for each group the monomer with the lowest mean pairwise RMSD. The representative intermediates from five of these groups are denoted as PRi.2, PRi.4, PRi.5, PRi.11, and PRi.12.
2.2. Molecular Dynamics Setup
The starting structures for the MD simulations of the OfCC and IfCC, respectively “MD1” and “MD2”, were taken from the corresponding PDB entries 2NWX and 3KBC. Calculation of pKa values for all titratable residues with the program MM_SCP31 showed that each titratable residue in both the OfCC and the IfCC is likely in a protonation state corresponding to standard aqueous conditions at pH = 7.0. To account for the recently reported transport stoichiometry of three sodium ions per substrate,12 we placed a third sodium ion (Na3) into the OfCC and the IfCC structures at a site near residues N310, D312, and T92 as identified in ref (19). For the OfCC, residues missing from the TM3–4 loop were modeled with the template-based loop structure prediction software ArchPRED.32
For the “MD2” simulations we constructed trimer intermediates, termed “MDi.x” (x = 2, 4, 5, 11), from each selected monomer PRi.x and added the substrate (aspartate) and sodium ions from the OfCC monomer to positions identified by superimposing the Cα atoms of HP1 and HP2 (which interact with the substrate) onto PRi.x (i.e., of residues 262–282, 342–367, RMSDs = 0.6–1.5 Å). Finally, each PRi.x monomer was triplicated and superimposed on each of the monomers of the OfCC’s crystal structure by matching only the residues in the central inner cavity of GltPh (i.e., Cα atoms of residues 60–64, 139–161, and 183–190). This procedure to construct trimer intermediates is made possible by the conserved structural frame of the trimerization domains observed in the crystal structures (Figure 1) and the symmetric monomer conformations in the OfCC and IfCC crystal structures. After this construction of a symmetric starting point, symmetry was not imposed on the monomers in the course of the MD simulations, which nevertheless remained substantially symmetrical except for a special case of asymmetry discussed below (section 3.3).
The N- and C-terminal end residues (including residues 1–11 in the OfCC and MDi.x intermediates, 1–5 in the IfCC, 417–422 in all conformations) that were not resolved in the crystal structures were modeled using the homology server FUGUE33 and available crystal data from the IfCC. For “MD2”, internal water molecules were calculated for each starting conformation with the programs Dowser34,35 and MMC36 (these waters left the TTDI in the end conformation during the simulations). After adding missing protein hydrogen atoms with the VMD plugin “psfgen”, each starting conformation for the “MD1” and “MD2” protocol (see below) was embedded in a POPC membrane bilayer model using guided positional information obtained from the program “TMDET”.37 A 10 Å layer of explicit “TIP3P” waters was added above and below each POPC–protein complex. With NaCl concentrations at 150 mM (VMD plugins “solvate”, “autoionize”38), the systems are composed of 250 000–300 000 atoms, including 50 000–70 000 waters and 700–900 lipid molecules in simulation boxes of 200 Å × 200 Å × 100 Å.
2.3. Molecular Dynamics Simulations
All MD simulations were performed with the all-atom CHARMM22 protein/water/ion force field (using CMAP corrections)39 with the program NAMD.40 The POPC molecules of the membrane were simulated with the CHARMM27 lipid force model in “MD1” (input for motion planning) and with CHARMM36 in “MD2” (used to analyze the MDi.x intermediates and the end conformations); CHARMM36 was not yet available for the “MD1” simulations. Each system was equilibrated with MD until all RMSDs of the protein with respect to the trimer and monomers of the two crystal structures and the protein’s starting conformation had converged (not shown). As a result, the OfCC was equilibrated for 105 ns, the intermediate MDi.2 for 107 ns, MDi.4 for 164 ns, MDi.5 for 178 ns, MDi.11 for 173 ns, MDi.12 for 109 ns, and the IfCC for 115 ns (the production phases were at least 40 ns long for each run), indicating that some of the modeled intermediates needed longer equilibration times than the crystal structures of the end conformations. We performed MD simulations with an integration step of 1 fs for the first 5 ns of equilibration and 2 fs thereafter, a temperature of 310 K, a Langevin damping coefficient of 5/ps, a nonbonded cutoff of 12 Å, switching distance of 10 Å, the particle-mesh-Ewald algorithm to treat electrostatic interactions, and the ShakeH algorithm41,42 to fix bonded interactions between hydrogens and heavy atoms (RigidBonds “all”). The first 0.5 ns of each MD equilibration was treated in the NVT and all subsequent phases of our MD simulation were in the semi-isotropic NPT ensemble (P = 1 atm with a 200 fs Nosé–Hoover Langevin barostat oscillation period and 50 fs damping time scale).
2.4. Domain/Helix (angle)/RMSD Definitions
The “transport domain” and “trimerization domain” are defined based on the crystal structures10 (i.e., residues 76–129, 226–422 and residues 1–75, 130–225, respectively). Helices are defined with the program STRIDE43 in VMD38 applied to the last 16 ns of both the OfCC and the IfCC MD-equilibrated trajectories, i.e., residues 14–30, 44–55, 59–65, 83–106, 143–146, 151–167, 175–199, 208–214, 227–243, 248–252, 259–262, 266–274, 281–290, 298–300, 302–303, 305–306, 313–328, 339–349, 363–364, 378–385, and 396–415. The angle θ between TM6 and the membrane normal was measured using the “AngleBetweenHelices” script in PyMol.44 All RMSDs in MD were calculated with VMD38 considering the Cα atoms of the helical residues only.
2.5. Alignment with the Reference Frame of the Lipid Membrane
Since the rotational orientation of our lipid–protein system was well maintained throughout the simulations, we first translated the latest snapshot of each MD-equilibrated simulation along the membrane normal, such that its membrane midplane would match the latest snapshot of the OfCC. Each snapshot was then translated perpendicular to the membrane normal, so that the center of mass of the central cavity of the trimer (Cα atoms of residues 60–64, 139–161, 183–190), projected on the midplane, matched the projected center of mass in the OfCC.
2.6. Distance Difference Matrices
Distance matrices were computed with the VMD plugin “iTrajComp”45 from average Cα–Cα distances over the last 16 ns of each MD simulation. These matrices were then converted to pairwise distances between structural elements by averaging over all Cα–Cα distances between each pair of these elements. Difference matrices were computed from these distance matrices by pairwise matrix subtraction.
2.7. Solvent-Accessibility Computations
Relative solvent-accessible surface areas (SASArel) were computed with the program NACCESS46 on the last 16 ns of each simulation, with the default probe radius of 1.4 Å. On the basis of single-residue-accessibility studies,47 we defined a residue to be solvent accessible if its average relative solvent-accessibility surface area (plus standard deviation) was larger than the threshold SASArel,thres. of 11% and to be solvent inaccessible otherwise.
2.8. Determination of the TTDI
A residue i is considered to be part of the TTDI if SASArel,i,isolated – SASArel,i,complex > SASATTDI ≡ 15%. SASArel,i,isolated is the SASArel of residue i in the context of an isolated domain (either transport or trimerization) to which it belongs; SASArel,i,complex is the SASArel of residue i in the context of the full trimerization/transport domain complex. This particular choice of SASATTDI yields a fairly robust interface definition, as the number of TTDI residues in any of our monomers changed by <16% when different values of SASATTDI were used for the definition (13%, 14%, 16%, 17%). The TTDI surface area ATTDI was calculated as48ATTDI ≡ SASAtrim.+ SASAtrans. – SASAtrim.+trans., where SASAtrim. and SASAtrans. represent the SASAs of the isolated trimerization and transport domains, respectively, and SASAtrim.+trans. is the SASA of the full trimerization–transport domain complex.
2.9. Mixed ENM Computations
mENMs were constructed between minimized, MD-equilibrated trimer conformations of the OfCC and IfCC. For these elastic networks, the uniform force constant γ was set to 0.03 kcal/mol/Å2 to normalize the calculated ENM fluctuations of the end conformations (at T = 310 K) to their corresponding experimental B factors. The distance cutoff of 15 Å for the models was chosen to maximize the correlations between calculated fluctuations and B factors. The mENM energy barriers were computed as described in ref (49) modifying an in-house ENM python script.50 In the absence of experimental data about the relative distributions of the end conformations, we assumed ε1 = ε2 = 0. In the mENMs, the reduction of TTDI contacts was modeled as a reduction in γ → 0.5γ for all elastic bonds between the transport and the trimerization domains (denoted as “w/<”).
3. Results
3.1. Structural Intermediates Obtained from Motion Planning and Molecular Dynamics
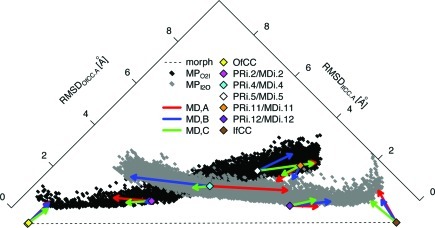
Substrate translocation in GltPh is a rare event, occurring on the time scale of micro- to milliseconds.51 Therefore, in order to characterize a putative accessible path connecting the two end structures of the STP, we modeled conformations with the motion planning (MP) approach to obtain reasonable intermediate structures that can serve as input for MD simulations. When applied starting from the outward- and the inward-facing conformations as described in Methods, the MP computations resulted in an ensemble of 23 000 monomer conformations. Figure 2 illustrates the progression of the structural intermediates obtained with this algorithm as expressed by their RMSD from the corresponding crystal structures of the monomers with chain identity A (see pdb entries 2NWX and 3KBC). The plot of RMSDOfCC.A against RMSDIfCC.A (Figure 2, black and gray points) is calculated for the Cα atoms of the helices in the compared structures. It shows that the intermediate conformations determined with MP span the entire RMSD range of the RMSD between the monomers in the OfCC and IfCC end structures, RMSDO,I = 9.1 Å.
Figure 2.
RMSD landscape of all computed conformations along the modeled translocation path of GltPh. Monomer Cα-RMSDs with respect to the A monomer in the OfCC crystal structure (RMSDOfCC.A) are plotted against the ones calculated with respect to monomer A of the IfCC crystal structure (RMSDIfCC.A) for all modeled MP monomers (“MPO2I” and “MPI2O”, black and gray filled circles, respectively); values of representative PRi.x (x = 2, 4, 5, 11, 12) intermediates are included. All monomers of the starting MDi.x (x = 2, 4, 5, 11, 12) intermediates and crystal monomer conformations are included (color-filled diamonds: OfCC in yellow, PRi.2/starting MDi.2 in magenta, PRi.4/starting MDi.4 in cyan, PRi.5/starting MDi.5 in white, PRi.11/starting MDi.11, orange, PRi.12/starting MDi.12, purple, and IfCC, brown). Red, blue, and green arrows point to the values for the corresponding monomers (monomers A, B, and C, respectively) after the MD simulations done in the context of the trimer. The linear interpolation between the two crystal structures is drawn as a black dashed line.
The representative intermediates PRi.x (x = 2, 4, 5, 11, 12) defined in Methods are depicted in Figure 3 in which their deviations from the crystal structures in Figure 2 are marked by filled diamonds. The rearrangements are detectable in Figure 3 in terms of a change in positioning of the transport domain (orange) relative to the trimerization domain (green). In this modeled path the transport domain moves toward the intracellular cytoplasm, while the tertiary structure of both domains is largely preserved. The TM3–4 loop (blue), which is expected to be highly flexible, appears fairly rigid along this path, although it is defined in the set of the degrees of freedom used by the motion planning algorithm (see Methods). Participation of this loop in the transition is revisited in the MD simulations discussed below.
Figure 3.
Sequential series of structural intermediates in the substrate translocation path (STP) modeled with Motion Planning, superimposed on the OfCC and IfCC crystal structures. Each monomer is represented in the reference frame of the trimerization domain. Transport and trimerization domains are shown as orange and green ribbons, respectively; the TM3–4 loop is colored in blue.
To evaluate the feasibility of the PRi.x intermediates calculated with the MP approach, each of the intermediates was used in turn to construct a symmetrical trimer MDi.x (x = 2, 4, 5, 11, 12), as described in Methods. Each one of these trimers and the two crystal trimers were simulated with all-atom MD for at least 100 ns in the context of a solvated POPC lipid membrane model. As seen from the positioning of the monomers in these trimers (RMSD plot in Figure 2), the intermediate structures evolve into MD-equilibrated conformations with RMSD values marked by the tip of the corresponding arrows (Figure 2). In MDi.2 and MDi.11, these equilibrated monomers have lower RMSDOfCC.A (higher RMSDIfCC.A) values compared to their starting values, whereas in MDi.5 and MDi.12 this trend is reversed. This indicates that the nearest feasible crystal structures are attraction points in the equilibration of the intermediates, with the exception of MDi.11, which appears to be caught near an intermediate state. A special feature of asymmetry developed in MDi.4, as individual monomers in this trimer were found to evolve toward either the OfCC (monomers B and C) or the IfCC (monomer A), thus generating an asymmetric structure; this is discussed further below (section 3.3). It is noteworthy that overall the converged RMSD values obtained from MD fall near the ones generated with MP, indicating that the structures are consistent in the two approaches.
3.2. Rearrangements of the Transport and Trimerization Domains
Comparison of the end-point crystal structures10,11 reveals large rearrangements of the transport domains, presumably outlining the changes required for substrate translocation. The corresponding conformational changes are evidenced in the MD-equilibrated conformations changing from the outward-facing structure, via the five MDi.x intermediates, to the inward-facing structure; this is illustrated in Figure 4 with respect to the surrounding lipid membrane. Along this modeled translocation path in the trimer, the three transport domains (orange ribbons) are seen to transition from the OfCC, along the membrane’s normal axis, toward the intracellular cytoplasm, displaced by as much as 11 ± 1 Å. This displacement is indicated by the change in position of the red bead marking their center of mass in all panels of Figure 4. These rearrangements of the transport domains are opposite in direction and much larger than those observed for the trimerization domains (green ribbons in Figure 4). By following the change in position of the trimerization domain’s center of mass (blue bead) in traversing the panels from the OfCC to the IfCC the repositioning of the domain is seen to be toward the extracellular cytoplasm by as much as 4 ± 1 Å along the same axis. Notably, there is also a tilt of the transport domain, measured by changes in the angle θ between TM6 and the membrane’s normal axis. As shown in Figure 4, the value of θ (averaged over all three monomers) changes along the modeled STP from 27 ± 3° in the OfCC to 44 ± 3° in the IfCC, which corresponds to a tilt of the transport domain by 17 ± 4°.
Figure 4.
MD-equilibrated trimers of the modeled substrate translocation path (STP) for GltPh shown in the reference frame of the lipid membrane (phosphor atoms as gray beads, lipid tail carbon atoms as cyan lines) for (a) OfCC, (b) IfCC, (c) MDi.4, and (d) MDi.5. The center of mass of the three transport domains (orange) is indicated by a red sphere; the center of mass for the trimerization domains (green) is marked by a blue sphere; residues 130–168 (TM4a–c) in monomer B were omitted for clarity. The angle between the membrane normal (black bar) and TM6 of monomer A (purple helix) is inscribed in black. Substrates are rendered as colored sticks.
The structural integrity of the simulated systems that exhibit these large rearrangements is evident in the distance difference matrices (DDMs). As described in Methods, these matrices were constructed from distances between structural segments (i.e., TM1–6, HP1, TM7, HP2, and TM8 of each monomer) with respect to the outward-facing crystal structure (Figure SI2, Supporting Information). The positions of the regions where the absolute differences are small, <3 Å, show that the tertiary structure of each monomer as well as the trimeric frame of the quaternary structure are largely preserved along the modeled translocation path.
3.3. Trimers of Intermediate States can be Asymmetric
Because the monomers in GltPh and EAATs have been suggested to transport substrate independently,15−17 we investigated whether monomers can adopt different conformations in our MD-equilibrated STP trimers. Table SI3, Supporting Information, shows that MDi.4 has the highest average RMSD between monomers (4.2 ± 0.1 Å), whereas the simulated OfCC and IfCC structures have the lowest ones of 1.0 ± 0.1 and 1.2 ± 0.1 Å, respectively. This observation suggests that the MDi.4 trimer is more asymmetric than other trimers along our modeled translocation path. The structural context of this asymmetry is evident from the comparison of two MDi.4 monomers in Figure 5. Clearly, the transport domain is positioned differently in monomer B (Figure 5a) than in monomer A (Figure 5b), i.e., more toward the extracellular region (into the figure plane) in monomer B than in monomer A. This observation is recorded by smaller values of RMSDOfCC.A (and larger RMSDIfCC.A) for monomers B and C than for monomer A (Figure 2).
Figure 5.
Two monomers illustrate the conformational asymmetry of the MDi.4 trimer intermediate: the transport domain in monomer “A” of MDi.4 (MDi.4.A) (b) has moved deeper toward the intracellular region than in monomer MDi.4.B (a) (the MD starting conformations of all monomers in a trimer are identical). Changes in the TM3–4 loop conformation (in green) along the modeled translocation path are shown with respect to every other residue of the monomer: Each such residue is colored by an average correlation coefficient (see text), i.e., in red if the residue tends to get closer to the TM3–4 loop along the path from the outward- to the inward-facing conformation and in blue if it tends to move farther away from the TM3–4 loop; residues colored in white are not correlated, on average, with the TM3–4 loop motion (TM3–4 is necessary for substrate transport and undergoes substrate-dependent conformational changes59). The other monomers in each figure are illustrated as cyan ribbons.
3.4. Conformation of the TM3–4 Loop Changes with Respect to the Transport Domain
A recent study on GltPh suggested that the TM3–4 loop is essential for substrate transport and undergoes substrate-induced conformational changes.52 Before investigating these changes along our modeled translocation path, we identified a conformational difference of this loop between monomer A and monomer B in MDi.4, which coincides with the different positioning of the transport domain, described above (Figure 5): with respect to the extracellular part of the transport domain, the TM3–4 loop (shown in green) is shifted inward in monomer B (Figure 5a) compared to the one in monomer A (Figure 5b). Thus, in monomer B this loop is closer to the tip of HP2 (average Cα–Cα distance between residues 108–127 and 352–357: d108–127,352–357 = 20.7 ± 0.7 Å) than to the loop between TM7b and HP2a (d108–127,330–337 = 23.8 ± 0.3 Å). For monomer A, which is closer to the intracellular end, we observe the opposite trend for the position of the TM3–4 loop (d108–127,352–357 = 32.1 ± 0.5 Å, d108–127,330–337 = 13.1 ± 0.2 Å).
To study the dynamics of loop TM3–4 along the modeled transition, we constructed a “translocation path series” from all 21 monomers of the six averaged, MD-equilibrated trimers ordered by the transition parameter λSTP = (ζ + RMSDO,I)/(2 × RMSDO,I) ϵ [0,1], where ζ ≡ RMSDOfCC.A – RMSDIfCC.A and RMSDO,I ≡ 9.1 Å is the RMSD between the OfCC and IfCC crystal monomers. To capture the loop’s different conformations along the path, we measured all possible values of dij, defined as the average (over the last 16 ns of each simulation) of Cα–Cα distance between a TM3–4 loop residue i, and any non-TM3–4 loop residue j of the same monomer. The Pearson correlation coefficients cij between each dij and λSTP quantify the trends of changes of the loop’s conformation along the modeled translocation path series. Figure 5 presents average values of the cij over all residues i (shown in green) mapped onto each residue j. Negative correlation coefficients indicate that the distance to the TM3–4 loop tends to decrease along the transition from the outward-facing toward the inward-facing conformation; positive correlations indicate residues for which the distance increases along the transition path. In contrast, residues colored in white have no correlation. Consequently, Figure 5 indicates the correlation between the movement of the transport domain and that of the TM3–4 loop is such that as the transport domain moves toward (or away from) the intracellular end, the TM3–4 loop moves outward (or inward), respectively, relative to the extracellular part of the transport domain. In movies available in SI4, Supporting Information, we present a molecular illustration of the rearrangements along λSTP, in an individual monomer, including the conformational changes of loop TM3–4.
3.5. Structural Changes in the Transport/Trimerization Domain Interface (TTDI)
The rearrangement of the spatial relationship between the transport and the trimerization domains is interpreted from a comparison of the crystallographic data as a change in their interface.10 Similar comparisons among the MDi.x intermediates and the end states reveal gradual changes in this interface (TTDI) along the modeled transition path. To characterize these changes quantitatively we used differences in relative solvent-accessible surface areas (SASAs) calculated as described in Methods. Figure 6 illustrates side views of the superimposed transport and trimerization domain of monomer A in the OfCC (a), MDi.4 (b), and IfCC (c) together with the corresponding TTDI residues. The “trimerization” side of the TTDI is seen to be largely preserved among these conformations and contains residues of transmembrane segments (TM) TM1 and 2, TM4a/c, and TM5. The changes in the “transport domain” side of the TTDI are greater in all three monomers, with the contacting residues coming from TM6, hairpin motif HP2a, and TM8a. Additional interface contacts are observed in some but not all monomers: residue contacts with HP1b and TM7a are formed only in the OfCC, residue contacts with HP1a are formed only in the OfCC and MDi.4, and contacts with HP2b are formed only in MDi.4 and the IfCC. In Figure 6, the TTDI in monomer A of MDi.4 (i.e., MDi.4.A) is seen to have a smaller area than the end states. In fact, the TTDI areas in the end conformations reach as high as 4000 Å2, whereas in the intermediates they may be as low as 2900 Å2. This intermediate reduction may affect greatly the energies of interactions and thus the dynamics of the interface along the translocation path. To estimate these effects in the form of changes in transition energy barriers between the outward- and the inward-facing conformations, we used mixed elastic network models (mENMs49,53) in which interactions are modeled as elastic bonds. In Figure SI5, Supporting Information, we plot the transition energy profiles of the “OCC↔IfCC” mENMs (“w/”, red) and the ones with reduced TTDI contacts (see Methods) in the OfCC (“w/<_f0”, blue) or the IfCC (“w/<_f1”, green). For this mENM, a reduction of TTDI contacts in either conformation lowers the transition energy barrier, indicating increased flexibility in the mENM transition between the two end conformations.
Figure 6.
Changes in contact surface in the transport–trimerization domain interface (TTDI) along the modeled translocation path: (a) monomer A of the OfCC, (b) MDi.4, and (c) IfCC. Residues at the interface are rendered as white surfaces on the structural cartoon of the transport domain (left, orange ribbons) and trimerization domain (right, green ribbons), respectively.
3.6. Changes in Residue Accessibility in the TTDI
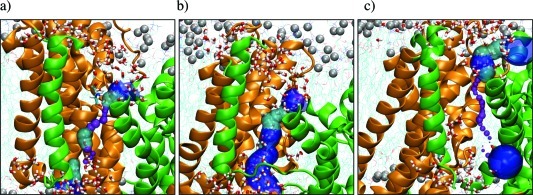
Concomitant with the reduction in the TTDI surface area, water molecules are observed to penetrate the TTDI region. This is illustrated by a snapshot of MDi.4.A in which a pore (semitransparent colored surfaces) of ∼20 water molecules is seen in the TTDI region (Figure 7b). Note that this water pore does not form in either the outward- (Figure 7a) or the inward-facing conformation (Figure 7c). On average, i.e., over the last 16 ns of each equilibrated trajectory (Table SI6, Supporting Information), the space at the TTDI contains as much as nwater = 15 ± 3 water molecules in the intermediates, significantly more than in the end conformations, which have no more than nwater = 5 ± 1.
Figure 7.
The interface between the transport and the trimerization domain (TTDI) shows water penetrating in the intermediates but much less so in the end-point conformations. The TTDI is shown for monomer A of the simulated OfCC (a), MDi.4 (b), and IfCC (c) from the structures shown in Figure 4. Explicit water molecules within 8 Å of residues 15–30 (TM1) and 207–216 (TM5) are visualized as red–white sticks; computed water pores are rendered as surfaces colored from purple via cyan to blue to represent small to large pore radii. Residues 36–45 (TM2) and 190–222 (TM5) are omitted for clarity.
The results indicating the existence of a water pore at the TTDI observed in the intermediates but much less so in the end states can be compared to results from experimental measurements of solvent accessibilities in the literature. To this end, we first determined the particular set X of TTDI residues that are solvent inaccessible in any monomer of the end conformations (see Methods) but are solvent accessible in the intermediates (i.e., for at least one intermediate monomer). We then classified any residue in the set X based on three criteria related to available experimental data (Table 1 and Figure SI7, Supporting Information) as “successful SCAM prediction” if this position is known (e.g., from published SCAMs5,54,55) to be solvent accessible (in either GltPh or its corresponding site in an EAAT homologue) and “unsuccessful SCAM prediction” if this position has been tested, e.g., with SCAM, but not found to be solvent accessible.54 We classify as “new SCAM prediction” those residues that should be accessible but to the best of our knowledge have not been reported out from any solvent-accessibility measurements. The three “successful SCAM” positions identified in this way among the nine positions in the TTDI support the validity of our model and the identified water pores at the TTDI. We predict that residue V209, the only apparently “unsuccessful SCAM prediction” residue, would become accessible with SCAM using a smaller reagent than MTS, such as HgCl, as was used in ref (5). We note the remaining five positions identified here as “new SCAM prediction” positions that can be tested experimentally to further validate and understand the STP model.
Table 1. All Residues in the Set X (i.e., solvent-accessible in the intermediates but inaccessible in the simulated crystal conformations, see text) That Belong to the TTDIa.
| “int.-solv.-acc.” | max SASArel (OfCC,IfCC) [%] | |
|---|---|---|
| successful SCAM predictions | I61, I213, M395? | 3.5, 2.3, 13.1 |
| unsuccessful SCAM predictions | V209? | 4.8 |
| new SCAM predictions | L54, V62, L66?, V198, A205 | 2.1, 0.0, 3.7, 2.7, 0.8 |
Solvent-accessible residues predicted from the simulations are listed as “successful SCAM prediction” if the position is known (e.g., from published SCAMs5,54,55) to be solvent accessible in GltPh or its corresponding site of an EAAT homologue; it is identified as “unsuccessful SCAM prediction” if this position has been tested, e.g., with SCAM but not found to be solvent accessible so far;54 it is listed in “new SCAM predictions” if to date, to the best of our knowledge, no solvent-accessibility measurements have been performed on this residue in GltPh or its EAAT counterpart. Residues marked as ? also showed some solvent accessibilty in the end conformations, measuring one or more average water molecules within 3 Å of the residue’s side chain (see Figure SI7, Supporting Information). In the “max SASArel” column, for each residue in the set X we list the maximum SASArel values observed in the OfCC and IfCC.
4. Discussion
The availability of crystal structures for the outward- and inward-facing states of GltPh10,11 has given a strong structural context to the studies of GltPh and EAATs that identify mechanistic elements of binding,5,19−22,56 extracellular capture,23,57 and intracellular release24 of both substrate and ions. Since these two structures are considered to represent the end states of GltPh’s substrate translocation mechanism, it became clear from their differences that significant rearrangements of key functional domains are central to this mechanism. In spite of the very attractive hypothesis presented on the basis of these two end-point structures, the path leading from the outward- to the inward-facing state remained unexplored.
In the present study, we obtained and evaluated dynamic molecular models of structural intermediates along GltPh’s substrate translocation path obtained from application of a combination of computational methods (motion planning, molecular dynamics, mixed elastic network models) to seek out salient conformational changes and mechanistic elements. Motion planning, with which we calculated intermediate conformations of GltPh monomers, is well known in computer science and robotics25 and was recently adapted to study proteins as large as the KcsA potassium channel.27,58 It was selected here as a relatively inexpensive computational tool for modeling the transition paths in terms of clash-free conformations as input for MD simulations exploring the dynamic properties of these states. From the MD simulations of the intermediate structures identified with PathRover, our results specify the rearrangements in the reference frame of the surrounding lipid membrane in terms of relative movements between the transport and the trimerization domains. These movements are in opposite directions along the membrane normal, and the computational results confirm as well a tilt of the transport domain with respect to this axis (cf. Figure 5 in ref (10)).
The dynamic role of the TM3–4 loop in the mechanistic substrate translocation pathway model resulting from our study agrees with the suggestion that this loop is involved in GltPh’s substrate transport,52 undergoing substrate-induced conformational changes. Indeed, a comparison between the outward- and the inward-facing crystal structures10,11 suggests a repositioning of this loop with respect to the transport domain. However, since parts of the 60 Å loop are unresolved in the outward-facing crystal structure, it remained unclear whether this conformational difference distinguishes the OfCC from the IfCC and how this conformational change is accomplished. Our study proposes a path for this conformational change of the loop with respect to the transport domain, which correlates well with the larger transitions along the translocation path (see movies in SI4, Supporting Information). Comparing the conformations of the TM3–4 loop in our modeled PRi.x (Figure 3) and MDi.x (Figures 4 and 5) intermediates, we observed that after motion planning alone (Figure 3) this loop appears intrinsically less flexible than is expected from the data for residue-specific, substrate-dependent solvent-accessibility changes in this loop.52 Much longer MD simulations will be required to cover the likely complex spectrum of dynamics of this 60 Å long loop.
We observed in our results a specific dynamic context for available experimental data indicating that GltPh and EAAT monomers function independently15−17 and “move stochastically and independently”.10 This appeared in one of the MD simulations where a trimer intermediate was shown capable of adopting structural asymmetry, despite the fact that all the starting structures had identical monomer conformations (Figure 5).
The mixed elastic network model approach, which had been used successfully to reproduce protein fluctuations from crystallographic data to predict large collective conformational changes and to identify minimum energy conformations therein,53,60−62 served here to examine further the dynamics of the transition between the outward- and the inward-facing conformation. Combined with the structural pathway indicated by our MP and MD simulations, the findings provide details of the pathway that agrees substantially with the inferences from the crystal structures of GltPh regarding a transport mechanism in which the transport domain undergoes a large vertical repositioning with respect to the trimerization domain in a rearrangement inferred to involve a rigid-bundle movement that preserves GltPh’s tertiary structure and its quaternary frame. However, accessibility studies using the SCAM method63 suggested that the intermediates between the two crystal structures representing the OfCC and the IfCC must involve intricate rearrangements. In particular, these studies identified as accessible some residues positioned in the interface between the transport and the trimerization domains (the TTDI), although this interface is compact in both crystal structures, and not suggestive of solvent (or reagent) accessibility to the sites identified as reactive with the SCAM approach. While remaining in agreement with the inferences from crystallographic data, our model of the translocation path resolves this apparent conflict as it describes significant changes in contact area of the TTDI in transition intermediates and shows significant water penetration in the interface region in the intermediate conformations equilibrated computationally. Thus, the contact area of the TTDI is reduced along our modeled translocation path by nearly 20% compared to the end states. This reduction is consistent with facilitated dynamics along GltPh’s substrate translocation path (Figure SI5, Supporting Information) and exposes some of the residues near the TTDI to solvent (Figure 7 and Table SI6, Supporting Information).
Our model is supported on a residue-specific level by experimental accessibility (SCAM) results. In contrast to the interface observed in either the outward- or the inward-facing structure of GltPh, which would not allow reagent accessibility to residues I61, I213, and M395,5,54,64,65 we show these to be accessible in the intermediates. Moreover, we predict residues L54, V62, L66, V198, and A205 to become solvent accessible in the intermediates but not in the end conformations of GltPh’s substrate translocation path, thus suggesting direct modes of experimental validation of the modeled STP, e.g., via SCAMs. With our current approach, we were unable to distinguish whether the water pore along the modeled STP is initiated from the extra- or intracellular region.
During the final preparation of this manuscript, a new crystal structure of an asymmetric intermediate of GltPh was reported66 featuring two monomers in the inward-facing conformation (RMSDIfCC.A = 0.7 Å) and one monomer in an intermediate conformation (RMSDOfCC.A = 3.0 Å, RMSDIfCC.A = 6.8 Å). This structure (PDB accession code 3V8G) exhibits remarkable similarity to the first intermediates in our modeled STP. Thus, with respect to this crystal intermediate monomer “iOFS”, which is monomer C (“iOFS.C”), our MP conformations have a minimum RMSDiOFS.C of 1.9 Å (not shown). The PRi.2 conformation has the lowest RMSDiOFS.C (2.3 Å) among all PRi.x intermediates (Table SI8, Supporting Information). Notably, the MDi.2 monomers conformations exhibit even lower minimum RMSDiOFS.C values (1.7 Å) (Table SI9, Supporting Information), with the RMSDiOFS.C for their average structure being 1.8 Å (Figure SI10, Supporting Information). All these RMSD values are smaller than the crystallographic resolution of 3.5 Å for the GltPh-s. Taken together, these structural comparisons support the validity of the intermediates modeled from our computations, which have remarkable resemblance to available crystallographic data of GltPh.
Acknowledgments
We thank Dr. Olga Boudker for invaluable insights and discussions regarding the GltPh structure and function, Dr. Barak Raveh for help with the Motion Planning “PathRover” source code,27 Dr. Lei Shi for helpful insights and technical advice, Dr. Willy Wriggers for Elastic Network Model scripts,50 Dr. Mihaly Mezei for his MMC program,36 Dr. Michelle A. Sahai, Dr. Niklaus Johner, and Jason Banfelder for discussions, and the Weill Cornell PBtech Staff for computational support. This work was supported by NIH Grants DA012408, U54GM087519, and 1S10RR026553-01, the computational resources of the Institute for Computational Biomedicine at Weill Medical College of Cornell University, and the New York Blue Gene Computational Science facility housed at Brookhaven National Laboratory.
Glossary
List of Abbreviations:
- DDM
distance difference matrix
- EAAT
excitatory amino acid transporter
- GltPh
bacterial EAAT homologue from Pyroccocus horikoshii
- HP
hair pin structural motif
- IfCC
inward-facing, closed (occluded) conformation
- MD
molecular dynamics
- mENM
mixed elastic network model
- MDi.x
molecular dynamics intermediate (see text)
- PRi.x
motion planning intermediate (see text)
- OfCC
outward-facing, closed (occluded) conformation
- PDB
Protein Data Bank, www.pdb.org
- POPC
1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine
- RMSD
root mean square deviation
- RRT
rapidly exploring random tree
- TM
transmembrane domain
- TTDI
transport trimerization domain interface
- SASA
solvent-accessible surface area
- SCAM
substituted cysteine-accessibility method
- STP
substrate translocation path
Supporting Information Available
Figures and Tables SI1–SI11 and two movies “SI4.a.mpg” and “SI4.b.mpg”. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Levy L. M.; Warr O.; Attwell D. Stoichiometry of the glial glutamate transporter GLT-1 expressed inducibly in a Chinese hamster ovary cell line selected for low endogenous Na+-dependent glutamate uptake. J. Neurosci. 1998, 18(23), 9620–9628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerangue N.; Kavanaugh M. P. Flux coupling in a neuronal glutamate transporter. Nature 1996, 383(6601), 634–637. [DOI] [PubMed] [Google Scholar]
- Fairman W. A.; Vandenberg R. J.; Arriza J. L.; Kavanaugh M. P.; Amara S. G. An excitatory amino-acid transporter with properties of a ligand-gated chloride channel. Nature 1995, 375(6532), 599–603. [DOI] [PubMed] [Google Scholar]
- Miller C. A leak in the EAATs. Nat. Struct. Mol. Biol. 2007, 14(5), 356–357. [DOI] [PubMed] [Google Scholar]
- Ryan R. M.; Mitrovic A. D.; Vandenberg R. J. The chloride permeation pathway of a glutamate transporter and its proximity to the glutamate translocation pathway. J. Biol. Chem. 2004, 279(20), 20742–20751. [DOI] [PubMed] [Google Scholar]
- Dingledine R.; Borges K.; Bowie D.; Traynelis S. F. The glutamate receptor ion channels. Pharmacol. Rev. 1999, 51(1), 7–61. [PubMed] [Google Scholar]
- Maragakis N. J.; Rothstein J. D. Glutamate transporters: animal models to neurologic disease. Neurobiol. Dis. 2004, 15(3), 461–473. [DOI] [PubMed] [Google Scholar]
- Bailey C. G.; Ryan R. M.; Thoeng A. D.; Ng C.; King K.; Vanslambrouck J. M.; Auray-Blais C.; Vandenberg R. J.; Bröer S.; Rasko J. E. J. Loss-of-function mutations in the glutamate transporter SLC1A1 cause human dicarboxylic aminoaciduria. J. Clin. Invest. 2011, 121(1), 446–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boudker O.; Ryan R. M.; Yernool D.; Shimamoto K.; Gouaux E. Coupling substrate and ion binding to extracellular gate of a sodium-dependent aspartate transporter. Nature 2007, 445(7126), 387–393. [DOI] [PubMed] [Google Scholar]
- Reyes N.; Ginter C.; Boudker O. Transport mechanism of a bacterial homologue of glutamate transporters. Nature 2009, 462(7275), 880–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yernool D.; Boudker O.; Jin Y.; Gouaux E. Structure of a glutamate transporter homologue from Pyrococcus horikoshii. Nature 2004, 431(7010), 811–818. [DOI] [PubMed] [Google Scholar]
- Groeneveld M.; Slotboom D.-J. Na+:Aspartate Coupling Stoichiometry in the Glutamate Transporter Homologue GltPh. Biochemistry 2010, 49(17), 3511–3513. [DOI] [PubMed] [Google Scholar]
- Gendreau S.; Voswinkel S.; Torres-Salazar D.; Lang N.; Heidtmann H.; Detro-Dassen S.; Schmalzing G.; Hidalgo P.; Fahlke C. A trimeric quaternary structure is conserved in bacterial and human glutamate transporters. J. Biol. Chem. 2004, 279(38), 39505–39512. [DOI] [PubMed] [Google Scholar]
- Yernool D.; Boudker O.; Folta-Stogniew E.; Gouaux E. Trimeric subunit stoichiometry of the glutamate transporters from Bacillus caldotenax and Bacillus stearothermophilus. Biochemistry 2003, 42(44), 12981–12988. [DOI] [PubMed] [Google Scholar]
- Grewer C.; Balani P.; Weidenfeller C.; Bartusel T.; Tao Z.; Rauen T. Individual subunits of the glutamate transporter EAAC1 homotrimer function independently of each other. Biochemistry 2005, 44(35), 11913–11923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch H. P.; Brown R. L.; Larsson H. P. The glutamate-activated anion conductance in excitatory amino acid transporters is gated independently by the individual subunits. J. Neurosci. 2007, 27(11), 2943–2947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leary G. P.; Stone E. F.; Holley D. C.; Kavanaugh M. P. The glutamate and chloride permeation pathways are colocalized in individual neuronal glutamate transporter subunits. J. Neurosci. 2007, 27(11), 2938–2942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang J.; Shrivastava I. H.; Watts S. D.; Bahar I.; Amara S. G. Large collective motions regulate the functional properties of glutamate transporter trimers. Proc. Natl. Acad. Sci. U.S.A. 2011, 108(37), 15141–15146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z.; Tajkhorshid E. Identification of the third Na+ site and the sequence of extracellular binding events in the glutamate transporter. Biophys. J. 2010, 99(5), 1416–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanner B. I.; Bendahan A. Binding order of substrates to the sodium and potassium ion coupled L-glutamic acid transporter from rat brain. Biochemistry 1982, 21(24), 6327–6330. [DOI] [PubMed] [Google Scholar]
- Larsson H. P.; Wang X.; Lev B.; Baconguis I.; Caplan D. A.; Vyleta N. P.; Koch H. P.; Diez-Sampedro A.; Noskov S. Y. Evidence for a third sodium-binding site in glutamate transporters suggests an ion/substrate coupling model. Proc. Natl. Acad. Sci. U.S.A. 2010, 107(31), 13912–13917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao Z.; Rosental N.; Kanner B. I.; Gameiro A.; Mwaura J.; Grewer C. Mechanism of cation binding to the glutamate transporter EAAC1 probed with mutation of the conserved amino acid residue Thr101. J. Biol. Chem. 2010, 285(23), 17725–17733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrivastava I. H.; Jiang J.; Amara S. G.; Bahar I. Time-resolved mechanism of extracellular gate opening and substrate binding in a glutamate transporter. J. Biol. Chem. 2008, 283(42), 28680–28690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dechancie J.; Shrivastava I. H.; Bahar I. The mechanism of substrate release by the aspartate transporter Glt(Ph): insights from simulations. Mol. Biosyst. 2011, 7(3), 832–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latombe J.-C.Robot Motion Planning; Kluwer Academic Publishers: Norwell, MA, 1991. [Google Scholar]
- Tirion M. M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77(9), 1905–1908. [DOI] [PubMed] [Google Scholar]
- Raveh B.; Enosh A.; Schueler-Furman O.; Halperin D. Rapid sampling of molecular motions with prior information constraints. PLoS Comput Biol 2009, 5(2), e1000295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohl C. A.; Strauss C. E. M.; Misura K. M. S.; Baker D. Protein structure prediction using Rosetta. Methods Enzymol. 2004, 383, 66–93. [DOI] [PubMed] [Google Scholar]
- Lavalle S. M.;Kuffner J. J. Jr.. Rapidly-Exploring Random Trees: Progress and Prospects of Algorithmic and Computational Robotics: New Directions; Kluwer Academic Publishers: Norwell, MA, 2000; Chapter 1, 293–308. [Google Scholar]
- Groeneveld M.; Slotboom D.-J. Rigidity of the subunit interfaces of the trimeric glutamate transporter GltT during translocation. J. Mol. Biol. 2007, 372(3), 565–570. [DOI] [PubMed] [Google Scholar]
- Mehler E. L.; Guarnieri F. A self-consistent, microenvironment modulated screened coulomb potential approximation to calculate pH-dependent electrostatic effects in proteins. Biophys. J. 1999, 77(1), 3–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Fuentes N.; Zhai J.; Fiser A. s. ArchPRED: a template based loop structure prediction server. Nucleic Acids Res. 2006, 34(Web Server issue), W173–W176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi J.; Blundell T. L.; Mizuguchi K. FUGUE: sequence-structure homology recognition using environment-specific substitution tables and structure-dependent gap penalties. J. Mol. Biol. 2001, 310(1), 243–257. [DOI] [PubMed] [Google Scholar]
- Gumbart J.; Trabuco L. G.; Schreiner E.; Villa E.; Schulten K. Regulation of the protein-conducting channel by a bound ribosome. Structure 2009, 17(11), 1453–1464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.; Hermans J. Hydrophilicity of cavities in proteins. Proteins: Struct, Funct, Genet 1996, 24(4), 433–438. [DOI] [PubMed] [Google Scholar]
- Mezei M.; Beveridge D. L. Generic solvent sites in a crystal. J. Comput. Chem. 1984, 5(6), 523–527. [Google Scholar]
- Tusnady G. E.; Dosztanyi Z.; Simon I. TMDET: web server for detecting transmembrane regions of proteins by using their 3D coordinates. Bioinformatics 2005, 21(7), 1276–1277. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual molecular dynamics. J. Mol. Graphics 1996, 14(1), 33–38. [DOI] [PubMed] [Google Scholar]
- Brooks B. R.; Brooks C. L.; Mackerell A. D.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30(10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26(16), 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen H. C. Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 1983, 52(1), 24–34. [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23(3), 327–341. [Google Scholar]
- Frishman D.; Argos P. Knowledge-based protein secondary structure assignment. Proteins 1995, 23(4), 566–579. [DOI] [PubMed] [Google Scholar]
- Dixson S.; Smondyrev A. M.; Rao S. N. PHASE: A Novel Approach to Pharmacophore Modeling and 3D Database Searching. Chem. Bioline Drug Des. 2006, 67, 370–372. [DOI] [PubMed] [Google Scholar]
- Gracia L.iTrajComp: interactive Trajectory Comparison; http://physiology.med.cornell.edu/faculty/hweinstein/vmdplugins/itrajcomp/. [Google Scholar]
- Hubbard S. J.; Thornton J. M.. NACCESS, Computer Program; Department of Biochemistry and Molecular Biology, University College: London, 1993. [Google Scholar]
- Beuming T.; Weinstein H. A knowledge-based scale for the analysis and prediction of buried and exposed faces of transmembrane domain proteins. Bioinformatics 2004, 20(12), 1822–1835. [DOI] [PubMed] [Google Scholar]
- Janin J. l.; Bahadur R. P.; Chakrabarti P. Protein-protein interaction and quaternary structure. Q. Rev. Biophys. 2008, 41(2), 133–180. [DOI] [PubMed] [Google Scholar]
- Zheng W.; Brooks B. R.; Hummer G. Protein conformational transitions explored by mixed elastic network models. Proteins 2007, 69(1), 43–57. [DOI] [PubMed] [Google Scholar]
- Stember J. N.; Wriggers W. Bend-twist-stretch model for coarse elastic network simulation of biomolecular motion. J. Chem. Phys. 2009, 131(7), 074112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watzke N.; Bamberg E.; Grewer C. Early Intermediates in the Transport Cycle of the Neuronal Excitatory Amino Acid Carrier EAAC1. J. Gen. Physiol. 2001, 117(6), 547–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compton E. L. R.; Taylor E. M.; Mindell J. A. The 3–4 loop of an archaeal glutamate transporter homolog experiences ligand-induced structural changes and is essential for transport. Proc. Natl. Acad. Sci. U.S.A. 2010, 107(29), 12840–12845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu F.; Hummer G. Gating transition of pentameric ligand-gated ion channels. Biophys. J. 2009, 97(9), 2456–2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seal R. P.; Leighton B. H.; Amara S. G. A model for the topology of excitatory amino acid transporters determined by the extracellular accessibility of substituted cysteines. Neuron 2000, 25(3), 695–706. [DOI] [PubMed] [Google Scholar]
- Shachnai L.; Shimamoto K.; Kanner B. I. Sulfhydryl modification of cysteine mutants of a neuronal glutamate transporter reveals an inverse relationship between sodium dependent conformational changes and the glutamate-gated anion conductance. Neuropharmacology 2005, 49(6), 862–871. [DOI] [PubMed] [Google Scholar]
- Ryan R. M.; Kortt N. C.; Sirivanta T.; Vandenberg R. J. The position of an arginine residue influences substrate affinity and K coupling in the human glutamate transporter, EAAT1. J. Neurochem. 2010, 114(2), 565–575. [DOI] [PubMed] [Google Scholar]
- Focke P. J.; Moenne-Loccoz P.; Larsson H. P. Opposite Movement of the External Gate of a Glutamate Transporter Homolog upon Binding Cotransported Sodium Compared with Substrate. J. Neurosci. 2011, 31(16), 6255–6262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enosh A.; Raveh B.; Furman-Schueler O.; Halperin D.; Ben-Tal N. Generation, comparison, and merging of pathways between protein conformations: gating in K-channels. Biophys. J. 2008, 95(8), 3850–3860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compton E. L. R.; Taylor E. M.; Mindell J. A. The 3–4 loop of an archaeal glutamate transporter homolog experiences ligand-induced structural changes and is essential for transport. Proc. Natl. Acad. Sci. U.S.A. 2011, 107(29), 12840–12845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normal mode analysis: theory and applications to biological and chemical systems; Chapman & Hall/CRC Mathematical & Computational Biology: London, 2006. [Google Scholar]
- Tozzini V. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 2005, 15(2), 144–150. [DOI] [PubMed] [Google Scholar]
- Zheng W. Anharmonic normal mode analysis of elastic network model improves the modeling of atomic fluctuations in protein crystal structures. Biophys. J. 2010, 98(12), 3025–3034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liapakis G.; Simpson M. M.; Javitch J. A.. The Substituted-Cysteine Accessibility Method (SCAM) to Elucidate Membrane Protein Structure; John Wiley & Sons, Inc.: Hoboken, NJ, 2001. [DOI] [PubMed] [Google Scholar]
- Slotboom D. J.; Konings W. N.; Lolkema J. S. Cysteine-scanning mutagenesis reveals a highly amphipathic, pore-lining membrane-spanning helix in the glutamate transporter GltT. J. Biol. Chem. 2001, 276(14), 10775–10781. [DOI] [PubMed] [Google Scholar]
- Zhang X.; Qu S. The Accessibility in the External Part of the TM5 of the Glutamate Transporter EAAT1 Is Conformationally Sensitive during the Transport Cycle. PLoS One 2012, 7(1), e30961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdon G.; Boudker O. Crystal structure of an asymmetric trimer of a bacterial glutamate transporter homolog. Nat. Struct. Mol. Biol. 2011, 19(3), 355–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.