Towards the prediction of order parameters from molecular dynamics simulations in proteins

Abstract

A molecular understanding of how protein function is related to protein structure requires an ability to understand large conformational changes between multiple states. Unfortunately these states are often separated by high free energy barriers and within a complex energy landscape. This makes it very difficult to reliably connect, for example by all-atom molecular dynamics calculations, the states, their energies, and the pathways between them. A major issue needed to improve sampling on the intermediate states is an order parameter – a reduced descriptor for the major subset of degrees of freedom – that can be used to aid sampling for the large conformational change. We present a method to combine information from molecular dynamics using non-linear time series and dimensionality reduction, in order to quantitatively determine an order parameter connecting two large-scale conformationally distinct protein states. This new method suggests an implementation for molecular dynamics calculations that may be used to enhance sampling of intermediate states.

INTRODUCTION

Proteins represent complex dynamical systems with multiple stable states. Sampling protein motions has shown itself to be complicated by the multiple time scale problem¹ with many different wells and barrier heights being found. Despite considerable effort, there is currently no rapid way to determine the range of stable states from a single structure or from sequence alone. Because biological function is intrinsically linked to the large scale conformational change of proteins, an improved understanding of how conformational change in the complex energy landscape of the protein is determined will provide important insights on both biological and physical questions.

When the state change is connected by an obvious low-dimensional reaction coordinate, specialized sampling methods have been developed that can reliably enhance the collection of intermediate states and the understanding of the relative free energy change.^{2, 3, 4, 5, 6} For example, the passage of an ion through a channel, simple alchemical changes, certain types of conformational change where the movement is mainly hinge-like or otherwise obvious on inspection fall into this category.^{7, 8} But, for many biological problems, the low-dimensional reaction coordinate that optimally predicts functional behavior is not at all obvious from the structure. As the set of solved x-ray structures has continued to grow, there has been an increasing number of situations where alternative structures for the same protein have been determined.⁹ Ideally these alternate structures would also suggest the reaction coordinate that connects one conformation to the other. But, despite many outstanding efforts to design sampling methods, a strong limitation is that an order parameter to enable sampling has been difficult to determine from either single or pairs of static x-ray structures.

Some groups have suggested, in this situation, that harmonic analysis from diagonalization of the second derivative matrix (the Hessian) would be sufficient to find the most important collective modes.^{10, 11, 12, 13, 14, 15, 16} The findings from the coarse-grained model community, in particular, have suggested that this approach can reveal important details about how a protein is connected to large conformational change.¹⁷ Other groups have cautioned that the harmonic model is lacking and have suggested instead focusing on determining effective collective modes from the covariance fluctuation matrix (quasi-harmonic, essential dynamics, or principal component analysis).^{18, 19, 20, 21, 22} These calculations has demonstrated that the low frequency collective motions inferred from the covariance matrix differ from the harmonic analysis. Recently there has been considerable efforts towards further improving on the linear assumptions in principal component analysis, using such tools as kurtosis and quasi anharmonic analysis to further elaborate on the deviations from Gaussian behavior that are found in (MD) molecular dynamics trajectories.^{23, 24, 25, 26}

To directly sample on large-scale conformational change there have been many methods proposed.^{27, 28, 29, 30, 31, 32, 33, 34, 35, 36} The most well known contemporary method is transition path sampling and uses a small number of conformations along a candidate transition pathway with a Monte Carlo move set to anneal an optimal prediction of intermediates in a conformationally changing system.^{37, 38} Alternative methods have used the RMS differences between states as an order parameter to control change,^{39, 40} directly adding a new force that biases motion along the root mean square (RMS) gradient. We developed a method, called dynamic importance sampling (DIMS)^{41, 42, 43, 44, 45, 46, 47, 48, 49, 50} that uses concepts from stochastic differential equations⁵¹ to create a family of independent transitions that together define the likelihood of different pathways and the kinetics of the transition with sufficient sampling. However, similar to the RMS based methods, the DIMS method requires a progress variable for use during the computed transitions and to create the biasing and its correction for an unbiased estimate of pathways, kinetics, and states.

In this paper, we describe the use of effective transfer entropy for the determination of a reduced set of degrees of freedom that can be used to define order parameters behind large scale conformational change. Our approach combines insights from the physics of non-linear time-series analysis, dimensionality reduction, and the chemical physics of protein motions on a complex energy surface to enable the dynamics of the complex system to define an order parameter candidate. This improves on other methods for the determination of order parameters where the candidate order parameter was inferred from empirical analysis of the static structure or simply assumed to correlate with the RMS between two different states. In the calculations to follow, we mainly use the receiver domain of nitrogen regulatory protein C (NtrC) (Fig. 1), in addition, we have performed steered molecular dynamics and checks of the implementation on the glucose-galactose binding protein (GGBP).

Figure 1.

Lowest frequency mode from PCA analysis for the inactive-state of NtrC.

PRINCIPAL COMPONENT ANALYSIS

The method of principal component analysis (PCA) has been used in the analysis of protein motions for many years.^{18, 22, 52, 53, 54, 55, 56, 57} This approach depends on the determination of a set of effective collective modes that define the complex motions that have been seen in the dynamics.⁵² While the initial excitement over the method as a way to sample on longer time-scales seems to have faded, there remains much effort to use this approach as a tool for the analysis of conformational change. A caution in that analysis has been the suggestion that PCA may lead to significant systematic error when there are multiple stable states separated by a large barrier.⁵³

To compute the PCA modes a MD trajectory is used along with the determination of the average fluctuations in the simulation. Then, from the MD trajectory $\vec{q}\left(t\right)=(q_1\left(t\right),q_2\left(t\right),...,q_{3N}\left(t\right)))$ of a protein with N atoms, the covariance matrix σ is built as follows:

$$\sigma =⟨(\vec{q}\left(t\right)-⟨\vec{q}\left(t\right)⟩)(\vec{q}\left(t\right)-⟨\vec{q}\left(t\right)⟩)⟩,$$ (1)

where the brackets (⟨…⟩) denote time averages. The orthonormal basis vectors (principal components/PC) ${\vec{\eta }}_{\alpha }$ are determined by the eigenvalue problem ${\lambda }_{\alpha }{\vec{\eta }}_{\alpha }=\sigma$.

The lowest frequency modes from PCA are normally associated with slow, collective motions and have been used to try and predict intermediate states.²⁰ Figure 1 depicts the lowest frequency mode obtained by applying Eq. 1 and, solving the eigenvalue problem for our 600 ns trajectory of NtrC. On this plot the porcupine spines are located at the C_α atoms and their magnitude and direction shows the type of motion involved in the mode.

To connect the PCA modes with conformational transitions between two structures, we use the involvement coefficient. This is defined in the following way. For a given mode α, the involvement coefficients (IC) is

$${\nu }_{\alpha }=\Vert {\vec{\eta }}_{\alpha }·({\widehat{q}}^A-{\widehat{q}}^B)\Vert ,$$ (2)

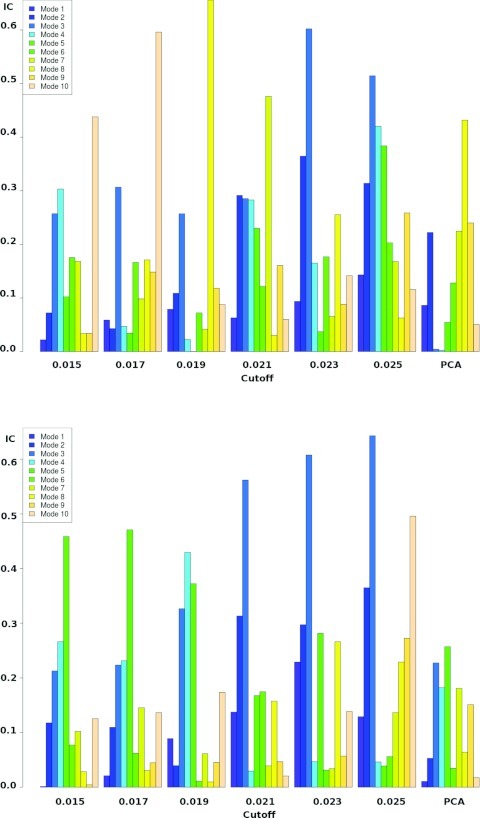
where ${\widehat{q}}^{A,B}$ indicates the set of normalized coordinates (${\widehat{q}}^{A,B}·{\widehat{q}}^{A,B}=1$) that represent the active-state and inactive-state conformations, respectively. Therefore, the ICs measure the amount of overlap between a principal component and the direction defined by the displacement vector between structures. In the case of hinge-bending motions, PCA shows higher values for the ICs compared to those from more complex motions. For instance, in the case of Adenalyte Kinase (AdK), the ICs for the first two modes are 0.49 and 0.63, respectively,^{58, 59} thus it is possible to characterize most of the transition just by using these two modes. In a previous study, we explored the fact that the structural difference between the apo and the holo states of AdK are almost completely captured by linear correlations within our DIMS framework in order to elucidate ensembles of candidate pathways;⁴¹ in a similar way, another study⁶⁰ was able to obtain intermediate states of the AdK transition by computing the normal modes from an elastic network model during short simulations (≈10¹ ps).

In the case of NtrC, the ICs are much lower (Fig. 4), in consequence the directions of the first PCs of both stable states are not pointing directly towards the other end state and therefore are not characterized by linear correlations. What is more, in another study, by using a set of order parameters based on observations of both stable structures, it was possible to obtain higher ICs values.⁵⁹ These order parameters involve only localized regions of the system and are proposed in an orderly series of events, that is, by using a single order parameter it is not possible to characterize the whole transition between the two states.

Figure 4.

Involvement coefficients for the two states of NtrC for different cutoffs D_cutoff.

One of the ideas behind our goal of looking for an order parameter is that a few degrees of freedom dominate part of or the entire transition, while the rest of the system would follow. Therefore finding an order parameter is equivalent to locating such leading modes. In this paper, we use an information theoretical approach to identify the leading modes by measuring the transfer entropy between pairs of residues. The more dominant residues are those that transfer the largest amount of entropy to the rest of the system.

INFORMATION FLOW IN PROTEINS

The networks of interactions between atoms and residues define the web of dependencies and patterns of dynamic coupling between domains in a protein, characterized by the directed flow of information spanning multiple spatial and temporal scales. An initial application of transfer entropy to DNA binding proteins was the first to apply the asymmetry of information transfer to protein molecular motions.⁶¹ Let X be the time series for the center of mass of the ith residue and, p(X) its probability distribution. Therefore it is possible to measure the average number of bits needed to optimally encode independent draws by using the Shannon entropy H_X = −∑_xp_xlog p(x),^{62, 63} where the sum extends over all the states that X can reach.

Transfer entropies

For a residue j ≠ i with a center of mass Y and, probability distribution p(Y); one could say that its trajectory is independent of that of residue i if

$$p\left(y_{n+1}\right|y_n)=p\left(y_{n+1}\right|y_n,x_n),$$ (3)

where p(y_{n + 1}|y_n) is the conditional probability to find residue j at state y_{n + 1} given its past y_n, …, y₁ and p(y_{n + 1}|y_n, x_n) is the conditional probability to find residue j at state y_{n + 1} given the past of both i and j. In the case where there is not a flux of information from X to Y then Eq. 3 is correct. On the other hand, in the event that there is flux of information in any direction, the divergence from correctness of Eq. 3 can be quantified by the Kullback-Leibler entropy⁶⁴ hence defining the transfer entropy,⁶⁵

$$T_{X\to Y}=\sum p(y_{n+1},y_n,x_n)\log \frac{p\left(y_{n+1}\right|y_n,x_n)}{p\left(y_{n+1}\right|y_n)}.$$ (4)

The transfer entropy between i and j is minimum and equal to zero when the two residues are independent and there is a maximum and equal to the entropy rate,

$$h_Y=-\sum p(y_{n+1},y_n)\log p\left(y_{n+1}\right|y_n),$$ (5)

when the residues are completely coupled. In order to minimize artifacts within the time series, we use the normalized effective transfer entropy given by^{66, 67}

$$T_{X\to Y}^E=\frac{1}{h_Y}\left(T_{X\to Y}-\frac{1}{N_{\mathrm{trials}}}\sum _{n=1}^{N_{\mathrm{trials}}}{T}_{X_{\mathrm{surrogate}}\to Y}\right),$$ (6)

where the second term is the average transfer entropy from N_trials surrogated samples of X, to Y.

The set Γ of most dominant residues

The total flux between two residues X and Y, can be calculated by the equation,

$$D_{X\to Y}=T_{X\to Y}^E-T_{Y\to X}^E.$$ (7)

Residues are selected according to the following rules: i is selected if D_{X → Y} > 0, residue j is selected if D_{X → Y} < 0 and, if D_{X → Y} = 0 then no residue is selected. The set of most dominant residues Γ is then defined as the set of residues that follow the rules above and also that are above a fixed cutoff |D_{X → Y}| ⩾ D_cutoff.

EXPERIMENTS WITH GGBP

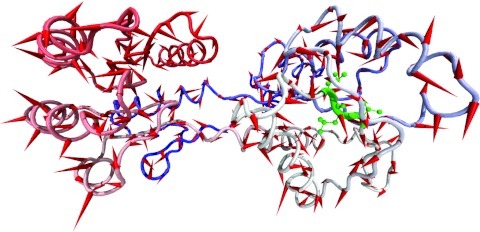
To verify that our implementation was correct, we performed analysis of coupled chaotic Ulam maps, for Henon maps and for autoregressive processes. In addition, as a more challenging test case, we used the Glucose-galactose binding protein (GGBP).⁶⁸ The two domains of GGBP exhibit a 0.5 rad hinge opening motion from one state to the other. The structure of the open state for an unbound glucose-galactose binding protein (GGBP) was crystallized by Borrock et al. (PDBID:2FW0) (Ref. ⁶⁸) at 1.55 Å. For the purpose of testing we used both DIMS transitions and we applied a constant pulling force along the line determined by residues Phe:142 and Leu:144 to create a system with a known directional change (highlighted in green in Figure 2). The size of this force was very small, sufficiently so that inspection of unsteered versus steered simulations in visual molecular dynamics (VMD)⁹⁰ would look identical. Thus, the applied force was meant only to enable us to simulate a situation with a clear set of degrees of freedom that lead and others that should lag, rather than a simulation that was dramatically and artificially shifted too strongly to a non-equilibrium situation.

Figure 2.

A pulling force is applied along the line defined by residues Phe:142 and Leu:144 (highlighted in green). The arrows in red represent the modes determined from a PCA of the pulling trajectory.

As a comparison point for our methods, we performed a PCA analysis over the trajectory generated by this same pulling along the residues Phe:142 and Leu:144. With the transient nature of the pulling, it can be seen how PCA is unable to detect the pulling direction (Figure 2). We now describe the data treatment and some results from our initial testing for the transfer entropy analysis that we propose.

Time series treatment

The time series from MD describing the atomic motions of proteins are generally double precision real-valued entries. Previous work on the application of time-series analysis has shown that to determine the joint probability densities in Eq. 4, from real valued data is not only computationally expensive but unnecessary. For example, it has been shown that the amplitude of collective excitations, representing correlated global motions in the protein, samples multicentered distributions.²⁰ Therefore, although single or double precision arithmetic is necessary for the stability and accuracy of the simulations themselves, the accuracy of the analysis does not require this same level of precision. This can greatly aid the determination of the probability distributions while greatly reducing noise and increasing computational efficiency. We optimize our implementation by incorporating high performance computing techniques (massively parallel calculations extended over thousands of cores) and by applying dimensionality reduction and data mining techniques that we briefly describe in the following sections. In other applications of transfer entropies^{61, 66, 67, 69, 70} discretization of the data is performed mainly by using symbolization techniques. In some cases the discretization maps the data to a single bit time series (spikes), for example in the situations where this analysis has been applied to data from neurophysiological in epilepsy patients.

Piecewise aggregate approximation (PAA)

A time series $\vec{q}\left(t\right)=(q_1\left(t\right),q_2\left(t\right),...,q_{3N}\left(t\right)))$ of length n can be represented by a second time series $\vec{Q}\left(t^{\prime }\right)=(Q_1\left(t^{\prime }\right),Q_2\left(t^{\prime }\right),...,Q_{3N}\left(t^{\prime }\right)))$ of length w < n, where each element $\vec{Q}\left(t^{\prime }\right)$ is computed according to⁷¹

$$\vec{Q}\left(t^{\prime }\right)=\frac{1}{\Delta t}{\int }_{t^{\prime }}^{t^{\prime }+\Delta t}\vec{q}\left(t\right)\mathrm{d}t,$$ (8)

where Δt = n/w. In other words, each vector of the time series $\vec{Q}\left(t^{\prime }\right)$ is simply the average, over a time range Δt, of the time series $\vec{q}\left(t\right)$. When Δt is constant, PAA can be seen as an attempt to approximate the original time series with a series of linear functions. Other approaches of PAA include using an adaptive mechanism to adjust Δt according to certain rules, i.e., defining a threshold such that σ(t = T) < ⟨q(t) − ⟨q(t)⟩_{t = 1…T}⟩_{t = 1…T}. For all calculations we set the time range Δt = 0.1 ns.

Transfer entropies from DIMS trajectories

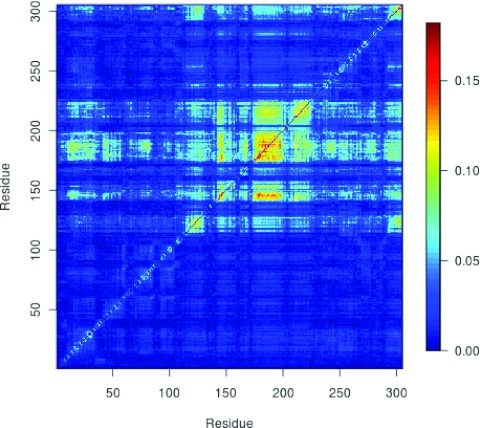
In previous work, we generated a set of transitions for GGBP;⁴⁴ the simulations were carried out using CHARMM27FF with crossterm map (CMAP)⁹¹ (Ref. ⁷²) with our implementation of DIMS and using an implicit solvent model (ACE2).⁷³ The rotational and translational degrees of freedom were removed by rms fitting the target structure to the evolving system and, the alignment atoms were selected on the N-terminal domain (Residues 111 to 252 and, 293 to 305). By applying our transfer entropy analysis we were able to identify the key residues in the DIMS transition (Figure 3). The results show that the leading residues for the transition are located in the three-segment hinge that connects the N- and C-termini 3.

Figure 3.

Transfer entropies computed for DIMS trajectories for GGBP.

FINDING THE LEADING MODES ON NTRC

The structures of the inactive-state and active-state conformations of NtrC have been solved by NMR.^{74, 75, 76} At room temperature NtrC samples both conformational states, however after phosphorylation the active states dominate the ensemble set of populations. Recent studies suggest that the transition pathway between the two conformations can be decomposed in a series of segmented progress variables (order parameters).⁵⁹ For this study both states were solvated in box of dimensions 20 Å × 20 Å × 20 Å with TIP3 waters, equilibrated for 15 ns; the total number of atoms, including solvent and ions, is 12 168 and 13 688 for the active and inactive states respectively. Production runs were performed for 600 ns using NAMD2.7 (Ref. ⁷⁷) at NICS-Kraken. Analysis of the trajectories was executed using our code at NCSA-Abe/Lincoln.

Computing the modes

A key insight is that the atoms with the strongest leading effective transfer entropy can be used as a subset of degrees of freedom to define collective modes that are new candidate order parameters. To accomplish this goal, once a cutoff and a time-length for the interrogation of the dynamics has been defined, is straightforward. The modes are determined by fluctuations of the leading effective transfer components and together describe a set of collective motions.

For the residues in the set Γ we compute the covariance matrix as in Eq. 1 over the full trajectory and obtain a set of modes ${\vec{\eta }}_{\alpha }^{\prime }$. The involvement coefficients (Eq. 2) for different values of the cutoff D_cutoff are presented in Figure 4. As the cutoff increases fewer residues are selected as dominant, however, the involvement coefficients are clearly increasing. This suggests that the most dominant modes ${\vec{\eta }}_{\alpha }^{\prime }$ are pointing towards the end structure. Since the modes are transferring entropy to the entire system biasing along these modes would result in a collective bias for the entire system.

Since η_α is an orthonormal base we can define the cumulative involvement coefficient μ_α of the first α principal components as

$${\mu }_{\alpha }=\sum _{i=1}^{\alpha }{\nu }_i^2,$$ (9)

and measure how much of the overall difference is accounted by the first α modes.

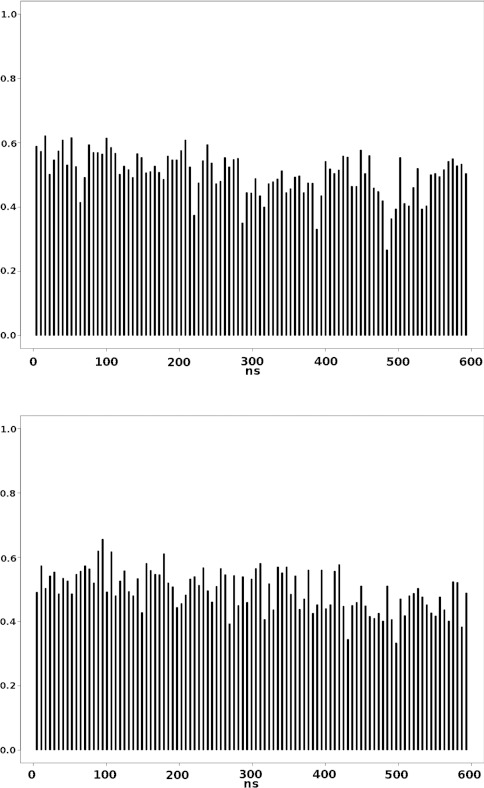
This last figure suggests that relatively short molecular dynamics simulations are converging onto the important degrees of freedom determined by the effective transfer entropy analysis (Fig. 5). It suggests that an algorithm for the use of the effective transfer entropy modes can be readily defined in CHARMM or other computer code. In that algorithm the lowest frequency modes would be the direction of biasing that is applied through DIMS or another approach (e.g., transition path sampling or targeted MD). The modes would be defined by a relatively short unbiased simulation and then followed by biasing for a similar amount of time to the mode determination. For example, this figure would suggest that 5 ns of sampling for the effective modes followed by 5 ns of sampling along the modes could be used to improve the confidence that the most important intermediate states are being reached. This would then be repeated with unbiased sampling including light restraints on the backbone atoms to define a new set of effective transfer entropy modes. By continuing this process until the end state is reached, a transition pathway would be defined. If this process is then repeated for multiple starting points with various sampling windows and different random number seeds, along with a random selection of cutoffs and mode selections, then a good sampling of the intermediate space should be obtained.

Figure 5.

Cumulative involvement coefficient as a function of time (ns) for the first α = 20 modes.

COMPARISON TO OTHER METHODS AND ASSUMPTIONS

It needs to be emphasized that the proposed method requires dynamic information for the calculation. The time-series comparisons that underlie the proposed method may be sensitive to the system choice and the total amount of information that is captured. Our results in this paper suggest that the total time needed to capture the leading and lagging degrees of freedom is much less than we might have initially assumed. But, the appropriate amount of time needed to collect dynamic information before a calculation of the effective transfer entropies is still an open question. It should be noted that there should be no pulling forces applied or other biasing if the suggestions for an order parameter are to correctly reflect motions from the unbiased state towards other directions. In a similar way, though we have assumed that two conformations are available for the calculation of the utility of the approach for conformational change, there is no restriction to two or more conformations for the calculation of the effective transfer entropy. Instead, the method outlined suggests that an effective order parameter that leads out from a particular conformational state may be defined by this approach and does not require that the order parameter, by itself, lead towards a specific endpoint. In that regard, then, the approach may also be helpful for sampling on multiple intermediate states that connect different larger conformational states. We have yet to fully test the utility of this thought, so the directions that the order parameter may lead could be coupled, as we outlined here, to computational efforts for understanding conformational change between states, or for the purposes of enhancing sampling away from one state and towards other, yet unexplored, states.

In addition, the method should be contrasted with other approaches that have attempted to determine subsets of states from long molecular dynamics data and then by extension to define intermediates and their connections to the states.⁷⁸ For example, the Head-Gordon group has suggested using instantaneous normal modes to define changes in the AdK system.⁶⁰ This relates to efforts using modes defined by essential dynamics analysis to sample on conformational change in the same system,⁷⁹ to work with Monte Carlo methods and collective modes^{80, 81} as well as to efforts using amplified collective modes.⁸² Our work on AdK suggests that the conformational change is much simpler than in NtrC, and that the optimal order parameter may be easier.⁴¹ Other groups have emphasized that cracking of secondary structural elements may be important for conformational change in AdK and should be considered in conformational change.⁸³ The current approach does not make any assumptions about the nature of the secondary structure of the domain motions needed for the conformational change.

In a related way, there is research from the Pande and other groups that is attempting to define Markov models based on long-dynamics simulations. In principle, the Markov models should also define the reduced descriptors needed for transitions between the Markov defined states. In practice, the approach outlined in this contribution may help with improving sampling between the states defined by the Markov models, since the intermediates may well be undersampled relative to the states themselves.⁸⁴

Work within the Thorpe group has suggested that conformational change can be considered in terms of the pebble game and degrees of freedom that are available from a static structure.⁸⁵ In that regard the current contribution may be thought of as finding those most important subsets of degrees of freedom that lead the change, as opposed to defining solely the available subset. It may be fruitful to define more fully what types of correlated motions are most likely to lead to order parameters and what less likely. This would be another interesting extension of this work and would complement work on static structural analysis. In a somewhat similar manner, simpler chemical systems have suggested that algorithms can be designed to follow peaks and valleys on adiabatic surfaces based on a single structure to define transition states.^{86, 87} Others have suggested that an improved understanding of the connections between temperature and transitions would aid an understanding of the intermediates.⁸⁸

Finally, there is a growing body of work addressing the limitations of principal component analysis and this suggests that there may be connections between the effective transfer entropy and the improved resolution of non-Gaussian analysis of long molecular dynamics trajectories.²⁶ While the nature of these connections remains to be understood, it suggests that the non-Gaussian components of motion may be the most important determinants of change out from the system. This could also tie into work from the Clementi group that is trying to find dimensionally reduced representations of dynamic conformation space.⁸⁹

CONCLUSIONS

A molecular understanding of how protein function is related to protein structure will require an ability to understand large conformational changes between multiple states. Unfortunately these states are often separated by high free energy barriers and within a complex energy landscape. This makes it very difficult to reliably connect, for example, by all-atom molecular dynamics calculations, the states, their energies, and the pathways between them. A major issue needed to improve sampling on the intermediate states is an order parameter – a reduced descriptor for the major subset of degrees of freedom – that can be used to aid sampling for the large conformational change. In this paper, we present a way to combine information from molecular dynamics using non-linear time series and dimensionality reduction, in order to quantitatively determine an order parameter connecting two large-scale conformationally distinct protein states. The results presented show that the leading modes can be computed from short simulations. This new method suggests an implementation for molecular dynamics calculations that may dramatically enhance sampling of intermediate states.