Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2012 Apr 24;39(5):2765–2770. doi: 10.1118/1.3701775

Measurement of magnetic nanoparticle relaxation time

John B Weaver 1,a), Esra Kuehlert 2
PMCID: PMC3350541  PMID: 22559648

Abstract

Purpose: Nanoparticle relaxation time measurements have many applications including characterizing molecular binding, viscosity, heating, and local matrix stiffness. The methods capable of in vivo application are extremely limited. The hypothesis investigated by the authors was that the relaxation time could be measured quantitatively using magnetic spectroscopy of nanoparticle Brownian motion (MSB).

Methods: The MSB signal (1) reflects the nanoparticle rotational Brownian motion, (2) can be measured from very low nanoparticle concentrations, and (3) is a function of the product of the drive frequency and the relaxation time characterizing Brownian motion. To estimate the relaxation time, the MSB signal was measured at several frequencies. The MSB signal for nanoparticles with altered relaxation time is a scaled version of that for reference nanoparticles with a known relaxation time. The scaling factor linking the altered and reference MSB measurements is the same factor linking the altered and reference relaxation times. The method was tested using glycerol solutions of varying viscosities to obtain continuously variable relaxation times.

Results: The measured relaxation time increased with increasing viscosity of the solution in which the nanoparticles resided. The MSB estimated relaxation time matched the calculated relaxation times based on viscosity with 2% average error.

Conclusions: MSB can be used to monitor the nanoparticle relaxation time quantitatively through a scale space correlation of the MSB signal as a function of frequency.

INTRODUCTION

The relaxation time is a measure of a nanoparticle’s (NP) rotational freedom. The rotational freedom has been used to characterize several phenomena: viscosity, chemical binding, and the stiffness of the matrix to which NPs are bound. Many of these phenomena have important biological applications but none can be measured in vivo at depth. For example, the stiffness of the cytoskeleton has been measured using SQUID measurements of the relaxation time of magnetic nanoparticles bound to integrins on the cell surface.1 The signaling pathways secondary to mechanical stiffness have been extensively studied and suggest that stiffness is linked to cell motility, angiogenesis, and cell adhesion that are all key to carcinogenesis.2 The importance of chemical binding in biology is fairly obvious, but two specific classes of binding have outsized importance in medical applications. Antibody binding is critical to many diagnostic and therapeutic applications, and “personalized medicine” relies largely on the specificity of antibody binding. Pharmaceutical binding determines its function. Binding can be measured optically in vitro and in vivo at very shallow depths.3 Other in vitro tools exist4, 5 and more are being developed.6, 7 Methods of estimating binding in vivo using a model of the kinetics and the activity of radioactive agents present at various times following injection exist but depend heavily on assumptions to solve the transport equations and can never distinguish binding affinity from the number of available binding sites8 or transport effects.9 Viscosity also has important medical applications.10, 11 The methods of measuring viscosity at small scales in vitro are also being developed.12 There are currently no methods of measuring the relaxation times capable of in vivo application at depth that do not make assumptions for which there are no measured data. This paper demonstrates quantitative measurement of the relaxation time using a method capable of in vivo application.

Magnetic spectroscopy of NP Brownian motion (MSB)13 is a new method that has been used to measure temperature with high accuracy14 and is sensitive to viscosity15 and bound state.16 MSB estimates properties related to rotational Brownian motion. The basic measurement is of the harmonics of the magnetization produced by magnetic nanoparticles in a sinusoidal applied magnetic field. The harmonics reflect the shape of the magnetization. The magnetization is a slightly distorted sinusoid because the magnetization is nonlinear with applied field. On a microscopic scale, the distortion of the magnetization as it approaches saturation is caused by the inability of the NPs to align with the applied field because of thermal effects. Therefore, the shape of the magnetization reflects a balance between the magnetic forces tending to align the NPs and rotational Brownian motion tending to randomize their directions. MSB generally uses the ratio of the fifth over the third harmonics as a concentration-independent measure. Because there are no other signals at the frequencies of the higher harmonics, they can be measured with very high sensitivity. It has been shown in other applications17 that the higher harmonics can be measured in vivo at nanogram NP concentrations,18 so MSB should function in vivo as well as in vitro.

Because MSB is sensitive to many phenomena, the key to extracting quantitative estimates from MSB is to isolate calibration data for the desired phenomena. For example, temperature has been measured quantitatively using calibration data obtained by sweeping the amplitude of the applied field.14 The calibration curve is valid for a given set of state variables including size distribution, solvent viscosity, and bound state. In this application, we sweep the frequency of the applied field to provide calibration data necessary to quantify the change in relaxation time caused by viscosity or binding. This is an extension of our previous multifrequency work19, 20 and has been anticipated by similar methods.21 In this report, we used the known viscosities of different glycerol solutions to validate the method.

METHODS

Theoretical basis

The magnetization formed from an ensemble of magnetic NPs can be described using the Fokker–Planck, Smoluchowski, equation for the distribution of magnetization directions. The magnetization’s time dependence allows us to scale the MSB signal as a function of frequency to estimate the relaxation time. For an alternating applied field, the magnetization, M(t), is a function of the product of the frequency, ω, and relaxation time, τ, of the magnetization. This is true for noninteracting NPs (Ref. 22) as well as interacting NPs (Ref. 23) in small and large alternating fields. It is explicit in the linear Debye approximation15, 18, 24, 25 for small applied fields

M(t)=χoHo(11+(ωτ)2cos(ωt)+(ωτ)1+(ωτ)2sin(ωτ)), (1)

where t is time, χo is the equilibrium susceptibility, and Ho and ω are the amplitude and frequency of the applied magnetic field, respectively. The relaxation time of the magnetic nanoparticles, τ, characterizes the ability to retain the magnetization direction after the aligning field is removed. It reflects the influences of Brownian and Neel relaxation, although the Brownian component almost always dominates for the frequency range (290–2110 Hz) and nanoparticle sizes we employ. The functional dependence on the ωτ product is true for the more general nonlinear formulations as well as the linear Debye formulation.

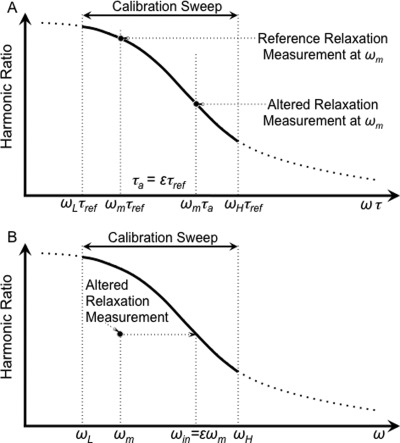
The method we are introducing rests on the functional dependence on the ωτ product. Changes in the MSB signal produced by increases in one variable can be exactly compensated by decreasing the other variable. Let ƒ(ωτ) be the ratio of the fifth over the third harmonics as a function of the ωτ product for a given ensemble of NPs, τref is the relaxation time of NPs in the reference state, and τa is the relaxation time of NPs in the altered state. A calibration curve taken with NPs in the reference state would be ƒ(ωj τref) ωj ∈ [ωL, ωH]. The measurement of the NPs in the altered state at one or more frequencies, ωm, would be ƒ(ωm τa). τa can be related to τref with a scaling factor

τa=ɛτref. (2)

A scale change in frequency by ɛ achieves equal harmonic ratios: ƒ(ωm τa) = ƒ(ɛ ωm τref). The process is shown graphically in Fig. 1.

Figure 1.

Figure 1

Open in a new tab

The method estimating the relative relaxation time quantitatively. The MSB signal (a) as a function of the product of frequency and relaxation time, ωτ, and (b) as a function of frequency, ω. (a) The harmonic ratio for an ensemble of NPs over a range of ωτ. The harmonic ratio for reference NPs and NPs with altered relaxation both taken at one frequency, ωm, are shown for comparison. The altered relaxation time, τa, is ɛτref. (b) The calibration curve and the signal with the altered relaxation as a function of ω. The relative relaxation time, τa/τref = ɛ can be estimated as the scaling factor aligns the MSB signal for the altered relaxation with the reference curve.

The least squares estimate of the scale change necessary to match the harmonic ratios for the altered relaxation with that for reference relaxation can be obtained. The interpolated frequencies, ωin, at which the harmonic ratio for the altered state equals that of the reference state, ƒ(ωm τa) = ƒ(ωin τref), can be obtained by spline interpolation. The least squares estimate of the scale, ɛ, is

ɛ=ΣωmωinΣωmωm. (3)

The interpolation is simple when (a) ƒ(ωτ) is monotonic which is generally true for reasonably narrow size distributions and (b) the calibration curve is sampled over a wide enough range of frequencies so ωL < ωin < ωH. The size distribution for which the method is accurate depends on the NP average size and the frequency range and amplitude of the applied field. Alternatively, the calibration curve and the altered data can be fit to polynomials and the least squares fit accomplished on the coefficients. Because each of the polynomial terms is related by ɛ to the power of the polynomial term, the optimization must be iterative for polynomials higher than linear. Clearly, conditioning limits the power of the polynomial used. Polynomial estimation is useful if ωa < ωLor ωa > ωH, which happens if the frequency range swept is too narrow.

The energy change associated with the change in relaxation time can also be estimated from the Stokes–Einstein formulation, which relates the relaxation time for Brownian rotation to the ratio of the work necessary to rotate the NP in a viscous fluid and the thermal energy

τ=3ηVHkT, (4)

where VH is the hydrodynamic volume and η is the viscosity. This approximation is well recognized and has been shown to work well. Therefore, the scaling factor ɛ can be thought of as the ratio of the effective binding energy of the altered state over the effective binding energy of the reference state. Although this is only valid for spherical NPs and isotropic binding such as hydrogen bonding which dominates the viscosity in water, one expects it to hold for randomly oriented anisotropic bonds as well.

Experimental methods

The method described was tested using the viscosity of glycerol solutions that are related to the relaxation time with the Stokes–Einstein relationship in Eq. 4. The solution with no glycerol was used as the reference state and each concentration of glycerol provided another altered state.

Two NP samples were used: 1250 μg of 100 nm bionized nanoferrite (BNF) NPs coated with starch (Micromod Partikeltechnologie GmbH, Rostock-Warnemuende, Germany) in 200 μl of PBS and 20 μg of 40 nm iron oxide NPs coated with PEG (Ocean NanoTech, Springdale, AR) in 200 μl of buffer. The mean hydrodynamic diameter measured using the Malvern (Worcestershire, UK) ZetaSizer Nano ZS was 113 nm for the 100 nm NPs and 65 nm for the 40 nm NPs. A sample of NPs was drawn and diluted to provide the reference sample. Increasing amounts of glycerol were added to the sample to increase the viscosity for the same ensemble of NPs. The percentage of glycerol was calculated based on weight and was used to calculate the viscosity by interpolating from measured values.26

Three data sets were accumulated: (1) To measure precision, four consecutive measurements were taken for each glycerol concentration for one sample of 100 nm NPs. (2) To measure accuracy, 12 samples of 100 nm NPs were measured for 7 glycerol concentrations. (3) A sample of 40 nm NPs was measured in two glycerol concentrations to evaluate the effects of NP size.

The spectrometer used to measure the magnetization was a modified version of the one described previously13 and is diagramed in Fig. 2. Briefly, the drive field was generated using a pure sinusoidal voltage, generated by an SR830 phase-locked amplifier (Stanford Research Systems, Sunnyvale, CA) and amplified by an audio power amplifier (QSC PL 236) driving a resonant coil. The only change from the previously described system was the addition of a computer-controlled relay bank used to switch different capacitors into series with the drive coil to change the resonant frequency of the coil. Seven capacitors were used to obtain the seven resonant frequencies: 290, 510, 755, 1050, 1270, 1740, and 2110 Hz. The applied magnetic field induced a magnetization in the NP sample that was recorded by the pickup coil. The pickup coil was connected in series with a balancing coil with opposite polarity and placed far from the NP sample, so it only recorded the drive field. The pickup coil and balancing coil combination effectively canceled the current generated by the drive field. The phase-lock amplifier was used to amplify and record the harmonics generated by the NP sample. Another coil was used to monitor and adjust the amplitude of the applied field, which was maintained at 10 mT/μo for all frequencies.

Figure 2.

Figure 2

Open in a new tab

Diagram of the apparatus used to measure the MSB signal from samples of nanoparticles. The pickup coil and balancing coil were fixed inside the coil producing the drive field. The pickup and balancing coils were in series and the output was measured using the phase-lock amplifier. The computer controlled the phase-lock amplifier and the switched capacitors, which together determined the drive field amplitude and frequency. The computer also sampled the phase-lock amplifier measurements of the harmonics. The ADC card in the computer sampled the drive field as the phase-lock amplifier sampled the harmonics to maintain the field at the desired amplitude.

RESULTS

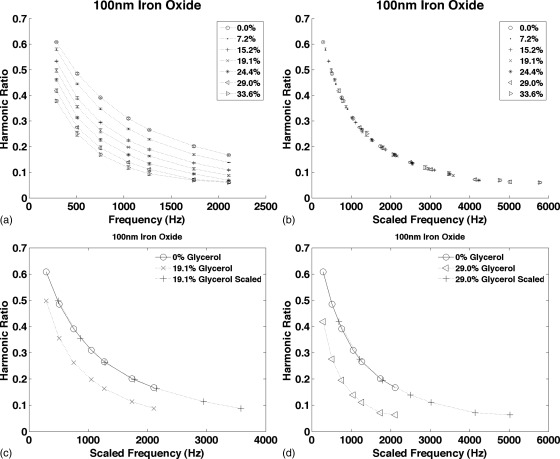
Figure 3 shows the harmonic ratio from starch coated 100 nm iron oxide NPs in water and in six glycerol solutions plotted as functions of frequency in Fig. 3a and as a function of the scaled frequency, ɛω, in Fig. 3b. When plotted as a function of ɛω, all the data fall on the same curve. Figures 3c, 3d compare the curves for two glycerol concentrations plotted as functions of ω and ɛω compared to the 0% glycerol reference curve. The average error in the MSB scaling factor was 3.0%.

Figure 3.

Figure 3

Open in a new tab

The harmonic ratio from starch coated 100 nm iron oxide NPs measured at seven frequencies between 290 and 2110 Hz. (a) The signal from the same NPs was measured in PBS and as more glycerol was added to the sample to increase the viscosity. The curves for each glycerol concentration are shown. (b) The curves in (a) were scaled plotted as a function of ɛω to demonstrate that all the curves are scaled version of the same function. (c) The 19.1% glycerol curve plotted as a function of ω and ɛω compared to the 0% glycerol curve. (d) The 29% glycerol curve plotted as a function of ω and ɛω compared to the 0% glycerol curve. Each measurement was taken four times; the average is plotted and the error bars show the standard deviation.

Four identical measurements were taken of each glycerol concentration, so precision was calculated from the 16 estimates of the scaling factor for each glycerol concentration. The precision averaged 1.91%. The precision was best, 1.4%, for low glycerol concentrations where the MSB signal at most of the frequencies was within the range of MSB values for the reference solution. The precision was worst, 3.0%, for high glycerol concentrations where MSB values at only two frequencies were within the range of MSB values for the reference solution.

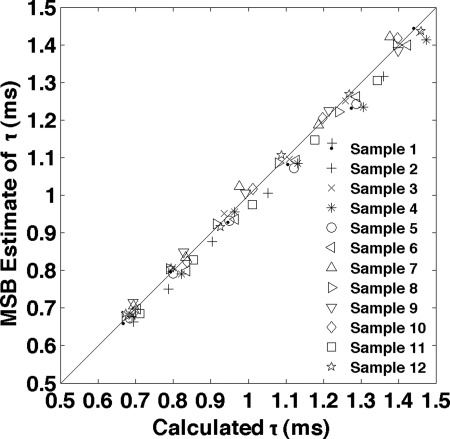
Measurements were collected for twelve 100 nm NP samples, each of which had six glycerol concentrations as well as pure water (0% glycerol). The MSB relaxation times, for each solution were plotted vs that calculated from the glycerol concentration in Fig. 4. The mean error was 1.8% and the correlation coefficient was 0.9972 with very high significance (P-value was zero to machine accuracy) supporting the linear relationship between the MSB measured relaxation and the relaxation calculated from the glycerol concentration.

Figure 4.

Figure 4

Open in a new tab

The data produced for the sample in Fig. 3 were taken for 12 other samples. Each sample had six glycerol concentrations as well as pure PBS (0% glycerol). All 72 relaxation times calculated from the MSB measures are plotted as a function of the relaxation time calculated from the glycerol concentrations. The RMS error was 2.51% and the correlation coefficient was 0.9972 with very high significance (P-value was zero to machine accuracy) supporting the linear relationship between the MSB relaxation times and the ones calculated based on glycerol concentration. The reproducibility estimated from repeated measurements of an identical NP sample in buffer averaged 1.25%. The reference relaxation time of NPs in PBS was based on temperature of 20 °C, viscosity of water at that temperature of 1.0019 mPa·s (Ref. 27), and effective NP diameter of 113 nm.

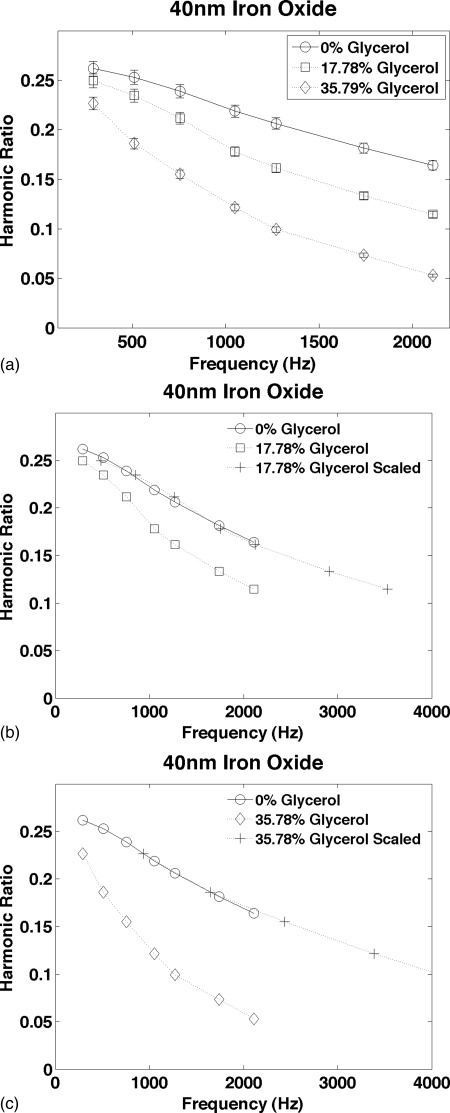
The results for the 40 nm iron oxide NP are shown in Fig. 5. The average error in the MSB relaxation time was 1.15%. The reproducibility of the individual measurements used to estimate the scaling factors was estimated from repeated measurements of an identical 40 nm NP sample in buffer; it averaged 2.8% compared to 1.5% for the 100 nm NPs. The difference in the reproducibility of individual measurements is roughly proportional to the amount of iron in the samples.

Figure 5.

Figure 5

Open in a new tab

The harmonic ratio measured from amphiphilic polymer coated 40 nm iron oxide nanoparticles in solutions of glycerol and water. The curves are presented in the same format as Figs. 3a, 3c. The reproducibility estimated from repeated measurements of an identical NP sample in buffer averaged 2.8%.

DISCUSSION

MSB is clearly very sensitive to relaxation time. However, it is challenging to obtain and relate calibration data that isolate the effects of relaxation time. The proposed method quantifies relaxation effects accurately.

The relative relaxation time calculated from MSB measurements was linearly related to that calculated from the viscosities with high significance indicating that there was little bias in the estimates of the relaxation time. The errors in the raw measurements at each frequency were not unduly amplified by the method used to calculate the relative relaxation times. The average error in the MSB relaxation times, 1% to 3%, resulted from 2% to 3% uncertainties in the individual measurements at each frequency. The relaxation time errors are predicated on the frequency range taken for the reference solution being large enough to allow the altered relation MSB measurements for at least one frequency to be within the range of MSB measurements in the reference data. The interpolation precludes direct propagation of error, but initial simulations showed that the uncertainties in the individual MSB measurements accounted for essentially all of the error in the relaxation times.

Faster updates can be obtained by using measurements at only one frequency for the solutions with altered relaxation times. Measurements at a range of frequencies are needed for the reference solution, but single measures are sufficient for the solutions with altered relaxation times. The average error for the 12 samples increased only marginally from 1.8% to 2.1% when only using one MSB measurement on the altered solution. The ability to take fast measurements allows dynamic processes to be monitored effectively.

The ratio of the harmonics has been used because it is a concentration-independent measure of the shape of the magnetization allowing estimates of relaxation times during concentration fluctuations as long as the size distribution of the ensemble does not change. The individual harmonics should also provide a measure of the relaxation time using the same method, but it would be sensitive to NP concentration so it would be more difficult to use in vivo.

The method is reasonably accurate for both nanoparticle sizes used indicating that NP size is not an important factor. However, in very limited experiments, the width of the size distribution is important. A very wide size distribution or extensive aggregation seems to cause the method to fail. We have not explored the effect, but it is possibly due to the use of the ratio of the harmonics rather than the harmonics themselves.

It should be pointed out that the method assumes that the relaxation time of the NPs in the original sample, the reference relaxation time, is known. If the reference relaxation time is not available, then the method only produces a relative change in relaxation time. Generally, Eq. 4 can be used to provide the reference relaxation time for almost all samples because the hydrodynamic volume can be measured optically and the viscosity for water at various temperatures is well known.

Relaxation times characterize effects ranging from viscosity changes to chemical binding. However, quantitating chemical binding is a more difficult task and has not been attempted yet. Viscosity is directly proportional to relaxation time, so the percentage errors for the estimation of viscosity directly are identical to those for relaxation time.

CONCLUSIONS

The MSB signal is very sensitive to changes in the rotational freedom of magnetic NPs. Relaxation time characterizes the rotational freedom and can reflect changes in viscosity, chemical binding, or matrix rigidity. The method proposed here allows the relaxation time to be quantified accurately. A range of relaxation times achieved using different viscosities of glycerol solutions were characterized with 2% average error. The method functioned using two different size NPs with relatively narrow size distributions. The accuracy was primarily limited by equipment imperfections rather than limitations in the theory. The harmonics measured in MSB are also used to image NPs in vivo in nanogram quantities, so MSB should be capable of measuring relaxation times in vivo as well.

ACKNOWLEDGMENT

This work was supported by NIH-NCI Grant No. 1U54CA151662-01.

References

  1. Wang N., Butler J. P., and Ingber D. E., “Mechanotransduction across the cell surface and through the cytoskeleton,” Science 260, 1124–1127 (1993). 10.1126/science.7684161 [DOI] [PubMed] [Google Scholar]
  2. Berrier A. L. and Yamada K. M., “Cell-matrix adhesion,” J. Cell. Physiol. 213, 565–573 (2007). 10.1002/jcp.21237 [DOI] [PubMed] [Google Scholar]
  3. Berk D. A., Yuan F., Leunig M., and Jain R. K., “Direct in vivo measurement of targeted binding in a human tumor xenograft,” Proc. Natl. Acad. Sci. U.S.A. 94, 1785–1790 (1997). 10.1073/pnas.94.5.1785 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Choo-Smith L. P., Edwards H. G., Endtz H. P., Kros J. M., Heule F., Barr H., J. S.Robinson, Jr., Bruining H. A., and Puppels G. J., “Medical applications of Raman spectroscopy: From proof of principle to clinical implementation,” Biopolymers 67, 1–9 (2002). 10.1002/bip.10064 [DOI] [PubMed] [Google Scholar]
  5. Schwieters C. D., Kuszewski J. J., Tjandra N., and Clore G. M., “The Xplor-NIH NMR molecular structure determination package,” J. Magn. Reson. 160, 65–73 (2002). 10.1016/S1090-7807(02)00014-9 [DOI] [PubMed] [Google Scholar]
  6. Baksh M. M., Jaros M., and Grove J. T., “Detection of molecular interactions at membrane surfaces through colloid phase transitions,” Nature (London) 427, 139–141 (2004). 10.1038/nature02209 [DOI] [PubMed] [Google Scholar]
  7. Chung S. H., Hoffmann A., Bader S. D., Liu C., Kay B., Makowski L., and Chen L., “Biological sensors based on Brownian relaxation of magnetic nanoparticles,” Appl. Phys. Lett. 85, 2971 (2004). 10.1063/1.1801687 [DOI] [Google Scholar]
  8. Innis R. B. et al. , “Consensus nomenclature for in vivo imaging of reversibly binding radioligands,” J. Cereb. Blood Flow Metab. 27, 1533–1539 (2007). 10.1038/sj.jcbfm.9600493 [DOI] [PubMed] [Google Scholar]
  9. Minchinton A. I. and Tannock I. F., “Drug penetration in solid tumours,” Nat. Rev. Cancer 6, 583–592 (2006). 10.1038/nrc1893 [DOI] [PubMed] [Google Scholar]
  10. Yarnell J. et al. , “Fibrinogen, viscosity, and white blood cell count are major risk factors for ischemic heart disease. The Caerphilly and Speedwell collaborative heart disease studies,” Circulation 83, 836–844 (1991). [DOI] [PubMed] [Google Scholar]
  11. Zurovsky Y., Mitchell G., and Hattingh J., “Composition and viscosity of interstitial fluid of rabbits,” Exp. Physiol. 80, 203–207 (1995). [DOI] [PubMed] [Google Scholar]
  12. Calero-DdelC V. L., Santiago-Quiñonez D. I., and Rinaldi C., “Quantitative nanoscale viscosity measurements using magnetic nanoparticles and SQUID AC susceptibility measurements,” Soft Matter 7, 4497 (2011). 10.1039/c0sm00902d [DOI] [Google Scholar]
  13. Weaver J. B., Rauwerdink A. M., Sullivan C. R., and Baker I., “Frequency distribution of the nanoparticle magnetization in the presence of a static as well as a harmonic magnetic field,” Med. Phys. 35, 1988 (2008). 10.1118/1.2903449 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Weaver J. B., Rauwerdink A. M., and Hansen E. W., “Magnetic nanoparticle temperature estimation,” Med. Phys. 36, 1822 (2009). 10.1118/1.3106342 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Rauwerdink A. M. and Weaver J. B., “Viscous effects on nanoparticle magnetization harmonics,” J. Magn. Magn. Mater. 322, 609–613 (2010). 10.1016/j.jmmm.2009.10.024 [DOI] [Google Scholar]
  16. Rauwerdink A. M. and Weaver J. B., “Measurement of molecular binding using the Brownian motion of magnetic nanoparticle probes,” Appl. Phys. Lett. 96, 033702 (2010). 10.1063/1.3291063 [DOI] [Google Scholar]
  17. Gleich B. and Weizenecker J., “Tomographic imaging using the nonlinear response of magnetic particles,” Nature 435, 1214–1217 (2005). 10.1038/nature03808 [DOI] [PubMed] [Google Scholar]
  18. Ferguson R. M., Minard K. R., and Krishnan K. M., “Optimization of nanoparticle core size for magnetic particle imaging,” J. Magn. Magn. Mater. 321, 1548–1551 (2009). 10.1016/j.jmmm.2009.02.083 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Weaver J. B. and Rauwerdink A. M., “Quantitation of nanoparticle concentrations in microscopic bound states,” Med. Phys. 37, 358 (2010). 10.1118/1.3469126 [DOI] [Google Scholar]
  20. Weaver J. B. and Rauwerdink A. M., “MSB estimation chemical binding affinity,” Proc. SPIE, Paper No. 7965-33 (2011).
  21. Wawrzik T., Remmer H., Ludwig F., and Schilling M., “Determination of core- and hydrodynamic size distribution by magnetic particle spectroscopy,” Biomed. Tech. 56, 59 (2011). [Google Scholar]
  22. Felderhof B. U. and Jones R. B., “Nonlinear response of a dipolar system with rotational diffusion to an oscillating field,” J. Phys.: Condens. Matter 15, S1363–S1378 (2003). 10.1088/0953-8984/15/15/305 [DOI] [PubMed] [Google Scholar]
  23. Felderhof B. U. and Jones R. B., “Mean field theory of the nonlinear response of an interacting dipolar system with rotational diffusion to an oscillating field,” J. Phys.: Condens. Matter 15, 4011 (2003). 10.1088/0953-8984/15/23/313 [DOI] [Google Scholar]
  24. Debye P., Polar Molecules (Dover, New York, 1929). [Google Scholar]
  25. Sánchez J. H. and Rinaldi C., “Rotational Brownian dynamics simulations of non-interacting magnetized ellipsoidal particles in d.c. and a.c. magnetic fields,” J. Magn. Magn. Mater. 321, 2985–2991 (2009). 10.1016/j.jmmm.2009.04.066 [DOI] [Google Scholar]
  26. Hodgman C., Handbook of Chemistry and Physics, 42nd ed. (The Chemical Rubber Publishing Co., Cleveland, OH, 1960). [Google Scholar]
  27. Swindells J. F., J. R.Coe, Jr., and Godfrey T. B., “Absolute viscosity of water at 20 °C,” J. Res. Natl. Bur. Stand. 48, 1–31 (1952). [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES