A scaling transformation for classifier output based on likelihood ratio: Applications to a CAD workstation for diagnosis of breast cancer

Abstract

Purpose: The authors developed scaling methods that monotonically transform the output of one classifier to the “scale” of another. Such transformations affect the distribution of classifier output while leaving the ROC curve unchanged. In particular, they investigated transformations between radiologists and computer classifiers, with the goal of addressing the problem of comparing and interpreting case-specific values of output from two classifiers.

Methods: Using both simulated and radiologists’ rating data of breast imaging cases, the authors investigated a likelihood-ratio-scaling transformation, based on “matching” classifier likelihood ratios. For comparison, three other scaling transformations were investigated that were based on matching classifier true positive fraction, false positive fraction, or cumulative distribution function, respectively. The authors explored modifying the computer output to reflect the scale of the radiologist, as well as modifying the radiologist’s ratings to reflect the scale of the computer. They also evaluated how dataset size affects the transformations.

Results: When ROC curves of two classifiers differed substantially, the four transformations were found to be quite different. The likelihood-ratio scaling transformation was found to vary widely from radiologist to radiologist. Similar results were found for the other transformations. Our simulations explored the effect of database sizes on the accuracy of the estimation of our scaling transformations.

Conclusions: The likelihood-ratio-scaling transformation that the authors have developed and evaluated was shown to be capable of transforming computer and radiologist outputs to a common scale reliably, thereby allowing the comparison of the computer and radiologist outputs on the basis of a clinically relevant statistic.

INTRODUCTION

Diagnostic computer aids that provide estimates of a lesion’s probability of malignancy (PM) are currently being explored as a way to improve radiologists’ performance in the task of diagnosing cancer. One way to evaluate the effect of computer-aided diagnosis (CAD) on radiologists’ performance is to perform an observer study in which radiologist observers are shown case images without and with the computer-aid and asked to give a rating between 0% and 100% that represents their confidence that each case or lesion is malignant.^{1, 2, 3, 4, 5, 6, 7} Such ratings are analogous to the PM ratings provided by some computer classifiers, in that both the computer and radiologist ratings are provided on a quasicontinuous ordinal scale between 0% and 100% (or equivalently, between 0 and 1), with higher ratings corresponding to greater probability of malignancy. Substantial variation among physicians in clinical probability-estimation tasks has been well known for some years—e.g., see Refs. ^{8, 9}. As we will show, different radiologists may “scale” such ratings quite differently. For example, some radiologists may tend to give ratings that are clustered at the lower and upper ends of the scale, while others may tend to give ratings that are spread in the middle of the scale.

The possibility that a radiologist gives ratings clustered in one way or another is an issue independent of the radiologist’s classification performance as described by a receiver operating characteristic (ROC) curve.¹⁰ In fact, ROC studies typically ignore classifier scale and focus on the scale-independent ROC curve and associated figures of merit, such as area under the curve, which quantify classification performance. However, a better understanding of a radiologist’s scale is of general interest. Differences in radiologists’ scales make it difficult to compare the confidence ratings provided by one radiologist with those of another or to compare a radiologist’s confidence ratings with a computer’s ratings. For example, one radiologist may assign a particular value of confidence to malignant lesions far more often than to benign lesions while another radiologist tends to assign that same value to malignant and benign lesions in nearly equal proportions. Another way of stating this scenario is that the likelihood ratio (LR) of the particular rating is greater than one for the first radiologist and about equal to one for the second. Relating the confidence rating to likelihood ratio therefore provides a quantitative basis for comparing confidence ratings: as measured by LR, the first radiologist is in fact more confident of malignancy than the second when using that particular rating. More generally, two radiologists may be indicating very different interpretations when they assign the same rating. Likewise, two different ratings, each from a different radiologist, may correspond to the same value of LR, in which case the two radiologists are indicating similar interpretations even though their ratings are quite different. These difficulties in comparing and interpreting values of classifier output can be addressed by considering the scales of the classifiers. In this paper, we present a principled approach to defining classifier scale based on the relationship of classifier output to statistics derived from classifier output densities-statistics such as likelihood ratio. From these definitions, we then develop and test algorithms that estimate scaling transformations that relate the output from one classifier to the output of another.

Although the term “scaling transformation” sometimes indicates a particular type of linear transformation, we will consider more general scaling transformations in this paper. Specifically, for classifiers with output in the interval [0,1], we define a scaling transformation to be a nonlinear, strictly increasing function that maps subintervals of [0,1] to other subintervals of [0,1]. Because all ROC curves are invariant under monotonic transformations of the decision variable, scaling transformations do not change the ROC curve associated with any classifier’s output. In developing CAD, the question of how to rescale a computer’s quantitative output most effectively—that is, the question of which particular monotonic transformation to employ for the interface between a CAD computer’s “native” output and the radiologist user—must begin with the question of how best to relate different scales. In this paper, we define notions of scale on the basis of LR, true positive fractions (TPF = sensitivity), false positive fractions (FPF = 1 − specificity), and cumulative distribution functions (CDF). Our LR-scaling transformation is the one that scales in a way such that, to the extent possible, the LRs of the two classifiers are identical for every value of classifier output. In exploring these transformations, we consider four different notions of “scaling,” which we refer to as LR scaling, TPF scaling, FPF scaling, and CDF scaling, respectively.

Because the user interface is an important component of any CAD scheme, a greater understanding of the different kinds of scales that radiologists use, and especially their relationship with those of computer classifiers, may prove useful in the development and evaluation of CAD workstations. Although the classification performance levels of the computer and of the radiologist are independent of their respective scales, it is not at all clear that the ability of the radiologist to employ a computer aid effectively is independent of the computer’s scale. That is, it may be that the aided radiologist’s performance depends upon the computer’s output scale. For example, when a radiologist attempts to use a computer aid that employs an output scale substantially different from his or her own, the consequent discordance between the radiologist’s and the computer’s rating may confuse the radiologist and thereby lead to ineffective use of the computer aid, both in observer studies and in clinical practice. Scaling the computer output to be “less discordant” with the radiologist’s rating scale may therefore provide added value to the radiologist. On the other hand, the performance of the radiologist with the computer aid may prove independent of the computer’s scale. For example, it may be that, within reason, whatever the scale of the computer, the radiologist adapts to the peculiarities of that scale. Whether or not the scale of the computer output affects aided radiologist performance is, to our knowledge, an open question that must be addressed in observer studies and lies beyond the scope of this paper. The methods we develop here are a first step toward concepts and methods that can be used to design CAD systems that account appropriately for differences in scale.

In what follows we describe algorithms that estimate the LR, TPF, FPF, and CDF scaling transformations; and methods that transform the computer’s output to the LR, TPF, FPF and CDF scale of the radiologist, respectively. We then evaluate the accuracy of these estimated transformations on simulated datasets for which the scaling transformations are known. Moreover, we report results obtained from the use of real data to study variation in radiologists’ rating scales and to provide examples of the scaling transformations implemented on our intelligent workstation for breast CAD.

MATERIALS AND METHODS

Databases

Three retrospectively collected databases of breast lesions were used in this study. The first two contain 319 mammographically imaged lesions (cancer prevalence 0.57) and 358 sonographically imaged lesions (cancer prevalence 0.19), respectively. The third comprised both mammograms and breast sonograms (cancer prevalence 0.37) from 97 lesions and is independent from the first two databases. All three databases have been described in detail elsewhere.⁷ The mammographic and sonographic databases were used to train our mammographic and sonographic classifiers, respectively, as well as to generate the mammographic and sonographic histograms displayed on our intelligent workstation.^{11, 12} We emphasize that the computer classifiers were trained on one database and tested on another, independent database. For a given lesion, both of our computer classifiers compute an estimate of the PM by merging automatically extracted features with Bayesian neural networks. The prevalences inherent in the sonographic and mammographic PM estimates are those of the training databases, 0.19 and 0.57, respectively. The independent two-modality database was used in a multimodality observer study⁷ in which 10 radiologists reported their confidence (rating) that a given lesion is malignant on a scale of 0% to 100%, both without and with the computer aid. Therefore, each radiologist’s rating was analogous to the computer’s PM estimate for the same lesion. In this paper, we will focus on the radiologists’ unaided ratings that had been obtained in that previously published observer study.⁷ The institutional review board approved the HIPAA-compliant observer study, with signed informed consent from the observers.

Scale: A real data example

To begin to understand the issue of scale in classifier output, it is useful to consider a real data example. The scatter plot and normalized histograms¹³ in Fig. 1 show the ratings produced by a computer classifier and independently by an unaided radiologist classifier for the two-modality database of 97 lesions. We see that 93 of the 97 lesions received a higher rating from the radiologist than from the computer; that the computer most frequently assigned lesions to the bin containing ratings between 0 and 0.1; and that the radiologist assigned no lesions at all to that bin. Differences of this kind caused the authors to wonder whether the radiologist and computer were operating on very different “scales.” Moreover, such differences between the computer and radiologist might lead the radiologist to misinterpret the computer’s output.

Figure 1.

A real data example of a radiologist and computer classifier operating at different “scales.” The plots show the ratings of our sonographic computer classifier and a radiologist for 97 clinical cases depicting breast lesions. The distributions of ratings for malignant and benign cases are shown by different histograms.

In what follows, it is important to distinguish between various ways of measuring the difference in the output of the two classifiers (one human and one machine, in the above example). We can measure differences in (1) classifier performance, as summarized by ROC curves; (2) case-by-case rankings, or rank order, with respect to suspicion of malignancy;¹⁴ and (3) classifier scale, according to measures that we describe below.

The example above concerns a particular application: the diagnosis of breast lesions during workup. However, we expect the scaling methods described in this paper to be useful also in other applications. Therefore, we will use word “lesion” when referring to the specific application of the diagnosis of breast masses and the word “case” when no specific application is being referenced.

ROC analysis, rank order correlation, and scale

ROC analysis¹⁰ is the current standard for assessing the performance of a given classifier, whether human or machine, in the task of differentiating diseased from nondiseased cases. The rank order of a sample of actually positive and actually negative cases determines the ROC curve associated to that sample, but not vice versa, because the same ROC curve can be produced by different rank orderings of individual cases. As is well known, the ROC curve and rank order are invariant under monotonic transformation, so both the ROC curve and the rank order are independent of scale. It follows that, in changing the scale of the output of a classifier, we will not be changing either the ROC curve or the rank order associated with that output. We emphasize that the purpose of scaling the output of one classifier to the scale of another is to reduce differences in classifier scales, so as to provide a basis for more meaningful comparisons: not to reduce differences in the ROC curves or the rank order. Nor is the purpose to reduce the difference in the outputs of the two classifiers for a given case.

It is important to note that case-by-case rank order variation is to be expected. Indeed, if there were perfect rank order correlation between human and machine, the use of a computer aid would not yield any diagnostic benefit, because gains in accuracy can be obtained from replicated readings only when discrepancies exist between ratings.¹⁶

Although the ROC curve associated to a particular classifier is independent of scale, a classifier’s scale does affect the value of the decision-variable threshold at which a particular point on the ROC curve is obtained.¹⁷ To use a diagnostic classifier, a single threshold and resultant ROC operating point must be chosen such that every case with classifier output greater than the threshold is classified as diseased whereas every case with classifier output less than the threshold is classified as nondiseased. The particular combination of TPF and FPF that the classifier achieves in this way depends upon the value at which the threshold is set. This means, for example, that in order to use two classifiers with the same ROC curve but different scales to achieve the same combination of TPF and FPF, two different thresholds must be chosen on the different scales.

Bayesian classifiers

In exploring classifier output scale, it is useful to have an example of a classifier with known properties that can be simulated. In addition to the kind of real rating data considered above, we looked at classifiers that produce estimates of the PM. Using Bayes’ rule, one can derive the following relationship of the (posterior) PM to the likelihood ratio R and prevalence of cancer, η:

$$\mathit{PM}(x)=\frac{\mathit{kR}(x)}{1+\mathit{kR}(x)}\mathrm{,}\mathrm{where}k\mathrm{=}\frac{\eta }{1-\eta },$$ (1)

and where x is the test result (for example, a feature vector). We will call classifiers that provide PM output “Bayesian classifiers.” To simulate the output of a Bayesian classifier, we will use a pair of normal distributions (i.e., a binormal distribution¹⁸) to generate normal samples of diseased and nondiseased cases, together with associated likelihood ratios, from which the PM can be computed from Eq. 1 for a particular choice of prevalence. Bayesian classifiers with output so constructed are related to the “proper” binormal model^{19, 20} and will therefore be referred to as “proper Bayesian classifiers.” With the proper binormal model, it is assumed that the classifier output and likelihood ratio are related by an unknown monotonic relationship. The proper Bayesian model that we studied is specified by the particular monotonic relationship between R(x) and PM(x) given in Eq. 1. To simulate the output of two proper Bayesian classifiers on the same database of cases, we used a bivariate form of the proper Bayesian classifier. The univariate proper Bayesian model depends on three parameters: the usual binormal ROC curve parameters a and b (or equivalently, d_a and c) together with a scaling-prevalence value η. The bivariate proper Bayesian model, which is equivalent to the conventional binormal model²¹ but with ROC curves based on marginal likelihood ratio rather than marginal normally distributed outcome, depends on eight parameters: $a_1$, $b_1$, and η₁ for classifier 1;$a_2$, $b_2$, and η₂ for classifier 2; and the conditional bivariate correlation coefficients for the malignant and benign populations, ${\rho }_{+}$ and ${\rho }_{-}$, respectively. The details of the univariate and bivariate proper Bayesian models can be found in Appendix 1, available online through the Physics Auxiliary Publication Service.²² Note that the conditional bivariate correlation coefficients, which quantify linear correlation in the latent decision variables of the two classifiers separately for actually positive and for actually negative cases, differ from the rank order correlation coefficients referred to in footnote.¹⁴

The proper Bayesian classifier is an accurate model for our computer classifier, which in fact estimates PM given a particular feature vector. However, in our experience, human classifiers tend not to give ratings that can be related to likelihood ratio according to Bayes’ rule [Eq. 1]. Even though we are primarily interested in scaling the output of a (Bayesian) computer classifier to the scale of a (non-Bayesian) radiologist or vice versa, we will still learn much from considering scaling between two Bayesian classifiers.

In another paper, we have shown that changing the prevalence in Bayesian PM output represents a type of scaling.¹⁷ For example, our mammographic computer classifiers were trained on a database with a prevalence of 0.57 and, therefore, produce PM estimates calibrated to that prevalence. On the other hand, for certain applications, one might wish to scale the mammographic computer output to reflect a prevalence of 0.04093,^{23, 24} the reported cancer prevalence in the population of U.S. women over the age of 40 receiving a diagnostic mammography examination. We can use Eq. 1 with η = 0.57 to find the likelihood ratio associated to the original mammographic PM output. Then using Eq. 1 again with η = 0.04093, we determine the new output, $\mathit{PM}\text{'}$, which reflects the clinical prevalence. In general, given a particular value of PM from a Bayesian classifier with prevalence η, we can scale that output to a new value, $\mathit{PM}\text{'}$, which reflects another prevalence, $\eta \text{'}$, using the modified prevalence transformation:¹⁷

$$\mathit{PM}\text{'}=\frac{\kappa \mathit{PM}}{(\kappa -1)\mathit{PM}+1}\mathrm{,}\mathrm{where}\kappa \mathrm{=}\frac{\eta \text{'}(1-\eta )}{\eta (1-\eta \text{'})}.$$ (2)

We will refer to the prevalence η in Eq. 1 as the PM-prevalence, and we will vary it in our simulations to explore scale for Bayesian classifiers.

The simple case: Identical ROC curves

To motivate the definitions of the scaling transformations analyzed in this paper, we consider examples of two classifiers with the same ROC curve under four different scaling and case-by-case rank order conditions on the classifier ratings: (1) the same scale and same rank order, (2) the same scale and different rank order, (3) different scale and same rank order, and (4) different scale and different rank order. For each of these conditions, we use a bivariate, proper Bayes distribution (see Appendix 1, available online through the Physics Auxiliary Publication Service²²). For Bayesian classifiers, the same and different scales are achieved by choosing the same or different PM-prevalence, respectively. Figures 23 show the scatter plots for 100 pairs of simulated PM output for the cases of identical and different scale, respectively. Note that the underlying conditional distributions for the malignant and benign ratings are identical for the output in Figs. 2a, 2b and can be made identical by a monotonic transformation in Figs. 3a, 3b.

Figure 2.

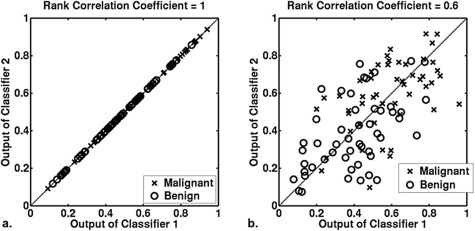
Simulated examples showing two classifiers with the same scale. The same scale is achieved by using the same PM-prevalence (η = 0.5) for two Bayesian classifiers, both of which have the same ROC curve (AUC = 0.76, a = 1, b = 1). The case-by-case rank order of the outputs from the two classifiers is the same (rank correlation coefficient = 1) and different (rank correlation coefficient = 0.6) in panels (a) and (b), respectively.

Figure 3.

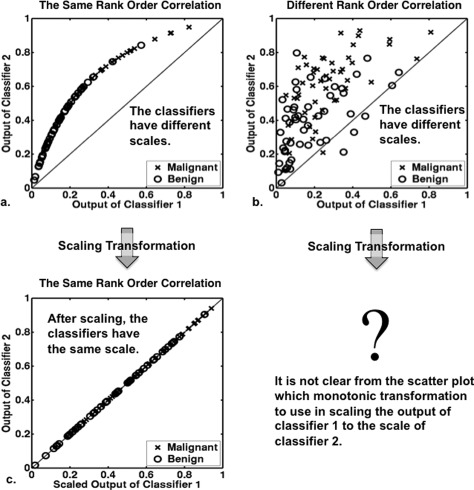
Simulated examples showing two classifiers with different scales. The difference in classifier scale was achieved by using different PM-prevalence for the two Bayesian classifiers (prevalence of 0.2 and 0.5 for classifiers 1 and 2, respectively), both of which have the same ROC curve (AUC = 0.76, a = 1, b = 1). The case-by-case rank order of outputs from the two classifiers is the same (rank order correlation = 1) and different (rank order correlation = 0.6) in panels (a) and (b), respectively. When the rank order is the same, panel (c) shows the effect of transforming the output of classifier 1 in panel (a) to the scale of classifier 2 by using the monotonic function shown in panel (a). However, when the rank order is different, as in panel (b), how best to transform output from classifier 1 to the scale of classifier 2 is not as clear.

In Figs. 2a, 2b, the two classifiers have the same ROC curves and the same scales (that is, the same PM-prevalence). In panel (a), the two classifiers yield the same rating for every case. In panel (b), the ratings given by classifiers 1 and 2 differ on a case-by-case basis, although these ratings are drawn from identical conditional distributions.

On the other hand, in both Figs. 3a, 3b, the two classifiers have the same ROC curves but different scales; in other words, the PM-prevalences of classifiers 1 and 2 differ so that the output of classifier 1 is necessarily on a different scale than the output of classifier 2. In Fig. 3a, for which the case-by-case rank order of the two classifiers is the same, the output of classifier 1 is related to the output of classifier 2 by a particular monotonic transformation. It should be intuitive that the monotonic function shown in Fig. 3a can be used to scale the output of classifier 1 to the scale of classifier 2. The scaled output of classifier 1 is then identical to the output of classifier 2 for every case [Fig. 3c]. On the other hand, from the scatter plot in Fig. 3b, it is not clear which monotonic transformation to use in scaling the output of classifier 1 to the scale of classifier 2. However, since we know that the output of the two classifiers are drawn from distributions with the same ROC curve, we can transform the output of classifier 1 such that, after the scaling transformation is applied, all thresholds produce the same TPF, FPF, and LR for both classifiers.

The special case of two classifiers associated with the same ROC curve, which is the situation considered up to this point, motivates three scaling transformations that can be used even when the ROC curves of the two classifiers differ. Therefore, we will scale the output of classifier 1 so that both classifiers produce (1) the same LRs at all thresholds [Fig. 4b]; (2) the same TPFs at all thresholds [Fig. 4c]; or (3) the same FPFs at all thresholds [Fig. 4d]. We will consider also a fourth scaling transformation based on the cumulative distribution function, which, as we will see Sec. 2F , is a linear combination of TPF and FPF. With this fourth scaling transformation, we scale so that both classifiers produce the same CDF at all thresholds.

Figure 4.

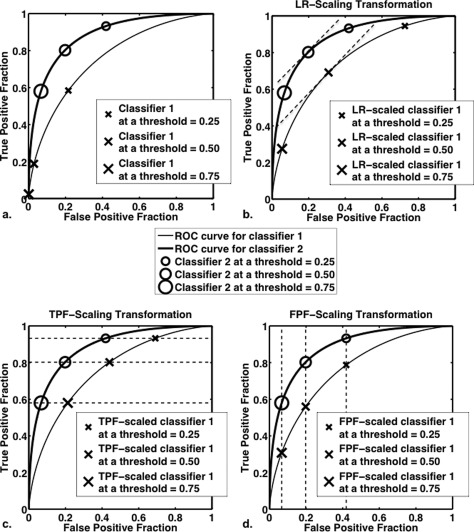
Graphical representation of the ideas behind LR scaling, TPF scaling, and FPF scaling. The ROC curves for two classifiers together with their (FPF, TPF) pairs at various thresholds are shown: (a) before scaling; (b) after transforming the output of classifier 1 to the LR-scale of classifier 2; (c) after transforming the output of classifier 1 to the TPF scale of classifier 2; and (d) after transforming the output of classifier 1 to the FPF scale of classifier 2. In panel (b), the slope of the two ROC curves is equal when equal thresholds are applied to the output of classifier 2 and to the output of classifier 1 after it has been scaled to the LR scale of classifier 2.

When the ROC curves associated to the two classifiers are identical, these four scaling transformations are identical because, in this situation, “matching” any one of LR, TPF, FPF, or CDF results in the matching of the other three. However, in general, when the ROC curves associated to the two classifiers differ, these four scaling transformations differ.

Classifier LR, TPF, FPF, and CDF functions

Before defining our scaling transformations, we will review the four functions upon which our transformations rely. We begin with the TPF, FPF, and CDF functions, which are given by

$$\mathit{TPF}(Y)=P(\mathrm{output}\mathrm{of}\mathrm{a}\mathrm{malignant}\mathrm{lesion}\mathrm{>}Y)={\int }_Y^1{f}_y(t|+)\mathit{dt},$$

$$\mathit{FPF}(Y)=P(\mathrm{output}\mathrm{of}\mathrm{a}\mathrm{benign}\mathrm{lesion}\mathrm{>}Y)={\int }_Y^1{f}_y(t|-)\mathit{dt},$$

$$\mathit{CDF}(Y;{\eta }_{\mathit{pop}})=P(\mathrm{output}\mathrm{of}\mathrm{any}\mathrm{lesion}\mathrm{<}\mathrm{Y})=1-{\eta }_{\mathit{pop}}\mathit{TPF}(Y)-(1-{\eta }_{\mathit{pop}})\mathit{FPF}(Y),$$

where 0 < Y< 1 is a particular classifier output value; where the non-negative functions $f_y\left(t|+\right)$ and $f_y\left(t|-\right)$ are the classifier output’s conditional density functions for malignant and benign cases, respectively; and where η_pop is the prevalence of cancer in the population from which the case in question is drawn.²⁵ According to the definitions above, the TPF and FPF functions are nonincreasing whereas the CDF function is nondecreasing—all with a range of [0,1]. In fact, in this paper, we will limit ourselves to classifiers for which the TPF and FPF functions are strictly decreasing whereas the CDF function is strictly increasing. Because it is common in ROC analysis to consider TPF as a function of FPF, we wish to emphasize that TPF as a function of classifier output is very different than TPF as a function of FPF: the former is independent of the ROC curve and depends upon the distribution of output values from actually-malignant cases, whereas the latter is the ROC curve. Because the classifier TPF function is independent of ROC, we can rescale the classifier output so that the TPF function is any nonincreasing function taking values between 0 and 1. (Of course, changing the TPF function affects the FPF function as well.) The independence of the classifier TPF function from the ROC curve means that two classifiers may have the same ROC curve but different classifier TPF functions or different ROC curves but the same classifier TPF function. Similarly, a classifier’s FPF and CDF are independent of the ROC curve.

The classifier LR function is defined by

$$\mathit{LR}(y)=\frac{p(y|\mathrm{malignant})}{p(y|\mathrm{benign})}.$$

The LR function is not necessarily monotonic (e.g., in general, the decision variable of the conventional binormal model is not related monotonically to likelihood ratio¹⁹). In this paper, we will assume that the relationship between the classifier output and LR is strictly increasing. The limitations of this assumption are described in Sec. 2G. Although the likelihood ratio in general can take on any value between 0 and ∞, a particular classifier’s minimum LR may be greater than 0, while that classifier’s maximum LR may be less than ∞. Because the LR associated with a particular threshold equals the slope of the ROC curve at that threshold, the maximum and minimum values of LR are also the maximum and minimum slopes of the ROC curve, respectively. This means the range of a classifier’s LR function is related to that classifier’s ROC curve—specifically, the minimum and maximum LR-range values define the slope in the upper-right-hand and lower-left-hand corners, respectively (assuming a strictly increasing LR function).

The LR, TPF, FPF, and CDF functions specified above define four different notions of classifier scale. For example, we will say that the TPF function of a particular classifier defines that classifier’s TPF scale. When we speak of scaling classifier 1 to the TPF scale of classifier 2, we mean that we monotonically transform the output of classifier 1 so that the transformed output has the same TPF function as that of classifier 2. In other words, for each value of y₁ (an output value from classifier 1), we wish to find a value y (the corresponding value on the TPF scale of classifier 2) such that

$$\mathit{TP}{F}_2(y)=\mathit{TP}{F}_1(y_1).$$

Formally solving this equation for y yields

$$y={\mathit{TPF}}_2^{-1}\circ \mathit{TP}{F}_1(y_1).$$

Here, y is the value of y₁ after transformation from the TPF-scale of classifier 1 to the TPF-scale of classifier 2. We therefore use the notation

$$y_{1\to 2}={\mathit{TPF}}_2^{-1}\circ \mathit{TP}{F}_1(y_1).$$ (3)

See Fig. 5 for an example. We emphasize that the output $y_{1\to 2}$ specified by Eq. 3 corresponds to the same ROC curve as classifier 1 but the same TPF function as classifier 2. Note that Eq. 3 is defined because the range of both TPF functions is the same ([0,1]) and because the TPF function is invertible (according to our assumption that TPF functions are strictly decreasing). We will refer to the transformation defined in Eq. 3 as “the TPF-scaling transformation,” with analogous transformations defined for LR, FPF, and CDF.

Figure 5.

Scaling classifier 1 to the TPF scale of classifier 2. In panel (a), the TPF functions of two classifiers are shown, together with arrows indicating how an output value of 0.2 from classifier 1 changes to 0.68 after it has been transformed to the TPF scale of classifier 2. Panel (b) shows the TPF-scaling transformation that maps the output of classifier 1 to the TPF scale of classifier 2.

Scaling transformation: Likelihood ratio

The ubiquity of the likelihood ratio makes it a natural basis for defining scale. For example, the likelihood ratio (or any monotonic transformation thereof) is the optimal decision variable.²⁶ Moreover, as defined by maximizing the utility function,²⁷ the optimal operating point on a “proper” ROC curve is a monotonic function of the likelihood ratio.^{28, 29} We are therefore interested in obtaining a scaling transformation that is based on matching likelihood ratio. That is, we are interested in the transformation

$$T_{1\to 2;\mathit{LR}}={\mathit{LR}}_2^{-1}\circ L{R}_1,$$ (4)

where LR₁ and LR₂ are the LR functions of classifiers 1 and 2, respectively. Here the notation “$1\to 2$; LR” means that the output of classifier 1 is being scaled to the LR-scale of classifier 2. Recall that we will assume that all classifier LR functions are strictly increasing, so that the inverse of LR₂ exists and $T_{1\to 2;\mathit{LR}}={\mathit{LR}}_2^{-1}\circ L{R}_1,$ is monotonic.

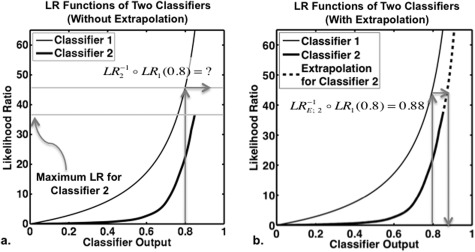
However, in general, the transformation given in Eq. 4 may not be defined, because the range of $L{R}_2$ may not be a subset of the range of $L{R}_1$, in which case the likelihood ratio of classifier 1 achieves values that likelihood ratio of classifier 2 does not [Fig. 6a]. To overcome this problem, we propose to extrapolate the function $L{R}_2$ such that the range of the extrapolated function $L{R}_{E;2}$ is [0,∞), the region of all possible values of likelihood ratio [Fig. 6b]. Then, we define the LR-scaling transformation as

$${\tilde{T}}_{1\to 2;\mathit{LR}}={\mathit{LR}}_{E;2}^{-1}\circ L{R}_1.$$ (5)

The method of extrapolation is based on Bayes rule and is detailed in Appendix 2, which is available online through the Physics Auxiliary Publication Service.²² Here it suffices to say, first, that $L{R}_2$ and $L{R}_{E;2}$ are identical over the domain of $L{R}_2$, so that the likelihood ratio of the two classifiers’ will match wherever possible. Second, in the case of diagnostic breast imaging, extrapolation only tends to be needed, if at all, for classifier output corresponding to regions of high or low sensitivity. For example, for the ten radiologists in our observer study,⁷ extrapolation is necessary in the computer-to-radiologist LR-scaling transformation only for computer output corresponding to TPF > 0.99 or TPF < 0.55. Since diagnostic breast radiologists tend to operate at a TPF far greater than 0.55 and at a TPF somewhat less than 0.99, extrapolation is for our application a technical convenience unlikely to affect clinical outcomes.

Figure 6.

Extrapolation used for the LR-scaling transformation. Panel (a) shows the LR functions of two classifiers with unequal ranges: the maximum possible LR value from classifier 2 is less than that from classifier 1. This means that when classifier 1 output is to be transformed to the LR scale of classifier 2, the LR scaling transformation is not defined for some output values from classifier 1 unless some method is used to extrapolate the LR function of classifier 2. An example is shown in panel (a), where arrows indicate that the transformation is not defined for a classifier 1 output value of 0.8. Panel (b) shows the process of Bayesian extrapolation for the LR function of classifier 2, together with arrows indicating how the classifier 1 output of 0.8 changes to 0.88 when the output of classifier 1 is scaled to the LR scale of classifier 2. Under this extrapolation, the LR-scaling transformation is defined for all values of classifier 1 output.

We remark that our assumption that the classifiers’ LR functions are strictly increasing represents a limitation for the LR-scaling transformation. On the other hand, there is evidence that such a limitation on the classifiers’ LR function may be fairly flexible. Recall that a classifier’s output is related monotonically to likelihood ratio if and only if its ROC curve has monotonically decreasing slope.^{19, 20} The proper binormal model is one model that satisfies this assumption and evidence supports its flexibility.¹⁹ Any proper model results in convex ROC curves—i.e., curves with nonincreasing slope, and consequently, nonincreasing LR functions as one moves from lower left to upper right along the curve. As described in a recent paper,²⁰ (1) nonconvexity in the population ROC curves implies the use of an irrational decision strategy, and (2) nonconvexity in the sample ROC curve can frequently be ascribed to chance, the sampling process or fitting artifact. Such results indicate that the assumption of strictly increasing LR functions for the radiologist and computer classifiers is not a particularly strong limitation.

If the classifier output y approximates the (Bayesian) posterior probability of malignancy with prevalence η, then Eq. 1 implies that the likelihood ratio function may be estimated by

$$\mathit{LR}(y)=\frac{(1-\eta )y}{\eta (1-y)}.$$ (6)

This function has domain [0,1) and range $[0,\infty )$. If both classifiers are approximately Bayesian, then the LR transformation reduces to the prevalence-scaling transformation discussed in a previous paper.¹⁷ Since our computer classifiers are Bayesian neural networks, we will assume that the likelihood ratio of the computer-estimated output can be approximated by the Bayesian relationship given in Eq. 6.

For human (radiologist) classifiers, however, the Bayesian relationship is not tenable, and some other approach must be used to estimate likelihood ratio for each case. There are many parametric and nonparametric ways to estimate the likelihood ratio of a classifier output. In this paper, we are guided by previous research in ROC analysis and model the radiologist classifier output using the proper binormal model,^{19, 20} which assumes that some monotonic transformation of the classifier output (decision variable) yields the likelihood ratio. We use the computer software PROPROC (Refs. ^{30, 31}) to determine the maximum likelihood estimates of the likelihood ratio, which are used in turn to compute the sequence of operations that defines the LR-scaling transformation as defined by Eq. 5—for details, see Appendix 3, which is available online through the Physics Auxiliary Publications Service.²²

TPF, FPF, and CDF-scaling transformations

We will also consider three other scaling transformations, based on matching TPF, FPF, or CDF. The TPF and FPF scaling transformations that we wish to approximate are

$$T_{1\to 2;\mathit{TPF}}={\mathit{TPF}}_2^{-1}\circ \mathit{TP}{F}_1\mathrm{and}{T}_{1\to 2;\mathit{FPF}}={\mathit{FPF}}_2^{-1}\circ \mathit{FP}{F}_1,$$ (7)

where $\mathit{TP}{F}_1$ and $\mathit{TP}{F}_2$ are the TPF functions for classifiers 1 and 2, respectively, and similarly for $\mathit{FP}{F}_1$ and $\mathit{FP}{F}_2$. We will assume that the classifier TPF and FPF functions are both strictly decreasing functions of classifier output with a range of [0,1], so that the inverse of $\mathit{TP}{F}_2$ and that of $\mathit{FP}{F}_2$ exist, and both ${\mathit{TPF}}_2^{-1}\circ \mathit{TP}{F}_1$ and ${\mathit{FPF}}_2^{-1}\circ \mathit{FP}{F}_1$ are defined and monotonic.

The CDF-scaling transformation is given by

$$T_{1\to 2;\mathit{CDF};{\eta }_{\mathit{pop}}}={\mathit{CDF}}_2^{-1}\circ \mathit{CD}{F}_1,$$ (8)

where $\mathit{CD}{F}_1$ and $\mathit{CD}{F}_2$ are the functions giving the CDF as a function of classifier output for classifier 1 and 2, respectively. Recall that CDF is related to TPF and FPF by

$$\mathit{CDF}(y;{\eta }_{\mathit{pop}})=1-{\eta }_{\mathit{pop}}\mathit{TPF}(y)-(1-{\eta }_{\mathit{pop}})\mathit{FPF}(y),$$ (9)

where η_pop represents the prevalence of actually positive cases for the population studied. Because our goal is to relate the scales of two classifiers by comparing their outputs from a single population of cases, the same value of η_pop will be used for both $\mathit{CD}{F}_1$ and $\mathit{CD}{F}_2$. Note from Eq. 9 that the prevalence parameter η_pop determines the relative weights placed on TPF and FPF in forming the CDF function. For example, taking η_pop = 0.04093, the reported prevalence of cancer in the diagnostic mammography population,²⁴ yields a CDF dominated by the FPF function, and the resulting CDF-scaling transformation will be somewhat similar to the FPF-scaling transformation, whereas setting η_pop = 0 or 1 yields the FPF and TPF transformations, respectively. Taking η_pop = 0.50, the prevalence of cancer in the databases frequently used to train computer classifiers yields a CDF in which the contributions of the TPF and FPF functions are equal. We will use η_pop = 0.50 in this paper. We emphasize that using different values for η_pop will result in different CDF-scaling transformations. Note also from Eq. 9 that our assumption that a classifier’s TPF and FPF functions are strictly decreasing implies that the classifier’s CDF is strictly increasing.

Just as with the LR, there are many ways to estimate TPF, FPF, and CDF as functions of classifier output. To estimate the LR function, we used the semiparametric proper binormal model,¹⁹ as noted above, and we will use the same model to estimate the TPF, FPF, and CDF functions. By using a given classifier’s LR estimates that PROPROC provides for the individual cases in a case sample, the proper binormal TPF and FPF functions can be calculated analytically,¹⁹ with the CDF determined subsequently from Eq. 9. The sequence of operations that defines the TPF, FPF, and CDF-scaling transformations are then constructed from these proper binormal TPF, FPF, and CDF functions, respectively. The details of this procedure are provided in Appendix 3, which is available online through the Physics Auxiliary Publications Service.²²

The TPF-scaling transformation determines the relationship between two classifier’s output scales that “matches” classifier sensitivity, without any consideration of classifier specificity. Similarly, the FPF-scaling transformation “matches” classifier specificity, without any consideration of classifier sensitivity. Because the cumulative distribution function of a classifier output is a linear combination of TPF and FPF, “matching” CDFs involves both the TPF functions and FPF functions of the two classifiers.

Applications to intelligent CAD workstations

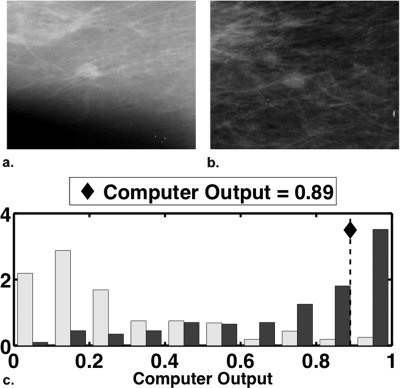
Our intelligent workstation for the diagnosis of lesions on mammography and breast sonography currently displays the computer’s PM estimate in an absolute numerical sense as well as relative to the computer’s PM histograms from the mammographic and sonographic training databases.^{11, 12} Figure 7 shows an example of the mammographic computer output, expressed in terms of both a numeric PM value and its location (♦) relative to the computer’s PM histogram from a relevant database. We explore two options in which the scaling transformations above can be used: (1) transform both the computer’s numeric PM estimate and the computer’s PM histogram to the scale of the radiologist or (2) transform the radiologist’s ratings to the scale of the computer and display them relative to the computer’s PM histogram. With option 1, the computer output is scaled “into the language” of the radiologist, presumably enabling the radiologist to better interpret the computer output. However, option 1 also introduces some variability into CAD workstations, as every radiologist will then view a different form of the computer output. With option 2, every radiologist will see the same form of the computer output, but the radiologist’s rating of a particular case is scaled into the language of the computer. Both options provide the basis of a more meaningful comparison between the radiologist and computer ratings, as with both options, the two ratings will be “in the same language,” be that “language” of the radiologist or the computer based on LR, TPF, FPF, or CDF.

Figure 7.

Our workstation’s mammographic computer output for a malignant case with computer-estimated PM = 0.89. Shown are (a) a region of interest taken from the mediolateral mammographic view and (b) a region of interest taken from the craniocaudal view. Panel (c) displays histograms of the mammographic computer output from an estimation database of 354 mammographic cases (prevalence of approximately 0.50), with the computer’s estimate (0.89) of the probability of malignancy for the case shown in (a) and (b) indicated by a dashed vertical line. The histograms for benign and malignant cases are shown by light gray and dark gray bars, respectively.

Evaluation of scaling transformations

In Sec. 3, we report three investigations: (1) we show the effects of all four scaling transformations on simulated bivariate proper Bayesian data; (2) we explore the two display options described above using actual rating data, performing both the radiologist-to-computer and the computer-to-radiologist estimations and displays, using all four scaling transformations; and (3) we compute the average mean square error (MSE) between the estimated and known transformations. We describe the average mean square error evaluation in Sec. 2K.

Average mean square error evaluation

Using simulated data, we calculated the average MSEs between the estimated and known scaling transformations. We emphasize that the purpose of this analysis is to evaluate our ability to estimate the scaling transformations described in this paper—not to evaluate whether or not such transformations result in improvements in radiologists’ performance. The MSE evaluation also allows us to determine the number of cases required to estimate the scaling transformations reliably. All of our simulations were based on the following sequence of operations: (1) generating samples of conventional binormal ratings, with the parameters of the binormal model set equal to those of the relevant classifier; (2) determining for each binormal rating the corresponding binormal LR; and (3) transforming the samples of binormal LRs to samples of classifier output using the inverse of that classifier’s LR function. For the computer classifier, we assumed the Bayesian model, so that the computer classifier’s LR function is derived from Bayes’ rule, and its inverse is analytically defined in Eq. 1. However, as we have mentioned, the Bayesian model is not appropriate for human classifiers. In order to model more realistically a range of radiologists’ rating behavior—that is, a variety of radiologists’ scales—we considered the unaided ratings of the ten radiologists from our prior multimodality observer study⁷ and chose, from this sample of ten, three radiologists whose LR-functions represent three different kinds of rating behavior. For each of the ten radiologists, we used PROPROC (Ref. ³⁰) to estimate the radiologist’s LR-function and then smoothed the resulting numerically defined function. The estimated ROC curves and smoothed (via moving average) log LR functions for all ten radiologists are shown in Fig. 8, in which the ROC curves and log LR functions of the three chosen radiologists are highlighted. As a basis for comparison, the ROC curve and log LR function for the computer classifier are also shown in Fig. 8. For each of the three highlighted radiologists, we then obtained simulated output for that radiologist by transforming samples of binormal LRs (obtained as described above from samples of conventional binormal ratings) to samples of radiologist output using the inverse of the relevant radiologist’s smoothed LR function. Because this function is defined numerically, rather than analytically, interpolation was employed to obtain the values of radiologist output from the simulated values of binormal LR. The binormal parameters used for the simulations are listed in Table TABLE I.. We emphasize that we used univariate, rather than bivariate, distributions for our simulations; thus, joint LR, TPF, FPF, or CDF functions for the computer and radiologist did not need to be estimated from a database of the same cases, because we wished to model the clinical application for which the computer and radiologist functions may be estimated using different databases.

Figure 8.

(a) The ROC curves and (b) log of the smoothed LR functions, determined using PROPROC on rating data from each of 10 radiologists for 97 cases. We will focus on the scale of radiologists 1, 2, and 3 in this paper. For comparison, the ROC curve and log LR function of the computer classifier are also shown by dotted lines.

TABLE I.

The binormal parameters used in the MSE simulation studies—see Appendix 1 available online through the Physics Auxiliary Publication Service (Ref. ²²) for details on the model. Note that although conventional binormal parameters are given, all simulations assumed the “proper” model.

	a	b	AUC
Computer	1.6508	0.9165	0.89
Radiologist 1	1.9967	1.3537	0.88
Radiologist 2	1.2637	0.8795	0.83
Radiologist 3	1.5525	0.8769	0.88

We now define the average MSE evaluation of the computer-to-radiologist scaling transformations, which scale the computer output to the scale of the radiologist, using LR, TPF, FPF, or CDF matching. The average MSE evaluation of the radiologist-to-computer scaling transformations is similar. Letting $T_{\mathit{com}\to \mathit{rad}}$ denote the actual LR, TPF, FPF, or CDF computer-to-radiologist-scaling transformation, we define the MSE for $T_{\mathit{com}\to \mathit{rad}}$ by

$$\mathit{MS}{E}_{\mathit{com}\to \mathit{rad}}(D_{\mathit{com}},D_{\mathit{rad}},V_{\mathit{com}})=\left(\frac{1}{N_V}\right)\sum _{y_i\in V_{\mathit{com}}}({(T_{\mathit{com}\to \mathit{rad}}(y_i)-{\hat{T}}_{\mathit{com}\to \mathit{rad}}(y_i|D_{\mathit{com}},D_{\mathit{rad}}))}^2,$$

where ${\hat{T}}_{\mathit{com}\to \mathit{rad}}(y_i|D_{\mathit{com}},D_{\mathit{rad}})=$ estimate of the computer-to-radiologist scaling transformation using databases $D_{\mathit{com}}$ and $D_{\mathit{rad}}$ at the computer output value y_i; $D_{\mathit{com}}=$ estimation database of N_D samples from the simulated computer classifier, used to estimate the computer classifier function (LR, TPF, FPF or CDF); $D_{\mathit{rad}}=$ estimation database of N_D samples from the simulated radiologist classifier used to estimate the radiologist classifier function (LR, TPF, FPF or CDF); ${\mathrm{V}}_{\mathit{com}}=$ evaluation database of N_V samples from the simulated computer classifier, used to evaluate the scaling transformation; and $y_i=$ sample from the computer evaluation database ${\mathrm{V}}_{\mathit{com}}$.

The estimated computer and radiologist classifier functions (LR, TPF, FPF, or CDF) were used to estimate each of the scaling transformations given in Eqs. 4, 6, 7. From $\mathit{MS}{E}_{\mathit{com}\to \mathit{rad}}(D_{\mathit{com}},D_{\mathit{rad}},V_{\mathit{com}})$, we define the average MSE for the computer-to-radiologist-scaling transformation by

$$\begin{array}{c}\multicolumn{1}{c}{{\varepsilon }_{\mathit{com}\to \mathit{rad}}(N_D,N_V,N)=\frac{1}{N}\sum _{i=1}^N\mathit{MS}{E}_{\mathit{com}\to \mathit{rad}}(D_{\mathit{com},i},D_{\mathit{rad},i},V_{\mathit{com},i}),}\end{array}$$

where computer and radiologist estimation databases ($D_{\mathit{com},i}$ and $D_{\mathit{rad},i}$, respectively), as well as computer evaluation databases ($V_{\mathit{com},i}$) have each been generated N times. Analogously, the standard error on the MSE is estimated by

$$\begin{array}{c}\multicolumn{1}{c}{{\sigma }_{\mathit{com}\to \mathit{rad}}(N_D,N_V,N)=\sqrt{\frac{1}{N(N-1)}\sum _{i=1}^N{(MS{E}_{\mathit{com}\to \mathit{rad}}(D_{\mathit{com},i},D_{\mathit{rad},i},V_{\mathit{com},i})-{\epsilon }_{\mathit{com}\to \mathit{rad}}(N_D,N_V,N))}^2}.}\end{array}$$

Average MSE and standard error for the radiologist-to-computer-scaling transformation are defined similarly. We fixed N_V = 200 and N = 200, and considered estimation datasets of size N_D = 100, 200, 300, …, 600. Note that, in this study, for a given scaling transformation, we used the same size dataset to estimate the LR, TPF, FPF, or CDF functions for both the computer and the radiologist. In real applications, obtaining a large number of ratings from the radiologists takes time, so that the size of the dataset available for estimating the radiologist functions may be smaller than the size available for estimating the computer functions. The prevalence of cancer in all datasets was fixed at 0.50.

RESULTS

Simulated bivariate proper Bayesian data

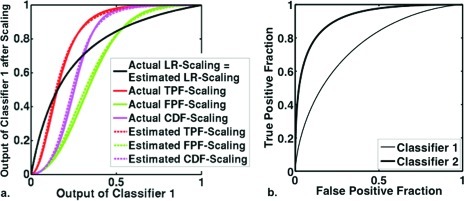
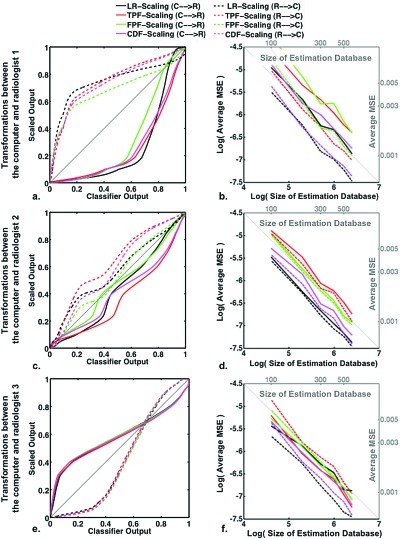
To better understand the effect of scaling transformations, we first estimated the LR, TPF, FPF, and CDF scaling transformations from simulated bivariate proper Bayesian data (a sample of 500 PM outputs for each of two classifiers). The actual and estimated scaling-transformations for classifier 1 to classifier 2 are shown in Fig. 9. The effects of the four scaling transformations on the simulated data are shown in Figs. 1011. To highlight the effects of scaling, we have chosen here to look at two highly correlated (${\rho }_{+}$ = ${\rho }_{-}$ = 0.8) classifiers with very different accuracies and PM prevalences: a low-performing classifier whose PM estimates reflect a prevalence of 0.30 (classifier 1, with $a_1$ = 1.0, $b_1$ = 1.0, and AUC = 0.76) and a high-performing classifier whose PM estimates reflect a prevalence of 0.70 (classifier 2, with $a_2$ = 2.0, $b_2$ = 1.0, and AUC = 0.92). Note from Fig. 9 that the four transformations are quite different, as is expected when the ROC curves of the two classifiers differ significantly. Note also that, when both classifiers are Bayesian with known PM-prevalence, the LR transformation is the modified prevalence transformation given by Eq. 2. The analytic form of the LR transformation is therefore known, in this situation, and need not be estimated.

Figure 9.

(a) The actual and estimated scaling transformations that map Bayesian classifier 1 to the scale of Bayesian classifier 2. (b) The ROC curves of classifier 1 and 2.

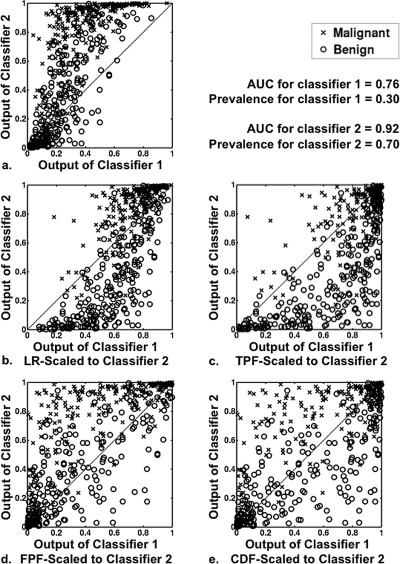
Figure 10.

Scatter plots showing effect of transforming the output of classifier 1 to the scale of classifier 2. Pairs of classifier outputs for 500 cases (250 malignant and 250 benign) were simulated from proper Bayesian bivariate distributions ($a_1$ = 1.0, $b_1$ = 1.0, $a_2$ = 2.0, $b_2$ = 1.00, ${\rho }_{+}$ = ${\rho }_{-}$ = 0.8, PM-prevalence for classifier 1 = 0.30 and PM-prevalence for classifier 2 = 0.70). Panel (a): a scatter plot showing the outputs of classifiers 1 and 2 before scaling. Panels (b), (c), (d), and (e): scatter plots of the output of classifier 2 versus the scaled output of classifier 1 after each the four scaling transformations (LR, TPF, FPF, and CDF, respectively). Note that the rank order correlation of this sample is 0.81.

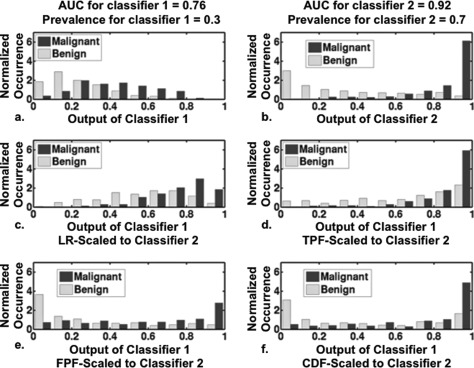
Figure 11.

Histogram plots showing effect of transforming the output of classifier 1 to the scale of classifier 2. Pairs of classifier outputs for 500 (250 malignant and 250 benign) cases were simulated from proper Bayesian bivariate distributions ($a_1$ = 1.0, $b_1$ = 1.0, $a_2$ = 2.0, $b_2$ = 1.0, ${\rho }_{+}$ = ${\rho }_{-}$ = 0.8, PM-prevalence for classifier 1 = 0.30 and PM-prevalence for classifier 2 = 0.70). Panels (a) and (b): conditional histograms of the outputs from classifiers 1 and 2 before scaling, respectively. Panels (c), (d), (e), and (f): the conditional histograms of the output of classifier 1 mapped to the scale of classifier 2 according to each of the four scaling transformations (LR, TPF, FPF, and CDF, respectively).

The scatter plot in Fig. 10a shows the original, simulated output for classifiers 1 and 2 on 500 cases—with classifiers 1 and 2 each estimating the PM given a prevalence of 30% and 70%, respectively. Figure 10b shows the output of classifier 2 and that of classifier 1 after transformation to the LR-scale of classifier 2, with both outputs estimating the same statistically relevant quantity—namely, the PM given a prevalence of 70%. Now compare the scatter plots after LR and CDF-scaling [Figs. 10b, 10e], and note that scaling classifier 1 to the CDF-scale of classifier 2 [Fig. 10e] results in the most even distribution of the two sets of classifier outputs across the identity line. However, the output of classifier 2 and the CDF-scaled output of classifier 1, shown together in Fig. 10e, do not estimate the same statistical quantity. CDF-scaling the output of classifier 1 modifies the original output, which estimates PM, to some other quantity, which, in general, does not estimate PM. The fact that LR-scaling [Fig. 10b] results, in this particular situation, in outputs with a “sigmoidal” joint distribution is a natural consequence of classifier 2 (AUC = 0.92) being much better than classifier 1 (AUC = 0.76) in differentiating malignant from benign lesions.

Note also that the malignant-case histogram of the output of classifier 1 transformed to the TPF scale of classifier 2 [the black bars in Fig. 11c] “looks most like” the malignant-case histograms of classifier 2 [the black bars in Fig. 11b]. On the other hand, the benign-case histogram of the output of classifier 1 transformed to the FPF scale of classifier 2 [the gray bars in Fig. 11d] looks most like the benign-case histograms of classifier 2 [the gray bars in Fig. 11b]. However, using the CDF, TPF, or FPF-scaling transformations on output that estimates PM from classifiers with different ROC curves results in scaled data that, in general, does not estimate PM. Only the LR-scaling transformation scales the output of classifier 1 so that the Bayesian relationship given in Eq. 1 holds. Before the output of classifier 1 is LR-scaled to the output scale of classifier 2, Eq. 1 holds for η₁, whereas after that LR-scaling, Eq. 1 holds for η₂.

Examples of the two display options using actual rating data

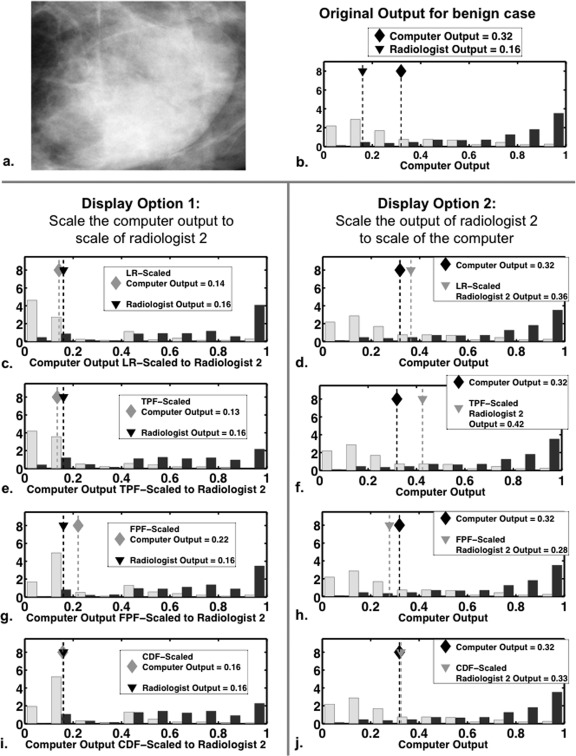
The prior illustrative example is not typical of clinical breast diagnosis, for three reasons. First, the radiologist is not generally a Bayesian classifier. Second, the ROC curves of the radiologist and computer are usually more similar. Finally, rank order correlation between the radiologist and computer output is typically not as large as that of the sample shown in Fig. 10 (rank order correlation = 0.81). In Fig. 12, we explore a real data example and show how the four scaling transformations would affect the display of the mammographic computer analysis for a particular benign case and a particular radiologist. The radiologist output shown is the rating that radiologist 2 gave for the depicted benign case during a previous observer study.⁷ The effect of the scaling transformations is given for both display options described in Sec. 2I . Notice that under display option 1, the scaled computer histograms depend on which of the four scaling transformations was used. In general, the more the ROC curves of the radiologist and the computer differ, the more the LR-scaled computer histograms will differ from the scaled histograms derived from the other scaling transformations.

Figure 12.

The two display options (described in the Sec. 2I) for the computer output given to radiologist 2 for a benign lesion under all four transformations. Diamonds indicate computer output, whereas triangles indicate the output of radiologist 2. Black diamonds and triangles indicate original output, while gray diamonds and triangles indicate scaled output. (a) An ROI of the lesion. (b) The original computer histograms and output for the benign lesion, together with the rating of radiologist 2. Panels (c), (e), (g), and (i): The computer display under display option 1, in which the computer output has been LR-, TPF-, FPF-, or CDF-scaled to the scale of radiologist 2, respectively. Panels (d), (f), (h), and (j): The computer display under display option 2, in which the output of radiologist 2 has been LR-, TPF-, FPF-, or CDF-scaled to the computer, respectively.

Before scaling, the computer gives the benign case shown in Fig. 12 a rating of 0.32, which is 0.16 higher than the rating given by radiologist 2. After scaling by any of the four methods, the ratings of the computer and radiologist more nearly agree, at least in this particular case. However, the purpose of scaling is not to produce more agreement but to provide a basis for more meaningful overall comparison of the ratings of two classifiers (here, a particular radiologist and the computer). For some particular cases, classifiers whose ratings agree before scaling may disagree after scaling.

Average mean square error evaluations

The results of the simulation study determining average MSE (between the estimated and actual scaling transformations) are shown in Fig. 13 for each of the three simulated radiologists, along with the actual LR-, TPF-, FPF-, and CDF-scaling transformations used to generate the simulated data. The actual scaling transformations were obtained by determining the sequence of operations [Eqs. 4, 6, 7] from the actual LR, TPF, FPF, and CDF functions. The actual LR functions, used in simulating the radiologists’ and computer output, are shown in Fig. 8b.

Figure 13.

Panels (a), (c), and (e): The actual scaling transformations for radiologists 1, 2, and 3, respectively. Panels (b), (d), and (f): Log of the average MSE for each scaling transformation as a function of the log of the size of the database used to estimate those transformations. The corresponding average MSE and estimation database size are given on the right and top, respectively. In all situations, the standard error on the average MSE is an order of magnitude less that the average MSE itself.

The actual TPF and FPF functions were determined analytically from the binormal LR function,¹⁹ and then the actual CDF function was determined from TPF and FPF using Eq. 8. For all three radiologists, the standard error on the average MSE obtained with each size of estimation database was an order of magnitude less than that of the average itself. The average MSE shown in Fig. 13 gives an indication of the kind of reliability achieved using databases of size 100 to 600 cases (50% cancer) to estimate the scaling transformations. Note that the log of the average MSE appears linearly related to the log of the estimation database size with a slope of −1, indicating that MSE varies approximately as one over the estimation database size, as one might expect.

Some scaling transformations can be expected to be more difficult to estimate than others. For example, the scaling transformations associated to radiologist 1 are fairly steep for some output values [Fig. 13a]. In the case of the computer-to-radiologist, the transformations are steep for output values greater than 0.60, while in the case of the radiologist-to-computer, the transformations are steep for output values less than 0.20. In steeper regions of a transformation, more data are required for an accurate estimate. Although there is a greater density of radiologist output in the steepest part of the radiologist-to-computer transformations, the density of the computer output is rather flat, so that a smaller portion of output values are used in the estimation of the steepest portion of the computer-to-radiologist transformation. These kinds of differences may account for the higher average MSE found in the computer-to-radiologist transformations than for the radiologist-to-computer transformations in the case of radiologist 1 [Fig. 13b].

DISCUSSION

In this paper, we have approached the problem of comparing and interpreting values of output from two classifiers on the basis of likelihood ratio, a clinically relevant statistic that can be estimated from each classifier’s output from a sample of cases. A radiologist’s confidence rating for any particular case, in isolation, may be subject to a variety of interpretations. However, if the output value of a particular classifier, human or machine, can be related quantitatively to a clinically relevant statistic such as likelihood ratio, then a way of interpreting that output value is provided. Moreover, matching scales on the basis of likelihood ratio provides a way to transform the output of one classifier to the scale of another. Such matching provides a basis for comparing classifier output on a given case. For example, when the LR-scaled computer output for a particular case is greater than the raw output from of the radiologist, one can conclude that the computer is associating a higher likelihood ratio to that case than does the radiologist. This conclusion can be drawn because LR is monotonically related to Bayesian probability but independent of disease prevalence; therefore, it follows that, regardless of disease prevalence, when the LR-scaled computer output for any particular case is greater than the LR-scaled raw output of the radiologist for that case, it follows that, regardless of prevalence, the probability that that case is malignant is judged to be higher by the computer than by the radiologist.

The TPF-scaling transformation can be used to scale the computer output so that the malignant-case histogram of the scaled output “looks more like” the malignant-case histogram of the radiologist output; thus; using the same threshold for the TPF-scaled computer classifier output and for the raw radiologist output will yield the same sensitivity. Similarly, the FPF-scaling transformation can be used to scale the computer output so that the benign-case histogram of the scaled output looks more like the benign-case histogram of the radiologist output; thus, applying the same threshold to the FPF-scaled computer classifier output and to the raw radiologist output will result in the same specificity. The major problem with either of these methods is that sensitivity and specificity are rarely considered independently.

With CDF-scaling, a linear combination of TPF and FPF is matched instead. When the radiologist’s task is to make a biopsy decision and when the prevalence used to construct the CDF [see Eq. 9] is the prevalence of cancer in the clinical population, the CDF at a particular threshold yields the biopsy rate (fraction of total cases biopsied) for that threshold. Thus, the same threshold for the CDF-scaled computer classifier output and the raw radiologist output results in the same biopsy rate. However, if the performance of the radiologist is much lower than that of the computer, then the radiologist should probably be recommending biopsy for a greater portion of cases than should the computer classifier—i.e., should be operating at a higher biopsy rate. Of course, the same threshold does not need to be used for both classifiers, but this means that the user must keep two thresholds in mind, instead of one.

The LR-scaling transformation, on the other hand, can be used to scale the computer output so that applying the same threshold to the radiologist and scaled computer outputs causes both classifiers to operate with the same critical likelihood ratio—i.e., with the same minimum strength of evidence before a case is classified as malignant. In particular, the LR-scaling transformation causes the optimal operating points on the proper ROC curves for the two classifiers to be achieved at the same decision-variable threshold, because optimizing expected utility reveals that the optimal operating point on any ROC curve is located where the curve slope—and therefore, critical likelihood ratio—has a particular value determined by the prevalence of the disease in question and by the various costs and benefits of the decision consequences.^{28, 29}

In this paper, the proper binormal model was used to estimate LR, TPF, FPF, and CDF, but as we have commented already, there are many other ways to estimate these quantities. Previously,³¹ we reported on a nonparametric method for estimating the TPF, FPF, and CDF functions, which used normalized histograms and could also be used to estimated the CDF-scaling transformation. That nonparametric method for the estimation of TPF, FPF, and CDF produces similar scaling transformations, as does the semiparametric method we have reported on in this paper for the estimation of the same. We have not explored any nonparametric methods for the estimation of the LR-scaling transformation. To determine precisely any of the scaling transformations for a particular radiologist, the radiologist needs to evaluate numerous cases—potentially hundreds—as a basis for estimating the relationship between output and likelihood ratio. Time-consuming calibration of this kind is a limitation of our proposed methods.

We have focused on scaling between two classifiers, one Bayesian and the other not. We used the Bayesian nature of the computer output to estimate the LR from Bayes’ rule. However, if the computer is not Bayesian, then one can estimate the computer’s LR function as we have estimated the radiologist’s LR function and match as in Eq. 5. In other words, the techniques outlined in this paper can be used to scale between any two quasicontinuous classifiers that yield proper ROC curves, regardless of whether those classifiers estimate PM or not.

We also have proposed two ways to use scaling transformations in the presentation of computer output by an intelligent workstation. As mentioned in Sec. 1, we do not know whether the radiologist’s aided performance depends substantially on the scale of the computer output. Moreover, we do not know to what extent the radiologist’s scale remains constant over time or whether it is affected by the computer’s scale over time. Such questions seem potentially important to the development of CAD tools and should be addressed in future studies.

Although we expect that the aided radiologist’s performance will prove to depend on the computer’s output scale, we are currently unaware of any way to predict the “optimal” transformation, in part because of the difficulty of modeling human decision-making in diagnostic tasks. It is impossible to test all ways of scaling computer output, of course, but a reasonable and practical approach might be to investigate principled methods that can be interpreted in a clinically relevant manner, as we have done in this paper. The LR-transformation is a good candidate in this sense, because it takes into account estimates of both the malignant and benign case densities, requires no knowledge of disease prevalence, and is amenable to a clear clinically relevant interpretation.

CONCLUSION

We have developed and evaluated four transformations to scale the output of one classifier to the scale of another, each based on matching some statistical characteristic that is, in theory, monotonically related to classifier output. The resulting transformations also are monotonic and do not affect the performance of the classifier but allow for a more meaningful comparison of the output of two classifiers. We have argued that the ubiquity of the likelihood ratio makes it a natural basis for defining scale. In particular, the LR-scaling transformation scales so that the optimal operating points on proper ROC curves of the two classifiers are achieved at the same threshold of classifier output.

We have also presented two options for using scaling transformations to present the computer analysis to the radiologist on a CAD workstation. In the first, a scaling transformation (dependent on a statistical characteristic such as LR, TPF, FPF, or CDF) is used to map the computer’s probability-of-malignancy output onto the confidence scale of a particular radiologist, and the radiologist’s rating is shown together with the scaled computer analysis. In the second, the rating of the radiologist is scaled onto the probability of malignancy scale of the computer, with the scaled radiologist rating shown together with the original computer analysis.

This paper gives the conceptual basis and mathematical framework for a particular approach to scaling classifier output. Further research is needed to assess the practical implications and possible benefits of scaling computer output to the scale of the radiologist or vice versa.