Abstract
C-arm cone-beam CT (CBCT) could replace preoperative multi-detector CT (MDCT) scans in the cardiac interventional setting. However, cardiac gating results in view angle undersampling and the small size of the detector results in projection data truncation. These problems are incompatible with conventional tomographic reconstruction algorithms. In this paper, the prior image constrained compressed sensing (PICCS) reconstruction method was adapted to solve these issues. The performance of the proposed method was compared to that of FDK, FDK with extrapolated projection data (E-FDK), and total variation-based compressed sensing (TVCS). A canine projection dataset acquired using a clinical C-arm imaging system supplied realistic cardiac motion and anatomy for this evaluation. Three different levels of truncation were simulated. The relative root mean square error and the universal image quality index were used to quantify the reconstruction accuracy. Three main conclusions were reached. (1) The adapted version of the PICCS algorithm offered the highest image quality and reconstruction accuracy. (2) No meaningful variation in performance was observed when the amount of truncation was changed. (3) This study showed evidence that accurate interior tomography is possible for realistic objects if a prior image with minimal artifacts is available.
1. Introduction
Operative image guidance has enabled the development of numerous percutaneous interventions in cardiology (Topol, 2011), vascular medicine (Valji, 2006), and oncology (Geschwind and Soulen, 2008). In electrophysiological (EP) procedures, volumetric image datasets are used to produce a roadmap of the atria which is registered to fluoroscopic images during catheter ablation procedures for the treatment of cardiac arrhythmias (Ejima et al., 2010, Cappato et al., 2010). Novel stem cell injection procedures for myocardial regeneration (Stamm et al., 2003) may also benefit from volumetric roadmaps. The 3D dataset used in these procedures can be obtained using a preoperative multi-detector CT scan (MDCT). However, the repeated image registration required between the MDCT image volume and images acquired using the real time imaging devices in the surgical room can significantly prolong the procedure. Therefore, it is highly desirable to directly use the cone-beam CT (CBCT) imaging capability provided by the digital flat panel-based interventional imaging suites to generate the necessary roadmap for such interventions. Due to cardiac motion, it may also be desirable to obtain a separate roadmap for different cardiac phases for optimal guidance. Such time-resolved navigation would require 4D CBCT imaging.
However, time-resolved interventional cardiac CBCT is technically challenging for two reasons. First, high temporal resolution images must be obtained using a C-arm gantry. Such a system has a relatively slow period of rotation, which allows several heart contractions to occur during the scan. The acquired projection data are retrospectively sorted into different cardiac phases. Each gated dataset is used to reconstruct a separate image volume for each phase. The first challenge originates from the fact that these gated datasets are highly undersampled with respect to view angles. If a conventional filtered backprojection (FBP) reconstruction algorithm -- such as the FDK algorithm (Feldkamp et al., 1984) -- is used, the reconstructed images are contaminated by a high level of streaking artifacts. The second challenge is caused by the small size of the detector only about 20 cm across in most cases. This results in a small scanning field of view (SFOV), which is often too small to cover the entire width of adult patients. Consequently, the system is prone to data truncation artifacts if FBP methods are used. These two challenges severely limit the quality of the current cardiac C-arm CBCT images.
Given that images are known a priori to be sparse under a particular transform, a possible approach to relax the classical Nyquist-Shannon sampling requirements is to use compressed sensing (CS) (Donoho, 2006, Candes et al., 2006, Candes and Tao, 2006). The CS approach used in this paper is called prior image constrained compressed sensing (PICCS) (Chen et al., 2008). PICCS improves on CS by incorporating a prior image similar to that to be reconstructed into a sparsifying transformation. This was shown to improve the undersampling capabilities of the CS framework and the noise properties of the images reconstructed (Chen et al., 2008). PICCS was applied to dynamic CBCT in image-guided radiation therapy (Leng et al., 2008) and in image-guided cardiac interventions (Chen et al., in press). In these applications, the prior image is reconstructed using the non-gated, fully-sampled projection dataset. However, the data truncation problem was not addressed in these initial publications.
The problem of image reconstruction from truncated projections has been studied extensively (Natterer, 1986). It is well known that it results in severe cupping artifacts. Several exact and approximate methods have been suggested to improve image quality. The projection data extrapolation method aims to approximate the missing projection segments using some a priori information (Herman and Lewitt, 1981, Ogawa et al., 1984, Ohnesorge et al., 2000, Ruchala et al., 2002, Hsieh et al., 2004, Sourbelle et al., 2005, Starman et al., 2005, Wiegert et al., 2005, Anoop and Rajgopal, 2007, Zamyatin and Nakanishi, 2007, Maltz et al., 2007, Kolditz et al., 2010, Kolditz and al., 2011, Zhao et al., 2011). It is also possible to increase the spatial and angular sampling to mitigate cupping artifacts moderately. Such an increase minimizes the impact of missing segments in the center of the field of view. The idea of differentiated backprojection (DBP) has been shown to enable exact reconstruction in cases of partial data truncation (Chen, 2003, Noo et al., 2004, Zou and Pan, 2004, Zhuang et al., 2004, Pan et al., 2005, Defrise and et al., 2006). The DBP can be used to exactly reconstruct images from fully-truncated projection data using a projection onto convex sets algorithm (POCS) provided that accurate information about the image object is know for a small region of interest inside the object (Ye et al., 2007a, Ye et al., 2007b, Li et al., 2009, Yu et al., 2008, Kudo and et al., 2008, Ye et al., 2008). Recently, the reconstruction of piecewise constant image objects from truncated projections was been shown to be possible using total variation based compressed sensing (TVCS) (Yu and Wang, 2009, Yu et al., 2009, Han et al., 2009). In these publications, TVCS was applied to fully-sampled projection datasets. Higher-order TVCS has also been shown to enable the exact reconstruction of piecewise polynomial objects (Yang et al., 2010). A method combining the TVCS and the POCS approaches has been suggested (Taguchi et al., 2011). Hardware solutions such as multi-resolution (Maass et al., 2011) acquisitions and x-ray filtration (Schafer et al., 2010) have also been investigated.
In this paper, we address both challenges encountered in cardiac C-arm CBCT by adapting the PICCS (Chen et al., 2008) to account for projection data truncation. The prior image for the PICCS reconstruction is reconstructed using the conventional FDK algorithm combined with a projection data extrapolation scheme. Furthermore, the PICCS objective function is modified to account for truncated projections.
The layout of the article is as follows. Section 2 briefly reviews the PICCS algorithm and its application to cardiac CBCT. Section 3 describes the data extrapolation method used to produce the prior image. The adapted version of the PICCS algorithm is presented in section 4. The methods and materials are described in section 5, while the results are presented in section 6, discussion in section 7, and the conclusions in section 8.
2.Review of prior image constrained compressed sensing (PICCS)
CS is a technique that aims to find solutions to underdetermined linear systems. One of its enabling ideas is sparsity. If a signal is known to be sparse under a certain transform, then it is possible to reconstruct the signal with high accuracy using a number of samples considerably lower than that dictated by the Nyquist-Shannon criterion. In practice, the reconstruction is accomplished by a constrained norm minimization since this procedure is tractable and is known to promote sparsity.
| (1) |
where x̂ is the reconstructed signal, Ψ is a transformation under which x is sparse, A is the measurement system matrix and y is the measurement data vector. Another possible formulation of this problem is closely related to basis pursuit denoising (Chen, 2001):
| (2) |
The generalization of Eq. (2) in the context of statistical image reconstruction was presented in (Tang et al., 2009).
In x-ray CT applications, the gradient norm transformation is often used because it greatly sparsifies piecewise-constant images (Rudin et al., 1992, Chen et al., 2008, Sidky and Pan, 2008, Nett et al., 2008, Tang et al., 2009, Jia et al., 2010, Choi et al., 2010, Bian et al., 2011a, Bian et al., 2011b, Defrise and et al., 2011, Ouyang et al., 2011, Ritschl et al., 2011). If one stores an M by N image as a vector using lexicographical ordering x∈RMN×1, the norm of the gradient transformation is equal to the total variation (TV):
| (3) |
where ε is a small constant which ensures that the TV is differentiable at the origin.
In medical imaging, an image similar to the one to be reconstructed is often available. The PICCS algorithm takes advantage of this prior image in order to sparsify the reconstruction using a difference operation. This operation also enables the target image to partially inherit the noise characteristics of the prior image. Formally, the reconstruction can be accomplished by solving the following optimization problem (Chen et al., 2008, Theriault-Lauzier et al., in press):
| (4) |
where xp is the prior image and α is the prior image parameter that controls the relative weight of the two sparsity-promoting terms of the objective function. λ is the regularization parameter to tradeoff the PICCS regularization function term and the data fidelity term.
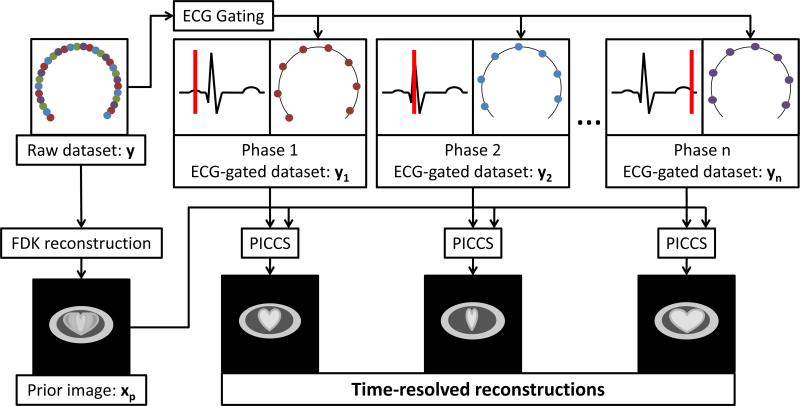
The nature of the prior image is application specific (Nett et al., 2008, Leng et al., 2008, Chen et al., 2009a, Tang et al., 2010, Szczykutowicz and Chen, 2010, Ramirez-Giraldo et al., 2011, Lubner et al., 2011). In the case of time-resolved cardiac CBCT, an interventional cardiac C-arm gantry with a flat-panel detector is used to acquire the projection dataset using a single slow (8 to 14 seconds) rotation (Chen et al., 2009b, Chen et al., 2011). Several cardiac contractions occur during the acquisition of over 400 view angles. A reconstruction of the whole dataset using FDK yields a temporally-averaged image volume with a relatively high SNR and a low level of streaking artifacts. These characteristics make this image a prime candidate to be used as a prior image. To recover temporal information, the projection dataset is retrospectively gated using the electrocardiogram (ECG) signal recorded during the acquisition. Each gated dataset only includes 14 to 30 view angles depending on the heart rate of the subjects. This makes the reconstruction of time-resolved images a highly underdetermined inverse problem, which is solved using the PICCS algorithm. The workflow described above is summarized schematically in FIG 1.
FIG 1.
Schematic workflow of the PICCS-based 4D cardiac CBCT image acquisition and reconstruction framework. The raw projection dataset is acquired in a single rotation. The gated datasets do not share common projection view angles with each other; in other words, the gating procedure sorts a particular view angle into a single gated dataset.
The potential limitations of the approach are described in (Chen et al., 2011). The minimal number of projection view angles per gated dataset that allowed the recovery of temporal information was determined to be 14. For a 14-second acquisition, the subject's heart rate should be above 60 bpm, which is not difficult to fulfill in clinical practice.
3.Projection data extrapolation
The prior image used in cardiac CBCT PICCS is reconstructed using the FDK algorithm. Images reconstructed using FDK with truncated projection data suffer from considerable artifacts. To mitigate these artifacts, projection data extrapolation is used in this study.
The goal of projection data extrapolation is to mitigate truncation artifacts and to moderately extend the field of view that is reconstructed accurately. The approach used in this study approximates the support of the object by an ellipsoid (Kolditz and al., 2011). The investigation of specific methods of obtaining the approximate support -- such as projection-based, camera-based, or a priori volume techniques -- is out of the scope of this research. It is assumed for the rest of this article that an approximate support is known a priori.
Given a truncated cone-beam projection dataset y(u, v, t), where u, v, and t parameterize respectively the in-plane dimension, the axial dimension and the view angle, the algorithm used to generate the prior image from truncated projection is described below.
| ALGORITHM: Projection data extrapolation FDK (E-FDK) |
| INPUT: truncated projection data y, ellipsoid support parameters (a, b, c) and center (x0, y0, z0) |
| OUTPUT: reconstructed prior image xp |
| yellipsoid(u, v, t) ← SIMULATE cone beam projection data of ellipsoid (a, b, c, x0,y0, z0) |
| FOR all rows v and view angles t DO |
| (u0, u1) ← DETEMINE edges of truncated projection |
| FOR all u < u0 DO |
| yextrapolated(u, v, t) ← y(u0, v, t) / yellipsoid(u0, v, t) × yellipsoid(u, v, t) |
| END |
| FOR all u > u1 DO |
| yextrapolated(u, v, t) ← y(u1, v, t) / yellipsoid(u1, v, t) × yellipsoid(u, v, t) |
| END |
| END |
| xp(x, y, z) ← PERFORM FDK reconstruction (yextrapolated) |
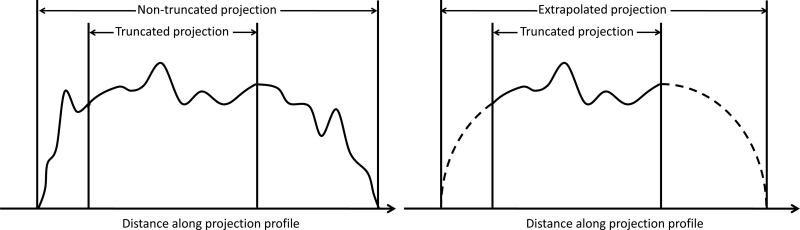
This method ensures continuity at the boundary between the measured and extrapolated regions. A schematic representation of an in-plane projection profile after the extrapolation procedure (yextrapolated) is illustrated in FIG 2.
FIG 2.
Illustration of the projection data extrapolation method. The extrapolated segments are the dashed lines.
4.4D cardiac CBCT using adapted PICCS
The PICCS algorithm can be modified in order to reconstruct images from fully truncated projection datasets. Specifically, the various terms of the objective function are calculated from specific regions of the image volume. The objective function is modified in the following manner:
| (5) |
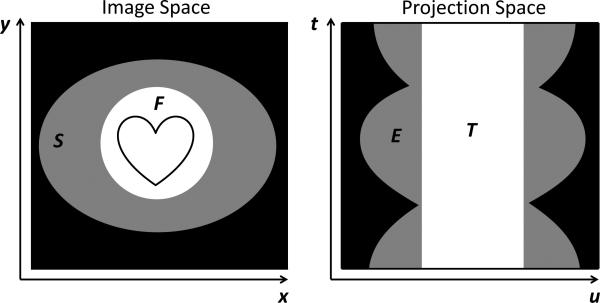
In this objective function, each term is calculated over the specific regions of the image object. The definition of the regions and the corresponding labels are given in Figure 3. To be more specific, let us define the terms of the objective function as:
| (6) |
| (7) |
and
| (8) |
FIG 3.
Illustration of the various image and projection space regions. F is the scanner field of view (SFOV). S corresponds to the assumed object support excluding the SFOV. E is the extrapolated region of projection space. T is the region of projection space for which data are acquired.
The regions of image and projection space used in equations (4-7) are illustrated in FIG 3. NF, , and NT are the number of voxels in each associated image region. Region S is excluded from the f1 term since the prior image is not expected to be accurate in that region. For the same reason, the f3 term excludes the extrapolated region E. f3 also excludes the region of the image outside in order to improve the convergence speed and accuracy. However, the term f2 includes region S since it is desirable that the image be approximately piecewise constant in that region.
As previously discussed, it was demonstrated in (Yu and Wang, 2009, Yu et al., 2009, Han et al., 2009) that piecewise-constant objects can be reconstructed from fully-truncated projections using TVCS. In the case of TV-based PICCS, this result applies in two ways. First, images of the cardiac ROI are mostly piecewise-constant since the contrast agent has a relatively constant concentration within the heart chambers. The TV term, f2, applies a penalty which favors a piecewise-constant image x. Second, the difference image x - xp is expected to also be mostly piecewise-constant. The prior image has only minimal truncation artifacts and temporal inconsistencies in xp mostly manifest themselves as large scale changes in contrast. The proposed approach takes advantage of these characteristics via the prior image term f1. This term promotes the reconstruction of a target image x that yields a piecewise-constant difference image x - xp.
The hypothesis investigated in this study was that the adapted PICCS reconstruction algorithm mitigates both truncation and undersampling artifacts in the context of 4D cardiac CBCT.
5.Methods and materials
The strategy used to evaluate the hypothesis was to acquire non-truncated projections using a clinical interventional system in an animal model and to truncate the projections artificially. This ensured that a non-truncated reconstruction was available for comparison. The amount of truncation was varied to simulate different detector dimensions. Four algorithms were used to reconstruct the datasets: FDK, EFDK, TVCS, and PICCS.
The dataset used in this study was acquired in vivo in a canine model. The study had Institutional Animal Care and User Committee (IACUC) approval. The subject was a one-year-old beagle with a weight of 9.8 kg. It was intubated, and its heart rate averaged 95 bpm during the scan. Prior to the scan, 37 mL of iodixanol-320 contrast agent (Visipaque, GE Healthcare, Waukesha, WI) were diluted in 113 mL of saline. The solution was injected using an automated injector (Medrad, Warrendale, PA). A GE Innova 4100 interventional imaging system (GE Healthcare, Waukesha, WI) with a detector size of (40×40) cm was used to acquire 420 projection view angles over a short-scan angular range of 210°. The total scan time was 14 seconds during which mechanical ventilation was suspended. The projections were retrospectively gated into 20 cardiac phases, each with 20 to 21 projection view angles. After reconstruction, each gated projection dataset yielded an independent image volume. In all cases, the image matrix size was set to 256×256×128 with an isotropic voxel size of 0.68 mm.
The ECG-based gating was performed using MATLAB (MathWorks, Natick, MA). Both TVCS and PICCS were implemented using the non-linear conjugate gradient method with backtracking line search (Nocedal and Wright, 1999). For all algorithms, the forward and back-projection, as well as the filtration operations were implemented using CUDA (Nvidia, Santa Clara, CA). The underlying optimization algorithm was coded using C++. A workstation equipped with a Q6700 Core 2 Quad CPU (Intel, Santa Clara, CA) and a GeForce GTX 560 Ti (Nvidia, Santa Clara, CA) was used to process the reconstructions.
Three levels of truncation were simulated, corresponding to flat panel sizes of (20×20) cm, (15×15) cm and (10×10) cm. The projection data outside the artificial scanner field of view (SFOV) was set to zero for the FDK reconstruction. This method is expected to produce images with both truncation and undersampling artifacts. The E-FDK algorithm described above was also applied to the gated projections; the reconstructions are expected to have mitigated truncation artifacts, but to be affected by undersampling. To conform with the method proposed in (Yu and Wang, 2009), all voxels of the initial guess image were set to zero for the TVCS reconstructions. In the case of PICCS, the prior image was used as an initial guess. This image was reconstructed using E-FDK from the full 420-view angle dataset. The PICCS reconstruction parameters α and λ were set based on the results from (Chen et al., 2011). α was set to 0.5 in all cases.
Reference images were reconstructed from the non-truncated datasets using the PICCS algorithm. To evaluate the reconstruction accuracy achieved by each algorithm, two quantitative metric were used. The first metric, the relative root mean square error (rRMSE), was measured within the SFOV for each approach:
| (9) |
where NSFOV is the number of voxels within the SFOV. The functions max() and min() yield the maximal and minimal voxel value within the SFOV of the reference image xref. The second metric, the universal quality index (UQI) (Wang and Bovik, 2002), is defined as:
| (10) |
where
and NSFOV is the number of voxels within the SFOV. The UQI takes values between 0 and 1. Large values correspond to high agreement in terms of correlation, mean image intensity value, and the contrast curve.
The left ventricular volume (LVV) was measured by manual delineation of every slice of each image volume for all cardiac phases. Because of the subjectivity of the measurement procedure, the LVV was not meant to be fully quantitative. It is only used to illustrate the temporal dynamics of the dataset and a potential clinical use of 4D cardiac imaging.
6.Results
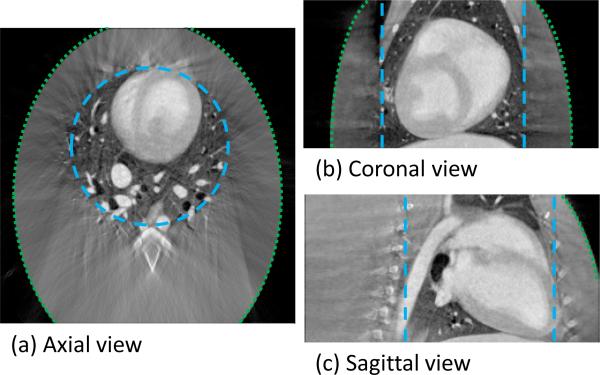
The prior image used for the PICCS reconstructions with a simulated detector size of (15×15) cm is presented in FIG 4. The E-FDK algorithm was used to reconstruct this image. The boundary of the SFOV is indicated by the blue long-dashed line in Figure 4, while the green short-dashed line encircles the assumed ellipsoidal object support.
FIG 4.
Three orthogonal slices through the PICCS prior image reconstructed using E-FDK. The long-dashed line encircles region F and the short-dashed line encircles region S. The truncation level simulated the use of a (15×15) cm detector.
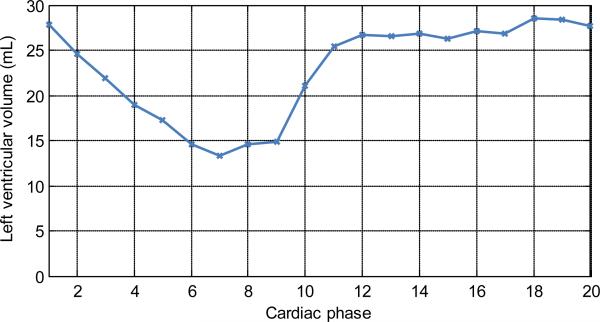
The gated datasets with a simulated detector size of (15×15) cm was used to investigate the performance of the four algorithms. In order to illustrate the dynamics present in the datasets, the LVV was measured from the truncated PICCS reconstructions (FIG 5). Again, this measurement was not meant to quantitatively evaluate the performance of the algorithm, but rather to show a potential clinical application.
FIG 5.
Plot of the left ventricular volume (LVV) as a function of cardiac phase. This plot is meant only as an illustration of the contraction dynamics at all 20 phases reconstructed. Phase 1 corresponds to the QRS complex.
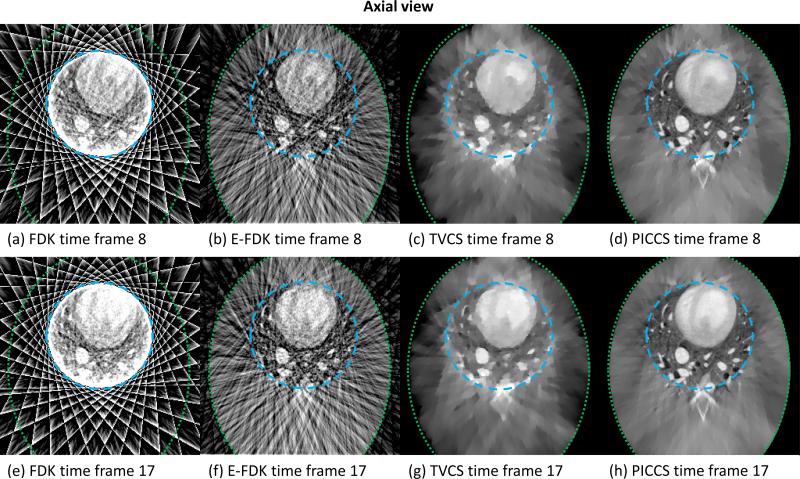
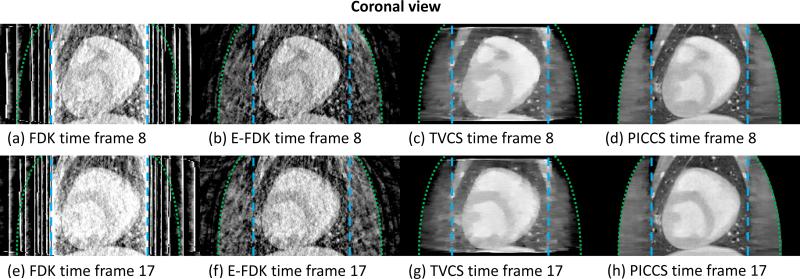
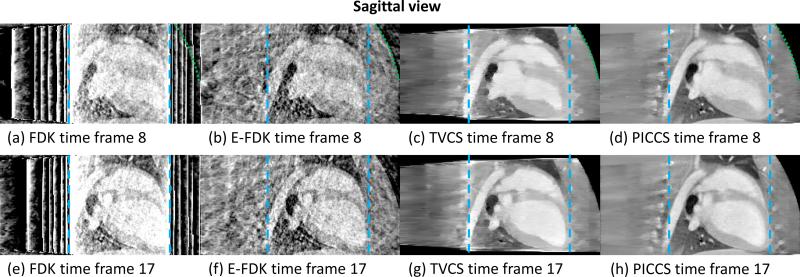
The images reconstructed using FDK, E-FDK, TVCS, and PICCS are presented in FIG 6 (axial view), FIG 7 (coronal view), and FIG 8 (sagittal view).
FIG 6.
Axial slice through the reconstructions from truncated projection dataset simulating a (15×15) cm detector size for the four reconstruction algorithms studied. Time frame 8 is at the end of the systole and time frame 17 is at the end of the diastole. The long-dashed line encircles region F and the short-dashed line encircles region S.
FIG 7.
Coronal slice through the reconstructions from truncated projection dataset simulating a (15×15) cm detector size for the four reconstruction algorithms studied. Time frame 8 is at the end of the systole and time frame 17 is at the end of the diastole. The long-dashed line encircles region F and the short-dashed line encircles region S.
FIG 8.
Sagittal slice through the reconstructions from truncated projection dataset simulating a (15×15) cm detector size for the four reconstruction algorithms studied. Time frame 8 is at the end of the systole and time frame 17 is at the end of the diastole. The long-dashed line encircles region F and the short-dashed line encircles region S.
As shown in FIGs 6, 7, and 8, the level and nature of artifacts varies between images reconstructed using different algorithms. The FDK reconstructions are plagued by a high level of truncation (cupping) and undersampling (streaks) artifacts. The latter artifacts also contaminate the E-FDK images. However, truncation artifacts are mostly corrected on these E-FDK images. The TVCS method mitigated both cupping and streaks. However, the object studied is only approximately piecewise-constant. The use of TVCS results in images which contain a large amount of patchy artifacts. These are particularly visible in the axial view since the TV is calculated in that plane. Small scale and low contrast structures are particularly degraded by this algorithm. The images reconstructed using PICCS have mitigated both undersampling and truncation artifacts. Furthermore, the algorithm accurately reconstructs both small scale and low contrast structures and does not result in obvious patchy artifacts.
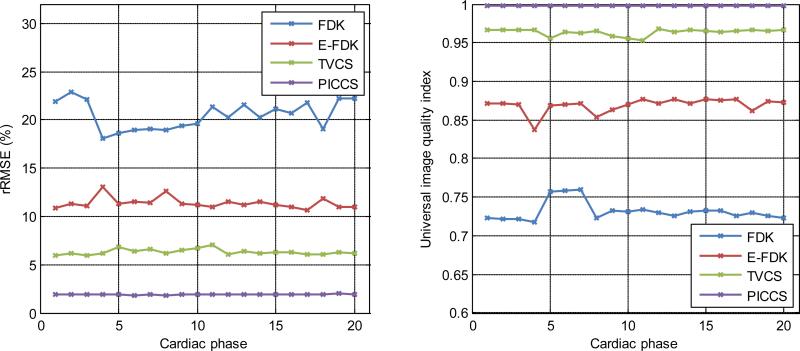
In order to quantify the reconstruction accuracy, the rRMSE and the UQI were measured for all images reconstructed with a simulated detector size of (15×15) cm. The results are plotted in FIG 9. The reference image used was the non-truncated PICCS reconstruction. The quantitative accuracy of each algorithm increases as expected from the qualitative evaluation. The average rRMSE over the 20 cardiac phases was 20.5% for FDK, 11.4% for E-FDK, 6.3% for TVCS, and 1.91% for PICCS which indicated that the PICCS reconstructions have the highest accuracy. The average UQI over the 20 cardiac phases was 0.732 for FDK, 0.869 for E-FDK, 0.964 for TVCS, and 0.998 for PICCS which indicated the image appearance is the most similar to the non-truncated case for the PICCS reconstructions.
FIG 9.
Plots of the quantitative image quality metrics for reconstructions produced using the four algorithms studied at all cardiac phases. The non-truncated PICCS reconstruction is taken as the reference. The truncation level simulated the use of a (15×15) cm detector.
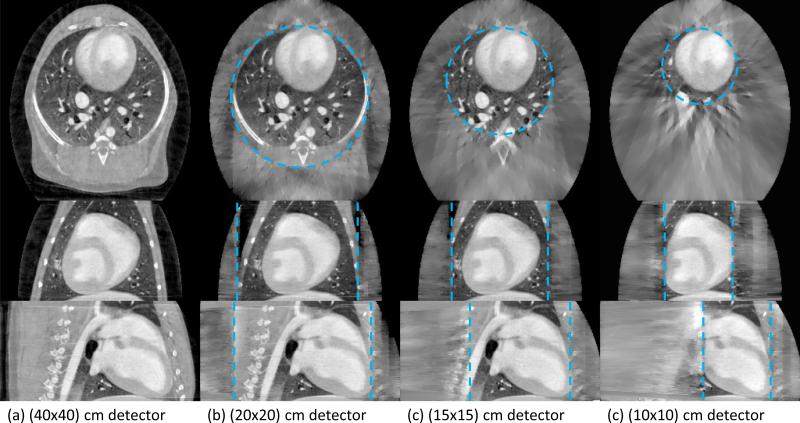
The first time frame of the dynamic dataset was used to evaluate the performance of the proposed approach with respect to the amount of truncation present at three simulated detector sizes. The reconstructions with various levels of truncation are presented in FIG 10. In each case, the reconstruction is only expected to be accurate within the SFOV denoted by the blue dashed line. Except for the reduction in SFOV size, no qualitative difference is observed within the SFOV.
FIG 10.
Images reconstructed using PICCS with varying levels of truncation. Three orthogonal slices are presented: axial (top row), coronal (middle row), and sagittal (bottom row). The dashed line encircles the SFOV in each case.
For all truncation cases, the rRMSE was measured to be very close to 1.6% and the UQI of about 0.996. Within the precision given, no dependence on the amount of truncation was observed. To ensure consistency between levels of truncation, all measurements were carried out within the SFOV of the (10×10) cm detector case using the non-truncated (40×40) cm detector image as a reference.
7.Discussion
A potential limitation of the quantitative measurements presented is that the reference image was produced using the non-truncated PICCS algorithm, which could have given PICCS an advantage over the other algorithms. However, a fully sampled reference image was not available in this case. While this may limit the strength of the conclusion about the advantage of PICCS over other algorithms, the results strongly support the hypothesis that the adapted PICCS mitigates both truncation and undersampling artifacts.
Another potential limitation of this study is the use a single canine dataset. Differences between the anatomy of the subject and that of patients are likely to result in variations in size and position of the regions described in FIG 3. The evaluation with respect to the amount of truncation present showed no meaningful dependence of the reconstruction accuracy on the size of the SFOV. This suggests that the proposed approach is rather robust with respect to geometrical variations. Further investigations, including a large-scale human subject validation, will answer this question more definitively in the future.
The datasets used in this study, like the vast majority of medically relevant cases, were only approximately piecewise-constant. Also, they were highly undersampled. Both of these factors explain the presence of patchy artifacts and consequently, the poor image quality of TVCS images. The results presented here expand on those of (Yu and Wang, 2009), where fully-sampled projection datasets were used. It is demonstrated that the images reconstructed using TVCS with truncation and undersampling suffer from the same types of artifacts as images with no truncation. Furthermore, the results presented here suggest that the requirement of TVCS approaches (Yu and Wang, 2009, Yu et al., 2009, Han et al., 2009, Yang et al., 2010) with regard to the properties of the object can be somewhat relaxed in practice. Indeed, it is demonstrated that realistic objects for which a prior image with minimal artifacts is available can be reconstructed with high accuracy using PICCS. This result is not specific to cardiac CBCT imaging, but rather is general to all types of truncated CT imaging.
It should be noted that the adaptation of the PICCS algorithm presented in this article is not fundamentally different from the formulation from (Chen et al., 2008). Essentially, the region of the image from which the terms of the objective function are calculated and the algorithm used to reconstruct the prior image are the only differences between the implementation used here and that used in other PICCS applications.
Finally, beyond the advantages relating to the less stringent detector size constraints, the results presented in this paper are also significant in terms of radiation dose reduction. Based on these results, it can be readily concluded that a high image quality can be maintained even if the x-ray beam is collimated down to cover only a volume of interest. A reduction in the width of the beam results in a reduction of the volume irradiated and in the overall radiation dose. This may have clinical significance.
8.Conclusion
Four algorithms were studied with regard to their ability to reconstruct time-resolved cardiac images from fully truncated projections acquired using a cardiac C-arm interventional system. A canine projection dataset was acquired in realistic conditions and supplied realistic cardiac motion. Three main conclusions can be drawn from the results. (1) The adapted version of the PICCS algorithm was shown to offer the highest image quality and reconstruction accuracy when compared with other approaches. (2) No meaningful variation in performance of PICCS was observed when the amount of truncation was varied. (3) This study showed evidence that accurate interior tomography is possible for realistic objects if a prior image with minimal artifacts is available to be used in PICCS.
Acknowledgements
The authors wish to acknowledge funding support from the National Institutes of Health (R01 EB009699), a GE Healthcare research grant, and a doctoral scholarship from NSERC-CRSNG (P.T.L). They are also grateful for stimulating discussions with Dr. Cyril Riddell. Finally, the authors thank Mr. John Garrett for his editorial assistance in preparation of the paper.
Footnotes
PACS 87.57.qp Computed tomography
87.57.nf Reconstruction
87.57.cp Artifacts and distortion
References
- Anoop KP, Rajgopal K. IEEE EMBS. Cité Internationale; Lyon, France: 2007. Estimation of missing data using windowed linear prediction in laterally truncated projections in cone-beam CT. pp. 2903–6. [DOI] [PubMed] [Google Scholar]
- Bian J, Han X, Sidky EY, Cao G, Lu J, Zhou O, Pan X. Investigation of Sparse Data Mouse Imaging Using Micro-CT with a Carbon-Nanotube-Based X-ray Source. Tsinghua Sci Technol. 2011a;15:74–78. doi: 10.1016/s1007-0214(10)70012-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian J, Siewerdsen JH, Han X, Sidky EY, Prince JL, Pelizzari CA, Pan X. Evaluation of sparse-view reconstruction from flat-panel-detector cone-beam CT. Phys Med Biol. 2011b;55:6575–99. doi: 10.1088/0031-9155/55/22/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candes EJ, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Information Theory. 2006;52:489–509. [Google Scholar]
- Candes EJ, Tao T. Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? IEEE Trans Information Theory. 2006;52:5406–5425. [Google Scholar]
- Cappato R, Calkins H, Chen SA, Davies W, Iesaka Y, Kalman J, Kim YH, Klein G, Natale A, Packer D, Skanes A, Ambrogi F, Biganzoli E. Updated worldwide survey on the methods, efficacy, and safety of catheter ablation for human atrial fibrillation. Circ Arrhythm Electrophysiol. 2010;3:32–8. doi: 10.1161/CIRCEP.109.859116. [DOI] [PubMed] [Google Scholar]
- Chen G-H, Theriault-Lauzier P, Tang J, Nett B, Leng S, Zambelli J, Qi Z, Bevins N, Raval A, Reeder SB, Rowley H. Time-resolved interventional cardiac C-arm cone-beam CT: an application of the PICCS algorithm. IEEE Trans Med Imaging. doi: 10.1109/TMI.2011.2172951. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen GH. A new framework of image reconstruction from fan beam projections. Med Phys. 2003;30:1151–61. doi: 10.1118/1.1577252. [DOI] [PubMed] [Google Scholar]
- Chen GH, Tang J, Hsieh J. Temporal resolution improvement using PICCS in MDCT cardiac imaging. Med Phys. 2009a;36:2130–5. doi: 10.1118/1.3130018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen GH, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys. 2008;35:660–3. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen GH, Tang J, Nett B, Leng S, Zambelli J, Qi Z, Bevins N, Reeder S, Rowley H. High temporal resolution cardiac cone-beam CT using a slowly rotating C-arm gantry. SPIE; Orlando, FL: 2009b. [Google Scholar]
- Chen GH, Theriault-Lauzier P, Tang J, Nett B, Leng S, Zambelli J, Qi Z, Bevins N, Reeder S, Rowley H. Time-resolved interventional cardiac C-arm cone-beam CT: An application of the PICCS algorithm. 2011. in press. [DOI] [PMC free article] [PubMed]
- Chen S. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2001;43:129. [Google Scholar]
- Choi K, Wang J, Zhu L, Suh TS, Boyd S, Xing L. Compressed sensing based cone-beam computed tomography reconstruction with a first-order method. Med Phys. 2010;37:5113–25. doi: 10.1118/1.3481510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Defrise M, et al. Truncated Hilbert transform and image reconstruction from limited tomographic data. Inverse Problems. 2006;22:1037. [Google Scholar]
- Defrise M, et al. An algorithm for total variation regularization in high-dimensional linear problems. Inverse Problems. 2011;27:065002. [Google Scholar]
- Donoho DL. Compressed sensing. IEEE Trans Information Theory. 2006;52:1289–1306. [Google Scholar]
- Ejima K, Shoda M, Yagishita D, Futagawa K, Yashiro B, Sato T, Manaka T, Nakajima T, Ohmori H, Hagiwara N. Image integration of three-dimensional cone-beam computed tomography angiogram into electroanatomical mapping system to guide catheter ablation of atrial fibrillation. Europace. 2010;12:45–51. doi: 10.1093/europace/eup371. [DOI] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. J. Opt. Soc. Am. A. 1984;1:612–619. [Google Scholar]
- Geschwind J-FH, Soulen MC. Interventional oncology: principles and practice. 2008 [Google Scholar]
- Han W, Yu H, Wang G. A General Total Variation Minimization Theorem for Compressed Sensing Based Interior Tomography. International Journal of Biomedical Imaging. 2009 doi: 10.1155/2009/125871. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herman GT, Lewitt RM. Evaluation of a preprocessing algorithm for truncated CT projections. J Comput Assist Tomogr. 1981;5:127–35. doi: 10.1097/00004728-198102000-00026. [DOI] [PubMed] [Google Scholar]
- Hsieh J, Chao E, Thibault J, Grekowicz B, Horst A, Mcolash S, Myers TJ. A novel reconstruction algorithm to extend the CT scan field-of-view. Med Phys. 2004;31:2385–91. doi: 10.1118/1.1776673. [DOI] [PubMed] [Google Scholar]
- Jia X, Lou Y, Li R, Song WY, Jiang SB. GPU-based fast cone beam CT reconstruction from undersampled and noisy projection data via total variation. Med Phys. 2010;37:1757–60. doi: 10.1118/1.3371691. [DOI] [PubMed] [Google Scholar]
- Kolditz D, Al. E. Comparison of extended field-of-view reconstructions in C-arm flat-detector CT using patient size, shape or attenuation information. Physics in Medicine and Biology. 2011;56:39. doi: 10.1088/0031-9155/56/1/003. [DOI] [PubMed] [Google Scholar]
- Kolditz D, Kyriakou Y, Kalender WA. Volume-of-interest (VOI) imaging in C-arm flat-detector CT for high image quality at reduced dose. Med Phys. 2010;37:2719–30. doi: 10.1118/1.3427641. [DOI] [PubMed] [Google Scholar]
- Kudo H, et al. Tiny a priori knowledge solves the interior problem in computed tomography. Physics in Medicine and Biology. 2008;53:2207. doi: 10.1088/0031-9155/53/9/001. [DOI] [PubMed] [Google Scholar]
- Leng S, Tang J, Zambelli J, Nett B, Tolakanahalli R, Chen GH. High temporal resolution and streak-free four-dimensional cone-beam computed tomography. Phys Med Biol. 2008;53:5653–73. doi: 10.1088/0031-9155/53/20/006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Kang K, Chen Z, Zhang L, Xing Y. A general region-of-interest image reconstruction approach with truncated Hilbert transform. J Xray Sci Technol. 2009;17:135–52. doi: 10.3233/XST-2009-0218. [DOI] [PubMed] [Google Scholar]
- Lubner MG, Pickhardt PJ, Tang J, Chen GH. Reduced image noise at low-dose multidetector CT of the abdomen with prior image constrained compressed sensing algorithm. Radiology. 2011;260:248–56. doi: 10.1148/radiol.11101380. [DOI] [PubMed] [Google Scholar]
- Maass C, Knaup M, Kachelriess M. New approaches to region of interest computed tomography. Med Phys. 2011;38:2868–78. doi: 10.1118/1.3583696. [DOI] [PubMed] [Google Scholar]
- Maltz JS, Bose S, Shukla HP, Bani-Hashemi AR. IEEE EMBS. Cité Internationale; Lyon, France: 2007. CT truncation artifact removal using water-equivalent thicknesses derived from truncated projection data. pp. 2907–11. [DOI] [PubMed] [Google Scholar]
- Natterer F. The mathematics of computerized tomography. SIAM; 1986. [Google Scholar]
- Nett B, Tang J, Leng S, Chen GH. Tomosynthesis via Total Variation Minimization Reconstruction and Prior Image Constrained Compressed Sensing (PICCS) on a C-arm System. Proc Soc Photo Opt Instrum Eng. 2008;6913:nihpa92672. doi: 10.1117/12.771294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nocedal J, Wright SJ. Numerical optimization. Springer; New York: 1999. [Google Scholar]
- Noo F, Clackdoyle R, Pack JD. A two-step Hilbert transform method for 2D image reconstruction. Phys Med Biol. 2004;49:3903–23. doi: 10.1088/0031-9155/49/17/006. [DOI] [PubMed] [Google Scholar]
- Ogawa K, Nakajima M, Yuta S. A reconstruction algorithm from truncated projections. IEEE Trans Med Imaging. 1984;3:34–40. doi: 10.1109/TMI.1984.4307648. [DOI] [PubMed] [Google Scholar]
- Ohnesorge B, Flohr T, Schwarz K, Heiken JP, Bae KT. Efficient correction for CT image artifacts caused by objects extending outside the scan field of view. Med Phys. 2000;27:39–46. doi: 10.1118/1.598855. [DOI] [PubMed] [Google Scholar]
- Ouyang L, Solberg T, Wang J. Effects of the penalty on the penalized weighted least-squares image reconstruction for low-dose CBCT. Phys Med Biol. 2011;56:5535–52. doi: 10.1088/0031-9155/56/17/006. [DOI] [PubMed] [Google Scholar]
- Pan X, Zou Y, Xia D. Image reconstruction in peripheral and central regions-of-interest and data redundancy. Med Phys. 2005;32:673–84. doi: 10.1118/1.1844171. [DOI] [PubMed] [Google Scholar]
- Ramirez-Giraldo JC, Trzasko J, Leng S, Yu L, Manduca A, Mccollough CH. Nonconvex prior image constrained compressed sensing (NCPICCS): theory and simulations on perfusion CT. Med Phys. 2011;38:2157–67. doi: 10.1118/1.3560878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritschl L, Bergner F, Fleischmann C, Kachelriess M. Improved total variation-based CT image reconstruction applied to clinical data. Phys Med Biol. 2011;56:1545–61. doi: 10.1088/0031-9155/56/6/003. [DOI] [PubMed] [Google Scholar]
- Ruchala KJ, Olivera GH, Kapatoes JM, Reckwerdt PJ, Mackie TR. Methods for improving limited field-of-view radiotherapy reconstructions using imperfect a priori images. Med Phys. 2002;29:2590–605. doi: 10.1118/1.1513163. [DOI] [PubMed] [Google Scholar]
- Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena. 1992;60:259–268. [Google Scholar]
- Schafer S, Noel PB, Walczak AM, Hoffmann KR. Filtered region of interest cone-beam rotational angiography. Med Phys. 2010;37:694–703. doi: 10.1118/1.3284540. [DOI] [PubMed] [Google Scholar]
- Sidky EY, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol. 2008;53:4777–807. doi: 10.1088/0031-9155/53/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sourbelle K, Kachelriess M, Kalender WA. Reconstruction from truncated projections in CT using adaptive detruncation. Eur Radiol. 2005;15:1008–14. doi: 10.1007/s00330-004-2621-9. [DOI] [PubMed] [Google Scholar]
- Stamm C, Westphal B, Kleine HD, Petzsch M, Kittner C, Klinge H, Schumichen C, Nienaber CA, Freund M, Steinhoff G. Autologous bone-marrow stem-cell transplantation for myocardial regeneration. Lancet. 2003;361:45–6. doi: 10.1016/S0140-6736(03)12110-1. [DOI] [PubMed] [Google Scholar]
- Starman J, Pelc N, Strobel N, Fahrig R. Estimating 0th and 1st moments in C-arm CT data for extrapolating truncated projections. Proceedings of SPIE. 2005 [Google Scholar]
- Szczykutowicz TP, Chen GH. Dual energy CT using slow kVp switching acquisition and prior image constrained compressed sensing. Phys Med Biol. 2010;55:6411–29. doi: 10.1088/0031-9155/55/21/005. [DOI] [PubMed] [Google Scholar]
- Taguchi K, Xu J, Srivastava S, Tsui BM, Cammin J, Tang Q. Interior region-of-interest reconstruction using a small, nearly piecewise constant subregion. Med Phys. 2011;38:1307–12. doi: 10.1118/1.3549763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J, Hsieh J, Chen GH. Temporal resolution improvement in cardiac CT using PICCS (TRIPICCS): performance studies. Med Phys. 2010;37:4377–88. doi: 10.1118/1.3460318. [DOI] [PubMed] [Google Scholar]
- Tang J, Nett BE, Chen GH. Performance comparison between total variation (TV)-based compressed sensing and statistical iterative reconstruction algorithms. Phys Med Biol. 2009;54:5781–804. doi: 10.1088/0031-9155/54/19/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theriault-Lauzier P, Tang J, Chen G-H. Prior Image Constrained Compressed Sensing (PICCS): Implementation and Performance Evaluation. in press. [DOI] [PMC free article] [PubMed]
- Topol EJ. Textbook of interventional cardiology. 2011 [Google Scholar]
- Valji K. Vascular and interventional radiology. 2006 [Google Scholar]
- Wang Z, Bovik AC. A universal image quality index. Signal Processing Letters, IEEE. 2002;9:81–84. [Google Scholar]
- Wiegert J, Bertram M, Netsch T, Wulff J, Weese J, Rose G. Projection extension for region of interest imaging in cone-beam CT. Acad Radiol. 2005;12:1010–23. doi: 10.1016/j.acra.2005.04.017. [DOI] [PubMed] [Google Scholar]
- Yang J, Yu H, Jiang M, Wang G. High Order Total Variation Minimization for Interior Tomography. Inverse Probl. 2010;26:350131–3501329. doi: 10.1088/0266-5611/26/3/035013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye Y, Yu H, Wang G. Exact interior reconstruction with cone-beam CT. Int J Biomed Imaging. 2007a;2007:10693. doi: 10.1155/2007/10693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye Y, Yu H, Wang G. Exact interior reconstruction from truncated limited-angle projection data. Int J Biomed Imaging. 2008;2008:427989. doi: 10.1155/2008/427989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye Y, Yu H, Wei Y, Wang G. A general local reconstruction approach based on a truncated hilbert transform. Int J Biomed Imaging. 2007b;2007:63634. doi: 10.1155/2007/63634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Wang G. Compressed sensing based interior tomography. Phys Med Biol. 2009;54:2791–805. doi: 10.1088/0031-9155/54/9/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Yang J, Jiang M, Wang G. Supplemental analysis on compressed sensing based interior tomography. Phys Med Biol. 2009;54:N425–32. doi: 10.1088/0031-9155/54/18/N04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Ye Y, Wang G. Interior Reconstruction Using the Truncated Hilbert Transform via Singular Value Decomposition. J Xray Sci Technol. 2008;16:243–251. [PMC free article] [PubMed] [Google Scholar]
- Zamyatin AA, Nakanishi S. Extension of the reconstruction field of view and truncation correction using sinogram decomposition. Med Phys. 2007;34:1593–604. doi: 10.1118/1.2721656. [DOI] [PubMed] [Google Scholar]
- Zhao S, Yang K, Yang X. Reconstruction from truncated projections using mixed extrapolations of exponential and quadratic functions. J Xray Sci Technol. 2011;19:155–72. doi: 10.3233/XST-2011-0284. [DOI] [PubMed] [Google Scholar]
- Zhuang T, Leng S, Nett BE, Chen GH. Fan-beam and cone-beam image reconstruction via filtering the backprojection image of differentiated projection data. Phys Med Biol. 2004;49:5489–503. doi: 10.1088/0031-9155/49/24/007. [DOI] [PubMed] [Google Scholar]
- Zou Y, Pan X. Exact image reconstruction on PI-lines from minimum data in helical cone-beam CT. Phys Med Biol. 2004;49:941–59. doi: 10.1088/0031-9155/49/6/006. [DOI] [PubMed] [Google Scholar]