A new algorithm quantifies the roles of wind and midge flight activity in the bluetongue epizootic in northwest Europe

Abstract

The 2006 bluetongue (BT) outbreak in northwestern Europe had devastating effects on cattle and sheep in that intensively farmed area. The role of wind in disease spread, through its effect on Culicoides dispersal, is still uncertain, and remains unquantified. We examine here the relationship between farm-level infection dates and wind speed and direction within the framework of a novel model involving both mechanistic and stochastic steps. We consider wind as both a carrier of host semio-chemicals, to which midges might respond by upwind flight, and as a transporter of the midges themselves, in a more or less downwind direction. For completeness, we also consider midge movement independent of wind and various combinations of upwind, downwind and random movements. Using stochastic simulation, we are able to explain infection onset at 94 per cent of the 2025 affected farms. We conclude that 54 per cent of outbreaks occurred through (presumably midge) movement of infections over distances of no more than 5 km, 92 per cent over distances of no more than 31 km and only 2 per cent over any greater distances. The modal value for all infections combined is less than 1 km. Our analysis suggests that previous claims for a higher frequency of long-distance infections are unfounded. We suggest that many apparent long-distance infections resulted from sequences of shorter-range infections; a ‘stepping stone’ effect. Our analysis also found that downwind movement (the only sort so far considered in explanations of BT epidemics) is responsible for only 39 per cent of all infections, and highlights the effective contribution to disease spread of upwind midge movement, which accounted for 38 per cent of all infections. The importance of midge flight speed is also investigated. Within the same model framework, lower midge active flight speed (of 0.13 rather than 0.5 m s⁻¹) reduced virtually to zero the role of upwind movement, mainly because modelled wind speeds in the area concerned were usually greater than such flight speed. Our analysis, therefore, highlights the need to improve our knowledge of midge flight speed in field situations, which is still very poorly understood. Finally, the model returned an intrinsic incubation period of 8 days, in accordance with the values reported in the literature. We argue that better understanding of the movement of infected insect vectors is an important ingredient in the management of future outbreaks of BT in Europe, and other devastating vector-borne diseases elsewhere.

1. Introduction

Bluetongue (BT) is a vector-borne viral disease of domestic and wild ruminants. The virus is transmitted by biting midges, Culicoides (Diptera: Ceratopogonidae), and causes disease with severe adverse effects on ruminant livestock. These effects include reduced productivity in cattle and fatal disease in sheep. Despite what is known about BT transmission, the rapid spread of BT across the landscape of northwest Europe during the 2006 outbreak was a surprise to many veterinarians and entomologists, and remains largely unexplained.

Many insects use wind for dispersal or migration and can, when infected with a pathogen, introduce diseases into new areas. To date, there is no evidence that midges belonging to the genus Culicoides actively migrate in ways shown by many other insects such as locusts [1]. Nevertheless, wind-borne dispersal of Culicoides from infected areas has been implicated as an explanation for the introduction of bluetongue virus (BTV) over both sea and land in the absence of recorded movements of their vertebrate hosts, for example, from Cuba to Florida, USA [2], from Morocco to Portugal [3], from Turkey or Syria to Cyprus [3], from Sardinia to the Balearic Islands [4] and from Mexico to Montana, USA [5]. These studies stratified vector dispersal (via suitable winds) into either local or long-distance spread without using any statistical assessment of the agreement between the speculated wind-borne midge trajectories and the diseases they might have been carrying. The primary ‘confirmation’ of wind-borne spread was therefore from qualitative correspondence of disease and wind patterns, alone.

The inland spread of bluetongue virus-serotype 8 (BTV-8) across northwest Europe in 2006 [6] elicited a few studies on the relationship between wind and the epizootic [7] among a large body of literature on its epidemiological characteristics [8,9]. Apart from the wind, other factors may have contributed to the BTV-8 epizootic, such as random midge flight [10] and human transport of the virus, host and/or midges [11–16]. The inclusion of processes beyond wind alone, however, considerably increases the complexity of the models involved, and often reduces our ability to understand the relative importance of each of the many factors potentially involved in the 2006 outbreak: midge flight capability [17], local spatial scale dynamics and characteristics (topography, land use, farm management, etc. [18]), climate [19], virus mutation rate [20], vector competence for specific virus serotypes, transmission parameters and incubation period [21]. Moreover, there are no direct measurements of how wind affects midge flight, although it might be expected that small insects such as Culicoides have limited flight capacity and are unlikely to take off and fly at all above certain wind speeds, as suggested by the negative correlation between midge numbers (or rate of midge biting on hosts, as in Carpenter et al. [17]) and wind speed found for the obsoletus group, common Culicoides spp. in northwest Europe [22,23].

Despite improvements in the methods used to describe winds and wind dispersion over the sea [24], there is still a lack of quantitative methods to relate wind fields and disease outbreaks in inland areas. The aim of this paper is to present a robust statistical evaluation of the relationship between wind fields, midge movements and the 2006 BTV-8 epizootic in northwest Europe. The algorithm developed here (called ‘spatiotemporal wind-outbreak trajectory simulation’, SWOTS) identifies possibly important winds, and related midge movements, and reports their correlation with the developing epizootic.

2. Methods

(a). Data

The data used in this study were the farms infected with BTV-8 in 2006 (longitude, latitude and confirmation date of infection), as reported to the World Organization for Animal Health (OIE), in Germany, France, Belgium, the Netherlands and Luxembourg (electronic supplementary material, figure S1, and supplementary data table). The wind fields used in the simulations reported here were produced from the UK Met Office's Unified Model as hourly wind speed and direction estimated at a nominal height of 10 m above ground level at the point locations of all the farms that eventually reported infections. These wind speeds were then interpolated to a height of 2 m to represent surface conditions experienced by midges before and on becoming airborne.

(b). Assumptions about midge behaviour

Predictions of the model are affected by the assumptions made in it for midge behaviour and movement, summarized in table 1, including midge distribution, midge infectivity, host distribution, active midge flight speed, time spent by the midge in the air, the total daily flight duration, midge take-off conditions, midge flight movement conditions, host attraction, and intrinsic incubation period (IIP; full description in the electronic supplementary material). The robustness of the model's results to some of these assumptions was examined in various ways, as explained later (see §2f).

Table 1.

Parameters used in the SWOTS algorithm. R, random movement; D, downwind movement; U, upwind movement.

	D	U	R	mixed R–D	mixed R–U
active midge flight speed (m s−1)	0.5	0.5	0.13	0.13 (R) and 0.5 (D)	0.13 (R) and 0.5 (D)
midge flight speed in wind (m s−1)	0.5 + wind speed	0.5 − wind speed	0.13	0.13 (R) and 0.5 + wind speed (D)	0.13 (R) and 0.5 − wind speed (D)
maximum time of flight (h)	10a	4	10a	10a	10a (R) and 4 (U)
maximum wind speed for flight (m s−1)	11	0.5	—	11	0.5
maximum wind speed to take off (m s−1)	3	0.5	—	3	0.5
common parameters
distance at which the host can be targeted by the midge (m)	300
farm buffer radius (m)	750
intrinsic incubation period (days) [IIP]	from 1 to 21
time spent by the midge in the air travelling from farm to farm (days) [DT]	from 1 to 21

^aThis is the value used for SWOTS analysis using average wind conditions over the 24 h daily period. For the alternative analyses using the five periods within each 24 h day, this figure was reduced to 4 h.

(c). Spatio-temporal wind-outbreak trajectories simulation algorithm

In this paper, we propose a novel algorithm (electronic supplementary material, figure S2), SWOTS (available from the corresponding author), to quantify analyses of disease spread that are often conducted using only qualitative methods [2,5,7]. It includes five types of Culicoides movement (downwind, upwind, random, downwind and random, and upwind and random) and combines a search-fitting model with a stochastic simulation analysis.

For clarity in what follows, we use the term ‘infected midges’ to indicate carriers of BTV-8 between farms. We use the term ‘vector’ in its mathematical sense, a variable with both magnitude and direction (e.g. as applied to wind, or the movement of infected midges). Hence, an ‘infection vector’ is the mathematical vector between an already infected farm and a susceptible farm that may be infected by it through the movement of infected midges. The track of an infected midge over the landscape is referred to as a ‘trajectory’ (electronic supplementary material, figure S3).

By exploring the correlations [25] between the wind fields and the infection vectors at each plausible spatial and temporal scale, SWOTS identifies optimal parameter values to describe the data and then simulates disease spread using the midge movements obtained by the combination of local stochastic wind fields and midge flight assumptions. The parameters optimized by SWOTS are the host IIP, the number of days of midge travel from farm to farm (days travelled, DT) and the time of day (TOD) (associated with changes in both wind speed and direction) and the type of wind averaging. The host IIP together with the vector's extrinsic incubation period (EIP) constitute the overall incubation period [26], which is estimated to be between 8 and 37 days (depending on temperature, being shorter at higher temperatures [19]).

Once the parameters are optimized, SWOTS simulates the outbreak by re-calculating the midge trajectories according to the optimized parameters and a stochastic wind field, assuming pre-defined distributions for wind angle and speed. This is motivated by the fact that, within a few hours, the wind can show a considerable variation in speed and direction. In the SWOTS analysis, each wind trajectory is recalculated 1000 times with different values of speed and direction. Hence each infected farm in each interval is associated with many different possible infected midge trajectories going from it. Some of these trajectories will end up on uninfected farms and eventually infect them. SWOTS examines the associations between suspected movement of infected midges from infected farms to susceptible farms, and identifies the most likely source and route of infection to each susceptible farm (see electronic supplementary material, equations S12 and S13). The infecting farms and the type of prevalent midge movement were estimated according to their probability values (full description in the electronic supplementary material).

3. Results and discussion

(a). The main types of midge movement explaining the outbreak

Using finer resolution surface wind information (at the heights of 2 and 10 m rather than 1 km) and more biologically realistic assumptions about midge movement than have been used previously (table 1 and electronic supplementary material, table S1), our simulations show that downwind movement alone is not sufficient to explain the 2006 BT outbreak in northern Europe and that upwind midge flight is also needed to describe the observed spread of disease (an animated simulation can be found in the electronic supplementary material, Epidemic Spread Video). All types of midge movements considered here were found to be significantly correlated with the BTV-8 outbreak: random movement (correlation value 0.65 and p = 0.0143), downwind movement (correlation value 0.59, p = 0.0057) and upwind movement (correlation value 0.74 and p = 0.0002). The average direction of all the infection vectors was 18° from north (where compass direction north is 0°); i.e. in the mean direction of approximately north–northeast.

For any particular farm-to-farm infection, it was usually found that a single type of midge movement was most probably (p ≥ 0.90) responsible for that infection. Taking all such trajectories with a probability equal to or greater than 0.90 (electronic supplementary material, figure S4), farms were mostly connected by either downwind or upwind midge movements (figure 1) that together accounted for 77 per cent of all infections. A further 17 per cent of modelled infections involved mixed random and downwind movement (13%), mixed random and upwind movement (2%) and random movement alone (2%). Only 6 per cent of all infections remain unexplained by the model (table 2 and figure 2).

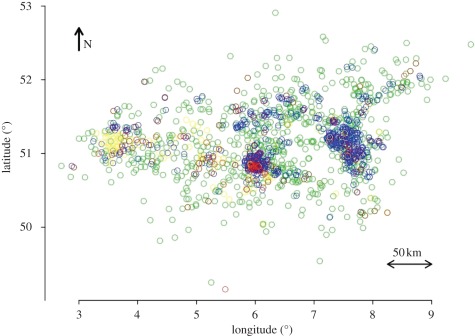
Figure 1.

Probable types of midge movement infecting farms, as determined by the SWOTS simulations. Blue circles show locations of farms infected by upwind midge movement; green circles, farms infected by downwind midge movement; and yellow circles, farms infected by other midge movements (random, mixed downwind and random, and mixed upwind and random). The red circles show the 6% of farms whose infections could not be explained by the SWOTS analysis. Farm locations are based on GPS readings (World Geodetic System 1984 (WGS84) datum), expressed in degrees.

Table 2.

Simulation analysis. Number of connected (i.e. infected) farms (N_c) and number of departing (i.e. infectious) farms (N_d) for each type of midge movement. N_d is less than N_c since one ‘departing farm’ might infect more than one ‘connected farm’. The last three columns show the proportion of each individual movement in the farm connections.

	Nc	Nd	%downwind	%upwind	%random
downwind	798	236	100	0	0
upwind	771	525	0	100	0
random	42	24	0	0	100
mixed R–D	257	23	83	0	17
mixed R–U	43	10	0	15	85

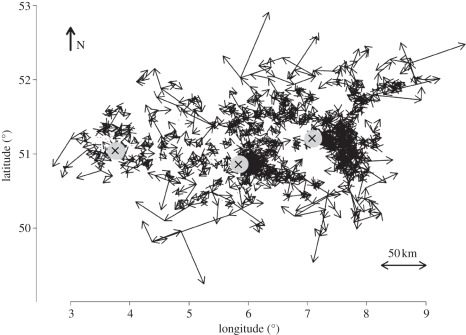
Figure 2.

Reconstructed BTV-8 epidemic in North Europe. The arrows show the direction of infection movement from infected farms (arrow origins) to farms that they infect (tips of arrows). In crossed grey circles and from left to right are three major cities: Ghent, Maastricht and Cologne. Farm locations are based on GPS readings (WGS84 data), expressed in degrees.

In the mixed movement models, the random component accounted for less than 20 per cent of the distance covered by the midges to arrive at, and infect, uninfected farms (table 2), because of the lower velocity of this type of movement in the model (table 1).

In all cases, the total distances covered by the midges were greater than the straight-line distances between farms because of the high variability in wind directions that resulted in midges covering larger distances before arriving at the next uninfected farm. In the electronic supplementary material, table S2, the lower average distances of mixed movement infections of farms is owing to the fact that such infections occurred between neighbouring farms rather than distant ones. It is clear that upwind movement was more important in the short distance infections, especially in Ghent and Cologne (figures 1 and 2).

(b). The spatial characteristics of the spread of bluetongue virus-serotype 8 between farms

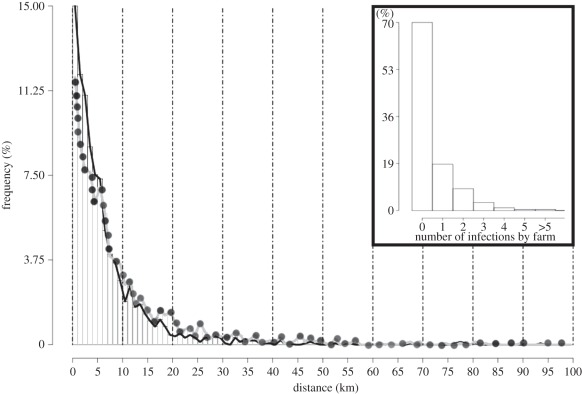
Of the 94 per cent of all outbreaks explained by SWOTS analysis, 54 per cent were found to be within Hendrickx et al.'s [7] short-range category, 38 per cent in their medium-range category and only 2 per cent in their long-range category (figures derived from figure 3, black line). Figure 3 shows that the vast majority of infections appear to have occurred over distances of 5 km or less. This result is in contrast to the conclusions of Hendrickx et al. [7], who considered only downwind movements at medium and long distances (i.e. not random, upwind or mixed movements) and assumed that, over short distances, all midge movements are effectively random, on the basis of Gerbier et al. [10], who applied standard cluster analysis to a small region of the same outbreak data.

Figure 3.

Histograms of the lengths of successful connections (in kilometres) explaining outbreaks on 94% of all the farms in the database. The histogram with the smoothed black line refers to the trajectories unconstrained by any EIP limitation, while the histogram with the smoothed grey line with dots shows the effect of requiring an EIP of at least 7 days in trajectories connecting infectious and infected farms. The dashed vertical lines are at 10 km intervals. In both histograms, the modal value is less than or equal to 1 km. Inset is a histogram of the frequency distribution of the number of new farms infected by the infectious farms during the 2006 outbreak; most (ca 70%) of the infected farms did not infect any other farm.

The different results of Hendrickx et al. [7] are also determined by their use of wind fields recorded at an average altitude of 1450 m rather than the much lower altitudes (i.e. surface layer conditions) used in the present analysis. Winds at high altitudes tend to move faster than those nearer the ground [27], may be in a different direction, and are much more stable, leading to a possible overestimate of long-range effects. Culicoides are usually sampled at low altitudes [28–34]; a recent analysis of the composition of insects in the air (sampling conducted for three/four weeks in July from 1999 to 2007, excluding 2001 and 2003) showed that only 14 Culicoides were caught at 170/200 m altitude over the entire sampling period [35]. We do not deny that midges (and many other insects) occur at altitudes up to 1 km, or even higher; we simply query the epizootiological/epidemiological importance of such records.

(c). The temporal scale and the estimated intrinsic incubation period during the outbreak

Because SWOTS analyses the time course of infections during the season, it is able to provide estimates of epizootiologically relevant parameters. The strongest correlations between farm infections and wind chatacteristics within each day were found for the wind vectors between 16.00 and 21.00 h rather than at any other time of day, or for the whole day combined (i.e. the summed daily wind vectors). This is also the time when peak midge activity occurs in the field [36–38].

The strongest correlation between infection and wind vectors was obtained with an IIP of 8 days. The midges needed between 1 and 20 days of winds (average time spent by the midge in the air = 7 days, less at short distances between farms) to reach the subsequent farm. The average speed of epizootic spread estimated by SWOTS in the 2006 outbreak was 1.8 km per day, with a maximum of 51 km in 1 day. This latter high value is alarming and emphasizes the need for continuous surveillance to detect when and where vector abatement or animal housing are required [39]. The more quickly the first infection is detected, the sooner disease spread can be restricted.

The IIP of 8 days means that if a farm was deemed infected on the 9^th of September (on which it is assumed the farm animals showed clinical symptoms, and were infectious to midges, for the first time), the infectious and infecting midge arrived at this farm on the 1st September (i.e. 8 days of IIP). This SWOTS-estimated value of the IIP for BTV-8 is consistent with what is described in the literature (4 to 12 days in Darpel et al. [40]).

(d). Further consideration of the extrinsic incubation period

For simplicity, we did not consider the midge's EIP, assuming that midges leaving an infected farm are infectious by the time they reach a susceptible farm (i.e. either they are infectious when they leave or else, being infected, they become infectious during their travels). The SWOTS model estimates that 62 per cent of the infected farms have a travel time (DT) of between 7 and 20 days, long enough for the EIP to have been completed before arrival at, and infection of, the next farm. For the remaining 38 per cent of the farms, we back-tracked along the trajectory beyond the first potentially infecting farm to previously potentially infecting farms. Seventy-nine per cent of these (i.e. 31% of the total of all infected farms) could have been infected by the second closest farm ‘in track’; a further 6 per cent (2% of all infected farms) by the third closest farm, and almost 3 per cent (1% of all infected farms) from the fourth closest farm. Only 12 per cent of the 38 per cent of farms (4% of all infected farms) remain with DTs less than the EIP (electronic supplementary material, figure S5). This change in the likely identity of the infecting farm increases the average length of the trajectories involved, as shown in figure 3 (grey line), but the effect is rather small (because the infecting farms involved are not widely scattered). The modal value for all infection distances remains at less than 1 km, with the majority of the distances within the short (43%) and medium (46%) ranges (of Hendrickx et al. [7]). Long-range movement accounts for only 5 per cent of the total.

(e). Robustness of spatio-temporal wind-outbreak trajectories simulation

The values estimated here for IIP, DT and TOD were the key parameters for the subsequent stochastic simulation from which were derived some of the results described above (e.g. the percentage of farms infected, and the routes of infection, whether upwind, downwind or by random movements, or some combination of these routes). We tested the robustness of SWOTS by verifying the conclusions drawn after taking out the data for half of the farms and re-estimating the parameters and variables. This exercise gave the same values as before for the temporal parameters, but with a slightly different correlation value for downwind movement (the correlation decreased from 0.59 to 0.55) and random movement (correlation decreased from 0.65 to 0.63) but not for upwind movements (correlation unchanged). This result suggests that any farms missed in the original dataset (i.e. the problem of under-ascertainment of infections) are unlikely to have influenced the parameter estimates of the model, unless such omitted farms were in some way ‘different’ from the reporting farms. If not, then inclusion of non-reporting farms is likely to increase rather than decrease the power of the SWOTS model, since they would provide an increased number of infections that could be successfully connected by the stochastic simulation.

(f). Sensitivity analysis

Sensitivity analysis was carried out in SWOTS investigating inter alia, the importance of host detection distance by the midges, and midge flight speed (electronic supplementary material, table S3). Keeping the farm radius constant at 750 m (ca half of the average minimum distance between two farms) and testing a range of potential detection distances (from 0 to 400 m), SWOTS shows a maximum reduction of 1 per cent of explained farms when this parameter is set to 0. This effect was largely owing to a change in mixed downwind-random movement. Assuming a detection distance of 0 m, and a farm radius at 375 m, reduces by 35 per cent the number of infections explained by SWOTS. It is evident that the midge's ability to detect hosts plays a crucial role at short farm radii.

Model results are also sensitive to midge flight speeds. By varying flight speeds, we tested the relative importance of upwind and downwind flight. Using a value of 0.13 m s⁻¹ (the one applied to random movement), upwind flight becomes effectively irrelevant, because wind-speed is usually greater than this (in which case only downwind, random or mixed downwind and random movements of midges are possible). The SWOTS model suggests that increasing the midges' flight speeds results in upwind farm infections becoming gradually more important until they become the main component of disease spread at flight speeds in excess of 0.5 m s⁻¹. In other words, the greater the midge's active flight speed, the greater is the non-downwind component of disease spread.

(g). Implications for disease control and management

Understanding the role of different types of midge movement in disease spread greatly enhances the design of appropriate target zones for surveillance and control. Long-range movements do not seem to have been an important ingredient in the 2006 outbreak (midge movements at distances larger than 100 km occur only with very low probability) but the potential exists for such movement to spread BTV-8 well outside the original outbreak area because we cannot exclude the possibility that a midge (once in the air) can reach altitudes higher than those used in this analysis, and hence may be carried by strong winds for long distances (e.g. 5 m s⁻¹ for 10 h corresponds to 180 km). This is probably the case for movements over the sea that are characterized by different conditions of atmospheric turbulence, surface roughness and the availability of midge food, as described by NAME, a Lagrangian dispersion model [41] developed by the UK Met Office to identify possible windborne routes of BTV spread from northwest Europe to the UK [24,42] and Sweden [43]. However, NAME assumed only downwind movement and was applied only at medium and large spatial scales, to investigate quite different phenomena from the much shorter-range dispersal that seems to have characterized the overland spread of the BTV-8 outbreak in northwestern Europe modelled here.

According to our analysis, 70 per cent of infected farms in the 2006 BT outbreak are transmission ‘end points’, and infect no other farms (inset in figure 3), either because of their spatial position relative to other farms and the prevailing wind conditions or, more simply, because they are infected at the end of the transmission season (brought about by on-coming winter conditions). Hence, some farms are more important than others in respect of any control or intervention strategy (akin to the ‘super-spreader’ idea in human disease epidemiology). For example, our simulations suggest that the very first farm recorded as infected in 2006 went on to infect 15 other farms during the rest of that year, and was also the most infective farm during the year.

SWOTS is an advanced alternative for investigating and forecasting flying insect-borne disease outbreak events (or even insect-related damage to crops/vegetation). Its application can be extended beyond the simple wind/outbreak relationship if any other relevant environmental factors can be converted to analogous geometric vectors (representing fluxes/directional gradients, etc.). Although the SWOTS algorithm took a considerable time to run on the present dataset (the parameter search took almost 7 days), its performance improves with more initial information (for example, prior estimates of incubation periods, time of the day of vector activity, etc. … ) or with fewer data points. For example, given prior estimates of the relevant parameters, and known wind fields, the model takes 1.5 days to predict the next 121 days of the outbreak. If the parameters are unknown, and so must be estimated from the data, SWOTS takes about 1 h to run on a dataset of 100 records over 7 days, as might be the case at the start of an epizootic. At such a stage of any new outbreak, parameter estimates are likely to be quite variable and so will need to be updated as more data accumulate. In this case, however, model updates can start with the previously estimated parameter values, so reducing algorithm running times.

This research is significant for many important actors in the study and control of vector-borne and other diseases: for public health actors and veterinary health managers who need to consider the different spatial and temporal scales of disease outbreaks to increase the efficacy of monitoring, surveillance and intervention during future outbreaks; for epidemiological scientists who need to consider different types of midge movements in future research correlating BT outbreaks and winds; and for entomological and physical scientists from whom we require more information about midges, their upwind flight speed, the time they spend each day in the air, their willingness or otherwise to fly at high altitude, etc. If these parameters can be estimated correctly, much easier (and faster) SWOTS frameworks can be applied in the future.

(h). Spatio-temporal wind-outbreak trajectory simulation limits

The unexplained portion of the BTV-8 epizootic (6% of the reported infected farms; electronic supplementary material, figure S2) might be due to human transport of midges or virus, to animal movement, or simply to erroneous estimation of the date of infection. The role of animal transportation in the dissemination of BTV-8 in northwest Europe may have been significant [44].

This outbreak was a new incursion initially affecting domestic animals but eventually spreading to local wild ungulate populations as well, for example, deer in Belgium [45,46]. Should the latter event result in more widespread and continuous infections of wild animals, we expect that our modelling approach will have less predictive power until it also incorporates characteristics of these wildlife populations (their distribution, abundance, movement patterns and infection status), quite different from those of domestic stock.

4. Conclusions

Careful analysis of the 2006 outbreak data suggests that the spatial and temporal pattern of BTV-8 movement across northwest Europe was driven by both downwind and upwind midge movements, with a small amount of random (i.e. non-wind related) movement. The SWOTS model developed here determines the extent of each sort of movement and is able to describe 94 per cent of the total of 2025 reported farm infections.

We recognize that certain critical assumptions had to be made in this simulation, stemming from incomplete knowledge of the life cycle of Culicoides. Key among these, and for which we require further information to improve our model's predictions, are midge responses to environmental variables (topography and weather) [18,47,48], flight properties (survival at different flight height, flight behaviour at different wind speeds), seasonality [48] and population parameters (reproductive status, age and local population density) [21].

This analysis gives only one picture of one disease outbreak, but is sufficient to draw the conclusion that studies of different types of insect vector flight behaviour at multiple spatial and temporal scales are needed in order to understand completely the unfolding events of a major disease epizootic. By calling into question the claims previously made for the frequency and therefore importance of long range, down-wind only infection events during the 2006 BTV-8 outbreak, and for the importance of high-rather than low-altitude wind fields, our study highlights the importance of finding out more about hitherto little-known and understood aspects of Culicoides behaviour. Only better knowledge of this behaviour, within a robust model framework, will prepare us for future similar outbreaks and provide the tools for implementing effective control.