Not an ancient relic: the endemic Livistona palms of arid central Australia could have been introduced by humans

Abstract

Livistona mariae is an endemic palm localized in arid central Australia. This species is separated by about 1000 km from its congener L. rigida, which grows distantly in the Roper River and Nicholson–Gregory River catchments in northern Australia. Such an isolated distribution of L. mariae has been assumed to have resulted from contraction of ancestral populations as Australia aridified from the Mid-Miocene (ca 15 Ma). To test this hypothesis at the population level, we examined the genetic relationships among 14 populations of L. mariae and L. rigida using eight nuclear microsatellite loci. Our population tree and Bayesian clustering revealed that these populations comprised two genetically distinct groups that did not correspond to the current classification at species rank, and L. mariae showed closest affinity with L. rigida from Roper River. Furthermore, coalescent divergence-time estimations suggested that the disjunction between the northern populations (within L. rigida) could have originated by intermittent colonization along an ancient river that has been drowned repeatedly by marine transgression. During that time, L. mariae populations could have been established by opportunistic immigrants from Roper River about 15 000 years ago, concurrently with the settlement of indigenous Australians in central Australia, who are thus plausible vectors. Thus, our results rule out the ancient relic hypothesis for the origin of L. mariae.

1. Introduction

Australian biodiversity has long been recognized as distinctive and globally significant [1–3]. The island continent's diverse and highly endemic biota is thought to have developed through allopatric speciation and adaptive diversification driven by over 30 Myr of geological isolation and aridification since the Mid-Miocene (15 Ma) [4–7]. Following the onset of desiccation, a number of endemic species are thought to have become restricted to isolated permanent water bodies in arid central Australia [8–10].

Livistona mariae F. Muell is endemic to the MacDonnell Ranges bioregion in arid central Australia, restricted to a small portion of the Finke River and its tributaries known as the Palm Valley Oasis (figure 1a; [11,12]). This species is the only palm occurring in arid central Australia. The extent of occurrence is less than 60 km², and the area occupied is less than 50 ha [13,14]. Livistona mariae is separated by about 800–1000 km from its nearest congener L. rigida Beccari which inhabits the Roper River at Mataranka Hot Springs and the Nicholson–Gregory catchment in Lawn-Hill National Park, respectively, in the Top End and Carpentaria regions of northern Australia (figure 1b,c) [11,12]. Such an isolated and localized distribution pattern of L. mariae has been described as ‘ancient’ and ‘relictual’, and has been assumed to have resulted from contraction of ancestral populations as Australia aridified during the Cenozoic (the relic hypothesis, 15 Ma; [5,10,11,13,15]).

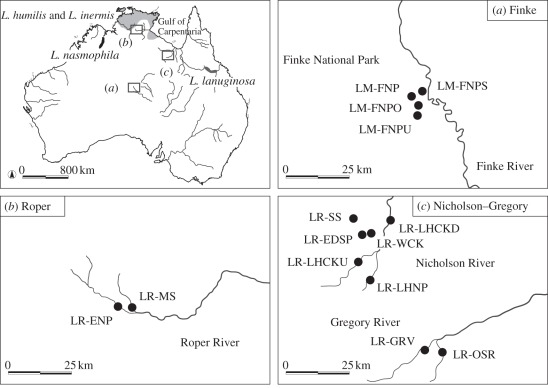
Figure 1.

(a) Location of the four Livistona mariae populations from Finke River and (b) 10 L. rigida populations from Roper River and (c) Nicholson–Gregory catchment. Shading (pale grey, dark grey and black) indicates the range of L. humilis and L. inermis, L. lanuginosa and L. nasmophila, respectively [12].

Recent molecular data, however, show that the isolation of L. mariae is scarcely ‘ancient’. Despite the large geographical gap, it is identical to L. rigida across 4 kb of chloroplast and nuclear sequences, and a previous estimate of the divergence time between these taxa ranges from 0.3 to 3 Ma [16]. In fact, the last likely connection between the Finke River (where L. mariae occurs) and Nicholson–Gregory catchments (where L. rigida occurs) occurred during the Pliocene (5–2 Ma; [17]) and this period overlaps with the estimate of the divergence time. During the past 2 Myr, the Nicholson River was intermittently linked to the Roper River (where the other population of L. rigida occurs) when the sea level was lower, converting the Gulf of Carpentaria to ‘Lake Carpentaria’ [17,18]. Therefore, the geographical disjunctions both between the two Livistona species and among populations of L. rigida could have been induced by successive historical river connections and disconnections corresponding to the geological and climatic changes during the relatively recent epoch, combined with their river-dependent dispersal syndrome (the Pliocene river connections hypothesis, 5–2 Ma; [16]).

In this study, we examine the genetic relationships among populations of L. mariae and their closest relative L. rigida using eight nuclear microsatellite loci to test the aforementioned two predictions of species range formation, i.e. the relic hypothesis (15 Ma; [13]) and the Pliocene river connections hypothesis (5–2 Ma; [16]), at the population level. We discuss the origin and the process of species range formation that could explain how the endemic palm L. mariae came to be localized in arid central Australia.

2. Material and methods

(a). Sample collection

We sampled four L. mariae populations along the Finke River and its tributaries in central Australia throughout the species' range (figure 1a). Additionally, two and eight populations of the closest relative L. rigida in the Roper River and Nicholson–Gregory catchments were sampled, respectively (figure 1b,c). The sample size ranged from eight to 10 individuals per population (mean: 9.86), with a total sample size of 38 and 100 individuals for L. mariae and L. rigida, respectively (table 1). We also sampled four relatives: L. humilis, L. inermis, L. lanuginosa and L. nasmophila (figure 1). L. humilis and L. inermis are widely distributed in open forests and woodlands in the northern part of the Northern Territory adjacent to the Roper River where L. rigida occurs (figure 1; [11,12]). Although habitat requirements of L. humilis and L. inermis differ greatly from riparian L. mariae and L. rigida, they shared a common cpDNA haplotype across 2.5 kb sequences [16]. L. lanuginosa is endemic to tropical east Queensland, being restricted to a small area of the Burdekin River basin (figure 1; [11,12]). L. lanuginosa showed the closest affinity with L. mariae and L. rigida in the phylogenetic analyses of all 18 Australian Livistona species based on 4 kb of chloroplast and nuclear sequences combined [16]. Morphology also indicates close similarity between them in the trunk base, waxy leaf undersides, inflorescence architecture and scales on the rachis bracts [11]. L. nasmophila is distributed along permanent watercourses in the central and northeastern Kimberley region (figure 1; [12]). L. nasmophila was clearly distinct from the other five species in the phylogeny based on 2.5 kb of chloroplast sequences [16] but was included in the present sample because it had been considered a subspecies of L. mariae [11,12]. We sampled populations of L. humilis (n = 4), L. inermis (n = 2), L. lanuginosa (n = 2) and L. nasmophila, (n = 3) with a respective sample size of 40, 20, 40 and 58 individuals for each species (details on the sampling location of four relatives are provided in the electronic supplementary material, table S1). In total, we sampled 296 individuals from 25 populations of six Livistona species.

Table 1.

Location, sample size and genetic diversity parameters for each of the 14 populations of Livistona mariae and L. rigida. We divided the 14 populations into three regional groups based on their locations. n, sample size; H_E, expected heterozygosity; allele richness [16], allelic richness; private allele, mean number of private alleles (i.e. those that are unique to a given population, p and region, r) per individual. Allelic richness values denoted by the same letters are not significantly different from each other at the p < 0.01 level (Scheffé's multiple comparison test.)

species	regional group	population code	latitude	longitude	n	HE	allele richness [16]	allele richness (means)	private allele (p)	private allele (r)
L. mariae	Finke	LM-FNPO	−24°04′23	132°43′90	10	0.08	1.35	1.60a	0.30	1.18
		LM-FNPS	−24°01′62	132°44′15	8	0.06	1.25		0.88
		LM-FNP	−24°02′68	132°42′27	10	0.13	1.85		0.30
		LM-FNPU	−24°06′58	132°43′48	10	0.19	1.94		0.50
L. rigida	Roper	LR-MS	−14°55′38	133°08′10	10	0.28	2.48	2.56b	0.40	0.25
		LR-ENP	−14°54′74	133°05′36	10	0.35	2.64		0.10
L. rigida	Nicholson–Gregory	LR-LHCKU	−18°43′02	138°28′46	10	0.25	1.95	1.89a	0.00	1.18
		LR-LHNP	−18°46′67	138°30′37	10	0.25	2.12		0.00
		LR-WCK	−18°36′67	138°30′81	10	0.19	1.80		0.10
		LR-SS	−18°33′23	138°27′02	10	0.18	1.90		0.00
		LR-EDSP	−18°37′10	138°29′41	10	0.20	1.80		0.10
		LR-LHCKD	−18°34′05	138°35′15	10	0.24	1.95		0.30
		LR-OSR	−19°01′48	138°45′90	10	0.18	1.60		0.00
		LR-GRV	−19°01′16	138°43′46	10	0.20	2.00		0.00

(b). DNA extraction and microsatellite analysis

We isolated total genomic DNA from approximately 50 mg of frozen leaf tissue from each of the 296 Livistona individuals using the hexadecyltrimethylammonium bromide miniprep procedure [19]. We used a total of eight microsatellite loci developed from L. rigida [20]. PCR amplifications were performed with a GeneAmp PCR System 9600 thermal cycler (Applied Biosystems, Foster City, CA, USA). The amplified products were analysed using an ABI 3100 autosequencer (Applied Biosystems), and their sizes were determined using the genescan analysis software (v. 3.7; Applied Biosystems). A significant population-wide presence of null alleles was not observed at all eight loci within 14 populations of L. mariae and L. rigida (Micro-Checker, v. 2.2.3; [21]), and the overall genetic parameters for each of the eight microsatellite loci indicated that they were suitable for population-level analysis of L. mariae and L. rigida (electronic supplementary material, table S2).

(c). Statistical analysis

(i). Genetic relationships among the populations of six Livistona species

To clarify the genetic relationship of L. mariae populations to the nearest congener L. rigida, we quantified the relationships among the 25 populations of six Livistona species using Cavalli-Sforza & Edward's [22] chord distances (D_C) and the neighbour-joining method [23] available in the phylip software, v. 3.6 [24]. The genetic distance of Cavalli-Sforza & Edward's [22] was chosen because it seems to be the most efficient distance to obtain a correct tree topology in closely related species and recently diverged populations [25]. D_C values were generated in the GENDIST module of phylip. From these distance matrices, we used the neighbour-joining method in the NEIGHBOR module to generate population trees, and used CONSENSE to generate a consensus tree with bootstrap values from 1000 replicated datasets created in SEQBOOT. We generated dendrograms in DRAWTREE. For this analysis, we excluded the locus LR 46 which could not be amplified in the four outgroup species (see the electronic supplementary material, table S3).

(ii). Individual-based genetic relationships both between L. mariae and L. rigida, and among the regions

To clarify the individual-based genetic relationships both between L. mariae and L. rigida, and among their populations, we performed a Bayesian cluster analysis using the method implemented in structure, v. 2.2 [26]. Simulations were replicated using 20 runs for each value of K between 1 and 14, with the following software settings: admixture model (initial α = 1.0), no population information, correlated allele frequency, a burn-in length of 10 000 and a Markov chain Monte Carlo (MCMC) length of 100 000. We then plotted the log probability of the data [ln P(D|K)] as a function of K across the 20 runs and looked for the value that captured the major structure in the data according to the structure manual [26]. We also used the ΔK statistical approach proposed by Evanno et al. [27] to select a K value. Once values of K had been chosen, the genetic contribution of each inferred cluster to the populations as well as to each individual was investigated.

(iii). Estimation of divergence time and migration rate both between L. mariae and L. rigida and among the regions

To find out the most likely historical scenario creating the disjunct distribution both between L. mariae and L. rigida, and among populations of L. rigida, we used the isolation-with-migration model implemented in the program im [28]. The model used coalescent simulations within a Bayesian inference framework to estimate marginal probability distributions for six demographic parameters scaled by the mutation rate per generation μ, assuming a stepwise mutation model (SMM) of microsatellite evolution: the time since population-splitting (T = tμ), measures of neutral population genetic diversity of the two current and one ancestral population (θ₁, θ₂, θ_A), proportional to their effective population sizes, N_e (θ = 4 N_eμ) and bidirectional migration rates (M₁ = m₁/μ, M₂ = m₂/μ) [28]. The estimations were based on the marginal a posteriori densities, and credibility intervals were obtained using the 90% of highest posterior density interval (HPDI) and the 95% CI. MCMC simulations started with a burn-in period of 10⁶ steps so that the state of the chain was independent of the starting point. After the burn-in period, simulations were continued for at least 30 million steps and genealogies were recorded every 100 steps over the course of the run. Analyses were considered to have converged upon the stationary distribution if independent runs generated similar posterior distributions, with each having a lowest effective sample size (ESS) of 50 for each estimated parameter as recommended in Hey & Nielsen [28]. We used a value of 5.00 × 10⁻⁴ mutations per generation, which is considered to be the average mutation rate over many species [29,30]. We also used a slower mutation rate (2.34 × 10⁻⁴) obtained from the direct estimation of mutation rates for microsatellite loci in plants [31]. The slower mutation rate might be more appropriate for trees, such as palms, with a long-generation time. Assuming a generation time (G) of 25 years for L. mariae and L. rigida, population-splitting time (T) can be converted to calendar years (t). The generation time was estimated from the annual growth rate of L. mariae in Finke River and the minimum palm height at which full reproductive capacity is achieved [13]. Although the frequency distribution of alleles at seven of the eight microsatellite loci except for locus LR 10 indicates a two-phase model (TPM) of evolution which allows a proportion of mutations to involve changes greater than single repeats, the frequency of alleles with sizes greater than single repeat changes was low. This limits the impact that a TPM, as opposed to the SMM assumed by im, might have on the analyses. In other Bayesian methods that infer past demographic changes from microsatellites, the analyses are robust to moderate departures from a strict SMM in the data [32]. Therefore, the biases in the estimations originating from such deviations from the strict SMM were considered small.

(iv). Geographical patterns of genetic differentiation between the two species and among the regions

We also investigated the patterns of spatial genetic structure by testing for isolation by distance (IBD). We calculated pairwise F_ST values [33] using fstat, v. 2.9.3 [34]. The distances between pairs of populations were calculated from the linear distances between mean latitudes and longitudes for each population. We performed a Mantel test with 999 random permutations between the populations [F_ST/(1–F_ST)], and the matrix of distances. We performed the analyses using the genalex software (v. 5.1) [35] both for the whole dataset and separately for pairwise comparisons of the three regional groups of populations: L. mariae and L. rigida each in Roper River and Nicholson–Gregory catchment.

(v). Geographical structure of genetic variation

To assess whether the genetic variation differed between the above regions, we calculated the average values of allelic richness within each population. We used the rarefaction method [36], which employs resampling of the genotype data to produce sample sizes equal to the smallest population. We tested differences in these parameters among the three regional groups by 1000 random permutations of population using fstat followed by Scheffé's multiple comparison test. We also calculated the mean number of private alleles (alleles that were unique to one population or region) per individual in each population and each region.

3. Results

(a). Genetic relationships among the populations of six Livistona species

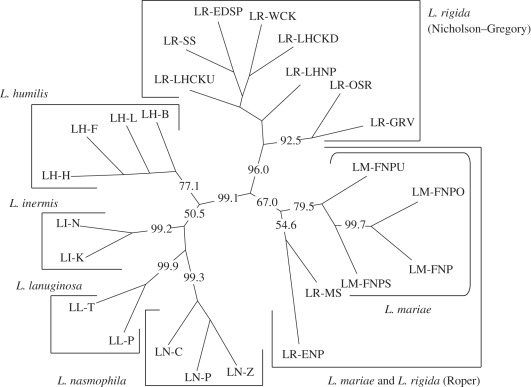
In our population tree of the 25 populations from six Livistona species, the four L. mariae and 10 L. rigida populations formed a cluster with strong bootstrap support for their genetic distinctness from the other four species in the analysis (figure 2; 99.1%). This cluster was classified into two groups. In the first group, the four L. mariae populations formed a separate cluster with strong bootstrap support (79.5%) and these clustered with two L. rigida populations from Roper River, although with only 67 per cent bootstrap support. The other group was composed of all eight L. rigida populations from Nicholson–Gregory catchment, with strong support (96%). In other words, the L. rigida populations from the two disjunct river systems were separated into two different clusters and L. rigida from the Roper River showed closer affinity with L. mariae than with L. rigida from Nicholson–Gregory. Each of the other four species (L. humilis, L. inermis, L. lanuginosa and L. nasmophila) formed a cluster with strong bootstrap support for the basal nodes (77.1%, 99.2%, 99.9% and 99.3%, respectively). A similar pattern of population grouping in L. mariae and L. rigida was also observed when we used Nei's genetic distance [37] which assumes that mutations change the allele frequencies (see the electronic supplementary material, figure S1), rather than genetic drift as in the chord distance method.

Figure 2.

Neighbour-joining population tree for the 25 populations of six Livistona species based on Cavalli-Sforza & Edward's [22] chord distances. Bootstrap support at internodes is shown if the value is more than 50%.

(b). Individual-based genetic relationships between L. mariae and L. rigida, and among the regions

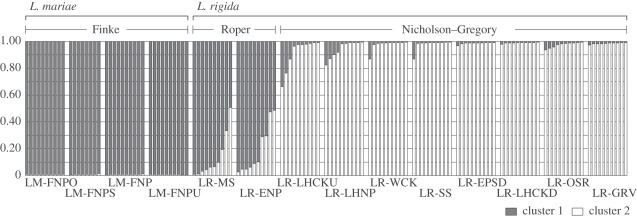
The results of the Bayesian cluster analysis for L. mariae and L. rigida obtained with different numbers of inferred groups are summarized in the electronic supplementary material, figure S2. Although increasing K values produced higher log probability values, they were decreasing with large standard deviations at K > 6, suggesting that K > 6 could not be the most likely number of K populations. On the other hand, the ΔK statistics supported K = 2 with a strong signal. Although there is debate on how to estimate the number of clusters [26–38], we place our focus on K = 2 detected by the ΔK statistics as an uppermost level of population structure. The results of group assignment of each individual at K = 2 indicated a pattern similar to that produced by the population tree approach, and they did not reflect the current classification at species rank (figure 3). All 38 individuals from four L. mariae populations were completely assigned to cluster I with extremely high probability. L. rigida individuals from Roper River and Nicholson–Gregory catchment were predominantly assigned to cluster I and II, respectively. L. rigida individuals from Roper River showed closer affinity with L. mariae than that with L. rigida from Nicholson–Gregory catchment. On the other hand, admixtures of two inferred clusters, i.e. in which the probability that an individual belonged to a particular cluster was less than 85 per cent, were observed in individuals from Roper River and two populations within Nicholson–Gregory catchment (LR-LHCKU and LR-LHNP). A similar pattern of Bayesian population assignment, i.e. distinct difference in inferred clusters between L. rigida from Nicholson–Gregory catchment and L. mariae, and close affinity between L. rigida from Roper River and L. mariae (LM-FNPU), was also found at K = 3. L. rigida from Roper River contains high levels of admixture from the other populations at K = 4, and at K = 5–6 it is separated into a different cluster, indicating divergence of this population from the other populations studied (electronic supplementary material, figure S3).

Figure 3.

Regional variation in the proportions of each individual in each of the two inferred clusters defined using the Bayesian cluster approach of Pritchard et al. [39]. Bars represent individuals grouped by sampling location and the proportion of shading in each bar indicates the probability that each individual belongs to the two groups.

(c). Estimation of divergence time and migration rate between L. mariae and L. rigida, and among populations

On the basis of results from the population tree (figure 2) and Bayesian clustering (figure 3), we analysed divergence time and bidirectional migration rates first between the two regional populations of L. rigida, i.e. (i) all eight L. rigida populations from Nicholson–Gregory catchment and (ii) both L. rigida populations from Roper River. Then, we repeated these analyses between (iii) both L. rigida populations from Roper River and (iv) all four L. mariae populations from Finke River.

Results from the im model for the divergence of the two regional populations of L. rigida (between Nicholson–Gregory and Roper) are summarized in table 2. The ESS values for each of the six estimated parameters are over 50, except for θ_N−G (ESS for Nicholson–Gregory catchment = 43). The divergence-time estimates based on the marginal a posteriori densities were 9750 (90% HPDIs: 4250–20 250, 95% CI: 5250–26 750) and 20 833 year BP (90% HPDI: 9081–43 269, 95% CI: 11 218–57 158), depending on the average and slower mutation rates per generation of 5 × 10⁻⁴ and 2.34 × 10⁻⁴, respectively (table 2). The migration rates were very low in both directions (from Roper to Nicholson–Gregory catchment: 0.00042 (90% HPDI: 0–0.00356, 95% CI: 0.00012–0.00455), opposite direction: 0.00406 (90% HPDI: 0.00191–0.00499, 95% CI: 0.00121–0.00492) depending on average mutation rate; table 2). The effective population sizes of Nicholson–Gregory and Roper River were 108.3 and 162.4 individuals, respectively (depending on average mutation rate; table 2).

Table 2.

The estimates of divergence time (t) and migration rates per generation (m) between the regional populations based on population tree (figure 2), and effective population sizes (N_e). Divergence time was converted into calendar years using generation time (G) of 25 years [13], and per-generation mutation rates of 5.0 × 10⁻⁴ [29,30] and 2.34 × 10⁻⁴ [31]. Migration rate per generation was also converted using two mutation rates. The estimations were based on the marginal a posteriori densities, and credibility intervals were obtained using the 90% of highest posterior density interval (HPDI) and the 95%.

pair of regional populations		mutation rate (µ)	divergence time (t) in yr		migration rate per generation (m)		effective population size (Ne)
population 1 (P1)	population 2 (P2)		Highest posterior value (upper; 90% HPDI, lower; 95% CI)		m to P1	m to P2	P1	P2
Nicholson–Gregory	Roper	5.00 × 10−4	9750	(4250–20 250)	0.00042	0.00406	108.3	162.4
				(5250–26 750)
		2.34 × 10−4	20 833	(9081–43 269)	0.00020	0.00190	231.4	347.0
				(11 218–57 158)
Roper	Finke	5.00 × 10−4	15 375	(6625–30 875)	0.00207	0.00026	178.6	226.1
				(7625–38 875)
		2.34 × 10−4	32 852	(13 632–63 529)	0.00097	0.00012	381.6	483.1
				(16 293–83 066)

Results for the divergence between L. rigida populations from Roper River and L. mariae populations from Finke River are summarized in table 2. The ESS values for each of the six estimated parameters are over 50. The divergence is estimated to have occurred 15 375 (90% HPDI: 6625–30 875, 95% CI: 7625–38 875) and 32 852 year BP (90% HPDI: 13 632–63 529, 95% CI: 16 293–83 066), depending on the average and slower mutation rates, respectively (table 2). The migration rates were very low in both directions (from Roper to Finke River: 0.00207 (90% HPDI: 0.00047–0.00578, 95% CI: 0.00053–0.00680), opposite direction: 0.00026 (90% HPDI: 0–0.00171, 95% CI: 0.00003–0.00261) depending on average mutation rate; table 2). The effective population sizes of Roper and Finke River were 178.6 and 226.1 individuals, respectively (depending on average mutation rate; table 2). The marginal posterior probability distribution of both the time since divergence in years and migration rates showed a clear peak for each of the two analyses (electronic supplementary material, figure S4).

(d). Geographical patterns of genetic differentiation among populations

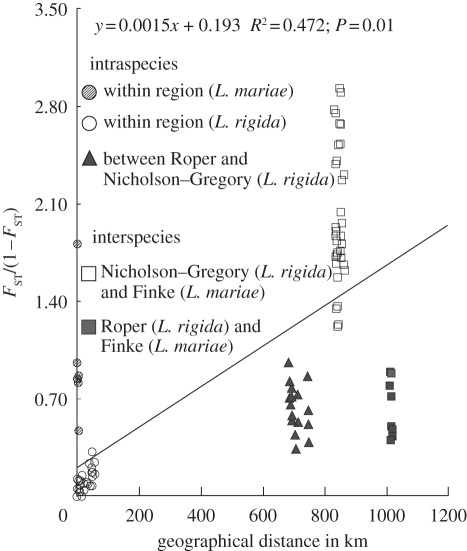
Across all 14 populations, the IBD test revealed a positive but weak relationship between genetic differentiation [F_ST/(1 − F_ST)] and the straight-line distance (R² = 0.472, p = 0.01; figure 4). The highest genetic differentiation was observed between the Nicholson–Gregory catchment (L. rigida) and Finke River (L. mariae), which are separated by 800 km. On the other hand, population pairs between Roper River (L. rigida) and Finke River (L. mariae) showed much lower genetic differentiation, even though these populations are separated by more than 1000 km. Furthermore, the levels of genetic differentiation between Roper River (L. rigida) and Finke River (L. mariae) were almost the same as those between the two regions of L. rigida, which are separated by 700 km.

Figure 4.

The relationships between the pairwise genetic differentiation (genetic distance) described as F_ST/(1 − F_ST) and the geographical distance between populations. Each combination of regions is represented by a different symbol.

(e). Geographical structure of genetic variation

Measures of genetic diversity within each population and region are presented in table 1. There was a significant difference in allelic richness among the three regional groups (p < 0.01). Scheffé's multiple comparison test indicated that allelic richness was significantly highest in the L. rigida populations from the Roper River (mean: 2.56), followed by the L. rigida populations from Nicholson–Gregory catchment (1.89) and L. mariae populations in Finke River (1.60, p < 0.01; table 1). Conversely, the mean number of private alleles per individual was lowest in L. rigida populations from the Roper River (mean: 0.25), whereas the L. rigida populations from Nicholson–Gregory catchment and L. mariae populations have the same mean number of private alleles (1.18 respectively; table 1).

4. Discussion

(a). Relationship between L. mariae and its closest relative L. rigida

In previous taxonomic arrangements, L. rigida was treated as a subspecies of L. mariae because of morphological similarities that distinguish both from related species (e.g. the trunk base, waxy leaf undersides, inflorescence architecture and bract scales; [11]). Recently, these taxa have been distinguished as separate species based on small quantitative differences in their morphological characters [12]. However, more recent molecular research showed that they are identical across 4 kb of chloroplast and nuclear sequences despite the large geographical gap between them [16]. Thus, the distinction between these taxa at the species level remains unclear. In our population tree, based on microsatellite polymorphism, the 14 populations of L. mariae and L. rigida formed a cluster with strong bootstrap support for the basal nodes (figure 2; 99.1%), and within this cluster, they were classified into two groups (bootstrap support for the basal nodes, 67% and 96%). However, these groups do not reflect the current classification at species rank, whereas each of the other four species (L. humilis, L. inermis, L. lanuginosa and L. nasmophila) formed a cluster with strong bootstrap support for the basal nodes (figure 2). In our Bayesian population assignment, a similar grouping of L. mariae with L. rigida (from Roper River) was found (figure 3). Additionally, an analysis of molecular variance (AMOVA; [40]) indicated that grouping by species accounted for a smaller amount of the total variation (42.94%) compared with grouping by both region (46.84%) or by the two groups observed in both Bayesian clustering and population tree (44.65%; details on AMOVA results are provided in the electronic supplementary material, table S4). All these results suggest that current species delimitation, based on the morphological characteristics, does not reflect the difference in genetic compositions among L. mariae and L. rigida populations. Thus, L. mariae and L. rigida should not be considered to be distinct species, although the high levels of genetic differentiation (figure 4) and the difference in inferred clusters at higher K values among three regions (K = 5, 6; electronic supplementary material, figure S3) indicate that they are in the process of speciation according to geographical isolation.

(b). The origin of the isolated L. mariae and L. rigida populations

The distribution of L. mariae, which is highly disjunct from its nearest congener L. rigida, has been assumed to have resulted from contraction of ancestral populations as Australia aridified from 15 Ma [5,10,11,13,15]. Recently, Crisp et al. [16] reconstructed the phylogeny of all 18 Livistona species in Australia and showed that L. mariae and L. rigida are identical across 4 kb of chloroplast and nuclear sequences, and that the estimated divergence time between these taxa ranges from 0.3 to 3 Ma. Because the last likely connection between the Finke River (where L. mariae occurs) and the Nicholson–Gregory catchment (where L. rigida occurs) occurred during the Pliocene (5–2 Ma; [17]), and this period overlaps with the estimates of the divergence time, they noted that L. mariae could be a ‘relictual’ species in arid central Australia resulting from the fragmentation of the Pliocene river. Likewise, Crisp et al. [16] also suggested that such historical river connections could have led to the range expansion of L. rigida between the Nicholson and Roper River catchments because they were intermittently connected when lower seas levels changed the Gulf of Carpentaria to Lake Carpentaria during the Quaternary (2 Ma) [17,18]. This scenario is plausible given that L. mariae and L. rigida are strictly riparian, and that their seeds are probably dispersed by stream flow [26]. According to this scenario, the genetic divergence between L. mariae and L. rigida should be deeper than that between two L. rigida populations (Roper River and Nicholson–Gregory catchment), and the deepest genetic divergence should be observed between L. mariae and L. rigida populations from Roper River. However, our patterns of IBD did not support this hypothesis (figure 4). Although much deeper genetic differentiation was observed between L. mariae populations and L. rigida populations from the Nicholson–Gregory catchment than that between two regional populations of L. rigida, the genetic differentiation between L. mariae and L. rigida populations from Roper River was almost equal to that between the two regional populations of L. rigida, despite the large geographical gap and the lack of a direct historical river connection between them. Furthermore, our population tree also showed that the L. mariae populations are more closely related to the L. rigida populations in Roper River than to L. rigida populations in the Nicholson–Gregory catchment, which conflicts with the predictions of the scenario described earlier (figure 2).

The levels of genetic diversity within each region suggest alternative explanations of the range formation processes in these taxa. The genetic diversity is generally expected to decline with increasing distance along a colonization route as a consequence of successive founder events during the range expansion [41]. In our calculations of the genetic parameters within each region, the highest observed values of allelic richness were statistically significant in the L. rigida populations from the Roper River (mean: 2.56, p < 0.01; Scheffé's multiple comparison test; table 1), followed by the L. rigida populations from the Nicholson–Gregory catchment (1.89) and the L. mariae populations in the Finke River (1.60). Conversely, the mean number of private alleles per individuals was the lowest in L. rigida populations from the Roper River (mean: 0.25), whereas the L. rigida populations from Nicholson–Gregory catchment and L. mariae populations have the same mean number of private alleles (1.18, respectively; table 1). Taken together, such geographical patterns of genetic variation indicate that the range expansion appears most likely to have been from Roper River eastward towards the Nicholson and southward towards the Finke River. Range expansion, via successive founder events, that was subsequently compounded by restricted gene flow among regional populations, appears to account for the decline of allelic richness and accumulation of mutations in both Nicholson and Finke River populations. Although the admixtures of two inferred clusters occurred in individuals from Roper River, the Nicholson and Finke River populations are more genetically homogeneous, and were assigned to different clusters (figure 3). Thus, we conclude that the deep genetic divergence observed between the Nicholson and Finke River populations reflects differences in colonization routes, and not the fragmentation of a Pliocene river system.

Our results support the hypothesis of Crisp et al. [16] that the range expansion of L. rigida from Roper River towards the Nicholson–Gregory catchment could have been induced by intermittent connections of these rivers when sea level was lower during the glacial period. The present Roper River and Nicholson–Gregory catchments have been repeatedly connected by marine regression during the glacial periods, and isolated by the marine transgression during the interglacial periods [42,43]. While individuals from Roper River and Nicholson–Gregory catchment were predominantly assigned to the different clusters, our Bayesian cluster analysis revealed genetic admixtures in some individuals from the Roper River population and in two populations within Nicholson–Gregory catchment (figure 3). Such patterns of Bayesian population assignment could reflect the population divergence and subsequent gene flow between Roper and Nicholson–Gregory populations corresponding to the intermittent historical river connections and fragmentations. In fact, similar patterns of Bayesian population assignment corresponding to the structure of the river system were also observed between present Nicholson and Gregory River populations at higher K values (K = 5, 6; electronic supplementary material, figure S3). Furthermore, the divergence between these two regional populations of L. rigida was estimated to have occurred 9750 years ago (90% HPDI: 4250–20 250 year BP, depending on the assumed mutation rate) and migration rates estimation only showed negligible gene flow between them after population-splitting (table 2). Our estimated divergence time was considered to reflect the most recent connection between the Roper River and Nicholson–Gregory catchment occurred during the last glacial period (from 60 to 10 kyr BP) and isolation occurred 11 000 years ago as a result of marine transgression [43]. In sum, the estimated divergence time (4250–20 250 year BP; table 2) and the admixtures of two inferred clusters within L. rigida populations (figure 3) could reflect the intermittent connections between L. rigida populations across the ancient Carpentaria river system. Because such inferences naturally depended on a specific mutation rate (i.e. 5.00 × 10⁻⁴ mutations per generation), the departure from them may induce some bias in our estimates. However, it was considered that the biological congruence between our genetic inferences and palaeogeographical records suggests the model captures the essential aspects of this range expansion process of L. rigida.

All 38 individuals from four L. mariae populations were completely assigned to a single cluster with extremely high probability in the Bayesian cluster analysis (figure 3). Such a pattern was also observed at the higher K values (from K = 3 to 6), although they were assigned to two clusters (electronic supplementary material, figure S3). This suggests that there has been no gene migration from either the Roper River or the Nicholson–Gregory catchment after the establishment of the L. mariae population. Furthermore, the low genetic differentiation between the Roper and the L. mariae population despite the large geographical gap indicates that the establishment of the Roper River population has occurred relatively recently. In fact, the divergence between L. mariae in the Finke River and L. rigida in the Roper River was estimated to have occurred 15 375 years ago (90% HPDI: 6625–30 875 year BP, depending on the assumed mutation rate; table 2), just after the last glacial maximum (18 kyr BP), when many organisms had started to expand their range as temperatures rose [44–46]. Even in the conservative case that we used the slower mutation rate, the divergence is estimated to have occurred about 32 852 years ago (90% HPDI: 13 632–63 529; table 2), which decisively rules out both the relic hypothesis (15 Ma; [13]), and the Pliocene river connections hypothesis (5–2 Ma; [16]). Additionally, the estimated migration rates were extremely low in both directions (table 2), suggesting there was either no or only little gene flow between the two regions via seeds and pollen after population establishment in the Finke River. Considering the lack of historical river connections between the Roper and Finke Rivers, it is likely that the L. mariae populations were established by opportunistic immigrants via long-distance seed dispersal over the 1000 km gap. Although passive movement by water is thought to be the main mode of seed dispersal in Livistona species, their seeds are also consumed and distributed by fruit-eating birds and bats [26]. However, it is unlikely that these small animals could fly over 1000 km across barren landscape and reach the Finke River frequently without elimination of seeds along the way, unless there were intermediate populations of L. mariae or L. rigida established on springs that are now extinct. On the other hand, Livistona species are known to be among the few edible and cultivable native plants in Australia, and descendants of indigenous Australians sometimes eat their ‘cabbages’ or the immature palm fronds, and use their fibrous bark as fishing lines and woven basket material [47]. The ancestors of the indigenous people reached the Australian continent from the north about 40–45 kyr ago when this landmass formed part of the Sahul continent which connected to the island of New Guinea via a land bridge [48,49], and then they intermittently migrated from northern to central Australia since around 20–30 kyr ago [50–52]. This period overlaps with the estimates of the divergence time between L. mariae in Finke River and L. rigida in Roper River (6625–30 875 years ago). Although it remains unclear which vectors introduced L. mariae to arid central Australia over such a huge distance and across a hostile landscape, it is as likely that it is a legacy of Aboriginal dispersal as it is that it was carried there by animals.