Consequences of fisheries-induced evolution for population productivity and recovery potential

Abstract

Fisheries-induced evolution has become a major branch of the research on anthropogenic and contemporary evolution. Within the conservation context, fisheries-induced evolution has been hypothesized to negatively affect the persistence and recovery potential of depleted populations, but this has not been explicitly investigated. Here, we investigate how fisheries-induced evolution of Atlantic cod (Gadus morhua L.) life histories affects per capita population growth rate, a parameter negatively correlated with extinction risk. We simulate the evolutionary and ecological dynamics of a cod population for a 100 year period of size-selective harvesting, followed thereafter by 300 years of recovery. To evaluate the relative importance of harvest-induced evolution, we either allowed life histories to evolve during and after the fishing period, or we assumed that fisheries-induced evolution was absent. Population growth rates did not differ appreciably between the evolutionary and non-evolutionary simulation scenarios, despite the emergence of rather pronounced differences in life histories. The underlying reason was that in the absence of fishing the cumulative lifetime reproductive outputs were very similar among differing life histories. The results suggest that fisheries-induced evolution might not always have as clear-cut an effect on population growth rate as previously anticipated.

1. Introduction

Harvesting has the potential to produce evolutionary changes in life history [1,2]. It often results in differential mortality among phenotypes for heritable traits, such as body size because of differential vulnerabilities generated by harvesting gear, fishing regulations or hunter preference [3–5]. Fishing is almost always size-selective, often targeting larger or intermediate-sized individuals, depending on the applied gear (reviewed in Kuparinen et al. [6]). As a consequence, fishing is hypothesized to drive evolution towards earlier maturation at a smaller size [7,8]. Fisheries-induced evolution has become a major branch of the study of anthropogenic evolution and possible evolutionary responses to fishing have been investigated in numerous species (reviewed in earlier studies [9–11]). While much of this research effort has been invested in detecting evolutionary shifts in life histories potentially attributable to fishing, markedly less attention has been focused on the ecological and demographic feedbacks of such life-history change [12]. The few existing attempts have examined the demographic feedbacks exclusively from a fisheries-based perspective, such as the influence of life-history evolution on yield, spawner–recruitment relationships [13] and natural mortality [14,15].

Important as this research is from a fisheries perspective, these approaches are less informative within a conservation context from which key questions are those that focus on the ability of populations (or species) to recover, or simply persist, following depletion. In this regard, some researchers have suggested that fisheries-induced evolution reduces recovery potential [16,17]. The fundamental link that exists between individual life histories and per capita rate of population growth provides a basis for testing this hypothesis given that, all else being equal, population growth rate (r) is negatively linked with extinction risk and positively associated with rate of recovery [18–20]. Here, we address this question by simulating the ecological and evolutionary dynamics of a fish population for a period of selective fishing followed by a period of recovery during which fishing had ceased. Extinction risk can, of course, potentially be related to factors such as extremely low abundance, habitat loss and genetic stochasticity, which we have not accounted for here; however, these variables appear not to be universal correlates of recovery for marine fishes, given the positive growth responses experienced by many (although not all) populations for which fishing mortality has been reduced [21].

Atlantic cod (Gadus morhua L.) is the species for which the effects of overfishing have been best documented. The Canadian population of northern cod, for example, provides the most striking example, as reflected by a 99 per cent population depletion [22] and concomitant life-history changes that have been interpreted as evolutionary responses to fishing [16,23]. Despite dramatic reductions in fishing mortality since 1992, the population has shown little signs of recovery [24]. From this perspective, northern cod provides a widely known and timely system in which to examine how fisheries-induced evolution might affect population growth rate. Specifically, we investigate the extent to which the population growth rate is affected by fishing-induced life-history evolution in contrast to a scenario in which the proportional representation of genotypes in the population, from one generation to the next, is unaffected by fishing.

2. Methods

The objective of our study was to investigate the role of fisheries-induced evolution on the rate of population growth in Atlantic cod. To this end, we built an individual-based simulation model that incorporates quantitative genetics, ecological processes and empirical data on cod growth and fecundity. Given that the model has been described in detail elsewhere [25], we restrict our description to an overview of its main features.

(a). Model description

Our modelling approach is based on 258 empirically observed cod growth trajectories measured from otoliths collected from a landlocked population inhabiting Ogac Lake, Baffin Island, northern Canada [26]. This population is not influenced by fishing, thus reflecting natural variability in cod life histories. Although a meromictic lake environment is not typical for cod, many traits in this population, such as age and size at maturity, individual growth rate, and in some cases cannibalism [27] are not unusual relative to cod elsewhere [26,28]. For example, the von Bertalanffy growth parameters estimated for Ogac Lake cod do not differ from those of Northeast Arctic cod [26,28] and are intermediate to the parameter estimates that have been reported for this species (www.fishbase.org; accessed 17 January 2012).

We modelled individual growth trajectories using least-squared fits of von Bertalanffy growth trajectories, where length at age t, L(t), is given by L_∞ − (L_∞ − L₀)e^−kt, where L₀ is size at t = 0, L_∞ is asymptotic length, and k the intrinsic individual growth rate [29]. Our simulation approach is based on two fundamental life-history invariants: (i) the strong negative correlation between von Bertalanffy growth parameters L_∞ and k, and (ii) the ratio of length at maturity and L_∞ [30]. For the first relation, regression analysis yielded an equation log(k) = −0.609–0.013 × L_∞ (with residual s.e. = 0.305), and the second was assumed to be 66 per cent [31]. Constructed in this manner, we could track the inheritance of L_∞, from which other relevant life-history traits could then be estimated. The value of k was generated using the above-mentioned regression (with a normally distributed random residual), and maturation was set to occur when L(t) exceeded 0.66 × L_∞. Quantitative traits are coded by a large number of loci each assumed to have small effect [32], such that L_∞ was assumed to be coded through the additive effects of 10 diploid loci with two alleles (0 or 1) in each. In this manner, the sum of allelic values (0–20) on the top of which some normally distributed environmental variation was added (s.d. = 3.5; calibrated to yield a realistic heritability of 0.2–0.3; [33]) was linearly translated into the value of L_∞ in the range 30–130 cm, a range observed in the empirical cod growth data. Thus, the model can be viewed as a means of describing the inheritance of alternative life-history types (e.g. large-growing late-maturing versus small-growing early-maturing).

Density-dependence was incorporated in the model through its effects on the growth of an individual along its growth trajectory (as defined by its L_∞ and k) and by the effects of body size (at each age) on fecundity. Reduction in growth owing to density-dependent competition was implemented in such a way that within one year an individual grows from length L(t) to L(t + Δt), where 0 < Δt < 1, and L(t + Δt) is then considered as the individual's length at age t + 1. Δt was defined through a logistic equation Δt = e^{15–17.6 × c} (1 + e^{15–17.6 × c})⁻¹, where c is the ratio of population biomass to the carrying capacity (set to 5000 kg), e.g. Δt = 0.5 if the population is at 85 per cent of its carrying capacity. While the choice of this equation is somewhat arbitrary, its sole purpose is to ensure that population biomass is bounded by the carrying capacity.

Fecundity was described through the model of egg production and survival to age 3 years [16] (eggs = ((0.48 × ((female weight + 0.37)/1.45) + 0.12) × 10⁶); survival = 1.13 × 10^–6), and by drawing the final number of juveniles surviving up to 3 years from a respective binomial distribution. The relationship between fecundity and weight for northern cod was estimated in the early 1960s [34] when the population might have been near the level at which the maximum sustainable yield from the population could have been obtained [24,35], meaning that it was at approximately 30–40% of its carrying capacity [36]. Therefore, in accordance with the stock–recruitment relationship predicted by the Beverton–Holt model for cod [37], we scaled the fecundity up or down depending on whether c (ratio of current biomass to carrying capacity) was below or above 0.4, such that final fecundity ranged between 174 per cent (at c ≈ 0) and 61 per cent (at c ≈ 1) of that given by the equation earlier. A weight–length relationship (weight = 3.52 × 10⁻⁶ × length^3.19) was obtained from the empirically observed cod growth histories.

The instantaneous rate of natural mortality (M) was partitioned into the background natural mortality assumed to be equal among all individuals, and the survival cost of reproduction that increased the mortality of mature individuals [38]. Background mortality was set to M = 0.12, to which a survival cost of 0.10 was added for mature individuals. These particular values were chosen as the simulated growth histories in a population that had adapted to this mortality regime provided a good match with the growth histories observed in the wild (electronic supplementary material, figure S1; [25]). Moreover, in an adapted population at equilibrium in our simulations these components of natural mortality yielded an overall mortality of 0.154, which falls well within the range estimated for Southern Gulf of St Lawrence cod in the 1970s (0.1–0.2; [15]). A maximum lifespan was set to 25 years. Fishing mortality was described by an overall instantaneous rate of fishing mortality of F = 0.2 (i.e. 18.1% of population biomass harvested every year) and a trawling selectivity curve e^{−12.5 + 0.25 × length}/(1 + e^{−12.5 + 0.25 × length}), which was obtained by fitting a logistic selectivity curve by eye to the size-dependent capture probabilities for northern cod [39].

The model described earlier was run for a set of individuals over discrete time steps and, at every time step, the processes of natural and fishing mortality, growth, maturation and reproduction were simulated at an individual basis. To this end, binomial random numbers were drawn for each individual to determine whether an individual died owing to natural mortality or was captured by fishing. Those individuals that did not die grew along their growth curves, such that the annual growth increment along the curve depended on the population density. Individuals matured once they had reached the threshold body length of 0.66 × L_∞, after which they produced juveniles, the average number of which depended on the size of the female fish and the population density, and was determined based on a binomial random number. Genotypes of the juveniles followed classical Mendelian inheritance and their phenotypes were determined based on their genotypes and the environmental variation around the genotypic trait value (see above). Sex of each juvenile was set randomly and L₀ was 4 cm, to roughly mimic larvae size during the first year (discrete time step, t = 0).

In order to investigate the ecological role of fisheries-induced evolution of life histories, we produced an evolutionary and a non-evolutionary version of the above-mentioned model. In the evolutionary model, the juvenile genotypes (and thus phenotypes) always depended on the genotypes of their parents. In the non-evolutionary model, after fishing had started, juvenile genotypes were drawn from a ‘parental pool’ of genotypes that had been recorded over a period of 30 years in the fully adapted, but non-fished, population. Therefore, fishing had no genetic impact on the population in the non-evolutionary model version. However, all the ecological impacts of fishing (e.g. density-dependent feedbacks, size-dependent fishing mortality) were similar in both evolutionary and non-evolutionary model versions, allowing for the investigation of the role of evolution in isolation from the direct ecological impacts of fishing.

(b). Simulation design

At first, we simulated the model for 2800 years in the absence of fishing, and recorded the fully adapted population every year for the last 100 years to create a set of 100 adapted populations to be used to initiate the final simulation runs (5578–6210 individuals). In addition, the fitness of genotypic trait values, as expressed by the average lifetime juvenile production plotted against the genotypic trait value of the individual (hereafter called ‘genotypic fitness function’), was recorded for the last 1000 years of the adaptation run. After these initial preparations, we started the final simulation runs that described the population before, during and after fishing. In each run, an initial population was first sampled from the 100 recorded ones and the model was run for 100 years in the absence of fishing. This was then followed by 100 years with fishing and then again 300 years in the absence of fishing. At each time step, we recorded several population and life-history metrics as well as the heritability (the ratio of genotypic variance to phenotypic variance) of the trait value coding L_∞ (and thus the life-history type) and the selection differential for the trait value (calculated based on the Breeder's equation from the previous year's heritability and the difference in the average trait value between previous and current year). For every cohort, we also recorded the average lifetime juvenile production R₀ (per-generation population growth rate) and calculated the population growth rate per unit time, r = log(R₀)/T, where T is the generation time, estimated by the average age of mature individuals over the cohort's lifespan. We further estimated the genotypic fitness function for those cohorts affected by fishing throughout their lifetimes. The simulation runs were produced for both the evolutionary and the non-evolutionary models, using 20 replicated runs for each.

Most previously published simulations that have modelled the evolutionary responses in life histories to fishing have assumed there to be no survival cost associated with reproduction [40], thus excluding a fundamental life history trade-off [38] and an important component of natural selection [25]. But, to allow our results to be comparable with previous work, and to evaluate the potential general applicability of our findings, we repeated the above-mentioned simulation design by not incorporating a survival cost but setting the overall mortality rate for all individuals (irrespective of whether they attained maturity or not) at 0.154 (see above). All simulations and analyses were conducted with R v. 2.10.0 [41].

3. Results

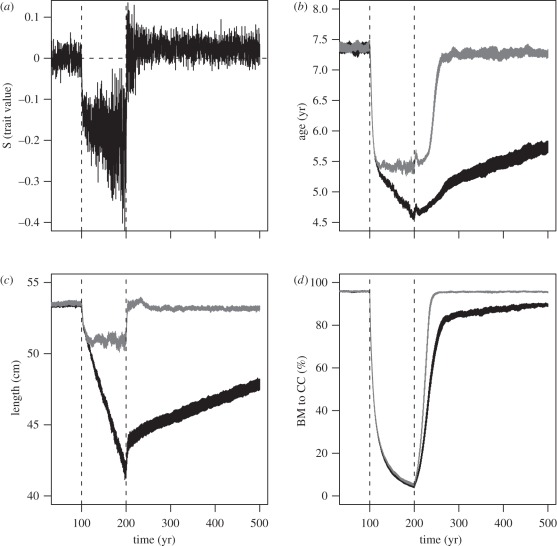
During the first 100 years of the simulation runs, the populations were fully adapted to the prevailing conditions as reflected by the lack of temporal trends in life-history traits and population abundance (figure 1). The beginning of fishing (at year 100) caused rapid declines in age and size at maturity because of increased mortality among large individuals (figure 1a–c and see also the electronic supplementary material, figure S2; note that changes in L_∞ are analogous to changes in size at maturity, given that the size at maturity was set to occur at 0.66 × L_∞). In addition, population abundance also declined from its pre-fished equilibrium (figure 1d). After about 20 years of fishing, the age and size at maturity began to deviate between the evolutionary and non-evolutionary models (figure 1b,c) because of the evolutionary adaptation of the life histories to fishing (figure 1a), which was allowed by the evolutionary model. After 100 years of fishing, the relative differences in the age and size at maturity as estimated by the evolutionary and the non-evolutionary models were 15 per cent and 18 per cent, respectively. During the fishing period, maximum age did not change and the 75 per cent quantile for lifespan decreased by only one year (from 12 to 11).

Figure 1.

Selection differentials and changes in life-history traits and population biomass during the simulation period. Selection differentials (S) on the trait value coding the life history are shown in (a), whereas age and length at maturity are given in (b) and (c), respectively, and biomass-to-carrying-capacity ratio (BM to CC) in (d). Black shade denotes evolution and grey shade denotes no evolution. Shaded areas encompass 95% CI of the averages of 20 replicated simulation runs. Dashed vertical lines indicate the beginning and the end of fishing. Runs are repeated with a model that allows the life histories to evolve as well as with a model that does not allow evolution, as indicated in the legend, except that selection differentials are only shown for the evolving population.

After the cessation of fishing (at year 200), the life histories began to evolve back towards the pre-fishing state in the evolutionary model (figure 1a–c), but the rate of evolution was slow, so that after 300 years of recovery age and size at maturity were still 22 per cent and 11 per cent lower than what they were before fishing (and compared with the life histories in the non-evolutionary model). The same pattern was also reflected by the heritabilities of the genotypic trait values. Prior to fishing, heritability averaged 0.27, decreasing to 0.22 by the end of the 100 year fishing period, and then slowly increasing to 0.25 by year 500. Evolutionary changes in life histories also affected the biomass rebuilding after the cessation of fishing in the evolutionary model, such that the population increased towards a new, lower equilibrium biomass than in the non-evolutionary model, which rebuilt rapidly back to its pre-fished biomass level (figure 1d).

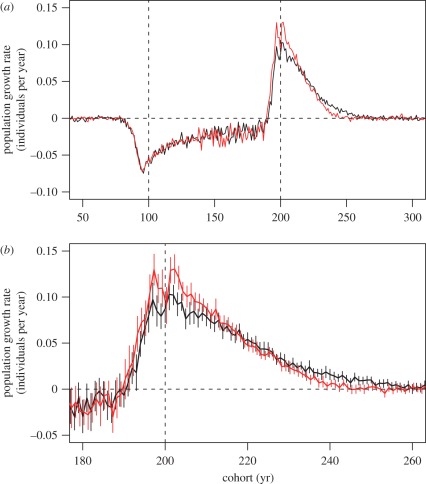
While evolutionary and non-evolutionary models showed clear differences in life histories during fishing and throughout the 300 year recovery period, the population growth rates calculated for each cohort remained similar (figure 2a). In both simulation scenarios, the initiation of fishing caused population growth rates to decline from the pre-fished level of approximately zero, indicating that the populations were declining. Once fishing has ceased, growth rates exceeded zero (indicative of positive population growth) until the populations had once again attained an equilibrium: the non-evolutionary model approximately by the year 245 and the evolutionary model by the year 260 (figure 2b). A difference in growth rates was discernable for the cohorts born during years near the time of cessation of fishing (year 200) and those born around year 250 (figure 2a), although a closer investigation of these time periods showed that in most years the 95% CI overlapped (figure 2b).

Figure 2.

Population growth rates per unit time (years) calculated for each cohort. The averages of 20 replicated simulation runs with evolutionary and non-evolutionary models (see §2 for further details) are shown in (a). (b) zooms into the time span where growth rates based on the evolutionary and the non-evolutionary model differ most and, in addition to averages, 95% CI are shown by vertical lines. Dashed vertical lines indicate the beginning and the end of fishing. Notice that the x-axis indicates the year in which a cohort is born. Cohorts born close to the begin of fishing were exposed to fishing later in life, whereas cohorts born close to the end of fishing were no longer exposed to fishing later in life. Consequently, growth rates of these cohorts were affected by the presence/absence of fishing later in life. Black curve denotes evolution; red curve denotes no evolution.

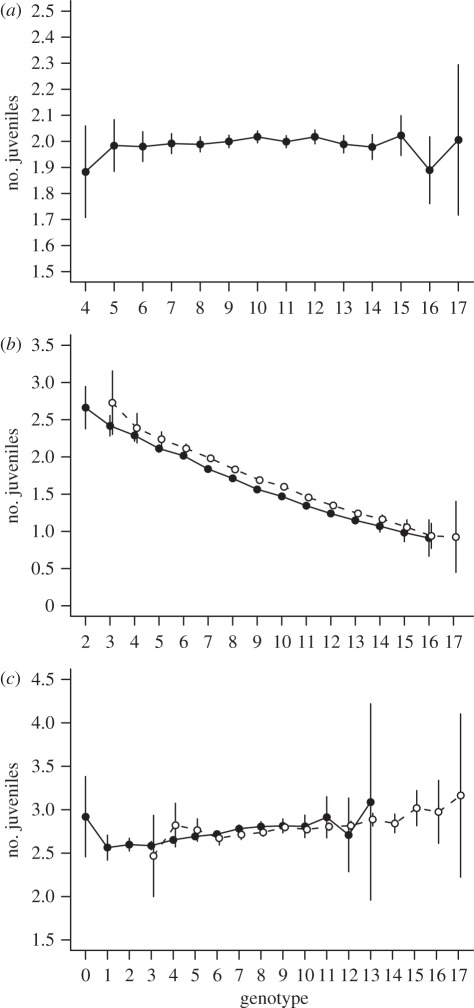
An explanation for the similarity in population growth rates, despite marked differences in life history between the evolutionary and non-evolutionary models, was provided by the genotypic fitness functions. In the absence of fishing, the fitness function was markedly flat across a wide range of genotypic trait values (and thus phenotypes), such that the cumulative lifetime reproductive output was very similar among differing life-history types (figure 3a). By contrast, during fishing, the early- and small-maturing life-history types (low genotypic trait values) had a higher fitness compared with the late- and large-maturing life-history types (high genotypic trait value; figure 3b). This resulted in evolution towards lower genotypic trait values during the fishing period (figure 1). But as soon as fishing had ceased, the fitness function again became flatter (figure 3c) resulting in similar rates of population growth, despite differing genotype distributions. Notably, the fitness function recoded for the cohorts born during the first 40 years of the recovery was slightly increasing along the genetic trait values (figure 3c), as a result of the combined effects of the population being below its equilibrium as well as the natural selection towards higher age and size at maturity (figure 1). As a result, in the absence of evolution (higher trait values more abundant), the equilibrium was reached slightly faster than in the presence of evolution (figure 2b).

Figure 3.

Genotypic fitness functions: (a) before, (b) during and (c) after fishing. Fitness is described as lifetime cumulative juvenile productions, and the genotypic trait value is the sum of allelic values of the individual (see §2 for further details). Averages are given by solid bullets and 95% CI are encompassed by vertical lines. Fitness before fishing is recorded for over 1000 years in a fully adapted population and the function given in (a) is restricted to genotypes of which there were over 1000 observations during this period. During fishing, fitness is recorded for those cohorts that were affected by fishing throughout their lifetime, over 20 replicated simulation runs, using the model with/without evolution (solid/dashed line and filled/open symbols). After fishing had ceased, the fitness is recorded for cohorts for the first 40 years thereafter (the population had not yet attained an equilibrium). In (b,c), functions are restricted to genotypes for which there were more than 100 observations.

Results of the simulations that excluded a survival cost of reproduction were qualitatively analogous to those in which the cost was accounted for (electronic supplementary material, figure S3). Population growth rates resulting from the evolutionary and non-evolutionary models largely overlapped and recovery times did not differ. Interestingly, comparing the results between the evolutionary and non-evolutionary models, the differences in population growth rate for the cohorts born close to the cessation of fishing were smaller than those documented in the presence of the survival cost (figure 2 and electronic supplementary material, figure S3).

4. Discussion

Our investigation of the evolutionary and ecological dynamics of Atlantic cod during a period of size-selective fishing, followed by a period of recovery, suggests that fisheries-induced evolution might not have a substantive effect on the rate of population growth. Given that population growth rate is intimately linked to extinction probability and recovery potential from low abundance [18–20], our findings imply that fisheries-induced evolution might not negatively affect population persistence or recovery. From a fisheries perspective, the impacts of fisheries-induced evolution are generally considered negative owing to a lower biomass yield and reduced catches [8,9,13]. From a conservation perspective, however, our findings suggest that the influence of fisheries-induced evolution might be lower than previously hypothesized [16,17].

Although the estimation of population growth rates has comprised a fundamentally important component of some fisheries-related research [42,43], population growth rate has attracted comparatively little attention in studies of fisheries-induced evolution (but see earlier studies [44–46] for closely related examples). In this respect, the analysis by Hutchings [16] was a rare attempt to estimate how life-history changes in an exploited fish stock affect the rate of population growth. However, by suggesting that the life-history changes observed in northwest Atlantic cod might indeed reduce population growth rate, the outcome of this study is in contrast to the findings of the present work. In part, this disagreement may be attributable to the fact that Hutchings’ [16] analyses did not account for the trade-off between individual growth speed (k) and asymptotic body size, nor did they account for density-dependent processes, primarily because population projections were not integral to his work; the analyses were projections of population growth rate under two life-history scenarios rather than temporal population projections that would have necessitated an incorporation of population dynamical processes, as we attempted here. The discrepancy nonetheless stresses the importance of incorporating ecological realism in the forecasts of fisheries-induced evolution. Density-dependence and life-history trade-offs are fundamental in shaping the selection and demographic feedbacks of evolution (see Dunlop et al. [40] and references therein as well as [47,48]).

The minor effect of fisheries-induced evolution on population growth rate found in our study was attributed to the flatness of the genotypic fitness function (expressed as lifetime reproductive output) in the absence of fishing (figure 3). It should be emphasized here that the shape of the fitness function was not an assumption of the simulation model but a model outcome, resulting from the trade-off between age and size at maturity and the effect of body size on individual fecundity. Interestingly, our finding is consistent with work reported by Law & Grey [49]: when estimating the selection pressures associated with the fishing of North Sea cod, they found the lifetime reproductive output to be very similar across a range of ages at maturity. More generally, these findings also match well with theoretical expectations. In the absence of disturbances, natural fish populations often show a broad level of diversity in life histories, suggesting that fitness functions might rather be flat across a range of life histories than dome-shaped around a single life-history optimum [7,50]. However, while the flatness of the fitness function implies that the population growth rate may not be largely affected by fisheries-induced evolution, it also means that the evolutionary changes in life histories do not reverse quickly in the absence of fishing [47]. This was seen in our simulations (figure 1) and has also been documented in previous modelling studies [13,40].

As discussed in §1, the interest in Atlantic cod goes beyond being just a study species, owing to its prominence in the research on the consequences of overfishing [51] and fisheries-induced evolution [10,23,49,52]. While our study was, by its nature, a theoretical investigation and was not intended to provide a detailed, realistic description of any particular cod stock, our results nonetheless suggest that fisheries-induced changes in cod life histories might not account for slow recovery following reductions in fishing pressure. This conclusion is also supported by recent findings by Swain [15], who showed that the rapidly increased natural mortality in the Southern Gulf of St Lawrence cod was not associated with changes in cod life histories concomitant with potential fisheries-induced changes in individual growth rate. Instead, reasons impeding cod recovery may be linked to changes in predator–prey interactions and in the entire food web (owing to dramatic reduction in cod abundance) as well as Allee effects at low population abundance, rather than fisheries-induced evolution per se [15] (see also Law & Grey [49]). Taking such ecological effects into account in the forecasts for fish stock recovery is a challenging yet necessary task for future fisheries stock assessment and management.

While our simulation of the Atlantic cod population suggests that fisheries-induced evolution might not largely affect population growth rate and, thus, extinction risk and recovery potential, generalizations based on our results should be performed very cautiously. As with any modelling study, our simulation approach carries many simplifying assumptions (for discussion of the model, see also Kuparinen et al. [25]). In our simulation design, one notable feature was that both mature and immature individuals were exposed to fishing similarly, so that no spatial aggregation of fishing between spawning and feeding grounds was considered. Law & Grey [49] showed that this does not affect the flatness of the fitness function. However, unaccounted processes such as growth or body-size effects on natural mortality [53], the effect of body size on sexual selection [54], density- and frequency-dependent effects on behaviour, maturation and plasticity of phenotypes [40,48], as well as body-size and age effects on egg quality [55] and juvenile survival [56], all might alter relative fitness of different life-history types. Similarly, we did not consider variability in the environment and its effects on population dynamics. Although recruitment variability in Atlantic cod is below the average for marine fishes [57], it can play an important role in fish population dynamics and select for the older age and large size at maturity characteristic of a bet-hedging life history in fishes [58], thus making the fitness function less flat than what was predicted by our model. Unfortunately, data on such processes are exceedingly limited for wild populations, and, thus, incorporation of them to the simulations would involve considerably high levels of uncertainty. Given that our study can be viewed as one of the first attempts to understand the role of fisheries-induced evolution in population growth, our aim was to keep the model simple and well data-supported. Nonetheless, we acknowledge that further research on the effects of the above-listed processes on phenotypic fitness and population growth rate is needed, and we stress that any interpretations based on our findings should be conditioned on the model assumptions made.

Caution is also required when generalizing the results of this study to a wider context of fisheries research and management. In addition to exploring the sensitivity of the model results to the assumptions discussed earlier, it would be instructive to contrast predictions of population growth rates in different fish species and populations relevant for the studies of fisheries-induced evolution. Such investigations would be useful to assess how consistent the findings are across species and life-history types and, conversely, to illuminate the circumstances under which fisheries-induced evolution might substantially affect population growth rate. It should also be borne in mind that even if fisheries-induced changes in life histories did not affect population growth rate directly, they may still affect a population's ability to cope with environmental fluctuations [59]. In cod, for instance, a population of early- and small-maturing individuals has been hypothesized to be more vulnerable to climate change [60,61]. All such features need to be carefully accounted for when evaluating conservational consequences of anthropogenic evolution [62].