How the type of anthropogenic change alters the consequences of ecological traps

Abstract

Understanding altered ecological and evolutionary dynamics in novel environments is vital for predicting species responses to rapid environmental change. One fundamental concept relevant to such dynamics is the ecological trap, which arises from rapid anthropogenic change and can facilitate extinction. Ecological traps occur when formerly adaptive habitat preferences become maladaptive because the cues individuals preferentially use in selecting habitats lead to lower fitness than other alternatives. While it has been emphasized that traps can arise from different types of anthropogenic change, the resulting consequences of these different types of traps remain unknown. Using a novel model framework that builds upon the Price equation from evolutionary genetics, we provide the first analysis that contrasts the ecological and evolutionary consequences of ecological traps arising from two general types of perturbations known to trigger traps. Our model suggests that traps arising from degradation of existing habitats are more likely to facilitate extinction than those arising from the addition of novel trap habitat. Importantly, our framework reveals the mechanisms of these outcomes and the substantial scope for persistence via rapid evolution that may buffer many populations from extinction, helping to resolve the paradox of continued persistence of many species in dramatically altered landscapes.

1. Introduction

The rapid pace of ongoing environmental change continues to threaten plant and animal populations by altering both ecological and evolutionary dynamics [1,2]. At the nexus of altered eco-evolutionary interactions lies the concept of evolutionary traps. Evolutionary traps occur when formerly adaptive behaviours become maladaptive (sensu [3,4]) because cues used for decision-making become decoupled from the resulting fitness consequences, such that previously adaptive choices result in lower fitness [5]. This decoupling can arise from habitat alteration or the production of novel anthropogenic stimuli that resemble food, mates, nest-sites or other resources [5,6]. Evolutionary traps are of extreme interest for both basic and applied reasons, as the study of evolutionary traps provides an opportunity to simultaneously investigate ecological and evolutionary forces that shape contemporary dynamics relevant to ecology, evolutionary biology and conservation [7–9].

One important type of evolutionary trap that has received considerable theoretical and empirical attention is an ecological trap, which occurs when individuals come to prefer settling in poor-quality habitats over better alternatives [5,10]. The concepts of ecological traps and source–sink dynamics are related [7,11], where preferred sinks are often considered ecological traps; yet traps focus on habitat selection behaviour, whereas source–sink dynamics can occur in the absence of habitat selection [12]. Although ecological traps are poorly documented and understood in nature [7,13], theory in the past decade has made great strides in highlighting the potentially dire implications of these phenomena for population dynamics and conservation strategies [14–17]. Results of these models suggest that traps generally promote population declines and can facilitate extinction [7].

However, it remains unclear how applicable these models are to real-world problems for two reasons. First, models have seldom acknowledged that traps not only influence ecological dynamics, but also evolutionary dynamics, such that populations may potentially ‘escape’ from traps via natural selection for adaptive preferences or through existing phenotypic plasticity (‘escape’ hereafter [6,17]). Second, models have not addressed the fact that traps can arise through different types of anthropogenic change [5,13]. For instance, anthropogenic alteration can degrade the fitness value of habitats without altering available habitat selection cues, such as habitat alterations causing changes in predator communities that result in heightened predation rates of prey [18,19]. Traps can also emerge when novel cues or habitats are triggered by anthropogenic change. For example, oil slicks and asphalt roads polarize sunlight and consequently mimic the appearance of water, which results in aquatic insects preferring to oviposit on them [20,21]. While these alternative types of traps have been emphasized, the resulting ecological and evolutionary consequences remain unexplored, in part because a general framework for tracking eco-evolutionary dynamics from traps has yet to emerge.

We contrast the effects of different types of anthropogenic change that trigger ecological traps using a framework uniquely suited for interpreting the eco-evolutionary implications of traps. The foundation of this framework is drawn from the Price equation, from evolutionary genetics [22]. Our approach allows for explicit tracking of ecological and evolutionary processes on population dynamics, and it identifies fundamental partitions that drive such dynamics. We first describe the general framework, and subsequently use this framework to interpret the dynamics and outcomes that arise when migratory birds are exposed to different types of traps. Our findings illustrate how the type of ecological trap and the characteristics of the trapped population interact to affect the fate realized by trapped populations.

2. Methods

(a). Applying the Price equation to interpret effects of ecological traps

The Price equation provides a novel framework for understanding the effects of ecological traps because it allows for simultaneously tracking the ecological and evolutionary forces influencing the dynamics and outcome of traps. In the Price equation, evolutionary change is tracked by

2.1

where w is a measure of fitness, z is the character of interest, i reflects different states/groups with the same character value (e.g. different individuals and patches), and Cov and E are standard statistical notations reflecting definitions of covariance and expectation, respectively [23]. Fitness is defined as w_i = n_i′/n_i, where primes denote a second population derived from the first (e.g. offspring derived from parents) and n denotes weights reflecting the absolute or relative number of individuals in i; note the similarity to the finite rate of increase, λ = n_t+1/n_t. Much of the focus of the Price equation has centred on discrete, non-overlapping generations in a population genetics framework. Nonetheless, the approach is a general formalism of selection and evolutionary change under all conditions, such that it can be applied to any form of selection [24], and can be extended to incorporate both continuous time [25] and overlapping generations [26].

For ecological traps, the value of the character of interest, z, can be described by either innate habitat preference or the habitat selected by an individual along an environmental gradient. In field investigations on ecological traps, often we simply have information on the habitats selected by individuals, which are presumably a function of innate preferences and environmental constraints. For simplicity, we consider a dichotomous situation where there are two types of habitats. To apply the framework of the Price equation to ecological traps, we define z_i as an arbitrary habitat value (e.g. poor habitat = 0 and good habitat = 1) that individual i selects in a landscape, with i = 1, … N, where N is the number of individuals in the landscape. We start by assuming no constraints on habitat choice occur (see below for relaxing this assumption). The relationship between the habitat selected along an environmental gradient (z_i) by individual i can be explained by innate preferences, g_i, or the probability of selecting high-quality habitat if all resources were equally available (and 1 – g_i is the probability of selecting low-quality habitat), where E(z_i) = g_i (for a Bernoulli trial). Consequently, the relationship for tracking the evolution of preference, g, becomes

2.2

Ecological dynamics regarding changes in population size can be examined by rearrangement of terms in equation (2.2) to yield

2.3

In the context of ecological traps, the term Cov(w_i, z_i) in the general Price equation (equation 2.1) identifies the ‘selection effect’, or the potential strength of the trap, where a large negative covariance highlights a strong trap. The related terms in equations (2.2) and (2.3) have a similar interpretation when no constraints on habitat selection occur (although the selection effect is scaled based on average fitness or average change in preference). The last term in equation (2.1), E(w_iΔz_i), identifies the fidelity of transmission of the habitat choices from parents to offspring (in equations (2.2) and (2.3), the last term identifies scaled measures of the fidelity of preference), which can occur genetically and/or culturally, and may be influenced by several ecological and evolutionary factors, such as variation in resource availability and mutation rates for alleles associated with preference. This term should not be confused with a measure of heritability, h², which can be partitioned from the covariance term in the Price equation under some conditions (see [23,27]). This second term is a strength of this framework, because it provides a flexible structure for tracking the fidelity of transmission (see below). Finally, using weights, n_i, based on absolute numbers of individuals, enables tracking the absolute change in population size, which will provide insight into the probability of population extinction.

(b). Modelling alternative types of ecological traps

We extend previous models regarding ecological traps to explicitly track ecological and evolutionary dynamics that arise under two general types of environmental perturbations that can generate ecological traps [13]. Both scenarios start with the same initial conditions, with two habitat types that vary in quality but both have λ > 1, and individuals prefer the highest-quality habitat (adaptive behaviours where no traps occur). In our first scenario, what we term a ‘degradation trap’, habitat quality is reduced in the formerly highest-quality habitat, leading to λ < 1 in that habitat, but preference for this habitat remains (at least initially) unchanged (electronic supplementary material, figure S1). This scenario is similar to that considered by Kokko & Sutherland [17]. The second scenario we consider occurs when habitat quality of the original habitat remains unchanged, but novel cues make unsuitable habitat attractive. This is accomplished in a way that allows the same amount and quality (λ) of trap habitat to be created as in the degradation trap scenario by causing non-habitat (i.e. the matrix) to be converted to a novel habitat type that mimics high-quality habitat but has λ < 1 [5], which we term a ‘novel habitat’ trap (electronic supplementary material, figure S1). While the prevalence of these types of traps is currently unknown, there is empirical evidence for each. Habitat degradation resulting in lower-quality habitats being preferred has been documented in several systems [18,19]. Novel habitat additions creating ecological traps from former non-habitat have not been explicitly considered in models of ecological traps, although some traps, such as the creation of roads, buildings and photovoltaic solar farms catalysing oviposition by wetland insects, clearly fall within this realm [20,28,29].

To understand the consequences of these types of ecological traps, we focus on modelling demography and habitat selection of migratory birds. Migratory birds are useful in this regard because several models on ecological traps focus explicitly on avian dynamics [15,17,30]. Several putative examples of ecological traps also occur for migratory birds [31–33]. We emphasize that our approach is very general and only uses birds as a means to bound demographic rates (electronic supplementary material, table S1), however, such that results are likely to be applicable to many taxa.

In the spirit of Schlaepfer et al. [5], our model begins with a landscape that has two different types of habitat, one of which is of high quality (λ ≈ 1.07) and the other slightly lower in quality, but the latter is still a habitat source (λ ≈ 1.02; ‘moderate quality’ hereafter), embedded in a matrix of non-habitat (cf. [17]). Individuals have adaptive preferences by tending to settle in high-quality habitat, but will have a lesser tendency to also settle in moderate-quality habitat. Sequential habitat selection by individuals is modelled by drawing from principles of resource selection modelling [34], and once a territory is selected it is no longer available to other individuals [35,36]. This assumption is consistent with site-pre-emptive selection and territoriality observed in many migratory birds [35,37]. We identify the proportion of high-quality habitat available in the landscape A_i for individual i (where 1 – A_i is the proportion of low-quality habitat available). Then the probability Pr(z_i) that individual i will select high-quality habitat is

2.4

where g_i is the ‘innate’ preference of individual i for high-quality habitat, or the probability that high-quality habitat would be selected if all resources were equally available [38]. Once settled, individuals attempt to breed. Fecundity varies between habitat types using estimates from previous models (electronic supplementary material, table S1; [15]). Annual survival rates of individuals were taken from other models on avian demography, where offspring have lower survival probabilities than adults and were constant between habitats, consistent with previous models [15,17]. We follow Frank [23] to model juvenile preference for habitats as a function of their parents’ preference,

2.5

where γ ∼ N(0, σ²) (see electronic supplementary material, figure S3). This phenomenological representation draws from quantitative genetics, is based on the idea that preference is generated from a small effect of many loci, and is intended to capture broad variation in transmission [23,39]. When σ² = 0, this reduces to the haploid inheritance used by Kokko & Sutherland [17]. We note that using a simple mutation rate for preference as the error in transmission [40] provides similar results to those presented here (R. J. Fletcher 2011, unpublished data). All processes were modelled through stochastic realizations from relevant probability distributions (electronic supplementary material, table S1).

We ran the model for 20 years with an adaptive situation of preference for high-quality habitat and then initiated two scenarios that encapsulate two major types of traps arising from perturbations on the landscape (electronic supplementary material, figure S1). While these types of traps could potentially be modelled in different ways, we explicitly designed these simulations such that the initial conditions, the amount of trap habitat created and the quality of trap habitat created were identical across these two scenarios, thereby allowing for seamless relative comparisons of the dynamics resulting from these different types of traps. However, this type of perturbation clearly results in a lower global λ (i.e. the habitat-weighted λ for the entire landscape, in the absence of habitat selection) for the degradation trap scenario, because after the perturbation, the highest-quality habitat (λ = 1.07) no longer remains. In the electronic supplementary material, figures S4–S7, we also compare a situation where the initial conditions, the amount of trap habitat created and the global λ were identical between these two types of traps by altering the severity of the trap habitat created in the degradation trap scenario.

For all simulations, we initialized a landscape with habitat that could accommodate 1000 individuals (approx. carrying capacity, K), reflecting a territory size of 1 ha. We initialized the model with 50, 100, 250, 500 or 750 individuals and ran the model for 20 years prior to the occurrence of a trap and 100 years after the trap began [15]. We used a form of ceiling density dependence [41], where if population size grew to be greater than K in the landscape, excess individuals permanently emigrated or died [15].

At each time step, we calculated the finite rate of increase (λ = N_t+1/N_t) and used the Price equation to partition changes in preference () and habitat selected (). Furthermore, we track both the selection and transmission effects over time. At the end of 100 years after the perturbation, we further determined if populations persisted with continued preference for traps, went extinct or escaped traps (i.e. the population persists and the average preference is no longer for low-quality habitat). We varied the following parameters in a factorial fashion across a broad parameter space (electronic supplementary material, table S1): initial preference for high-quality habitat (g_int), the likelihood of transmission of preferences, γ, and the amount of perturbation (trap habitat). For each combination, we ran 50 replicate simulations. To interpret the relative effects of these parameters and trap type on population outcomes, we used a multinomial generalized linear model (GLM). In simulation models, small differences may yield statistical significance because of the ability to produce large sample sizes. Consequently, we focus on the relative magnitude of F-values rather than p-values to interpret the relative effect of parameters on outcomes [42].

3. Results

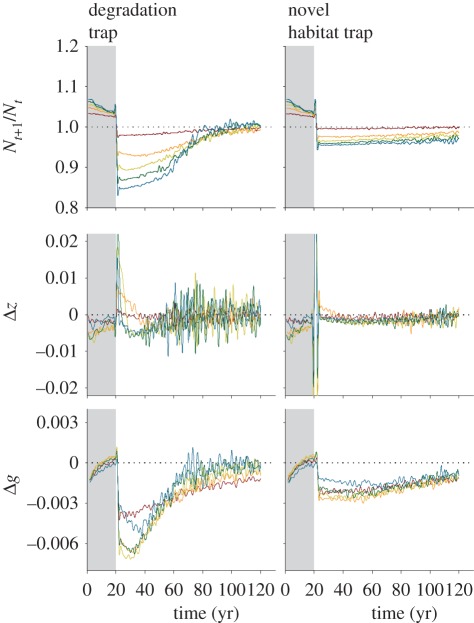
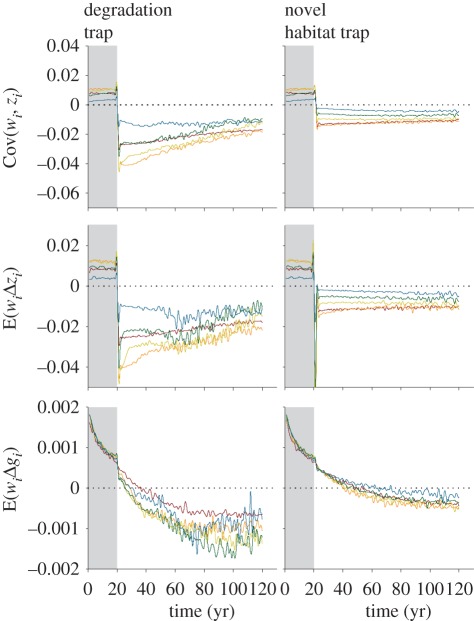
Prior to perturbations that created traps (years 1–20), changes in habitat preference via natural selection were small (figure 1), but tended to be negative owing to the fact that as populations grew, a greater fraction of individuals used less-preferred habitat where λ was still positive. The Price equation showed a positive covariance between habitat selection and fitness (figure 2), which is expected under these adaptive conditions. Similarly, the transmission in habitat selection was also positive, as was the transmission in preference, highlighting that the more successful individuals with adaptive preferences were contributing more to populations in subsequent time steps.

Figure 1.

Changes in population growth (N_t+1/N_t), habitat selection () and habitat preference () over time for two types of ecological traps under different amounts of trap habitat created (ha). Grey shading denotes initial dynamics that occur prior to trap formation. Marginal means from 37 500 simulations are shown for each type of trap. Brown line, 100; orange line, 300; green line, 500; dark green line, 700; blue line, 900.

Figure 2.

Partitioning the effects of two types of ecological traps under different amounts of trap habitat created (ha) using the Price equation. The Price equation partitions effects based on the selection effect, Cov(w_i,z_i), and transmission effects, shown here as transmission of habitats selected E(w_iΔz_i) and habitat preference E(w_iΔg_i). Figure formatting is the same as figure 2. Brown line, 100; orange line, 300; yellow line, 500; green line, 700; blue line, 900.

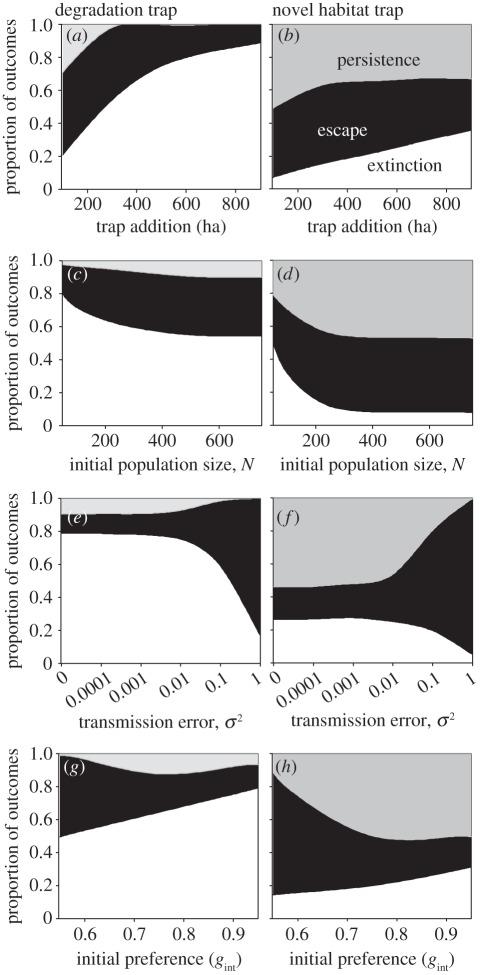
When perturbations occurred, we found that population dynamics from the same amount of trap perturbation were strikingly different depending on the trap type, where populations were more likely to suffer extinction from degradation traps than novel habitat traps (figure 3). Novel habitat traps were more likely to persist because some high-quality habitat remained on the landscape, diluting the negative effects arising for preference for the novel habitat. Changes in growth rates, habitat selection and preference were stronger for degradation traps, and also more variable over time, which was driven by stronger selection pressures and reduced population size (electronic supplementary material, figure S4), leading to increased stochastic variation in these parameters. A multinomial GLM suggested that the population outcome was most sensitive to initial preferences and transmission error, and least sensitive to initial population size (electronic supplementary material, table S2); habitat amount and transmission error also showed greater interactive effects with trap type than initial preferences or population size in determining outcomes. When we contrasted these scenarios holding the global λ constant, these effects remained, although the magnitude of effects was less (electronic supplementary material, figures S5–S8 and table S2).

Figure 3.

Population outcomes in response to two types of ecological traps as a function of: (a,b) the amount of trap habitat created (ha); (c,d) initial population size (N); (e,f) errors in transmission of preference (σ²); and (g,h) strength of initial preference (g_int). For each scenario, initial landscape conditions were composed of the same amount of high-quality and moderate-quality habitat. Outcomes were defined as population extinction (white region) when N = 0, escape (black region) when N > 0 and population preference for low-quality habitat was eliminated, or persistence (grey region) when N > 0 and preference for low-quality habitat remained.

When partitioning responses using the Price equation, we found that selection effects, Cov(w_i,z_i), showed similar trends to transmission effects on habitat selection (figure 2). For all scenarios, transmission effects on habitat preference, E(w_iΔg_i), were an order of magnitude smaller than transmission effects on habitat selection, E(w_iΔz_i).

4. Discussion

Understanding ecological and evolutionary dynamics that arise from ecological traps is important because traps may represent an underappreciated source of population endangerment [7], and because contemporary evolution may play a pivotal role in affecting persistence in the face of anthropogenic habitat and climatic change [2,43,44]. Using a novel framework guided by the Price equation, our results illuminate three key points regarding ecological traps. First, the likelihood of population adaptation, persistence despite continued preference for poor-quality habitat or extinction hinges crucially on the type of ecological trap that arises from anthropogenic change. Second, our model provides a mechanistic explanation for the common observation that trapped populations continue to persist despite frequent theoretical predictions to the contrary [15,45]. Third, by utilizing a flexible, powerful approach built on the Price equation, our work reveals how transmission error plays an important, yet generally unappreciated role in affecting the fate of populations. Below, we discuss each of these points, as well as the implications of our results for applied conservation and rapid evolution.

(a). The profound influence of the type of ecological trap

Our model shows that traps arising from habitat degradation of former high-quality habitat may increase population vulnerability to extinction more than the addition of novel habitats that results in ecological traps. Furthermore, ecological and evolutionary dynamics were highly variable across these scenarios, such as the magnitude of the selection effect, even while initial conditions and other aspects of model structure (e.g. preference and amount of habitats perturbed) were structurally the same.

Previous modelling efforts on ecological traps have not explicitly considered these different types of ecological traps on ecological and evolutionary dynamics. Rather, most models have begun with a scenario where traps already exist and low-quality habitat is preferred by individuals over existing high-quality habitat [14–16]. The only exception was the model by Kokko & Sutherland [17], which tracked an initially adaptive situation that was perturbed in a manner similar to our scenario where traps arise from the degradation of high-quality habitat. Our results illustrate that explicit consideration of the way a trap arises is critical because it affects the likely fate of trapped populations. This finding is particularly relevant because of the pragmatic likelihood that traps of different origins (like those modelled here) are likely to be common in modern anthropogenic landscapes [13]. By identifying how traps arise, we may be able to better understand the persistence and evolution of populations exposed to traps.

(b). Persistence of trapped populations need not be paradoxical

Although recent reviews highlight the difficulty of accurately identifying ecological traps in nature [13], a growing concern is that trapped populations may be relatively common in contemporary landscapes [7]. While earlier modelling approaches suggest that the persistence of trapped populations may not be likely [14–17], our model illustrates several cases where persistence occurs. Trapped populations are most likely to persist when traps arise from novel habitat being created on landscapes, where some high-quality habitat still remains owing to reduced selection and transmission effects. We caution, however, that our results also illustrate that ecological traps consistently reduce population size (electronic supplementary material, figures S4 and S8), thereby leaving populations more susceptible to stochastic extinction.

Allee effects can arise from ecological traps when, at low population densities, individuals can act on their maladaptive habitat preferences, but at higher densities spillover into less-preferred habitat occurs, which can help bolster population persistence when traps occur [5,17]. In our model, this effect can be seen through changes in the amount of the trap perturbation relative to population sizes. Our model highlights that the key to interpreting Allee effects and the potentially rapid extinction of species under some population threshold is a function not just of population densities, but of the availability of trap habitats (electronic supplementary material, figures S3 and S6).

(c). The role of transmission error in affecting the response to traps

The likelihood of transmission of maladaptive traits can be highly influential in evolutionary responses. For instance, Gomulkiewicz & Holt [46] considered the general situation of the ability of natural selection to prevent extinction in organisms faced with a new environment. Results from their quantitative-genetics model suggest that as heritability of maladaptive traits increases, the likelihood of extinction decreases. Our results provide contrasting results for ecological traps as transmission error declines. This discrepancy can be explained by the fact that moderate levels of transmission error provide variation in preference for natural selection to act on and that heritability in the Price equation is partitioned from the covariance term, rather than the transmission term [23,27]. Gomulkiewicz & Holt [46] further show that the ability of natural selection to prevent extinction is strongly influenced by the degree of maladaptation, which is consistent with our results regarding the strong effects of initial strength of habitat preference on observed outcomes (electronic supplementary material, table S2).

Kokko & Sutherland [17] have also formally considered the possibility of evolutionary response to selection from ecological traps. However, in their approach, inheritance was assumed to be exact haploid inheritance of preference. The Price equation framework can readily capture these dynamics: in such a situation, Δg_i = 0 and the Price equation reduces to the first term in equation (2.1). Yet variation in trait transmission from parents to offspring is possibly common in nature [47]. Our framework allows for errors in inheritance (potentially from genetic, cultural and/or environmental sources) and suggests that this factor is an important determinant of the outcome of traps. Furthermore, by incorporating evolutionary dynamics, inferences on the likelihood of extinction also changed relative to previous efforts: a primary determinant of the probability of extinction was the error in transmission of preference across generations. By expanding upon recent modelling efforts for understanding the implications of ecological traps [14–17], our framework clearly demonstrates that more consideration is needed on the potential for evolutionary responses to traps.

5. Conclusions

Ecological traps are complex phenomena that incorporate both ecological and evolutionary issues operating at different levels of organization. Our work illustrates that the origins of traps and the magnitude of transmission error have profound effects on the outcome realized by a trapped population. In illuminating the importance of the type of environmental change and transmission of preferences, our work also highlights the lack of empirical information on both of these key components. Even so, the general flexibility of our framework makes it possible to evaluate a wide range of scenarios when trap type and transmission are not known with certainty, and this framework could be expanded to accommodate other types of evolutionary traps and issues, such as the role of phenotypic plasticity and cultural evolution. While recent modelling has laid the ground for understanding the implications of ecological traps [14–17], we suggest that more attention is needed on how traps arise and the potential for evolutionary responses to traps.