Hierarchical flexural strength of enamel: transition from brittle to damage-tolerant behaviour

Abstract

Hard, biological materials are generally hierarchically structured from the nano- to the macro-scale in a somewhat self-similar manner consisting of mineral units surrounded by a soft protein shell. Considerable efforts are underway to mimic such materials because of their structurally optimized mechanical functionality of being hard and stiff as well as damage-tolerant. However, it is unclear how different hierarchical levels interact to achieve this performance. In this study, we consider dental enamel as a representative, biological hierarchical structure and determine its flexural strength and elastic modulus at three levels of hierarchy using focused ion beam (FIB) prepared cantilevers of micrometre size. The results are compared and analysed using a theoretical model proposed by Jäger and Fratzl and developed by Gao and co-workers. Both properties decrease with increasing hierarchical dimension along with a switch in mechanical behaviour from linear-elastic to elastic-inelastic. We found Gao's model matched the results very well.

1. Introduction

Dental enamel is the highly mineralized (up to 80–90 vol%), hierarchically structured biological material that covers the crowns of teeth [1]. With all mammalian creatures, teeth play a vital role in the survival of the host as they are crucial for nutrition and mastication. Thus, nature has invented considerable optimization in the properties of the components of teeth. Enamel is by far the hardest and stiffest mineralized biological tissue and while it is non-vital, it plays a crucial role in sustaining the severe masticatory forces and at the same time protecting the vital dentine and pulpal structure of teeth. The specific enamel structure varies between classes and species, however in mammals, enamel is almost always composed of three hierarchical levels [2]. Figure 1 displays the structure of bovine enamel (which was used in this work): at the smallest structural level, hydroxyapatite (HAP) nano-fibres, approximately 50 nm in diameter and up to 100 µm in length [1], are glued together by proteins (level 1), which at the next level of hierarchy are bundled together to form micrometre-scaled fibre-bundles with a diameter of about 5 µm (the enamel rods, level 2), which in some parts of the tooth are periodically interwoven to form higher ordered interwoven patterns [1]. Groups of decussated rods with same orientation form the so-called Hunter–Schreger bands (level 3), which are—in bovine enamel—about 20–30 µm wide as indicated in figure 1c. Individual rods are assumed to span almost the entire enamel layer, hence, being up to 1 mm long, whereas the Hunter–Schreger bands span only the inner enamel layer (approx. 500 µm) [1]. It should be noted here that there exists no strict definition of the counting of hierarchical levels. In a previous study [3], we counted the levels of hierarchy of several biological materials from the first mineral–protein composite level up to the bulk and do this analogously in this work for enamel in concert with the counting of hierarchies used by Gao and co-workers [4–7].

Figure 1.

The hierarchical structure of bovine enamel. (a) Enamel on the smallest size scale consists of hydroxyapatite (HAP) nano-fibres, which are glued together by proteins (first hierarchical level). These nano-fibres are bundled together to form micro-fibres (a), building the so-called enamel rods. Hence, the first hierarchical level can also be called the ‘intra-rod structure’. The enamel rods are arranged straight and parallel in the enamel layer close to the tooth surface (b,d; second level of hierarchy; multiple rods) and form periodically interwoven decussation patterns in the enamel layer close to the inner dentin core of the tooth (c,d; third hierarchical level; decussated rods). Groups of rods of same orientation within the decussation structure form the so-called Hunter–Schreger bands. (e) Dental enamel is mineralized up to 80–90 vol% and covers the tooth crown.

Numerous indentation studies exist characterizing enamel at the micrometre-scale (e.g. [8–11]) with indents and correspondingly induced contact stress-fields commonly having dimensions of up to some tens of micrometres, covering several rods (rod diameter approx. 5 µm; [1]). Additionally, mechanical data are also available from bulk testing techniques, where all levels of hierarchy are included in the sample volumes being tested (e.g. [12–15]), additionally, Lawn et al. [16] have directed significant effort to obtaining a fundamental understanding of the mechanics of the entire tooth crown system.

However, as with other biological materials, hardly any other investigations exist for enamel that addresses the determination of certain mechanical properties at various levels of hierarchy apart from that of Ang et al. [17], where indentation modulus and indentation-induced elastic/inelastic transition were determined. Indentation approaches quantify material properties in highly constrained conditions that do not enable the more critical strength response to be determined. In addition with indentation approaches, it is difficult to identify quantitatively anisotropic material properties as is the case in enamel and most biological materials. In order to better assess the tensile hierarchical structure–mechanical property relations of enamel, a single mechanical testing technique is required that can be applied to all levels of hierarchy within a specific structure. In the study presented here, we use focused ion beam (FIB) milling to fabricate cantilever beams out of dental enamel. By varying the size and position of the cantilevers, it was possible to determine strength and elastic modulus at all three levels of hierarchy.

2. Material and methods

2.1. Material

Bovine enamel was investigated in this study; the specific structure is displayed in figure 1. Slices of around 2 mm thickness were cut out of the middle of five bovine incisors using a Buehler Isomet 4000 precision saw exposing cross sections such as the one shown in figure 1e. The cross sections were ground with 1200 grit SiC paper and further polished with 1 µm and 0.25 µm diamond suspension. The enamel layer was subsequently etched for 1 s using 36 per cent hydrochloric acid and again polished with 1 µm diamond suspension until the enamel rod structure was barely visible under a light microscope. Bovine samples were further bonded to electron microscope stubs using conductive silver paint and were vacuum dried for at least 2 days. Dried samples were then sputter-coated with a thin gold–palladium layer (some nanometres).

2.2. Focused ion beam sample preparation

Triangular cantilever beams were prepared as described by Chan et al. [14,15] using a Dual Beam Zeiss Supra 55VP FIB system First, a trench was milled using gallium ions at 30 kV and a current of 10 nA. The sample was then rotated by 90° and tilted by 30° with respect to the ion direction. Another trench was milled at this angle. The sample was then rotated by 180° and a further trench was milled at 30°. This results in a triangular cantilever beam structure. The process was repeated using gallium ions at 30 kV and a current of 2 nA to generate accurate and smooth cantilever sides. Two differently sized cantilever beams were prepared: small bars with approximately 15 µm length and approximately 4 µm height and width and large bars with approximately 40 µm length and approximately 10–13 µm height and width. The different sized bending bars were prepared randomly within the five teeth cross sections. Nine samples were prepared in summary, three individual samples for each level of hierarchy. Small bars (z = 3; in the following, the number of samples z of tested specimens is given in brackets) were positioned within single rods in the outer enamel region (intra rod, level 1), large bars were prepared within the outer enamel region containing several parallelly aligned rods (z = 3; multiple rods, level 2) and in the inner enamel region containing decussated rods (z = 3; decussation, level 3) as shown in figure 2. Sample dimensions of all samples prepared are listed in table 1.

Figure 2.

Positioning of focused ion beam (FIB) cantilevers within enamel microstructure. To determine the mechanical properties of all levels of hierarchy, positioning and size of FIB-prepared cantilevers of triangular-shaped cross sections were varied. (a,c) Small cantilever beams of approximately 4 µm width and height and approximately 15 µm length were prepared within single rods characterizing the intra-rod structure, which is built by HAP nano-fibres representing the first hierarchical level. Larger cantilevers of 10–13 µm width and height and approximately 40 µm length were positioned into the parallelly aligned outer enamel structure (a) and into the interwoven decussation structure of the inner enamel layer (b,d) to characterize the second and third levels of hierarchy, respectively.

Table 1.

Dimensions of all FIB cantilevers prepared: sample length l, sample height h and sample width b as measured using the Zeiss Supra 55VP scanning electron microscope system. Loaded cantilever length l* is also listed (for details please see figure 4).

sample	length l (µm)	height h (µm)	width b (µm)	loaded cantilever length l* (µm)
sample group 1: intra rod (level 1)
intra rod 1	15.75	4.84	4.15	13.43
intra rod 2	15.39	4.36	3.87	12.82
intra rod 3	16.17	5.28	4.86	14.18
sample group 2: multiple rods (level 2)
multiple rods 1	39.45	10.16	10.51	27.33
multiple rods 2	40.74	11.41	10.90	28.31
multiple rods 3	48.69	11.90	11.30	37.36
sample group 3: decussation (level 3)
decussation 1	37.25	9.23	9.23	26.78
decussation 2	38.82	14.11	12.67	27.85
decussation 3	45.02	13.23	12.50	28.16

The small bars with approximately 4 µm height and width contain several parallelly aligned nano-fibres (approx. 50 nm in diameter), whereas the larger bars within the outer enamel layer with approximately 10–13 µm height and width contain several parallelly aligned rods (approx. 5 µm in diameter) so that owing to cantilever size and placement, the first and second hierarchical levels can be tested appropriately. Owing to size limitations of the cantilevers according to FIB technology, the cantilever placed into the inner enamel region representing the third hierarchical level of enamel contains several decussated rods (figure 2b), but not several parallelly aligned Hunter–Schreger bands (width around 20–30 µm, figure 1c); so that characterization of the third hierarchical level might lack some accuracy.

Additionally, nano-fibre and rod length (100 µm and up to 1 mm, respectively) both exceed by far the cantilever lengths of the specific groups (15 µm and 40 µm, respectively), so that fibre and rod length within the cantilevers are limited by sample geometry and not by enamel structure.

Even though there are limitations associated with the FIB technique, it is to our knowledge the only method to fabricate bars of appropriate hierarchical length scales for the first and second hierarchical levels and also to take into account the anisotropy of the hierarchical microstructure.

2.3. Bending bar testing

FIB-prepared cantilever beams were tested using an MTS nanoindenter system (MTS, USA) equipped with a Berkovich tip. Cantilever testing required accurate alignment of the cantilever's free end with the nanoindenter tip. Using the nanoindentation system's optical microscope, the position of the cantilever was identified, and an indent was made close to the base of the cantilever for aligning the exact indenter position. This way, we maximized the positioning resolution of the instrument, so that the desired loading point is achieved for the bending experiment. The nanoindenter tip was then positioned at the cantilever's free end. Samples were loaded with a displacement rate of 0.2 nm s⁻¹ until fracture. The load applied to the sample and tip displacement was continuously measured.

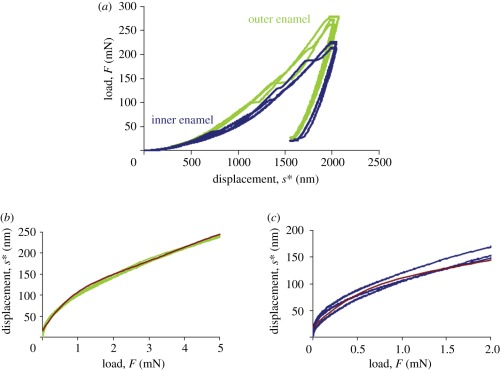
After testing, the indentation displacement had to be subtracted from the total measured displacement in order to assess for the deflection of the cantilever beam alone. This was achieved by carrying out indentations into the bulk material, and using the resultant load–displacement curves for subtracting the indent penetration, s*, from measured displacement, s, at a given load. s* was determined in the inner and outer bovine enamel regions. Three indent load–displacement curves were measured in each area (data shown in figure 3a). For each region of interest (inner and outer enamel), a polynomial function was fitted to those curves within the loading ranges applied during cantilever testing (up to 4 mN in intra rod and multiple rod samples (outer enamel) and up to 2 mN for decussation samples (outer enamel)) to calculate the tip penetration s* into the sample surface at a given load (figure 3b,c):

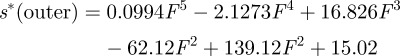2.1

and

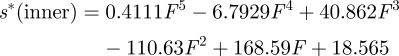2.2

with F in milliNewton and s* in nanometre.

Figure 3.

Data for sample displacement correction. Three indent load-displacement profiles (F(s*)) were monitored in the (a) outer and inner enamel regions, respectively. As the cantilevers were only loaded up to approximately 4 mN in the outer enamel region (intra rod and multiple rod samples) and up to approximately 2 mN in the inner enamel region (decussation samples), this very first part of the curves is plotted the other way round (s*(F)) in (b,c). The true cantilever displacement s_true was calculated by s_true = s − s* with s being the total displacement measured at the cantilever, and s* being the tip penetration into the sample surface at a given load. Red lines in (b,c) show the fitted polynomial functions approximating s* in the inner and outer enamel region: s*(outer enamel) = 0.0994F⁵ − 2.1273F⁴ + 16.826F³ − 62.12F² + 139.82F + 15.02 and s*(inner enamel) = 0.4111F⁵ – 6.7929F⁴ + 40.862F³ − 110.63F² + 168.59F + 18.565 with F in milliNewton and s* in nanometre.

2.4. Scanning electron microscopy

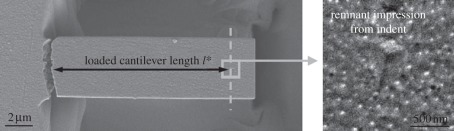
After fracture, samples were investigated using a Zeiss Auriga scanning electron microscope (3 kV, 10⁻⁶ mbar). The actual indenter loading point during cantilever testing was determined by identifying the residual impression of the indent left from cantilever loading. The cantilever length loaded during testing l* was measured accordingly for each sample (figure 4). Measured total cantilever lengths of tested cantilevers were compared with measured lengths before testing to eliminate errors owing to permanent deflections of the cantilevers. There was no significant difference in length before and after testing.

Figure 4.

Loaded cantilever length l*. After fracture, the actual indenter position during testing was determined within the scanning electron microscope by identifying the remnant indenter impression. The cantilever length under load l* was measured correspondingly.

2.5. Calculation

Stress–strain curves were calculated from the load–displacement data monitored using the following equations [18]:

2.3

and

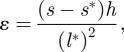2.4

where σ is the bending stress, F is the load on the bar, l* is the loaded cantilever length, b is the cantilever width, h the cantilever height, ɛ is the bending strain, s is the measured total tip displacement and s* is the tip penetration into the material at corresponding force F (figure 3).

The elastic modulus E was determined for the cantilever structures within the linear-elastic regions of the stress–strain curves following

2.5

In preliminary tests, the linear elastic behaviour of the intra-rod cantilevers was checked by sequentially loading and unloading. Loading, unloading and reloading curves showed identical slopes.

2.6. Statistics

Fracture stress, strain and elastic modulus values of the different sample groups tested were statistically analysed with t-tests. Differences in mechanical properties between groups were accepted at a level of significance p being 5 per cent or less (p < 0.05).

3. Results and discussion

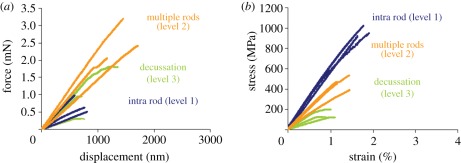
Force–displacement data measured and stress–strain curves calculated according to equations (2.3) and (2.4) (including displacement correction, figure 3) and using sample dimensions as listed in table 1 are shown in figure 5a,b. Fracture stress, fracture strain and elastic modulus are listed in table 2. The differences in fracture stress and elastic modulus were found to be statistically significant between all groups, the differences in fracture strain were statistically different only between multiple rod and decussation cantilevers.

Figure 5.

(a) Measured force–displacement and (b) calculated stress–strain data for all hierarchical levels in enamel. Stress–strain curves were calculated according to equations (2.3) and (2.4) using sample dimensions listed in table 1. Berkovich tip penetration into sample surface was eliminated (figure 3).

Table 2.

Fracture stress, fracture strain and elastic modulus for all cantilevers tested.

sample	fracture stress (MPa)	fracture strain (%)	elastic modulus (GPa)
sample group 1: intra rod (level 1)
intra rod 1	990	1.98	53
intra rod 2	1022	1.90	56
intra rod 3	921	1.70	54
mean ± s.d.	978 ± 52	1.86 ± 0.14	54 ± 2
sample group 2: multiple rods (level 2)
multiple rods 1	391	1.76	26
multiple rods 2	467	1.18	41
multiple rods 3	576	1.57	41
mean ± s.d.	478 ± 93	1.50 ± 0.30	36 ± 8
sample group 3: decussation (level 3)
decussation 1	127	0.79	17
decussation 2	126	1.07	12
decussation 3	199	0.91	27
mean ± s.d.	151 ± 42	0.92 ± 0.14	19 ± 8

Both fracture stress and elastic modulus decrease with additional hierarchical structuring (figure 5b and table 2). Additionally, deformation mode changes from almost linear-elastic (with only small deviations from linear elasticity) in intra rod and multiple rod samples to nonlinear material behaviour in decussation cantilevers. Fracture strain remained almost constant from level 1 (intra rods) to level 2 (multiple rods) and decreased then slightly in the decussation cantilevers.

The determined mechanical data for the smallest cantilever size in bovine enamel (intra rod, level 1: σ = 978 MPa, ɛ = 1,86, E = 54 GPa) fit very well to data determined by Chan et al. [14] for human enamel samples that match the size and orientation of the intra-rod samples. They measured elastic moduli between 42 and 51 GPa, strengths between 750 and 1420 MPa and strains around 2 per cent in human primary molars [14]. Sample treatment and experimental set-up were almost identical: samples were etched and sputter-coated. However, the samples were tested in a re-hydrated condition by placing Hank's balanced salt solution (HBSS) droplets on top of the bending bars half an hour prior to testing. Another study by the same authors showed that there is no statistical significant difference in strength of enamel if tested dry (without placing the HBSS droplet on the samples) or re-hydrated [15].

Scanning electron micrographs of fractured cantilevers are shown in figure 6. In the smallest bovine sample size (level 1), HAP nano-fibres were fractured and partially pulled out of the matrix as shown in the scanning electron micrograph in figure 6a. At the next level of hierarchy (level 2, multiple rods) where the bending bar contained several parallelly aligned rods, these rods were fractured, but one can see that cracks were partially deflected along rod boundaries (figure 6b) indicating the weakness of the protein-rich boundaries compared with the rods themselves [2]. For the third bovine sample group (figure 6c), the decussated rod structure provided weak rod boundaries perpendicular to cantilever long axes—and fracture consequently occurred along these boundaries. Close to the main crack, microcracking and crack branching along rod boundaries could be observed. Both mechanisms might be responsible for the nonlinear material behaviour that could be observed in the cantilevers, which contain the decussation structure. The protein-rich rod boundaries seem to be the preferred crack paths as crack deflection along rod boundaries in the multiple rod cantilevers and crack propagation within the decussation cantilevers shows.

Figure 6.

Fractured cantilever beams for all sample groups: nano-fibres and rods were fractured perpendicularly in (a) cantilevers containing nano-fibres and (b) parallelly aligned rods; however, (c) in decussation cantilevers, microcracking (rod boundary cracking) and crack branching along rod boundaries could be observed. In the latter sample group, fracture almost completely occurred within rod boundaries. This and crack deflection along (b) rod interfaces prove that the weak protein-rich interface between rods is the preferential crack path within enamel.

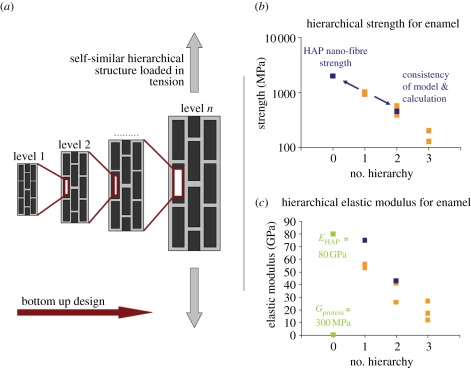
In a previous work [3], we demonstrated the applicability of a mechanics model proposed by Jäger & Fratzl [19] and developed by Gao and co-workers [4–7] for analysing experimental data of hierarchically structured biological materials. By applying fracture mechanics concepts to a two-dimensional, self-similar structure (figure 7a) consisting of hard particles embedded within a soft protein phase, Gao and co-workers derived formulae for hierarchical strength, stiffness and toughness under tensile load. However, up to now, only indentation data from Ang et al. [17] were available to demonstrate the model's applicability for hierarchical property analysis owing to a lack of other comprehensive datasets. As indentation causes highly complex multiaxial but predominantly compressive stress-fields within materials, there remains a discrepancy between model that was developed for structures tested in tension and experiment. With the bending data derived in this work, where fracture was induced in the tensile stress region of the cantilevers with the microstructure aligned parallel to the bar axes (levels 1 and 2), a much more profound verification of the model can be obtained.

Figure 7.

Principle of mechanics model owing to Gao and co-workers and application to experimental data. Gao developed a hierarchical mechanics model based on suggestions from Jäger and Fratzl, which consists of (a) a two-dimensional self-similar structure made of hard particles (black) embedded within a soft protein phase (bright grey). The composite structure at level n forms the hard particles at level (n + 1). The as-built structure is virtually loaded in tension and the basic assumption thereby is that the hard particles at each hierarchical level carry the tensile load that is transferred via shearing of the protein phase. By applying fracture mechanics concepts and geometrical considerations, Gao and co-workers developed formulae for hierarchical strength, elastic modulus and toughness. We show the applicability of the model to experimental results of real biological materials by predicting the strength of the second hierarchical level within enamel using experimental data from level 1—as can be seen (b), calculations and experiment fit quite well. Alternatively, it is possible to calculate (b) the HAP nano-fibre strength (2 GPa), which can hardly be determined experimentally. For (c) elastic modulus also, quite satisfying agreement of model and experimental results was found. Unfortunately, the model cannot be applied to the third level of hierarchy as decussation cantilevers owing to size limitations in fact contained several decussated rods, but not several aligned Hunter–Schreger bands (which would represent the ‘hard particles’ of the third level). (b) Orange regions, experimental data; blue regions, calculations owing to Gao. (c) Orange regions, experimental data; green regions, basic constituents; blue regions, calculations.

Gao's formula for strength is based on the assumption that the material phase failing first (hard particles of strength S_n or protein matrix of strength S_p) determines overall strength at level (n + 1) leading to the expression

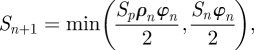3.1

where ρ_n is the aspect ratio of the hard particles and φ_n is the hard particle content. The intra-rod strength (and hence, the hard particle strength of the second hierarchical level) was measured to be S₁ = 978 MPa. For estimating the hard particle content φ_n of the different hierarchical levels, the following assumptions were made: in dental enamel, proteins are assumed to envelope individual nano-fibres as well as individual rods [1]. Furthermore, it can be assumed that proteins accumulate at sites where mineral density is low [2], which is considered the case between Hunter–Schreger bands, where rod orientation changes. This means that each additional level of hierarchy adds more protein to the composite structure. For calculations, we assumed that the volume fraction of protein added by each hierarchical level and the mineral volume fraction of each hierarchy were constant (φ_n = φ). Hence, the hard particle content of the composite structure at level n (which is φ_n) decreases with hierarchical structuring and can be calculated as Φ_n = φⁿ. φ was chosen to be 0.95, so that Φ₃ = φ³ = 0.85 (i.e. overall mineral volume fraction of enamel [1]).

The decrease in strength in this connection from level 1 to level 2 can be explained with the increasing amount of (weak) protein within the composite structure: in samples of level 1, protein is only present enveloping the pure mineral nano-fibres, whereas in level 2, proteins additionally accumulate within rod boundaries.

Using again the experimental data of the first hierarchical level, one can also calculate the nano-fibre strength of the HAP fibres as S₀ = 2S₁/φ₁ with S₁ = 978 MPa and φ₁ = 0.95, which results in approximately 2 GPa for HAP nano-fibre strength (figure 7b). In a previous study [3], we estimated the HAP nano-fibre strength as having theoretical strength (approx. E/10) of HAP (approx. 8–12 GPa) following suggestions from Gao and co-workers who emphasized in their work that in nature biological minerals are most probably nano-scale (especially the nano-sized crystallites present in bone and dentine) to reach the theoretical strength limit. Thus, these lower strengths of enamel crystallites may arise because of their high aspect ratio and additionally, high-resolution electron microscopy of enamel shows that natural sound HAP crystals are not perfect [20]. There are lattice striations and defects, edge and screw dislocations and even small angle boundaries within the HAP crystallites. Considering these aspects, a tensile strength of approximately 2 GPa for enamel crystallites is more realistic. It might also be possible that the ion beam used for cantilever preparation affects the mechanical properties of the protein or mineral phase. Chan et al. [14] conducted indentation measurements before and after enamel cantilever preparation close to the cantilever site. They found that hardness and elastic modulus were not affected by FIB sample treatment. This does not mean that strength cannot be affected, however, the interaction of the gallium ions with the cantilever should be limited to some tens of nanometres in depth (see data for silicon [21]; unfortunately, no comparable data are available for biological materials as enamel). Hence, most of the cantilever volume should not be affected by the gallium ions. In addition, owing to the correlation of measurements with ultrastructural observations, we assume that the imperfect structure of the HAP crystallites and not gallium ion damage reduces the strength to 2 GPa.

Unfortunately, Gao's model can not be applied to the third cantilever group (decussation) representing the third hierarchical level. It was not possible to manufacture FIB cantilevers larger than the ones prepared as the amount of material needed to be removed obviates the use of the FIB method owing to inefficiency and redeposition effects. The decussation cantilevers in fact contain decussated rods but not several parallelly aligned Hunter–Schreger bands as would be the requirement for further applying the Gao model. Nevertheless, it is interesting as to how the fracture mechanism changes from HAP fibre fracture to protein-mediated failure depending on the rod orientation in the cantilevers (parallel in multiple rod and interwoven in decussation cantilevers, figure 3b,c). Owing to this transition, the actual strength of the cantilevers largely decreases—but the fracture type changes from catastrophic linear-elastic fracture to ductile fracture including a substantial inelastic deformation portion of the stress–strain curve. Hence, at the expense of fracture strength, a more damage-tolerant structure is introduced by decussated rods on the third hierarchical level.

The comparison of model and experiment also shows similar trends in the elastic modulus that can be calculated owing to

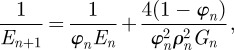3.2

with E_n+1 being the composite modulus at level (n + 1), E_n being the hard particle elastic modulus, φ_n being the hard particle content, ρ_n being the hard particle aspect ratio and G_n being the protein shear modulus.

For bovine enamel, the measured values are 54 and 36 GPa for the first and second hierarchical levels, respectively. Calculations following equation (3.2) can be made by using E₀ = 80 GPa (elastic modulus for artificial HAP determined in bending; [22]), φ = 0,95 and G_p = 300 MPa (G_p ∼ E_p/3 = 300 MPa; [23]). The aspect ratio of the HAP nano-fibres ρ₁ at this is not limited by the actual nano-fibre (approx. 100 µm long; [1]) but by the loaded cantilever length (approx. 15 µm) and is chosen to be ρ₁ = l₁/h₁ = 300 with l₁ being the cantilever length and h₁ being the HAP nano-fibre diameter (approx. 50 nm; [1]). The aspect ratio of nine determined for the 500 µm to 1 mm long enamel rods is calculated analogously with l₂ being the loaded cantilever length (45 µm) and h₂ being the rod diameter (5 µm; [1]). This results in 75 and 43 GPa as elastic moduli for levels 1 and 2 are predicted by the model (figure 7c). Though slightly high especially for the first hierarchical level, these calculations fit the experimental findings reasonably well. Overestimation might be due to the fact that the Gao model implicates the material to be perfect but in reality, natural material imperfections such as microcracks and pores might reduce the material's stiffness. An alternative explanation for the overestimation of the elastic modulus could be that the results were determined in cantilever ending flexure, where substantial gradients in tensile and shear stresses occur and some potential slippage between rods may have occurred. This would be expected to be more evident for the decussation beams, where the structure is not parallel to the loading axes (figure 2d). Following the calculations, decrease in elastic modulus from one to the next hierarchical level seems to be due to the decreasing hard particle aspect ratio from nano- to microstructure as well as to the increasing overall protein content. Increasing protein content most probably also influences the decrease from level 2 to level 3 though the experimental difficulty in fabricating sufficiently large cantilevers circumvents a theoretical investigation of this hierarchical level owing to Gao.

There are some limitations of the experimental set-up used in this study, especially owing to FIB preparation (de-hydration and sputter-coating of samples; exposing cutting edges to gallium ions). We do not know how this treatment finally affects strength and modulus measurements. However, owing to the lack of alternative experimental techniques with comparable ability of sample positioning and highly localized property assessment, we accept these uncertainties to at the least be able to determine overall trends of mechanical property variations with hierarchical structuring. Additionally, it was observed that fracture strain decreased from level 2 (multiple rods) to level 3 (decussation), although protein content should increase and hence, fracture strain was expected to increase as well. For clarification, if this unexpected trend in fracture strain results from protein damage owing to FIB preparation or has other reasons, further investigations are needed.

4. Conclusion

In this work, we determined both strength and elastic modulus of dental enamel at three hierarchical levels. Both values were found to decrease roughly by a factor of 2 with increasing hierarchical level. This is a very strong effect, which we attribute mainly to the increase of protein content with each hierarchical level. Our results of the third hierarchical level show the cross over from a stiff high-strength brittle material to a damage-tolerant low-strength material. To interpret the data obtained in more detail, we applied the hierarchical mechanics model developed by Gao and co-workers. By combining experiments and model, the HAP nano-fibre strength within enamel could be estimated to be 2 GPa, which is substantially lower than theoretical estimates previously used, but in keeping with ultrastructural observations of the defective nature of enamel crystallites. Although the maximum sample size is limited by the FIB technology itself, the FIB cantilever preparation technique was found to be suited for hierarchical, anisotropic, site-specific material property assessment.