Optimized nanoscale composite behaviour in limpet teeth

Abstract

Limpet teeth are striking examples of a biological fibrous nanocomposite consisting of goethite mineral within a polymeric chitin matrix. The mechanical function of limpet teeth is critically dependent on the efficient composite behaviour of goethite, formed as distinct discontinuous nanofibres, reinforcing the matrix. The mechanical properties of discrete volumes from a limpet tooth measured using atomic force microscopy indicate how the tooth structure can be approximated as a short fibre-reinforced composite. Short fibre composite analysis reveals how the goethite nanofibres have a length optimized for the transfer of stress from the matrix to fibre and highlight how this limpet tooth structure is efficient in a mechanical load-bearing function.

1. Introduction

Biology is adept at producing a range of organic–inorganic composite structures for specific mechanical function. Understanding the mechanical performance of these biological composites can often be achieved by applying theories developed for man-made composite materials. For example, bone has been extensively studied with a number of works applying composite mechanics concepts to quantify deformation at protein–mineral interfaces [1–3], elastic behaviour [4], failure [5,6] and toughness from structural orientation effects [7]. Indeed, toughness in biological materials has been extensively studied in layered structures [8–11] and provides pathways for constructing synthetic materials incorporating the sometimes remarkable mechanical properties of their biological equivalents [12,13]. Many biological materials use fibrous constituents as building blocks for structures with complex hierarchies and therefore can be considered as a fibre-reinforced polymer composite. Critically, a considerable body of composite theory exists for the study of short fibre-reinforced polymer composites, which is particularly relevant for biological composite structures, as the reinforcing phase is often discontinuous.

The teeth of limpets (Gastropoda) are a distinct product of biomineralization processes where the mineral phase is predominantly elongated nanofibre crystals of goethite (α-FeOOH) encapsulated within an organic chitin matrix. Thus, the goethite mineral can be essentially considered as a fibrous nanomaterial reinforcement within a polymeric matrix material. The primary function of limpet teeth is to remove algae from rock surfaces at near- and inter-tidal regions. The limpet's feeding mechanism requires rasping of the teeth over the rock surface, and therefore these teeth need to be mechanically robust under mechanical loading conditions. Previous work has examined limpet teeth using macroscopic testing methods, with results indicating an increase in the hardness at the leading posterior edge of the limpet tooth when compared with the trailing anterior edge [14]. While hardness measurement experiments are important in understanding the overall mechanical properties of limpet teeth, currently there is little understanding on how the nanoscale constituents define overall mechanical behaviour in these limpet teeth, or indeed other biological materials incorporating fibrous nano-biomineral constituents.

The structural organization of the limpet tooth is complex with many different goethite orientations found, but high-resolution electron microscopy of the microstructure indicates that the mineral appears as distinct short fibres, with lengths of a few micrometres, aligned within the organic chitin matrix [15]. Such structural examinations of limpet teeth bear a striking resemblance to man-made composite materials although the mineralized fibre diameters are tens of nanometres, whereas engineering fibre diameters approach 10 µm. Thus, the limpet tooth at micrometre length scales is particularly analogous to synthetic short fibre composite structures and the corresponding composite models used to describe their mechanical behaviour. Isolating discrete material volumes at micrometre length scales has been extensively achieved using focused ion beam (FIB) microscopy, particularly for preparation of samples for transmission electron microscopy [16], but was recently exploited for the measurement of mechanical properties. FIB micromachining, or milling, of slender beams for mechanical testing has been used for synthetic materials [17,18] and biological materials of human dental enamel [19]. Beam geometries allow the FIB-isolated volumes to be directly mechanically tested typically using nanoindentation [20,21] or atomic force microscopy [22–24] techniques that have sufficient load resolution to record deformation of the beam. Limpet teeth share the high volume fraction mineral phase of enamel, indicating the suitability of FIB for preparation, while possessing a clear short fibre composite-type organization. This paper, therefore, examines the mechanical properties of limpet teeth at micrometre length scale using FIB microscopy to isolate discrete volumes and applies conventional short fibre composite theory to determine the effectiveness of composite behaviour within limpet teeth biological structures. Mechanical studies of limpet teeth at these micrometres to sub-micrometre length scales, therefore, present an opportunity to elucidate behaviour in a structural short fibre biological composite and ascertain the influence of the fibrous mineral nanomaterial constituents on resultant mechanical performance in a biological system.

2. Material and methods

Samples of the limpet Patella vulgata were harvested in Southampton, UK. Limpets were fixed in sea water during transportation to the laboratory and rinsed in running tap water before dissection under an optical microscope. The radula, an appendage used to rasp limpet teeth present on its surface across rock faces, was dissected from the visceral mass of the limpet. Cutting and folding tissue around the head of the limpet exposes the whole radula length, usually found as a radula coil, which was then removed by the dissection process. The first 5–10 rows of teeth present at the mature end of the radula, shown in figure 1a and defined as the end of the radula closest to the limpet mouth when the radula is extended, were discarded as considerable wear was observed in these rows of teeth under the optical microscope. Individual limpet teeth were isolated by first cutting the remaining radula length into 3–5 mm sections using a sharp knife. Radula sections were mounted onto a standard electron microscopy aluminium stub using carbon tape. A droplet of water was added to the radula to ensure that the section on the stub was compliant and a fine stainless steel needle was used to straighten the radula on the stub. The radula was allowed to dry on the stub for 30 min to lower adhesion between the limpet teeth and radula surface. Individual teeth were scraped carefully away from the dry radula, shown in figure 1b, from the posterior to the anterior direction of the tooth using a razor blade. A polycarbonate film underneath the aluminium stub was used to collect the teeth removed from the radula in the scraping process. The limpet teeth were finally brushed from the film surface onto an additional aluminium stub containing a droplet of silver paint. Most of the limpet teeth became partially embedded within the paint and, after allowing to dry for 8 h, produced partially exposed individual limpet teeth from the paint surface, as shown in figure 1c. The anterior surface of limpet tooth was then imaged using scanning electron microscopy (SEM) in backscattered mode to highlight the contrast provided by the aligned goethite nanofibres as shown in figure 1d.

Figure 1.

(a) Optical image showing the dissection of a 7 cm long radula from the limpet mouth. (b) Scanning electron micrograph of the radula with rows of exposed teeth. (c) Scanning electron micrograph of an individual limpet tooth exposed from the silver paint surface prior to focused ion beam preparation. (d) Scanning electron micrograph of the tooth surface indicating the presence of fibrous goethite mineral. (Online version in colour.)

The mechanical properties of individual limpet teeth at micrometre/sub-micrometre length scales were found by first isolating relatively small sample volumes using FIB microscopy (Quanta 3D, FEI Company, EU/USA). Regions of the limpet tooth displaying regularly formed goethite short fibres were first selected at the anterior edge of the limpet tooth as shown in figure 1c. FIB was used for site-specific milling of subsurface structures of biological samples in order to select discrete rectangular beams. The FIB micro-cantilever technique as a local probe of mechanical properties in teeth samples was first demonstrated in Chan et al. [25]. The cantilevers in this previous work were produced with a triangular cross-sectional geometry so that the beams could be deflected to fracture. In our work, cantilevers with rectangular cross sections are fabricated using FIB for subsequent mechanical testing at smaller beam deflections within the elastic regime of the limpet tooth sample. Smaller deflections within the elastic regime are required; so established stress analysis can be applied to describe elastic properties and subsequent composite behaviour as defined below. Removal of material using FIB milling was conducted with gallium ions accelerated at 30 kV using a current of 1 nA. FIB milling was carried out following the methodology previously used to produce micro-beams in bone tissue [26]. The same methodology was applied to the limpet teeth of this work. Beams with defined geometries are produced using a series of cuts provided by the FIB and rotating the sample so that the FIB mills parallel to each face of the limpet tooth beam. In particular, regular rectangular beams can suffer from tapering when produced using FIB. In our experience, tapered beam geometries occur when the FIB milling process is carried out in one step, which removes a relatively large amount of sample in the milling process but promotes material re-deposition onto the beam that is responsible for the tapering. The limpet tooth beams in this work are produced using multiple FIB milling steps, i.e. beam edges are FIB-milled one at a time instead of all together so that only small amounts of material are removed, which produces regular beam geometries. Resultant material was removed from the limpet teeth so that beams with dimensions of approximately 10 × 2 × 1 µm were produced. We note that the FIB direction during milling was always parallel to the beam surfaces to avoid sample damage from the ion beam [27]. A series of arrays were produced at the anterior surface as shown in figure 2. The principal beam axis was varied relative to the principal axis of the limpet tooth, indicated as angle (θ) in order to determine any potential orientation effects in the goethite mineral organization. Thus, if the goethite mineral orientation is effectively unidirectional, then mechanical properties will vary as a function of this off-axis angle θ. A total of four different rectangular beam array regions were produced, labelled A, B, C and D, corresponding to different values of θ. The aluminium stub containing the limpet teeth patterned from the FIB milling procedure was removed and placed into an atomic force microscope (AFM) for subsequent mechanical testing.

Figure 2.

Scanning electron micrograph showing the focused ion beam-milled regions A, B, C and D at the anterior side of limpet tooth used for mechanical bending tests.

Mechanical testing was carried out on the limpet tooth material in air at high humidity (approx. 80% relative humidity) using AFM (NTegra, NT-MDT, Russia). AFM allows both high-resolution imaging of nanostructures prior to mechanical testing [28,29] and the accurate application of force to deform a range of different nanostructures [30,31]. The FIB-milled beams were located using AFM in a semi-contact mode as shown in figure 3a using an AFM cantilever spring constant of 200 N m⁻¹. The choice of such a large cantilever spring constant allows the application of large forces to the sample during mechanical testing.

Figure 3.

(a) Atomic force microscope (AFM) topography image of the focused ion beam (FIB)-milled rectangular beams exposed at the anterior surface of the limpet tooth. (b) Schematic showing the mechanical test configuration used to bend individual FIB-milled limpet tooth beams using AFM mechanical testing. (Online version in colour.)

Following AFM imaging and location of a single beam, the scanning AFM probe was contacted with the free end of the beam and the piezo-scanner of the AFM extended to push the AFM probe into the beam. Extension of the piezo-scanner caused the AFM probe to deflect the beam with the corresponding bending of the AFM cantilever recorded using an optical sensor situated above the AFM cantilever. A schematic of the test is shown in figure 3b. The spring constant of the AFM cantilever (k) was calculated by the thermal noise method [32]. The force (F) applied to the beam was calculated using

2.1

where δ_AFM is the deflection of AFM cantilever recorded by the optical sensor. The deflection of the limpet tooth beam was found by

2.2

where δ_total is the extension of the piezo-scanner measured from the AFM.

The elasticity of the beams within the four regions on the anterior surface was measured using the AFM to mechanically bend individual beams and evaluate the mineral orientation effect on the mechanical properties of limpet teeth. A total of four to six beams were mechanical-tested in each region.

3. Results

The force applied to individual limpet tooth beams against deflection is shown in figure 4 for all beam arrays examined. All force–deflection curves showed an initial linear region corresponding to elastic deformation of the beam by the AFM probe. Deviation from this linear behaviour was observed for all beams at relatively large beam deflections, indicating potential plastic deformation. The resistance of the FIB-milled limpet beams to deflection by the AFM probe increases when the beam axis is parallel to the principal axis of the limpet tooth, i.e. small values of θ, with region A showing the highest resistance to beam bending as indicated by the largest force–deflection gradient in figure 4. The elastic modulus of the rectangular beams shown in figure 2 can be calculated from the applied force–beam deflection curves of figure 4 using Euler–Bernoulli beam bending theory

3.1

where F and δ are the force applied by the AFM probe and resultant beam deflection, respectively, given by the gradient of the curve in figure 4, and E is the elastic modulus of the beam. The breadth (b), thickness (h) and length (L) of the beam is measured from SEM images. Therefore, the resistance of limpet tooth beams to bending from the AFM probe can be quantified from the elastic modulus calculated using equation (3.1). The variation of limpet beam elastic modulus with beam orientation can be plotted as shown in figure 5.

Figure 4.

Force–beam bending deflection curves for the mechanical testing of rectangular beams at the anterior surface of the limpet tooth. Curves A–D correspond to the mechanical properties of beams located at the four regions defined in figure 2.

Figure 5.

Plot of the variation of elastic modulus with beam long axis orientation for mechanical testing of rectangular beams at regions A, B, C and D on the anterior surface of the limpet tooth.

The elastic modulus of the mechanically tested limpet tooth beams in figure 5 is critically dependent on the orientation of beam relative to the principal axis of the limpet tooth. The results in figure 5 suggest that the goethite nanofibres may be oriented along the principal axis of the limpet tooth, producing the highest elastic modulus values for the rectangular beams in region A, with mechanical testing at orientations deviating from this principal axis, such as in region D, resulting in relatively low beam elastic modulus values. Previous structural investigations of limpet tooth structure using high-resolution electron microscopy to elucidate goethite mineral organization correlate with our mechanical testing results, indicating uniaxial fibrous orientation [14,15]. These observations support the claim that limpet teeth structures are analogous to an aligned short fibre composite materials.

4. Composite analysis

In order to evaluate the composite mechanical behaviour of the limpet tooth, we apply conventional short fibre composite theory in order to assess the efficiency of the limpet tooth structure composed of the goethite nanofibres and the polymeric chitin matrix. Short fibre composite theory defines the mechanical efficiency of the composite in terms of the orientation of the short fibres and the fibre length. Figure 6 schematically highlights two different short fibre composites where relatively short fibres distributed randomly provide ineffective reinforcement, with a resultant drop in composite elastic modulus, whereas fibres that are relatively long and oriented in the direction of the load will give an increase in composite elastic modulus. The elastic modulus of a short fibre composite can therefore be expressed in terms of fibre orientation and length, as well as the composition of the composite, according to Jayaraman & Kortschot [33]

4.1

where χ₁ and χ₂ are the orientation and fibre length factors, respectively. The composition of the composite is described by the volume fraction V_f of the fibres, with an elastic modulus of E_f, and the elastic modulus of the matrix E_m of volume fraction V_m. The fibre orientation factor χ₁ is a complex function of the fibre orientation angle according to

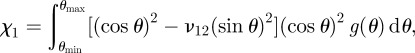4.2

where ν₁₂ is the Poisson's ratio of goethite. The fibre orientation factor χ₁ can therefore be calculated from equation (4.2) by knowing the fibre orientation distribution function g(θ), which is stated as [34,35]

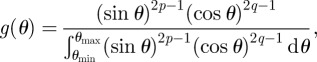4.3

where p and q are shape parameters used to determine the shape of the fibre orientation distribution curve. Thus, measuring the orientation angle θ of every short fibre in a composite can provide an orientation distribution and give fibre orientation distribution function g(θ) using equation (4.3). However, for short fibre composites that possess some degree of fibre alignment, equation (4.3) can be simplified by considering the mean fibre orientation θ_mean, and the maximum and minimum mineral orientation angles of θ_max and θ_min, respectively, in the milled beams as follows

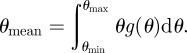4.4

Figure 6.

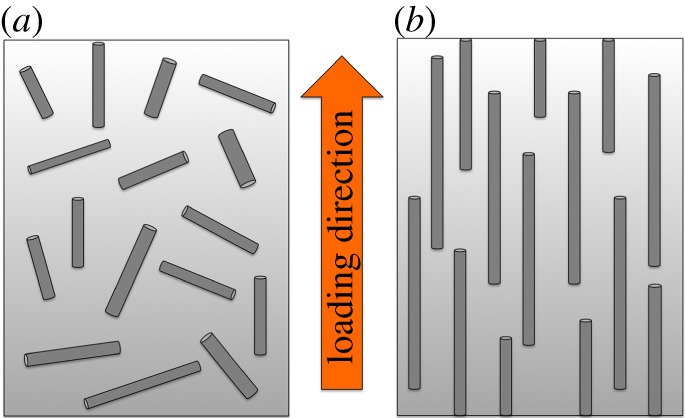
Schematic showing ineffective fibre reinforcement within a composite structure (a) incorporating relatively short fibres randomly distributed throughout the composite and (b) longer fibres oriented in the direction of the load for effective reinforcement. (Online version in colour.)

The mean, maximum and minimum goethite nanofibre orientation was measured from backscattered images of the limpet tooth regions and analysed using ImageJ (US National Institutes of Health, USA) and the fibre orientation distribution function g(θ) determined from equation (4.4). Equation (4.2) was subsequently used with the fibre orientation distribution function values to calculate the fibre orientation factor χ₁ values as shown in table 1 for the four different regions examined. Image analysis also revealed an average goethite volume fraction of 81 per cent and a mean goethite nanofibre length of 3.1 µm. As the elastic modulus of the composite beams has been measured using AFM bending experiments, equation (4.1) can be solved in order to reveal the fibre length factor parameter χ₂. Simplification of equation (4.1) can be made as the goethite mineral nanofibres dominate the mechanical behaviour of the composite, i.e. E_f ≫ E_m and V_f ≫ V_m, thus V_mE_m → 0 in equation (4.1). The fibre length factor parameter χ₂ is therefore calculated from equation (4.1) using the calculated fibre orientation factors χ₁ in table 1 (taken from equation (4.2)), the E_c of the limpet tooth beams measured using AFM and the elastic modulus E_f of the goethite mineral estimated as 200 GPa, which is reasonable considering that bulk goethite has been recently reported in this range [36].

Table 1.

Mechanical properties, fibre orientation and length factor of focused ion beam-milled beams selected from regions A, B, C and D at the limpet tooth anterior edge.

	region A	region B	region C	region D
θmean (°)	5	17	26	41
Ec(GPa)	140	118	93	52
χ1	0.98	0.83	0.65	0.34
χ2	0.88	0.89	0.88	0.93

The parameter χ₂ is important in defining the efficiency of the short fibres in acting as a composite reinforcement. Critically, the efficiency of the goethite nanofibrous material as reinforcement, and indeed the efficiency of biominerals in structural applications, is an unexplored area of research despite the known importance of the mineral in mechanical performance of mineralized biological tissue [37–39]. The fibre length factor for the different limpet teeth regions is shown in table 1 and is a relatively constant value of χ₂ = 0.90 ± 0.03, as would be expected for goethite nanofibres with a relatively uniform length across the regions examined. The fibre length factor is dependent on the average length of the goethite nanofibres L in the limpet teeth and the critical fibre length L_c. Critical fibre length is a key short fibre composite parameter that defines the length at which stresses can be transferred from the matrix in order to fracture the reinforcing fibre during external loading. Short fibre composites with a relatively large critical fibre length are poor reinforcements materials, whereas small critical fibre lengths are indicative of efficient stress transfer that result in fracture of the reinforcement, especially when the critical fibre length is much smaller than the average fibre length, and is a large energy-absorbing feature of load-bearing composite structures [40–42]. The fibre length factor can be written fully as

4.5

As the average nanofibre length L is known and χ₂ calculated in table 1, the critical fibre length L_c can be determined using equation (4.5) and gives a value of 610 ± 190 nm. This critical fibre length is significantly smaller than the mean goethite nanofibre length of 3.1 µm, highlighting how the limpet tooth goethite nanofibre–chitin matrix structure is an efficient load-bearing composite material. This critical fibre length for the biological limpet tooth nanocomposite is also comparable with values for synthetic carbon nanotube–polymer nanocomposites where the carbon nanotube surface was chemical functionalized to increase stress transfer efficiency [43]. Interestingly, classical work on short fibre composites has shown an almost plateau in fibre reinforcement efficiency at L : L_c ratios of 5 [44]. Our results indicate a comparable L : L_c of 5.1, thus highlighting how the growth of the goethite fibrous crystal phase reaches an optimal length for structural composite mechanical function.

5. Conclusions

The mechanical properties of rectangular micrometre-sized beams isolated from different regions of the anterior surface of a limpet tooth have been measured using AFM. The FIB-isolated beams represent a model short fibre nanocomposite system, thus allowing the application of conventional composite theory to describe their structure–mechanical property dependence. Evaluation of these short nanofibre composites indicate considerable reinforcement efficiency of the goethite nanofibrous phase and suggest an optimized goethite nanofibre length for load-bearing applications achieved within the biological limpet tooth structure.