Determination of the layer-specific distributed collagen fibre orientations in human thoracic and abdominal aortas and common iliac arteries

Abstract

The established method of polarized microscopy in combination with a universal stage is used to determine the layer-specific distributed collagen fibre orientations in 11 human non-atherosclerotic thoracic and abdominal aortas and common iliac arteries (63 ± 15.3 years, mean ± s.d.). A dispersion model is used to quantify over 37 000 recorded fibre angles from tissue samples. The study resulted in distinct fibre families, fibre directions, dispersion and thickness data for each layer and all vessels investigated. Two fibre families were present for the intima, media and adventitia in the aortas, with often a third and sometimes a fourth family in the intima in the respective axial and circumferential directions. In all aortas, the two families were almost symmetrically arranged with respect to the cylinder axis, closer to the axial direction in the adventitia, closer to the circumferential direction in the media and in between in the intima. The same trend was found for the intima and adventitia of the common iliac arteries; however, there was only one preferred fibre alignment present in the media. In all locations and layers, the observed fibre orientations were always in the tangential plane of the walls, with no radial components and very small dispersion through the wall thickness. A wider range of in-plane fibre orientations was present in the intima than in the media and adventitia. The mean total wall thickness for the aortas and the common iliac artery was 1.39 and 1.05 mm, respectively. For the aortas, a slight thickening of the intima and a thinning of the media in increasingly distal regions were observed. A clear intimal thickening was present distal to the branching of the celiac arteries. All data, except for the media of the common iliac arteries, showed two prominent collagen fibre families for all layers so that two-fibre family models seem most appropriate.

1. Introduction

Alterations of the underlying mechanical principles of the healthy arterial wall (for example, changes in the wall constituents) are believed to have implications upon arterial disease and degeneration [1]. Available evidence suggests that intimal thickening is owing to specific mechanical stresses [2], atherosclerosis may be related to increased arterial wall stiffness [3], aortic disease may be linked to differences in the tissue organization and content in the proximal and distal regions of the aorta [4], and enlargement of intracranial aneurysms may result from growth and rearrangement of collagen owing to stress (increasing the risk of rupture with a related mortality rate of 35–50%) [5]. Ageing processes such as stiffening of the vessel wall [6–8] are related to an increase in collagen content relative to elastin [9,10], fibrosis and continuous depositions of amorphous substances for the elastin, and increased cross-linking of collagen; all of which lead to reduced mobility of the arterial wall constituents [11]. Additionally, for the human abdominal aorta, sex-dependent differences in the degrees of stiffening have been reported [7], and generally, the interaction of the structural vessel wall components with the different constituents of the extracellular matrix is believed to be a key factor in understanding diseases [11].

The (passive) mechanical behaviour of arterial walls is mainly determined by elastin and collagen in the media and adventitia [12]. These two constituents are embedded in an extracellular, non-fibrous, glycosaminoglycan-rich matrix [10], forming a complex three-dimensional network including smooth muscle cells [13]. The structural subdivision of the collagen fibre into fibrils and micro-fibrils significantly increases its flexibility (which is directly proportional to the number of subunits) and reduces the risk of rupture because cracks cannot easily propagate across multiple fibrils [14–16]. With an ultimate tensile strength in the range 50–100 MPa [17], it is the collagen fibres that give the arterial wall its strength and ability to resist loads. Thus, with regard to strength and load resistance, collagen fibres are mechanically the most important tissue constituents [16,18,19]. Together with proteoglycans, it is the elastin with its nearly perfect elastic properties which is responsible for the resilience of the matrix [20]. Elastin is load-bearing at low and high strains, with a less significant contribution at higher strains owing to the increased bearing of load through collagen.

In humans, there are 28 known different types of collagen; however, the collagen fibres investigated in this study are limited to the major types present in arterial walls, namely the classical fibrillar collagen of types I and III [21]. Collagen types IV, V and VI are also present in human arteries (among others), but these constitute only about 0.5–1.0% of the total arterial collagen.

While the significance of collagen fibre orientation and dispersion on the mechanical properties of arterial walls have been well established [18,22,23], and two- and three-dimensional data of collagen organization for human vessels have been published [5,24–27], limited structural data are available to date regarding collagen orientation in the human aorta and common iliac artery. In young and healthy arteries, the intima consists of a single layer of endothelial cells with no structural importance to the wall. It becomes mechanically significant with ageing and the associated onset of arteriosclerosis [28]. In the media, the collagen fibre arrangement in human cerebral arteries is circumferential [29]. For the adventitia of human coronary arteries (fixed at distending pressure), a single circumferential order of collagen has been reported in Canham et al. [24], while for cerebral arteries, a wide range of orientations are present [26].

It is known that variations exist in both the structural composition and the mechanical properties of arteries from different species, as well as in different regions of the same arteries, and that they both influence the mechanical response of the vessels [30–32]. Differences were observed in intimal and internal muscular layers between different ethnic groups [2], and are also expected (in all likelihood) among different age groups of a single species [7,33]. In the human aorta, the elastin-to-collagen ratio decreases in progressively distal regions making the aorta most flexible at proximal regions [3]. Such differences in morphology among arteries may change the influence of pressure and wall shear stresses upon the vessels [34,35]. Hence, experimental data on the collagen arrangement from human tissue samples of specific blood vessels are indispensable to facilitate better understanding of disease progression and improve modelling of the cardiovascular system.

The approach taken in this study differs from related research on cerebral arteries [23,25] and intracranial aneurysms [5,27], where investigations into the collagen fibre orientations were performed. We use the well-established method of picrosirius-polarization [36,37], in combination with a universal stage, similar to the method pioneered and described in Smith et al. [38], to study samples from healthy, non-atherosclerotic, human aortas and common iliac arteries for, to our knowledge, the first time. The birefringent feature of the collagen fibres is used for the measurement of the collagen fibre orientations. Picrosirius red was used as a birefringence enhancement stain for collagen [36]. Qualitative and quantitative data with respect to the fibre alignments were obtained using polarized light microscopy [39]. To approximate the in vivo strain state of the blood vessel, all of the samples investigated were pre-stretched biaxially with a specially designed fixture, followed by chemical fixation in formalin while distended [2]. This process resulted in improved fibre orientation coherence [26,30,40]. The measurements were performed using a Zeiss universal stage attached to a Zeiss polarizing microscope (Carl Zeiss IMT GmbH, Vienna, Austria) [27], enabling the measurement of two Euler angles and thus fully defining the local orientation of the mostly straightened fibres in the three-dimensional space. The measured data were fitted with the von Mises distribution allowing the determination of the orientation density function characterizing the three-dimensional distribution of collagen fibre orientations in the (unloaded) reference configuration [22].

The quantitative structural information obtained through this study will not only improve our understanding of the biomechanical behaviour of arterial walls, but will also have a broader impact on the modelling of the cardiovascular system, providing fundamental parameters for mathematical models, which are becoming more widely used, and will even become more important in clinical decision-making.

2. Material and Methods

2.1. Tissue preparation

Eleven human non-atherosclerotic, descending aortas including the common iliac arteries (all are elastic-type vessel walls) were harvested within 24 h from death (63.0 ± 15.3 years, mean ± s.d., six women ranging from 48 to 91 and five men ranging from 43 to 83). Precaution was taken not to include samples showing type IV lesions or higher, or other pathologies [41].

Seven square samples were removed from each axially cut vessel at specific locations labelled as T1, T2, T3, A1, A2, A3 and CI (figure 1). The labelling T and A refer to the descending thoracic region T1–T3 and the abdominal region A1–A3 of the aorta, respectively, while CI refers to the common iliac artery. Anatomic landmarks like the branching of the celiac arteries were used to ensure consistent, repeatable sample locations. Samples from different vessels were always taken from the same seven locations and measured 15 × 15 mm. Two corners of each sample were removed to mark the circumferential direction of the vessel. Four black markers were placed at the centre of each sample, separated by a distance of approximately 6 mm in each coordinate direction, for tracking with the video extensometer. A coordinate system was applied to this reference geometry, where X is the circumferential direction, Y the axial direction and Z indicates the direction of the sample thickness. This geometry is referred to as the unloaded configuration, while in the deformed configuration, the axes are labelled with lower case characters (x, y, z) to unambiguously distinguish between them.

Figure 1.

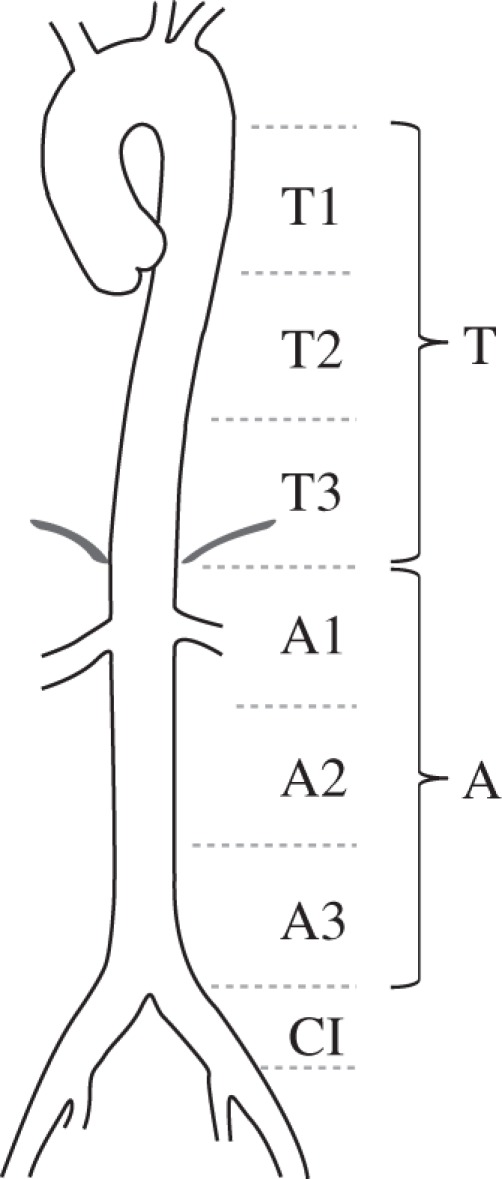
Seven locations T1, T2, T3, A1, A2, A3 and CI along the aortas and the common iliac arteries from which samples were extracted. T and A denote the descending thoracic and abdominal part of the aorta, and CI the common iliac arteries.

To approximate the in vivo stress/strain state of the vessel wall and to ensure (mostly) straightened collagen fibres, a biaxial stretch was applied with a specially designed fixture. The consideration of a biaxial pre-stretch is an important part of the sample preparation method because a pre-stretch has a substantial influence on the organization of the layered microscopic structure of collagen and muscle fibres [42]. To minimize boundary effects during the sample stretching, a suture-based gripping method was chosen with three hooks, serving as suture attachments for each edge of the sample. The three hooks spanned about 10 mm, and the area between the four markers was approximately 6 × 6 mm in the (planar unstretched and unloaded) reference configuration.

Before stretching the sample, the distance between the markers in the X- and Y-directions, and the sample thickness (the Z-direction), was measured using a video extensometer, yielding the geometries of the unloaded configurations of the specimens. Using a displacement-controlled protocol, a strain of 22 per cent in the circumferential direction and 12 per cent in the axial direction was then applied with a custom made fixture. Our value for the axial strain is based on the lower bound of in vivo values reported in Learoyd et al. [43], and for the circumferential strain, we used a similar value as described in Labrosse et al. [44]. Figure 2 shows a tissue sample mounted in the fixture before stretching it biaxially. Applying a controlled stretch was essential during tissue preparation since it not only approximates the in vivo conditions of the vessel wall, but also straightens the collagen fibres, resulting in an increasingly coherent orientation necessary to perform accurate angular measurements [26,40,45]. The stretched sample and fixture were then put into a bath of 4 per cent formaldehyde for chemical fixation. After approximately 10 h in the formaldehyde bath, the sample was removed from the stretching fixture and sewn into a specially designed aluminum frame to maintain the stretched state, while the sample was dehydrated, and embedded in paraffin wax. At the beginning of the embedding process, the specimen was dipped into the first hot paraffin bath, while still mounted in the fixture to counteract shrinking owing to the rapid temperature change of about 40°C. The sample was then removed from the aluminum frame for further processing.

Figure 2.

Tissue sample mounted in the test fixture under biaxial stretch to approximate the in vivo strain state prior to chemical fixation in 4% formaldehyde while distended. Four black markers at the centre of the sample are used for measuring the biaxial stretch via a video extensometer.

The resulting paraffin block (with the embedded tissue sample) was cut into two halves, one was used to obtain in-plane sections (x–y plane) and the other to obtain transverse sections (x–z plane). A series of planar sections were made according to the following protocol: (i) begin sectioning from the luminal side (intima is sectioned first), (ii) make six subsequent sections at 8 µm, and (iii) leave a gap of 100 µm before starting with the next series of six sections. This was repeated throughout the entire embedded sample as many times as possible. The preferred section thickness of 8 µm was determined in a pilot study on pig aortas during which we tested section thicknesses ranging from 2 to 12 µm (in 2 µm steps). We found that histological sections with a thickness below 7 µm were sometimes very fragile and often contained cracks and/or tears, while sections with a thickness above 8 µm often displayed a three-dimensional topography, which made it difficult to focus or achieve proper extinctions.

Every first section out of each series of six was then stained with picrosirius red, a well-known birefringent enhancement stain for collagen that does not change the optical axis of the unstained fibres [36]. Every second section was stained with haematoxylin and eosin for standard histological analysis to detect atherosclerotic lesions of type IV or higher according to Stary [41], to determine if the sample could be included in this study. All sections were cut with a Microm HM 335 (Microm, Walldorf/Baden, Germany).

To ensure that the sample preparation process caused no geometrical changes (for example, a shrinking of the wall during the fixing in paraffin), we measured the wall thicknesses of the stretched samples before paraffination and compared these with the thicknesses obtained from the microscopic images. In all cases, the same results were obtained within the tolerance of the measurement procedures.

2.2. Method of measurement

A Zeiss three-axis universal rotary stage attached to the main stage of a Zeiss polarizing microscope was used for the determination of the three-dimensional distribution of collagen fibre orientations. Each microscope slide with the histological section was fixed between two glass hemispheres, thus ensuring that the polarized light always enters the glass perpendicularly and minimizing light reflections in tilted positions. The hemispheres have an index of refraction of 1.516; additionally, to minimize internal reflections and refractions, the inner surfaces were coated with glycerol (index of refraction approx. 1.47). The area of interest on the tissue section was centred between the two glass hemispheres to avoid distortions that occured on the outer rim.

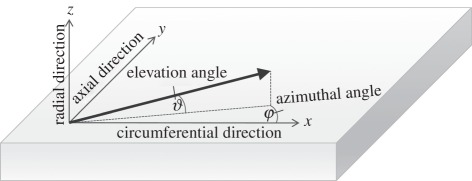
The universal stage allowed the tissue sections to be tilted and rotated in angled planes around its three axes. All rotational angles can be measured. For an unambiguous definition of the orientation of a line (idealized straightened collagen fibre) in three dimensions, two Euler angles may be used. In our coordinate system, the azimuthal angle φ denotes the in-plane rotations (circumferential-axial plane) of the sample, where φ = 0° is then the circumferential direction. The elevation angle ϑ denotes the out-of-plane rotations (circumferential-radial plane) with ϑ = 0° denoting no radial component in the orientation of the fibre (figure 3).

Figure 3.

Definition of the coordinate system and two Euler angles φ and ϑ on a biaxially stretched tissue sample.

To measure the collagen fibre directions, the polarizer and the analyser were preset at extinction so that only the birefringent components of the tissue were visible. It has long been established that type I and type III collagen, the major types in arterial walls [46], exhibit a positive intrinsic and form birefringence [39]. In order to determine the best sample location for the angular measurements (for example, to avoid regions that were damaged during the tissue preparation process), the entire tissue section was first scanned with a relatively low magnification (2.5× objective lens). The region of interest was then centred and aligned to the in-plane (ϑ = 0°) and circumferential (φ = 0°) direction. A 10× objective lens was then used for all measurements. The slide was rotated in the azimuthal plane until the collagen fibres reached its darkest position, yielding the first Euler angle φ, followed by tilting the slide in the elevation plane without further changing the azimuthal angle until the final darkest position was found, yielding the second Euler angle ϑ. Images of transversally cut tissue samples with the polarizing microscope were also taken, allowing the elevation angle ϑ to be measured directly from the images using standard software (Axiovision 40, Carl Zeiss IMT GmbH, Vienna, Austria). To determine the layer-specific thicknesses of the arterial walls, images were taken from each transversely cut tissue sample from all vessels. Using Axiovision 40, approximately 20 thickness measurements for each of the intima, media and adventitia were performed from each image. The average thickness for each of the three layers was obtained by calculating the mean value and the standard deviation of the 20 measurements. To obtain the total wall thickness, the three mean values were added, the total standard deviation was calculated by using 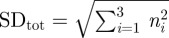, where n is the standard deviation of each layer.

2.3. Data analysis

The collagen fibre directions φ, ϑ were measured in the deformed configuration to mimic the in vivo stress/strain condition and to ensure (mostly) fibre straightening. In the unstressed state, the fibres generally exhibit wavy patterns, often without a clear spatial direction which is difficult to measure. However, material models consider the fibre directions in the reference configuration [18,22]. To ensure unambiguous differentiation between the two configurations, all axes, vectors and angles are now denoted with lower case characters for the deformed configuration and with upper case characters for the reference configuration.

In the following, we briefly introduce the required nonlinear kinematics. By Ω₀, we denote the reference configuration of a sample, while the deformation χ: Ω₀ → ℝ³ transforms a material point X ∈ Ω₀ to a new position x = χ(X) ∈ Ω in the deformed configuration [47]. As a deformation, we introduce the deformation gradient as F(X) = ∂χ(X)/∂X. We consider the artery wall to be incompressible, which yields the condition λ_xλ_yλ_z = 1 for the three stretch ratios λ_x, λ_y and λ_z. Hence, for the biaxial pre-stretch in the x-, y-plane, when stretched along the fibres, the deformation gradient F in matrix notation takes on the form

2.1

It is worth remarking here that it is important to minimize shear during biaxial stretching because of the inability to impose and control shear stresses. Shearing strains are usually much smaller than the extensional strains [48]; we therefore treated the shearing strains as negligible. For more details on this issue, see [49].

All measured azimuthal and elevation angles from the deformed tissue samples are now described as a unit vector with the Cartesian components x = cosϑ cosφ, y = cosϑ sinφ and z = sinϑ, yielding a spatial fibre vector field corresponding to the measured fibre directions themselves in the deformed state. In the following, we simply use the inverse deformation gradient F⁻¹ for mapping back the vector field from the deformed to the reference configuration. Owing to this pull-back operation, the corresponding X-, Y- and Z-coordinates in the reference configuration (assuming homogeneous deformation) result as

2.2

To obtain the elevation angle Θ and the azimuthal angle Φ in the reference configuration, the following relations are used (see also [45]):

2.3

All angle data in the reference configuration from all vessels were then averaged, resulting in mean values for the intima, media and adventitia for the locations T1 to CI. The angles were plotted with a 5° resolution, generating the fibre density, say ρ_m, of the measured data (indicated by the index m) as a function of Θ and Φ.

Since we ultimately desire to use the measured data in an existing constitutive model [22], we need to transform the Euler angles Θ and Φ from our coordinate system (figure 3) to the coordinate system used in Gasser et al. [22]. We denote the transformed angles by 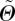and 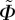. Thus,

2.4

In the new Cartesian coordinate system, the distributed collagen fibre orientations in Ω₀ are characterized by a density function 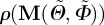with respect to the undeformed orientation of an arbitrary unit vector M. With 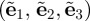, an orthonormal Cartesian basis, and with the two Euler angles 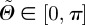and 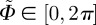, the unit vector M takes on the form

2.5

For simplicity, the distribution of the experimentally measured collagen fibre family is assumed to have rotational symmetry about a principal direction a₀, consistent with Gasser et al. [22]. Representation of a single collagen fibre family, which does not include dispersion, can be accomplished using a structure tensor of the form a₀ ⊗ a₀ [18]. By fibre family, we mean a group of fibres oriented along a single common direction of alignment with some dispersion.

Without loss of generality, the preferred direction of the unit vector a₀ is now taken to have the same direction as the basis vector 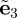, making the density function 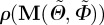independent of 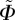, i.e. 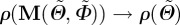. This allows the generalized structure tensor, which is an alternative measure of the fibre distribution in a continuum sense, to be written in the compact form [22]

2.6

with the identity tensor I and the dispersion (or structure) parameter κ, given by

2.7

To model the rotational symmetry about a preferred fibre direction a₀, a transversely isotropic and π-periodic von Mises distribution is used according to Gasser et al. [22], with the density function 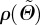as

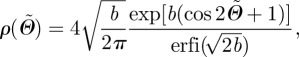2.8

where b > 0 is the so-called concentration parameter associated with the von Mises distribution, and erfi(x) = − ierf(ix) denotes the imaginary error function [50]. From equation (2.7), it is clear that the dispersion parameter κ describes the degree of dispersion in an integral sense, ranging from κ = 1/3 (b = 0), describing an isotropic distribution of fibres in a continuum sense, to κ = 0 (b → ∞), describing perfect alignment of the collagen fibres. In the latter case, the density function 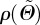in equation (2.8) becomes the Dirac delta function.

The method of least squares was applied to determine the best fit for the fibre density 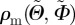, by using the π-periodic von Mises distribution as a function of the concentration parameter b, the elevation angle 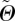and the azimuthal angle 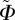. To facilitate fitting, the volumes enclosed by ρ_m and the von Mises distribution ρ were both normalized to 4π. The optimized value of the least-squares fit was then obtained by minimizing the residual sum of squares given by

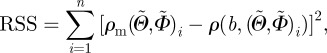2.9

where n denotes the number of observed angle pairs 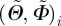, binned on a 5 × 5° grid, ranging from −90° to +90°, and RSS denotes the squared distance between the (measured) fibre density 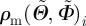of every angle and the corresponding density 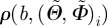of the von Mises distribution. Although the von Mises distribution is independent of 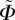, we used it to obtain the values for 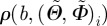in equation (2.9). As a measure of the goodness-of-fit, we calculated the coefficient of determination r² as

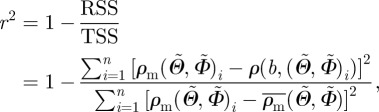2.10

where 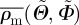denotes the overall mean of the measured fibre density ρ_m for all angle pairs 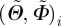and TSS is the sum of the squared distances between every individual density value of the measured angle pairs and the overall mean fibre density. Hence, r² yields values between 0 and 1; the better the von Mises distribution ρ fits the measured data ρ_m, the closer the value of r² is to unity.

3. Results

Approximately 50 fibre angles were measured for each histological tissue section. Depending on the width and the quality of the samples, we were usually able to obtain one to two picrosirius red-stained planar sections from the intima, two to three from the adventitia and three to four from the media from each sample. Given the number of samples (11 human aortas, including the common iliac arteries), the total number of recorded fibre angles from all tissue sections was over 37 000. Analysis of the layer-specific data from the samples investigated for the locations T to CI allowed us to determine: the number of fibre families, the mean angular data such as the azimuthal mean (Eulerian) angle Φ_m and the elevation mean (Eulerian) angle Θ_m, the corresponding angular deviation (AD), the dispersion parameter κ, and the minimized r²-value as a measure of the goodness-of-fit. Because no significant difference between the mean fibre directions was found among the locations T1–T3 and A1–A3, we summarized these data into the thoracic region T and the abdominal region A. All resulting data are summarized in table 1.

Table 1.

Layer-specific data from all 11 subjects of the descending thoracic aorta T, the abdominal aorta A and the common iliac artery CI (compare also with figure 1). (Summarized are the number of fibre families, mean angular data such as azimuthal mean angle Φ_m and elevation mean angle Θ_m, then corresponding angular deviation (AD), dispersion parameter κ and minimized r²-value.)

		azimuthal data (°)		elevation data (°)		fitting data
location	no. of fibre families	Φm	AD	Θm	AD	κ	r2
intima
T	2–4	41.15	22.07	4.02	9.44	0.052	0.60
		−39.48	23.11
A	2–4	38.37	23.39	1.42	8.53	0.048	0.55
		− 37.14	23.92
CI	2–3	45.02	24.73	0.63	9.49	0.055	0.18
		−42.37	23.94
media
T	2	27.75	15.30	1.66	7.89	0.046	0.74
		−27.19	15.18
A	2	24.79	14.44	0.14	7.51	0.039	0.82
		−24.91	14.96
CI	1	−0.11	19.70	−0.34	8.58	0.060	0.63
adventitia
T	2	53.21	17.30	−0.99	9.47	0.055	0.73
		−50.55	16.74
A	2	50.09	18.76	1.07	9.45	0.059	0.64
		−47.75	18.76
CI	2	53.30	17.55	1.43	9.32	0.054	0.69
		−54.27	18.08

Note that the listed mean fibre angles are obtained from the entire data using all subjects, hence yielding the overall mean values Φ_m and Θ_m. The dispersion parameter κ also represents a mean value, however, it is obtained by fitting the model only to data relating to two fibre families in the intima (omitting fibre orientations in the circumferential and axial directions) and to all data for the media and the adventitia. As can be seen from the table, we found that the mean angle Θ_m is close to 0° for all locations and for all three arterial layers. Consequently, the collagen fibres at all locations of the investigated vessels are located close to the tangential plane, i.e. the x–y plane.

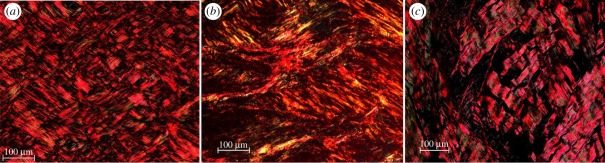
Overall, the arterial layers from all locations showed two very distinct counter rotating fibre families, with a few exceptions, i.e. for the media of the common iliac artery, and the intima along the aortas and the iliac artery. Figure 4 for example, displays three representative images from the intima, the media, and the adventitia at location T2, all showing two distinct fibre families located in the x–y plane. We observed that in the media and adventitia, the two collagen fibre families are organized in separate layers (each layer containing one preferred fibre direction), which is observable by the appearance of a kind of ‘plywood’ structure when cutting through several of such layers. In the intima, this organization in layers was less clear, the two fibre families displayed a ‘carpet-like’ structure, as shown in figure 4a.

Figure 4.

Representative polarized light micrographs, using crossed polars, of picrosirius red-stained sections of (a) the intima, (b) the media and (c) the adventitia of the thoracic aorta. All three images show two distinct collagen fibre families located in the x–y plane of the arterial wall. The horizontal and vertical sides of the image denote the circumferential and axial directions, respectively. (Online version in colour.)

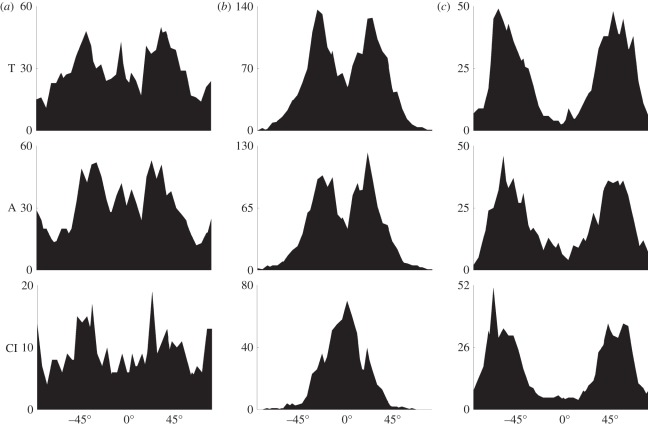
Remarkably, in the media of the common iliac artery, we observed a very different result from two distinct fibre families to only one, which is oriented in the circumferential direction. In the case of the intima, we observed a higher fibre dispersion with a varying number of fibre families, ranging from two to four. The intimas of the thoracic and abdominal aortas showed up to four fibre families, while the intima of the common iliac arteries showed up to three. It is important to emphasize that not all intimas investigated had more than two fibre families, but that two prominent fibre families, placed between the major axes in the x−y-plane, were always visible. Several intimas showed a third peak in the axial direction and a fourth peak oriented circumferentially. To visualize the varying number of fibre families between the different locations, we provide an overview of the azimuthal angles Φ of the data from all samples in figure 5.

Figure 5.

Layer-specific overview of the totality of the azimuthal angles Φ with respect to the reference configuration (Φ = 0° is circumferential) from all subjects as a function of the location along the aortas and the common iliac arteries. The X-axis denotes Φ ∈ [−90°, 90°], the Y-axis denotes the density of the measured angles for the descending thoracic aorta T, the abdominal aorta A and the common iliac arteries CI. (a) Intima, (b) media and (c) adventitia.

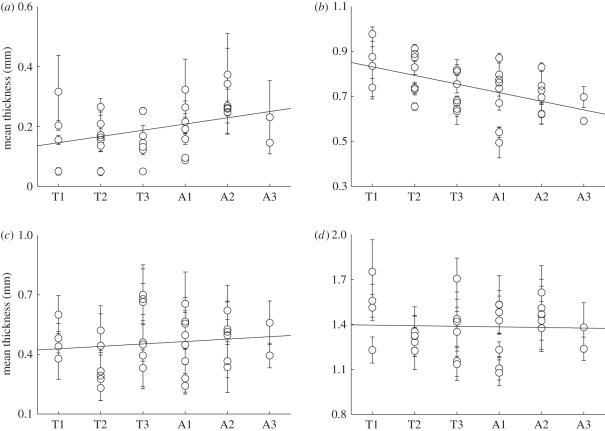
The analysis of the total wall thickness for the descending thoracic and abdominal aortas and the common iliac arteries yielded 1.39 ± 0.18 mm, 1.39 ± 0.16 mm and 1.05 ± 0.15 mm, respectively. No significant variations in the thicknesses between the locations T1–T3 and A1–A3 were observed. While the descending thoracic and abdominal walls have the same thickness, we found a decrease of about 25 per cent for the wall of the common iliac artery. Layer-specific changes in the thickness along the descending aorta, from T1 to A3, are shown in figure 6. Owing to the much thinner wall of the common iliac artery, we decided not to include these data in figure 6, because it would have distorted trends in the linear regression. Although not statistically significant, the overall wall thickness appeared to remain almost constant (r² = 0.17), while a slight thickening of the intima (r² = 0.26) and a thinning of the media (r² = 0.75) in increasingly distal regions were observed. No significant variations were found for the adventitia (r² = 0.27).

Figure 6.

Layer-specific thickness data from locations T1 to A3 according to figure 1. To avoid distortions in the linear regression, data from the much thinner common iliac arteries were not included. (a) Intima, (b) media, (c) adventitia and (d) entire wall.

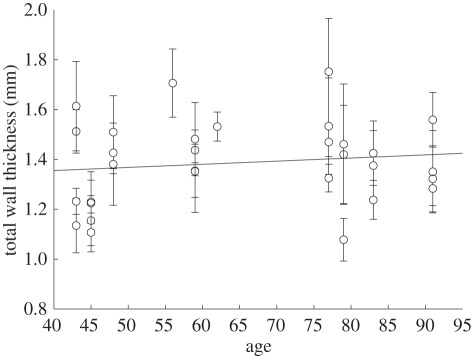
Because the thickness of the arterial intima is not uniform owing to adaptive intimal thickening [46], and the absolute thickness values might be misleading, we also provide intima/media and intima/media/adventitia ratios in table 2. The listed values in table 2 were calculated from the averaged mean thickness data using all subjects, therefore, yielding mean values for the thickness ratios. In figure 7, we illustrate the total wall thickness for the thoracic and abdominal aortas as a function of age for the limited number of subjects available (the positive slope of the linear regression is statistically not significant: r² = 0). An analysis of sex-related thickness variations for the total wall also showed no significant results.

Table 2.

Intima/media and intima/media/adventitia arterial wall thickness ratios (in percentages) for the descending thoracic T1–T3, the abdominal aortas A1–A3 and the common iliac arteries CI. (All values were obtained from the averaged mean thickness data using all subjects.)

location	I/M (%)	I/M/A (%)
T1	21/79	12/57/31
T2	20/80	13/61/26
T3	20/80	10/52/38
A1	27/73	14/52/34
A2	41/59	20/48/32
A3	29/71	14/49/37
CI	33/67	14/44/42

Figure 7.

Age dependency of arterial wall thickening.

4. Discussion

The importance of collagen fibre angles on the mechanical behaviour of arterial walls has been well studied and established in the literature [18,22,27,51]. Because of strong legal and institutional restrictions, only limited structural data on many human tissues are currently available. To our knowledge, this is the first experimental investigation on the structure of collagen fibres in human aortas and common iliac arteries with non-atherosclerotic intimal thickening. We were able to quantify the layer-specific distribution of collagen fibre orientations along the aortas and the common iliac arteries for the first time, providing essential data on the structural composition of the vessel walls. This study has demonstrated the strong variation and dependence of the distribution of collagen fibre orientations on the specific tissue location and especially on the wall layer.

4.1. Fibre angle measurements

In our experiments, we measured over 37 000 fibre angles from non-atherosclerotic descending thoracic and abdominal aortas and from common iliac arteries, providing a large body of data relative to previous studies on different arteries [23,26]. The results of our analysis show two clear fibre families for the intima, media and adventitia in both the thoracic and abdominal aortas, with often a third and sometimes a fourth family of fibres present in the intima in the axial and circumferential directions. For the investigated human aortas, the two families are almost symmetrically arranged with respect to the cylinder axis and are closer to the axial direction in the adventitia, closer to the circumferential direction in the media and in between in the intima, as shown in table 1 and figure 5. The same trend was found for the intima and the adventitia of the common iliac arteries; however, there was only one fibre family present in the media of the common iliac arteries. The differences of the mean fibre angles among different layers of the thoracic and abdominal aortas (more circumferential for the media and more axial for the adventitia) were expected to a certain degree. These differences correlate well with the mechanical response demonstrated in uniaxial tension tests on human iliac arteries, where a higher stiffness for the adventitia tested axially and the media tested circumferentially has been reported [28,32]. However, it is important to note that the biaxial layering of the collagen fibres in the descending aortic media is not a universal quality among elastic arteries, as our results for the fibre distribution of the media in the common iliac artery show, where a unimodal distribution was observed (table 1 and figure 5).

In human brain arteries, a highly aligned medial collagen in the circumferential direction has been documented [23,26]. This result correlates well with our findings for the media in the common iliac arteries, but differs significantly for the media in the thoracic and abdominal aortas. The differences are not unexpected owing to the different functions of the human aorta, which is exposed to high circumferential elastic strain, and a smoothing of blood pressure (systolic-diastolic) is important, versus brain arteries that are of the muscular type. Two helically arranged fibre families (with different orientations in different layers) in the elastic aorta allow for the necessary distensions to absorb pulsating pressure waves originating from the heart, and also form a net-like structure to prevent the vessel wall from overstretching at increased blood pressures. A widely distributed collagen fibre orientation about a mean axial direction was reported for the adventitia in the brain arteries [23]. A mean helical orientation of 53° (0° is circumferential) was documented in Finlay et al. [26], but the presence of two fibre families was not reported. At physiological (in vivo) pressures, the media is the mechanically most significant layer with its more circumferentially oriented fibres in a healthy artery. The less stiff adventitia, however, adds additional structural integrity to the wall by forming a ‘jacket-like’ tube at elevated pressures [18].

In the intimal layer, we consistently observed two fibre families, while often a third and sometimes a fourth (additional) fibre family was found in the axial and circumferential directions, respectively. Our finding of two prominent helically organized fibre families in the intima (symmetrically arranged with respect to the cylindrical axis) was also documented for the subendothelium of human brain arteries in Finlay et al. [52]. As depicted in figure 5, there is generally a much wider range of fibre orientations present in the intima than in the media and adventitia. We did not find any significant correlation between the additional (third/fourth) fibre families and age or sex for our limited number of 11 subjects.

4.2. Statistics

We fitted the dispersion in prominent fibre families with a rotationally symmetric π-periodic von Mises distribution, as suggested in Gasser et al. [22].

The listed dispersion data κ in table 1 are mean values of both main fibre families (figure 5), except for the media of the common iliac artery, where only one fibre family was detected. A third or fourth fibre cluster in the intima was not included in the analysis. The dispersion parameter κ is lower in the media when compared with the adventitia, in the regions T and A. The result is also visible in figure 5, where the peaks in the adventitia plots are slightly wider than the peaks in the media plots.

The r²-values show that the symmetric von Mises distribution is certainly not an ideal statistical distribution for the obtained experimental data. While other non-symmetrical distributions might be more suited to fit our data, we want to emphasize that the rotationally symmetric von Mises was specifically chosen because it allows for the calculation of a single dispersion parameter κ (as introduced in Gasser et al. [22]), yielding a quantitative value for the anisotropy within the framework of a two-fibre family material model, which has been implemented in various finite-element analysis programmes, such as ABAQUS (Simulia Corp., RI, USA) and FEAP (University of California at Berkeley, CA, USA).

Although the study of Haskett et al. [53] documents some salient structural quantities with regard to arterial morphology, this present work highlights the fact that these quantities are highly layer-specific. We made no a priori assumptions regarding the number of fibre families; we measured distributions as a function of direction. From these data then we concluded mean fibre directions, fibre families and corresponding dispersions. By pre-stretching the arterial samples, we have attempted to properly account for the in vivo condition. For the specific choice of circumferential and axial tissue pre-stretch (22% and 12%, respectively) we were guided by the work of Learoyd & Taylor [43] and Labrosse et al. [44]. The 22 per cent circumferential strain is not matched with a known transmural pressure. While we believe that our data representation of overall mean values is well suited for illustrating the layer-specificity of our findings (table 1), we want to emphasize that one must always be respectful of the variability among different subjects, for example, in the present study a specific mean azimuthal angle can vary up to 8° among individual subjects. Although our reported ADs capture such variabilities statistically, we would like to accentuate that one needs to recognize such biological variations rather than seeking universal ‘truths’ in biological, physiological or anatomical function.

4.3. Wall thickness measurements

We performed detailed thickness measurements, which resulted in a mean total wall thickness for the descending aorta of 1.39 ± 0.18 mm, 1.39 ± 0.16 mm for the abdominal aorta, and 1.05 ± 0.15 mm for the common iliac arteries. These values correlate well with the thicknesses documented in Holzapfel et al. [54] for the non-atherosclerotic abdominal aortas, while in a multi-ethnic study of atherosclerosis, the observed aortic wall thicknesses were significantly higher, in the range 2.11–2.32 ± 0.06 mm [55]. A similar result was shown for aortas with second- or third-degree atherosclerosis, where increased wall thickness was documented [56].

Our layer-specific analysis of the thoracic and abdominal aortas demonstrated a slight thickening of the intima and a thinning of the media in increasingly distal regions, while the overall tissue thickness remained constant. Based on guidelines from the American Heart Associations' Council on Arteriosclerosis [46], we calculated the intima/media ratio as a method to determine normal intima thickness, and our results of 0.3–0.7 (table 2) are well within the range of normal human arteries. Interestingly, while the intima/media ratio remains almost constant for the thoracic aorta, a clear intimal thickening can be observed distal to location A1, starting at the branching of the celiac arteries where constant blood flow is disturbed. This regional observation also correlates well with the preferred locations for diffuse intimal thickening, between the orifice of the inferior mesenteric artery and the bifurcation of the common iliac arteries [46].

Despite the limited number of subjects and their relatively advanced age (63.0 ± 15.3 year) we found that wall thickening depends (slightly) on age, as shown in figure 7. While the overall trend is consistent with documented data [55,56], we would expect a stronger dependence of tissue thickness with age if younger subjects (with very little or no intimal thickening) were included in our analysis.

4.4. Implications for vascular physiology

Our results provide novel data on the structure of human arterial walls, with implications for the physiological performance of arteries with non-atherosclerotic intimal thickening. Significant differences in the mechanical behaviour in both axial and circumferential directions have been established in the literature [32], but the underlying principle of such an anisotropic behaviour has yet to be fully understood. While some authors already hypothesized that fibre angles might be responsible for the mechanical behaviour [28], our structural data have the potential to provide a foundation for understanding these experimental observations.

The different responses of arteries (for example, aorta versus cerebral artery) are governed by the structure of the wall. Since the collagen fibres are the structurally most important constituent of the wall, and the significant influence of fibre dispersion on the mechanical properties has been established [51], our layer-specific data on the number of fibre families and the fibre angles (including their dispersion) constitute a step forward in the biomechanical understanding of the functions of human aortic walls and the walls of common iliac arteries.

Our expected observation of differences in fibre arrangement between the intima, media and adventitia explains the previously reported mechanical and functional differences of the three arterial layers [18,28]. One of our key results show a variation of fibre distribution of the media among elastic arteries (descending aortic media versus common iliac media). This affirms that structural vessel composition cannot be assumed to be the same even within a single species, much less among different species [30]. Therefore, experimental data from human tissues like those presented here will become increasingly indispensable for identification of pathological progressions and material modelling of arteries. In the future, studies of the influences of cardiovascular diseases such as atherosclerosis on the collagen fibre distribution in arterial tissue (compared with healthy tissue) would be a natural extension of the work presented here.

4.5. Limitations

To approximate in vivo stretches and ensure straightened collagen fibres, our samples were stretched biaxially, yielding a planar geometry for each tissue sample. While this geometry was necessary to obtain in-plane histological sections for microscopical measurements, it does deviate from the (uncut) cylindrical in vivo shape of arteries, which could have caused slight changes in the mean fibre directions.

When measuring collagen fibre angles using polarized light, it is a great challenge to ensure correct fibre sampling because the nature of the method ‘invites’ the microscopist to preferably measure the more visible (brighter) fibres, therefore, possible biasing away from weaker fibres. Additionally, the usage of the universal stage does not allow for the use of a grid pattern in deciding on the location of the measurements in a practical manner. With this in mind, we tried to sample as fairly as possible, but cannot completely exclude some human bias during measurements.

Another limitation of this study is that it does not allow the measurement of fibre angles continuously throughout the entire wall (in the radial direction; figure 3), and we want to emphasize that our results are mean values for each layer. Because of the small variations in mean fibre directions among our investigated samples (see §3), we do not believe that major changes occur within each arterial layer.