Changes in kinematics and aerodynamics over a range of speeds in Tadarida brasiliensis, the Brazilian free-tailed bat

Abstract

To date, wake measurements using particle image velocimetry (PIV) of bats in flight have studied only three bat species, all fruit and nectar feeders. In this study, we present the first wake structure analysis for an insectivorous bat. Tadarida brasiliensis, the Brazilian free-tailed bat, is an aerial hunter that annually migrates long distances and also differs strikingly from the previously investigated species morphologically. We compare the aerodynamics of T. brasiliensis with those of other, frugivorous bats and with common swifts, Apus apus, a bird with wing morphology, kinematics and flight ecology similar to that of these bats. The comparison reveals that, for the range of speeds evaluated, the cyclical pattern of aerodynamic forces associated with a wingbeat shows more similarities between T. brasiliensis and A. apus than between T. brasiliensis and other frugivorous bats.

1. Introduction

Most studies of bats have focused on aspects of ecology, echolocation or conservation rather than wing motion or aerodynamics [1–6]; hence, we have much less-detailed understanding of flight mechanics. Simultaneous high-speed videography and time-resolved particle image velocimetry (PIV) allow analysis of complex wing motion in relationship to the development of force generation over a wingbeat cycle, but studies of wake patterns and the changes in kinematics in relation to flight speed have been undertaken in only three of the more than 1200 living species of bats to date [7–13]. As a consequence, there is much yet to learn about even straight, forward flight—the simplest of flight behaviours.

Within the extant diversity of the order Chiroptera, body sizes range from 2 to over 1200 g, and there is a substantial variety of wing morphologies. However, although there have been speculations about the relationship of morphology with ecology and flight performance, there have been few quantitative measurements [14]. At present, our knowledge of force generation based on wake measurements is limited to two relatively small nectar-feeding, hovering bats, Glossophaga soricina (approx. 10 g) and the closely related Leptonycteris yerbabuenae (approx. 23 g) [7–9,13], and a medium-sized fruit bat, Cynopterus brachyotis (approx. 35 g) [11,12,15].

In this study, we examine the aerodynamics and kinematics of Tadarida brasiliensis, the Brazilian free-tailed bat, a species that differs from those studied previously in several significant ways. Tadarida brasiliensis is a member of the family Molossidae, a lineage of bats that is believed to have had an evolutionary history distinct from those of the previously studied species for at least 52 Myr [16]. It is insectivorous and a skilled aerial hunter, catching its prey during flight, and is described as having a high wing aspect ratio [17,18]. Tadarida brasiliensis typically emerges from cave roosts at dusk in very large columns at exceptionally high densities [19,20]. These dense columns disperse a few miles from the caves, and it is believed that individual T. brasiliensis may fly up to 50–100 km daily during each foraging bout [21] and during their migration in the autumn [22]. In contrast, G. soricina and C. brachyotis live in relatively small colonies of a few dozen to a few hundred animals and forage within a few kilometres of their roosts [23,24], and L. yerbabuenae live in colonies of 20 000–100 000 individuals, and migrate and forage 30–100 km per night [25,26].

By analysing kinematics and aerodynamics in a species that differs substantially from those previously investigated, we hope to gain insight into the functional, aerodynamic significance of wing structure and movement in general, and, in particular, of the distinctive condition embodied in T. brasiliensis. Comparative analysis will ultimately require study of many species to fully distinguish the effects of phylogeny, body size and ecology, but here we make a foundational step forward by providing the first detailed analysis of wing motions and the associated aerodynamic forces for a highly specialized insectivorous bat.

2. Material and methods

The methods used in this study are similar to those used previously [12], but are briefly summarized.

2.1. Bats

The study subjects were five T. brasiliensis (two females and three males), caught in Texas in April 2009, vaccinated against rabies and transported to Brown University. The bats were trained to fly in a wind tunnel over a range of speeds. Flights were recorded at 2.8, 3.8, 5.3, 6.8 and 8.3 m s⁻¹, with a target of five trials per individual per speed. Only two bats successfully carried out flights at 8.3 m s⁻¹. Each successful run was rewarded with a mealworm. Mealworm weight was measured so that the weight of the bat could be adjusted accordingly.

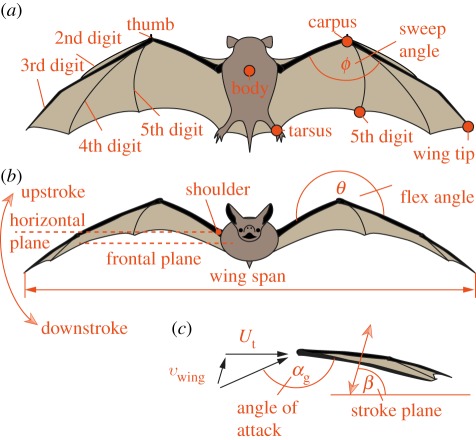
We employed kinematic results from low-speed flights to calculate morphological descriptors of each individual (figure 1). Wing span, b, was defined as twice the maximum distance between the point midway between the scapulae and the wingtip at mid-downstroke, and wing chord, c_V, as the maximum distance between the wrist and the tip of the fifth digit. The surface area, S, was the area enclosed by sternum, wrist, wingtip, tip fifth digit and foot markers at mid-downstroke. For chord, span, weight, wing surface area, aspect ratio (AR = b²/S) and wing loading (Q = mg/S), we calculated means and standard deviations for each bat from all available wingbeat cycles (table 1). Values for morphological parameters measured in this manner in flight can differ from those measured on bats placed in a maximally flattened posture with wing joints maximally extended, but are more directly relevant for specific flight conditions under study.

Figure 1.

Anatomical features, marker positions and kinematic parameters. (a) Top view, (b) front view, (c) side view (U_t, total forward speed; v_wing, wing velocity at wing span location). (Online version in colour.)

Table 1.

Mean and standard deviation of span, chord and weight surface area and aspect ratio of the five individual bats.

individual	sex	span b (m)	chord cV (m)	mass m (g)	S (m2)	AR (−)
bat I	female	0.26 ± 0.016	0.047 ± 0.023	11.8 ± 0.4	0.008 ± 0.0002	9.51 ± 0.5
bat II	female	0.25 ± 0.018	0.043 ± 0.005	13.2 ± 0.4	0.007 ± 0.0001	9.60 ± 0.8
bat III	male	0.26 ± 0.020	0.047 ± 0.022	11.0 ± 0.4	0.008 ± 0.0002	9.73 ± 0.7
bat IV	male	0.27 ± 0.018	0.045 ± 0.006	12.4 ± 0.6	0.007 ± 0.0001	10.2 ± 0.4
bat V	male	0.27 ± 0.020	0.045 ± 0.009	10.5 ± 0.4	0.007 ± 0.0002	9.92 ± 0.7
mean	—	0.26 ± 0.010	0.045 ± 0.002	11.8 ± 1.1	0.007 ± 0.0002	9.79 ± 0.3

2.2. Experimental setup

Measurements were made in a 0.60 × 0.82 × 3.8 m (height × width × length) test section of a closed-loop wind tunnel seeded with particles of DEHS (di-ethyl-hexyl-sebacate). Three high-speed video cameras (Photron 1024 PCI) recorded kinematics at 200 Hz in synchrony with PIV. Two PIV cameras were positioned to measure flow in a plane perpendicular to the flow stream. Kinematic and PIV cameras were triggered manually after the bat passed through the laser sheet.

Three-dimensional wing motion was reconstructed from markers painted on the tarsus, carpus, tip of the third and fifth wing digits, and body midline between the scapulae (figure 1). The start of each wingbeat cycle was designated as the upper reversal point of the wing tip. Wingbeat cycles were interpolated to 40 time increments per cycle.

A right-handed coordinate system, with its origin at the body marker was defined as: positive x in the wind direction, positive y from the body midline towards the tip of the right wing and positive z in the vertical upward direction.

Because all bats flew faster than the wind tunnel air speed, total flight speed, U_t, was determined from the pre-set wind tunnel speed, U_∞, plus the horizontal flight speed of the bat relative to the wind tunnel air flow, U_B. Horizontal and vertical accelerations, a_x and a_z, respectively, were calculated from the change in horizontal and vertical velocities observed through a full wingbeat cycle.

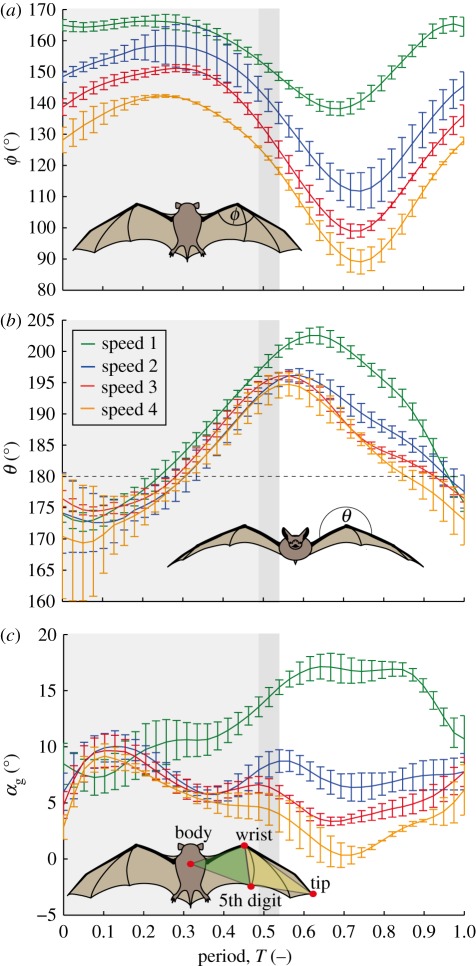
We calculated the following parameters using the global coordinate system: flapping frequency, f; geometric angle of attack, α_g; span ratio, SR; wrist sweep angle, ϕ; and wrist flexion angle, θ. α_g was computed as the angle between the wing surface and the air velocity, the vector sum of the net bat speed, U_t, and the wing velocity relative to the sternum. From sternum, wrist, wing tip and fifth digit markers, two surface planes can be defined to characterize the wing orientation (figure 4c): the armwing (wrist, sternum and fifth digit) and the handwing (wrist, tip and fifth digit). The calculations based on the two planes were similar, so we present only results based on the armwing calculation. We present statistics for α_g at mid-downstroke α_{g_md}, as well as α_{g_mean}, the average α_g over the wingbeat cycle. The span ratio, SR, which is the ratio of the wing span during the upstroke to that during the downstroke, was, calculated when the wing passed through the horizontal plane (figure 1). We quantify orientation of the handwing in relation to the armwing by wrist sweep angle (figure 4a), the rotation of the handwing along the axis defined by wrist and the fifth digit. A decrease in ϕ is thus a backward sweeping motion. Finally, wrist flexion angle, θ (figure 4b), describes the rotation of the handwing in the axis perpendicular to the armwing; an angle above 180° corresponds to a downward flexing motion.

Figure 4.

Wrist kinematics in relation to flight speed. Downstroke indicated by shading (downstroke is shorter at higher speeds, darker shade indicates period of variation). (a) Wrist sweep angle, ϕ. (b) Wrist flexion angle, θ. Dashed line represents no flexion between proximal and distal wing, essentially a ‘flat plate’ condition. (c) Geometric angle of attack in relation to the wingbeat cycle with respect to flight speed. Calculations of angle of attack are based on the armwing or proximal plane (shaded green in inset). Speed 1, green; speed 2, blue; speed 3, red; speed 4, orange.

DaVis v. 7.2 software (LaVision) was used to analyse the PIV recordings. Sequential cross-correlation with multi-pass iterations in decreasing size (128 × 128, two iterations to 64 × 64, two iterations, 50% overlap) was used to calculate vector fields. Vectors with a peak ratio Q < 1.2 and an average neighbourhood variation >1.5 × r.m.s. were replaced by post-processing interpolation and the application of a simple 3 × 3 smoothing filter. Vector fields were then exported and further processed in Matlab.

Vorticity and swirl were calculated to visualize wake structure [12]. Because swirl is always positive, the rotational direction of the vortices was determined from the sign of the vorticity. After processing with a 3 × 3 smoothing filter and swirl threshold (±25), swirl isosurfaces were then mapped as wake structures.

We calculated circulation for the four vortices that comprise the wake, tip vortex, root vortex, distal vortex pair [12] and displayed their development with respect to the timing of the wingbeat cycle. To calculate circulation for each vortex, we indentified vortex location manually and then integrated vorticity over the surrounding adjacent area following application of a 5 s⁻¹ threshold.

2.3. Statistics

Although wind tunnel speed was set at discrete values, the variation in the additional speed of the bat's progressive upstream flight resulted in a continuous distribution of total flight speeds. Therefore, for statistical evaluation, we treated speed as a continuous variable. However, to facilitate identification of changes in dynamics and kinematics in relation to speed, we grouped data into four speed ranges: below 5.5 m s⁻¹, between 5.5 and 7 m s⁻¹, between 7 and 8.5 m s⁻¹ and above 8.5 m s⁻¹. Only two bats flew at speeds higher than 8.5 m s⁻¹.

We analysed a total of 110 trials from five bats, using no more than three wingbeat cycles per trial, for a total of 247 wingbeat cycles. To account for pseudo-replication in the statistical analysis, we employed a mixed effect model with wingbeat cycle as a repeated measure and individual as a random effect; a significance level of 5% was used for all tests. We performed all statistical tests using SPSS v. 17.0 (SPSS Inc., Chicago, IL, USA).

To compare kinematic and aerodynamic data graphically, we first computed averages of the respective variables for all wingbeat cycles within a trial, then averaged all trials for each bat before computing averages for all bats (figures 2, 4, 6 and 7). Standard deviations are calculated over individuals.

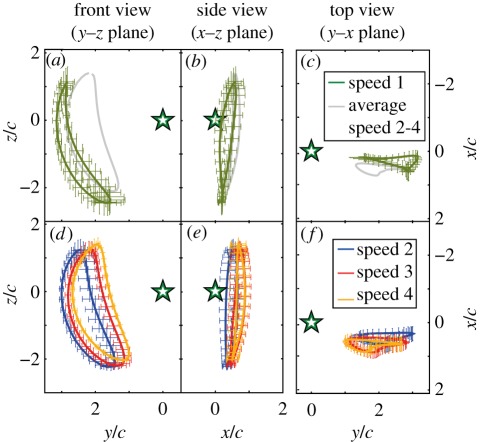
Figure 2.

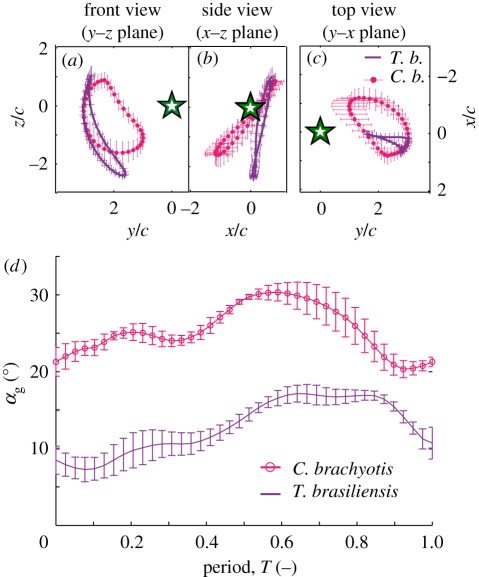
Average wingtip trajectory in body-referenced coordinate system, normalized by the wing chord c_V, in front, side and top views (note reverse ordinate for y–x plane). Star indicates body marker position. (a–c) Trajectories at speed below 5.5 m s⁻¹ (‘speed 1’, green) compared with the averaged trajectories of speeds above 5.5 m s⁻¹, grey; (d–f) trajectories for speeds between 5.5 and 7 m s⁻¹ (‘speed 2’, blue), 7 and 8.5 m s⁻¹ (‘speed 3’, red) and above 8.5 m s⁻¹ (‘speed 4’, orange).

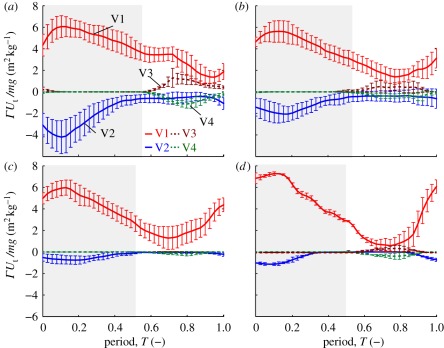
Figure 6.

Average body weight normalized circulation for V1–V4, for each speed category (a–d) speed 1–4 (n = 5 bats for speeds 1–3; n = 2 for speed 4). Shading denotes downstroke. (Online version in colour.)

Figure 7.

Average wingtip trajectory (a–c) and geometric angle of attack (d) of T. brasiliensis (two bats) and C. brachyotis (four bats) close to their respective minimum power speeds. Tadarida brasiliensis (v_mp = 3.8 m s⁻¹; displayed at 4–4.5 m s⁻¹); C. brachyotis (v_mp = 4.9 m s⁻¹; displayed at approx. 5 m s⁻¹). (a–c) Trajectory displayed in body-referenced coordinate system, normalized by the wing chord (note reverse ordinate for y–x plane). Star indicates body marker position. (Online version in colour.)

3. Results

3.1. Kinematics

U_B, the speed of the bats relative to the wind tunnel flow, was always greater than zero, but decreased significantly with increasing flow speed (table 2). This pattern varied among individuals in both slope and intercept (electronic supplementary material, figure S2).

Table 2.

p-Value, degree of freedom and t-value for change in kinematic parameters with respect to flight speed (number of individuals N = 5; number of wingbeat cycles used for calculation n = 247).

flight parameter	increase/decrease with flight speed	p-value	95% CI		t-value	d.f.
			lower bound	upper bound
additional bat speed, UB (m s−1)	↓	<0.001	0.1980	0.2453	18.5	239.0
frequency, f (Hz)	↓	<0.001	−0.5607	−0.4031	−12.1	101.1
amplitude, Θtip (°)	↑	<0.001	3.2766	5.3673	8.2	99.9
span ratio, SR (−)	↓	<0.001	−0.0638	−0.0452	−11.6	97.4
sweep angle, ϕ (°)	↓	<0.001	−10.2434	−8.4066	−20.2	87.9
flex angle, θ (°)	↓	<0.001	−1.6956	−1.0155	−8.0	86.5
downstroke ratio, τ (−)	↓	0.001	−0.0130	−0.0032	−3.3	118.6
horizontal acceleration, ax (m s−2)	—	0.359	−0.2328	0.0851	−0.9	90.7
vertical acceleration, az (m s−2)	↑	0.002	0.1364	0.5949	3.2	94.3
stroke plane angle, β (°)’	—	0.844	−1.4602	1.1968	−0.2	63.1
maximum span, b (m)	↓	<0.001	−0.0059	−0.0046	−16.1	106.5
maximum wing chord, cν (m)	—	0.478	−0.0010	0.0021	0.7	127.4
minimum distance body–wing tip, dmin (m)	↓	<0.001	−0.0125	−0.0097	−15.8	102.1
mean geometric angle of attack, αg_mean (°)	↓	<0.001	−3.4838	−2.4056	−10.9	86.1
geometric angle of attack mid-downstroke, αg_md (°)	↓	<0.001	−1.5949	−0.4692	−3.7	58.3

Increasing flight speed was accompanied by significant increases in wingbeat amplitude and vertical acceleration and decreases in flapping frequency, sweep angle, flex angle, downstroke ratio, wingspan, minimum body–wingtip distance, average angle of attack, α_{g_mean}, and mid-downstroke angle of attack, α_{g_md} (table 2). Stroke plane angle, wing chord and horizontal accelerations did not change with speed. Average and maximum accelerations were 0.64 ± 1.45, 4.68 and −1.64 ± 2.28, 8.70 m s⁻² in the horizontal and vertical directions, respectively.

Differences in wing motion between up- and downstroke are small at low speeds, and more distinct at higher speeds (figure 2). Below 5.5 m s⁻¹, up- and downstroke wingtip trajectories show minimal differences (figure 2a). There is only slight flexion of the wrist during the course of the upstroke. As speed increases, wrist flexion also increases, hence the distance between the wing tip and the body is substantially less during that upstroke than during downstroke (figure 2d). Above 5.5 m s⁻¹, landmark trajectories change little with flight speed, with the overall shape of the wingtip path remaining unchanged while the entire trajectory is translated medially (figure 2d). The side and top views demonstrate an almost vertical stroke plane at all speeds, with an average stoke plane angle over all speeds and bats of −84.4 ± 3.6° (figure 2b–f). The change in upstroke and downstroke wing extension (span) results in a significant decrease in span ratio with speed (table 3).

Table 3.

Mean value and standard deviation for span ratio and the change in wrist sweep and wrist flexion angle over the course of a wingbeat cycle for different speed categories (averaged first over bats individually than all bats).

flight parameter	speed 1	speed 2	speed 3	speed 4
SR	0.9 ± 0.04	0.72 ± 0.06	0.65 ± 0.04	0.61 ± 0.03
sweep angle, Δϕ (°)	25.4 ± 7.2	45.8 ± 9.0	51.7 ± 5.9	47.8 ± 5.7
flex angle, Δθ (°)	30.4 ± 6.1	24.2 ± 4.3	21.9 ± 1.8	25.4 ± 6.5

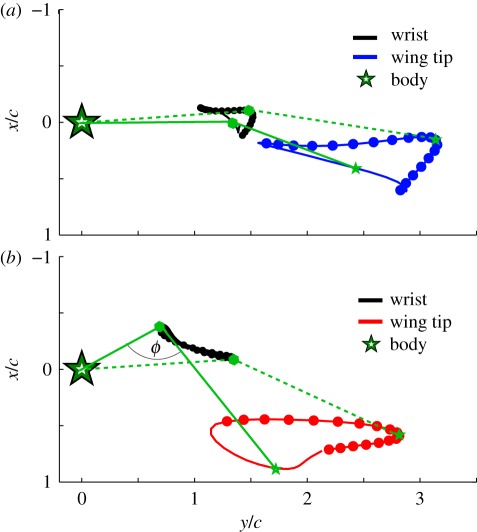
Based on the higher wing retraction in the upstroke at higher speeds, one might expect a substantial difference in upstroke and downstroke trajectory in side view (x–z plane). However, wingtip path in lateral view is similar at all speeds (figure 2b,e). Analysis of wrist movement reveals that the relatively narrow path of the side view trajectory at higher speeds is achieved by anterior motion of the wrist, synchronized with posterior motion of the wing tip (figure 3).

Figure 3.

Average wrist and wingtip trajectory in the body-referenced coordinate system, normalized by wing chord (top view). Dots indicate successive time increments during downstroke. Solid green line represents virtual leading edge at mid-upstroke, dashed line at mid-downstroke, green stars are wing tip, and hexagons are wrist positions at mid-upstroke and downstroke. Wrist flexion angle, ϕ, is the angle between the two vectors representing the leading edges of the proximal and distal portions of the wing. (a) Speeds below 5.5 m s⁻¹; (b) speeds between 7 and 8.5 m s⁻¹. (Online version in colour.)

Reduction in wing extension during upstroke is correlated with a decrease in wrist sweep angle, ϕ (figure 4a). In slow flight (<5.5 m s⁻¹) with high SR, the wing starts out almost fully extended (close to 180°) and the angle changes by about 25°; however, at faster speeds (>5.5 m s⁻¹), the wing already starts out less extended and the changes are considerably larger (approx. 50°; table 3). Wrist flexion angle, θ a descriptor of out-of-plane wing shape, changes less (table 3 and figure 4b). The wrist is slightly hyperextended at the beginning of the downstroke, where θ = 175°, then the arm- and handwing align to bring θ to 180° at about mid-downstroke, followed by flexion through the second half of downstroke and the majority of upstroke, with values of up to 200° shortly after the onset of the upstroke.

The geometric angle of attack, α_g, changed continuously through the wingbeat cycle, and differed substantially between flight speeds (figure 4c). Average α_g changed significantly with speed for all bats. However, mid-downstroke α_g differed significantly among speeds for only two of five bats. Below 5.5 m s⁻¹, α_g is visibly different than at higher speeds: values are substantially higher in the last two-thirds of downstroke, and α_g increases continuously until the end of the first quarter of the upstroke, the angle remains constant during the middle half of upstroke, then it decreases in the last third of the upstroke. For speeds higher than 5.5 m s⁻¹, α_g is similar during the downstroke, reaching its maximum at the end of the first third of the downstroke and decreasing thereafter. At higher speeds, α_g decreases over the course of the downstroke and reaches its minimum at mid-upstroke. However, at lower flight speeds, α_g increases slightly again around the lower reversal point, and stays constant during the upstroke. The lowest speeds, in contrast, show an increasing α_g during the downstroke and the first third of the upstroke where it reaches its highest values.

3.2. Wake structure

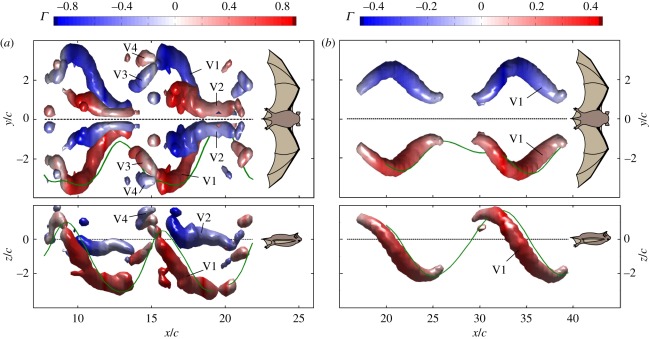
Previous studies have identified four re-occurring vortices in the wake of flying bats [8,12]. We have previously referred to these vortices as the tip vortex (V1), the near-body or root vortex (V2), and the distal vortex pair (V3, V4) [12] and employ that nomenclature here.

Figure 5 shows representative isosurface reconstructions of the wake for lower and higher speed flight. At all speeds, the main structure was the tip vortex (V1), visible over most or all of the wingbeat cycle. Development of the tip vortex was accompanied by appearance of the root vortex (V2), whose strength and duration varied considerably with flight speed. At higher speeds, root vortices, if present at all, were often too weak to appear in isosurface reconstructions. A distal vortex pair (V3, V4) of varying strength appeared towards the end of the upstroke, with rotation opposite to the tip and root vortex system, indicating negative lift generation.

Figure 5.

Top and side view reconstruction of the wake structure for two wingbeat cycles. Isosurfaces of the transverse swirl are shown based on the two-dimensional PIV data. The wake is displayed in the body-reference coordinate system, and time was converted into space to allow spatial display of the wake structure behind the bat. Body (dashed line), right wingtip (solid green line). Vortices are coloured based on their strength and rotational direction, with counter-clockwise rotating vortices positive (red). (a) Total speed: 5.1 m s⁻¹; (b) total speed: 7.0 m s⁻¹.

For all speeds, the circulation of V1 reaches its maximum shortly after the beginning of downstroke and then decreases continuously until 70–80% through the cycle, after which it increases. The magnitude and timing of the minimum strength of the tip vortex changes with speed, decreasing in strength and advancing to mid-upstroke at the higher speeds. At speeds below 5.5 m s⁻¹ (figure 6a), V2 strength almost equals that of V1 at the beginning of the downstroke, reaches a maximum in synchrony with the tip vortex peak, then decreases in strength faster than V1 until the wingtip lower reversal point. During the upstroke, V2 strength remains nearly constant, then increases close to the upper reversal point. The distal vortex pair appears during the first third of the upstroke, gains strength, diminishes and then disappears near the upper reversal point. At the highest speeds studied, V3 and V4 were not or just barely discernible (figures 5b and 6d).

Owing to the large measurement field required to capture wake structure over the entire wingbeat, measured vorticity absolute magnitude is likely slightly lower than true values [27]. This is an intrinsic shortcoming of the transverse plane PIV technique with the available instrumentation. However, this underestimation of vortex strength is a consistent effect and thus does not affect description of either spatial structure or the relative strength of specific vortices [27] (see electronic supplementary material).

4. Discussion

Although multiple studies have analysed the kinematics of bat flight [1,2,4,28–30], the detailed structure of wakes has been analysed in only three bat species: G. soricina, L. yerbabuenae and C. brachyotis [7–10,13]. All feed primarily on nectar or fruit, all possess wings with a relatively low aspect ratio (AR approx. 6), and G. soricina and C. brachyotis forage close to their roosts [31–33]. In comparison, T. brasiliensis is quite distinctive. Of the diets of bats studied to date, only that of T. brasiliensis comprises food capable of active, indeed rapid, escape. Aerial pursuit predators, Brazilian free-tailed bats feed on diverse flying insects, chiefly lepidopterans and coleopterans, but also hymenopterans and dipterans [34–36]. In a single night, a lactating female can capture well over 25 per cent of her body weight in prey. Tadarida brasiliensis regularly fly over 50 km in single foraging bouts [21], they forage over 2500 m above ground [22,37] and can migrate nearly 2000 km yearly [38,39]. Morphologically, wing shape of T. brasiliensis differs substantially from that of other bats studied; T. brasiliensis having a much greater aspect ratio, published values ranging from 8.12 to 8.6 [40–43]; and in this study we compute estimates as high as 9.8 when wing span and area are based on the natural, in-flight postures.

In this study, we explore aerodynamics and kinematics in T. brasiliensis, and make comparisons between the patterns observed in this species and those seen in other bat and bird species, with particular focus on C. brachyotis, whose flight we have studied in detail. It is impossible, however, to unequivocally interpret the differences among taxa at present. Brazilian free-tailed bats differ from other bats whose flight has been studied intensively in multiple ways: ecologically, morphologically, physiologically, and phylogenetically. As a consequence, lacking good phylogenetic control, differences in flight mechanics could be owing to any one or a combination of factors [44,45]. Nonetheless, these results, the first detailed analysis of wing motions and their aerodynamic consequences in an insectivorous bat, represent a substantial step forward in our understanding of bat flight, and set the stage for more robust comparative analyses.

4.1. Kinematics

There are striking differences in wing motion apparent when one compares, even qualitatively, high-speed video of T. brasiliensis and C. brachyotis in flight (see electronic supplementary material, videos). In contrast to species previously studied, T. brasiliensis shows little or no late downstroke wing ‘curling’, the characteristic combination of flexion at the wrist, metacarpophalangeal and interphalangeal joints observed in some bats. Its wing movement lacks the more complex three-dimensional changes in wing shape (e.g. curl of the wings) documented previously in other bat species [3,10,12,28,29]. Surprisingly, T. brasiliensis displays an almost vertical stroke plane at all flight speeds, unlike the common strategy seen in other bats, birds and insects, in which the stroke plane angle becomes increasingly vertical with speed [10,12,28,30,33,46–48].

Several kinematic parameters changed significantly with flight speed in this study (figure 4, tables 2 and 3). Wingbeat frequency, downstroke ratio, angle of attack, wrist flexion angle (θ), sweep angle (ϕ), maximum wing extension, span ratio and minimum body to tip distance all decreased with speed; in contrast, wingbeat amplitude increases with speed. Birds also decrease wing extension with speed, owing to the different demands of lift generation and drag reduction at low and high speeds [29,33,49]. At low speeds, lift is strongly dependent on wing area; so greater wing extension increases lift, simultaneously decreasing induced drag, the dominant drag component at low speeds. With increasing flight speed, the influence of induced drag decreases, but profile and parasite drag gain importance. Reduction in wing extension is then favourable, reducing those drag components while simultaneously decreasing inertial forces.

Span ratio was significantly higher at speeds below than above 5.5 m s⁻¹. This contrasts with previous observations in the flight of birds and bats in which slow flight is associated with reduced wing extension during the upstroke, making the upstroke largely aerodynamically passive [10,47,50,51]. Span ratio in T. brasiliensis is considerably higher than in most birds except Apodiformes, the swifts and hummingbirds. At higher speeds, span ratios of Tadarida are comparable with those measured for G. soricina [10], with values near 0.65–0.67. However, at low speed, span ratio in T. brasiliensis is as high as 0.9, much like the more rigid-winged swifts (SR = 0.7; [52]) and hummingbirds (SR = 0.9; [48]). In T. brasiliensis, the anterior motion of the wrist is linked to posterior sweep, producing little net change in the trajectory of wing tip in the x–z plane with increasing speed. This motion is similar to the anatomically coupled parallel motion of the humerus and metacarpus in bird flight [53,54].

To compare kinematics between species that differ substantially in body mass, a selection of appropriate speeds at which to carry out such a comparison is required. Bat flight shows no unambiguous gait transitions analogous to the walk–trot or trot–gallop transition of terrestrial vertebrates, so we chose to employ an aerodynamic model to select speeds at which to make our comparisons. Using an empirically derived equation that predicts minimum-power flight speeds of bats from body mass, wingspan and wing area [40], we see substantial differences in wingtip kinematics between C. brachyotis and T. brasiliensis at their respective minimum power speeds (figure 7a–c). Motions of the C. brachyotis wingtip show changes in trajectory between downstroke and upstroke, reflecting the greater flexion of the metacarpophalangeal and interphalangeal joints during the upstroke that we characterize as wing curling. Tadarida brasiliensis wingtip motion shows less variation between the downstroke and upstroke trajectories, demonstrates a nearly vertical stroke plane and reflects little flexion at any joints within the wing.

Angle of attack is substantially lower overall in T. brasiliensis than in C. brachyotis (figure 7d). At low and medium flight speeds, angle of attack increases during the second half of the wingbeat cycle in both species, and wing extension decreases with speed. However, there are striking differences in the way this is achieved. In T. brasiliensis, the wings are almost planar, with the handwing swept backward at the wrist, and relatively little ventral flexion. In contrast, in C. brachyotis, the wings ‘curl’, a motion dominated by ventral flexion of the handwing with less sweeping motion; at the end of downstroke, this flexion can be so extreme that the wingtips overlap (figure 8).

Figure 8.

Differences in wing curling for (a) C. brachyotis and (b) T. brasiliensis at lower reversal point.

4.2. Wake structure

We compared the three-dimensional wake structures associated with forward flight for T. brasiliensis with those of G. soricina, L. yerbabuenae, C. brachyotis and A. apus, the common swift, whose wake displays wing root vortices, a characteristic previously thought to be specific to bat flight [13]. Despite the substantial differences among bat taxa in wing shape and kinematics, the structure of their wakes is remarkably similar. All are dominated by the tip vortex, whose strength rapidly increases in the first half of the downstroke. In all three frugivorous bat species, the tip vortex circulation persists with little or no decrease in strength until around mid-upstroke, at which point it diminishes or disappears [8,12], while, simultaneously a counter-rotating distal vortex pair develops. Tip vortex circulation is a key characteristic of the upstroke in all frugivorous bat species at medium flight speeds, with a short period of reversed circulation at the distal part of the wing, indicating negative lift and thrust generation at the end of upstroke. Additionally, the frugivorous bats show the development of a root vortex at or shortly after the onset of the downstroke, with rotation opposite to that of the tip vortex. However, although the duration of the root vortex in C. brachyotis is rather short, and it disappears by mid-downstroke, it persists, at reduced strength, until the end of upstroke for G. soricina and L. yerbabuenae [13]. At very low flight speed (1.5 m s⁻¹), measurements of G. soricina show reverse circulation during the upstroke, indicating negative lift generation [7]. Additionally, a downstroke leading edge vortex (LEV) is present during hovering and low-speed flight in G. soricina [9], and speculation that LEVs could be involved in the flight of the larger-bodied L. yerbabuenae or at higher flight speeds in G. soricina is yet to be resolved [8].

The wakes of several bird species have been documented using PIV, and in comparison with bat wakes, those of birds have been considered rather simple, primarily comprising the tip vortex [55,56]. However, root vortices have now been seen in bird flight, first in blackcaps [57] and then in swifts [58]. In addition, swifts generate a pair of tail vortices [58] which have not been reported for bats, although no bat studied to date possesses a substantial tail membrane.

Tadarida brasiliensis is morphologically and ecologically quite distinct from the other bat species employed in PIV studies, and differs from these bats in the direction of swifts, birds with high wing aspect ratios (approx. 10), high span ratios (greater than 0.6) and rather planar wings with pointed tips. Given these similarities, we hypothesize that the commonalities in the wing form and flight performance of swifts and Brazilian free-tailed bats might be reflected in the structure and development of their respective wakes.

The time course of the development of the tip vortex differs considerably between narrow-winged swifts and Brazilian free-tailed bats on the one hand and broad-winged nectar and fruit eating bats on the other. In T. brasiliensis and swifts, circulation increases in strength in the first half of the downstroke, peaks at mid-downstroke, then decreases until approximately the midpoint of upstroke [58]. In contrast, in other bats, there is typically a plateau of constant circulation later in the upstroke [8,12].

The magnitude of aerodynamic force depends on circulation, speed and wing span. At higher speeds, low circulation combined with wing retraction leads to a largely aerodynamically passive upstroke in T. brasiliensis. We propose that this may be beneficial for an animal that typically forages at relatively high speed, in which the generation of a relatively high drag as a byproduct of generating lift during upstroke lift is particularly undesirable. Active upstrokes that generate considerable lift might be a necessity for species with higher wing loading, such as C. brachyotis, in which lift generation during downstroke alone might not be sufficient to counteract weight. Although lift decreases in this species when wings are retracted during the upstroke, upstroke circulation is still much higher than that observed in T. brasiliensis and in swifts. It is possible that C. brachyotis alters their aerodynamics to a more aerodynamically passive upstroke at considerably higher speeds than T. brasiliensis, but those speeds were not achieved in the previous PIV wind tunnel study.

In the observed speed range, there is little flight speed dependence of the overall development of the tip vortex during the wingbeat cycle for any bat species or for swifts, with exception of the distinctive hovering flight of L. yerbabuenae and G. soricina. However, in C. brachyotis and T. brasiliensis, the tip vortex strength starts to decline earlier with increasing speed so that the overall duration of the tip vortex diminishes with speed (electronic supplementary material, table S1). As a result of this, a slightly larger part of upstroke appears to be aerodynamically passive at higher speeds, increasing the gap between closed-ring vortex loops. This pattern is not consistent with previous observations in bird flight in which a ring vortex wake is hypothesized to be characteristic of slow flight [59–61].

The presence of a root vortex during low-speed flight in T. brasiliensis is consistent with wakes observed previously from both bats and swifts. Root vortices indicate that the body generates less circulation than each wing, and is not fully integrated into the lifting surface. The root vortices start to develop at or nearly at the same time as the tip vortex at the beginning of downstroke. In C. brachyotis, the root vortex disappears in the first half of downstroke, while the strength of the tip vortex is still increasing, indicating that, at this stage in the wingbeat cycle, the body and wings function as a single lifting surface [12]. In contrast, in G. soricina and L. yerbabuenae, the root vortex remains a distinct structure, although it diminishes in strength late in upstroke; the body does not reach the same circulation as the wings, generating less lift [13]. In swifts and T. brasiliensis, root and tip vortex strength peak simultaneously, although, depending on flight speed, at different absolute values. This indicates that the diminishing strength of the root vortex is due to a general decrease in circulation, not the further inclusion of the body in lift generation.

In swifts, peak tip and root vortex strength varies little with flight speed, although the root vortex is absent during part of the upstroke at slow speed. In T. brasiliensis, the root vortices are the most velocity-dependent (figure 6). At low speed, root vortices are strong and persist well into upstroke, although their strength decreases, ultimately to the point of total absence. This distinctive lack of a root vortex at higher speeds distinguishes the wake of T. brasiliensis from that of all other bats and of swifts. This wake pattern suggests that at high speed, the body participates fully in lift generation from the onset of downstroke, and allows us to reject the hypothesis that the body always presents a disruption on the lift-generating surface of the wings for these bats [58].

The appearance of distal vortices at the end of the upstroke seems to be a general characteristic of bat flight, not so far observed in birds. Tadarida brasiliensis fits the bat pattern until it reaches higher speeds, at which point this vortex pair is weak or non-existent. If these vortices arise from the highly negative angle of attack of the wing tip at lower speeds, the decrease in this angle with speed may lead to their absence. However, the distal vortex pair gains prominence with speed in G. soricina and L. yerbabuenae [13], suggesting that the mechanistic basis of this vortex structure is yet to be fully uncovered.

5. Conclusion

The structure of the wake of T. brasiliensis, a fast-flying aerial hunter, differs substantially from that of other bats from two distantly related lineages that are characterized by broader wings, lower typical flight speeds and frugivorous or nectarivorous diets. Instead, the wake of Brazilian free-tailed bats, particularly the tip vortex structure, is more similar to that recorded from swifts, with circulation peaking before the middle of the downstroke, and relatively little lift generated during the upstroke. This distinctive wake structure may arise, at least in part from distinctive wing kinematics. The wings of T. brasiliensis move in a manner similar to an oscillating flat plate, with little change in the three-dimensional shape of the wing other than a reduction of wingspan during the upstroke. Although T. brasiliensis sweeps the wings backwards to reduce wingspan, the downstroke wing motion shows little of the flexion of the joints in the arm and handwing, sometimes designated as curling, which is seen to varying degrees in other species of bats in the family Pteropodidae [12,29] and subfamily Glossophaginae [13,33]. The resemblance between the wake structure of T. brasiliensis and swifts might be explained by similar morphological and kinematic characteristics such as high aspect ratio, relatively pointed wings, sweeping wing motion to reduce wing span and high span ratio. In addition, ecological commonalities such as aerial predation and long-distance migration might suggest that T. brasiliensis' flight mechanics have more in common with swifts than with their nectar and fruit-eating relatives.

Full understanding of the aerodynamic significance, let alone the evolutionary history, of vertebrate wing form and kinematics will require denser taxonomic sampling than has yet been feasible with logistically challenging and labour-intensive techniques such as PIV. However, as researchers select study species to broaden insight, we can begin to discern the outlines of the characteristic patterns of wing motion and aerodynamic force production of particular groups of flying animals. By providing the first detailed experimental study of vortex wake structure of an insectivorous bat, we gain a new appreciation of the diversity of wake architecture in bats. At the same time, the comparison between swifts and T. brasiliensis shows that there might not be a clear distinction in the nature of aerodynamic force production between bats and birds, but rather a range of continuous variation. To discern features shared by all flying vertebrates, and to distinguish the specializations associated with the evolutionary acquisition of particular morphological or kinematic patterns will require that the experimental flight research community continues to extend their studies in a manner that will facilitate comparative analysis.