Amphiphilic Adsorption of Human Islet Amyloid Polypeptide Aggregates to Lipid/Aqueous Interfaces

Abstract

Many amyloid proteins misfold into β-sheet aggregates upon interacting with biomembranes at the onset of diseases, such as Parkinson’s disease and type II diabetes. The molecular mechanisms triggering aggregation depend on the orientation of β-sheets at the cell membranes. However, understanding how β-sheets adsorb onto lipid/aqueous interfaces is challenging. Here, we combine chiral sum frequency generation (SFG) spectroscopy and ab initio quantum chemistry calculations based on a divide-and-conquer strategy to characterize the orientation of human islet amyloid polypeptides (hIAPP) at lipid/aqueous interfaces. We show that the aggregates bind with β-strands oriented at 48° relative to the interface. This orientation reflects the amphiphilic properties of hIAPP β-sheet aggregates and suggests the potential disruptive effect on membrane integrity.

Introduction

Aggregation of amyloids at biomembranes is often associated with the onset of type II diabetes as well as Parkinson’s, Alzheimer’s and prion diseases.^1–3 In particular, human islet amyloid polypeptide (hIAPP) is implicated in the type II diabetes.^{4, 5} Previous in vitro studies show that negatively charged membrane surface can induce aggregation of hIAPP, suggesting a crucial role of interactions between the lipid membrane and hIAPP in the misfolding and aggregation of hIAPP.^6–8 On the other hand, the hIAPP misfolding process is suggested to disrupt the membrane integrity and cause permeability across the membrane, which is toxic to the pancreatic β cell.^8–10 This lipid-hIAPP interaction should closely correlate to the orientations of various protein secondary structures formed by hIAPP at membrane surfaces at different stages of aggregation. Upon interaction with lipid membranes, hIAPP cooperatively misfolds from disordered structures to α-helices and then to β-sheets.^{6, 7} Previous studies show that the hIAPP α-helical intermediates bound to the membrane with an orientation parallel to the membrane surface, in close contact with phospholipid headgroups.¹¹ However, the orientation of hIAPP β-sheets has yet to be established, limiting our understanding of how amyloid aggregates may affect membrane structure. Especially, recent studies show that the β-sheets oligomers and protofibrils can permeabilize membranes, and thus are cytotoxic.^12–14 However, the molecular mechanism of the interactions remains poorly understood. Here, we use chiral surface-specific vibrational sum frequency generation (SFG) spectroscopy in conjunction with ab initio simulations of the characteristic A and B amide I vibrational modes¹⁵ to determine the orientation of hIAPP aggregates at lipid/aqueous interfaces (Fig. 1).

Fig. 1.

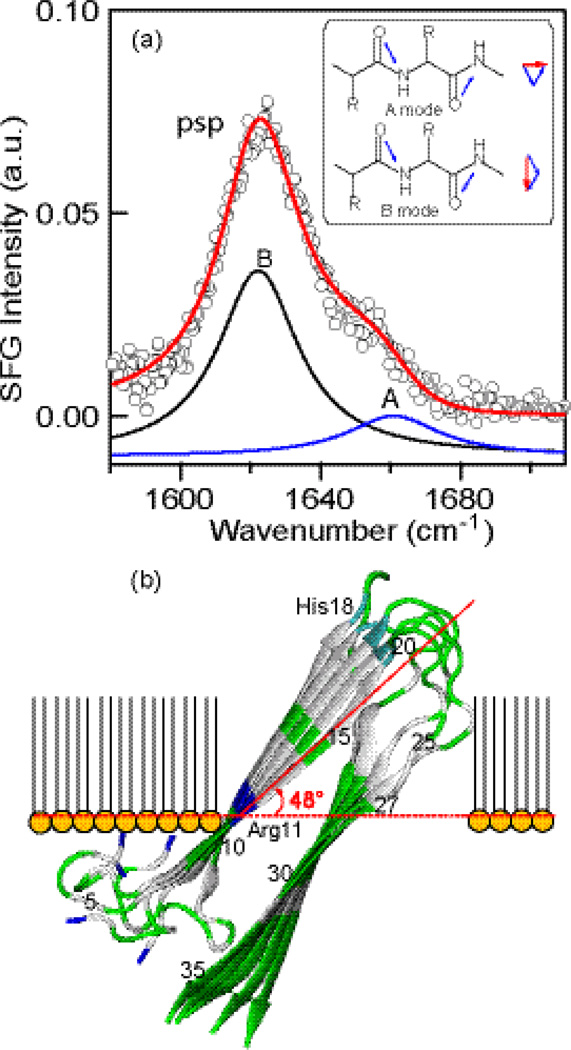
(a) SFG spectrum of hIAPP 10 hours after the addition of DPPG. The blue and black component peaks are ascribed to the A and B amide I modes, respectively, for parallel β-sheets (inset: the transition dipoles of the A and B modes are parallel and perpendicular to the peptide backbone, respectively). (b) Predominant orientation of the hIAPP aggregate at the lipid/aqueous interface (dashed line) determined by the ab initio analysis of the SFG spectrum. Color key: Hydrophilic amino acids (green) and hydrophobic amino acids (gray).

Human islet amyloid polypeptide (hIAPP) is a protein of 37 amino acids implicated in type II diabetes.^{4, 6, 7, 16} In its normal state, hIAPP is cosecreted with insulin from islet β-cells of pancreas and adopts an unstructured conformation. In the disease state, hIAPPs misfold into β-sheet-rich amyloids and deposits in the islet cells of pancreas. Tycko and coworkers have examined the structure of the hIAPP aggregates using solid-state NMR and showed that hIAPP aggregates consist of parallel β-sheets.¹⁶ Their conclusion is supported by electron paramagnetic resonance (EPR) spectroscopy and infrared reflection absorption spectroscopy (IRRAS) studies.^{17, 18} However, the orientation of the parallel β-sheets relative to the lipid membrane surface at the early stage of amyloid formation has yet to be established.

In our recent studies, we applied chiral SFG to investigating the early stage of the misfolding process of hIAPP at lipid/aqueous interfaces using phospholipids monolayer as a model membrane.^{19, 20} The phospholipid monolayer at amphiphilic interfaces has traditionally been used as biological membrane models.²¹ Although the monolayer only consists of one layer of lipid molecules, which is unlike the native bilayer membrane, the air phase is hydrophobic, mimicking the lipid environment. The simplified artificial model of lipid monolayer has been widely used to study the protein-membrane interactions at membrane surfaces, due to its stability and feasibility.²² By probing the chiral N-H stretch and amide I vibrational structures of the peptide backbone, we observed a conversion of hIAPP from disordered structures to α-helices and then to parallel β-sheets at a lipid/aqueous interface on the time scale of 10 hours in situ and in real time. At the end of the misfolding process, we observed a stable chiral amide I spectrum exhibiting a peak at 1620 cm⁻¹ and a shoulder at 1660 cm⁻¹ (Fig. 1), which are the characteristic B and A amide I modes of parallel β-sheets, respectively. In this study, we obtain the spectrum at a higher signal-to-noise level and introduce a quantitative method to analyze this spectrum to obtain the orientation of the parallel β-sheet hIAPP aggregate at the lipid/aqueous interface.

Our quantitative analysis is based on SFG theory^{23, 24} in conjunction with ab initio quantum chemistry calculations. Considering the symmetry of the A and B amide I modes of a parallel β-sheet, we first derive an analytical expression to describe the intensity of the B mode (1620 cm⁻¹) relative to the A mode (1660 cm⁻¹) as a function of hyperpolarizability and orientation of the parallel β-sheet. Subsequently, we establish a molecular model of the hIAPP aggregates based on the NMR structure. Using this model, we introduce a divide-and-conquer approach to calculate the hyperpolarizability tensor components. Compared to previously reported normal mode analyses of macromolecular structures, our divide-and-conquer approach uniquely includes all the possible strongly-coupled amide I vibrational modes and the inhomogeneous broadening effect of amide I bands due to the presence of various amino acid side-chains. Using the calculated hyperpolarizability and the derived expression of the intensity ratio of the B mode to the A mode, we simulate the chiral SFG spectra. The method thus represents a simple paradigm for simulating SFG spectra, based entirely on ab initio quantum chemistry methods. We then compare the experimental spectrum to the simulated spectra for the β-sheet aggregate model in various possible orientations, and obtain for the first time the orientation of hIAPP parallel β-sheet aggregates at the lipid/aqueous interface.

We find that the β-strands of the hIAPP aggregates are oriented at 48° relative to the surface (Fig. 1b). We speculate that the tilted insertion of a macromolecular β-sheet structure is likely to disrupt membrane integrity, which can potentially result in ion permeability across the cell membrane. This molecular picture is related to one of the proposed pathogenic mechanisms of type II diabetes. The proposed mechanism suggests that hIAPP induces ion permeability across cell membranes and becomes cytotoxic to islet β-cells of pancreas.^{10, 25, 26, 27} Hence, our work provides new insight at the molecular level into further investigation of this proposed pathogenic mechanism of type II diabetes and potentially other amyloid diseases.

Results

Chiral SFG spectrum of hIAPP aggregates

Fig. 1 shows a high signal-to-noise chiral SFG spectrum of amide I of hIAPP obtained using the psp (p-polarized SFG, s-polarized visible, and p-polarized infrared) polarization setting. The raw spectrum was processed as described previously.^{19, 20, 28} Two amide I vibration peaks appear in the chiral SFG spectrum. The strong peak at 1620 cm⁻¹ is ascribed to the amide I B mode, where the vibrational unit vector is perpendicular to the peptide backbone (inset in Fig. 1a). The shoulder peak at 1660 cm⁻¹ is ascribed to the amide I A mode, where the vibrational unit vector is parallel to the peptide backbone (inset in Fig. 1a). These two characteristic peaks indicate the presence of a parallel β-sheet structure in the hIAPP aggregates. The intensities of the two peaks were obtained by fitting the SFG spectrum using Eq. (1),

$$I_{\mathit{\text{SFG}}}\propto {\left|{\chi }_{\mathit{\text{NR}}}^{(2)}+{\displaystyle \sum _q}\frac{A_q}{{\omega }_{\mathit{\text{IR}}}-{\omega }_q+i{\mathrm{\Gamma }}_q}\right|}^2$$ (1)

where I_SFG is the SFG intensity, χ_NR is nonresonant 2^nd-order susceptibility, ω_IRis the input IR frequency, and A_q, ω _q, and Г_q are the amplitude, vibrational frequency, and damping factor for the q^th vibration mode, respectively. The fitting results for the parameters of A_q and Г_q for amide I B and A modes are shown in Table 1, where experimental errors were also reported. The relative intensity of the B to A mode is computed as

$$I_{B/A}={\left|\frac{A_B/{\mathrm{\Gamma }}_B}{A_A/{\mathrm{\Gamma }}_A}\right|}^2=4.8\pm 0.5$$ (2)

TABLE 1.

Parameters of the chiral amide I spectrum of hIAPP aggregates shown in Fig. 1.

Mode	A (a.u.)	ωq (cm−1)	Γ (a.u.)	χNR (a.u.)
A	−2.1 ± 0.16	1660 ± 1.3	16.0 ± 1.1	−0.02
B	3.9 ± 0.06	1622 ± 0.2	13.6 ± 0.3	±0.003

Relationship between chiral SFG spectra and orientation of parallel β-sheets

The relative chiral SFG intensity of the B mode to the A mode (I_B/A) can be analytically derived as a function of the orientation of hIAPP parallel β-sheets relative to the interface. The chiral SFG intensity measured using the psp polarization setting (I_psp) is related to the effective 2^nd-order susceptibility,

$$I_{\mathit{\text{psp}}}\propto {\left|{\chi }_{\mathit{\text{psp}}}^{(2)}\right|}^2$$ (3)

The effective 2^nd-order susceptibility results from a combination of susceptibilities of all the normal modes. For the q^th normal mode, the effective susceptibility is

$${\chi }_{\mathit{\text{psp}}}^{(2)}=L_{\mathit{\text{zyx}}}{\chi }_{\mathit{\text{zyx}},q}^{(2)}-L_{\mathit{\text{xyz}}}{\chi }_{\mathit{\text{xyz}},q}^{(2)}$$ (4)

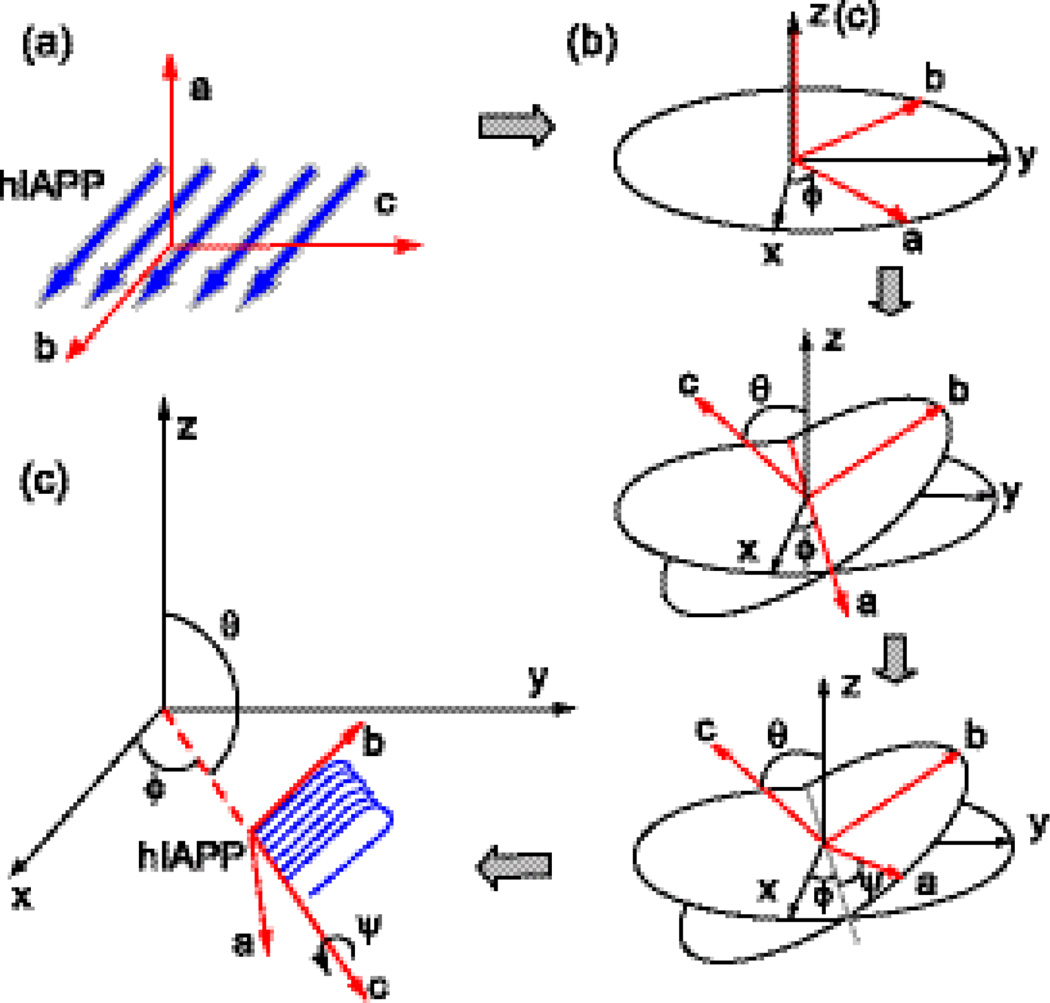
where L_zyx and L_xyz are the Fresnel factors, ${\chi }_{\mathit{\text{ijk}},q}^{(2)}$ (i, j, k = x, y, or z, which is the lab coordinate) is the tensor element of the macroscopic 2^nd-order susceptibility of the interface, defined by the vector sum of the microscopic vibrational hyperpolarizability β_lmn,q (l, m, n = a, b, or c, which is the molecular coordinate) via the Euler transformation:

$${\chi }_{\mathit{\text{ijk}},q}^{(2)}=N_s{\displaystyle \sum _{l,m,n}}\langle R_{\mathit{\text{il}}}{R}_{\mathit{\text{jm}}}{R}_{\mathit{\text{kn}}}\rangle {\beta }_{\mathit{\text{lmn}},q}$$ (5)

where N_s is the number density of the chromophores, 〈R_ilR_jmR_kn〉 is the average product of the Euler transformation matrix (see Supplementary Materials) for the projection from the molecular coordinate (a, b, c) onto the lab coordinate (x, y, z), and ϕ, θ, and Ψ are Euler angles defined in Fig. 2b. The chiral susceptibility elements, ${\chi }_{\mathit{\text{zyx}}}^{(2)}\text{ and }{\chi }_{\mathit{\text{xyz}}}^{(2)}$ (see Supplementary Materials), are obtained by an integration of the in-plane rotation angle ϕ from 0 to 2π as discussed by Simpson et al.²³ Hence, the effective 2^nd-order susceptibilities for the A modes (χ_psp,A) and B modes (χ_psp,B) are functions of θ, Ψ, and the β_lmn,q, elements. These functions can be simplified by eliminating the zero β_lmn,q elements and setting the Euler angle θ = π/2. The zero β_lmn,q elements are determined by the symmetry and the selection rule of SFG: only the vibrational modes that are both IR and Raman active are SFG active, as described by

$${\beta }_{\mathit{\text{lmn}},q}\propto \frac{\partial {\alpha }_{\mathit{\text{lm}}}}{\partial Q_q}\frac{\partial {\mu }_n}{\partial Q_q}$$ (6)

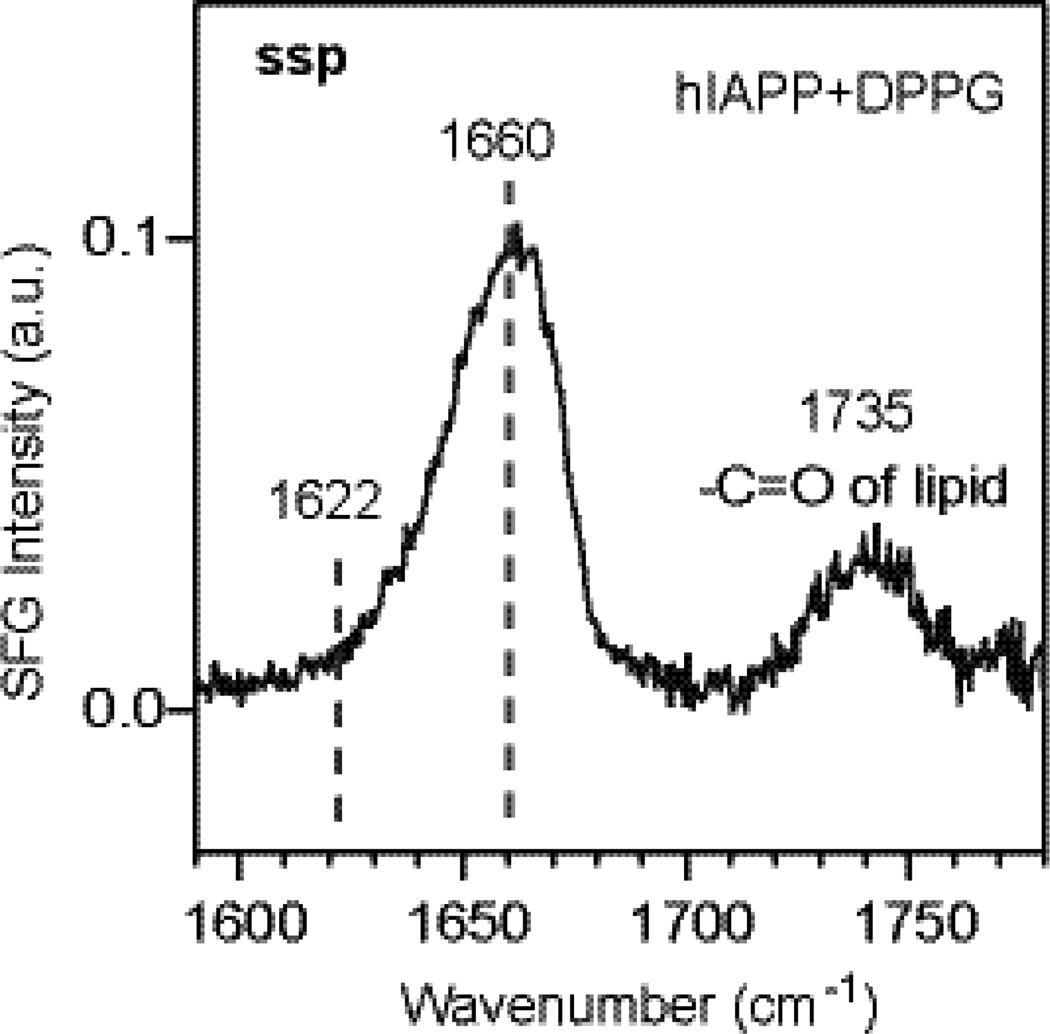
where α_lm and μ_n are the polarizability and dipole moment, respectively, and Q_q is the normal mode coordinate. The parallel β-sheet structure adopts C₂ symmetry, and the non-zero tensor elements of β_lmn,q are β_aab, β_ccb, β_acb=β_cab, and β_bbb for the A mode, and β_abc=β_bac, β_cbc=β_bcc, β_cba=β_bca, and β_aba=β_baa for the B mode.²⁹ The θ angle is set to π/2 such that the c axis is parallel to the surface (Fig. 2). This orientation is in agreement with the IRRAS study by Winter et al.¹⁸ It also agrees with our achiral spectrum of the hIAPP aggregates obtained using the ssp polarization setting (Fig. 3). The achiral spectrum shows only a peak at 1660 cm⁻¹ corresponding to the A mode, but no peaks at 1622 cm⁻¹ corresponding to the B mode (See Supplementary Materials). The ssp achiral SFG is sensitive to the vibrational mode whose dipole moment has the vertical component to surfaces. Thus, the absence of the B mode in the achiral SFG spectrum indicates that the dipole moment corresponding to the B mode (1622 cm⁻¹) is parallel to the interface, suggesting that the molecular c-axis (Fig. 2b) is parallel to the interface, i.e., θ = π/2. Subsequently, χ_psp,A and χ_psp,B, can be simplified to

$${\chi }_{\mathit{\text{psp}},A}^{(2)}=\frac{1}{2}{L}_{\mathit{\text{zyx}}}{N}_s\langle {\text{cos}}^2\psi \rangle {\beta }_{\mathit{\text{acb}},A}$$ (7)

$${\chi }_{\mathit{\text{psp}},B}^{(2)}=-\frac{1}{2}{L}_{\mathit{\text{zyx}}}{N}_s\left\{\langle {\text{sin}}^2\psi \rangle {\beta }_{\mathit{\text{bca}},B}+\left(\langle {\text{cos}}^2\psi \rangle -\langle {\text{sin}}^2\psi \rangle \right){\beta }_{\mathit{\text{bac}},B}\right\}$$ (8)

Hence, the relative SFG intensity of the B mode to the A mode is

$$I_{B/A}={\left|\frac{{\chi }_{\mathit{\text{psp}},B}^{(2)}}{{\chi }_{\mathit{\text{psp}},A}^{(2)}}\right|}^2={\left|\langle {\text{tan}}^2\psi \rangle \frac{{\beta }_{\mathit{\text{bca}},B}}{{\beta }_{\mathit{\text{acb}},A}}+\left(1-\langle {\text{tan}}^2\psi \rangle \right)\frac{{\beta }_{\mathit{\text{bca}},B}}{{\beta }_{\mathit{\text{acb}},A}}\right|}^2$$ (9)

Because I_B/A is an experimental observable, once the hyperpolarizability tensor elements β_bca,B, β_bac,B and β_acb,A are known, the orientation of the parallel β-sheet (Ψ) can be determined.

Fig. 2.

(a) Definition of molecular coordinates (a, b, and c) of a parallel β-sheet, (b) Euler transformation from the molecular coordinate (a, b, and c) to the lab coordinate (x, y, and z). (c) Orientation of the β-sheet at θ = π/2 and ϕ integrated from 0 to 2π.

Fig. 3.

The achiral ssp spectrum of the hIAPP aggregates. The 1660-cm⁻¹ peak and 1735-cm⁻¹ peak are assigned to the A amide I mode of parallel β-sheet, and carbonyl stretch of lipid, respectively.

Computation of hyperpolarizabilities: a divide-and-conquer ‘nearest-neighbor’ approach

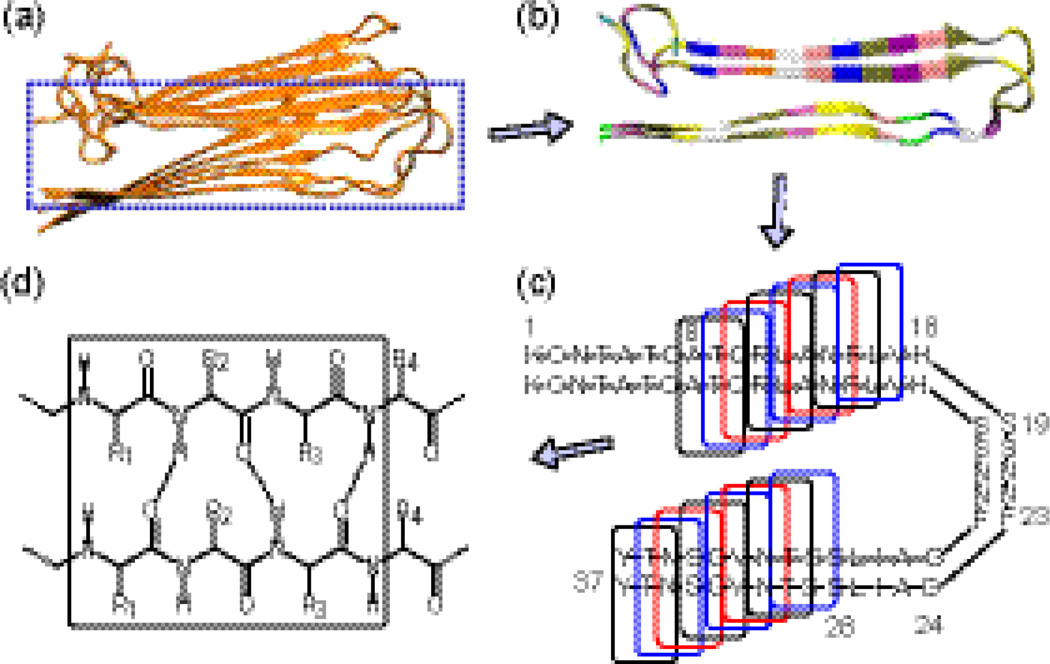
We computed hyperpolarizability elements using a molecular model of the parallel β-sheet structure. The model is built by two hIAPP molecules extracted from the NMR-structure (Fig. 4a). The β-sheet was divided into two β-sheet regions, the upper one (amino acid 8–17) and the lower one (amino acid 28–37). These two regions were subsequently subdivided into 16 partially overlapping tri-peptide pairs (tpp) (Fig. 4b–c). The covalency of the dangling bonds in the fragments was completed according to the link-H atom scheme, forming amine and amide groups in the N- and C-terminus ends, respectively (Fig. 4d). The geometry of each tpp was optimized, subject to the constraint of fixed backbone dihedral angles to preserve the β-sheet configuration. Energy minimization and normal mode analysis were then performed at the density functional theory (DFT) level, using the B3LYP functional and the 6-31G* basis set. Dipole derivatives of each vibrational mode were obtained using the keyword ‘iop(7/33=1)’ during a frequency calculation, and polarizability derivatives were obtained by performing the Raman vibrational analysis with the ‘polar’ keyword. Here, all of the calculations were performed using the Gaussian 03 program.³⁰

Fig. 4.

(a) The NMR structure of hIAPP aggregates. (b) Two hIAPP molecules extracted from the NMR structure. (c) The upper and lower β-strands subdivided into 18 subunits. (d) Each subunit containing six amino acids as a tri-peptide pair for ab initio normal mode analysis.

The ab initio normal mode analysis of the 16 tpp fragments yielded a total of 96 amide I normal modes, since each tpp includes 6 C=O groups and each C=O stretching mode has a single degree of freedom in vibration. The Supplementary Materials provides a detailed description of the amide I vibrational modes, which are classified into the A- and B- types according to the angles between the normal mode dipole derivatives and the peptide backbone axis. Here, the normal mode analysis was performed for the ttps in the gas phase to model the amide I modes in the experiment, as the amide I vibrations in the experimental condition were expectedly exposed in a low dielectric environment, where the amide I groups were embedded inside the hIAPP aggregates and were not directly in contact with the water or lipid molecules. In additional, the calculated vibrational frequencies were scaled by calibrating to the experimental peak of the amide I B mode to account for the influence of weak dielectric environment. As shown in the literature,³¹ the B3LYP/6-31G* usually has an uncertainty of ~2% for the scaling factor. This uncertainty is based on the calculation results of many different categories of molecules. Here, the vibrational analysis is performed for a specific category of molecules (i.e. peptides), thus the calculation error could be systematic (i.e. over-estimation of the frequencies). As the calculated frequencies are scaled by a common scaling factor to calibrate the experimental peak at 1622 cm⁻¹, the final calculation error of frequencies in the specific region of amide I bands could be fairly small compared to the experimental spectra.

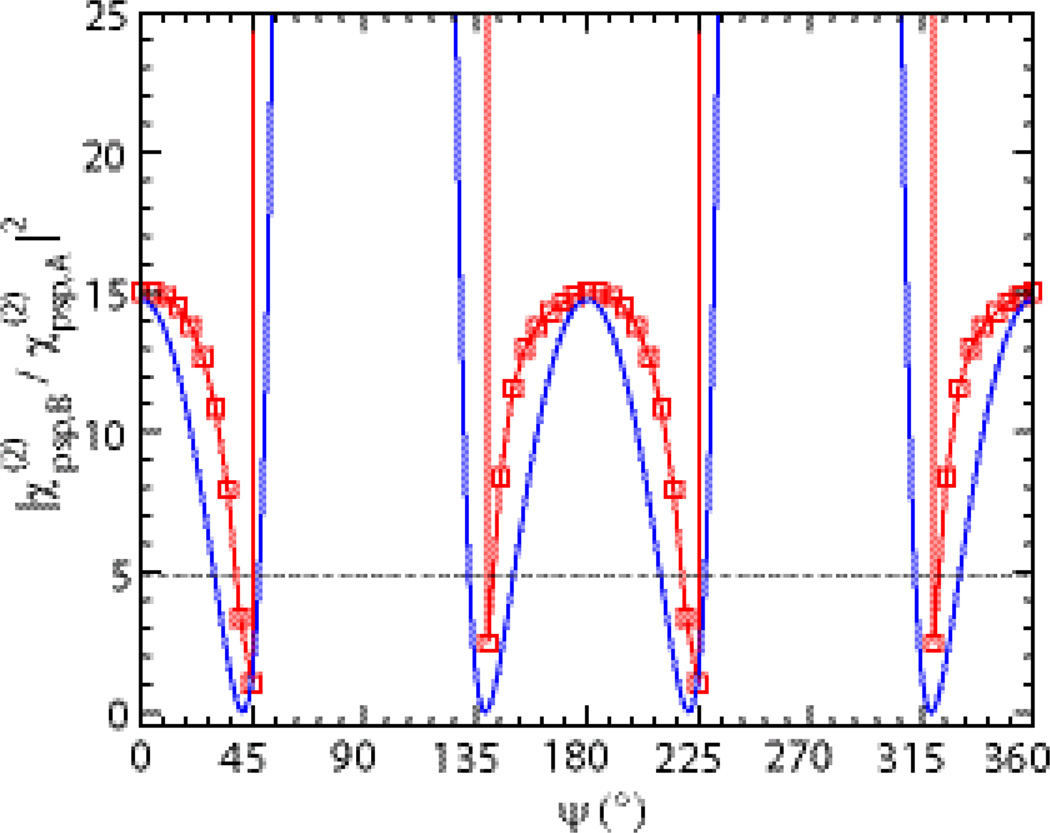
Based on the normal mode analysis, the β_lmn,q elements for each amide I mode were calculated using Eq. (6). The effective hyperpolarizability elements β_bca,B, β_bac,B and β_acb,A of the B and A modes were obtained from the calculated spectra of β_lmn components (see Supplementary Materials), which yields β_bca,B/β_acb,A = 1.2 and β_bac,B/β_acb,A = −3.8. According to Eq. (9), the relationship between I_B/A and ψ has a periodicity of π, as shown in the blue curve of Fig. 5. From the experimental SFG spectrum of hIAPP aggregates (Fig 1a), we obtained I_B/A = 4.8 ± 0.5 (see Supplementary Materials). By drawing a line of I_B/A = 4.8 (the dotted line) in Fig. 5, we find 4 possible ψ-angles within the period of π: 30°, 48°, 132°, or 150°, with an error of ± 1°. The error was estimated based on Eq. (9) (i.e. blue curve in Fig. 5) by the changes of the ψ-angles as I_B/A = 4.8 varies within the experimental error (i.e. from 4.3 to 5.3). Here, the estimated error is small because in the region of I_B/A = 4.8 ± 0.5, the angles are not sensitive to the variation of I_B/A. In the following, we will simulate the whole chiral SFG spectra using these 4 possible ψ-angles and then compare the simulated spectra with the experimental spectrum to determine ψ.

Fig. 5.

Square of the ${\chi }_{\mathit{\text{psp}}}^{(2)}$ ratio of the B-mode to the A-mode versus orientation angle ψ. The blue curve is obtained analytically using Eq. (9), while the red curve is obtained numerically using Eq. (S6) (see Supplementary Materials).

Simulation of chiral SFG spectra

The whole chiral SFG spectrum was simulated based on the calculated β_lmn, using the following steps. First, for a particular set of orientation angles (ϕ, ψ, θ), the 2^nd-order susceptibilities of each normal mode $({\chi }_{\mathit{\text{ijk}},q}^{(2)}(\varphi ,\psi ,\theta ))$ were computed from β_lmn,q via the Euler transformation using Eq. (5), with the transformation matrix that was not averaged. Second, since ϕ = 0–2π and θ = π/2, the ψ-dependent ${\chi }_{\mathit{\text{ijk}},q}^{(2)}$ were obtained by averaging over ${\chi }_{\mathit{\text{ijk}},q}^{(2)}(\varphi ,\psi ,\theta )$ with a complete set of ϕ-angles (here, ϕ is sampled numerically very 5° from 0 to 360°) using

$${\chi }_{\mathit{\text{ijk}},q}^{(2)}(\psi )={\displaystyle {\int }_0^{2\pi }}{\chi }_{\mathit{\text{ijk}},q}^{(2)}(\varphi ,\psi ,\theta =\pi /2)d\varphi$$ (10)

Then, from ${\chi }_{\mathit{\text{ijk}},q}^{(2)}(\psi )$, the effective susceptibilities ${\chi }_{\mathit{\text{psp}},q}^{(2)}$ were calculated using Eq. (4), where the Fresnel factors L_zyx and L_xyz, are 0.1927+i1.4739×10⁻⁵ and 0.2157−i1.9184×10⁻³, respectively, as determined by the geometry of the SFG setup.²⁸ Subsequently, we introduced a Gaussian function to account for the inhomogeneous broadening effect on ${\chi }_{\mathit{\text{psp}},q}^{(2)}$ for each normal mode. Thus, the overall effective susceptibility was calculated by

$${\chi }_{\mathit{\text{psp}}}^{(2)}(\omega )={\displaystyle \sum _{q=1}^{N_q}}g(\omega ,{\omega }_q){\chi }_{\mathit{\text{psp}},q}^{(2)}$$ (11)

which is frequency-dependent. Finally, the SFG chiral spectrum was computed by

$$I_{\mathit{\text{psp}}}(\omega )={\left|{\chi }_{\mathit{\text{psp}}}^{(2)}(\omega )\right|}^2$$ (12)

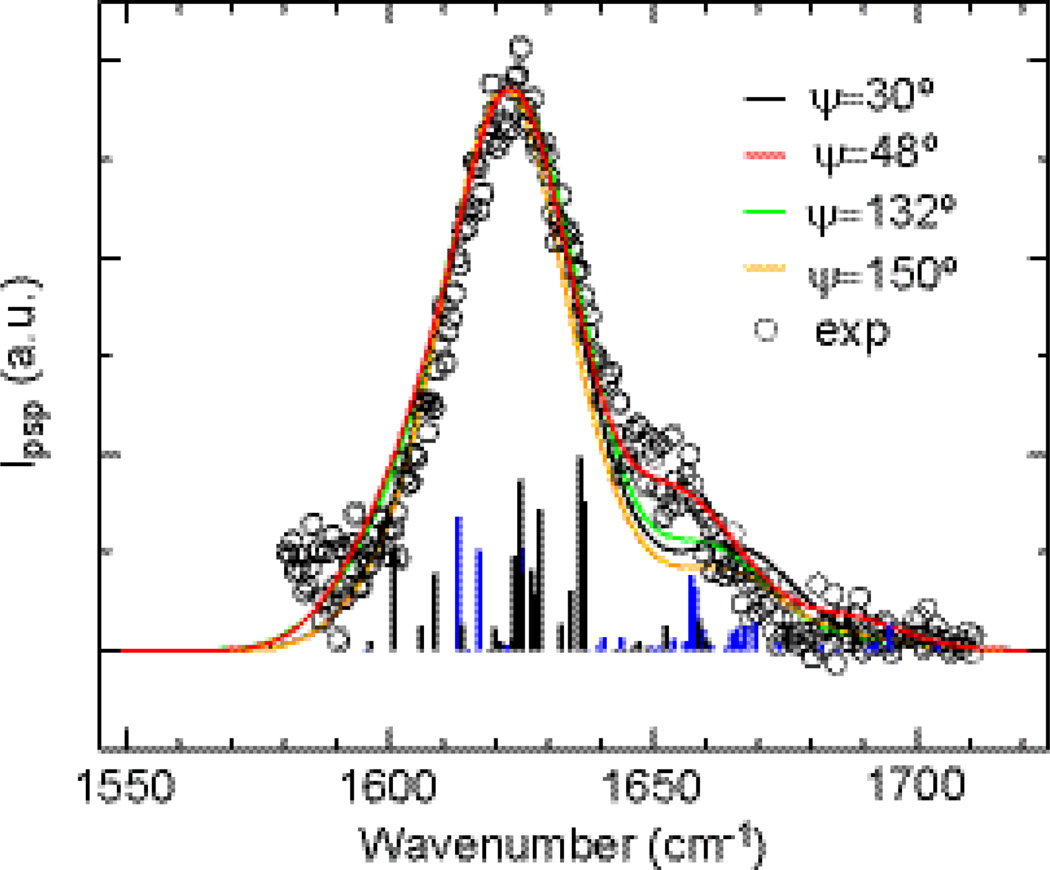
Fig. 6 shows the calculated SFG spectra for ψ = 30°, 48°, 132° and 150°, respectively, together with the experimental SFG spectrum. The calculated SFG spectrum with ψ = 48° shows the best agreement with the experimental data, suggesting that the hIAPP aggregates have a predominant orientation of β-sheets at ψ = 48 ± 1°. The analysis of the A and B mode contributions to the chiral SFG signals shows that the peak at 1622 cm⁻¹ originates predominantly from the B mode components (black bins), while the peak at 1660 cm⁻¹ results mostly from A mode components (blue bins), which is consistent with our assignment of peaks for the experimental SFG spectrum in Fig. 1a.

Fig. 6.

Comparison of chiral SFG spectrum (circles) and simulated spectra for ψ = 30° (black), 48° (red), 132° (green), and 150° (orange). The constituent B- and A-type normal mode components for ψ = 48° are represented as bins in black and blue, respectively, with heights given by the squared magnitude of the 2^nd-order susceptibility of individual normal modes. The calculated frequencies are scaled by 0.94 to facilitate the comparison with the experimental data.

The relationship of I_A/B versus ψ can also be obtained directly from the simulated SFG spectra with various ψ-angles (see Supplementary Materials). The red curves (with squares) in Fig. 5 shows the plot of I_B/A versus ψ that was obtained by the direct numerical simulation. On the other hand, the blue curve is the analytical description of I_B/A versus ψ (Eq. (9)) derived from the chiral SFG theory. The consistency between the red curve and the blue curve indicates that the ab initio analysis is consistent with the analytical expression derived from the chiral SFG theory. The ab initio simulation method on the basis of the divide-and-conquer ‘nearest-neighbor’ approach explicitly includes the couplings between nearest-neighbored amide-I vibrational modes and the inhomogeneous broadening of amide I bands due to side-chain interactions. As a step forward, this approach enables us to accurately predict the shape of the whole chiral SFG spectra of the protein secondary structures,

Absolute orientation of hIAPP aggregates

Because the intensity signal has a periodicity of π (Fig. 5), both ψ = 48° and 228° are possible orientation of the β-sheet structure at the lipid/aqueous interface. However, only ψ = 48° is consistent with the molecular amphiphilic properties of the hIAPP β-sheet aggregate (Fig. 1). At ψ = 48°, the hydrophobic β-strands (gray in Fig. 1) are inserted into the lipid phase while the hydrophilic β-strands (green in Fig. 1) remain in the water phase. Moreover, the hydrophobic hairpin β-turn of the misfolded hIAPP is inserted into the lipid phase and the hydrophilic N- and C-termini to the aqueous phase.

Discussion

hIAPP aggregates at membrane surfaces

Using the divide-and-conquer ‘nearest-neighbor’ approach, we simulate the chiral SFG spectrum of the β-sheet hIAPP aggregate at the lipid/aqueous interface (Fig. 1a and Fig. 6). We build a molecular model to describe the orientation and position of membrane-bound hIAPP β-sheet aggregates by setting ψ equal to 48° and submerging the entire hydrophilic β-strand (residues 28–37) into the aqueous phase as shown in Fig. 1b.

The molecular model present in Fig. 1b is consistent with previous experimental findings. First, previous experiments showed the disulfide bond to be mildly perturbed upon membrane insertion,³² suggesting that it is in the aqueous phase. Second, residues 20–27 were previously shown in a hydrophobic environment;^{33, 34} in our model they are in the lipid phase. Third, Ramamoorthy et al. found that deprotonated His18 at pH=7.5 caused more disruption than protonated His18 at pH=6.0.³⁵ In our model, His18 inserts into the lipid phase, and deprotonation at high pH energetically favors the insertion, potentially causing more disruption to the membrane. Finally, negatively charged lipids are known to induce aggregation of hIAPP.^{7, 8} In our model, the positively charged Arg11 is level with the negatively charged lipid head groups, facilitating the electrostatic interactions. It is known that the electrostatic interactions between the negatively charged dipalmitoylphosphoglycerol (DPPG) and hIAPP is crucial for the binding of hIAPP on membrane surfaces and subsequent hIAPP-induced ion permeability of lipid membranes.^{8, 9} It is also known that the DPPG lipid can significantly accelerate the aggregation process of IAPP at surfaces,^{6, 7, 36, 37} and thus can be used as a model system for studying the mechanism. Indeed, when we replaced negatively charged DPPG with zwitterionic dipalmitoylglycerophosphocholine (DPPC), we did not observe any chiral amide I signals corresponding to the formation of parallel β-sheet at the lipid/aqueous interface 15 hours after the addition of DPPC to the hIAPP solution. This result suggests that the negative charge of DPPG is crucial for inducing the formation of β-sheet aggregates under our experimental conditions.

Biomedical implications

Our molecular model guides us to a better understanding of the origin of hIAPP pathogenesis. There is evidence that hIAPP misfolding into oligomers can induce ion permeability across the membrane and cause the death of β-cells, leading to type II diabetes. However, the molecular mechanism of the hIAPP-induced ion permeability is still controversial.^{8, 9} Currently, two kinds of models predominate. The first involves pores or channels formed by hIAPP oligomers, whose structures remain largely uncharacterized.^{14, 26} The second model implicates less specific structures of hIAPP, e.g., by detergent-like solubilization.⁸ Along this line, Engel et al. proposed that ion permeability is caused by the process of hIAPP aggregation, rather than any structurally well-defined hIAPP species.³⁸ In our studies, we observed the initial misfolding β-sheet product and obtained the orientation of the β-strands with 48° tilted to the surface, which could be informative in terms of understanding the disruption of membrane integrity by hIAPP. Recent studies by Vivcharuk et al show that protegrin-1 peptide, which is known to disrupt the integrity of membrane, also adopts a β-sheet structure and inserts into the membrane at 42 ± 12°, as revealed by MD simulation.³⁹ The orientation angle obtained in this studies, combined with our earlier kinetic studies using chiral SFG spectroscopy, allows us to synthesize the following hypothesis. Initially, hIAPP adsorbing onto the membrane surface is relatively unstructured. Upon interaction with the membrane, hIAPP folds into α-helical intermediates lying flat at the surface. The subsequent conversion of the α-helical intermediates into parallel β-sheet structures inserts hIAPP into the membrane at a highly tilted angle (~48°) that may be related to its disruption of membrane integrity. Although the correlation between orientation and membrane disruption remains to be explored, it offers helpful guidance to the investigation of the pathogenic mechanism for type II diabetes and potentially other amyloid diseases.

Probing early stages of amyloid aggregation by chiral SFG

Our study establishes an experimental and theoretical framework to probe the early stages of amyloid aggregation at the membrane surfaces. Increasing evidence indicates that the aggregation of many amyloid proteins is catalyzed by membranes, and cytotoxicity could be arise from the intermediates rather than the end-product fibrils. Hence, understanding early-stage aggregation on the membrane surface is vital. However, conventional methods cannot distinguish signals generated from the bulk and from interfaces, making it difficult to study the role of membranes. We showed earlier that chiral SFG detects the misfolding of hIAPP from α-helices to β-sheets in situ and in real time on membrane surfaces. Here, we demonstrate that chiral SFG can be used to obtain the orientation of the early β-sheet aggregates on membrane surfaces. Hence, chiral SFG can be a new approach for investigating molecular mechanisms of amyloid diseases and effects of drug candidates targeting the early aggregation intermediates on membrane surfaces.

Moreover, the chiral SFG approach developed here can be complimentary to IRRAS. Both IRRAS and SFG are among the very few spectroscopic methods that are capable of in situ and real-time kinetic studies using only micrograms of sample and sensitive to structures, conformations, and orientations at interfaces. However, when IRRAS was applied to study hIAPP aggregation at lipid/aqueous interfaces, only the orientation angle of θ (= 90°) could be determined, but not ψ.¹⁸ In contrast, SFG allows determination of both, θ (= 90°) and ψ (= 48°). Because SFG is a second-order coherent method utilizing both IR and visible beams, the polarization of the two incident beams in the SFG experiments can be individually controlled, providing an additional dimension for probing the interaction of light and molecules to reveal orientation at interfaces.

Ab initio approach for analyzing experimental chiral SFG spectra

Previously, several research groups reported observations of chiral SFG signals from various molecular systems and developed theory to quantitatively describe the observations. Shen and coworkers reported the first observation of chiral SFG signal detected from bulk pure chiral liquids using transmission geometry.⁴¹ Subsequently, Chen and coworkers detected chiral SFG from an anti-parallel β-sheet model peptide adsorbed at the polystyrene-liquid interface.⁴² The Geiger group studied the chirality of DNA,⁴³ while the Ishibashi group probed thin films of porphyrin aggregates using double-resonance chiral SFG.⁴⁴ Recently, we have observed both chiral N-H stretch and amide I signals from peptide backbones.^{19, 20} In theoretical developments, Shen et al. applied first-order perturbation theory to describe the chiral signal detected from bulk chiral liquid and found that the anti-Stokes Raman tensor is responsible for this bulk signal.⁴⁵ Simpson et al. also used perturbation theory to treat hyperpolarizability (β) near and off resonance.⁴⁶ Analyzing the symmetry of vibrational modes, they determined the nonzero β tensor elements and calculated χ⁽²⁾ of the interface by considering a surface with C_∞ symmetry.⁴⁷ They proposed that achiral molecules arranged into macromolecular chiral structure can generate surface-specific chiral SFG signals. Wang et al. also investigated the chiral χ⁽²⁾ elements and deduced equations describing their contribution to the effective SFG optical response.⁴⁸

Nonetheless, among all previous studies, only Chen et al. applied a quantitative approach to analyze experimental chiral SFG spectra of macromolecular structures to obtain molecular orientations. They computed the chiral SFG spectra for an anti-parallel β-sheet model peptide at the polystyrene/liquid interface by including four typical coupled amide I vibrational modes based on a model anti-parallel β-sheet structure containing four repeating peptide units.⁴⁹ They obtained the SFG hyperpolarizability of the repeating unit by summing over individual IR transition dipole moments and Raman polarizability tensors, where the IR transition dipole moments were calculated based on the experimental results by Marsh,⁵⁰ and the Raman polarizability tensors were calculated from the experimental Raman spectra of a uniaxial tetragonal aspartame crystal.⁵¹

Our study improves upon these methods by introducing a new divide-and-conquer approach for ab initio calculations of hyperpolarizability, allowing us to simulate chiral SFG spectra entirely ab initio for the first time. The approach complements several alternative methods previously proposed for interpreting the vibrational spectra obtained by 1D or 2D infrared, vibrational circular dichroism, and SFG methods,^{15, 29, 52–56} including calculations of normal modes for the individual amino acid residues, the infinite periodic method based on ideal repeating units of peptides,^{54, 56} calculations for small portions of anti-parallel and parallel β-sheets,^{29, 55} and the partial Hessian vibrational analysis.^{15, 52, 53} Our method starts with fragmenting the β-sheet regions into all possible combinations of nearest-neighbor tripeptide pairs. We calculate the chiral SFG spectra of the β-sheets aggregates ab initio from the constituent tri-peptide pair fragments, including computations of hyperpolarizability and normal mode analysis. Hence, our calculation takes into account the contributions of vibrational coupling and inhomogeneous broadening of protein side chains to the backbone amide I modes. While the divide-and-conquer approach is applied for elucidating the orientation of hIAPP aggregates at interfaces, our results suggest that the approach is applicable to other secondary structures, and potentially other biomacromolecules, such as DNAs and RNAs. Hence, the approach is expected to extend the applicability and capacity of SFG in quantitative analysis of biomolecular structures at interfaces, solving problems related biological processes associated with membrane surfaces and surface characterization of biomaterials and biosensors, and beyond.

Conclusions

We conclude that hIAPP aggregates adsorb to lipid/aqueous interfaces by orienting the parallel β-strands at 48 ± 1° relative to the interface. The orientation is determined by the amphiphilic properties of the β-sheet aggregates with the hIAPP hydrophilic and hydrophobic parts exposed to the aqueous and lipid phases, respectively. We speculate that this detergent-like behavior might be detrimental to the cell membrane integrity. The reported results demonstrate a general methodology to characterize the orientation of chiral biomacromolecular structures at interfaces by combining chiral SFG spectroscopy and a new ab initio divide-and-conquer strategy for quantitatively simulating the whole SFG spectra of self-assembled protein structures. The combined methodology should be valuable for characterizations of a wide range of systems at interfaces, including but not limited to secondary and tertiary structures of proteins, DNA and RNA, and non-native materials such as peptiomimics and chiral polymers.

Materials and Methods

We obtained the SFG spectra of β-sheets formed by hIAPP at the lipid/aqueous interface using a broad-bandwidth SFG spectrometer as previously reported.^{19, 20, 28} To obtain high-quality spectra, we further improved the resolution of SFG spectrometer from 17 cm⁻¹ to 7 cm⁻¹. The chiral SFG spectra were obtained using the psp polarization setting (p-polarized SFG, s-polarized visible, and p-polarized infrared), while the achiral SFG spectra were obtained using the ssp polarization setting (s-polarized SFG, s-polarized visible, and p-polarized infrared). The DPPG lipid was chosen because previous studies showed that the negatively charged lipids trigger fibrillization of IAPP at membrane surfaces,^{6, 18} and thus can be used as a model for cell membrane to study the mechanism for the binding of hIAPP to membrane and the aggregation of hIAPP.

A solution of hIAPP (Keck Facility, Yale University) was added to a phosphate buffer (10 mM, pH = 7.4) to a final concentration of 4 µg/mL. The hIAPP sequence is H₂N-KCNTATCATQRLANFLVHSSNNFGAILSSTNVGSNTY-CONH₂. After the addition of hIAPP, the DPPG lipid (Avanti, AL) dissolved in a mixture of chloroform and methanol (3:1) was added at an area per molecule of ~100 Ų/DPPG. The solvent was allowed to evaporate. The actual area per molecule of DPPG could be lower than the apparent value of 100Ų/DPPG if considering the adsorption of hIAPP aggregates to the interface. The incident 800-nm and IR beams are directed to the sample surface in a co-propagation configuration, with incident angles of 56° and 69°, respectively. The IR and 800 nm beams are focused slightly below the sample surface to avoid photo-damage to the sample. The achiral and chiral spectra were taken. The SFG spectra were monitored every hour until no spectral changes were observed, which took roughly 10 hours as shown previously.^{19, 20} The incident laser beams were unblocked only during data acquisition.

Abbreviations used

SFG

sum frequency generation

hIAPP

human islet amyloid polypeptide

tpp

tripeptide pair

EPR

electron paramagnetic resonance

IRRAS

infrared reflection absorption spectroscopy

DFT

density functional theory

DPPG

dipalmitoylphosphoglycerol

DPPC

dipalmitoylglycerophosphocholine