Abstract
The merging of the computational theory of mind and evolutionary thinking leads to a kind of rationalism, in which enduring truths about the world have become implicit in the computations that enable the brain to cope with the experienced world. The dead reckoning computation, for example, is implemented within the brains of animals as one of the mechanisms that enables them to learn where they are (Gallistel, 1990, 1995). It integrates a velocity signal with respect to a time signal. Thus, the manner in which position and velocity relate to one another in the world is reflected in the manner in which signals representing those variables are processed in the brain. I use principles of information theory and Bayesian inference to derive from other simple principles explanations for: 1) the failure of partial reinforcement to increase reinforcements to acquisition; 2) the partial reinforcement extinction effect; 3) spontaneous recovery; 4) renewal; 5) reinstatement; 6) resurgence (aka facilitated reacquisition). Like the principle underlying dead-reckoning, these principles are grounded in analytic considerations. They are the kind of enduring truths about the world that are likely to have shaped the brain's computations.
Keywords: acquisition, extinction, partial reinforcement, spontaneous recovery, renewal, reinstatement, resurgence, information theory, Bayesian inference
In the common view, learning is mediated by an association-forming mechanism. Because this mechanism solves every problem, the structure of a particular kind of problem is irrelevant. The only question is, What gets associated with what? There are many mathematical formulations of the associative learning, but one looks in vain in textbooks on learning for a mathematical characterization of the problems posed by associative conditioning paradigms. Mathematical learning theory in its associative form is like a theory of vision in the absence of a theory of geometrical optics.
From a rationalist perspective, learning is mediated by problem-specific computational mechanisms (Gallistel 1990; 1992; 1995). The theorist's first and most important challenge is to correctly characterize the problems that the mechanisms informing the animal's behavior have evolved to solve. What are the equivalent in various learning domains of the geometrical optics considerations in the domain of vision and the acoustics considerations in the domain of audition? The problems posed by Pavlovian and operant protocols do in fact have an identifiable mathematical structure that sets them apart from other learning problems: they are multivariate, nonstationary time series problems (Gallistel 1999; Gallistel 2003)
A second challenge to the theorist with a rationalist bent is to identify the optimal computational solution to those problems, taking proper account of the conditions under which they are optimal. These may not be the conditions in the protocol, in which case the behavior that emerges in response to the protocol is often not optimal. The protocol may be a round hole into which the animal attempts to fit a square strategic peg. The behavior observed may be far from optimal, because the protocol does not reproduce the conditions under which the behavioral strategy the animal deploys is optimal (Breland and Breland 1961).
Optimality plays a role in rationalist theorizing, because the rationalist materialist assumes that the computational mechanisms that mediate learning have evolved through natural selection, just as have, for example, the sensory organs. Evolution by natural selection is an optimizing process; it tends to find approximately optimal solutions given the constraints that constitute the selection sieve. These constraints include, of course, computational tractability and physical realizability. If a computation is not physically realizable in a behaviorally appropriate amount of time, then it cannot be mediating the observed behavior. That said, basic evolutionary principles justify the assumption that natural selection will favor mechanisms that compute behaviorally important parameters of the animal's environment quickly and accurately over mechanisms that compute them slowly and inaccurately. It is clear that evolution has optimized the sensory organs. Optimizing the front end of the information-gathering machinery would not confer much benefit if the processing that followed was sloppy, slow and inaccurate, relative to what was in principle possible.
Although different learning problems require different computations, some computations are very broadly useful, so they appear as constituents of many more problem-specific computations. Two of these broadly useful computations are the computation of entropy and Bayesian marginalization. To say that they are broadly useful computations is not to say that they are general purpose computations. Marginalizing a likelihood function is as specific a computation as is integrating velocity with respect to time or inverting a matrix. There may be a general-purpose learning mechanism, but there are no general-purpose computations.
The Basic Information-Theoretic Computation
If we take the function of learning to be the reduction of an animal's uncertainties about behaviorally important parameters of the experienced world, then we expect to find many cases in which an information-theoretic computation is part of the learning mechanism. In Pavlovian conditioning, for example, the information communicated by the onset of the CS reduces the animal's uncertainty about when the next US may be expected. Computing the information conveyed by a CS solves both the temporal pairing problem and the cue competition problem in classical conditioning (Balsam and Gallistel 2009; Balsam, Drew et al. 2010).
The computation of entropy is the basic computation in information theory. Entropy measures the uncertainty in a distribution of probabilities over a set of possibilities. It also measures the information available about those possibilities, because the information carried by a signal (or a correlate) is the reduction in receiver uncertainty that would be effected if the receiver fully extracted the information about the source from the signal. The information communicated to the receiver of the signal is the difference in the entropy of the receiver's estimate of the probabilities before and after the signal is received (Shannon 1948; Gallistel and King 2009).
The entropy, H, of a probability distribution is: , where pi is the probability of the ith possibility. The set of mutually exclusive and exhaustive possibilities for which non-zero probabilities are defined is the support for the distribution1.
Mutual information, joint distributions, conditional distributions and contingency
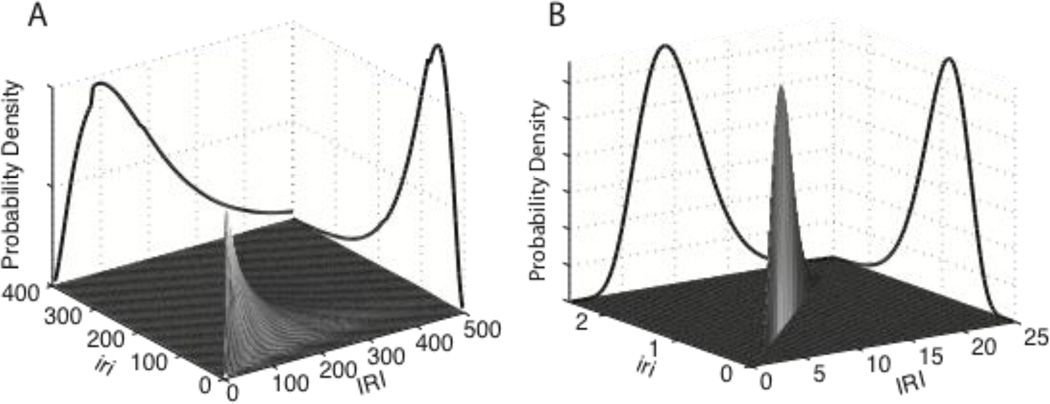
The mutual information between stochastic variables is the sum of the entropies of the two distributions minus the entropy of their joint distribution (Figure 1). The support for a joint distribution is the set of mutually exclusive and exhaustive combinations of the values for two variables.
Figure 1.
A. Illustrative joint probability distribution of inter-reinforcement interval (IRI) and average inter-response interval (iri = 1/λ), with the marginal distributions on the walls. The joint distribution was computed assuming a variable-interval (VI) 20s schedule of reinforcement and exponentially distributed inter-response intervals, with an expectation of 120 s (very slow, maximally random responding). The marginal distributions are the distributions of IRI and iri. They are not plotted to scale; for graphic purposes, they have been scaled down to make their height approximate the height of the joint distribution. The joint distribution and each of the marginal distributions contains a unit mass of probability. The marginal distributions may be thought of as produced by a marginalizing bulldozer that bulldozes the unit mass of probability in the joint distribution up against one or the other wall. This bulldozing is a metaphorical realization of the mathematical operation of integrating the joint distribution with respect to one of its dimensions (the dimension along which the bulldozer travels). The mutual information between IRI and iri is the combined entropy of the two marginal distributions minus the entropy of the joint distribution. In this example, the mutual information is 15.7% of the information (entropy) of the IRI distribution. The contingency between the behavioral measure (1/λ) and the duration of the inter-reinforcement interval (IRI) is weak, because the variation in the reinforcement-arming interval (the VI schedule) accounts for much of the variation in IRI. When smaller average inter-response intervals are assumed (that is, higher average response rates), the contingency decreases, because at very high response rates, the distribution of IRIs is almost entirely determined by the scheduling of response-contingent reinforcements at varying intervals after the preceding reinforcement, with the result that the stochastic variation in iri from one IRI to the next has very little effect on IRI. B. The joint distribution and the two marginals for an FR10 schedule (reinforcement of every 10th response). Here, the marginal distributions are to scale, because they have the same height as the joint distribution. All three distributions are the same curve in different planes, so, they all have the same entropy: HIRI = Hiri = Hj. Thus, the mutual information (the sum of the entropies of the two marginal distributions minus the entropy of the joint distribution) is 100% of the entropy of the IRI marginal distribution [(HIRI + Hiri − Hj)/HIRI = 1]--perfect contingency. Perfect contingency means that, given the average inter-response interval during an IRI, one can predict perfectly the duration of the IRI, because, with an FR(N) schedule, the IRI is always N times the iri.
Consider by way of illustration, two variables in operant experiments: 1) the inter-reinforcement interval (IRI), whose durations I denote by IRI; and 2) the average inter-response interval (iri) during an IRI, whose value I denote by iri.
λi is the rate of responding during the ith IRI; IRIi is the duration of that IRI; and ni is the number responses during that IRI.
The support for the joint distribution is the plane with orthogonal axes IRI and iri. The points on the plane represent the different possible combinations of the values of these two variables. The summation index, i, in the formula for entropy ranges over all the combinations (all the points in the support plane). The pi's are the relative frequencies with which those combinations occur.
The joint probability of the combination 〈IRIi, irij〉, that is, of an IRI of specified duration and a specified rate of responding, is the probability of an IRI of that duration times the conditional probability of observing the specified iri during an IRI of that duration:
The joint probability distribution is the complete set of joint probabilities, one for each possible combination.
A slice through a joint distribution parallel to one axis--when rescaled (normalized) to make it integrate to 1--gives a conditional distribution. A conditional distribution gives the probabilities of values of one variable under conditions where the value of another variable is held constant. If, for example, we make a slice parallel to the IRI axis at iri = 100 through the joint distribution in Figure 1A, we get the probability of different possible values for the IRI when the iri is 100 s. This conditional probability distribution differs from the unconditional probability distribution, which is the marginal distribution plotted on the IRI wall. It differs most conspicuously in that IRIs less than 100 have 0 probability in the conditional distribution, whereas they have substantial probability in the unconditional distribution. They have 0 probability in the conditional distribution because the interval between two reinforcements (the IRI) cannot be less than the interval between two responses (the iri). This constraint, arises from the fact that the reinforcements in a VI schedule are triggered by responses. Thus, the next reinforcement cannot come sooner than the next response. This constraint is the principal reason why there is a contingency between the average inter-response interval (iri) and the inter-reinforcement interval when a VI schedule is operative. It is this contingency that creates mutual information between the iri and the IRI. The information-theoretic measure of contingency is the ratio of the mutual information to the source information. It specifies the extent to which knowledge of the iri reduces ones uncertainty about the IRI. When there is 0 contingency, as with, for example, a variable time (VT) schedule of reinforcement, the iri does not alter the distribution of IRIs, hence there is no mutual information between the iri and the IRI. When there is perfect contingency, as with a fixed ratio (FR) schedule of reinforcement, the iri fully determines the IRI, the mutual information equals the source information, so their ratio is 1 (see Figure 1B).
The information-theoretic measure of contingency is quite generally applicable. To my knowledge, no generally applicable measure of behavior-reinforcement contingencies has previously been proposed, even though the concept of such a contingency has been central to operant thinking. Lord Kelvin (1883) wrote: "… when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely in your thoughts advanced to the state of Science…․" Those working in the operant tradition should embrace information theory if for no other reason than it provides a way of measuring something we have long been talking about.
The advantage of the information-theoretic measure of contingency over trial-based measures that have been proposed in the classical conditioning literature (Gallistel 2011) is that it does not depend the specification of "trials." An objectively justifiable specification of "trials" is generally not possible in operant paradigms and often not possible even in classical conditioning paradigms (Gallistel and Gibbon 2000 see also Gallistel, 2011). Unlike correlation, the information-theoretic measure does not assume linear dependence. To pursue this argument further, would digress to far from the focus of this paper. In the Supplementary Material, I show how to apply the information-theoretic measure to the response-reinforcement contingency, which is not the same as the contingency between iri and IRI, and I elaborate on it relevance to two other issues of fundamental importance, the temporal pairing problem and the assignment of credit problem.
The Basic Bayesian Computation
When an animal's behavior is governed by innate strategies for coping with uncertainties, the rationalist suspects that Bayesian inference may also be operative, because it is the optimal form of probabilistic inference (cf Courville, Daw et al. 2006).
Bayesian inference presupposes prior probability distributions in the minds/brains of animals. The prior probabilities play a strong role in determining behavior when there is little empirical evidence, as in the early stages of a conditioning protocol, the stages where an animal is learning the most. Bayesian priors provide a natural means for incorporating the guidance provided by both the evolutionary past and past experience into the processes that cope with an uncertain present.
Bayes Rule may be written,
In this notation, π(w) is the prior distribution. It specifies the probabilities (or probability densities) of different states of some aspect of the world, not taking into consideration some new data, D. The different possible states of that aspect of the world are symbolized by the variable w, which represents the support for the distribution, the set of mutually exclusive and exhaustive possibilities for which the function gives probabilities. L(w|D) is the likelihood function. It specifies the relative likelihoods of those different possible states of the world, given only the data, D. L(w|D, π(w)) is the posterior likelihood function; it specifies the relative likelihoods of those states after one has combined the information in the prior and the information in the likelihood function. When the posterior likelihood function is rescaled to make it integrate to one, it becomes the posterior probability distribution. The version of Bayes Rule given above omits this rescaling.
The Bayesian computation has two great virtues: 1) It adjudicates the trade-off between descriptive adequacy and descriptive complexity in building up behaviorally useful representations of past experience. This adjudication is unavoidable in good change-detecting algorithms, because, as explained below, detecting a change in a stochastic parameter requires deciding between competing descriptions of the history of the parameter's observed manifestation, descriptions that vary in their complexity. Because this fundamentally important aspect of Bayesian inference is not widely understood at this time a tutorial in the Supplementary Material, explains how it works. 2) The Bayesian computation makes optimal use of all available information in drawing inferences about the state of a world in which the animal constantly confronts uncertainties about behaviorally important parameters.
Bayesian framework and evolutionary considerations
The Bayesian framework encourages and rewards evolutionary thinking about learning mechanisms. Perhaps evolution created an association-forming mechanism and then rested on its laurels, leaving all else to experience; but it seems probable, to the rationalist at least, that many important principles are implicit in the computational structure of learning mechanisms because they confer advantages in coping with an uncertain world. An animal with a prior that assigns high probability to something that has been certain or highly likely since the paleozoic era will adapt faster to its environment than an animal that must learn the universal truths.
Problem-specific structure comes into the Bayesian computation in two ways. First, the support for the prior and the likelihood function (the x-axis and its higher-dimensional equivalents, see Figure S-2 in the Supplementary Material) is problem specific. In a navigation problem, where the uncertainty is about one's location, the support is the set of possible locations; in a cue-competition problem, where the uncertainty is about what predicts reinforcement, the support is the set of cues that might provide information about when to expect reinforcement. In spatial problems, the support is 2- or 3-dimensional space; in temporal problems, it is 1-dimensional. Second, the form of the likelihood function depends on the form assumed for the distribution from which the data are assumed to have come. This form often has some problem-specific, genetically specified structure. A similar point may be made regarding how problem-specific structure enters into information-theory computations: It does so via the support for the distributions, that is, the set of possibilities over which the inference is drawn. The support differs radically from one application of information theory to another.
Using Information Theory and Bayesian Inference
Among the uncertainties that animals face in conditioning experiments are these (CS--short for conditioned stimulus--refers to a possibly predictive cue; US--short for unconditioned stimulus--refers to a reinforcing event that it may predict; CR--short for conditioned response--refers to the measured anticipatory response that develops to the predictor):
What predicts and retrodicts what? And how well? As explained in the Supplementary Material, the mutual information between event times, for example between CS onsets and US onsets, measures the extent of the contingency between them. It determines the extent to which knowledge of the time at which one event occurred can reduce uncertainty about the time at which the other will (or did) occur. In operant protocols, the mutual information between response and reinforcement determines the extent to which a response can be expected to shorten the time to the next reinforcement.
How long can a perceived contingency be expected to last? In more technical language, how stationary is it?
On what is the contingency itself contingent? Does it hold only in the environment in which it has so far been experienced? Or, does it hold across a range of environments? Are there limits on that range?
On what are changes in contingency contingent? Are they signaled by changes in other variables?
To illustrate the relevance of information theory and Bayesian inference, I consider first the insight they provide in understanding two long-standing paradoxes surrounding the effects of non-reinforcement: 1) the fact that it does not increase the number of reinforcements required for a conditioned response to appear, and 2) the fact that it increases trials to extinction in proportion to the thinning of the reinforcement schedule (the partial reinforcement extinction effect).
In associative theorizing, the effects of non-reinforcement oppose the effects of reinforcement. They do so most straightforwardly by weakening the associations created by reinforcements (Rescorla and Wagner 1972; Mackintosh 1975). However, this "weakening" assumption has been mostly abandoned (see McLaren and Mackintosh 2000 for an exception) in the light of extensive experimental evidence that an association once established is never eliminated. Under the right circumstances, it can again control behavior (e.g., Pavlov 1927; Rescorla 1992; Rescorla 1993; Bouton and Ricker 1994; Delamater 1996; Rescorla 1996; Rescorla 1998). The view that now prevails is that non-reinforcements do not weaken the associations created by reinforcements; rather, they strengthen countervailing inhibitory associations (Pavlov 1927; Pearce and Hall 1980; Wagner 1981; Bouton 1993; Rescorla 1996).
But can non-reinforcements be treated as events, similar to reinforcements? Inhibitory associations are said to be produced by the pairing of a CS and a (or the?) no-US. There are, however, conceptual problems with the assumption that there is such a thing as a no-US (Gallistel 2011). An important property of a US (a reinforcement) is its onset time. The problem with the no-US construct comes into sharp focus when reinforcement during training is stochastic. How do associative theories explain extinction following training on VI (variable interval) or VR (variable ratio) or VT (variable time) schedules?--or following partial reinforcement of the CS in a Pavlovian protocol? In a VI protocol, the computer arms the reinforcement-delivering mechanism at a randomly determined interval following the harvesting of the previous reinforcement. In a VR protocol, the computer arms the mechanism after a randomly determined number of responses following the preceding reinforcement. In the VT protocol, the computer delivers reinforcement at a randomly determined interval after the previous delivery, regardless of what the subject does. In Pavlovian partial reinforcement, only randomly chosen CSs are reinforced. These stochastic reinforcement schedules are much closer to every day reality than are protocols in which there is no uncertainty about when or whether reinforcements will occur.
In associative theories, including what are called real-time associative theories (Wagner 1981; Sutton and Barto 1990; McLaren and Mackintosh 2000), reinforcements (aka USs) trigger an updating of the strengths of the associative bonds. And so do non reinforcements (no-USs)! Reinforcements are observable events, so there is an objectively specifiable time at which the updating occurs. The problem is that non-reinforcements do not actually occur, but the associative theorist is constrained to treat them as if they did. When reinforcement is stochastic, there is no observationally specifiable time at which a physically realized associative model should update associative strength in response to the "occurrence" of a non-reinforcement. When the time at which, or response after which, a reinforcement ought to occur is perfectly predictable, then theorists can and do assume that a non-reinforcement occurs when a reinforcement should have occurred but does not. However, in protocols in which the occurrence of a reinforcement is stochastic, there is no time (nor any response, nor any CS) at which (or following which) a reinforcement should occur. Thus, during extinction, there is no time at which, nor any response or CS following which, a non-reinforcement can objectively be said to have occurred. The updating in response to non-reinforcement must occur at a specific moment in time, but it is in principle impossible to say whether there was in fact a non-reinforcement at that moment or not. One may wonder how it is, then, that formalized associative models explain the consequences of non-reinforcements. In most cases, the answer is that a god outside the machine (the modeler) decrees the "trials" on which non-reinforcements occur.
Some models called real-time models (e.g., McLaren and Mackintosh, 2000) divide time into small bins called micro-trials. Associations are updated on every micro-trial. The problem in these models is that a no-US occurs on every micro-trial on which a US does not occur. Therefore, associations have an intrinsic half-life determined by the model's parameters. The association with reinforcement for any CS that endures for multiple micro-trials is decremented by some proportion on every micro-trial on which that CS is present but not reinforced, which is to say, on most of the micro-trials. Thus, for example, in a context-conditioning experiment in which the average inter-reinforcement interval is much longer than the half-life of an association, the strength of the association between the context and reinforcement sinks to 0 during many of the inter-reinforcement intervals.
One can put the problem with these real-time associative models in an operant context, by substituting 'response' for 'micro-trial. 'Suppose that the association between a response and reinforcement is decremented by some proportion whenever a response is not reinforced. The parameter of the model that specifies the decrement proportion determines how many unreinforced responses are required to reduce an association to half its initial value. This half-number is the equivalent of the half-life in a real-time associative model. If we choose a VR schedule with an expected number of responses between reinforcement substantially longer than this, the response-reinforcement association will often decay to 0 before the animal has made the number of responses required to produce the next reinforcement. As it decays, the tendency to continue to respond should get weaker (assuming that associative strength translates into an observable response frequency). This is not what happens: responding on VI and VR schedules is steady during the inter-reinforcement intervals. Similarly, conditioned responding to prolonged and/or partially reinforced CSs does not decay between reinforced trials (Prokasy and Gormezano 1979).
The problem of specifying when non-reinforcements "occur" may be the most intractable conceptual problem in associative theorizing about extinction, but there are several other problems. If the no-US is just as much an event as a US, why does pairing the CS and the no-US produce inhibitory associations to the US, rather than excitatory associations to the no-US. Should not an excitatory association form between the CS and the no-US, so that the CS comes to elicit whatever response it is that a (the?) no-US elicits? For still other problems with the no-US concept, see Gleitman, Nachmias and Neisser (1954).
Machado and Silva (2007) call for more careful conceptual analysis in psychology. Their call is germane when it comes to the treatment of non-reinforcement in theories of associative learning. These conceptual problems have long been apparent (Gleitman, Nachmias et al. 1954). Both Pavlov (1927) and Hull (1952) recognized that explaining the behavioral effects of events that failed to happen was a challenge for a theory based on the association-forming effects of event-triggered signals in the brain. The problem is not far to seek: the core idea in associative learning is that the learning mechanism is set in motion by the temporal pairing of the neural signals generated by events (see, for example, Gluck and Thompson 1987). When translated into neurobiological doctrine, this becomes "Neurons that fire together, wire together." Any theory founded on this idea is going to have trouble dealing with the behavioral consequences of non-events. It is going to have to treat non-events as if they were events; that assumption is going to pose difficult conceptual problems.
My focus, however, is on the empirical problems. If non-reinforcement has an effect opposed to that of reinforcement, then mixing non-reinforcements with reinforcements during conditioning should reduce net excitatory strength following any given number of reinforcements; hence, it should increase the number of reinforcements required before the conditioned response appears. Mixing reinforcements and non-reinforcement during initial conditioning should also result in a weaker (net) associative strength at the end of the conditioning phase; hence, fewer non-reinforcements should be required during extinction.
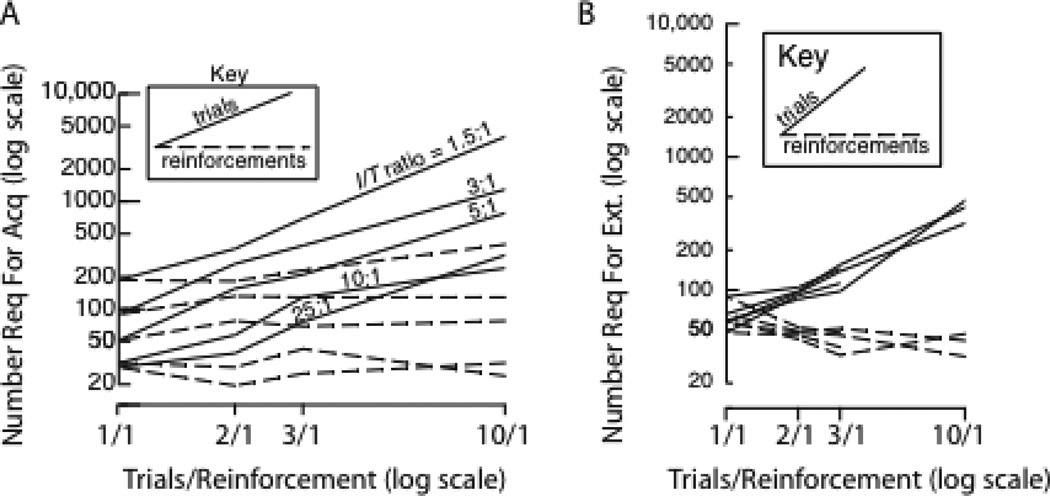
It has long been known that these predictions are false: Intermixing non-reinforced trials does not increase the number of reinforced trials required for the conditioned response to appear (Gibbon, Farrell et al. 1980; Williams 1981; Gottlieb 2004; Harris 2011)--see Figure 2A. Moreover, this intermixing does not hasten subsequent extinction. On the contrary, it prolongs trials to extinction in proportion to the admixture of unreinforced trials (Gibbon, Farrell et al. 1980; Gallistel and Gibbon 2000)--see Figure 2B. This partial reinforcement extinction effect has been known for the better part of a century (Humphreys 1939; Mowrer and Jones 1945; Katz 1955; Lewis 1960), and so has its theoretical importance: "The most critical problem facing any theory of extinction is to explain the effect of partial reinforcement. And, for inhibition theory, the difficulties are particularly great."--(Kimble 1961, p. 286)
Figure 2.
The lack of effect of partial reinforcement on reinforcements to acquisition and omitted reinforcements to extinction. A. The solid lines plot the number of trials required for the appearance of a conditioned pecking response in a pigeon autoshaping experiment as a function of the reinforcement schedule (trials per reinforcement) and the ratio between the intertrial interval (ITI) and the trial duration (T). The dashed lines plot the number of reinforcements required. Trials required increase in proportion to the reinforcement schedule, with the result that reinforcements required remain constant. B. Solid lines plot the number of unreinforced trials required to extinguish the conditioned as a function of the reinforcement schedule during the conditioning. Dashed lines plot the number of expected reinforcements omitted. Trials to extinction increases in proportion to the reinforcement schedule, with the consequence that the number of reinforcements omitted remains constant. The different lines are for different ratios between CS-US interval and the intertrial interval. This variable has no effect on trials to extinction, whereas it has a strong effect on trials to acquisition. (Reproduced from Gallistel and Gibbon 2000, Figures 8B Figure 14B, by permission of the American Psychological Association. Data first published in Gibbon, et al, 1980, and Gibbon et al, 1977)
From a rationalist perspective, neither result is paradoxical; they both follow from intuitive principles that would be expected to inform the structure of a mechanism optimized for solving non-stationary multivariate time series problems.
Partial reinforcement and acquisition
The lack of an effect of partial reinforcement on reinforcements to acquisition follows from the principle that the rate of conditioning (the inverse of trials to acquisition) is proportionate to what Balsam and Gallistel (2009) call the informativeness of the CS. The informativeness of a CS is the factor by which its onset reduces the expected time to reinforcement (the US). The greater this factor, the sooner the conditioned response appears. Balsam and Gallistel derive from this principle both cue competition and the dependence of the rate of conditioning on the relative proximity of the CS onset to the US onset (Balsam and Gallistel 2009; Balsam, Drew et al. 2010). Their derivation gives for the first time a quantitatively accurate account of the role of temporal pairing in Pavlovian conditioning. It is remarkable that the same principle explains both the data on temporal pairing and the data on cue competition. In associative theory, there is no conceptual connection between the temporal-pairing problem (the imagined "window of associability") and the cue competition problem.
This principle also explains why partial reinforcement does not affect the number of reinforcements required for the conditioned response to appear, as I now show. Following Balsam and Gallistel (2009), I assume that the problem facing the animal is to use available cues so as to reduce its uncertainty about when the next US may be expected to occur. The extent to which it is possible for a CS to reduce uncertainty about when the next US will occur is limited by the entropy of the US temporal distribution. This basal (contextual) entropy is the available information, the amount of information that could be communicated by the CS if CS onset eliminated altogether the subject's uncertainty about when the next US would occur.
On the assumption that USs in a given experimental context are approximately randomly distributed in time, the entropy per US is Hper US = log I̅US-US + k, where I̅US-US is the expected interval between USs (Balsam and Gallistel 2009). A continually reinforced CS reduces this uncertainty by the logarithm of the factor by which the expected interval to the next US is reduced by the onset of the CS. That factor is I̅CS-US/I̅US-US where I̅CS-US is the expected CS-US interval (the average interval from the onset of the CS to the onset of a US).
Partial reinforcement adds ambiguity and further uncertainty. The ambiguity arises because there are at least two different stochastic processes that may produce partial reinforcement. On the one hand, it may arise from randomness in the times of occurrence of USs relative to CS onsets and offsets. The partial reinforcement in Rescorla's truly random control (Rescorla 1968) is of this nature. In his experiment, a conditioned response to the CS appeared if and only if its onset signaled an increase in the rate of US occurrence and its offset a decrease. The random rate of US occurrence during the CS, however, was sufficiently low that there was no US during an appreciable fraction of the CSs. Thus, this was a partial reinforcement paradigm, albeit an unusual one.
In delay conditioning, US onset is coincident with CS offset, and both follow at a fixed interval following CS onset. Partial reinforcement adds uncertainty about whether the USs will occur at a time specified by CS onset.
The existence of two different explanations for the failure of a US to occur during every US is an example of the ambiguities that the brain of the animal must resolve one way or the other--on the representationalist assumption that the brain computes a useful description of the experienced world as a guide to future behavior. Bayesian considerations about the likelihood of "suspicious coincidences" relative to "typical2" times of occurrence will favor the second explanation in the delay conditioning paradigm and the first explanation in the Rescorla paradigm. However, either state of the world is a priori plausible until the animal has experiences that render the posterior likelihood of one state substantially greater than the posterior likelihood of the other.
Regardless of the stochastic process that produces partial reinforcement, it should not increase the number of reinforcements required for a CR to appear. On the temporal stochasticity model, deleting a fraction s − 1 of the reinforcements increases both I̅CS-US and I̅US-US by factor s, the schedule of reinforcement factor, so their ratio is unaffected. According to Balsam and Gallistel (2009), it is this ratio that determines the rate of acquisition. (This explains the effect of the ITI/T ratio seen in Figure 2A.)
If, instead, the subject represents US occurrences as occasioned by CS onset, with probability 1/S, then the uncertainty (entropy) surrounding the question whether the US will or will not occur at the CS-specified time is −log(1/S) = log(S). Thus, reinforcing only 1/S CS occurrences increases the uncertainty at CS onset by log(S). However, this intermittent CS reinforcement also adds log(S) uncertainty to the basal or contextual uncertainty, because it reduces the basal rate of US occurrence by S. The information communicated to the animal by CS onset is the difference in these two entropies. The log(S) term common to them both disappears from their difference.
In sum, one can use information theory to derive the important quantitative result about non-reinforcement from the principle that the informativeness of the CS determines the rapidity with which a CR appears. The result, which has been obtained in several different labs (Gibbon, Farrell et al. 1980; Williams 1981; Gottlieb 2004; Harris 2011), is that partial reinforcement does not affect the number of reinforcements required for the CS to appear (as shown by the flat dashed lines in Figure 2A). The result follows whether one computes the increase in entropy consequent upon partial reinforcement by time or by trials, and the derivation does not depend on parametric assumptions.
Partial reinforcement and extinction
The problem posed by extinction is non-stationarity: many CS-US and response-outcome contingencies are here today and gone tomorrow. The rationalist expects that an animal optimized for surviving in a non-stationary world will have approximately optimal computational mechanisms for detecting changes in stochastic parameters (Gallistel, Mark et al. 2001; Kheifets and Gallistel submitted). Any such mechanism will exhibit the partial reinforcement extinction effect, for an intuitively obvious analytic consideration. How we state this consideration depends, again, on the nature of the stochastic process we take to be at work: If USs are generated by a random rate process, then the lower the rate to begin with, the more time it will take to detect its decrease (Gallistel and Gibbon 2000). If, on the other hand, USs are occasioned by a CS with discrete probability 1/S, then the lower this discrete probability is to begin with, the more unreinforced CS occurrences will be required to detect its decrease (cf Haselgrove, Aydin et al. 2004; Courville, Daw et al. 2006). Thus, no matter how the brain figures it, whether by time or by trials (CS occurrences), if extinction is mediated by a computational mechanism that detects a decrease in either the rate or the probability of reinforcement, then partial reinforcement will increase time or trials to extinction.
The idea that the partial reinforcement extinction effect arises from the difficulty of distinguishing the extinction phase from the conditioning phase is an old one (Mowrer and Jones 1945; Kimble 1961, pp 318–329, see also Baum, this issue), but it has only recently been treated from a mathematical perspective (Courville, Daw et al. 2006). What follows is, I believe, the first quantitative derivation of the flatness of the dashed lines in Figure 2B, the results showing that the number of omitted reinforcements required to satisfy an extinction criterion is the same regardless of the partial reinforcement schedule during the training phase that preceded the extinction phase.
Extinction in a Bayesian Framework
Optimal change detection requires a Bayesian computation, because the question posed by change detection is whether the sequence of reinforcements so far experienced is better described by an encoding in which the stochastic parameter has changed or by an encoding in which it has not. The former encoding is more complex than the latter, because it uses more parameters to describe the experienced sequence. It is an analytic (hence, universal) truth that even sequences generated by an unchanging stochastic process will nonetheless be "better described" by a model that assumes changes, unless model complexity is taken into account. Thus, deciding which is the better description, change or no change, requires trading descriptive adequacy against simplicity. A conventional approach to deciding between competing models--testing a null hypothesis--does not provide a native means for adjudicating this trade-off; it does not correctly measure the relative likelihoods of competing descriptions; and it does not measure the strength of the evidence in favor of the simpler description when that is in fact the better one. The Bayesian computation does all three.
The no-change description of a random sequence uses a single parameter to describe it, namely, the p parameter of the Bernoulli distribution or the λ parameter of the Poisson process, depending on which stochastic model is assumed. The change description of the same sequence uses three parameters: the probability or rate before the change (pb or λb), the probability or rate after the change (pa or λa), and the change time or trial, tc, the point in the sequence where the change is assumed to have occurred. The dimensionality of the space in which a Bayesian prior distributes the unit mass of prior probability is the number of parameters in the description for which it is the prior. Thus, the more complex ("change") description distributes the unit mass of probability more diffusely, over a greater volume of possibilities. (See Supplementary Material for an illustration in the simplest case, where one pits a 0-dimensional prior (a point prediction) against a 1-dimensional prior (an interval prediction)).
If a one-parameter no-change model describes the sequence well, its marginal likelihood will be greater, because it has a less diffuse distribution of the unit mass of prior probability. It puts its money where the data imply the truth is. It does not waste prior probability. If, on the other hand, the sequence is better described by a model in which the p value changed at some point, then the marginal likelihood of the one-parameter description will be smaller than that of three-parameter description, because the overly simple no-change model puts 0 prior probability in the region of the parameter space where the data imply that the likelihood in fact lies. In this case, the simpler description places no bets in the part of the space where the likelihood resides, so it wastes likelihood (see Supplementary Material for further explanation and an illustration).
The effect of time and sequence length on the odds of a change
The Bayes factor, which gives the relative posterior likelihood of the competing descriptions of the data, is not the only relevant consideration when deciding whether there has been a change in a stochastic parameter. An optimal computation must take into account yet another analytic truth, namely, that the prior odds of a change increase with the length of the sequence considered. When the sequence is short relative to the expected number of trials (or expected interval) between changes, then the prior odds of its containing a change are low. If it is long relative to this expectation, then the prior odds that there has been a change somewhere in it are high. Thus, as a sequence grows longer in real time, the prior odds that it does contain a change grow higher. The growth of the prior odds of a change is independent of the pattern within the sequence; it depends only on its length. By contrast, the Bayes factor depends only on the pattern of events within the sequence. The posterior odds, which are the product of the prior odds and the Bayes factor, take both considerations into account.
In short, an approximately optimal change-detecting mechanism must have a prior distribution on the expected number of trials (or expected time) between the changes. The expectation of this distribution, which is the best estimate of the probability or rate with which changes occur, determines the growth of the prior odds that there has been a change as the length of the sequence increases (cf Gallistel et al under review).
In sum, optimal change-detecting computations bring into play two prior distributions: a prior on the rate or probability of reinforcement and a prior on the rate or probability of a change in this stochastic parameter. These priors will exert a strong influence on behavior early on, when the animal has little experience. However, the purpose of a prior is to become a posterior, that is, to be updated by experience so as to benefit both from relevant a priori considerations and from experience. Given appropriate priors, the posterior will soon be dominated by the effects of experience. Thus, in the long run experience determines the expectations of a Bayesian learner. However, learning focuses on beginnings, on early experience, for examples, the first encounter with reinforcement-predicting events in new environments and the first encounter with changes in reinforcement probability or frequency in those environments. In the early stages of new experiences, priors strongly influence expectations--and expectations strongly influence behavior. So we need to think about what these priors might be.
For the prior distributions on the rate or probability of US occurrence, one may reasonably conjecture the use of an uninformative prior that has a minimal effect on the posterior, making the result of the Bayesian computation maximally sensitive to experience. This conjecture rests on analytic considerations, not on speculation about the environment in which mammals evolved. Analytic considerations would suggest so-called Jeffrey's priors. A Jeffrey's prior is invariant under re-parameterization. In the present case, for example, this would mean that the results of the computation are the same whether the prior (hence, also the posterior) distribution is defined over λ, the rate of US occurrence, or over I̅ = 1/λ, the expected interval between USs. These analytically-arrived at priors may be thought of as the mathematically correct and inferentially optimal way for a rational agent to represent its uncertainty about a parameter of the world in the absence of any relevant experience.
The prior distribution on the rate or probability of a change in the rate or probability of a US is more problematic, which may also make it more theoretically interesting. It does not make sense to use uninformative Jeffrey's priors here, because these have inappropriate expectations and modes. The conjugate prior for the Bernoulli distribution is the beta distribution. The Jeffreys prior is a beta distribution with parameters α = β= 1/2. With this prior, the naive subject would expect a change on every other trial. Sequences in which changes were that frequent would be indistinguishable from sequences generated by a Bernoulli process with a stationary p.
Regardless of the assumption we make about the prior distribution on the trial-by-trial probability of a change, the detectability of a change will depend on its size; the lower the probability to begin with, the smaller the change when it drops to 0. Figure 3 shows this quantitatively; it plots the exponential growth of the posterior odds of a change in Bernoulli sequences as a function of the initial probability (the schedule of partial reinforcement) and the duration of the initial sequence (length of training), after different amounts of training, and for different assumptions about the prior odds. In this computation, the estimate of the expected number of trials between changes was scaled by the length of the sequence. Thus, as the sequences grew, the estimate of the number of trials expected between changes grew correspondingly. However, the computation began only with the last reinforcement. This is unrealistic from the point of view of a subject's brain, since it has no way of knowing that it has seen the last reinforcement. A subject using the even-odds prior (right column of Figure 3), would have detected many bogus decreases and increases during training. With this prior, it is even odds that a sequence of only two trials contains a change and even odds that a sequence of only four trials contains a change, and so on. Thus, with this prior, the change-detector would be too sensitive to purely stochastic runs.
Figure 3.
The odds that there was a decrease in the probability of reinforcement after the last reinforcement, as a function of the number of unreinforced trials (extinction trials), following training on continuous or partial reinforcement schedules. The trials/reinforcement during training are written by the curves in the upper left panel. Top row: minimal training (12 reinforcements); bottom row: extensive training (96 reinforcements). Left column: prior odds scaled so that in a sequence of any given length, there is a 1 in 10 chance that it contains a change; right column: even odds of a change in a sequence of a given length. Dashed horizontal lines indicate even odds. The trials required to reach this criterion increase roughly in proportion to the schedule parameter.
Figure 4 shows that regardless of our assumption about the prior probability of change, the expected number of trials to detect a decrease to 0 in the rate or probability of reinforcement increases in an approximately scalar manner with the dilution factor in a partial reinforcement training schedule. Thus Figure 4 shows the derivation of the experimental result shown in Figure 2. This derivation, like the previous derivation, does not depend on any assumption about the values of free parameters.
Figure 4.
Trials to extinction versus partial reinforcement schedule during training. These plots are plots of the trials at which the curves in the bottom panels of Figure 3 intersect the even odds criterion, that is, the trial during the extinction phase at which the odds shift in favor of the conclusion that there has been a decrease in the rate or probability of reinforcement. These plots approximately replicate the empirical results plotted in Figure 2B, although these are slightly concave upward, whereas the empirical plots are slightly concave downward. To a first approximation, a Bayesian change computation, based on the assumption that extinction is the consequence of an approximately optimal change-detecting computational mechanism, predicts quantitatively the relation between partial reinforcement and trials to extinction shown in Figure 2B.
Sequelae
The rationalist proposal is that extinction is mediated by a computational mechanism that detects changes in the rate or probability of reinforcement. In what follows, I give a rationalist theory for the unfolding behavioral consequences of this detection (the sequelae). Unlike those advanced above, these explanations do not include the mathematical derivation of experimental results, because the available results are not, I suggest, of a kind to support such derivations. The experimental results derived above were empirical trade-off functions. To my knowledge, there are no such results for the phenomena now to be discussed. The results now to be discussed are all psychometric functions. There is an important difference between trade-off functions and psychometric functions:
Psychometric functions and trade-off functions
A function that gives performance as a function of a stimulus (or protocol) parameter is a psychometric function. An example is the frequency-of-seeing function in visual psychophysics; it plots the probability that a subject detects a spot of light as a function of the intensity of the spot. The functions plotting number of conditioned responses in sessions following the first extinction session are also of this kind. These are the functions one sees in the literature on spontaneous recovery, renewal, reinstatement, and resurgence.
Trade-off functions, by contrast, specify combinations of conditions that produce a fixed behavioral effect. The scotopic spectral sensitivity function is the best-known example in vision. It specifies the combinations of wavelength and light intensity that produce the same frequency of seeing in the dark-adapted human observer.
The empirical functions explained by the preceding mathematical derivations were trade-off functions. The first specified the combinations of number of reinforcements and partial reinforcement values that produce the first significant increase in the probability of an anticipatory (i.e., conditioned) response in an autoshaping protocol. The second specified the combinations of partial reinforcement values during training and trials during extinction that produced the first significant decrease in the probability of a conditioned response.
Almost all of the theoretically important empirical functions in sensory psychophysics are trade-off functions, because trade-off functions reveal quantitative properties of underlying mechanisms, whereas psychometric functions rarely do. Psychometric functions are the composition of all the functions that intervene between the stimulus (protocol parameter) and the observed behavioral effect, so their quantitative form does not reveal the quantitative form of any one intervening process. Their form depends on innumerable different processes sensitive to a variety of extraneous factors, so there is little theoretical insight to be gained from modeling psychometric functions. Such modeling may provide a compact summary of the experimental results, but it rarely reveals quantitative properties of underlying mechanisms.
Trade-off functions, by contrast, reveal the quantitative manner in which stimulus (or protocol) parameters combine, at the stage of processing at which they combine, no matter how far back in the causal change that stage is (see Gallistel, Shizgal & Yeomans, 1981 for lengthy explanation and many examples). That is why the scotopic spectral sensitivity function gives the absorption spectrum of rhodopsin. The wavelength and intensity of light incident at the retina combine to determine the amount of rhodopsin isomerized in rod outer segments. A quantitative property of the rhodopsin molecule--its absorption spectrum--is revealed by the spectral sensitivity function of the human psychophysical observer, even though this light-sensitive molecule operates at the very first stage of a very long and almost entirely unknown chain of causes and effects, ending in the observed behavior of the psychophysical observer. The only condition that must be satisfied in order that a behaviorally determine trade-off function be the same as the trade-off function determined directly on the combinatorial mechanism itself is the monotonicity of the arbitrarily many function that intervene between the combinatorial stage and the observed behavioral effect (Gallistel, Shizgal et al. 1981).
One could obtain trade-off functions that shed light on quantitative properties of the mechanisms that mediate the sequelae to extinction. It is known, for example, that the strength of spontaneous recovery depends on both the interval between training and extinction and the interval between extinction and the test for spontaneous recovery (Rescorla 2004; Myers, Ressler et al. 2006; Johnson, Escobar et al. 2010). A trade-off function would specify the combinations of these two intervals that produce the same amount of spontaneous recovery. The experiment is tedious but doable.
Different trajectories for different CRs
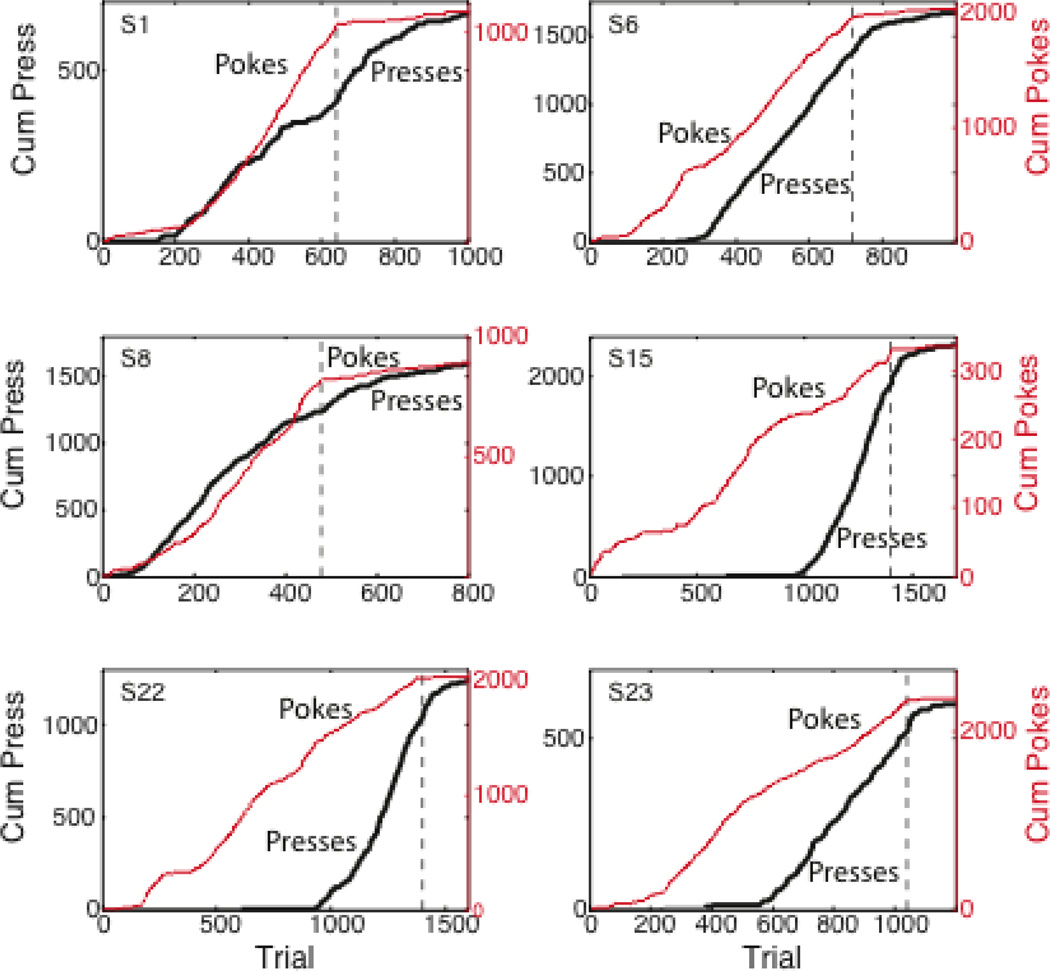
One puzzle about the behavior observed during extinction is why some conditioned responses persist long after the subject has given clear evidence of having detected the decrease in reinforcement rate or probability, while others cease more or less immediately. The number of trials to extinguish anticipatory poking into the feeding hopper in response to the extension of a lever in a continuously reinforced mouse autoshaping experiment occurs quickly and abruptly (Figure 5, red plots). Trials to the extinction of this CR are roughly in accord with what one would expect from computing the strength of the evidence that the probability that the extension of the lever will be followed by pellet release has decreased (the above-described change-detection computation). This behavior, which is directed to the site where the food is expected to appear, is called goal tracking (Boakes 1977, see also Staddon, 1971). By contrast, the extinction of sign tracking --in this case, lever manipulation--takes much longer (Figure 5, black plots, see also Boakes 1977 and Delamater 1996)3.
Figure 5.
Cumulative records of lever presses (plotted against left axis) and hopper entries (pokes, plotted against right axis) during continuously reinforced autoshaped lever-press conditioning in the mouse, followed by an extinction phase, which began at the dashed vertical line. There were 40 trials in each 2-hr session. The lever extended next to the hopper 10 seconds before pellet release and retracted upon its release. Note the rapid and abrupt cessation of poking (hopper entries) very early in the extinction phase, while pressing the lever persists. Striking individual differences in the relative amounts of sign tracking (lever pressing) and goal tracking (hopper entries) are also evident, as are striking differences in when these two CRs appeared in the course of conditioning. From an unpublished experiment by A.M. Daniel, G.P. Shumyatsky & C.R. Gallistel.
I would replace the terms 'sign-tracking' and 'goal-tracking' with 'foraging' and 'harvesting' behavior. There is no point in going to harvest a pellet that you do not expect to be delivered under current conditions (in the current state of the world), but there is every reason to continue checking on a foraging option from time to time to determine the magnitude of the decrease in the probability or rate of reinforcement to be expected from that option and how long the decrease persists. I suggest that the foraging behavior persists much longer and reappears more readily because it is governed by a strategy designed to determine both how low the decreased probability of reinforcement may now be and how long the decrease can be expected to last. This suggestion is in line with Timberlake's behavior systems theorizing (Timberlake 1993; Timberlake 1994; Timberlake 1995). On my version of this view, the function of foraging behavior is to gather information, whereas the function of hopper entries is to gather food. Visiting a foraging option gathers information, whether food is found or not, visiting the hopper gathers food only if there is food there.
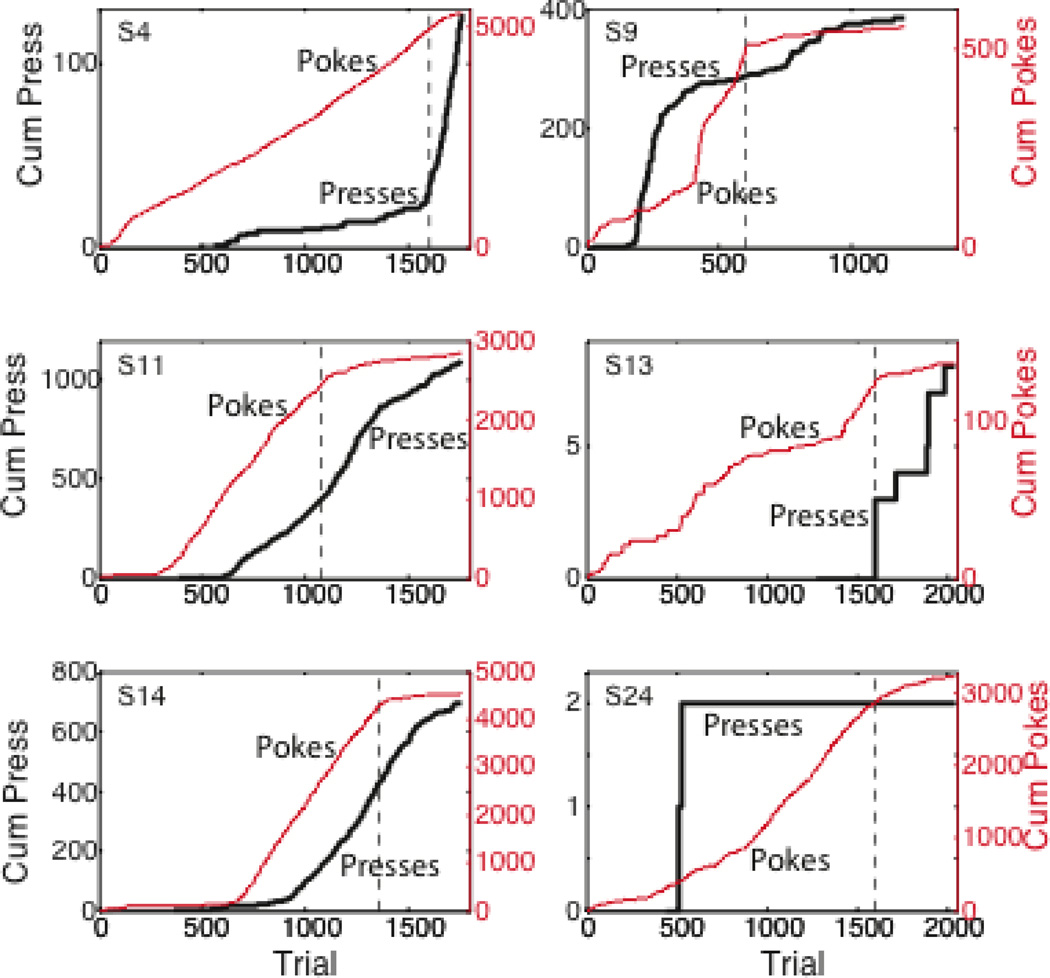
The difference in the behavior of these two CRs during extinction is even more striking when extinction follows partial reinforcement (Figure 6). In that case, several of the mice show an acceleration of lever pressing early in the extinction phase (cf Amsel 1962), but always a more or less immediate deceleration in poking into the hopper itself. One sees the partial reinforcement extinction effect for both kinds of conditioned responses (contrast plots in Figure 6 with those in Figure 5), but extinction comes much sooner for hopper entry than for lever manipulation following either continuous or partial reinforcement.
Figure 6.
Cumulative records of lever presses and hopper entries during partially reinforced autoshaped lever-press conditioning in the mouse, followed by an extinction phase that began at the dashed vertical line. A randomly chosen 12 of the 40 trials in each session were reinforced. In several subjects, the onset of extinction elicits an acceleration in lever pressing (a steepening of the black cumulative record), whereas, for every mouse, hopper entry rapidly decelerates--albeit not as rapidly as following continuous reinforcement, that is, the partial reinforcement extinction effect is apparent when one compares these plots to those in Figure 5. Note again the striking individual differences in the relative amounts of the two different CRs (compare red scales on right to black scales on left, within and between panels). From an unpublished experiment by A.M. Daniel, G.P. Shumyatsky & C.R. Gallistel.
The rapid extinction of the hopper-entry CR puts an upper limit on how long it takes the subject to detect the decrease in the probability of reinforcement. Sign tracking ("exploratory foraging"?) persists well after that, so the persistence of this CR is clearly being driven by a different strategy for coping with nonstationarity, rather than by the weakening of net excitatory association strength. I suggest that this difference in strategy arises because these two different "conditioned" behaviors come from repertoires that have different functions under natural circumstances (foraging vs harvesting, preparatory vs consummatory, cf Boakes, 1977; 1979). These data remind us once again of the importance of the learning-performance distinction. Our behavioral measures are not a simple reflection of some underlying associative strength. As Timberlake reminds us, they are consequences of behavior systems (Timberlake 1994). Despite the difference in strategy, both behaviors are sensitive to the detectability of the change. Both are prolonged in proportion as the change becomes less detectable, but the scale factor for this prolongation is much greater for the sign-tracking behavior than for the goal-tracking behavior, for reasons I have attempted to suggest.
Spontaneous recovery
In the rationalist view, extinction does not wipe out what has been learned (as it does in the enormously influential models of Rescorla and Wagner, 1971, and in the more recent real-time model of Mackintosh and McLaren, 2000). Nor is spontaneous recovery a consequence of the animal's forgetting the extinction experience (as in the theories of Bouton 1994; Bouton and Moody 2004). In the rationalist view, spontaneous recovery, reinstatement, renewal and resurgence are all manifestations of a foraging strategy whose function is to determine the durations and magnitudes of the ups and downs in a behaviorally important stochastic parameter, the probability of food availability. This strategy is in essence an instinct, that is, a complex knowledge-dependent pattern of behavior whose dominant features are genetically specified. It may also be thought of as an instance of a Timberlakian behavioral system (Timberlake 1993). The functioning of this strategy is predicated on the animal's remembering all the lessons of its past experience, both the ups and the downs. This suggestion is also in line with the theoretical and experimental work of the Devenports on foraging behavior in non-stationary naturalistic environments (Devenport and Devenport 1993; Devenport and Devenport 1994; Devenport, Hill et al. 1997; Devenport 1998; Devenport, Patterson et al. 2005).
If the animal were to forever abandon a foraging option at the first downturn in its richness, it would never learn if and when the good times there returned, nor how severe the downturn was. From a rationalist perspective, the properties of the behavior system that patterns the behavioral response to a decrease in the richness of a foraging option should be dominated by rational sampling considerations. These rational sampling considerations do not rest on speculative assumptions about evolutionary environments; they rest on an analysis of the sampling problem, that is, on considerations analogous to a consideration of geometrical optics in vision.
Sampling has a cost, so it should be efficient. Therefore, the sampling frequency should be proportioned to an estimate of the frequency with which the events of interest occur. The initial value for the sampling frequency should be set by the pre-extinction rate of reinforcement in a given environment, as this is the only empirical basis that the animal has for estimating how frequent reinforcement may be in that environment. If the pre-extinction rate of reinforcement sets the scale parameter for the decrease in sampling that occurs as extinction progresses, then the greater the pre-extinction rate of reinforcement in an environment, the more responding one will see during the subsequent extinction phase. This consideration would seem to explain a basic finding in the literature on behavioral momentum, which is that the rate of responding during extinction phases depends on the overall rate of reinforcement (both response-contingent and non-contingent) in the preceding phase (Nevin and Grace 2000; Lattal and St. Peter Pipkin 2009; Podlesnik and Shahan 2009).
The next question is, What should this estimate be when there have been no events (reinforcements) since the point at which the downturn in rate of reinforcement is estimated to have occurred, which will be at or after the last reinforcement? The only relevant information is the duration of the interval elapsed since that point. This duration puts an upper limit on a rational estimate of the new expected interevent interval (the post-change expectation). This suggests that the post-change rate of sampling should decrease in proportion to the reciprocal of the interval elapsed since the last reinforcement. I do not know of relevant published data, though the data to test this must exist in abundance in operant laboratories. The hypothesis needs to be tested against data from individual subjects, because the constant of proportionality probably differs from subject to subject. Generally speaking, the form of the average across a set of functions with a given form but different parameters does not itself have the same form as those functions (Estes 1956)
The second rational consideration that should govern the pattern of sampling behavior is aliasing. If the sampling is periodic, then events occurring with a period shorter than twice the sampling period (the Nyquist frequency, aka the folding frequency, Shannon 1948) will be misperceived as having a period greater than the sampling period. (Aliasing is what makes the wagon wheels appear to turn backwards in old movies.) A solution to this problem is to make the sampling aperiodic (random sampling, see Bilinskis and Mikelsons 1992; Masry 2006). If we add this conjecture to the preceding conjecture, the response pattern we expect to see during extinction is Poisson with a hyperbolically decreasing rate parameter.
On first consideration, these conjectures seem to be refuted by the data on spontaneous recovery, because it is well established that the degree of recovery (the number of conditioned responses observed in a test for spontaneous recovery) increases as the duration of the extinction-test interval increases. This may, however, be an instance of the effect of a round hole on a square peg, that is, it may be an artifact of the experimental protocols interacting with the sampling mechanism. In the natural world, the animal remains in its environment and is free to sample again at times of its choosing (though predation risks that may be higher at some times than at others may circumscribe this freedom, as may other opportunity-limiting factors). In the laboratory, the animal is removed from the foraging environment when it is judged to have quit responding (sampling the option that used to yield food) and returned to that environment at a time chosen by the experimenter. The question then becomes, What does a behavior system that controls sampling in accord with rational principles do when it no longer has control over sampling times? Perhaps it operates like the arming schedule in a queued-VI protocol. When it generates a command to sample, if the command cannot be executed, it goes into a queue. The longer the interval that elapses without the opportunity to sample, the more sampling commands there are in the queue (or, equivalently, the greater the sampling drive). This would nicely reflect an analytic truth already stressed in the discussion of the prior odds of a change, namely, the longer the interval that has elapsed since a non-stationary process was last sampled, the more likely it is to have changed (thus the greater the motivation for sampling it).
Renewal, reinstatement and resurgence
Not all of the innate principles that inform the behavior we observe in learning experiments are analytic. For example, naive subjects assume that the time of day is a causally important factor in their world. They have an internal clock whose genetically specified period has been shaped over evolutionary time to approximate the period of the earth's rotation. When, at a given time of day, they are shocked for entering the dark compartment in a passive-avoidance apparatus, they are most reluctant to enter that compartment again when tested at the same time the next day (see Gallistel 1990, for review of the experimental literature on time-of-day learning). That the earth turns with a 24-hour period is not an analytic truth, nor is it an analytic truth that states of the world, including states of mutual information between variables, tend to be driven by this rotation. Apparently, however, these are sufficiently stable and behaviorally useful truths about our world that, over evolutionary time, they have been incorporated into the prior distributions that enable diverse animals to make maximum use of minimum amounts of information. To the rationalist, the appeal of the Bayesian framework is the ease with which it accommodates both the analytic truths, which I take to be true in all habitable worlds for all time, and truths that are merely enduringly probable in our own speck of the universe.
The rotation of the earth is an example of a hidden variable with many causal effects. If the world has many such variables, then when one perceptible change in a state of the world is coincident with another, it becomes probable that there exists an underlying causal connection (cf Courville, Daw et al. 2004; Gershman, Blei et al. 2010). If two changes, such as a change in the experimental context and a change in the CS-US contingency, are causally connected, then a change back to the first context or a change to a third context increases the probability that a contingency between CS and US or between inter-response interval and inter-reinforcement interval that once existed may again exist. Insofar as the priors governing the subject's behavior in the face of these contextual changes reflect these a priori probabilities, one will see renewal: When returned to the original training environment or put in yet another environment, the animal will tend to respond to the CS as if it might again predict the US. In doing so, the animal expresses its inherited knowledge of how the world tends to work: it has hidden variables with many effects. This inherited knowledge is implicit in the experience-independent aspects of its prior probability distributions.
On this theory, reinstatement and resurgence are reflections of the same Bayesian inference mechanism. When the experimenter switches from a training protocol to an extinction protocol in either a Pavlovian or an operant paradigm, the subject experiences two changes: reinforcement is no longer predicted by the CS or the operant behavior (loss of contingency) and reinforcement no longer occurs in that context (drop in the base rate of reinforcement in that environment). If subjects' sampling strategy is informed by the fact that coincident changes are often linked through hidden causal variables, then the reappearance of reinforcements in that context increases the probability that the contingency between reinforcement and the CS or the discriminative stimulus or the operant may also have been restored. Reinstatement refers to the reappearance of conditioned responding when non-contingent reinforcements reappear in the training environment. Resurgence is the reappearance of a previously extinguished conditioned response during the extinction of the conditioned response to another CS or discriminative stimulus.
Learning to learn: the rapid acquisition of rapid acquisition and extinction
The acquisition of the commonly measured conditioned responses to appetitive reinforcers is slower than can plausibly be explained by the growth in the evidence of contingency (Kakade and Dayan 2002), and, as already noted, so is the extinction of sign-tracking behavior. The rationalist seeks a rationale: Why should this be?
I suggest two rationales: The first, which I think applies only to the slowness of acquisition, is that a prey animal must be convinced that a foraging option is relatively safe (cf Winterrowd and Devenport 2004). It must have evidence that in exercising a foraging option, it does not expose itself to predation. And predation events are relatively rare, so a sustained period of observation is necessary to gain assurance on this score. This rationale implies a trade-off between the strength of an appetitive contingency and the amount of reassurance a highly vulnerable prey animal needs before it ventures to exploit it. (This does not, however, explain why eyeblink conditioning takes so long in the rabbit; that remains a puzzle.)
The second rationale applies to the increase in rates of acquisition and extinction when the animal has repeated experience of the ups and downs of reinforcement (Bullock and Smith 1953; Lauer and Estes 1955; Woodard and Bitterman 1976; Couvillon, Brandon et al. 1980). Again, information-theoretic and Bayesian perspectives suggest explanations. I take the animal's problem to be learning how big the fluctuations in the stochastic parameter may be and how long they may be expected to last. In other words, the problem is to learn the distribution of the ups and downs. When learning a distribution, the initial observations--the one's not predicted well by what one already knows--provide much more information than the later observations (Cover and Thomas 1991).
From the Bayesian perspective, there must be an uninformative prior on the parameters of the to-be-learned distribution. This is a technical way of expressing the thought that there is no telling how long a newly discovered contingency may last or how safe exploiting it may or may not be. Just as the purpose of the Bayesian prior is to become a posterior, so also the purpose of the posterior is to become a prior, because the posterior as of the last experience serves as the prior for the next. When an animal first experiences conditioning and extinction, it has no idea what to expect--it has maximal uncertainty about the magnitude and duration of the contingencies it experiences. Its first few experiences are for that very reason highly informative; they have a strong effect on what it may expect. These experience-informed prior expectations facilitate its adaptations to further changes (subsequent acquisitions and extinctions).
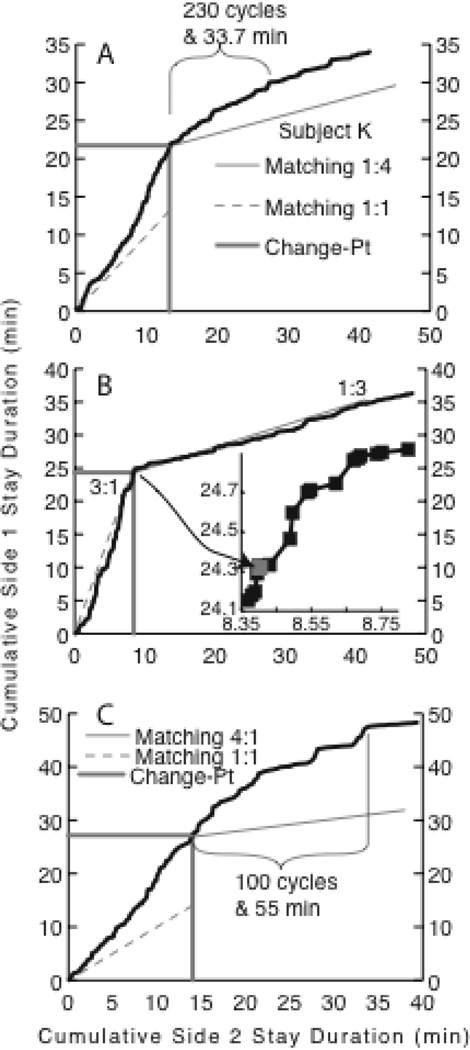
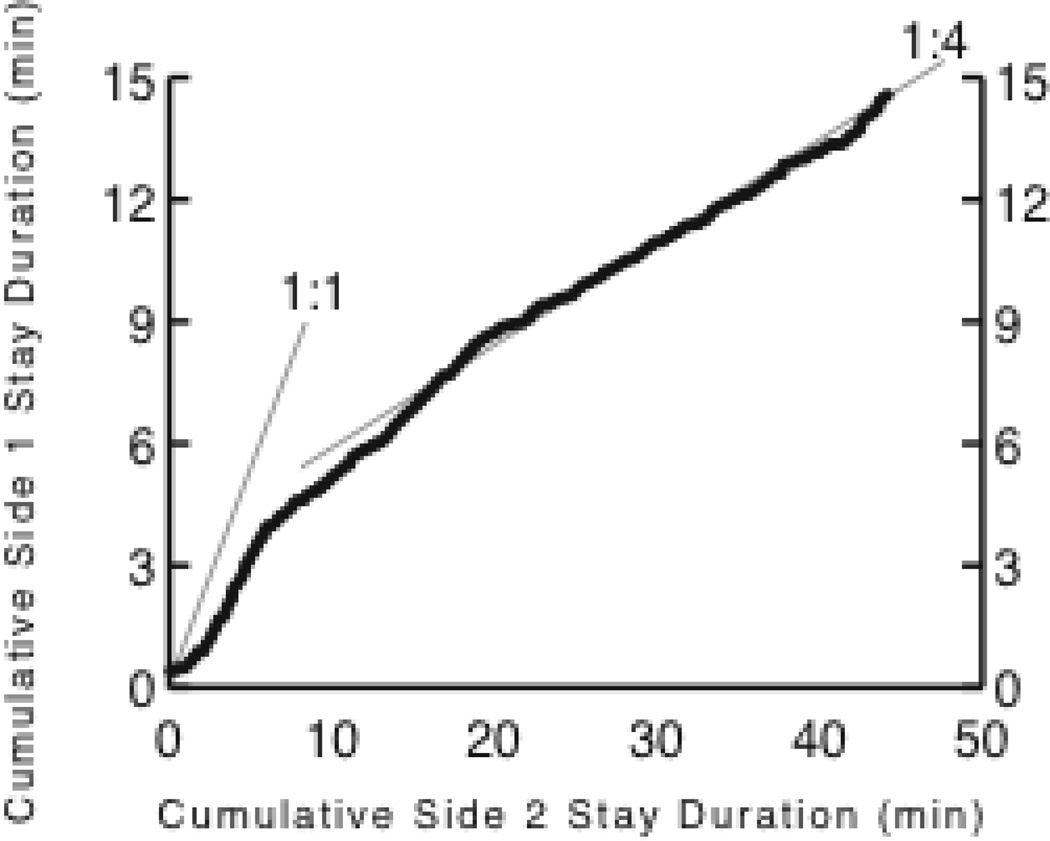
In my lab, we observed the effects of experience-derived prior expectations about the duration of stochastic parameters in a matching experiment. In that experiment, rats foraged on two different levers that produced brain stimulation reinforcements on concurrent variable interval schedules (Gallistel, Mark et al. 2001). Foragers match the ratio of their expected visit durations to the ratio of the incomes obtained from different foraging options. Income is amount of reinforcement per unit time. It is not to be confused with return, which is the amount of reinforcement per unit time invested, that is, per unit time spent visiting an option. In our experiment, there were daily 2-hour sessions, during which the rats were reinforced hundreds of times on each lever. For 30 days, the ratio of the incomes from the two levers never changed. This created a prior strongly favoring the stability of this parameter. Half way through the 31st session, the income ratio changed: it went from 4:1 to 1:4 or from 1:1 to 4:1 depending on the subject. In response to this first change, which occurred after a long period of stability, subjects adjusted the ratio of their visit durations slowly (Figure 7A).
Figure 7.
The duration of the behavioral adjustment to a change in a stochastic parameter depends on the current prior on the stability of the status quo ante: The thick somewhat irregular lines are plots of the cumulative duration of the visits to one lever versus the cumulative duration of the visits to the other during sessions in which there was an unsignaled step change in the ratio of the expectations of the concurrent variable interval schedules of brain stimulation reward. The slopes of these plots at any given point in a session give the ratio of the visit durations at that point in the session. For comparison, the thin straight lines plot the ratio of the two VIs; hence, to a first approximation, the ratio of the reinforcement incomes. When a thick line (plotting the behavioral ratio) has the same slope as the corresponding thin line (plotting the income ratio), the rat is matching the ratio of its visit durations to the ratio of the incomes. A. First change experienced by this subject, coming after a long period of stability in the income ratio. The dashed thin line is the VI/VI ratio prior to the change; the solid thin line, the ratio after the change. The subject's adjustment to the change extended over about 230 visit cycles (and roughly correspondingly numerous reinforcements). Note, however, that the adjustment began soon after the change. B. Same subject adjusting to an even bigger change under conditions where the VI/VI ratio changed from the end of each session to the beginning of the next and then again at an unpredictable time within each session. Under these conditions, subjects adjusted the ratio of their visit durations completely within a very few visit cycles, as shown by the inset, which plots the region around the change enlarged so that one can see every cycle. (The end of each cycle is marked by a square.) C. Same subject after it was returned to a regime in which the VI/VI ratio did not change for a month, at the end of which it experienced a final unsignaled change in the VI/VI ratio. The adjustments under these conditions of renewed stability were as slow as the first ones, even though the same subjects made maximally rapid adjustments during an intervening period when the changes in the VI/VI ratio occurred frequently. (Replotted from data in Gallistel, Mark et al. 2001.)
The new ratio held for another 20 2-hour sessions. Then, the regime changed from one of great stability to one of instability. In this new regime, the income ratio changed by an unpredictable amount between the end of every session and the beginning of the next, and it changed again at an unpredictable time during each session. After only four or five of these rapid-fire changes, subjects adjusted to them with great rapidity and with no reversions to the status quo ante (see below); they behaved like ideal detectors of these changes (Figure 7B). However, when stability was restored, so that the VI/VI ratio again remained the same for a month, then subjects adjusted to a final change as slowly as they had to the first change. Thus, it is not a matter of their learning to learn. Rather, it is their prior on how often changes may be expected and how long they may be expected to last. When recent experience testifies to the stability of a stochastic parameter, subjects adjust slowly to a change; when it testifies to the instability of that parameter, they adjust rapidly.
Spontaneous recovery of matching to the status quo ante
At the beginning of the first few sessions following the first change, our subjects showed that they expected the income ratio to revert to the status quo ante: The ratio of their visit durations returned to the value it had before the change that occurred in the middle of the previous session (Figure 8). When, however, they observed that the change persisted into this next session, they adjusted back to where they had been at the end of the previous session. More fleeting reversions to the behavioral status quo ante were seen at the starts of the next two sessions as well.
Figure 8.
Spontaneous recovery (reversion to the behavioral status quo ante) at the beginning of the session following the first change in the income ratio (same subject as in Figure 7). The thin line labeled 1:1 plots the income ratio that had been in effect at the beginnings of the 31 preceding sessions. The thin line labeled 1:4 plots the income ratio that was in effect throughout this session. The ratio of the subject's visit durations reflected at first what had been the case at the beginning of all previous sessions, then changed rather abruptly to reflect what was now the case.
These reversions to the status quo ante are instances of spontaneous recovery. They show yet again that a change in the value of a stochastic parameter does not wipe out the animal's memory of the value the parameter once had. What subjects learn is, in effect, "That was then; this is now." Under a variety of uncertainty-arousing conditions, their behavior is again informed by the unforgotten past. This is the function of the Bayesian prior; it carries forward the lessons of the past in the form of probability distributions. These distributions inform future behavior whenever conditions change in such a way as to make the animal uncertain about what to expect next. This uncertainty evokes a systematic sampling that is informed by both generally valid considerations and specific past experience.
Summary
The coming together of the computational theory of mind and the rationalist tradition in the philosophy of mind yields a perspective in which one assumes that the computational mechanisms mediating observed behavior reflect in their structure and operation implicit enduring truths about the world within which the brain attempts to direct behavior. Many of these principles endure because they are analytic. It is, for example, an analytic truth that probability distributions integrate to one. Another analytic truth is that if a parameter of the world has ever changed, then the more time has passed, the more likely it is to have changed again. Yet another analytic truth is that the uncertainties (entropies) from independent sources of uncertainty are additive. I have tried to show how these analytic truths structure the behavior phenomena surrounding non-reinforcement. I suggest they do so by way of information theoretic computations and the computations mediating Bayesian inference.
If the rate of conditioning is determined by the informativeness of the CS-US relation, as defined by Balsam and Gallistel (2009), then a simple information-theoretic calculation, making use of the additivity of information from independent sources, shows that intermixing reinforced and non-reinforced trials during conditioning should not increase the number of reinforced trials to acquisition. Thus, this one rationalist consideration explains the quantitative experimental facts about the effects of temporal pairing, cue competition, and partial reinforcement on the acquisition of a conditioned response to a CS. None of these derivations depends on parametric assumptions. The success of these quantitative derivations gives reason to believe that the computational mechanisms mediating the acquisition of conditioned responses have been informed over evolutionary time by the principles that are at the foundation of Shannon's (1948) theory of information. If we think it unremarkable that the principles underlying optical theory in physics have, over evolutionary time, informed the structure of the eye, then I suggest that it is no more remarkable that the principles underlying information theory have informed the mechanisms that enable an animal to exploit the mutual information between events.
In contemplating extinction, the rationalist conceptualizes the problem as one of perceiving non-stationarity in a stochastic parameter, that is, detecting a decrease in the mutual information between CS and US. If the behavior we observe is in fact the result of a change-detecting computation, then the partial reinforcement extinction effect follows from basic principles of Bayesian inference. These principles give mathematical rigor to the intuitively obvious--and mathematically provable--fact that the lower an initial probability (or rate) is, the longer it takes to detect a decrease to 0.
Rationalist considerations give similarly direct explanations for spontaneous recovery. Following extinction, the animal's past offers contradictory testimony about what to expect in the future (Devenport and Devenport 1994). The animal remembers that there once was mutual information between the CS and the US, which enabled it to better anticipate US occurrence. It also remembers that this state of the world only lasted for some while. More recently, there was no such useful mutual information between CS and US. Thus, it now knows that this aspect of the world is not stationary. Another analytic truth is that if something ever does change, then the more time passes, the more likely it is that it has changed. Thus, the more time that has elapsed since it was last able to sample that option, the more likely it is that the rate of reinforcement to be expected from exercising that option has changed again. In short, spontaneous recovery is generated by a mechanism that implements a rational sampling strategy.
Reinstatement, renewal and resurgence are generated by a mechanism whose structure is informed by the fact that our world has hidden variables with multiple causal effects. In such a world, coincident changes in two variables are evidence that both are driven by a hidden variable. In that case, a change in one of the observable variables increases the probability that the other has changed as well.
Associative theories have not explained either the lack of effect of partial reinforcement on reinforcements to acquisition or the extinction-prolonging effect of partial reinforcement. Nor have they explained spontaneous recovery, reinstatement, renewal and resurgence except by ad hoc parametric assumptions of the form, the animal forgets extinction faster than it forgets acquisition (cf Bouton 1994). I believe these failures derive from the failure to begin with a characterization of the problem that specific learning mechanisms and behavioral systems are designed to solve. When one takes an analysis of the problems as one's point of departure, and when one considers what would be the behavior of a computational mechanism optimized to solve those problems, insights follow and paradoxes dissolve. This perspective tends, however, to lead the theorist to some version of rationalism, because the optimal computation will reflect the structure of the problem, just as the structure of the eye and the ear reflect the principles of optics and acoustics.
Highlights.
>Bayesian inference explains partial reinforcement extinction effect (PREE) >Information theory explains why PR does not increase reinforcements to acquisition >Spontaneous recovery is a manifestation of a rational foraging strategy >Reinstatement, renewal and resurgence occur because suspicious coincidences indicate hidden common causes
Supplementary Material
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
When the distributions are continuous, one can compute an entropy by subdividing the distribution into 100 or so narrow rectangles. The probability mass in each rectangle is pw, where p is the height of the distribution at that point and w is the width of the rectangle. The resulting entropy depends on w, which is arbitrary, but one is generally interested only in differences in entropy; they are unaffected by w, provided it is much less than the width of the distribution.
'typical' is used here in its technical, statistical and information-theoretic sense to distinguish between the kind of sequence that would commonly be generated by a specified stochastic process versus the kind that would be generated only rarely (Cover & Thomas, 1991)
The results in Figure 2B are for the extinction of a sign-tracking behavior. The derivation of these results given above explains the flatness of the omitted-reinforcements-to-extinction function; it does not explain why so many omitted reinforcements are required.
References
- Amsel A. Frustrative nonreward in partial reinforcement and discrimination learning. Psychological Review. 1962;69:306–328. doi: 10.1037/h0046200. [DOI] [PubMed] [Google Scholar]
- Balsam P, Gallistel CR. Temporal maps and informativeness in associative learning. Trends in Neurosciences. 2009;32(2):73–78. doi: 10.1016/j.tins.2008.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsam PD, Drew MR, et al. Comparative Cognition & Behavior Reviews. Time and Associative Learning. 2010;5:1–22. doi: 10.3819/ccbr.2010.50001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bem DJ. Feeling the future: Experimental evidence for anomalous retroactive influences on cognition and affect. Journal of Personality and Social Psychology. 2011;100:407–425. doi: 10.1037/a0021524. [DOI] [PubMed] [Google Scholar]
- Bilinskis I, Mikelsons M. Randomized signal processing. London, UK: Prentice-Hall; 1992. [Google Scholar]
- Boakes RA. Associating a stimulus with positive reinforcement. In: Davis H, Hurvitz HMB, editors. Operant-Pavlovian interactions. Hillsdale, NJ: Lawrence Erlbaum Associates; 1977. pp. 67–101. [Google Scholar]
- Bouton ME. Context, time, and memory retrieval in the interference paradigms of Pavlovian learning. Psychological Bulletin. 1993;114:80–99. doi: 10.1037/0033-2909.114.1.80. [DOI] [PubMed] [Google Scholar]
- Bouton ME. Conditioning, remembering, and forgetting. Journal of Experimental Psychology: Animal Behavior Processes. 1994;20(3):219–231. [Google Scholar]
- Bouton ME, Moody EW. Memory processes in classical conditioning. Neuroscience & Biobehavioral Reviews. 2004;28(7):663–674. doi: 10.1016/j.neubiorev.2004.09.001. [DOI] [PubMed] [Google Scholar]
- Bouton ME, Ricker ST. Renewal of extinguished responding in a second context. Animal Learning and Behavior. 1994;22(3):317–324. [Google Scholar]
- Breland K, Breland M. The misbehavior of organisms. American Psychologist. 1961;16:681–684. [Google Scholar]
- Bullock DH, Smith WC. An effect of repeated conditioning-extinction upon operant strength. Journal of Experimental Psychology. 1953;46(5):349–352. doi: 10.1037/h0054544. [DOI] [PubMed] [Google Scholar]
- Courville AC, Daw N, et al. Model uncertainty in classical conditioning. In: Thrun S, Saul L, Schölkopf B, editors. Advances in neural information processing systems. Cambridge, MA: MIT Press; 2004. pp. 977–984. [Google Scholar]
- Courville AC, Daw ND, et al. Bayesian theories of conditioning in a changing world. Trends in Cognitive Sciences. 2006;10(7):294–300. doi: 10.1016/j.tics.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Couvillon P, Brandon S, et al. Performance of pigeons in patterned sequences of rewarded and nonrewarded trials. Journal of Experimental Psychology: Animal Behavior Processes. 1980;6(2):137–154. [Google Scholar]
- Cover TM, Thomas JA. Elements of information theory. 2nd ed. New York: Wiley Interscience; 1991. [Google Scholar]
- Delamater AR. Effects of several extinction treatments upon integrity of Pavlovian stimulus-outcome associations. Animal Learning and Behavior. 1996;24(4):437–449. [Google Scholar]
- Devenport JA, Devenport LD. Time-dependent decisions in dogs (Canis familiaris) Journal of Comparative Psychology. 1993;107(2):169–173. doi: 10.1037/0735-7036.107.2.169. [DOI] [PubMed] [Google Scholar]
- Devenport JA, Patterson MR, et al. Dynamic averaging and foraging decisions in horses (Equus callabus) Journal of Comparative Psychology. 2005;119(3):352–358. doi: 10.1037/0735-7036.119.3.352. [DOI] [PubMed] [Google Scholar]
- Devenport LD. Spontaneous recovery without interference: Why remembering is adaptive. Animal Learning and Behavior. 1998;26:172–181. [Google Scholar]
- Devenport LD, Devenport JA. Time-dependent averaging of foraging information in least chipmunks and golden-mantled squirrels. Animal Behaviour. 1994;47:787–802. [Google Scholar]
- Devenport LD, Hill T, et al. Tracking and averaging in variable environments: A transition rule. Journal of Experimental Psychology: Animal Behavior Processes. 1997;23(4):450–460. [Google Scholar]
- Estes WK. The problem of inference from curves based on group data. Psychological Bulletin. 1956;53:134–140. doi: 10.1037/h0045156. [DOI] [PubMed] [Google Scholar]
- Gallistel CR. The organization of learning. Cambridge, MA: Bradford Books/MIT Press; 1990. [Google Scholar]
- Gallistel CR. Classical conditioning as a non-stationary, multivariate time series analysis: A spreadsheet model. Behavior Research Methods, Instruments, and Computers. 1992;24(2):340–351. [Google Scholar]
- Gallistel CR. The Replacement of General Purpose Theories with Adaptive Specializations. In: Gazzaniga MS, editor. The Cognitive Neurosciences. Cambridge, MA: MIT Press; 1995. pp. 1255–1267. [Google Scholar]
- Gallistel CR. The replacement of general-purpose learning models with adaptively specialized learning modules. In: Gazzaniga MS, editor. The cognitive neurosciences. 2nd ed. Cambridge, MA: MIT Press; 1999. pp. 1179–1191. [Google Scholar]
- Gallistel CR. Conditioning from an information processing perspective. Behavioural Processes. 2003;62(1–3):89–101. doi: 10.1016/s0376-6357(03)00019-6. [DOI] [PubMed] [Google Scholar]
- Gallistel CR. Contingency in learning. In: Seel NM, editor. Encyclopedia of the sciences of learning. New York: Springer; 2011. [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107(2):289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, King AP. Memory and the computaitonal brain: Why cognitive science will transform neuroscience. New York: Wiley/Blackwell; 2009. [Google Scholar]
- Gallistel CR, Mark TA, et al. The rat approximates an ideal detector of changes in rates of reward: Implications for the law of effect. Journal of Experimental Psychology: Animal Behavior Processes. 2001;27(4):354–372. doi: 10.1037//0097-7403.27.4.354. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Shizgal P, et al. A portrait of the substrate for self-stimulation. Psychological Review. 1981;88(3):228–273. [PubMed] [Google Scholar]
- Gershman SJ, Blei DM, et al. Context, learning and extinction. Psychological Reivew. 2010;117:197–209. doi: 10.1037/a0017808. [DOI] [PubMed] [Google Scholar]
- Gibbon J, Farrell L, et al. Partial reinforcement in autoshaping with pigeons. Animal Learning and Behavior. 1980;8:45–59. [Google Scholar]
- Gibbon J, Farrell L, et al. Partial reinforcement in autoshaping with pigeons. Animal Learning & Behavior. 1980;8:45–59. [Google Scholar]
- Gleitman H, Nachmias J, et al. The S-R reinforcement theory of extinction. Psychological Review. 1954;61(1):23–33. doi: 10.1037/h0062623. [DOI] [PubMed] [Google Scholar]
- Gottlieb DA. Acquisition with Partial and Continuous Reinforcement in Pigeon Autoshaping. Learning & Behavior. 2004;32(3):321–335. doi: 10.3758/bf03196031. [DOI] [PubMed] [Google Scholar]
- Harris JA. The acquisition of conditioned responding. Journal of Experimental Psychology: Animal Behavior Processes. 2011;37:151–164. doi: 10.1037/a0021883. [DOI] [PubMed] [Google Scholar]
- Haselgrove M, Aydin A, et al. A Partial Reinforcement Extinction Effect Despite Equal Rates of Reinforcement During Pavlovian Conditioning. Journal of Experimental Psychology: Animal Behavior Processes. 2004;30:240–250. doi: 10.1037/0097-7403.30.3.240. [DOI] [PubMed] [Google Scholar]
- Hull CL. A behavior system. New Haven, CT: Yale University Press; 1952. [Google Scholar]
- Humphreys LG. The effect of random alternation of reinforcement on the acquisition and extinction of conditioned eyelid reactions. Journal of Experimental Psychology. 1939;25:141–158. [Google Scholar]
- Johnson JS, Escobar M, et al. Long-term maintenance of immediate or delayed extinction is determined by the extinction-test interval. Learning & Memory. 2010;17:639–644. doi: 10.1101/lm.1932310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kakade S, Dayan P. Acquisition and extinction in autoshaping. Psychological Review. 2002;109(3):533–544. doi: 10.1037/0033-295x.109.3.533. [DOI] [PubMed] [Google Scholar]
- Katz S. An experimental evaluation of the stimulus generalization interpretation of the partial reinforcement extinction effect. Dissertation Abstracts. 1955;151955:2583. [Google Scholar]
- Kelvin WT. Electrical units of measurement. London: Institution of Civil Engineers; 1883. [Google Scholar]
- Kheifets A, Gallistel CR. Mice take calculated risks. Nature. doi: 10.1073/pnas.1205131109. (submitted). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimble GA. Hilgard and Marquis' conditioning and learning. NY: Appleton-Century-Crofts; 1961. [Google Scholar]
- Lattal KA, St. Peter Pipkin C. Resurgence of previously reinforced responding: Research & application. The Behavior Analyst Today. 2009;10:254–265. [Google Scholar]
- Lauer D, Estes W. Successive acquisitions and extinctions of a jumping habit in relation to schedule of reinforcement. Journal of Comparative and Physiological Psychology. 1955;48(1):8–13. doi: 10.1037/h0045009. [DOI] [PubMed] [Google Scholar]
- Lewis DJ. Partial reinforcement: A selective review of the literature since 1950. Psychological Bulletin. 1960;57(1):1–28. doi: 10.1037/h0040963. [DOI] [PubMed] [Google Scholar]
- Machado A, Sliva FJ. Toward a richer view of the scientific method: The role of conceptual analysis. American Psychologist. 2007;62:671–681. doi: 10.1037/0003-066X.62.7.671. [DOI] [PubMed] [Google Scholar]
- Mackintosh NJ. A theory of attention: Variations in the associability of stimuli with reinforcement. Psychol. Rev. 1975;82:276–298. [Google Scholar]
- Masry E. Random sampling of deterministic signals: Statistical analysis of Fourier transform estimates. IEEE Transactions on Signal Processing. 2006;54(5):1750–1761. [Google Scholar]
- McLaren IPL, Mackintosh NJ. An elemental model of associative learning: I. Latent inhibition and perceptual learning. Animal Learning & Behavior. 2000;26(no. 3):211–246. [Google Scholar]
- Mowrer OH, Jones HM. Habit strength as a function of the pattern of reinforcement. Journal of Experimental Psychology. 1945;35:293–311. [Google Scholar]
- Myers KM, Ressler KJ, et al. Different mechanisms of fear extinction dependent on length of time since fear acquisition. Learning & Memory. 2006;13:216–223. doi: 10.1101/lm.119806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Grace RC. Behavioral momentum and the law of effect. Behavioral and Brain Sciences. 2000;23:73–130. doi: 10.1017/s0140525x00002405. [DOI] [PubMed] [Google Scholar]
- Pavlov I. Conditioned reflexes. New York: Dover; 1927. [Google Scholar]
- Pearce JM, Hall G. A model for Pavlovian learning: Variation in the effectiveness of conditioned but not of unconditioned stimuli. Psychol. Rev. 1980;87:532–552. [PubMed] [Google Scholar]
- Podlesnik CA, Shahan TA. Behavioral momentum and relapse of extinguished operant behavior. Learning & Behavior. 2009;37(4):357–364. doi: 10.3758/LB.37.4.357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prokasy WF, Gormezano I. The effect of US omission in classical aversive and appetitive conditioning of rabbits. Animal Learning and Behavior. 1979;7:80–88. [Google Scholar]
- Rescorla RA. Probability of shock in the presence and absence of CS in fear conditioning. Journal of Comparative and Physiological Psychology. 1968;66(1):1–5. doi: 10.1037/h0025984. [DOI] [PubMed] [Google Scholar]
- Rescorla RA. Response-independent outcome presentation can leave instrumental R-O associations intact. Anim. Lng. Behav. 1992;20(2):104–111. [Google Scholar]
- Rescorla RA. The preservation of response-outcome associations through extinction. Animal Learning and Behavior. 1993;21(3):238–245. [Google Scholar]
- Rescorla RA. Preservation of Pavlovian associations through extinction. Quarterly Journal of Experimental Psychology. 1996;49B:245–258. [Google Scholar]
- Rescorla RA. Spontaneous recovery after training with multiple outcomes. Animal Learning and Behavior. 1996;24:11–18. [Google Scholar]
- Rescorla RA. Instrumental learning: Nature and persistence. In: Sabourin M, Craik FIM, Roberts M, editors. Proceeding os the XXVI International Congress of Psychology: Vol. 2. Advances in psychological science: Biological and cognitive aspects. Vol. 2. London: Psychology Press; 1998. pp. 239–258. [Google Scholar]
- Rescorla RA. Spontaeous recovery. Learning & Memory. 2004;11:501–509. doi: 10.1101/lm.77504. [DOI] [PubMed] [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning II. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- Scott GK, Platt JR. Model of response-reinforcement contingency. Journal of Experimental Psychology: Animal Behavior Processes. 1985;11(2):152–171. [Google Scholar]
- Shannon CE. A mathematical theory of communication. Bell Systems Technical Journal. 1948;27:379–423. 623–656. [Google Scholar]
- Sutton RS, Barto AG. Time-derivative models of Pavlovian reinforcement. In: Gabriel M, Moore J, editors. Learning and compuational neuroscience: Foundations of adaptive networks. Cambridge, MA: Bradford/MIT Press; 1990. pp. 497–537. [Google Scholar]
- Timberlake W. Behavior systems and reinforcement: An integrative approach. Journal of the Experimental Analysis of Behavior. 1993;60(1):105–128. doi: 10.1901/jeab.1993.60-105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timberlake W. Behavior systems, associationism, and Pavlovian conditioning. Psychonomic Bulletin & Review. 1994;1(4):405–420. doi: 10.3758/BF03210945. [DOI] [PubMed] [Google Scholar]
- Timberlake W. Theories of behavior therapy: Exploring behavior change. Washington, DC: American Psychological Association; US; 1995. Reconceptualizing reinforcement: A causal-system approach to reinforcement and behavior change; pp. 59–96. [Google Scholar]
- Wagner AR. SOP: A model of automatic memory processing in animal behavior. In: Spear NE, Miller RR, editors. Information processing in animals: memory mechanisms. Hillsdale, NJ: Lawrence Erlbaum; 1981. pp. 5–47. [Google Scholar]
- Williams BA. Invariance in reinforcements to acquisition, with implications for the theory of inhibition. Behaviour Analysis Letters. 1981;1:73–80. [Google Scholar]
- Winterrowd MF, Devenport LD. Balancing variable patch quality with predation risk. Behav Processes. 2004;67(1):39–46. doi: 10.1016/j.beproc.2004.02.003. [DOI] [PubMed] [Google Scholar]
- Woodard WT, Bitterman M. Asymptotic reversal learning in pigeons: Mechanisms for reducing inhibition. Journal of Experimental Psychology: Animal Behavior Processes. 1976;2(1):57–66. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.