A graphical method for assessing risk factor threshold values using the generalized additive model: the multi-ethnic study of atherosclerosis

Abstract

Continuous variable dichotomization is a popular technique used in the estimation of the effect of risk factors on health outcomes in multivariate regression settings. Researchers follow this practice in order to simplify data analysis, which it unquestionably does. However thresholds used to dichotomize those variables are usually ad-hoc, based on expert opinions, or mean, median or quantile splits and can add bias to the effect of the risk factors on specific outcomes and underestimate such effect. In this paper, we suggest the use of a semi-parametric method and visualization for improvement of the threshold selection in variable dichotomization while accounting for mixture distributions in the outcome of interest and adjusting for covariates. For clinicians, these empirically based thresholds of risk factors, if they exist, could be informative in terms of the highest or lowest point of a risk factor beyond which no additional impact on the outcome should be expected.

1 Introduction

The National Cholesterol Education Program (NCEP) released in 2001 provides a guideline for non-lipid risk factors associated with increase of coronary heart disease (CHD) risk that physicians should consider in CHD preventive efforts (NCEP 2001). These factors include family history of premature CHD, gender, cigarette smoking status as well as blood pressure and cholesterol level control, and most importantly, advancing age. The NCEP went further by recommending that family history should be considered positive for premature CHD if clinical CHD or sudden cardiac death can be documented in first degree male relatives younger than 55 years of age and in first degree female relatives younger than 65 years of age. Such family history should then be used in the treatment decision making for patient care.

Even though the choice of the 55 and 65 years as age of onset of premature CHD for men and women respectively is mostly driven by clinical experiences (rather than by analysis of data) and without any consideration of covariate effects, such dichotomization is quite useful for the clinical practitioner in charge of patient care when age for example is a risk factor of interest in the medical decision making. For similar reasons, in risk prediction models of health (and social) outcomes, continuous predictors and confounders (such as patient age, blood pressure, body mass index, etc) are often dichotomized prior to entry in multivariate regression models (for example, old vs. young, high vs. low blood pressure) using prior knowledge or practical recommendations, allowing for easy interpretation and presentation of results. The dichotomization practice is widespread in clinical studies (Del Priore et al. 1997), but it is known to possibly result in biased estimation (Cumsille et al. 2000; Royston et al. 2006) and the inflation of the type-I error rate for tests of association (Altman et al. 1994; Austin and Brunner 2004), when not correctly done. Nevertheless, this need of categorization arises in other statistical practices as well, including regression tree fitting (Breiman et al. 1984), change point analysis (Pawitan 1998) and knot spline regression (Zhou and Shen 2001), and algorithms for threshold selection in piecewise-constant model fitting have been developed (Breiman et al. 1984; Braun et al. 2000; O'Brien 2004).

Even when variables are not dichotomized, most prediction models used in medical decision making are based on commonly used statistical techniques such as linear or logistic regression models that still make specific assumptions on the functional relationship between the outcome of interest and the regressors. While recognizing that ad-hoc thresholds or variable dichotomization can lead to a biased estimate of the relationship between variables, this article uses the semi-parametric method of the generalized additive model (Hastie and Tibshirani 1990) for the model fit and the improvement of outcome driven thresholds if such thresholds exist. The proposed method also accounts for skewedness as well as mixture distributions due to a substantial fraction of zeros in the outcome of interest using a two-part model regression technique (Duan et al. 1983; Mullahy 1998; Manning et al. 1981).

The layout of this paper is as follows. The linear and logistic generalized additive model (GAM), the two-part model and the recycled prediction methods that will be combined for threshold detection are presented in Sect. 2. Section 4 covers the example of threshold detection of the effect of family relative age of CHD onset on patients coronary artery calcium (CAC) score using the Multi-Ethnic Study of Atherosclerosis (MESA) study. Conclusions are presented in Sect. 5.

2 Methods and estimations

In health care cost studies, the large number of people who do not seek care in the period of interest spend no money on medical care while sick patients use a varying amount of medical care dollars with a few outliers having extremely expensive medical care. To understand the effect of a predictor on charges, the two-part model regression technique (Howard and McGowan 2004) will account for such data structure by modelling the use or not of the service as well as the log of positive charges given use of the service.

Similarly, in the MESA study data that is later used in this article, about half of study participants have a CAC score of zero and one will need to fit a two-part model, a mixture distribution model with a point mass component at zero. The zero/nonzero outcome will be modelled using binary regression techniques such as a logistic or a probit model and then the magnitude of non-zero responses will be modelled conditionally by a continuous distribution technique such as linear model. For the CAC score, the non-zero values were highly skewed and the analysis of such skewed data can often be simplified by applying a monotone transformation (such as log) to the outcome and then analyzing the data on the transformed scale.

Since the youngest age at onset of CHD for the first degree relatives, a continuous variable, is commonly used to determine a positive family history of premature CHD, the method of generalized additive model will be combined with the two-part model process to determine a covariate adjusted threshold for such family history of CHD if it exists. With the outcome transformations and the link functions used for the logistic as well as the linear fit, the technique of recycled prediction (Graubard and Korn 1999) will be applied to estimate the level of the different effects in the outcome scale. The following sections present these different statistical methods to be used for threshold detection and inference.

2.1 Two-part models

In a regression analysis with p covariates denoted by X_i = (X_1i,X_2i,...,X_pi)^T for the ith observation (i = 1,2,..., n) where the outcome variable Y_i has a mixture distribution with a mass point at Y_i = 0 and a highly skewed distribution for Y_i > 0, needing a monotone variable transformation $f\left(Y_i^{+}\right)\equiv f(Y_i\mid Y_i>0)$, a general setup for a two-part model consist of the following two model specifications:

$$\begin{array}{cc}\hfill (Part1:){\pi }_i=& Prob(Y_i>0\mid {\mathit{X}}_i)=\frac{1}{1+\exp (-{\beta }_0-{\beta }_1{X}_{1i}-\cdots -{\beta }_p{X}_{pi})}\hfill \\ \hfill (Part2:)f(Y_i^{+}\mid {\mathit{X}}_i)=& {\alpha }_0+{\alpha }_1{X}_{1i}+\cdots +{\alpha }_p{X}_{pi}+\epsilon \text{conditional on}{Y}_i>0\hfill \end{array}$$ (1)

where ε is the error term, assumed normally distributed with mean 0 and variance σ², conditional on a positive response and the logit link function assumed in Part 1 can be easily adapted to fit alternative models. The model structure in (Part 1) describes the odds of nonzero outcome whereas the second model (Part 2) describes the intensity of the outcome conditional on the realization that a patient has positive outcome measure. Note that the structure of the relationship between the outcome and the covariates can be different from one model to the other and inferences can be made separately on both sections of the outcome.

Even though studies of finite mixture models date back to at least the late 1800s (Pearson 1893), the method of two-part model considered here was developed in the 1980's by Manning and colleagues to analyze annual medical expenditures properly (Manning et al. 1981; Mullahy 1998; Duan 1983). Such expenditures have two characteristics that require special attention to obtain reliable estimates. A substantial part of the distribution is located at zero, and the distribution of positive expenditures is very skewed. In this compound model, a logistic or probit regression is commonly used to predict whether expenses are positive or zero, and a logarithmic transformation is used to make the positive expenditures more nearly symmetric.

To interpret results from these regressions in the natural scale of dollars, researchers need to re-transform the logistic regression to get the probability of positive spending, and the log-spending regression to get spending. Since 1981, this model has been used and studied in a multitude of articles in health economics, and can also be applied to health care outcomes such as CAC score that tend to have similar distributional characteristics as expenditures.

When prediction is of interest, estimates are always preferable in the original outcome scale. For the probability of having the outcome Y_i > 0 for an individual with characteristics X_i; an estimate of such probability can be obtained straightforwardly by using the estimated logistic model coefficients:

$${\widehat{\pi }}_i=\frac{1}{1+\exp (-{\widehat{\beta }}_0-{\widehat{\beta }}_1{X}_{1i}-\cdots -{\widehat{\beta }}_p{X}_{pi})}$$

If no transformation was performed in (part 2), i.e. $f\left(Y_i^{+}\right)=Y_i^{+}$, the same prediction construction can be obtained via the model estimates. In cases such as the CAC score where the skewness of the outcome requires a transformation, $f\left(Y_i^{+}\right)=log\left(Y_i^{+}\right)$, several estimation techniques of $E(Y_i^{+}\mid {\mathit{X}}_i)$ have been developed in the past two decades with Duan (1983) presenting the method of smearing estimate and McCullagh and Nelder (1989) proposing the widely used concept of generalized linear models. In this paper we will restrict our procedure to the use of the smearing estimates but similar developments could be done when using all other retransformation methods.

With the log transformation for example, $f\left(Y_i^{+}\right)=log\left(Y_i^{+}\right)$, a lognormal distribution theory shows that a consistent prediction for an individual with characteristics X_i will be obtained by $E(Y_i^{+}\mid {\mathit{X}}_i)=e^{0.5{\sigma }^2}\times \exp ({\alpha }_0+{\alpha }_1{X}_{1i}+\cdots +{\alpha }_p{X}_{pi})$ but this retransformation estimate hinges critically on Y⁺ being really lognormally distributed. Duan (1983) proposed a consistent retransformation factor $\widehat{\varphi }=\frac{1}{n_{+}}{\sum }_j\exp \left({\widehat{\epsilon }}_j\right)$, where n₊ is the number of participants with Y > 0 and ${\widehat{\epsilon }}_i$ the estimated error term, so that $\widehat{E}(Y_i^{+}\mid {\mathit{X}}_i)=\widehat{\varphi }\times \exp ({\widehat{\alpha }}_0+{\widehat{\alpha }}_1{X}_{1i}+\cdots +{\widehat{\alpha }}_p{X}_{pi})$. For any monotone transformation $f\left(Y_i^{+}\right)$ of the outcome, the general smearing estimate was defined as

$$\widehat{E}(Y_i^{+}\mid {\mathit{X}}_i)=\frac{1}{n_{+}}\sum _{j=1}^{n_{+}}{f}^{-1}({\widehat{\alpha }}_0+{\widehat{\alpha }}_1{X}_{1i}+\cdots +{\widehat{\alpha }}_p{X}_{pi}+{\widehat{\epsilon }}_j).$$ (2)

See Duan (1983) for more information on the smearing estimate technique.

It is sometimes useful to estimate the unconditional effect of the covariates on the outcome or the average estimated outcome for each level of a specific covariate after controlling for all the other ones. Under the two-part model, the commonly sought expected outcome for participants with characteristics X_i; not conditional anymore on having Y > 0, can then be estimated as

$$\widehat{E}(Y_i\mid {\mathit{X}}_i)={\widehat{\pi }}_i\times \widehat{E}(Y_i^{+}\mid {\mathit{X}}_i)$$

As will be shown later, this combined prediction technique can be used to estimate the effect of a specific covariate on the outcome of interest in the original outcome scale.

2.2 Generalized additive models and their visual plots

The logistic and linear models used in (1) assumed that the contribution of the different covariates X_k, k = 1,...,p toward the predicted outcome is linear through β_kX_k and α_k X_k respectively but in fact the relationship can be non-linear (Hastie and Tibshirani 1990). In generalized additive models (GAM), the contribution of each covariate X_k is generalized to semi-parametric functions, thus expanding (1) to

$$\begin{array}{cc}\hfill (Part1:){\pi }_i=& Prob(Y_i>0\mid {\mathit{X}}_i)=\frac{1}{1+\exp \{-{\beta }_0-h_1\left(X_{1i}\right)-\cdots -h_p\left(X_{pi}\right)\}}\hfill \\ \hfill (Part2:)f(Y_i^{+}\mid {\mathit{X}}_i)=& {\alpha }_0+g_1\left(X_{1i}\right)+\cdots +g_p\left(X_{pi}\right)+{\epsilon }_i\text{conditional on}{Y}_i>0\hfill \end{array}$$ (3)

where h_k and g_k are unknown functions that are estimated by a non-parametric approach in a GAM algorithm.

The functions h_k and g_k being estimated by the data will reveal the true relationship between the covariates and the outcome and such relationship can be shown in the plots of h_k(X_ki) and g_k(X_ki) on X_ki. If there are r thresholds t₁; t₂,..., t_r on the effect of a covariate X_k on the outcome of interest, such thresholds can be simply approximated by visual assessment of such plots. In the best case scenario of clean cut thresholds, each plot will be similar to a step function plot where for any value of X_k between two consecutively ordered thresholds t_l and t_l+1, the effect on the outcome will be mostly constant, but significantly different than the next threshold interval. So, visual detection of a threshold will consist of observing curvatures in the plot of h_k(X_ki) or g_k(X_ki) on X_ki and detecting break points where there are shifts in the effect.

GAM can sometimes produce poor estimates of the functions h_k(X_ki) and g_k(X_ki) when there are very few observations in a certain interval of the range of X_k and this can happen toward the end points of the range of X_k when there are outliers in the X_k observations. Special attention then need to be paid to outliers in the covariate when using GAM for threshold detection. Hastie and Tibshirani (1990) provide estimation techniques for pointwise 95 % confidence interval of the functions h_k(X_ki) and g_k(X_ki). Therefore, if we denote SE_hk(X_ki) such pointwise standard error of the function h_k(X_ki) estimated at the observation X_ki, a lower and upper 95 % confidence bound can be obtained by h_k(X_ki) – 1:96 × SE_hk(X_ki) and h_k(X_ki) + 1:96 × SE_hk(X_ki) respectively. The narrower the confidence interval, the more precise the estimate of h_k(X_ki). Because in two-part models, different functions h_k(X_ki) and g_k(X_ki) can be estimated for both parts of the relationship between Y and X; the method of recycled prediction presented next can be used to provide a threshold when the interest is on the effect of a covariate X_k on the unconditional outcome Y.

2.3 Recycled prediction

Recycled prediction also referred to as predictive margins (Graubard and Korn 1999) is a method that allows presentation of regression results in a meaningful scale when response transformation was involved in the fit. It can also be regarded as a method for estimation of average response associated with different risk factors after controlling for sample covariates that are imbalanced between different risk groups.

Consider for example the effect of X₁ = smoking status (taking value 1 for smokers and 0 for non smokers) on the likelihood of study participants having CAC score of 0 or not (yes/no), the logistic regression set up of (1) to be used for such estimation can then be written as

$${\pi }_i=Prob(Y_i>0\mid {\mathit{X}}_i)=\frac{1}{1+\exp (-{\beta }_0-{\beta }_{1}Smok{e}_i-{\beta }_1{X}_{12i}-\cdots -{\beta }_p{X}_{pi})}.$$ (4)

Even though the estimates ${\widehat{\beta }}_1$ and $\exp \left({\widehat{\beta }}_1\right)$ provide the log-odds and the odds ratio respectively of the effect of smoking on the likelihood of having positive outcome, it can be useful to interpret these estimates by the difference in probability of a positive outcome between smokers and non-smokers. This can be done by first using the estimated model coefficients to estimate the probability ${\widehat{\pi }}_i$ of each participant assuming that they are all smokers (i.e setting Smoke = 1 for all of them) but keeping their original values for all the other covariates X_ki; k = 2,...,p. The full sample average of such probability estimates will provide an estimate of the probability of having Y > 0 for smokers after controlling for all the other covariates. The same procedure will be conducted for non-smokers by setting Smoke = 0 for all participants. The difference between the two obtained probabilities provides an estimate in probability scale of the effect β₁ and reflects the net impact of smoking on the likelihood of positive score since both share the same sample of respondents. Formally

$$\begin{array}{cc}\hfill & {\widehat{\pi }}_{smokers}=\frac{1}{n}\sum _{i=1}^n{\widehat{\pi }}_i{\mid }_{smoke=1}=\frac{1}{n}\sum _{i=1}^n\frac{1}{1+\exp (-{\widehat{\beta }}_0-{\widehat{\beta }}_1\times 1-{\widehat{\beta }}_2{X}_{2i}-\cdots -{\widehat{\beta }}_p{X}_{pi})}\hfill \\ \hfill & {\widehat{\pi }}_{non-smokers}=\frac{1}{n}\sum _{i=1}^n{\widehat{\pi }}_i{\mid }_{smoke=0}=\frac{1}{n}\sum _{i=1}^n\frac{1}{1+\exp (-{\widehat{\beta }}_0-{\widehat{\beta }}_1\times 0-{\widehat{\beta }}_1{X}_{12i}-\cdots -{\widehat{\beta }}_p{X}_{pi})}\hfill \\ \hfill & \text{Probability effect size}{\widehat{\pi }}_{\text{effect}}={\widehat{\pi }}_{smokers}-{\widehat{\pi }}_{non-smokers}\hfill \end{array}$$

Standard error and confidence interval of ${\widehat{\pi }}_{\text{effect}}$ can be estimated using bootstrap methods (Efron 1987). (See Graubard and Korn (1999) for other estimators of ${\widehat{\pi }}_{\text{effect}}$ as well as standard error estimators). Recycled prediction is not restricted to logistic regression models, and the same prediction idea can even be applied to linear models with transformation, such as the one in (1), in order to present estimation and effect sizes in the untransformed outcome scale as will be shown in the next section.

2.4 Combination of all three methods

In the recycled prediction development, it is not essential that the predictor of interest (smoking status) takes only two values 0 and 1. For X₁ = OnsetAge, the youngest age at onset of CHD for first degree relative, a continuous covariate, the same method could determine the average difference in probability of a positive outcome between participants with relative OnsetAge = 50 compare to the ones with OnsetAge = 65. One will estimate for any age v

$${\widehat{\pi }}_{\text{OnsetAge v}}=\frac{1}{n}\sum _{i=1}^n\frac{1}{1+\exp \{-{\widehat{\beta }}_0-({\widehat{\beta }}_1\times v)-{\widehat{\beta }}_2{X}_{2i}-\cdots -{\widehat{\beta }}_p{X}_{pi}\}}$$ (5)

and then take the difference ${\widehat{\pi }}_{\text{effect}}={\widehat{\pi }}_{\text{OnsetAge}65}-{\widehat{\pi }}_{\text{OnsetAge}50}$. Furthermore the GAM semi-parametric model assumption flexibility can be injected in this setup. If one does not believe that the relationship between the logit transformation of the binary outcome and the predictors should be linear, the semi-parametric estimation method in (3) should be used instead and thus the average probability at onset age v will be estimated as

$${\widehat{\pi }}_{\text{GAM-OnsetAge v}}=\frac{1}{n}\sum _{i=1}^n\frac{1}{1+\exp \{-{\widehat{\beta }}_0-h_1\left(v\right)-h_2\left(X_{2i}\right)-\cdots -h_p\left(X_{pi}\right)\}}$$ (6)

where the value of the estimated h₁ function is fixed at h₁(v) and all the other functions are left to keep their values h_k(X_ki) assumed for the observation X_ki of the participant i. In light of this, while in the GAM, the plot of h_k(X_ki) on X_ki is used to visually estimate a threshold on the effect of X_k on Prob(Y_i > 0|X_i) where h_k(X_ki) is the logit scale value of that effect, a plot of ${\widehat{\pi }}_{\text{GAM-OnsetAge}\mathrm{v}}$ on v will reflect the same effect and threshold, but in the probability scale.

This can also be extended beyond the logistic model assumption. For any monotone outcome transformation f used in part 2 of (1), applying the smearing estimate in (2), we can estimate the recycled predicted outcome Y⁺ at an Onset Age v for example by positing for X₁ = OnsetAge

$$\begin{array}{cc}\hfill \widehat{E}\left(Y^{+}\text{at OnsetAge}v\right)=& \frac{1}{n_{+}}\sum _{i=1}^{n_{+}}\widehat{E}(Y_i^{+}\mid {\mathit{X}}_i,\text{OnsetAge}=v)\hfill \\ \hfill =& \frac{1}{n_{+}^2}\sum _{i=1}^{n_{+}}\sum _{j=1}^{n_{+}}{f}^{-1}\{{\widehat{\alpha }}_0+({\widehat{\alpha }}_1\times v)+{\widehat{\alpha }}_2{X}_{2i}+\cdots +{\widehat{\alpha }}_p{X}_{pi}+{\widehat{\epsilon }}_j\}.\hfill \end{array}$$ (7)

Even for the unconditional average response prediction, it is straightforward to have

$$\widehat{E}\left(Y\text{at OnsetAge}v\right)=\frac{1}{n_{+}}\sum _{i=1}^{n_{+}}{{\widehat{\pi }}_i\mid }_{(\text{OnsetAge}=\mathrm{v})}\times \widehat{E}(Y_i^{+}\mid {\mathit{X}}_i,\text{OnsetAge}=v)$$ (8)

Once again if the GAM semi-parametric model is used instead of the parametric one in (1) we can estimate the untransformed scale average expected outcome at Onset Age v

$$\begin{array}{cc}\hfill \widehat{E}\left(Y^{+}\text{at GAM-OnsetAge}v\right)=& \frac{1}{n_{+}^2}\sum _{i=1}^{n_{+}}\sum _{j=1}^{n_{+}}{f}^{-1}\{{\widehat{\alpha }}_0+g_1\left(v\right)+g_2\left(X_{2i}\right)+\cdots +g_p\left(X_{pi}\right)+{\widehat{\epsilon }}_j\}\hfill \\ \hfill \widehat{E}\left(Y\text{at GAM-OnsetAge}v\right)=& \frac{1}{n}\sum _{i=1}^n{{\widehat{\pi }}_i\mid }_{(\text{GAM-OnsetAge}=v)}\times \widehat{E}(Y_i^{+}\mid {\mathit{X}}_i,\text{GAM-OnsetAge}=v)\hfill \end{array}$$ (9)

In a two-part model setting, the estimate Ê(Y at GAM-OnsetAgev) has the advantage of combining the results for Y = 0 and Y > 0 and thus providing a single non-parametric function on the Y scale of the effect of the covariate on the outcome that can be used for threshold detection purpose if the interest is in such combined outcome score. The bootstrap method (Efron 1987) will be used for standard error (SE) estimation on all these estimated values. Even though non-linear transformations were conducted throughout this process, a ±1.96SE will be used for rough confidence interval estimates.

3 Performance of GAM plots for threshold detection

The performance of our proposed graphical method for threshold detection depends on users’ ability to identify thresholds by visually inspecting a GAM plot. We conduct simulation studies with emphasis on data sample size and the spread of thresholds to evaluate the ability of users correctly identifying thresholds visually using GAM plots. For two types of sample size (small N = 100 and large N = 5000), we generate N observations of an Age variable (integer) uniformly distributed between 30 and 80 and three covariates X₁, X₂ and X₃ normally distributed with different variances. We then selected two age thresholds T₁ and T₂ (with T₁ < T₂) also uniformly distributed between age 40 and 75 with the condition that the spread (d = T₂ – T₁) between the two thresholds be at least 5 years of age. We next generated an outcome variable Y with

$$Y_i={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\alpha }_{0}Age+{\alpha }_1(Age-T_1){\mathbb{I}}_{(\ge Age-T_1)}+{\alpha }_2(Age-T_2){\mathbb{I}}_{(\ge Age-T_2)}+\epsilon$$

where ε is a normally distributed random error and ${\mathbb{I}}_{(\ge Age-T_1)}$ and ${\mathbb{I}}_{(\ge Age-T_2)}$ are the indicator functions for age greater than T₁ and T₂ respectively. With this simulation, the slope of the step function representing the impact of Age on the outcome is α₀, α₀ + α₁ and α₀ + α₁ + α₂ in the age areas [30, T₁], [T₁, T₂] and [T₂, 80] respectively. For the simulated data, the first two slopes were fixed at α₀ = –5.2 and α₀ + α₁ = 0.3 and we vary α₀ + α₁ + α₂ to take values –6.2, –5.2 or –4.2. GAM analyses were then conducted, resulting in a total of 42 GAM plots, which represented combinations of different sample sizes, different threshold spread d and different slopes α₀ + α₁ + α₂ in the age area [T₂, 80].

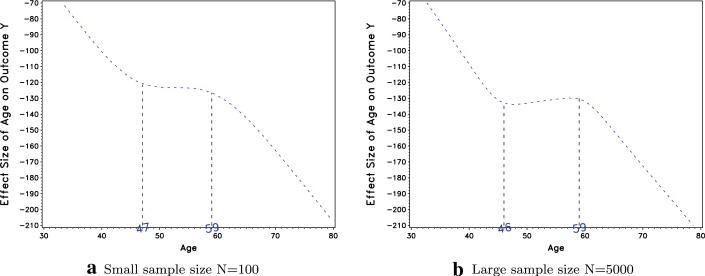
A sample of 31 prospective users were recruited to participate in the assessment of the performance of the GAM plots. Of the 31 users, 22 were students at Carnegie Mellon University with basic understanding of statistics and 9 were seasoned researchers with extensive knowledge of GAM. The students attended a 10-minute introduction session explaining GAM, and then were asked to evaluate the 42 GAM plots for estimates of the thresholds. The 9 researchers were also asked to evaluate all 42 GAM plots. Participants were not told about the number of thresholds used in the generation of the simulated data and were free to identify as many thresholds as they deemed fit. Two examples from the 42 GAM plots are presented in Fig. 1. These two GAM plot examples were generated using the same slopes and thresholds (T₁ = 45 and T₂ = 60), but Fig. 1a was generated with a small sample size, and Fig. 1b was generated with a large sample size. The estimated thresholds reported by one prospective user is also reported on the plot.

Fig. 1.

Simulated data GAM plots for T₁ = 45, T₂ = 60 with different sample sizes and a user estimated thresholds reported

The thresholds identified by the prospective users were analyzed and compared to the simulated true thresholds to evaluate prospective users’ accuracy in using GAM. In some cases, users reported only one reliable threshold (while in fact there were two thresholds), and such estimates were compared to the true threshold they were closest to. Our analysis involved first estimating the number of times thresholds were not identified even though the data was simulated with thresholds. Next, if any thresholds were identified, we computed the percentage of agreement, a measure of reliability defined as the ratio of the number of exact threshold agreement divided by the number of possible agreements (Hayes and Hatch 1999). Because age is a continuous variable and in practice, there is not much difference between for example, age 45 and age 46, we also computed these estimates with a relaxed definition, such that we considered an estimated threshold to be in agreement with the true threshold if the estimated threshold was within two years of the true threshold. We then relaxed the definition even further, such that we considered an estimated threshold to be in agreement with the true threshold if the estimated threshold were within five years of the true threshold. We also reported the Pearson's correlation and the Cronbach's alpha between the true and the estimated thresholds, both of which are measures of internal consistency between these two values. A common rule of thumb for evaluating alpha coefficients suggests that an alpha less than 0.7 is poor, between 0.7 to 0.8 is acceptable, between 0.8 and 0.9 is good, and between 0.9 and 1 is excellent (George and Mallery 2003; Nunnally and Bernstein 1994). Lastly, we assess the reliability of the estimates between prospective users using intra-class correlation coefficients (ICC), computed based on one-way analysis of variance that assesses the reliability of continuous measures. By convention, ICC estimates of 0.75 or more signify excellent agreement beyond chance.

The results of the simulations are reported in Table 1. Across all estimations, 11 % of the time, the prospective users reported no threshold while in fact there were thresholds. After further exploration of the data, the “no threshold” estimation was reported only 0.2 % of the time among simulations with a large sample size, and occurred more frequently with simulations involving a small sample size. The “no threshold” estimation was cited 44.8 % of the time when the sample size was small and the spread d between the thresholds was small (d ≤ 15) and only 2.4 % of the time when the sample size was small and the spread d was large (d > 15). When thresholds were estimated, users identified thresholds that were in exact agreement with the true simulated values only 40.4 % of the time, with researchers being much more likely than students to provide an exact match. Given that age is a continuous variable, it is not surprising that exact matches to the true simulated values are somewhat unlikely. However, across both researchers and students, 84 % of the thresholds were correctly estimated within two years of the true simulated threshold, and such agreement was at 96 % within five years of the true threshold. Matches were not as accurate for the small sample size data, but for N = 5000, the agreement within five years of the true simulated value was at 99.6 %. Even when exact agreements were not high (due to the continuous nature of the age variable), other measures of accuracy that take into account the continuous nature of the variable revealed excellent accuracy. For example, the correlations, ICC estimates, and Cronbach's alphas suggested that even for small sample sizes, excellent accuracy was still observed. In practice, when it comes to continuous variables such as age, decision makers will likely round the thresholds to the nearest multiples of 5. These results suggest that in practical situations, these GAM plots provide excellent estimates, even for users such as students that might be novice to using GAM.

Table 1.

Rater agreement and reliability estimates of simulated data

Simulation type	% of no detection	% agreement within			Cronbach alpha	Pearson correlation	Intra-class correlation
		0 year	2 years	5 years
Overall	11.0	40.4	84.0	96.0	0.989	0.982	0.982
N = 100	32.7	22.6	46.9	85.3	0.951	0.943	0.946
N = 5000	0.2	46.5	96.5	99.6	0.997	0.995	0.990
d ≤ 15	20.6	44.8	88.7	99.0	0.989	0.979	0.970
d > 15	0.5	36.6	79.9	93.4	0.989	0.984	0.990
N = 100, d ≤ 15	44.8	35.1	71.9	98.0	0.969	0.945	0.932
N = 100, d > 15	2.4	5.0	11.6	67.4	0.934	0.965	0.957
N = 5000, d ≤ 15	0.4	49.3	96.5	99.5	0.995	0.991	0.983
N = 5000, d > 15	0.0	44.4	96.6	99.7	0.998	0.996	0.993
Researchers	10.3	50.7	84.5	97.1	0.990	0.984	0.987
Students	11.3	36.2	83.8	95.6	0.989	0.981	0.981

4 Application to age of onset thresholds on CAC scores

4.1 The data

Atherosclerotic CHD, one of leading cause of death in men and women, has a lengthy induction period, during which biologic risk factors interact with genetic and environmental influences but more importantly, sudden death or myocardial infarction is often its initial manifestation (Kannel and Schatzkin 1985). Measurement of coronary artery calcium (CAC) has been proven to be an independent predictor of CHD events and, thus, a way to improve CHD risk assessment (Detrano et al. 2008; Pletcher et al. 2004). Physicians commonly use CAC scores as a surrogate for estimation of likelihood of CHD event on patients.

Family history of CHD is also well-known to be a significant risk factor of CHD, and Nasir et al. (2007) has shown that such family history, especially premature CHD in first degree relatives, is associated with the presence and advance of CAC in four separate ethnic groups and the relationship is independent of other commonly known CHD risk factors. Even the NCEP guideline (NCEP 2001) for non-lipid risk factors of CHD includes a family history of premature CHD: it recommends considering premature CHD in a first degree male relative when the age of onset is 55 or less or if the age of onset is less than 65 in a female first degree relative. We will use the statistical methods described in this article to empirically estimate the age at onset of family members where there is a shift in the effect of family history of CHD on CAC scores.

The MESA that we will use, began in July 2000 and is a cohort of 6,814 subjects without clinically apparent atherosclerotic vascular disease (e.g., no history of heart attack, angina, stroke, transient ischemic attack, or heart failure) at baseline, age 45 to 84, from 6 sites across the United States (Columbia University, Johns Hopkins University, Northwestern University, University of Minnesota, UCLA, and Wake Forest University). Participants were followed in order to investigate the prevalence, correlates, and progression of subclinical cardiovascular disease (CVD) in individuals without known CVD. Further details about the MESA study and sample design were reported in Bild et al. (2002), Nasir et al. (2007) and Scheuner et al. (2008).

While only 2,587 of participants reported having family members with history of CHD (we restrict history of CHD to events after 29 years of age since very early events are rare), 1,379 of them have only male relatives with a history of CHD, 693 have only female relatives with CHD history and 515 have both male and female relatives with CHD. Because of the extensive research and the perception among physician and policy makers about the difference in gender impact on people's likelihood of CHD, we will restrict our analysis to only the 1,379 participants with only male relatives with CHD. In this sample, the CAC score outcome of interest takes value 0 for 47 % of the sample (N = 651), and for participants with CAC score greater than 0, the CAC measurements range from 0.8 to 4602.1 with a median of 106.1 but a mean of 296.4 suggesting that even the conditional CAC score is highly skewed. Pletcher et al. (2004) made the same observation in population CAC scores and as they suggested, we will use a log-transformed CAC score (when CAC > 0) for normal approximation of its distribution for analysis purpose.

For each participant, data was collected on their gender (51 % female), race, age, education level, marital status, income, youngest age at onset of CHD of their first degree relatives, number of relatives in their family, as well as participant's general Framingham cardiovascular risk (FCR) categories—low, medium or high—(D'Agostino et al. 2008) estimated using their age, total cholesterol, HDL cholesterol, diabetes and smoking status. In the next section we present the analysis of the effect of study participant's family member's age at onset of CHD on their CAC scores while adjusting for those covariates.

We first started by fitting a generalized additive logistic regression model with the continuous variable family CHD onset age entered in the model through non-parametric functions as in (3) in order to estimate the likelihood of CAC score being positive. Then a log-transformed generalized additive linear model estimation was conducted on the positive scores. Finally, these two prediction models were combined using the technique described in Sect. 2.4. Graphs of the onset ages on their effects were plotted and impact thresholds were estimated visually for all three models. To evaluate the effectiveness of the threshold estimates obtained through our method with respect to the NCEP 55 years onset age threshold for premature CHD, different models with these threshold were fitted and compared to a model without a family history of CHD predictor.

4.2 Results

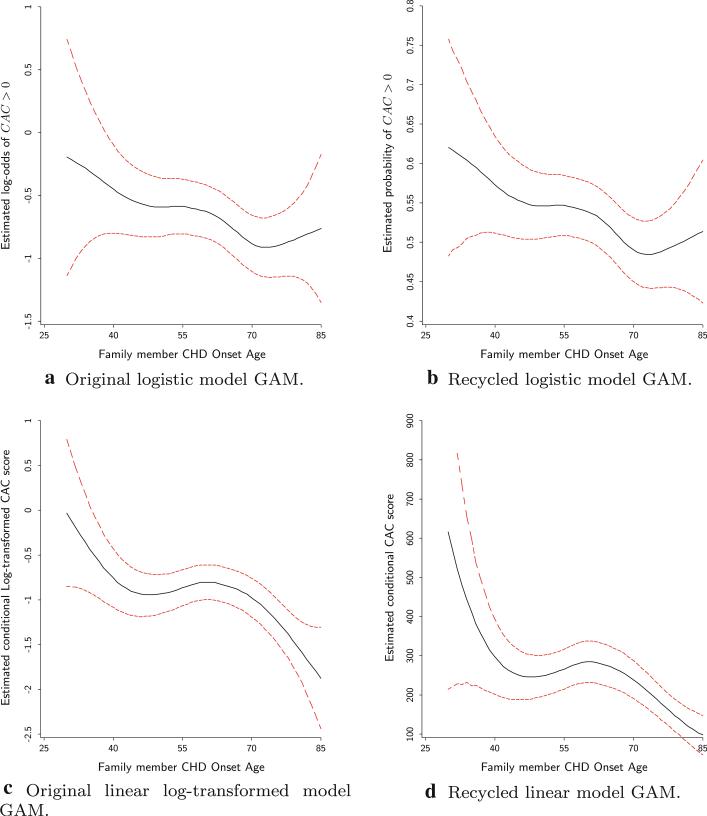
In the GAM, in order to assess both linear and nonlinear trend in the effect of family member CHD onset age, the unknown non-parametric functions were re-parameterized. So for example h_k(X_ki) was replaced by ${\beta }_k{X}_{ki}+h_i^{+}\left(X_{ki}\right)$ where any significant evidence of β_k ≠ 0 will mean the existence of linear trend in the relationship between the outcome and the predictor. For the binary outcome of CAC > 0, while a t-test reveals that there is a linear relationship between the likelihood of CAC > 0 and the CHD onset age (p-value = 0.029), a chi-squared test of the non-linear part $h_k^0$ comparing the deviance between the full model and the model without this non-linear part is far from significant (p-value = 0.416). When dealing with the continuous log(CAC) outcome model, both linear and non-linear trend tests turned out to be significant (p-values 0.002 and 0.006 respectively). In Figs. 2a and 2c, the CHD onset age variable was plotted against its logit for the likelihood of CAC > 0 and its log-transformed effect on the CAC score for participants with CAC > 0 respectively. The visual patterns in these plots support the significance inferences made earlier where in the logistic regression, the effect of CHD onset age, the estimated log odd of CAC > 0 slightly decreases with the age almost linearly from –0.2 to –0.9. Because this logit scale effect is not as easy to interpret as the probability of CAC > 0 that is usually of interest, a conversion of those log odd ratios into probabilities using recycling prediction resulted in Fig. 2b. It shows that, after adjusting for all covariates, the likelihood of a participant having CAC > 0 decreases almost linearly from 60 % for relative CHD onset age of 30 to 48 % for the onset age of 75 or above. For the linear log-transformed model, there seems to be a higher effect for very young CHD onset age and the effect decreases almost linearly up to around 40 years of age. Between ages 40 and 69 the effect does not change and then for onset age of at least 69, the effect decreases again one more time. With the back-transformation of the log scale effects into the CAC scale, Fig. 2d shows that, conditional on the CAC score greater than 0 and after adjusting for all covariates, from age 30 to 40, the predicted CAC score decreases from 600 to 300, but between the ages of 41 and 68 the predicted CAC score fluctuates between 250 and 300. For the ages of 69 and older, the predicted score once again decreases from 250 down to 100.

Fig. 2.

GAM plots depicting the relationship between family member CHD onset age and CAC score for the different models and outcome scales

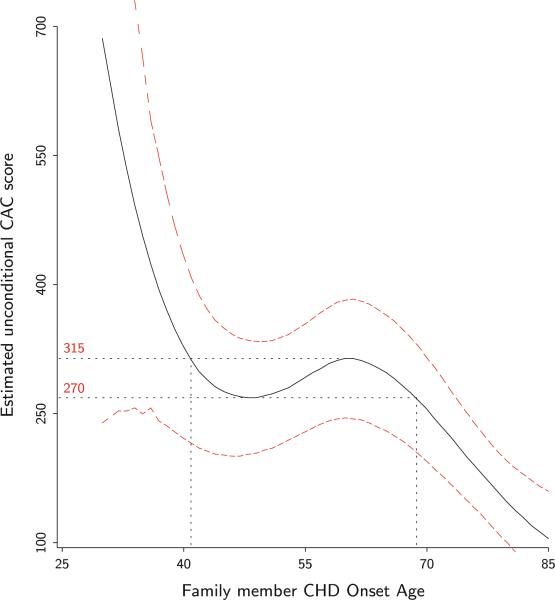
The two-part model combined (non-conditional) predicted outcome for family member CHD onset age is presented in Fig. 2. Once again between ages 40 and 69, the estimated CAC score varies little between 270 and 315 while it decreases outside that interval. To classify family members’ CHD onset age as a risk factor for patients CAC score and thus their likelihood of CHD event, these results are suggesting 69 years or older as normal age of onset, 41–68 years as early onset age and 40 years or younger as really premature onset age. Even with bootstrap estimated confidence interval, such normal onset age could be as large as 75 years. This empirical threshold estimate is significantly different from the 55 years old for premature CHD recommended by the NCEP and commonly used by physicians. To compare the predictive ability of our empirically observed threshold to the commonly used 55 years old, we fitted three models M₀, M₁ and M₂ with the CAC score outcome using two-part model techniques. In M₀ only the covariates gender, race, age, education level, marital status, income, number of relatives, and FCR were included as predictor. Model M₁ consisted of all the covariates in M₀ plus the family member age at onset of CHD variable split at 55 years (NCEP recommendation). The last model M₂ is comprised of all covariates in M₀ plus the family member age at onset of CHD variable split in three groups: [30, 40], [41, 68] and [69, +]. Because M₀ is nested in M₁ as well as in M₂, a χ² test was conducted for comparison of the nested logistic models while an F-test was conducted for the linear log-transformed models. The results of the model comparisons are presented in Table 2. While in the logistic as well as the linear model M₁ using the NCEP recommended cut seems to provide no improvement to the model M₀ without a family history of CHD, in both cases, our newly defined family history of CHD provides a significant improvement. While M₁ and M₂ are not nested and thus not directly comparable, the different likelihood ratio statistics as well as the F-statistics suggest a clear improvement from the use of the empirically estimated thresholds.

Table 2.

Logistic and Log-transformed models M₀, M₁ and M₂ comparison tests

Models	χ2 Test for logistic models comparison			Test for linear models comparison
	LR statistics	df	p-value	F-test statistics	df	p-value
M0 vs M1	2.157	1	0.142	0.70458	1, 709	0.402
M0 vs M2	8.692	2	0.013	5.930	2, 708	0.003

4.3 An analysis of CAC risk factors and inference

In this two part model setting, the method of recycled prediction provides an intuitive alternative way to present inference on the effect of the categorized family members CHD onset age on the CAC score outcome as well as all the other covariates. Table 3 reports the results (model estimates as well as recycled predictions) of CHD onset age and FCR in models M₁ and M₂, where practical differences between different groups can be assessed. Practical differences between the NCEP recommendation and the GAM visually assessed thresholds can also be examined. In this study, after adjusting for participants characteristics such as age, gender, race, income level, education and family size, using the NCEP age recommendation for premature CHD, we will have inferred that there is no relationship between family history of CHD and patients calcium scores, whether it is for the likelihood of a participant having a CAC above 0 or the trend in CAC specific scores above 0. But, using the GAM visually assessed thresholds we infer that the family history of CHD has a significant effect on participants’ calcium scores.

Table 3.

Estimated onset age and FCR effect on CAC scores in the two-part model with their recycled estimates and standard errors

Models	Covariates	n	Logistic model of CAC > 0			Log-transformed linear model			Combined CAC estim. (SE)
			Log odds	p-value	Adjusted prob. (SE)	Log estim.	p-value	CAC estim. (SE)
Model M1 with NCEP threshold	Onset age
	55 +	942			51.6 % (1 %)			336.5 (36)	176.6 (17)
	30–54	437	0.197	0.14	55.4 % (2 %)	0.11	0.40	375.0 (51)	206.5 (26)
	FCR
	Low	593			46.4 % (2 %)			178.5 (29)	84.0 (14)
	Medium	629	0.517	0.00	57.0 % (2 %)	0.60	0.00	326.6 (35)	178.8 (17)
	High	157	0.762	0.01	62.0 % (5 %)	1.04	0.00	503.0 (82)	291.7 (48)
Model M2 with GAM thresholds	Onset age
	69+	407			48.0 % (2 %)			254.5 (35)	128.5 (17)
	41–68	900	0.325	0.02	54.3 % (1 %)	0.36	0.00	366.4 (39)	199.4 (18)
	30–40	72	0.716	0.01	61.6 % (5 %)	0.82	0.01	576.3 (150)	337.7 (87)
	FCR
	Low	593			46.4 % (2 %)			180.0 (29)	84.7 (14)
	Medium	629	0.518	0.00	57.0 % (2 %)	0.60	0.00	327.9 (35)	178.8 (16)
	High	157	0.757	0.00	61.8 % (5 %)	1.01	0.00	493.4 (79)	284.3 (46)

Participants with family history of CHD with onset age at 69 or more have about 48 % chance of having positive CAC scores, while that change increases to 54 % for early family history of CHD (onset age between 41 and 68) and the people with really premature family history of CHD (onset age less than 40) have a 62 % chance of having positive calcium scores. Those probabilities were estimated through the logistic model as an odd ratio of 1.384 for early onset and 2.046 for the premature family history. Conditional on a participant having a positive CAC score, the average expected CAC score after all covariate adjustment was estimated to be about 255, 266 and 576 for the normal, early and premature family history groups, respectively. The unconditional CAC score using the two part model turned out to be 129, 199 and 338 for those groups.

Using the NCEP recommendation, family history of premature CHD (younger than 55 years old) will have resulted in a small insignificant increase of the chance of having positive CAC score from 52 % to about 55 %. Similarly, conditional on a participant having a positive CAC score, having a family history of premature CHD would have only resulted in an insignificant increase in CAC score from 337 to 375. Even qualitatively, the GAM visually assessed thresholds provides some significant differences in inferences that can be made about the impact of family history of premature CHD on participants CAC score and possibly their likelihood of having CHD events.

Similar results were obtained for the different levels of the Framingham risk. Because by design, the cardiovascular risk factors age and gender are major components of FCR, the estimated relationship between CAC score and FCR might be even stronger without age and gender adjustment.

5 Conclusion

Identification of key factors associated with the risk of developing a disease and quantification of such risk using statistical regression models are common practices in medical research. But for clinicians, empirically based risk factor thresholds such as age thresholds for determination of premature family history of CHD is desired especially if such thresholds can be translated into an estimated likelihood of disease event. In this paper, we used generalized additive models, recycled prediction and two-part models aided by data visualization to estimate existing empirical thresholds of a continuous clinical risk factor (youngest age at onset of family member with CHD) after adjusting for important covariates that might also have impact on the outcome of interest. The article shows an association between the risk factor and the outcome and uses GAM for a non-parametric approximation of the true relationship, thus accurately modeling it and adding to the efficiency and interpretability of any threshold observed.

We proposed a visualization of the GAM effect plot in order to decide thresholds, if they exists, where different inferences of the effect on the outcome can be made. Although dividing a risk factor into two or more levels may result in some loss of information, we believe it contributes to understanding crucial thresholds where significant change can be expected for patients in different groups. Our empirically based thresholds are improvements on the expert opinion thresholds commonly used in the literature.

Recycled predictions and the two-part model have an additional advantage. Even though outcome transformation procedures such as the logistic model produce estimates (e.g log odd or odd ratios) that researchers understand, recycling provides equivalent estimates in the natural outcome scale that can be useful for practitioners. So, for example in the logistic model, the log odd ratios 0.3 and 0.7 convey the information that participants with family history of CHD at early onset age (41–68 years) and very early age at onset (40 years or younger) are more likely to have positive CAC score than participants with later age at onset (69 years and older). But reporting the probability of having CAC > 0 to be 48, 54 and 62 % for participants with family history of very early, early and later age at onset might be more informative than those log odds. For the linear model with log-transformation, instead of differences in the log scale between risk factor groups for CAC scores, the expected real CAC scores in those groups are more consistent with how clinicians think about these measures in practice. The method can also be used to make outcome prediction when desired for a specific value of a continuous risk factor. In the two part model, combined model coefficient estimates cannot be provided, but this method allows for a combined unconditional estimate of the predictive value of the outcome in different risk groups that can be used for inference.

While this study has demonstrated the potential utility of GAM for establishing thresholds on risk factors such as the age of premature CHD, it is also important to address the limitations of the use of GAM for decision making. As it is based on users’ visual assessment, the method proposed does not reliably identify specific, unique thresholds, but instead can identify regions where those thresholds are likely to exist, if they exist at all. From one user to another, there can be slight differences in the interpretations of the GAM plots where the graphs can support different but equally viable alternative thresholds. For example, an argument can be made that in Fig. 3, the plot suggests the thresholds are located at 42 and 68, rather than the selected thresholds 40 and 69 used in our example. These thresholds may lead to slightly different definition of premature CHD, and any cut scores will artificially introduce variation between treatment of groups that are at the cusp of the thresholds. However, even the NCEP recommendation has such a limitation, and it would be unusual for clinical phenomena to have precise age thresholds.

Fig. 3.

Two-part model combined estimates GAM plot

Finally, with the general objective of a threshold detection method presented here being about the visual estimation of such threshold in the data in the presence of other covariates, users should always keep in mind that thresholds must be clinically or biologically meaningful.