Quantitative body DW-MRI biomarkers uncertainty estimation using Unscented Wild-bootstrap

Abstract

We present a new method for the uncertainty estimation of diffusion parameters for quantitative body DW-MRI assessment. Diffusion parameters uncertainty estimation from DW-MRI is necessary for clinical applications that use these parameters to assess pathology. However, uncertainty estimation using traditional techniques requires repeated acquisitions, which is undesirable in routine clinical use. Model-based bootstrap techniques, for example, assume an underlying linear model for residuals rescaling and cannot be utilized directly for body diffusion parameters uncertainty estimation due to the non-linearity of the body diffusion model. To offset this limitation, our method uses the Unscented transform to compute the residuals rescaling parameters from the non-linear body diffusion model, and then applies the wild-bootstrap method to infer the body diffusion parameters uncertainty. Validation through phantom and human subject experiments shows that our method identify the regions with higher uncertainty in body DWI-MRI model parameters correctly with realtive error of ~36% in the uncertainty values.

1 Introduction

Diffusion Weighted MRI (DW-MRI) is a non-invasive imaging technique that is rapidly evolving as a surrogate imaging biomarker for extra-cranial applications, including organ functionality evaluation [8,17], oncological disease classification [9], and early assessment of body tumor response to therapy [5,6].

DW-MRI is particularly appealing for pediatric patients undergoing multiple, repeat imaging examinations because a) it does not involve ionizing radiation associated with traditional imaging methods such as CT, MIBG, or FDG-PET; and b) it is performed without administration of intravenous contrast agents, which, in some patients, may be contraindicated [14].

In-vivo measurement of the body tissue diffusivity involves acquisition of a sequence of DW-MRI with multiple b-values, and estimation of the Apparent Diffusion Coefficient (ADC) from the sequence. Traditionally, the ADC value is computed for each voxel using the Stejskal-Tanner exponential model: S_b = S₀e^−b*ADC [13]. However, in living tissue, physiological motions unrelated to diffusion (e.g., the intra-voxel micro-capillary perfusion effect) can mimic diffusion processes and confound in-vivo measurements. Hence, accurate estimation of the ADC values requires fitting a multi-exponential model that describes both diffusion and perfusion effects [12,1].

Clinical applications of DW-MRI typically involve the comparison of mean or median ADC values in particular, Regions of Interest (ROI) [8]; or may use voxel-wise analysis [10] to visualize the change in the ADC over time. Estimation of ADC from multiple b-value images has an intrinsic uncertainty, however, due in part, to noise in the image acquisition process; and in part, to artifacts such as those caused by patient motion. The uncertainty that characterizes ADC value estimation is therefore needed to achieve quantitative ADC assessment in clinical applications.

Direct estimation of the ADC measurement uncertainty using traditional asymptotic estimators or the bootstrap technique [7] requires repeated acquisitions, however. These techniques are therefore impracticable in routine clinical use due to lengthy scan times per patient, and to resulting increases in artifacts. Moreover, model-based bootstrap techniques require homogeneous leverages of the different sample points. Although it is possible to rescale the heterogeneous leverages of different points using an underlying log-linear model derived from the Stejskal-Tanner exponential diffusion model in intra-cranial Diffusion Tensor MRI (DT-MRI) [3]; body DW-MRI exhibits a multi-exponential model [12,1] that cannot be linearized through a log transform. As a result, model-based bootstrap techniques cannot be utilized directly for the uncertainty estimation of body DW-MRI ADC.

We present a new model-based bootstrap technique to infer the measurement uncertainty in ADC estimation from body DW-MRI without acquiring additional images, thus eliminating the underlying linear model requirement. First, a multi-exponential model is fitted to the acquired data. Next, the residuals between the observed data and the estimated model are computed. Heterogeneous leverages scaling parameters are computed using the Unscented transform [11], and the residuals are scaled accordingly. Last, the wild-bootstrap resampling technique [4] is used to estimate the ADC distribution from which the model uncertainty can be derived. The estimated uncertainty values can then be used for further analysis of the change in the ADC values in response to the therapy. Our Unscented wild-bootstrap technique does not assume any linearity in the underlying model and thus can be utilized directly in other cases exhibiting underlying nonlinear models, such as crossing fibers in DT-MRI.

We compared the uncertainty estimation using our method to that which was obtained through repeated acquisitions of both phantom and human subject experiments. In all experiments, our method identified the regions with higher uncertainty in body DWI-MRI model parameters correctly with realtive error of ~36% in the uncertainty values. Thus, our method can provide the necessary information for reliable quantitative DW-MRI biomarkers assessment, without repeated acquisitions.

2 Method

The goal is to infer the uncertainty in ADC estimation from DW-MRI. Our proposed approach utilizes a body DW-MRI dataset consisting of six or more images acquired with different b-values in the range of 0–800 s/mm². First, a multi-exponential diffusion model is fitted to the data and the raw residuals between the obtained fit and the observed images are computed. Next, the Unscented Transform (UT) [11] is used to compute the scaling parameters required to account for heterogeneous leverages in the different sampling points, and the residuals are scaled accordingly to satisfy the wild-bootstrap method [4] conditions. Last, wild-bootstrap resampling is used to infer the uncertainty in the diffusion model parameters estimation. In the next section, we describe each step in detail.

2.1 Diffusion model fitting

The DW-MRI measurement of tissue diffusivity is affected by both thermal-driven water molecules diffusion and intra-voxel, randomly oriented, micro-capillary blood flow. Thus, the DW-MRI measurements should be modeled using a multi-exponential diffusion model [12,1]:

$$S(b)=S_0(f·\mathit{\text{exp}}(-b·\mathit{\text{PER}})+(1-f)·\mathit{\text{exp}}(-b·(\mathit{\text{ADC}}+\mathit{\text{PER}})))$$ (1)

where b is the b-value used to acquire the images, ADC is the Apparent Diffusion Coefficient (ADC) describing the signal attenuation due to the real diffusion effect; PER is the perfusion coefficient describing the signal attenuation due to the blood perfusion effect; and f is the fractional volume of the perfusion effect.

Assuming a Rician noise model with scaling parameter σ_R, the Probability Distribution Function (PDF) of the DW-MRI signal is given by:

$$P(M|S,{\sigma }_R)=\frac{M}{{\sigma }_R^2}\mathit{\text{exp }}(-\frac{M^2+S^2}{2{\sigma }_R^2}\left)I_0\right(\frac{\mathit{\text{MS}}}{{\sigma }_R^2})$$ (2)

where M is the observed value; S is the “true” underlying signal; and I₀(·) is the zero-ordered modified Bessel function of the first kind.

The likelihood of the diffusion model parameters Ω = {ADC, PER, f, S₀} given the observed data M and σ_R is:

$$L(\Omega ;M,{\sigma }_R)={\displaystyle \prod _{i=1}^N}P(M_i|\Omega ,{\sigma }_R)$$ (3)

where N is the number of the observations.

The Maximum Likelihood (ML) estimation of the model parameters Ω is computed by maximizing the following log-likelihood function:

$$\widehat{\Omega }=\underset{\Omega }{\text{argmax}}{\displaystyle \sum _{i=1}^N}{I}_0\left(\frac{S(b_i;\Omega )M_i}{{\sigma }_R^2}\right)-{\displaystyle \sum _{i=1}^N}\frac{S{(b_i;\Omega )}^2}{2{\sigma }_R^2}$$ (4)

where S(b_i; Ω) is the signal estimation at b-value b_i given the model parameters Ω computed using Eq. 1. The estimation of σ_R is computed by ML fitting of a Rayleigh distribution to a pre-defined background region on each image.

Initial estimation of the model parameters is obtained as in [2], and the maximization is done using the BOBYQA non linear optimization algorithm [15]. The raw residuals between the obtained fit and the observed images are then given by: ε_i = M_i − S(b_i)

2.2 Heterogeneous leverages scaling

The wild-bootstrap resampling technique assumes homogeneous leverage of the different sampling points. However, the estimation of model fitting uncertainty usually involves heterogeneous leverage. Appropriate rescaling of the raw residuals ε_i is required to satisfy this condition. In linear models, these rescaling parameters can be obtained directly from the model equation as in [3,4]. However, there is no direct way to compute the heterogeneous leverage of different points in the non-linear model underlying body DW-MRI.

To offset this limitation, we use the Unscented Transform (UT) [11] to estimate the heterogeneous leverage of different points by propagating a set normally distributed test points with μ = Ω̂ and σ = 1 throughout the non-linear model, and computing the variance of the propagated points.

Given the multi-exponential diffusion model (Eq. 1) and the estimated parameters Ω with n as the model parameters number; we define a set of 2n test points p as in [3]. A new set of model parameters with μ = Ω̂ and σ = 1 is then generated by adding each test point p_j to the estimated model parameters:

$$\widetilde{{\Omega }_j}=\widehat{\Omega }+p_j$$ (5)

Next, the DW-MRI signal values $S(b_i;\widetilde{{\Omega }_j})$ are computed for each b_i with the new model parameters $\widetilde{{\Omega }_j}$ using Eq. 1, and the variance of the propagated errors is given for each sampling point i by:

$$h_i=\frac{1}{2n}{\displaystyle \sum _{j=1}^{2n}}{(S(b_i;\widetilde{{\Omega }_j})-\overline{S(b_i;\widetilde{{\Omega }_j}}))}^2$$ (6)

Finally the scaled residuals $\widehat{{\epsilon }_i}$ are computed from the raw residuals εi by:

$$\widehat{{\epsilon }_i}=\frac{{\epsilon }_i}{\sqrt{1-h_i^2}}$$ (7)

2.3 Wild-bootstrap estimation of the model uncertainty

Following the method described in [4], the wild-bootstrap resampling is defined as:

$$S^{*}{(b_i;\widehat{\Omega })}_k=S(b_i;\widehat{\Omega })+t_k\widehat{{\epsilon }_i}$$ (8)

where S^*(b_i; Ω̂)_k is the resampled measure at the b-value b_i and t_k is a two-point Rademacher distributed random variable with P(t = 1) = 0.5 and P(t = −1) = 0.5 defined for each b-value separately.

The wild-bootstrap resamples are generated for the entire set of b_i values and a multi-exponential diffusion model is fitted using Eq. 4. Resampling and model fitting are repeated for a large number of fixed repetitions to obtain a large set of diffusion models. The estimation of the model uncertainty is then obtained by computing the standard deviation of the estimated model parameters from the set of bootstrap diffusion models.

3 Experimental results

We evaluated the performance of our Unscented wild-bootstrap uncertainty estimation method through DW-MRI scans of an American College of Radiology (ACR) MRI phantom and a human subject. In the following section, we describe each experiment in detail.

3.1 ACR phantom experiment

Ten DW-MRI datasets of an ACR MRI phantom were acquired using the gradient encoding scheme [16] on a 1.5T MRI machine (Magnetom Avanto, Siemens Medical Solutions, Erlangen, Germany). Each dataset consisted of diffusion images with values = [5, 50, 100, 200, 270, 400, 600, 800]s/mm². One out of the ten datasets was acquired during slight vibrations of the phantom to introduce motion artifacts and enlarge the model fit uncertainty. The additional 9 datasets were acquired with the stabilized phantom. A multi-exponential diffusion model was fitted to each dataset using Eq. 4. The performance of our method was evaluated using the Leave-One-Out (LOO) methodology, where the “ground-truth” uncertainty in model estimation was defined as the standard deviation of the ADC measure at each voxel over 8 out of the 9 stabilized acquisitions, and the ADC uncertainty was estimated from the additional dataset solely using our technique with a varying number of bootstrap resampling iterations between 50 and 1000. Finally, the Relative error between the estimated uncertainty and the “ground-truth” uncertainty was computed for each dataset. In addition, we compared the ADC uncertainty estimated from the vibrated phantom dataset to a “ground-truth” uncertainty obtained from the 9 stabilized phantom datasets.

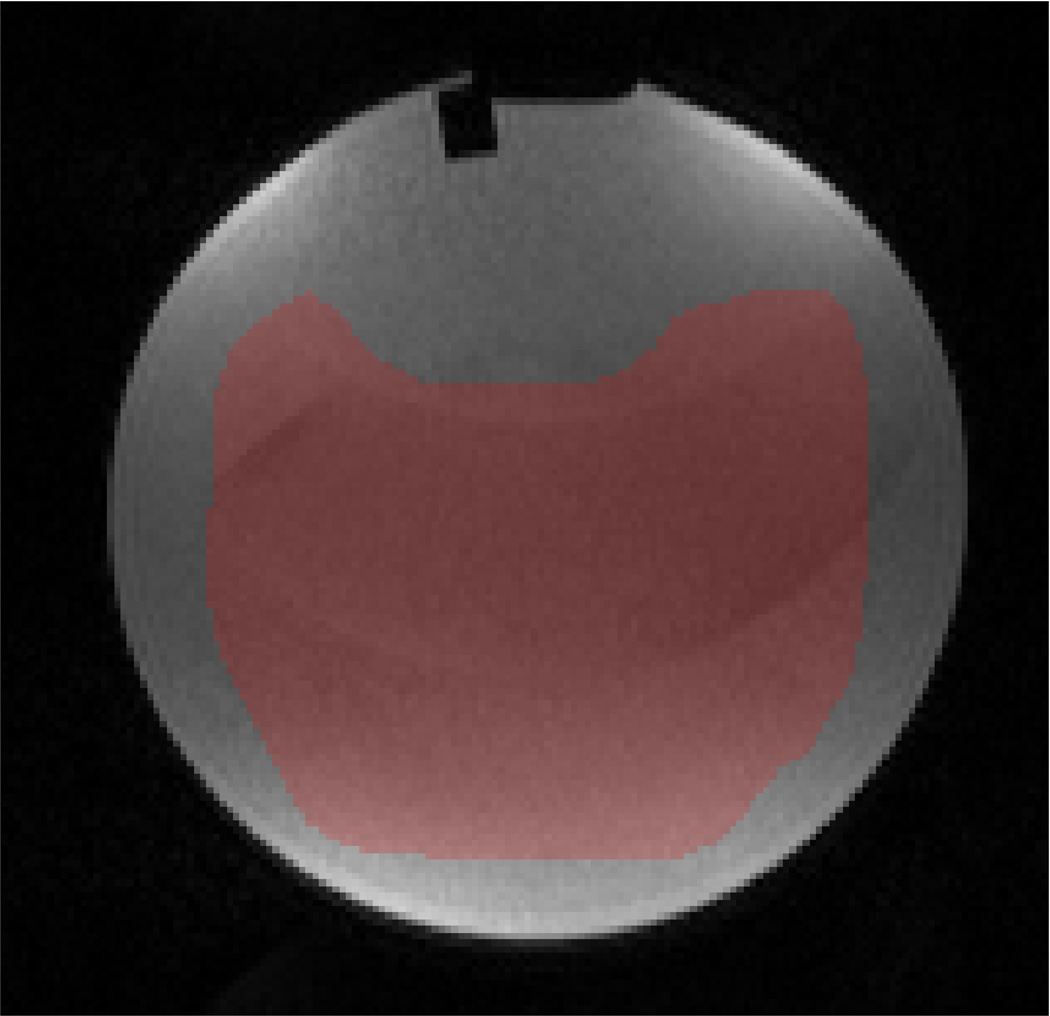
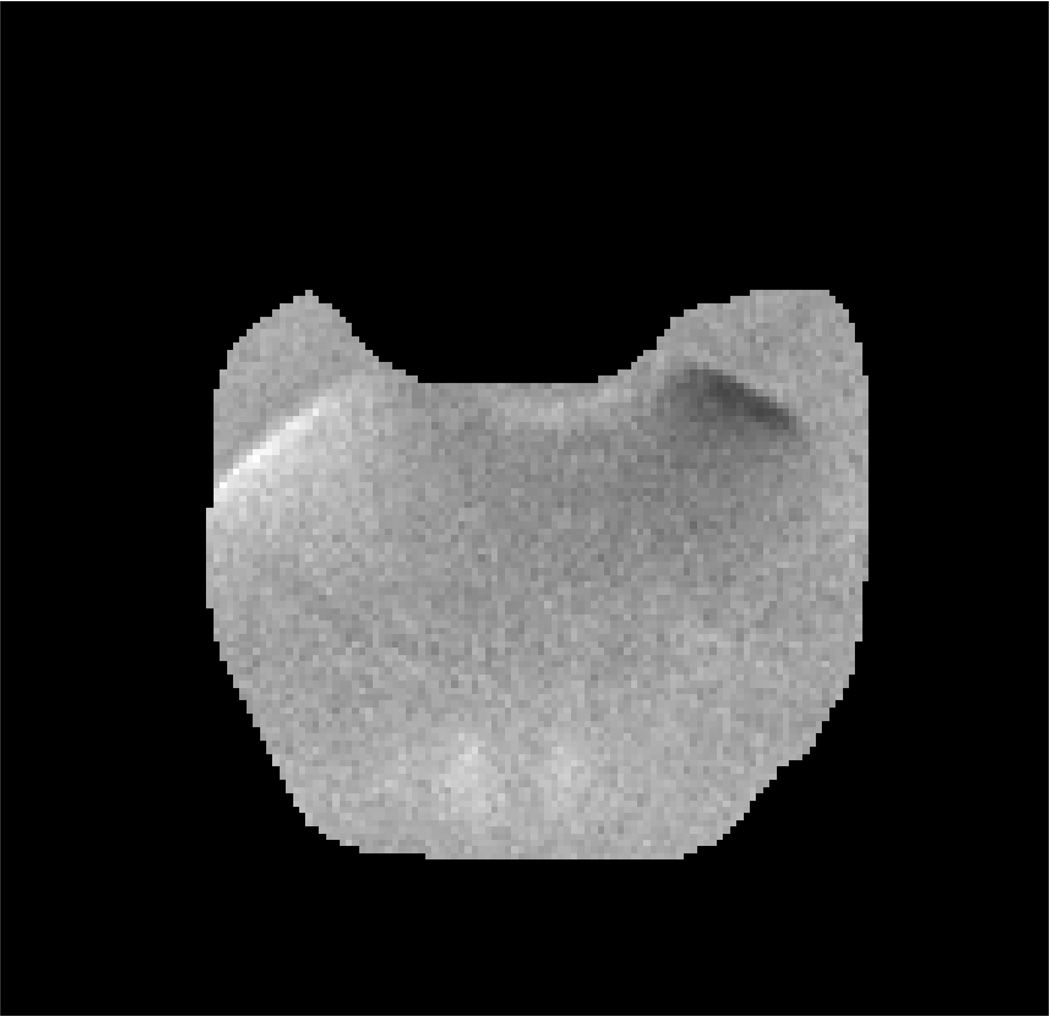
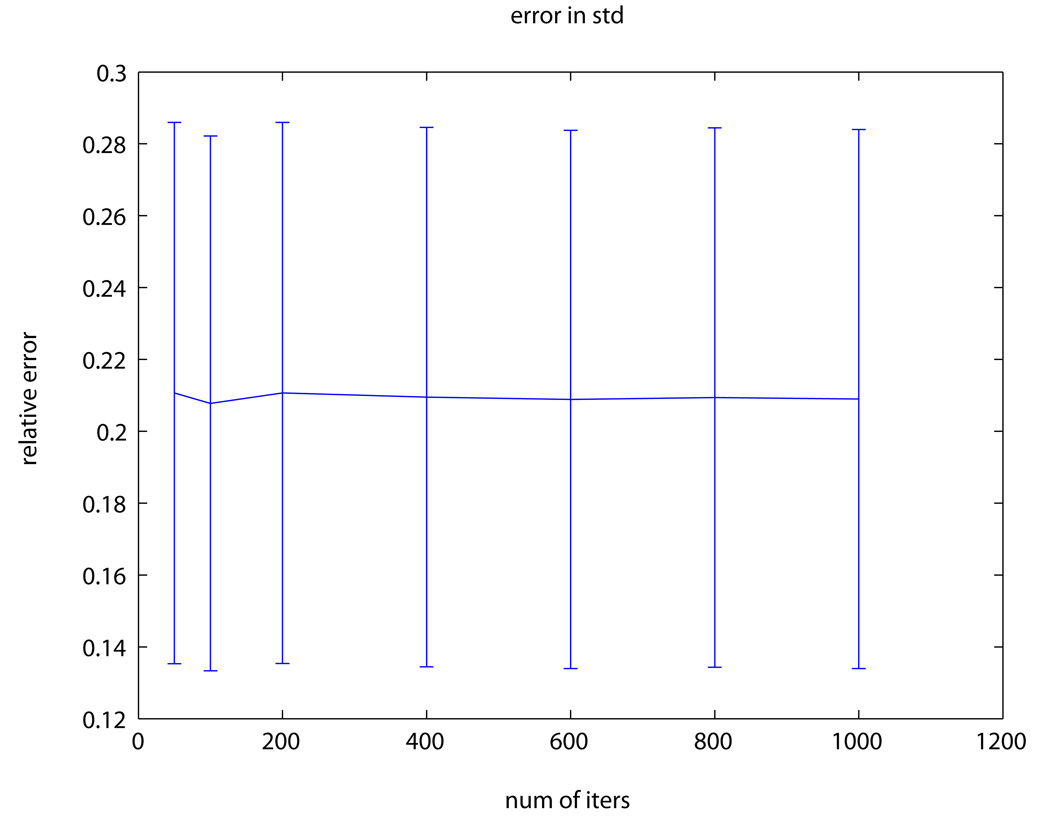
Fig. 1 presents the DW-MRI image used in the experiment, the “ground-truth” uncertainty map, the estimated uncertainty map computed from one of the stabilized phantom datasets and the estimated uncertainty computed from the vibrated phantom dataset. As expected, our method estimated higher uncertainty in the vibrated phantom dataset (41%) compared to the stabilized phantom datasets (~21%).

Fig. 1.

ACR phantom experiment: (a) DW-MRI image of the ACR phantom with b-value=50s/mm²; pixels used for evaluation are marked in red. (b) The “ground-truth” ADC uncertainty. (c–d) Estimated ADC uncertainty using our method from a (c) stabilized phantom dataset and (d) vibrated phantom dataset. (e) RMS error between our estimation and the “ground-truth” using a varying number of bootstrap resampling iterations.

Fig. 1e presents the relative error between the estimated and the groundtruth uncertainty maps. Our method estimated the uncertainty with an average (std) error of 21% (6.5%) of the “ground-truth” value. Increasing the number of bootstrap resampling iterations, however, did not yield any significant improvement in the uncertainty estimation accuracy.

3.2 Human subject experiment

Five (5) body DW-MRI datasets of a healthy human subject were acquired as in the ACR phantom experiment (Sec. 3.1) during free-breathing of the subject. A multi-exponential diffusion model was fitted to each dataset using Eq. 4. The performance of our method was evaluated using same methodology as in the ACR phantom experiment (Sec. 3.1).

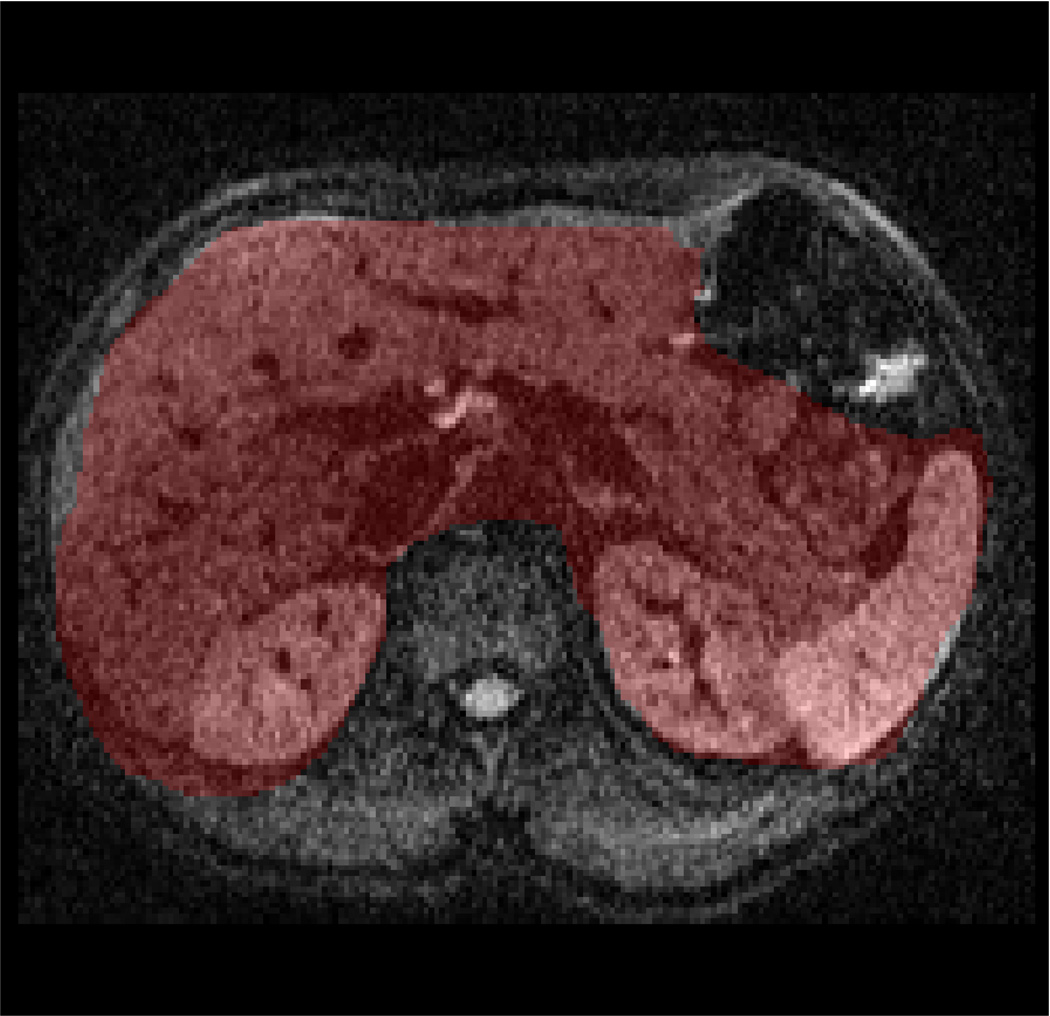
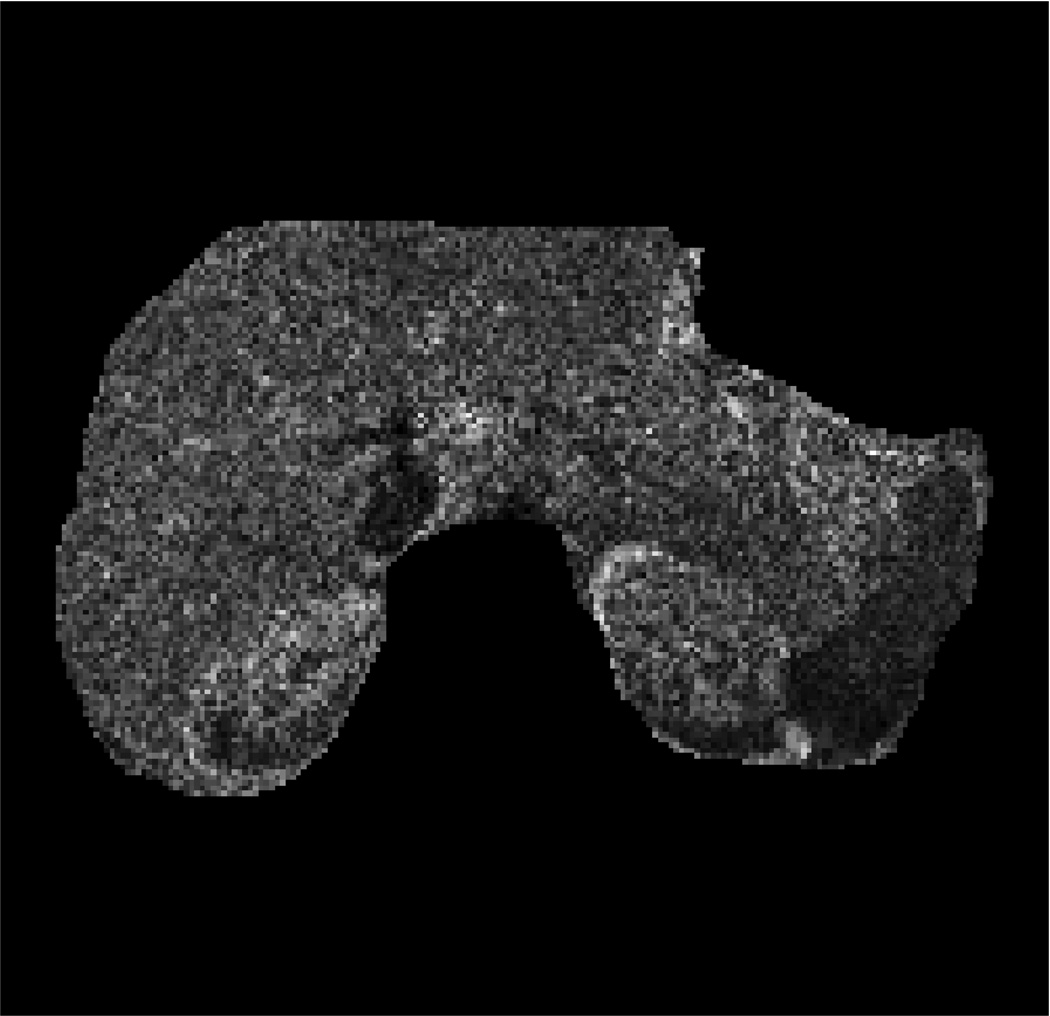
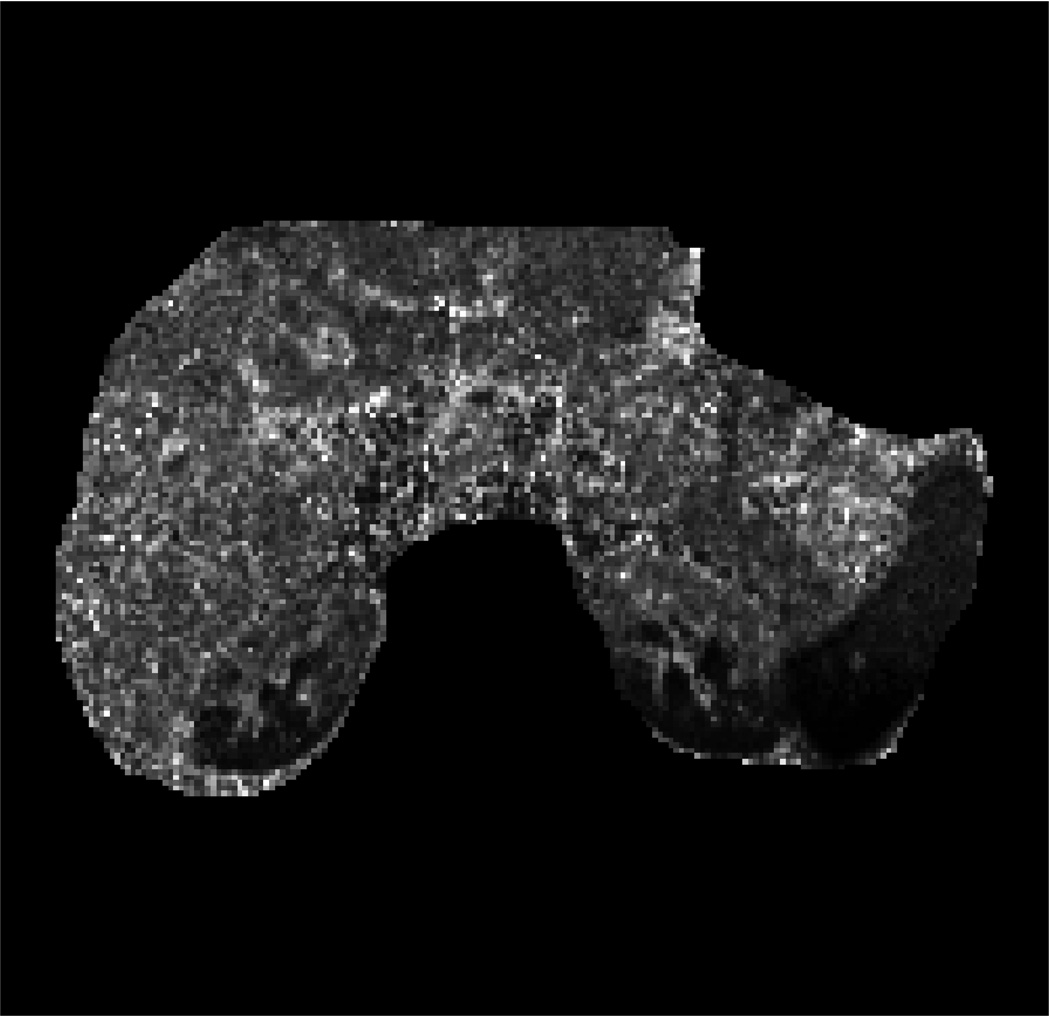
Fig. 2 presents the DW-MRI image acquired with b-value=200s/mm², the ADC map computed using one of the datasets, the “ground-truth” uncertainty map, and the estimated uncertainty map. Our method identify the organ boundaries as the regions with the highest uncertainty, due to the respiratory motion effect on these regions. The uncertainty in the liver is higher than that in the kidneys and the spleen due to the larger effect of respiratory motion on the liver.

Fig. 2.

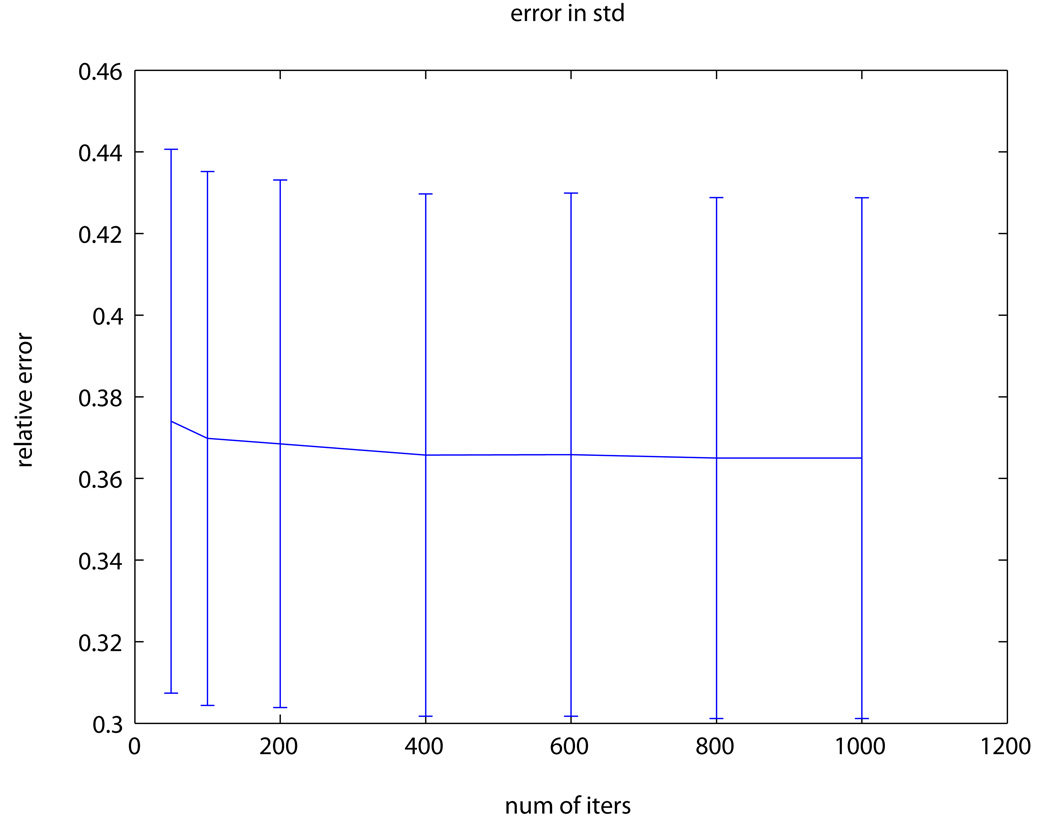
Human subject experiment: (a) Body DW-MRI image with b-value=200s/mm²; pixels used for evaluation are marked in red. (b) ADC map obtained by fitting the multi-exponential model to one of the datasets. (c) The “ground-truth” ADC uncertainty. (d) Estimated ADC uncertainty using our method from one of the datasets. (e) Relative error between our estimation and the “ground-truth” using a varying number of bootstrap resampling iterations.

Fig. 2e presents the relative error between the estimated uncertainty and the ground-truth uncertainty. Our method estimated the uncertainty accurately with an average (std) error of 36.8% (6.2%) of the ground-truth value. Increasing the number of bootstrap resampling iterations did not, however, yield significant improvement in the uncertainty estimation accuracy. Similar relative error was obtained for the estimation of the uncertainty in the perfusion comparatment (PER). Higher uncertainty values and larger estimation errors were observed in the human imaging study; these numbers are primarily driven by motion artifact (i.e., breathing) that typically takes place during any acquisition with DW-MRI.

4 Conclusions

We have presented a new Unscented wild-bootstrap method for the estimation of diffusion model parameters uncertainty in body MR-DWI imaging. The estimation of the model parameters uncertainty is necessary to achieve quantitative clinical assessment of body DW-MRI biomarkers. The main advantage of our method is two-fold: First, it does not require repeated acquisitions, which is undesirable in routine clinical applications; and second, it is not limited to underlying linear models that are less suitable in body DW-MRI. Evaluation of our method against uncertainty estimations obtained by repeated acquisitions of both phantom and human subject DW-MRI data shows that our method can estimate the uncertainty associated with a multi-exponential body diffusion model fit accurately without repeated acquisitions.