Abstract
A variable dielectric model based on residue types for better description of protein-ligand electrostatics in MM-GBSA scoring is reported. The variable dielectric approach provides better correlation with binding data and reduces the score dynamic range, typically observed in the standard MM-GB/SA method. The latter supports the view that exaggerated enthalpic separation between weak and potent compounds due to the lack of shielding effects in the model is greatly responsible for the wide scoring spread.
Introduction
Molecular Mechanics based scoring methods using all atom force fields coupled with Poisson-Boltzman (MM-PB/SA)1 or Generalized Born calculations (MM-GB/SA)2 to model solvation have recently seen an upsurge in popularity. When compared to docking scoring functions, the physics-based methods provide improved enrichment in the virtual screening of databases and better correlation between calculated binding affinities and experimental data.3 Their main purpose is to rescore docking poses in order to circumvent limitations of the docking scoring functions, in particular the ones associated with desolvation, intramolecular, and entropy penalties for the ligands upon binding.
We investigated the performance of our own flavor of MM-GB/SA when rescoring docking poses of congeneric series for pharmaceutically relevant targets.4 The correlations with experiment obtained with the physics-based scoring were far superior to the ones obtained with the Glide XP scoring function and competitive with the computationally intensive FEP methods.4,5 Despite showing good accuracy when applied within a series, much work is necessary to improve the MM-GB/SA method and gain greater efficiency in drug design. For example, MM-GB/SA suffers from poor estimation of protein desolvation and a large dynamic range observed in the scoring when compared to the experimental range.
In the case of the GB/SA protein desolvation, substituting this term by the free energy associated with displacing binding-site waters upon ligand binding estimated by the WaterMap method,6 which treats the solvent explicitly, provides superior results.4b,7 As for the large theoretical dynamic range for the binding energies, that seems to be a direct result of the degree of sampling since FEP simulations with restricted flexibility as well as MM-GB/SA approaches that make use of a single configuration for the protein-ligand complexes are plagued by this.4a Computational van’t Hoff analysis suggests that the wider scoring spread is not only affected by missing entropic contributions due to restricted sampling, but also exaggerated enthalpic separation between compounds.4a
One plausible cause for the exaggerated enthalpic gap is the application of an internal dielectric constant (εin) of 1 in a model where protein motions and polarization are not taken into account. Hence, electrostatic interactions are not shielded enough and protein-ligand electrostatic attractions and repulsions are overestimated, causing the large separation between potent and weak compounds.4a,4b As previously described, when the protein permanent dipoles are included explicitly but their relaxation, i.e., the protein reorganization, and the protein induced dipoles are considered implicitly, the value of εin is not well defined.8 Warshel and coworkers suggest that εin should be between 4 and 6 for dipole-charge interactions and 10 for charge-charge interactions.9,10 More recently, a variable dielectric model has been developed to increase the accuracy in protein side chain and loop predictions.11 The authors introduced an energy model where εin is allowed to vary as a function of the interacting residues.
In this work, we explore the use of a variable dielectric model based on residue types to alleviate the overestimation of electrostatic effects between protein residues and ligands for improved MM-GBSA scoring. Since poor description of protein-ligand electrostatic interactions could not only result in a wider scoring spread but also affect the correlation with experiment, we decided to use binding data to derive the set of variable dielectric constants. Specifically, the pharmaceutically relevant targets CDK2, FactorXa, p38, and PDE10A and respective congeneric series were considered in the optimization process that led to the set of variable dielectric constants, subsequently tested on two additional datasets, the human Carbonic Anhydrase (hCAII) and a second p38 chemical series.
Methods
Datasets and System Setup
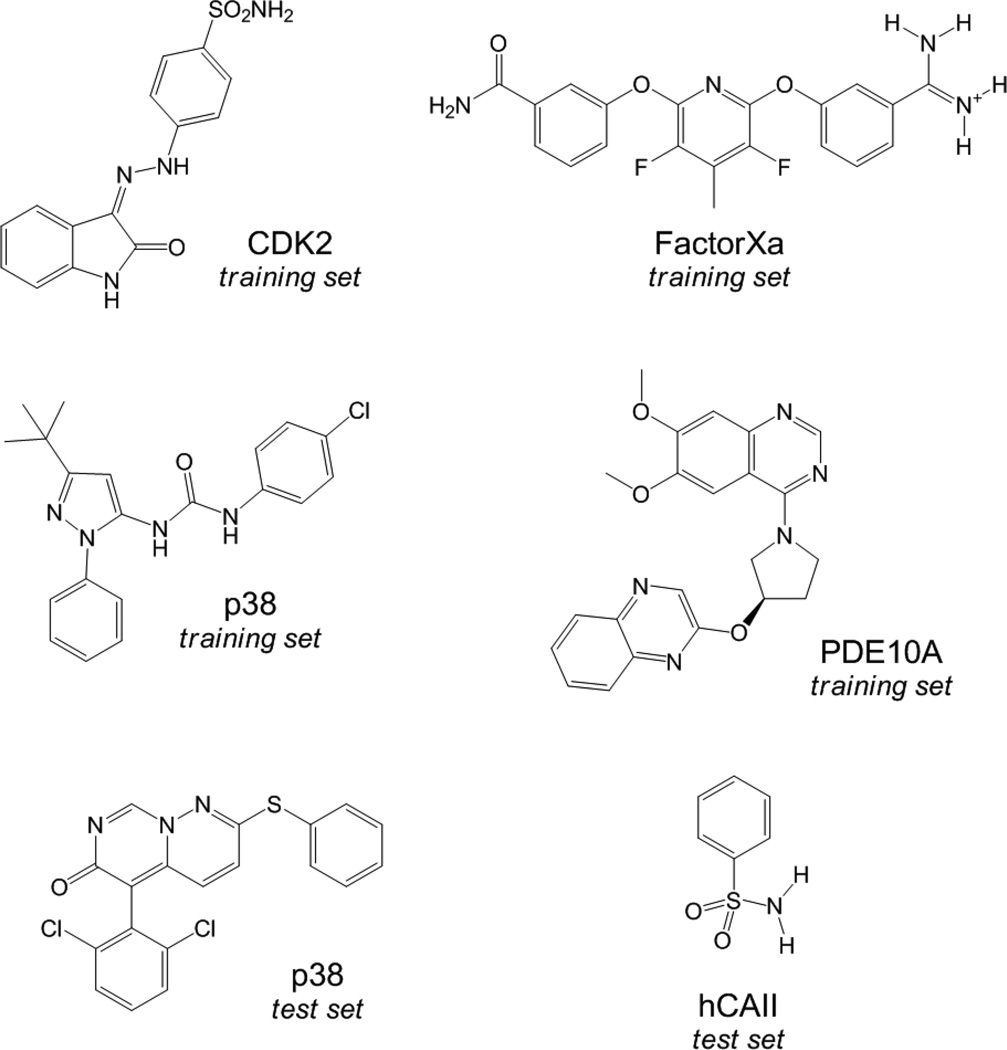
The crystal structures for CDK2 (PDB ID: 1E9H), FactorXa (PDB ID: 1FJS), PDE10A (unpublished structure), both p38 chemical series (PDB ID’s: 1KV1 and 1OUY), and hCAII (PDB ID: 2WEJ) were selected. The 1E9H CDK2 structure was modified as described before4c as it is not consistent with the conditions for the biological assay. All complexes were submitted to a series of restrained, partial minimizations using the OPLS_2005 force field12 within Macromodel.13 Prior to the docking calculations using Glide XP,14 the selected congeneric series of CDK2,15 FactorXa,16 PDE10A,17 p38,18,19 hCAII,20 were submitted to a pre-energy minimization using the OPLS_2005 force field and the GB/SA method as the implicit water model.21 Representative structures for each chemical series are illustrated in Figure 1. Tables with all derivatives and binding data can be found in the supporting information. In order to accommodate for the fact that the protein structure used for docking will not in general be optimized to fit a particular ligand, the van der Waals radii for non-polar protein atoms were scaled by a factor of 0.8, while those for the ligands were not scaled.
Figure 1.
Representative structures for the congeneric series used in this work. Tables with all derivatives and binding data can be found in the supporting information.
MM-GB/SA Rescoring
Our implementation of the MM-GB/SA rescoring procedure (eq 1) has been described in details elsewhere.4 In eq 1, ΔEintra and ΔGsolv are the intramolecular strain and desolvation penalty for each ligand upon binding. The conformational entropies (Sconf) in solution were computed from the probabilities (Pi) assuming a Boltzmann distribution (eq 2), where kB is the Boltzmann constant. In the bound state, it was assumed that there was only one conformation accessible to each ligand; its conformational entropy is therefore zero. Thus, −TΔSconf is the ligand conformational entropy penalty, multiplied by the temperature to convert it into energy. EVDW and EElect are the protein-ligand intermolecular van der Waals and electrostatic interaction energies, respectively. EPTN, the protein energy in the bound state, describes the protein deformation or strain imposed by each ligand. EGB is the solvent shielding of protein-ligand electrostatic interactions estimated by the GB model. This term, generally not included in the scoring as it has no significant impact on the MM-GB/SA results,4 is necessary here as it depends on εin. Finally, is the protein desolvation term calculated by the continuum model. The final ranking is obtained by calculating relative binding energies, ΔΔGbind, using the top-scoring inhibitor as reference.
| (1) |
| (2) |
The conformational search for the inhibitors in the unbound state and energy minimization for the complexes were performed with BOSS and MCPRO,22 respectively, instead of Macromodel.13 This was done with the purpose of facilitating the implementation of the variable dielectric approach. The Z matrixes for the complexes obtained from the docking calculations and ligands in the unbound state were prepared using the pepz program.22 The proteins were considered in their entirety. The protonation states of histidine side chains were assigned with the assistance of the software PROPKA 2.0.23 Charge neutrality for the protein systems in MCPRO was imposed by assigning normal protonation states at physiological pH to basic and acidic residues near the active site and making the adjustments for neutrality to the most distant residues. The OPLS-AA force field was used for the protein.12a The energetics for the ligands were represented with the OPLS/CM1A force field.24 The CM1A atomic charges for the neutral ligands were scaled by 1.14.25 The GB/SA solvation model implemented in BOSS and MCPRO was used.26
The variable dielectric formalism and implementation
The focus here is to obtain a set of dielectric constants based on residue types that improves MM-GB/SA scoring. Protein intramolecular electrostatic interactions were not considered in the optimization process as the set of optimal dielectric constants for each residue-residue pair is not necessarily the best it can be obtained to improve the description of ligand-residue electrostatic interactions. In addition, the EPTN values within a congeneric series generally fall in a very narrow range due to the constrains applied in the energy minimizations for the complexes.4 As this term behaves almost like a constant, it was excluded from the scoring equation used to develop the variable dielectric formalism. Although , like EPTN, depends on εin, it was also excluded from the scoring equation as it is usually very noisy and deteriorates the correlation with experimental data.4b,4c The energy minimizations for the complexes, however, are performed using GB/SA.
Eqs 3 and 4 describe the protein-ligand electrostatic interactions and the solvent shielding estimated by the GB model, respectively, where qi and qj are charges on atom i belonging to the protein and j belonging to ligand, rij is their distance, εin is the internal dielectric constant, εsol is the dielectric constant in water, and αij is the geometric average of the Born radii αi and αj.
| (3) |
| (4) |
If εin adopts different values depending on the residue type k interacting with the ligand, eqs 3 and 4 have to be rewritten as shown in eqs 5 and 6. The dielectric constant εin(k) is assigned for the interactions between all atoms i belonging to the residue type k and the ligand atoms j. The side chains for all polar (Ser, Thr, Asn, Gln) and ionizable residues (His, Lys, Arg, Asp, Glu), which are expected to be more polarizing, were considered individually in the optimization. All remaining residue side chains and backbone atoms were bundled in a group called “other”. For simplicity, neutral and protonated states of the ionizable residues were not treated separately. The dielectric constant εin(k) for a given residue-ligand pair is the same whether the residue interacts with a neutral or charged ligand.
| (5) |
| (6) |
Five different values (1, 2, 4, 8, and 20) were considered for every residue type (Ser, Thr, Asn, Gln, His, Lys, Arg, Asp, Glu, and other). Computational efficiency was achieved by obtaining the inner summation terms in eqs 5 and 6 for every residue k through one single point calculation per complex using the geometries obtained with εin equals 1. No cutoffs were applied to the protein-ligand electrostatic interactions. The inner summation terms were then combined with 510 dielectric constant permutations outside of MCPRO to generate the MM-GB/SA scores corresponding to each set of EElect and EGB values. Their performance against the experimental data was judged based on correlation coefficients (R2) and predictive indices (PI).19 The latter is a measure of how accurate the predicted rank order is compared to the experiment, with −1, 0, and +1 meaning opposite, random, or perfect predictions, respectively. The set of dielectric constants that overall provided the best R2 and PI values for the training set targets and ligands was selected and then tested on two additional datasets.
Results and Discussion
Residue-based dielectric constant optimization
In the optimization process, 510 combinations of dielectric constants based on the residue type were generated for each system in the training set, CDK2, FactorXa, PEDE10A, and the p38 urea series (p38_u). The combinations that provided the MM-GB/SA scores with the best agreement with binding data based on R2 and PI values for each target individually were set aside. Table 1 illustrates the combinations for each target that maximized R2 and PI separately. Although the combinations listed on Table 1 are the very best for each system according to each metric, there were few other solutions that provided just slightly worse results. The set of optimal dielectrics constants for all targets simultaneously was derived by verifying the combination whose R2 and PI values deviated the least from each individual’s best (Table 1).
Table 1.
Optimal set of residue-based dielectric constants (εin(k)) for the targets individually and best overall.
| Res Type | CDK2 | FactorXa | PDE10A | p38_u | Optimal | ||||
|---|---|---|---|---|---|---|---|---|---|
| Ser | 20 | 1 | 1 | 1 | 20 | 1 | 20 | 20 | 1 |
| Thr | 20 | 2 | 20 | 2 | 1 | 2 | 1 | 1 | 4 |
| Asn | 1 | 1 | 20 | 1 | 20 | 8 | 1 | 4 | 2 |
| Gln | 1 | 1 | 1 | 20 | 4 | 2 | 1 | 1 | 1 |
| His | 20 | 1 | 20 | 20 | 20 | 1 | 1 | 20 | 4 |
| Lys | 2 | 2 | 20 | 1 | 20 | 20 | 1 | 1 | 2 |
| Arg | 1 | 1 | 1 | 1 | 2 | 1 | 20 | 20 | 20 |
| Asp | 1 | 8 | 20 | 20 | 2 | 20 | 20 | 20 | 2 |
| Glu | 20 | 20 | 1 | 1 | 1 | 1 | 20 | 20 | 8 |
| Other | 1 | 1 | 4 | 8 | 20 | 4 | 20 | 2 | 4 |
| R2=0.56 | PI=0.76 | R2=0.68 | PI=0.90 | R2=0.53 | PI=0.71 | R2=0.58 | PI=0.75 | ||
Figure 2 shows the polar and ionizable residues within 6 Å from the ligands depicted in Figure 1 for not only the systems that belong to the training set, but also to the test set, hCAII and the p38 pyridazo-pyrimidinone (p38_pp) series. As electrostatic interactions are very long range, it is obvious that polar and ionizable residues beyond 6 Å are also relevant; their interactions with the ligands are included in EElect and EGB. Although the optimal set of dielectric constants is a function of the specific residue-ligand interactions in the training set and inaccuracies in the charges of the force-field of choice, it is tempting to physically interpret the εin(k) values obtained. Here, Arg and Glu have the largest εin(k) values, 20 and 8, respectively, which seems reasonable since those residues, very flexible and polarizing, can be more easily shielded. The optimal value for Asp, with a shorter side chain and reduced flexibility when compared to Glu, is 2. Interestingly, a much smaller dielectric constant was obtained for Lys in contrast to the one for Arg. In a study of residue density in proteins,27 it became evident that in spite of evolutionary relatedness, Arg is more buried, more frequently involved in salt bridges, hydrogen bonds, and cationic-aromatic contacts. It is then plausible that a larger εin(k) value than Lys emerges for Arg in the optimization process. In the case of the polar and the ionizable His residues, found to be in its neutral state in the majority of the cases here, the εin(k) values are fairly small, ranging from 1 to 4. For three of the five residues, the dielectric constants seem to be correlated with the magnitude of the side chain dipole moments, with the εin(k) value for His > Asn > Ser. As for Gln and Thr, the dielectric constants obtained seem to be counterintuitive when compared to their closest analogs, Asn and Ser, respectively. The optimal εin(k) value for the more flexible side chain of the pair is actually smaller; this might be a function of the specific residue distributions for the targets in the training set. Finally, the εin(k) value of 4 for the set that contains all remaining side chains might be somewhat high because it also contains all backbone atoms.
Figure 2.
Ligands in their binding sites. Only the polar and ionizable residues within 6 Å from each ligand are shown for CDK2, Factor Xa, PDE10A, hCAII, and p38 urea (p38_u) pyridazo-pyrimidinone (p38_pp) series.
Standard versus variable dielectric MM-GB/SA scoring
It should be noted that the variable dielectric approach was unable to recover some outliers in the training set in the preliminary rounds of dielectric constant optimization. Those compounds had to be ultimately excluded before the optimization round that led to the εin(k) values in Table 1. The number of outliers removed, both in the training and test sets, is listed in Table 2. Except for CDK2, the outliers represent between 0% and 15% of the compounds in each series and are highlighted in the Tables provided in the supporting information. The balance between the number of remaining binding datapoints in the training set (110) and the number of adjustable εin(k) values (10), a 11:1 ratio, seems appropriate and suggests that the set of dielectric constants obtained might be applied more widely. Table 2 illustrates the R2 and PI values obtained using the standard and variable dielectric MM-GB/SA scoring procedures, the latter using the optimal εin(k) values in Table 1. The results where EElect and EGB are removed from the scoring equation are also included for comparison. They provide a baseline for the cases where the standard dielectric MM-GB/SA performs poorly. In those cases, the variable dielectric approach should at least outperform the scoring equation with EElect and EGB removed.
Table 2.
MM-GB/SA results using standard and variable dielectric protein-ligand electrostatics.
| Target | Na | Outb | R2 STDc |
R2 NOd |
R2 VARe |
PI STD |
PI NO |
PI VAR |
DRf STD |
DR NO |
DR VAR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CDK2 | 36 | 7 | 0.48 | 0.41 | 0.52 | 0.69 | 0.66 | 0.73 | 17.6 | 13.7 | 13.1 |
| FactorXa | 22 | 3 | 0.59 | 0.09 | 0.66 | 0.84 | 0.37 | 0.87 | 14.8 | 6.3 | 9.3 |
| PDE10A | 28 | 0 | 0.47 | 0.52 | 0.51 | 0.65 | 0.69 | 0.67 | 8.3 | 6.7 | 7.1 |
| p38_u | 36 | 2 | 0.33 | 0.56 | 0.55 | 0.46 | 0.67 | 0.71 | 20.9 | 21.0 | 21.9 |
| hCAII | 17 | 2 | 0.32 | 0.39 | 0.58 | 0.63 | 0.74 | 0.75 | 11.9 | 10.9 | 7.8 |
| p38_pp | 17 | 3 | 0.41 | 0.49 | 0.43 | 0.68 | 0.70 | 0.70 | 10.5 | 9.4 | 10.5 |
Number of total compounds in each series.
Number of outliers removed.
Standard dielectric protein-ligand electrostatics (STD).
No protein-ligand electrostatics. EElect and EGB are removed from the scoring equation (NO).
Variable dielectric protein-ligand electrostatics (VAR).
Score dynamic range (DR) in kcal/mol.
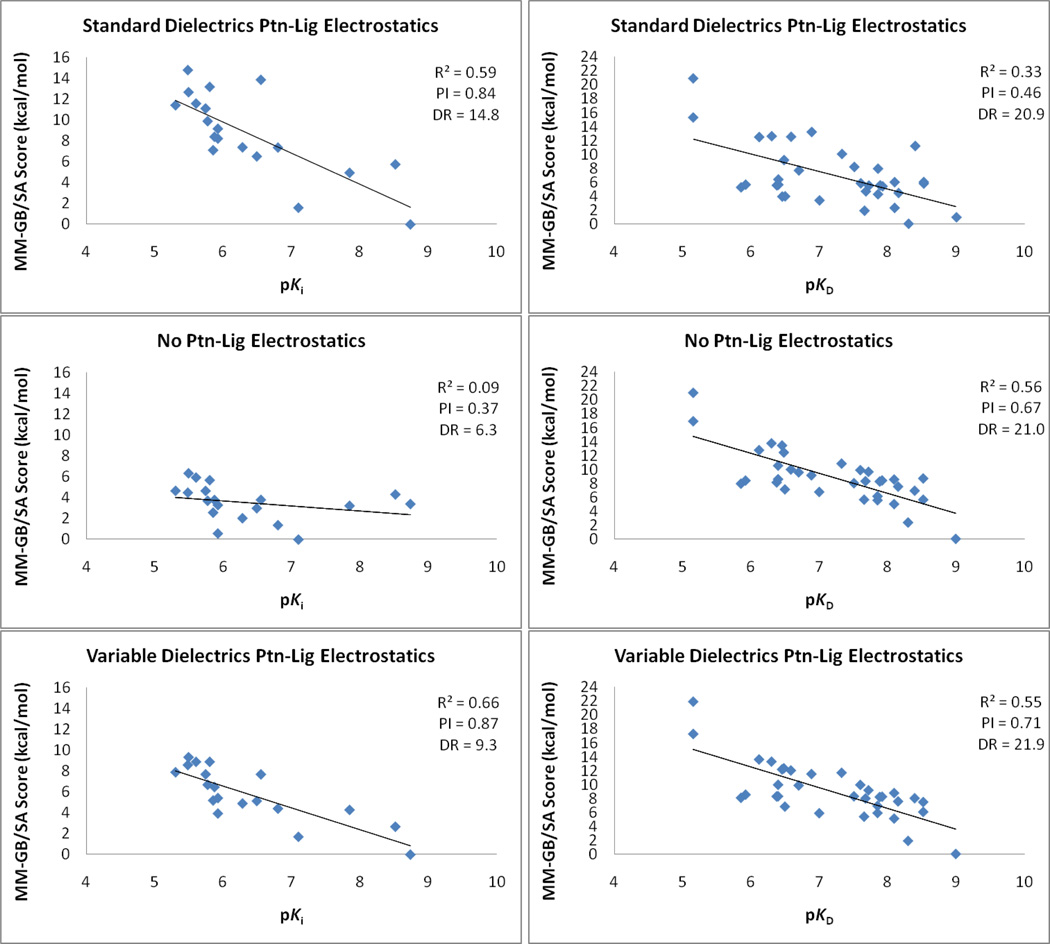
It is disturbing that the scoring equation with no protein-ligand electrostatics performs better than the standard MM-GB/SA in four out of the six systems (Table 2). Factor Xa, where EElect and EGB are critical, and CDK2, where they marginally improve the results, are the only exceptions. In Factor Xa, the most potent compounds of the series establish a key hydrogen bond with the catalytic triad Ser residue (Figure 2), unable to be described without the electrostatic terms. Although it is difficult to pinpoint whether the deterioration of the correlation with experimental data when EElect and EGB are introduced has its origin in the force field charges, the lack of explicit polarization, or the lack of dynamical screening due to the use of a single structure for the complex, it is clear that the variable dielectric approach improves the description of protein-ligand electrostatics. It performs better than standard dielectrics in all cases, including the two systems in the test set, hCAII and p38_pp. Figure 3 illustrates the results for Factor Xa and p38_u using the different MM-GB/SA scoring approaches. Plots for all systems can be found in the supporting information.
Figure 3.
MM-GB/SA scoring versus experiment using standard and variable dielectric protein-ligand electrostatics, and with the EElect and EGB terms removed for two systems, Factor Xa (left) and p38_u (right).
It is also reassuring that the performance of the variable dielectric approach is at least equivalent or superior to the scoring equation with EElect and EGB removed. A scoring method that describes protein-ligand electrostatic interactions properly as well as the fine balance with the desolvation penalty process is highly desirable since the introduction of polarity, which drives the compound to a better property space,28 often kills or attenuates binding affinity. One should note that the variable dielectric approach will not necessarily provide significant improvements over the standard electrostatic treatment for all cases. This is illustrated in Table 2 for a couple of systems, PDE10A and p38_pp. In those instances, the residues around the ligand are mostly non-polar, and the electrostatic interactions between them are not appreciably large (Figure 2). Specifically, the combined EElect and EGB terms for all ligands in the congeneric series obtained with εin equals 1 range from −1.9 to −0.2 kcal/mol and −3.6 to 0.0 kcal/mol for PDE10A and p38_pp, respectively. In other words, protein-ligand electrostatic interactions play a minor role in the rank-ordering for the PDE10A and p38_pp and the attenuation or exclusion of EElect and EGB has no impact on the results. This contrasts to p38_u, for example, with a much wider range (−11.8 to +1.9 kcal/mol) for the combined EElect and EGB terms. The protein conformation (DFG out) for p38, the chemical series, and binding mode are very different, with the urea group establishing hydrogen bonds with a Glu residue and a backbone NH (Figure 2). In this case, the variable dielectric approach greatly help since EElect and EGB are relevant. Finally, Table 2 indicates that the variable dielectric approach reduces the score dynamic range (DR) in four of the six systems, although no attempt has been made to improve DR in the optimization process. This supports the view that the exaggerated protein-ligand electrostatic interactions due to the lack of shielding effects in the standard MM-GB/SA model is indeed a key factor in its wide scoring spread.
Supplementary Material
Acknowledgements
The authors thank the Computational Sciences Center of Emphasis at Pfizer and the National Institutes of Health (GM32136 and AI44616) for support.
Footnotes
Supporting Information. Tables with all derivatives and binding data and plots of the multiple MM-GB/SA approaches against the experiment for all systems can be found in the supporting information.
References
- 1.Barril X, Gelpí JL, López JM, Orozco M, Luque FJ. How accurate can molecular dynamics/linear response and Poisson–Boltzmann/solvent accessible surface calculations be for predicting relative binding affinities? Acetylcholinesterase huprine inhibitors as a test case. Theor. Chem. Acc. 2001;106:2–9. [Google Scholar]
- 2.Kuhn B, Kollman PA. Binding of a diverse set of ligands to avidin and streptavidin: An accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. J. Med. Chem. 2000;43:3786–3791. doi: 10.1021/jm000241h. [DOI] [PubMed] [Google Scholar]
- 3.(a) Hou T, Wang J, Li Y, Wang W. Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. J. Chem. Inf. Model. 2011;51:69–82. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Haider MK, Bertrand H-O, Hubbard RE. Predicting fragment binding poses using a combined MCSS MM-GBSA approach. J. Chem. Inf. Model. 2011;51:1092–1105. doi: 10.1021/ci100469n. [DOI] [PubMed] [Google Scholar]; (c) Lee MR, Sun Y. Improving docking accuracy through molecular mechanics generalized Born optimization and scoring. J. Chem. Theory Comput. 2007;3:1106–1119. doi: 10.1021/ct6003406. [DOI] [PubMed] [Google Scholar]; (d) Foloppe N, Hubbard R. Towards predictive ligand design with free-energy based computational methods? Curr. Med. Chem. 2006;13:3583–3608. doi: 10.2174/092986706779026165. [DOI] [PubMed] [Google Scholar]; (e) Huang N, Kalyanaraman C, Irwin JJ, Jacobson MP. Physics-based scoring of protein-ligand complexes: Enrichment of known inhibitors in large-scale virtual screening. J. Chem. Inf. Model. 2006;46:243–253. doi: 10.1021/ci0502855. [DOI] [PubMed] [Google Scholar]; (f) Huang N, Kalyanaraman C, Bernacki K, Jacobson MP. Molecular mechanics methods for predicting protein–ligand binding. Phys. Chem. Chem. Phys. 2006;8:5166–5177. doi: 10.1039/b608269f. [DOI] [PubMed] [Google Scholar]; (g) Lyne PD, Lamb ML, Saeh JC. Accurate prediction of the relative potencies of members of a series of kinase inhibitors using molecular docking and MM-GBSA scoring. J. Med. Chem. 2006;49:4805–4808. doi: 10.1021/jm060522a. [DOI] [PubMed] [Google Scholar]
- 4.(a) Guimarães CRW. A direct comparison of the MM-GB/SA scoring procedure and free-energy perturbation calculations using Carbonic Anhydrase as a test case: Strengths and pitfalls of each approach. J. Chem. Theory Comput. 2011;7:2296–2306. doi: 10.1021/ct200244p. [DOI] [PubMed] [Google Scholar]; (b) Guimarães CRW, Mathiowetz AM. Addressing limitations with the MM-GB/SA scoring procedure using the WaterMap method and free-energy perturbation calculations. J. Chem. Inf. Model. 2010;50:547–559. doi: 10.1021/ci900497d. [DOI] [PubMed] [Google Scholar]; (c) Guimarães CRW, Cardozo M. MM-GB/SA rescoring of docking poses in structure-based lead optimization. J. Chem. Inf. Model. 2008;48:958–970. doi: 10.1021/ci800004w. [DOI] [PubMed] [Google Scholar]
- 5.(a) Guimarães CRW, Boger DL, Jorgensen WL. Elucidation of fatty acid amide hydrolase inhibition by potent α-ketoheterocycle derivatives from Monte Carlo simulations. J. Am. Chem. Soc. 2005;127:17377–17384. doi: 10.1021/ja055438j. [DOI] [PubMed] [Google Scholar]; (b) Simonson T, Georgios A, Karplus M. Free energy simulations come of age: Protein-ligand recognition. Acc. Chem. Res. 2002;35:430–437. doi: 10.1021/ar010030m. [DOI] [PubMed] [Google Scholar]; (c) Jorgensen WL. Free energy changes in solution. In: Schleyer PvR., editor. Encyclopedia of Computational Chemistry. Vol. 2. New York: Wiley; 1998. pp. 1061–1070. [Google Scholar]; (d) Kollman PA. Free energy calculations: Applications to chemical and biochemical phenomena. Chem. Rev. 1993;93:2395–2417. [Google Scholar]; (e) Jorgensen WL. Free energy calculations: A breakthrough for modeling organic chemistry in solution. Acc. Chem. Res. 1989;22:184–189. [Google Scholar]
- 6.Abel R, Young T, Farid R, Berne BJ, Friesner RA. Role of the active-site solvent in the thermodynamics of Factor Xa ligand binding. J. Am. Chem. Soc. 2008;130:2817–2831. doi: 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Abel R, Salam NK, Shelley J, Farid R, Friesner RA, Sherman W. Contribution of explicit solvent effects to the binding affinity of small-molecule inhibitors in blood coagulation factor serine proteases. ChemMedChem. 2011;6:1049–1066. doi: 10.1002/cmdc.201000533. [DOI] [PubMed] [Google Scholar]
- 8.Schutz CN, Warshel A. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 9.Sham YY, Muegge I, Warshel A. The effect of protein relaxation on charge– charge interactions and dielectric constants of proteins. Biophys. J. 1998;74:1744–1753. doi: 10.1016/S0006-3495(98)77885-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Muegge I, Schweins T, Langen R, Warshel A. Electrostatic control of gtp and gdp binding in the oncoprotein p21 ras. Structure. 1996;4:475–489. doi: 10.1016/s0969-2126(96)00052-4. [DOI] [PubMed] [Google Scholar]
- 11.Zhu K, Shirts MR, Friesner RA. Improved methods for side chain and loop predictions via the protein local optimization program: Variable dielectric model for implicitly improving the treatment of polarization effects. J. Chem. Theory Comput. 2007;3:2108–2119. doi: 10.1021/ct700166f. [DOI] [PubMed] [Google Scholar]
- 12.(a) Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]; (b) Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WJ. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- 13.MacroModel. version 9.0. New York, NY: Schrödinger, LLC; 2005. [Google Scholar]
- 14.(a) Friesner RA, Banks JL, Murphy RB, Halgren TA, Klicic JJ, Mainz DT, Repasky MP, Knoll EH, Shelley M, Perry JK, Shaw DE, Francis P, Shenkin PS. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem. 2004;47:1739–1749. doi: 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]; (b) Friesner RA, Murphy RB, Repasky MP, Frye LL, Greenwood JR, Halgren TA, Sanschagrin PC, Mainz DT. Extra precision Glide: docking and scoring incorporating a model of hydrophobic enclosure for protein-ligand complexes. J. Med. Chem. 2006;49:6177–6196. doi: 10.1021/jm051256o. [DOI] [PubMed] [Google Scholar]
- 15.Bramson HN, Corona J, Davis ST, Dickerson SH, Edelstein M, Frye SV, Gampe RT, Harris JPA, Hassell A, Holmes WD, Hunter RN, Lackey KE, Lovejoy B, Luzzio MJ, Montana V, Rocque WJ, Rusnak D, Shewchuk L, Veal JM, Walker DH, Kuyper LF. Oxindole-based inhibitors of Cyclin-Dependent Kinase 2 (CDK2): Design, synthesis, enzymatic activities, and X-ray crystallographic analysis. J. Med. Chem. 2001;44:4339–4358. doi: 10.1021/jm010117d. [DOI] [PubMed] [Google Scholar]
- 16.(a) Phillips G, Davey DD, Eagen KA, Koovakkat SK, Liang A, Ng HP, Pinkerton M, Trinh L, Whitlow M, Beatty AM, Morrissey MM. Design, synthesis, and activity of 2,6-diphenoxypyridine-derived Factor Xa inhibitors. J. Med. Chem. 1999;42:1749–1756. doi: 10.1021/jm980667k. [DOI] [PubMed] [Google Scholar]; (b) Phillips G, Guilford WJ, Buckman BO, Davey DD, Eagen KA, Koovakkat S, Liang A, McCarrick M, Mohan R, Ng HP, Pinkerton M, Subramanyam B, Ho E, Trinh L, Whitlow M, Wu S, Xu W, Morrissey MM. Design, synthesis, and activity of a novel series of Factor Xa inhibitors: Optimization of arylamidine groups. J. Med. Chem. 2002;45:2484–2493. doi: 10.1021/jm0200660. [DOI] [PubMed] [Google Scholar]
- 17.(a) Verhoest PR, Chapin DS, Corman M, Fonseca K, Harms JF, Hou X, Marr ES, Menniti FS, Nelson F, O’Connor R, Pandit J, Proulx-LaFrance C, Schmidt AW, Schmidt CJ, Suiciak JA, Liras S. Discovery of a novel class of Phosphodiesterase 10A inhibitors and identification of clinical candidate 2-[4-(1-Methyl-4-pyridin-4-yl-1H-pyrazol-3-yl)-phenoxymethyl]-quinoline (PF-2545920) for the treatment of schizophrenia. J. Med. Chem. 2009;52:5188–5196. doi: 10.1021/jm900521k. [DOI] [PubMed] [Google Scholar]; (b) Chappie TA, Humphrey JM, Allen MP, Estep KG, Fox CB, Lebel LA, Liras S, Marr ES, Menniti FS, Pandit J, Schmidt CJ, Tu M, Williams RD, Yang FY. Discovery of a series of 6,7-dimethoxy-4-pyrrolidylquinazoline PDE10A inhibitors. J. Med. Chem. 2007;50:182–185. doi: 10.1021/jm060653b. [DOI] [PubMed] [Google Scholar]
- 18.Regan J, Breitfelder S, Cirillo P, Gilmore T, Graham AG, Hickey E, Klaus B, Madwed J, Moriak M, Moss N, Pargellis C, Pav S, Proto A, Swinamer A, Tong L, Torcellini C. Pyrazole urea-based inhibitors of p38 MAP kinase: From lead compound to clinical candidate. J. Med. Chem. 2002;45:2994–3008. doi: 10.1021/jm020057r. [DOI] [PubMed] [Google Scholar]
- 19.Pearlman DA, Charifson PS. Are free energy calculations useful in practice? A comparison with rapid scoring functions for the p38 MAP kinase protein system. J. Med. Chem. 2001;44:3417–3423. doi: 10.1021/jm0100279. [DOI] [PubMed] [Google Scholar]
- 20.Scott AD, Phillips C, Alex A, Flocco M, Bent A, Randall A, O’Brien R, Damian L, Jones LH. Thermodynamic optimization in drug discovery: A case study using Carbonic Anhydrase inhibitors. Chem. Med. Chem. 2009;4:1985–1989. doi: 10.1002/cmdc.200900386. [DOI] [PubMed] [Google Scholar]
- 21.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990;112:6127–6129. [Google Scholar]
- 22.Jorgensen WL, Tirado-Rives J. Molecular modeling of organic and biomolecular systems using BOSS and MCPRO. J. Comput. Chem. 2005;26:1689–1700. doi: 10.1002/jcc.20297. [DOI] [PubMed] [Google Scholar]
- 23.Bas DC, Rogers DM, Jensen JH. Very fast prediction and rationalization of pKa values for protein–ligand complexes. Proteins. 2008;73:765–783. doi: 10.1002/prot.22102. [DOI] [PubMed] [Google Scholar]
- 24.Jorgensen WL, Tirado-Rives J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. USA. 2005;102:6665–6670. doi: 10.1073/pnas.0408037102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Udier-Blagovic M, Morales De Tirado P, Pearlman SA, Jorgensen WL. Accuracy of free energies of hydration from CM1 and CM3 atomic charges. J. Comput. Chem. 2004;25:1322–1332. doi: 10.1002/jcc.20059. [DOI] [PubMed] [Google Scholar]
- 26.Jorgensen WL, Ulmschneider JP, Tirado-Rives J. Free energies of hydration from a Generalized Born model and an all-atom force field. J. Phys. Chem. B. 2004;108:16264–16270. [Google Scholar]
- 27.Baud F, Karlin S. Measures of residue density in protein structures. Proc. Natl. Acad. Sci. USA. 1999;96:12494–12499. doi: 10.1073/pnas.96.22.12494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.(a) Hughes JD, Blagg J, Price DA, Bailey S, DeCrescenzo GA, Devraj R, Ellsworth E, Fobian YM, Gibbs ME, Gilles RW, Greene N, Huang E, Krieger-Burke T, Loesel J, Wager T, Whiteley L, Zhang Y. Physiochemical drug properties associated with in vivo toxicological outcomes. Bioorg. Med. Chem. Lett. 2008;18:4872–4875. doi: 10.1016/j.bmcl.2008.07.071. [DOI] [PubMed] [Google Scholar]; (b) Wager TT, Hou X, Verhoest PR, Villalobos A. Moving beyond rules: The development of a central nervous system multiparameter optimization (CNS MPO) approach to enable alignment of druglike properties. ACS Chem. Neurosci. 2010;1:420–434. doi: 10.1021/cn100008c. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.