Neural Modulation Tuning Characteristics Scale to Efficiently Encode Natural Sound Statistics

Abstract

The efficient-coding hypothesis asserts that neural and perceptual sensitivity evolved to faithfully represent biologically relevant sensory signals. Here we characterized the spectrotemporal modulation statistics of several natural sound ensembles and examined how neurons encode these statistics in the central nucleus of the inferior colliculus (CNIC) of cats. We report that modulation-tuning in the CNIC is matched to equalize the modulation power of natural sounds. Specifically, natural sounds exhibited a tradeoff between spectral and temporal modulations, which manifests as 1/f modulation power spectrum (MPS). Neural tuning was highly overlapped with the natural sound MPS and neurons approximated proportional resolution filters where modulation bandwidths scaled with characteristic modulation frequencies, a behavior previously described in human psychoacoustics. We demonstrate that this neural scaling opposes the 1/f scaling of natural sounds and enhances the natural sound representation by equalizing their MPS. Modulation tuning in the CNIC may thus have evolved to represent natural sound modulations in a manner consistent with efficiency principles and the resulting characteristics likely underlie perceptual resolution.

Introduction

According to ecological and efficiency principles, neural systems have evolved elaborate strategies to faithfully represent sensory signals experienced by an organism in its natural habitat (Attneave, 1954; Barlow, 1961). In the auditory system, sound information is first decomposed in the cochlea by a bank of frequency-selective hair cells. The structure and organization of this filterbank mirrors a short-term spectral decomposition that is near optimal for natural sounds (Lewicki, 2002; Smith and Lewicki, 2006). Unlike the cochlear receptors, neurons in central auditory structures are not only selective for the frequency content of a sound, but are also selective for spectrotemporal modulations that are found in wide variety of natural sounds (Theunissen et al., 2000; Escabí et al., 2003; Woolley et al., 2005) and are key information-bearing attributes (Chi et al., 1999; Singh and Theunissen, 2003; Elliott and Theunissen, 2009).

Analysis of natural sound has demonstrated that several statistical characteristics are highly conserved across natural sound ensemble (Voss and Clarke, 1975; Attias and Schreiner, 1998a; Nelken et al., 1999; Escabí et al., 2003; Singh and Theunissen, 2003). In particular, temporal modulations in natural sounds exhibit long-term temporal correlations that manifest as a 1/f modulation power spectrum (MPS). Several studies have argued that peripheral and central auditory neurons make use of such statistical regularities and are adapted and possibly optimized to efficiently encode natural sounds (Rieke et al., 1995; Attias and Schreiner, 1998b; Nelken et al., 1999; Escabí et al., 2003; Woolley et al., 2005; Lesica and Grothe, 2008; Holmstrom et al., 2010). Yet, it is presently not clear whether and to what extent the structure and organization of the ensemble of neural modulation filters in central auditory stations confer advantages for encoding natural sounds.

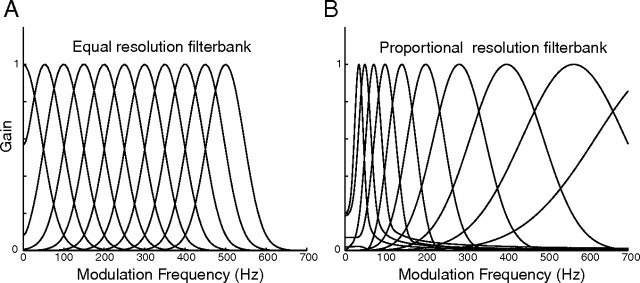
Neural sensitivity to sound modulations vary considerably across the population of neurons in the central nucleus of the inferior colliculus (CNIC) (Schreiner and Langner, 1988; Krishna and Semple, 2000; Woolley et al., 2005; Rodríguez et al., 2010). We consider the possibility that this extensive representation allows for a more efficient encoding strategy for natural sounds. To do so we compare two candidate “modulation filterbank” models and compare these to the modulation filtering characteristics of the CNIC (illustrated in Fig. 1). An equal resolution modulation filterbank (Fig. 1A) would essentially preserve the power distribution of the incoming sensory signal. In this scheme, modulation filter bandwidths are constant regardless of the filter modulation frequency so that the output of each filter is proportional to the incoming signal power and the sensory signal is directly represented by the firing rate distribution of the neural array. Under such a scheme, neural responses to high modulation frequency signals would be limited and difficult to detect because high modulations frequency signals are under-represented in natural sounds (i.e., 1/f modulation power spectrum). In the present study we propose an alternate scheme that may account for the wide range of response resolutions observed in CNIC neurons and which may underlie perceptual resolution to amplitude modulations. For neurons in this proportional resolution filterbank, response resolution (modulation bandwidth) varies systematically across the array so that it scales with the characteristic modulation frequency of each neuron (Fig. 1B) thus following an approximate inverse relationship to the 1/f MPS of natural sounds. According to this second model, neurons that respond to high modulation frequencies would integrate and respond to an extensive range of modulation frequencies in effect boosting the response power in the high-frequency modulation channels, thus equalizing or “whitening” natural sensory signal (Field, 1987). From an efficiency perspective, such equalization would enhance detection of weak high-frequency components in natural sounds that are susceptible to noise and evenly distribute encoding resources across the neural ensemble allowing for more efficient transfer of information.

Figure 1.

Hypothetical modulation filterbank models. A, An equal resolution filter (constant filter bandwidth) preserves the power of the signal across all frequencies. B, The filter bandwidths of a proportional resolution filterbank scale with frequency. This scaling can augment the power of the incoming signals for higher frequencies as a consequence of the larger bandwidths. The filterbank models are shown for temporal modulations; however, an equivalent framework can also be applied for spectral modulations.

Here we characterize the MPS of natural sound ensembles and compared these statistics with the modulation filtering characteristics of CNIC neurons. We demonstrate that modulation-tuning scales in the CNIC and neurons approximate proportional resolution filters that equalize the MPS of natural sounds. The findings provide evidence consistent with efficiency coding principles and which closely mirror perceptual sensitivity.

Materials and Methods

Spectrotemporal modulation analysis of natural sounds

Natural sounds were obtained from commercially available compilations and consisted of animal vocalizations (109 min), human speech (46.6 min), background environmental sounds (18.9 min), and white noise (10 min). Vocalizations and background sounds were obtained from the Macaulay Library of Natural Sounds at Cornell University (Storm, 1994a,b; Emmons et al., 1997). Human speech consisted of a radio broadcast reproduction of the William Shakespeare play Hamlet (Shakespeare, 1992). These same sound ensembles were previously analyzed using a complementary approach (Escabí et al., 2003). All sounds were sampled at a rate of 44.1 kHz and 16-bit resolution.

Natural sounds and white noise were decomposed into their spectral and temporal components with a physiologically motivated filterbank that resembles the filtering characteristics of the peripheral auditory filters in mammals and perceptual filtering characteristics of humans. The filterbank model is similar to that described by Escabí et al. (2003). All sounds were first filtered with an array of third-order (n = 3) gamma-tone filters (Irino and Patterson, 1996) with impulse response functions of the form h_k(t) = tⁿ⁻¹ · cos (2πf_kt) · e^{(−2*π*b(f_k)*t)} where f_k represents the frequency of the kth filter and b(f_k) the filter bandwidth. The spectrotemporal envelope (s(t,x_k)) of each sound was obtained by passing the sound through the auditory filterbank and subsequently computing the magnitude of the analytic signal for each frequency channel:

Here s(t) is the input sound, s_k(t) is the extracted envelope for the kth channel, * represents the convolution operator, x_k is the frequency variable in octaves, and H{·} is the Hilbert transform. Filter center frequencies (f_k) were logarithmically spaced (1/8 octave spacing) between 500 Hz and 16 kHz and filter bandwidths [b(f_k)] were chosen to follow perceptual critical bandwidths (Fletcher, 1940; Zwicker et al., 1957): b(f_k) = 25 + 75 · [1 + 1.4 · f_k²]^0.69. The temporal modulations within each frequency channel were then band limited to 500 Hz by filtering the temporal envelope with a b-spline lowpass filter. This upper limit was chosen to allow comparisons with CNIC neurons which do not exhibit substantial phase-locking to spectrotemporal modulations above this range (Joris et al., 2004).

Once the sounds were decomposed into their spectrotemporal envelopes, we computed the MPS of each ensemble (Singh and Theunissen, 2003). The MPS characterizes the signal modulation power as a function of the sound's temporal and spectral modulation. The MPS of each sound was obtained by segmenting the spectrotemporal envelope of each sound ensemble into nonoverlapping half-second blocks, s_n(t, x_k), and averaging the MPS of each block:

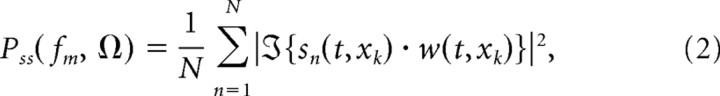where N is the number of blocks, ℑ{·} is a two-dimensional Fourier transform, w(t,x_k) is a two-dimensional Kaiser window (β = 3.4), f_m is the temporal modulation frequency (TMF, in Hz) and Ω is the spectral modulation frequency (SMF, in cycles/octave). Finally, we computed the temporal and spectral MPS of each ensemble by considering a singular value decomposition of the joint MPS (Singh and Theunissen, 2003). The joint MPS of each ensemble was decomposed according to:

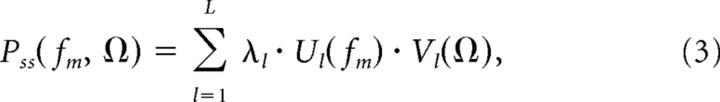where λ₁ > λ₂ > … > λ_L are the singular values and U_l(f_m) and V_l(Ω) are the singular vectors. The temporal and spectral MPS were then defined by the first singular vectors, U₁(f_m)and V₁(Ω) respectively (Singh and Theunissen, 2003).

Surgical procedure.

Animals were housed and handled according to approved procedures by the University of Connecticut Animal Care and Use Committee and in accordance with National Institutes of Health and the American Veterinary Medical Association guidelines. The surgical and experimental procedures have been reported in detail previously (Zheng and Escabí, 2008; Rodríguez et al., 2010) and are briefly outlined here.

Experiments were performed in an acute recording setting (48–72 h). Cats were initially anesthetized with a mixture of ketamine (10 mg/kg) and acepromazine (0.28 mg/kg, i.m.). A tracheotomy was performed to ensure adequate ventilation and reduce the nasal cavity acoustic noise. Exposure of the inferior colliculus was then performed either under sodium pentobarbital (30 mg/kg) or isoflurane gas mixture (3–4%). The inferior colliculus (IC) was exposed by removing the overlying bone and tissue in the occipital cortex and part of the bony tentorium. Following surgery, the animal was maintained in a nonreflexive state by continuous infusion of ketamine (2 mg · kg⁻¹ · h⁻¹) and diazepam (3 mg · kg⁻¹ · h⁻¹), in a lactated Ringer's solution (4 mg · kg⁻¹ · h⁻¹). Biological data (heart rate, temperature, breathing rate and reflexes) was monitored and used as physiological criteria.

Acoustic stimuli and delivery.

Sounds were delivered dichotically to the animal in a sound-shielded chamber (IAC) via hollow ear-bars (Kopf Instruments), attached to a closed binaural speaker system. The system was calibrated (flat spectrum between 1 and 47 kHz, ±3 dB) with a finite impulse response inverse filter (implemented on a Tucker-Davis Technologies RX6 Multifunction Processor). Sounds were delivered with either a Tucker-Davis Technologies RX6 or an RME DIGI 9652, through electrostatic or dynamic speaker drivers (Tucker-Davis Technologies EC1; or Beyer DT770).

To identify recording locations within the central nucleus, we first presented a random sequence of pure tones (50 ms duration tone pips with 300 intertone interval spanning 1–47 kHz and 5–85 dB SPL in 1/8 octave and 10 dB steps). This allowed us to measure the frequency response area of each unit and to verify the tonotopic gradient of the CNIC (Merzenich and Reid, 1974; Semple and Aitkin, 1979). Recording locations were selected only if a consistent tonotopic gradient was present. The recorded neurons had a median best frequency of 7.8 kHz and spanned a range from 1.1 kHz to 19.5 kHz. Next, a dynamic moving ripple (DMR) sound was presented to measure the spectrotemporal preferences of CNIC neurons (Escabi and Schreiner, 2002). DMR were generated digitally using a sampling rate of 96 kHz and 24-bit resolution. Two 10 min segments of the DMR sequence were presented (20 min total) at 80 dB SPL (65 dB spectrum level per 1/3 octave). The DMR consists of a time-varying broadband sound that covered a frequency range from 1 to 48 kHz and probed spectrotemporal preferences with a maximum temporal and spectral modulation of 500 Hz and 4 cycles per octave, respectively. For the purpose of this study only spectrotemporal receptive fields (STRFs) for the contralateral ear are considered as these characterizes the dominant phase-locked response of CNIC neurons (Qiu et al., 2003).

Electrophysiology

Neural data were obtained from 353 recording locations in the central nucleus of the inferior colliculus. Of the 353 recording locations, 262 passed stringent selection criteria to qualify as single unit activity as described below. Acute 4-tetrode (16 channel) recording probes (NeuroNexus Technologies) with 150 μm electrode separation and 177 μm² contact area (impedance 1.5–3.5 MΩ at 1 kHz) or single parylene-coated tungsten electrodes were used for the neural recordings (impedance 2.5–3.5 MΩ at 1 kHz). The probes or single electrodes were first positioned on the surface of the IC with the assistance of a stereotaxic frame (Kopf Instruments) at an angle of ∼30° relative to the sagittal plane (orthogonal to the isofrequency-band lamina) (Schreiner and Langner, 1997). Electrodes were inserted into the IC with either an LSS 6000 Inchiworm (Burleigh EXFO) or a hydraulic microdrive (Kopf Instruments). Neural responses were digitized and recorded digitally for offline analysis with an RX5 Pentusa Base station (Tucker-Davis Technologies). Neural data obtained with tungsten electrodes was spike-sorted offline with a Bayesian sorting algorithm (Lewicki, 1994). For the tetrode data, neural signals were first digitally bandpass filtered (300–5000 Hz). The covariance of the signals was computed and 4-sample vectors that exceeded a hyperellipsoidal threshold of 5 were detected as candidate action potentials (Rebrik et al., 1999). Spike waveforms were sorted using 4-vector peak values and first principle components with an automated clustering software (KlustaKwik software) (Harris et al., 2000). Sorted units were classified as single units only if the signal-to-noise ratio exceeded 5.

Temporal and spectral resolution analysis.

Spectrotemporal receptive fields were obtained for the contralateral ear of identified CNIC single neurons using a spike-triggered averaging procedure (Escabi and Schreiner, 2002). Significance testing was performed against a noise STRF obtained for a Poisson neuron of identical spike rate (Escabi and Schreiner, 2002). A two-tailed test was performed and significant STRF regions were defined by the positive and negative fluctuations that exceeded 3.09 SDs of the noise STRF. This criterion guarantees that we detect STRF components at a significance level of p < 0.002 (p < 0.001 for excitation and p < 0.001 for inhibition) relative to those expected for a purely random firing neuron. To assure that we only analyze clean, well defined noise-free STRFs, we required that the signal-to-noise ratio of the STRF exceed 5 (i.e., 14 dB). This criterion guarantees that we accurately measure response parameters with minimal estimation error. Applying the selection criteria to the spike waveforms (SNR > 14 dB, previous paragraph) and STRF (SNR > 14 dB) resulted in a reduction of the number of neurons in our sample (from 353 to 262). However, similar results were obtained with less stringent selection criteria (using all recording sites; data not shown). As described in detail previously, the color spectrum in all plots indicates spike rate relative to the mean such that blue and red denote decrease or increase below and above the mean, respectively (Escabi and Schreiner, 2002).

The temporal and spectral resolution of each unit was quantified by considering the temporal and spectral extend of each STRF (Rodríguez et al., 2010). This analysis is motivated by the uncertainty principle where the spectral and temporal resolution of a filter is derived by considering the spectral and temporal power distributions of a filter and measuring the average spread (i.e., the SD) across the spectral and temporal dimensions (Gabor, 1946; Cohen, 1995). Briefly, for each STRF we defined the receptive field time-frequency power distribution by the magnitude of the analytic signal STRF (Qiu et al., 2003; Rodríguez et al., 2010):

where H{·} is the Hilbert transform. The spectral and temporal power marginals were obtained by collapsing p(t,x) along the temporal and spectral dimensions and normalizing for unit area, respectively:

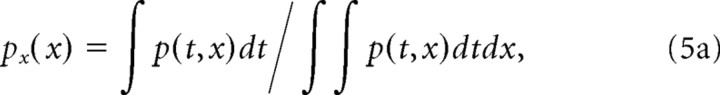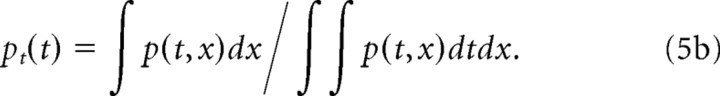The center of mass values from the response power marginals define the average STRF latency (t̄) and best frequency (x̄). The STRF integration time (Δt) and octave bandwidth (Δx) were defined as twice the SD of the spectral and temporal distributions:

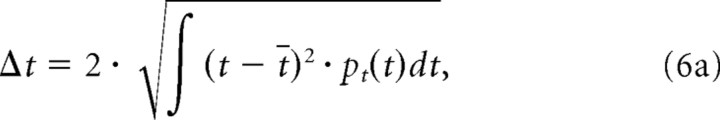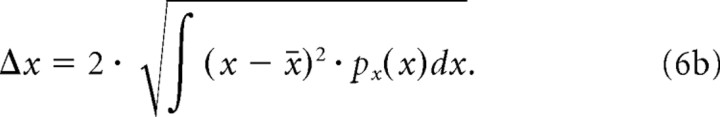Modulation tuning and bandwidth analysis.

The spectral and temporal modulation resolutions of each unit were obtained directly from the ripple transfer function (RTF). Specifically, we sought to characterize the relationship between each unit's characteristic temporal modulation frequency and modulation tuning bandwidth to identify whether CNIC neurons approximate proportional resolution modulation filters (as in Fig. 1B). The RTF of each neuron was obtained by performing a two-dimensional Fourier transform (ℑ₂{·}) of the STRF and subsequently computing the magnitude as described previously (Escabi and Schreiner, 2002):

Here f_m is the temporal modulation frequency variable and Ω is the spectral modulation frequency. The spectral and temporal MTF (sMTF and tMTF) were then obtained by computing the power marginals of the RTF and subsequently normalizing for a unit area:

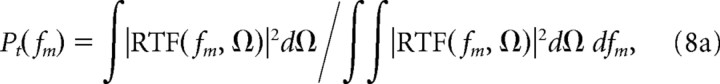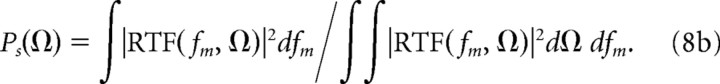The modulation tuning characteristics were obtained for each unit by considering the region and extent of maximal neural activity directly from the power marginals. The characteristic temporal and spectral modulation frequencies of each unit were derived by computing the centroids from the modulation power marginals:

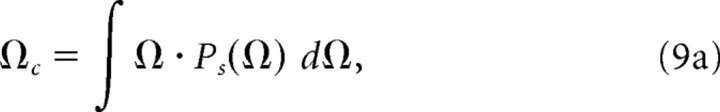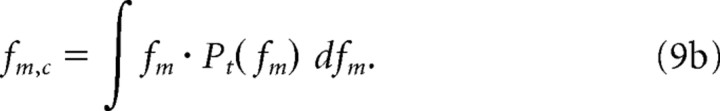Next, we estimated the spectral and temporal RTF bandwidths as the average width of the power marginals. The modulation bandwidths were defined as two SDs relative to the centroid values:

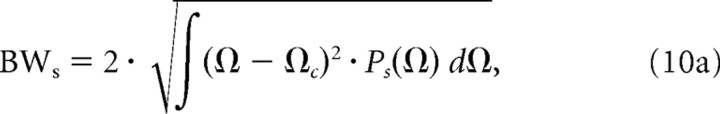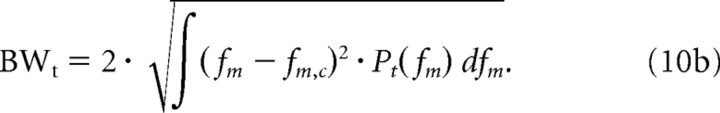Finally, for each unit we also computed the spectral (Q_s = Ω_c/BW_s) and temporal (Q_t = f_m,c/BW_t) quality factors as a way of quantifying the sharpness of modulation tuning.

Modulation power gain.

To relate the bandwidth of each neuron to its sensitivity (gain), we estimated the gain of the tMTF (G_temporal) and sMTF (G_spectral) that was strictly associated with the bandwidth of the modulation filter. The modulation power gain was defined by the output power in response to a white noise signal of unit variance. Temporal and spectral MTFs were normalized for a peak gain of 1 (i.e., 0 dB) and the modulation gain associated with the bandwidth of the filter was estimated by integrating the amplitude normalized tMTF and sMTF.

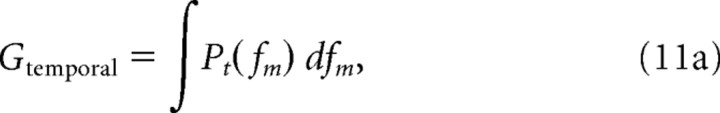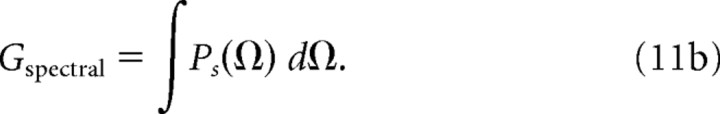Predicting the MPS output of the CNIC.

For each of the three natural sound ensembles (speech, vocalizations, environmental background sounds), we predicted the MPS output that would result after passing the natural sounds through a CNIC model filterbank. To do this, we devised a modulation filterbank that was composed of rectangular filters with unity gain across the filter passband. The filters were designed so that the modulation frequency versus modulation bandwidth relationship observed for CNIC neurons was preserved. Temporal and spectral modulation filter bandwidths were chosen to follow the best-fit power-law relationship to the CNIC data shown below in Figure 6:

This assures that the model filters scale according to the observed bandwidth relationship for CNIC neurons. The simulation was performed using temporal modulation filters between 5 and 350 Hz and spectral modulation filters within 0.25–2.65 cycle/octave. We choose filters limited to this range so that the filter upper cutoff frequencies do not exceed the maximum MPS frequencies in the sound analysis (500 Hz temporal; 4 cycles/octave). The output MPS for the CNIC model was obtained by passing the spectral and temporal MPS of each sound ensemble through the CNIC model filterbank.

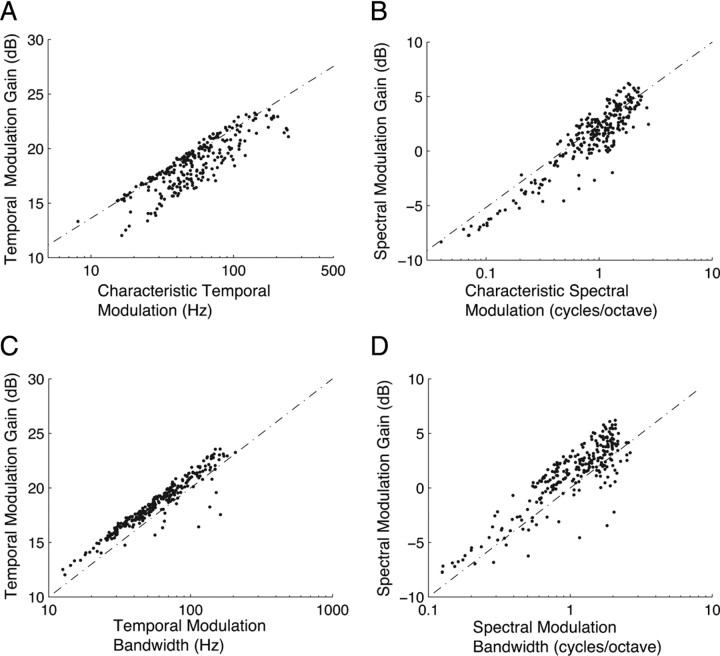
Figure 6.

Modulation gains increase systematically with characteristic modulation frequencies and bandwidths. A, Temporal modulation gain is strongly correlated with cTMF (A, r = 0.79 ± 0.02, p < 0.01) while spectral modulation gains are strongly correlated with cSMF (B, r = 0.78 ± 0.03, p < 0.01). These trends are even stronger when one considers the relationship between modulation gains and modulation bandwidths. C, D, As can be seen there is a marked correlation between these parameters (C, r = 095 ± 0.01, p < 0.01; D, r = 0.94 ± 0.02, p < 0.01) and a significant increase in power with modulation frequency (7.65 dB/decade for temporal; 8.2 dB/decade for spectral). These trends oppose the MPS of natural sounds where the modulation power decreases with modulation frequency (Fig. 2C,D).

For reference, we also filtered the natural sound MPS with an equal resolution filterbank where modulation filter bandwidths are constant. To allow for direct comparisons between the CNIC filters and equal resolution filters, the bandwidth of the equal resolution filters was matched to the smallest bandwidth for the CNIC filterbank. This normalization allows for a common reference point since it guarantees that the first filter in both filterbanks have identical gain and produces identical output.

Ensemble efficiency.

As a metric of performance, we compared the efficiency of both filterbanks for encoding spectral and temporal sound modulations. Hypothetically, an efficient strategy for encoding natural sound modulations across a neural ensemble is to represent all the modulations in that sound with equal power so that the corresponding power spectrum is flat or “white”. Under such a scenario, each neural filter produces identical response power regardless of its characteristic modulation frequency so that encoding resources are evenly distributed across the neural ensemble. Thus, an ensemble has 100% efficiency if all the neurons in the ensemble produce identical output power. The spectral and temporal ensemble efficiency are defined as the average normalized modulation power:

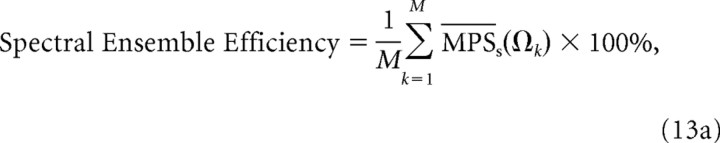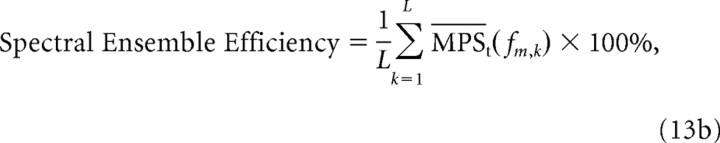where MPS_s and MPS_t are the spectral and temporal modulation power spectrums of the sound after being filtered by the neural ensemble of interest (CNIC filterbank or equal bandwidth filterbank). For the purposed of calculating efficiency, MPS_s and MPS_t are normalized for a maximum power of 1 (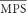_s = MPS_s/max[MPS_s] and 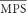_t = MPS_t/max[MPS_t]). Thus the ensemble efficiency corresponds to the average power per neural receptor after being normalized to the receptor that produces maximum power. Note that the ensemble efficiency is precisely 100% if the resulting MPS is “white” (i.e., flat modulation spectrum so that _s and _t = 1 for all frequencies).

Results

We present results for the natural sound modulation statistics first (Fig. 2) and subsequently describe the filtering characteristics of single CNIC neurons (Figs. 3–6) and their unique benefits for encoding natural sounds (Figs. 7, 8).

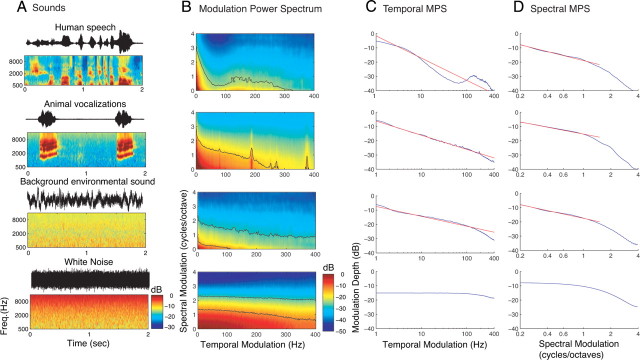
Figure 2.

Ensemble characteristics of natural sounds. Natural sounds waveforms (A, black waveforms) were decomposed by an auditory filterbank model into a spectrotemporal representation (A, color panels) that depicts the sound power as a function of time and frequency. Representative 2 s segments from speech (male speaker; “If she unmask her beauty to the moon.”), an animal vocalization (wild cat; Felis herpailurus yaguarondi), background sound (rain), and white noise (top to bottom). For vocalizations the sound power is coherently modulated over frequency and time, whereas for background sounds and white noise the modulations are random. For white noise the power at high frequencies is accentuated because the auditory filterbank bandwidths are larger for higher frequencies. B, The MPS depicts the signal power as a function of temporal and spectral modulation frequency. Black contours in the MPS denote the modulation space that accounts for 90% and 50% of the MPS power. For all three natural sounds, a tradeoff between temporal and spectral modulations is observed. C, D, The temporal and spectral modulation power spectrum was obtained by decomposing the MPS into its strictly spectral and temporal components (see Materials and Methods). A strong decrease in the modulation power of all natural sounds approximates a power law function (straight line on a doubly logarithmic plot). A comparable decrease in the modulation power is not observed for white noise. Red curves in C and D designate the optimal-fit power law.

Figure 3.

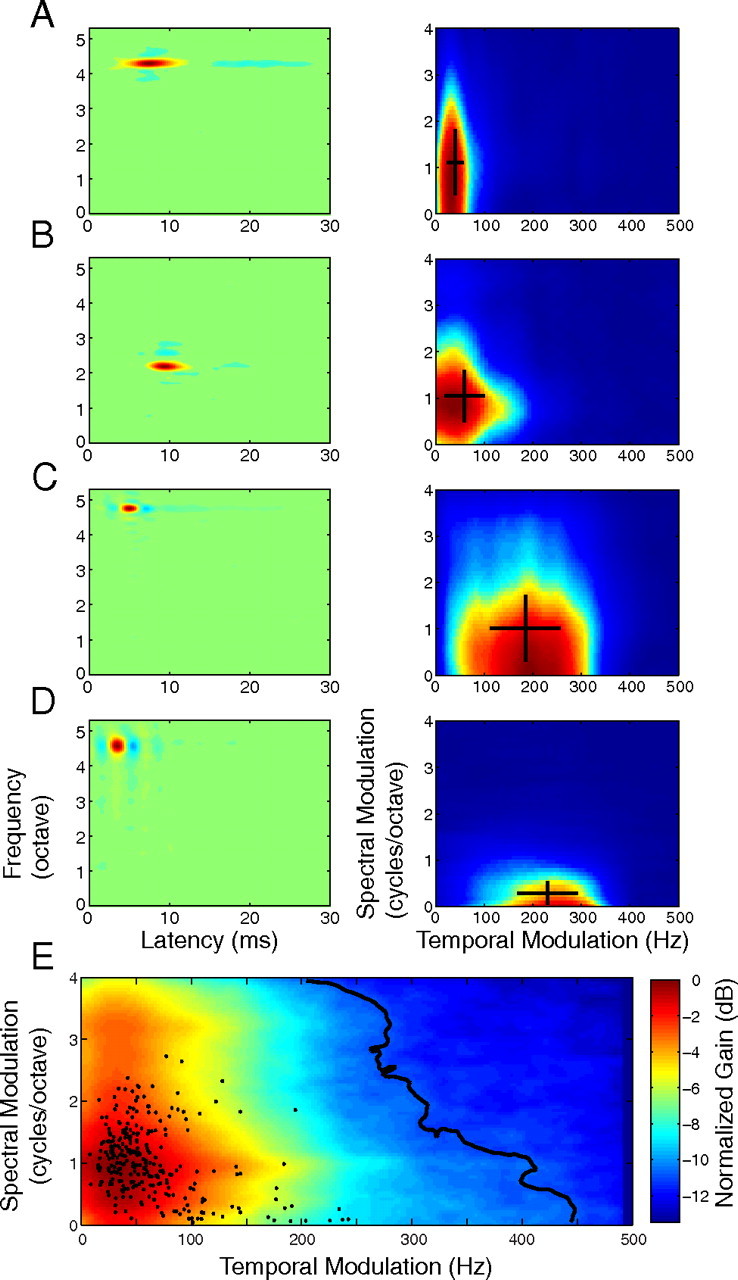
Tradeoff in neural spectrotemporal tuning in the inferior colliculus. A–D, Example STRF and the corresponding MTFs from four CNIC neurons. The example STRFs (A–D, left) are ordered from slow to fast integration times (A, 6.6 ms; B, 3.92 ms; C, 2.12 ms; D, 2.13 ms). The STRF bandwidths for these examples represent the average width of the STRF (A, 0.20 octave; B, 0.25 octave; C, 0.18 octave; D, 0.43 octave). As can be seen, neurons can be sharply or broadly tuned in frequency or can alternately exhibit short or long integration times. The STRF structure is directly related to the modulation tuning characteristics of each neuron (A–D, MTF shown on right). STRFs with slow integration times (A) prefer slower temporal modulation while faster STRFs prefer higher temporal modulations (D). Similarly, narrowband STRFs with strong sideband inhibition tend to prefer higher spectral modulations (A) while broadband STRFs prefer slower spectral modulations (D). Temporal and spectral modulation bandwidths account for the sharpness of modulation tuning and are depicted by the horizontal and vertical black bars. The intersection of these bars represents the characteristic temporal and spectral modulation of each neuron. E, The ensemble average MTF for the CNIC shows the gain of the ensemble as a function cTMF and cSMF (color plot). Dots represent the cTMF and cSMF of each neuron and black contours represent the region of the MTF space that accounts for 90% of the response power. Note that at the extremes, neurons can respond to fast temporal modulations (high cTMF) or fine spectral modulations (high cSMF), but not both.

Figure 4.

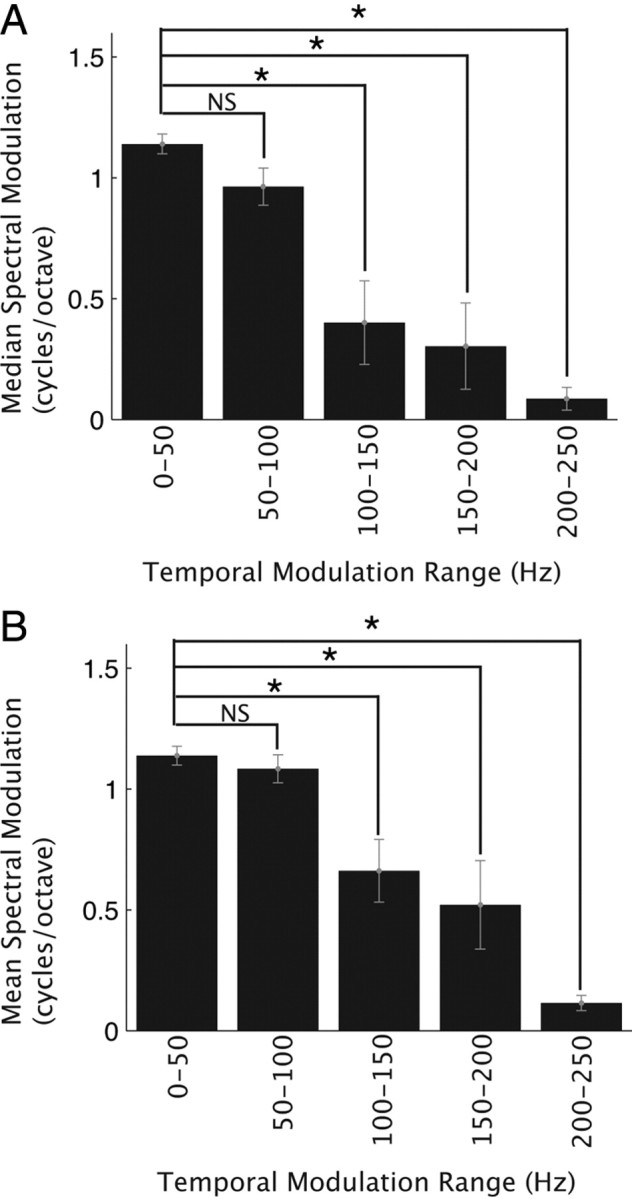
Modulation tradeoff statistics. A, B, Median (A) and mean (B) cSMF as a function of cTMF range. The neural ensemble was partitioned into nonoverlapping cTMF ranges (0–50, 50–100, 100–150, 150–200, 200–250 Hz). Both the median and mean cSMF decreased systematically with increasing cTMF range. Error bars designate the bootstrapped SE and * designates significant results (median, Wilcoxon rank-sum, p < 0.05 with Bonferroni correction; mean, paired t test, p < 0.05 with Bonferroni correction).

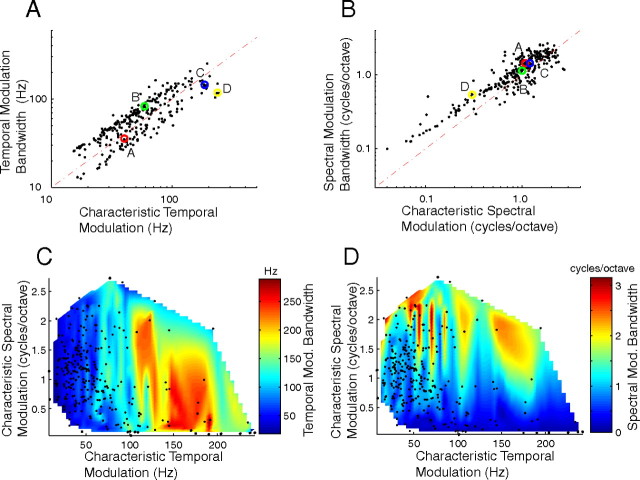
Figure 5.

Modulation tuning characteristics scale in the CNIC. A, B, Temporal and spectral modulation bandwidths show a clear increase as function of their respective characteristic modulation frequency (slope of increment for temporal: 0.8, p < 0.01; spectral: 0.75, p < 0.01). The selected examples from Figure 3 are indicated by A–D. C and D show the relationship between temporal (C) and spectral (D) modulation bandwidths (surface color plots) as function of cTMF and cSMF (black dots, indicate the cTMF and cSMF of each neuron). Note that temporal modulation bandwidths scale most prominently with cTMF. Likewise, spectral modulation bandwidths scale most prominently with cSMF.

Figure 7.

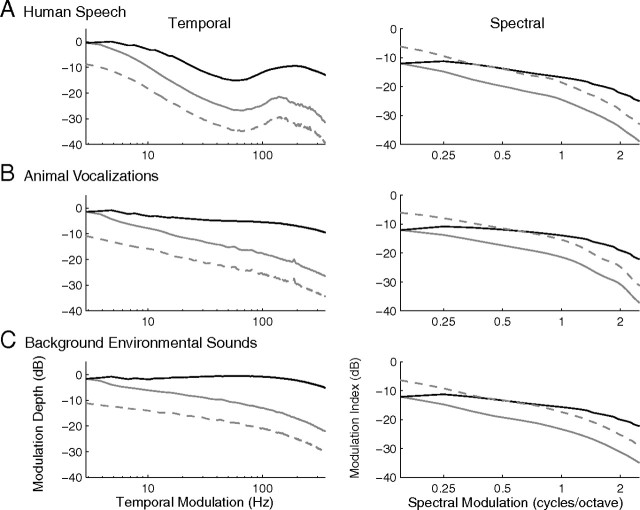
CNIC filtering characteristics equalize the modulation power of natural sounds. A–C show the temporal (left) and spectral (right) MPS (dashed gray lines) for the three natural sound ensembles (human speech, animal vocalizations and background environmental sounds; same as in Fig. 2). To determine the degree of power equalization conferred by the CNIC ensemble, the MPS of natural sounds were passed through a modulation filterbank in which modulation bandwidths scale as for the CNIC neural ensemble (see Materials and Methods). Black lines in A–C represent the CNIC model filterbank output MPS. For reference the MPS were also filtered with an equal resolution filterbank analogous to Figure 1A (gray lines). There is marked flattening in the modulation power at the output of the CNIC model but not for the equal resolution filters.

Figure 8.

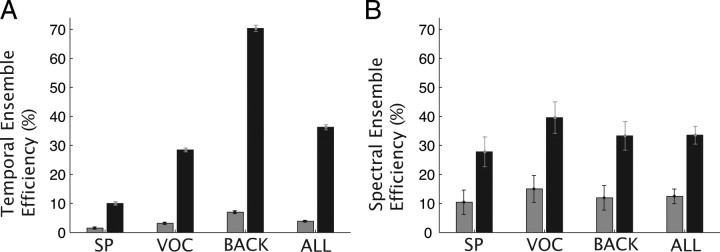
CNIC filtering characteristics enhance encoding efficiency for natural sound ensembles. A, Temporal ensemble efficiency for an equal resolution filterbank (gray) and a proportional resolution filterbank where filter bandwidths scale as for CNIC (black). The CNIC filterbank exhibits significantly higher temporal efficiency (p < 0.01, bootstrap t test) for all three natural sound ensembles tested (SP, speech; VOC, animal vocalizations; BACK, background; ALL, SP+VOC+BACK). B, Spectral encoding efficiency is shown for the equal resolution filterbank (gray) and CNIC model filterbank (black). The spectral ensemble efficiency is significantly higher for the CNIC model filterbank for all natural sound ensembles tested (p < 0.01, bootstrap t test). Error bars designate SEM.

Natural sounds exhibit spectrotemporal modulation tradeoff and power-law scaling

We examined how a biologically plausible peripheral filter bank model decomposes a variety of natural sound ensembles. The model consists of an array of filters with frequency-tuning bandwidths that scale with the filter center frequency as observed in the auditory nerve of mammals (Kiang et al., 1965; Lewicki, 2002; Mc Laughlin et al., 2007) and which exhibit low-frequency tails (Kiang et al., 1965; Kiang and Moxon, 1974). Natural sound ensembles consisted of a large repertoire of animal vocalizations (109 min), human speech (46.6 min), and background environmental sounds (18.9 min). Figure 2A shows the sound waveforms (black waveform) and the spectrotemporal decomposition obtained from a peripheral auditory model (color panels) for representative two-second segments from, animal vocalizations, background sound and white noise (ordered from top to bottom). As can be seen, the peripheral model decomposition of speech and other animal vocalizations reveals coherent spectral and temporal modulations compared with the more homogeneous modulations of background sounds and white noise. The modulation statistics of each ensemble are represented by the average MPS (Fig. 2B). The MPS shows the sound's modulation power as a function of the temporal and spectral modulation frequencies. Fast temporal modulations (>100 Hz) tended to occur whenever vocalizations had coarse spectral modulations (<1 cycles/octave) as evident in the joint MPS. Conversely, fine spectral modulation (>1 cycle/octave) were prominent primarily when sounds had slow temporal modulations (<100 Hz). Vocalizations rarely contained fast temporal modulations when spectral modulations were >1 cycle/octave (Fig. 2B). This tradeoff between spectral and temporal modulations was evident from the prominent portion of the MPS for the three natural sound ensembles examined (Fig. 2B, black contours circumscribe 90% of the modulation power). In contrast the joint MPS of white noise is much more uniform for temporal and spectral modulations up to ∼400 Hz and ∼1.5 cycles/octave, respectively. Thus natural sound ensembles exhibited a distinct modulation tradeoff that was not present for white noise.

The spectrotemporal tradeoff in the sound decomposition by the peripheral auditory filterbank serves to enhance temporal modulations in speech. As can be seen from the speech MPS, a prominent lobe with increase power is seen in the vicinity of 100–300 Hz for coarse spectral modulations <1 cycle/octave (Fig. 2B, top). The increased power in this region is due to the fact that speech contains prominent harmonics associated with voicing pitch that are created by oscillations of the vocal chords. When these harmonics are passed through peripheral filterbank with physiologically plausible bandwidths they are transformed into temporal modulations whenever the harmonics are unresolved (i.e., multiple harmonics fall within a single filter) (Schouten, 1940). Thus voicing pitch is evident within the 100–300 Hz region of the MPS well within periodicity pitch range of hearing. This enhanced temporal representation for speech is not observed in spectrogram models that employ high-resolution constant bandwidth filters capable of resolving the harmonics of the sound (Singh and Theunissen, 2003; Elliott and Theunissen, 2009). These spectrogram models tend to enhance spectral modulations while severely limiting temporal modulations (to mostly <50 Hz), so that voicing pitch can only be detected in the spectral modulations (Elliott and Theunissen, 2009). By comparison, auditory filters tend to enhance temporal modulations at the expense of limiting spectral modulations. The ability of the proposed peripheral model to enhance temporal modulations (over constant bandwidth filterbanks used previously) is illustrated for three harmonic complex sounds (100 Hz, 200 Hz and 300 Hz; supplemental Fig. S1, available at www.jneurosci.org as supplemental material).

A precipitous decrease in the modulation power is observed with modulation frequency when the MPS is decomposed into its strictly spectral or temporal components (Fig. 2C,D). This decrease approximates a power-law (straight line on double logarithmic plot) as previously described for temporal modulation (Attias and Schreiner, 1998a; Singh and Theunissen, 2003). The temporal MPS of all three natural sound ensembles (Fig. 2C) exhibited approximately power-law behavior for frequencies extending to several hundred hertz. In the case of speech, the trend deviated somewhat from a strictly linear decrease as a result of the strong modulation power within the voicing pitch region (100–300 Hz). Nonetheless, the modulation power of all three natural sound ensembles decreased substantially with increasing temporal modulation frequency (Fig. 2C, fitted optimal power law are shown in red; slopes for speech = −15.6 dB/decade; vocalizations = −10.0 dB/decade; background = −7.0 dB/decade). A similar trend is also observed for the spectral MPS of all three natural sound ensembles for spectral modulation frequencies up to ∼1.5 cycles/octave (Fig. 2D). Similar to the temporal MPS, spectral modulation power decreased at a rate of ∼15 dB/decade within this range (Fig. 2D, fitted optimal power law are shown in red; slopes for speech = −15.9 dB/decade; vocalizations = −12.2 dB/decade; background = −13.7 dB/decade). The reduced power for spectral modulations >1.5 cycles/octave in all natural sound ensembles (and white noise) is attributed to the critical-band bandwidths (∼1/3 octave) of the peripheral filterbank model (Fletcher, 1940; Zwicker et al., 1957), which substantially limits spectral modulations beyond this point. In contrast to natural sounds, the modulation power of white noise tended to be relatively constant throughout comparable range of temporal (Fig. 2C, bottom) and spectral modulations (up to ∼1.5 cycles/octave) (Fig. 2D, bottom). Thus, the approximate power-law scaling observed for natural sounds was not present for white noise.

Modulation filtering tuning and scaling

Ideally if auditory neurons use an efficient strategy to encode natural sounds they would show complementary modulation tuning statistics to those described above. Here we measured STRFs and MTFs from an ensemble of single neurons in the CNIC (N = 262) to compare the tuning of neurons with the MPS of natural sounds. STRFs were obtained as illustrated for four example neurons (Fig. 3A–D, left) along with the corresponding MTF (Fig. 3A–D, right). The STRF indicate the preferred sound modulation pattern that evokes a time-locked response to the sound. In a complementary manner, the MTF of each neuron depicts the preferred response as a function of the temporal (TMF) and spectral (SMF) modulation frequency of the sound (red correspond to strong activity while blue indicates low activity). CNIC neurons were tuned to a restricted range of sound modulations (Fig. 3A–D, right) and these tuning properties were directly related to the STRF structure (Fig. 3A–D, left). The first two example neurons preferred relatively long duration sounds as they exhibit a brief (∼5 ms) excitatory peak followed by a slower suppression (∼10 and ∼5 ms, respectively; blue) along the time axis of the STRF. These STRFs had narrow spectral bandwidths (0.2 and 0.25 octave, respectively) and relatively long STRF integration times (6.6 and 3.9 ms). Because of the relatively long response times these neuron have a slow characteristic temporal modulation frequency (cTMF = 40.1 Hz and 58.9 Hz, respectively). Spectrally, the STRF of both neurons exhibited an interleaved pattern of excitation and inhibition extending along the spectral axis over a range of ∼1 octave. Thus these neurons respond preferentially to fine spectral modulations (cSMF = 1.1 and 1.1 cycles/octave, respectively) as can be seen from their MTF (Fig. 3A,B, right). The second two example neurons (Fig. 3C,D) exhibited on-off-on temporal STRF pattern with substantially shorter integration times (2.1 and 2.1 ms). Accordingly, the MTFs for these neurons are tuned for faster temporal modulations (cTMF = 191.8 and 254.5 Hz; cross in Fig. 3C,D, right). Spectrally, the neuron of C is narrowly tuned (0.18 octave bandwidth) with well defined lateral inhibition and thus it is optimally tuned to spectral modulation ∼1.2 cycles/octave (cSMF). By comparison, the neuron of D has no lateral inhibition and is more broadly tuned (0.4 octave). This neuron thus prefers sounds that lack spectral modulations (on spectral patterns, 0 cycles/octave) and it is tuned to low spectral modulations (cSMF = 0.2 cycles/octave). For these exemplar cells, the width of the STRF in spectral and temporal dimensions is inversely related to the temporal (BW_t) and spectral modulation bandwidths (BW_s), respectively. This general behavior was observed across the neural ensemble (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Neurons with short STRF integration times (Fig. 3D) tended to have broader BW_t while neurons with sharply tuned STRFs tended to have larger BW_s (Fig. 3A). These general relationships between the STRF and modulation domains are expected a priori because the Fourier transform and uncertainty principle dictate that the integration time of a system (average temporal width) is inversely related to the systems bandwidth in the Fourier domain (Gabor, 1946; Cohen, 1995). Empirically, we observe that this is the case (supplemental Fig. S2, available at www.jneurosci.org as supplemental material) and, throughout, we therefore focus on the MTF parameters.

The distribution of modulation tuning parameters for CNIC neurons was complementary to the MPS pattern of natural sounds. Specifically, neural selectivity exhibited an inverse-like dependence between the cTMF and cSMF of each neuron across the neural ensemble. Figure 3E shows the ensemble averaged MTF (shown in color) along with the cTMF and cSMF for individual single neurons (superimposed dots). At the extremes, neurons tended to prefer either fast temporal modulations or fine spectral modulations, but generally not both. This behavior is seen in the ensemble averaged MTF and the corresponding contour accounting for 90% of the MTF power (Fig. 3E, black contour). This contour does not encompass the region of high cTMF and high cSMF values and is well approximated by a straight line of negative slope (slope = −4 cycles/octave per 250 Hz, p < 0.01). At the extremes, the 90% contour extends to 450 Hz when spectral resolution is poor (cSMF = 0 cycles/octave). By comparison, the contour is temporally restricted to 200 Hz for higher spectral modulations (4 cycles/octave). This tendency to tradeoff spectral for temporal modulations at the extremes is also evident from the cTMF and cSMF of each neuron (Fig. 3E, black dots), which exhibited a significant negative correlation (log₁₀(cTMF) versus log₁₀(cSMF), r = −0.44 ± 0.05, p < 0.01). Furthermore, cTMFs were strongly correlated with 1/cSMF (r = 0.55 ± 0.07, p < 0.01) implying an inverse dependence between spectral and temporal modulation sensitivity. Statistics for this behavior are shown in Figure 4. Neurons were grouped according to their cTMF (0–50, 50–100, 100–150, 150–200, 200–250 Hz) and the median (Fig. 4A) and mean (Fig. 4B) cSMF were computed for each of the cTMF ranges. As can be seen, the median and mean cSMF exhibited a significant decrease with increasing cTMF (Wilcoxon rank-sum test with Bonferroni correction p < 0.05; paired t test with Bonferroni correction p < 0.05). Thus analogous to the MPS of natural sounds, neural modulation tuning was confined to a select region of the modulation space and mirrored the inverse dependence observed in the MPS of natural sounds.

Although the CNIC response parameters were highly overlapped with the MPS of natural sounds, changes in MTF bandwidths opposed the natural tendency for sound modulation power to decrease with increasing frequency (Fig. 2C,D). Figure 5 shows that modulation bandwidths and characteristic modulation frequencies of CNIC neurons are strongly correlated with one another. This result is not expected a priori and is consistent with the proposed scaling modulation filterbank model (Fig. 1B). Note that the characteristic modulation and modulation bandwidth can in fact be completely independent of one another. For instance, in the absolute resolution modulation filterbank proposed in Figure 1A, the filter integration times (or bandwidth for the spectral dimension) are constant regardless of the filter cTMF (or cSMF, for spectral dimension), which is inconsistent with the observed measurements (supplemental Fig. S2, available at www.jneurosci.org as supplemental material A and B). As can be seen temporal modulation bandwidth was strongly correlated with the characteristic temporal modulation frequency (cTMF vs BW_t, Fig. 5A; r = 0.79 ± 0.02, p < 0.01) with slope near unity (log(cTMF) vs log(BW_t); slope = 0.8, p < 0.01; best fit power-law: tBW = 2.5 · cTMF^0.8). Similarly, spectral modulation bandwidths were strongly correlated with cSMF (Fig. 5B; cSMF vs BW_s, r = 0.78 ± 0.03; slope = 0.75, p < 0.01; best fit power-law: sBW = 1.2 · cSMF^0.75). Thus, neurons that responded optimally to slow temporal (low cTMF) and coarse spectral (low cSMF) modulations tended to have narrow spectral or temporal modulation bandwidths, respectively. Stated in another way, modulation bandwidths scaled with the neuron's characteristic modulation frequency.

Interactions between temporal and spectral response sensitivities were examined as previous studies have suggested systematic relationships (Qiu et al., 2003; Rodríguez et al., 2010). Although cTMF and cSMF were good predictors of the temporal and spectral modulation bandwidths, respectively, the converse was not true. Temporal modulation BW was only weakly related to the spectral characteristics (i.e., cSMF) while spectral modulation BW was weakly dependent on temporal characteristics (i.e., cTMF). In Figure 5C, the temporal modulation BW is shown as a function of cTMF and cSMF (surface color plot designates BW_t; dots represent the cTMF and cSMF of each neuron). A weak inverse correlation (r = −0.24 ± 0.06, p < 0.01) was observed between the temporal modulation bandwidth and characteristic spectral modulation (cSMF). Likewise, there was a small but significant correlation (r = −0.40 ± 0.05, p < 0.01) between spectral modulation bandwidth and characteristic temporal modulation (BW_s vs cTMF, Fig. 5C). Thus response dependencies across spectral and temporal components were evident although not as strong as those within (Fig. 5A,B).

Modulation power equalization, whitening, and efficiency

The observed neural scaling could theoretically enhance the representation of natural sound modulations by equalizing the power output of the neural ensemble. Given that natural sound power decreases as an approximate power-law with modulation frequency, it is required that gain of the neural ensemble would increase in a power-law fashion with modulation frequency to compensate for the reduction in sound modulation power. Mechanistically, this boost in the modulation power could be achieved through scaling because the high modulation frequency neurons would integrate over a larger region of the modulation space (compared with low modulation frequency neurons) leading to a boost in the modulation power output for high modulation frequency neurons.

To test for this possibility, we computed the modulation power gain of each neuron that was strictly associated with the filter modulation bandwidth (see Materials and Methods). As can be seen (Fig. 6A), temporal modulation gain was strongly correlated with the cTMF (r = 0.85 ± 0.01, p < 0.01). Similarly, the spectral modulation gain was also strongly correlated with the cSMF (Fig. 6B, r = 0.91 ± 0.01, p < 0.01). The modulation power gain in either spectral or temporal dimension increased approximately in proportion to the corresponding characteristic modulation frequency of the neuron (temporal slope = 7.65 dB/decade; spectral slope = 8.2 dB/decade). Ideally, if the characteristic modulation frequency is equal to the modulation bandwidth (as would be the case for equivalent rectangular bandwidth bandpass filters with quality factor 1), the slope of the resulting curve would be precisely 10 dB/decade. In the CNIC, modulation filter bandwidths were slightly smaller than the characteristic modulation frequency (median quality factor: Q_t = 0.7 for temporal; Q_s = 0.89 for spectral; supplemental Fig. S3, available at www.jneurosci.org as supplemental material) and thus the corresponding slopes were slightly <10 dB/decade. Furthermore, there was a subtle but significant correlation between cTMF and Q_t (r = 0.44 ± 0.07, p < 0.01) and cSMF and Q_s (r = 0.41 ± 0.07, p < 0.01) indicating that neurons with higher characteristic modulation frequency where more sharply tuned (Fig. S3A,B available at www.jneurosci.org as supplemental material). The correlation between modulation bandwidth and modulation gain were high for both temporal (Fig. 6C, r = 0.95 ± 0.01, p < 0.01) and spectral (Fig. 6D, r = 0.94 ± 0.02, p < 0.01) dimensions, suggesting that the modulation gain was strongly dependent on the modulation bandwidth. Overall, these trends oppose the MPS for natural sounds, where power decreases with increasing modulation frequency (Fig. 2B), thus providing a viable mechanism to equalize the modulation power output of the CNIC for natural sounds.

To determine the degree of power equalization that could be conferred by the CNIC filtering characteristics, we filtered the MPS of natural sounds with a modulation filterbank model composed of rectangular filters in which bandwidths scale with characteristic modulation frequencies as for the CNIC neural population (see Materials and Methods). For comparison, the natural sounds were also filtered with an equal resolution filterbank with constant modulation bandwidths (as in Fig. 1A). Figure 7, A–C, shows the temporal and spectral MPS for the three natural sound ensembles after being filtered with the equal resolution (gray lines) or the CNIC filterbank (black lines). For reference, the original MPS are shown in each panel (dashed gray lines). As can be seen, the output spectral and temporal MPS for the CNIC model filterbank is substantially flatter. This flattening behavior is not seen for the equal resolution filterbank, which exhibits a similar pattern to the original MPS. For both the equal resolution and CNIC filterbank, there is an offset in the MPS as a result of the minimum gain provided by the filter bandwidth (e.g., approx. +12 dB for temporal and −7 dB for spectral in Fig. 5C,D). For all three natural sound ensembles, there was a substantial flattening of the MPS after filtering with the CNIC model as indicated by the reduced model output MPS slopes (speech: temporal slope = −2.0 dB/decade; spectral slope = −8.6 dB/decade; vocalizations: temporal slope = −4.4 dB/decade; spectral slope = −5.5 dB/decade; background: temporal slope = −2.6 dB/decade; spectral slope = −6.4 dB/decade).

For both the equal resolution and CNIC modulation filterbank models, we computed the ensemble encoding efficiency for the three natural sound ensembles. From an efficiency perspective, each receptor in the filterbank should produce identical output power (flat MPS) to maximize resource utilization across the neural ensemble. Thus an ensemble efficiency of 100% indicates that the output power is equalized across the receptors (or equivalently across modulation frequencies). Figure 8A demonstrates an enhancement in the temporal ensemble efficiency for the CNIC filterbank over the equal resolution filterbank (36.3% versus 3.9%; p < 0.01, bootstrap t test). This was true for all three natural sound ensembles tested with speech and background sounds exhibiting the lowest (10.5%) and highest (70.4%) efficiency, respectively. A similar enhancement in efficiency is also observed for the CNIC spectral modulation filterbank over the equal resolution spectral filterbank (Fig. 8B). Spectral ensemble efficiency of the CNIC filterbank was significantly higher for all three natural sound ensembles when compared with the equal resolution filterbank (33.5% versus 12.5%; p < 0.01, bootstrap t test).

Discussion

Previous studies have demonstrated that individual auditory midbrain neurons respond efficiently to sounds with natural-like statistical characteristics (Attias and Schreiner, 1998b; Escabí et al., 2003; Lesica and Grothe, 2008). Here, we provide further evidence that tuning characteristics of CNIC neurons are optimized across the neural ensemble so as to equalize the modulation power of natural sounds. Thus, our data provide a link between the ensemble characteristics of natural sounds and the characteristics of the ensemble filtering properties of the CNIC.

Neural modulation bandwidths scaled in such a way that they approximately canceled the observed 1/f MPS of natural sounds. Specifically, modulation bandwidths increased nearly proportional to the characteristic modulation frequency of each neuron. Consequently modulation-filtering resolution is traded-off for filter gain to assure sufficient modulation power transfer. Within this framework, CNIC neurons exhibit high resolution (small bandwidths) and low sensitivity for low modulation frequencies where the signal power is high and lower resolution (large bandwidths) and higher sensitivity at high modulation frequencies where the signal power tends to be low for natural sounds. This trend was present for both spectral and temporal modulations and the overall degree of scaling was similar for each.

CNIC neurons exhibited inverse dependencies between spectral and temporal sound modulation sensitivity that mirrored the spectrotemporal modulation tradeoffs observe in natural sounds. For each of the natural sound ensembles the joint MPS exhibited an inverse-like dependence in which temporal and spectral modulations are not independent (Fig. 2). CNIC neurons exhibited a similar dependency between characteristic spectral and temporal modulations (Figs. 3E, 4). Previous studies have demonstrated that spectral and temporal modulations in natural sounds are not independent (Singh and Theunissen, 2003) and exhibit a number of structural regularities (Voss and Clarke, 1975; Attias and Schreiner, 1998a; Escabí et al., 2003; Singh and Theunissen, 2003). Prior studies also find that the distribution of single neuron MTFs in the songbird auditory system (midbrain: Mld and forebrain structures: Field L, and CM) are optimized to minimize redundancies and enhance the sound representation within the low-frequency region of the MPS (<50 Hz) (Woolley et al., 2005). Our results differ and complement their findings in a number of important ways. First, spectral-temporal tradeoffs described here were not observed in the songbird auditory pathways (Woolley et al., 2005). Although it is possible that this difference is species-specific, it is not likely due to species-specific differences in temporal modulation sensitivity alone as these appear to be very similar in mammalian and songbird IC (Woolley and Casseday, 2005). In the previous study the temporal modulations examined were restricted by the spectrogram decomposition and sounds used primarily to the rhythm range of hearing (<50 Hz; supplemental Material, Fig. S1, available at www.jneurosci.org as supplemental material), which is well below the limits of phase-locking in the cat auditory midbrain which has been estimated at ∼300 Hz (Joris et al., 2004). Thus, the findings from this prior study do not generalize to the faster temporal modulations examined here such as those that are important for roughness and pitch perception. Cat CNIC neurons were tuned out to ∼250 Hz and a substantial amount of power in the ensemble MTF was present out to 450 Hz (Fig. 3E). Previous studies in the bat IC using ripple sounds and STRFs have observed a similar range of modulation sensitivities (Andoni et al., 2007). Second, the whitening mechanism and CNIC filter-bank model proposed here relies on the concept of bandwidth scaling where the modulation bandwidths grow proportionally to the characteristic modulation frequencies of CNIC neurons. This proposed scaling behavior and the resulting equalization has not been described previously. For frequencies between 0 and 30 Hz this prior study finds a net gain of ∼4.5 dB (Woolley et al., 2005, their Fig. 3). Although this net gain can serve to help equalize modulation power in the low modulation frequency range as proposed in that study, it does not fully compensate for the 1/f decrease in modulation power observed for natural sounds. In contrast, the estimated gain across the population of cat CNIC neurons produces ∼8 dB boost in the modulation power per decade which amounts to ∼20 dB gain over an extensive range of temporal modulations (up to 500 Hz). Finally, the present study demonstrates similar whitening for both spectral and temporal dimensions, which has not been reported previously.

The observed modulation filtering characteristics differ dramatically from auditory nerve fibers which strictly exhibit lowpass modulation filtering and are inconsistent with the concept of modulation tuning (Joris and Yin, 1992). Although we can only speculate about the exact mechanisms underlying the transformation from lowpass modulation selectivity in the auditory nerve to bandpass selectivity in the brainstem and CNIC, it is apparent that inhibition in the brainstem and midbrain sharpen modulation selectivity and could partly underlie the observed tuning behavior (Andoni et al., 2007; Rodríguez et al., 2010).

Like the peripheral auditory filters, our data indicate that neural tuning characteristics may have evolved to efficiently represent natural sensory signals that exhibit 1/f spectrotemporal modulations. The tuning characteristics of the peripheral auditory filters are optimized for low-order statistics of natural sounds (Lewicki, 2002; Smith and Lewicki, 2006). An intriguing aspect of the present study is the implication that different forms of scaling occur at different levels of the auditory system (e.g., carrier frequency and modulation frequency). Frequency tuning bandwidths in the auditory nerve scale systematically with increasing characteristic frequency (Kiang et al., 1965). This cochlear bandwidth scaling enhances temporal modulations at the expense of removing detailed spectral modulations when compared with a conventional spectrogram (supplemental material Fig. S1, available at www.jneurosci.org as supplemental material). Ultimately, the combined scaling behavior for the frequency tuning filters in the cochlea and the modulation filtering in CNIC leads to an enhancement in the encoding efficiency for representing spectrotemporal modulations in natural sounds (Fig. 8). The results complement previous findings in the periphery since they suggests that the CNIC tuning characteristics are specialized to enhance the representation of higher-order acoustic features in natural sounds. Future studies need to identify how this ensemble representation is further enhanced or used at higher levels of processing, including the auditory thalamus and cortex.

The proposed response organization is also consistent with psychoacoustical studies on humans, which have demonstrated that perceptually derived spectrotemporal modulation filters have bandpass shape and approximate proportional resolution filters. Specifically, temporal modulation tuning characteristics for human listeners are well approximated by bandpass filters with a quality factor of ∼1 (Ewert and Dau, 2000). This result generalizes for spectrotemporal modulations since perceptually derived spectrotemporal modulation filters are bandpass tuned with quality factors of ∼1 (Verhey and Oetjen, 2010). In our data, modulation tuning bandwidths scaled with similar quality factors (median of 0.7 for temporal and 0.89 for spectral modulation tuning supplemental Fig. S3, available at www.jneurosci.org as supplemental material). Furthermore, the scaling behavior in the CNIC extended beyond 100 Hz analogous to human data where detection of temporal modulations and scaling is evident to several hundred Hz (Viemeister, 1979; Dau et al., 1997). Neural tuning characteristics in the CNIC have been shown to resemble a number of psychophysical phenomena. In particular, the frequency tuning and laminar organization of the CNIC (Schreiner and Langner, 1997; Malmierca et al., 2008) may serve as the substrate for 1/3 octave critical band perceptual resolution observed in humans (Fletcher, 1940) and other species (Pickles, 1979; Langemann et al., 1995). Our findings provide evidence that modulation-tuning in the CNIC closely mirrors and may serve as a neural substrate for psychophysical modulation sensitivity.

Power-law scaling may be a general strategy of the brain to efficiently encode natural sensory stimuli. For example, natural visual scenes also exhibit long-term spatiotemporal correlations and power law scaling (Field, 1987; Ruderman and Bialek, 1994) analogous to temporal modulations in natural sounds (Voss and Clarke, 1975; Attias and Schreiner, 1998a; Singh and Theunissen, 2003). Like their auditory counterparts, its been demonstrated that single neurons in the visual system can respond efficiently to natural visual scenes (Dan et al., 1996; Vinje and Gallant, 2000). An intriguing finding is that an optimal coding strategy for natural visual scenes is to employ spatially compact oriented Gabor-like filters, which resemble the receptive field structure of neurons in the primary visual cortex (Olshausen and Field, 1996). Aside from the fact that CNIC temporal preferences are approximately an order of magnitude faster than visual cortex, STRFs in the CNIC are well approximated by nearly identical spectrotemporal Gabor functions (Qiu et al., 2003). Our results lend support to the general hypothesis that tuning characteristics of sensory systems can exploit high-level sensory features in natural signals in a manner that enhances sensory representations and which may ultimately underlie perceptual sensitivity.