Abstract
The softening of the radial breathing mode (RBM) of metallic single walled carbon nanotubes (m-SWNTs) due to electron-phonon coupling has been studied by observing the Fermi level (εF) dependence of the RBM Raman peak. In situ Raman spectra were obtained from several individual m-SWNTs while varying εF electrochemically. The RBM frequency of an intrinsic m-SWNT is shown to be down-shifted relative to highly doped tubes by ~2 cm−1. The down-shift is greatest for small diameter and small chiral angle SWNTs. Most tubes show no change in RBM linewidth. A comparison is drawn between the RBM and the G band (ALO phonon) with respect to the εF dependence of their frequencies and linewidths.
Electron-phonon (e-ph) interactions govern many aspects of the physical properties of materials. In graphene and single walled carbon nanotubes (SWNTs), the coupling between electrons and the in-plane C-C stretching optical phonon modes (G-band phonons) influences the phonon structure [1,2], electrical transport [3], and optical transition properties of these materials [4]. Thus, significant effort has been devoted to this subject recently. Another phonon mode of interest in SWNTs is the isotropic radial deformation of the nanotube called the radial breathing mode (RBM). This optical phonon is solely the result of the one-dimensional tubular structure of SWNTs and its deformations are very different from those of the optical stretching modes that are common to all other graphitic materials. e-ph coupling of the RBM is important because it provides a new scattering channel for electrons that is absent in higher dimensional forms of carbon. Being a low energy optical phonon, the RBM could be a significant scatterer of low energy electrons such as in electrical transport at low biases [5].
In metallic SWNTs (m-SWNTs) e-ph coupling can be especially strong because a wide range of phonon energies is able to resonantly excite electrons across the linear electronic bands. Phonons that effectively couple to excitations near the Fermi surface experience lifetime broadening and energy renormalization [1,2]. This phenomenon is typically investigated by studying how the phonon energy and lifetime evolve as a function of the Fermi energy, εF. For the G− Raman peak of a m-SWNT, the observed up-shift and narrowing of the peak with doping has helped clarify the origin of the metallic G-band line shape and the role of electronic excitations in the softening of the ALO phonon at εF for the neutral m-SWNT [6]. A recent theoretical treatment of the εF dependence of the RBM predicts a similar, albeit weaker, softening of the RBM phonon with a significantly larger chiral angle dependence [7]. Because the RBM energy is so much smaller than the G band, the e-ph coupling is expected to be much more sensitive to the fine structure of the electronic bands near the Dirac point where the valence and conduction bands touch. An experimental study of the softening of the RBM frequency in m-SWNTs is therefore important to clarify the structure-dependent e-ph coupling phenomena associated with the RBM phonon.
In this Letter we present a careful analysis of the frequency ωRBM and linewidth γRBM of the RBM of individual SWNTs as a function of the electrochemical gating potential Vg. We observe an increase in frequency when the nanotube is doped with either electrons or holes. Our experimental results show a diameter (dt) and chiral angle (θ) dependence of the ωRBM softening.
We use a transparent polymer electrolyte (PEO/LiClO4) to electrochemically dope m-SWNTs. Long, gas flow aligned SWNTs are grown by chemical vapor deposition and then contacted by a Cr/Au electrode to form the working electrode of the electrochemical cell. The SWNTs are typically several hundred microns long and are separated from each other by 20–50 μm. A Pt counter electrode is controlled by a Princeton Applied Research 283 potentiostat to vary the potential (Vg) of an Ag pseudo-reference electrode with respect to the SWNTs [8]. Raman measurements are made through the transparent electrolyte. The nanotube metallicity is determined by placing ωRBM and the excitation energy Elaser on a Kataura plot, and by observing a broadening and shift of the G band [6]. The m-SWNTs under study are either isolated or in small bundles of two or three SWNTs. However, only one SWNT contributes to the signal for these measurements.
Figure 1(a) shows the RBM spectrum of a m-SWNT at several values of Vg. Here, a positive (negative) Vg corresponds to electron (hole) doping. A subtle up-shift of 2 cm−1 for both (±) polarities of Vg is observed. Changes in ωRBM are more evident after fitting the peaks, whereby the fit gives both ωRBM and the FWHM linewidth γRBM versus Vg, shown in Figs. 1(b) and 1(c), respectively. We use a Voigt profile to deconvolute the instrumental broadening from the Lorentzian linewidth of the RBM peak. The ωRBM of the m-SWNT shown in Fig. 1(b) makes an almost symmetric “V” shape about Vg = 0. Previous studies suggest that environmental effects such as the van der Waals interaction of the SWNT with the substrate or surrounding solution may modify ωRBM [9]. The latter effect presumably only contributes to a constant background with respect to Vg. The large drop in the peak intensity observed with increasing Vg may be caused by a change in the resonance condition. Because of the loss in peak intensity with increasing Vg, we are only able to follow ωRBM (Vg) for those m-SWNTs that have strong signals, which biases our sample set towards tubes with small θ values [7]. These m-SWNTs all exhibit a similar characteristic ωRBM (Vg) behavior. Meanwhile, the RBM peak for a semiconducting SWNT (s-SWNT) shows no appreciable change in ωRBM (Vg) as a function of Vg, as, for example, shown in the inset of Fig. 1(b). It is thus clear that the behavior in Fig. 1(b) is an effect specific to m-SWNTs.
FIG. 1.
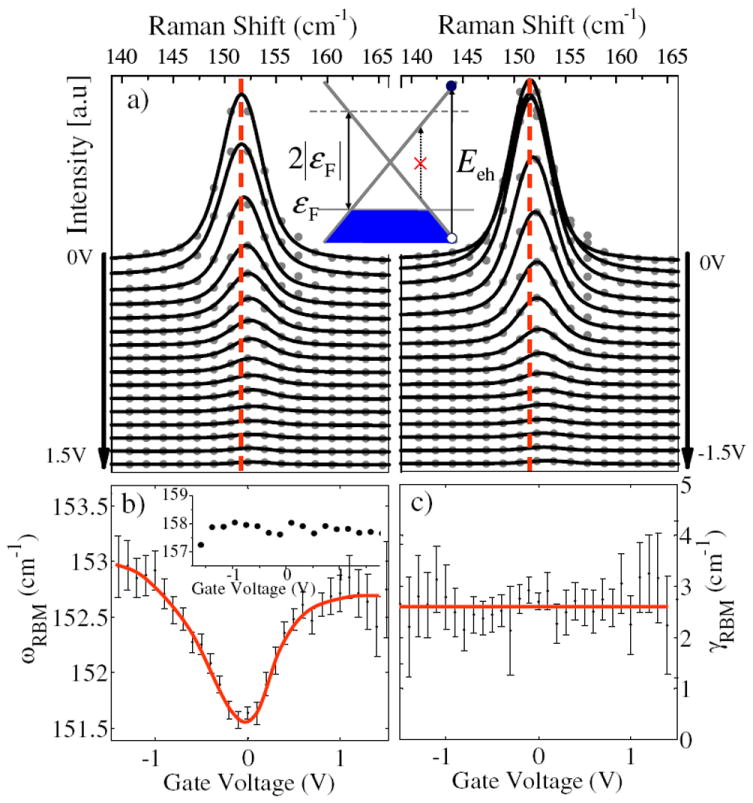
(color online). (a) Waterfall plots of the RBM spectra of a m-SWNT at several positive (left-hand panel) and negative (right-hand panel) values of gate potential Vg. To evaluate the ωRBM down-shift we use the vertical red lines as fiduciary marks indicating the peak frequency at Vg = 0. The inset of (a) is a schematic band structure of a m-SWNT illustrating the allowed e-h transitions. (b) Fitted frequency ωRBM and (c) FWHM linewidth γRBM values versus Vg. Error bars denote 95% confidence interval. Solid curves guide the eye. The inset of (b) shows the fitted ωRBM(Vg) for a s-SWNT.
The behavior of ωRBM for m-SWNTs can be understood by considering that, like the G-band phonons, the RBM is also an optical phonon capable of exciting vertical electron-hole (e-h) pairs across the linear k valence and conduction bands of the m-SWNT near the K (or K′) point. If the e-ph matrix element for such transitions is nonzero, these scattering events contribute to renormalizing the phonon energy and decreasing its lifetime. As illustrated in the inset of Fig. 1(a), the Pauli exclusion principle limits the available e-h pair transitions to those satisfying Ee-h > 2|εF|, thus giving rise to the Vg dependence of ωRBM. As εF is shifted away from the Dirac point, the number of excitations contributing to the dressed RBM phonon is reduced and ωRBM approaches the frequency of the bare RBM phonon [7].
In Fig. 2 we compare the εF dependence of the G− peak (ALO phonon) to ωRBM of a m-SWNT which we tentatively assign as a (13,4) SWNT (ωRBM = 193 cm−1, Elaser = 1.91 eV). We see a striking resemblance between the Vg dependence of ωG− and that of ωRBM, with both peaks displaying a minimum in frequency around Vg = 0. However, the γRBM behavior of the two peaks is quite different with the RBM peak showing no noticeable broadening in contrast to the 60 cm−1 broadening of the G− peak. The lack of broadening for the RBM indicates a negligible resonant decay of the RBM into an e-h pair.
FIG. 2.
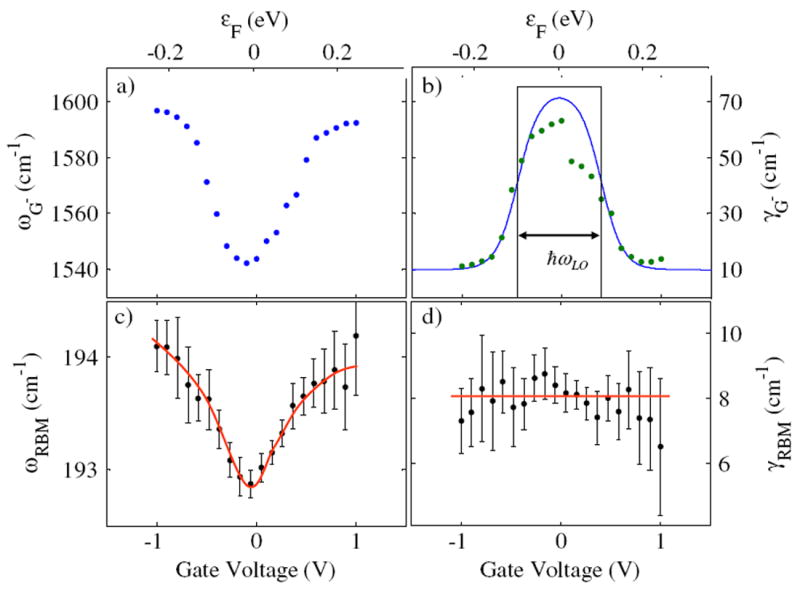
(color online). Comparing the G− and RBM peaks versus Vg for a (13,4) m-SWNT (ωRBM ~ 193 cm−1, Elaser = 1.91 eV). (a) the G− frequency and (b) G− linewidth versus Vg (bottom axis) and εF (top axis). The Vg dependence of the γG− is used to estimate the gating efficiency, α = 0.24 eV/V. The box in (b) gives the T = 0 energy range within which the LO phonon can excite real e-h pairs. (c) ωRBM and (d) γRBM for the same m-SWNT.
To understand why the RBM is down-shifted but not broadened, it is instructive to draw comparisons to the e-ph coupling of the optical phonons that contribute to the G band of graphene, m-SWNTs and s-SWNTs, which have recently been studied in great detail [6,10-13]. In m-SWNTs, the LO phonon (with energy 0.2 eV) is able to create real and virtual e-h pairs across the linear electronic bands, resulting in the strong broadening and downshift in frequency characteristic of the metallic G− peak as shown in Fig. 2. Similarly, in graphene, the G-band phonons are both broadened and down-shifted because they couple to e-h excitations near the Dirac point. In the case of s-SWNTs, the optical phonons do not have sufficient energy to excite e-h pair excitations across the large electronic energy gap. However, these optical phonons can still create virtual excitations which contribute to the down-shift of the phonon frequency. Since there is no decay into real states, there is no linewidth broadening and the frequency shift is modest compared to that of m-SWNTs, as recently verified in experiments [13,14].
Since ћωRBM is a small fraction of the LO/TO phonon energies, the e-h excitations for the RBM occur much closer to the Dirac point. On this energy scale a very small energy gap, such as the curvature-induced minigap, becomes significant. The latter, given by , is greatest for zigzag and absent for armchair m-SWNTs. The value of A is about 60 meV based on an extended tight-binding model [7]. From the perspective of the RBM phonon, the electronic bands of small diameter zigzag m-SWNTs with Egap > ћωRBM appear semiconductinglike. Only the armchair SWNTs have truly metallic bands when close to the Dirac point. Indeed, for the (13,4) SWNT shown in Fig. 2, Egap = 32 meV (dt = 1.2 nm, θ = 13°) exceeds the ћωRBM (24 meV) and hence no linewidth broadening is expected.
In Fig. 3 we show ωRBM for the (13,4) nanotube calculated from the effective mass theory in [7], which also predicts no change in γRBM as a function of εF and a ωRBM behavior qualitatively similar to what we observe in our measurements. For a quantitative comparison, we converted the Vg scale of Fig. 2 to an energy scale (bottom axis) using a gate efficiency of α = 0.24 (eV/V). The α value is determined by fitting the broadening window of the G− peak to γG− = γo + γEPC(Vg), as shown in Fig. 2(b). Here, γEPC, the linewidth due to e-ph coupling, is given by Eq. (29) of [1]. The Vg independent contributions to the linewidth are included in γo which is taken as 10 cm−1 based on our experimental results. Comparing Fig. 2(c) with Fig. 3 within the same εF range, we see that the experimental shift of ωRBM is approximately a factor of 2 smaller than that predicted.
FIG. 3.
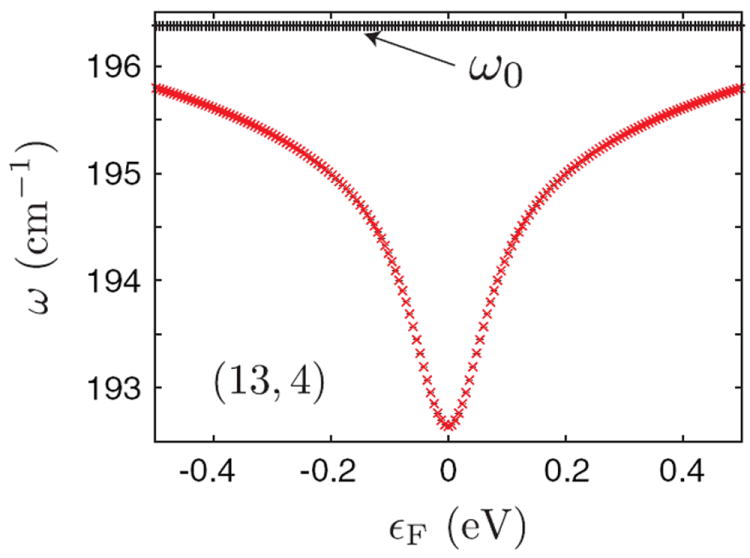
(color online). Calculated ωRBM versus εF for a (13,4) m-SWNT. For this m-SWNT the e-ph coupling contribution to the γRBM is zero. Black points ω0 give the bare ωRBM and gray (red) points give the corrected ωRBM [7].
It is important to know in what dt range the softening of ωRBM becomes significant. The down-shift in ωRBM is greatest in smaller dt m-SWNTs as seen in Fig. 4, which plots the observed frequency down-shift relative to Vg = V0 + 1V (black) and relative to Vg = V0 − 1V [gray (red)] as a function of 1/dt for several m-SWNTs, where V0 is the gate voltage where the minimum in frequency occurs. The e-ph matrix element and hence the frequency shift ΔωRBM at a constant Vg is expected to be linear in 1/dt [7]. The experimental data increase monotonically versus 1/dt with some variation that we attribute to the expected θ dependence of ωRBM [7]. Note that the shift on the negative gate side is in most cases greater than it is on the positive side. We attribute the mild asymmetry with respect to the sign of Vg to the C-C bond softening (stiffening) due to charging the lattices with electrons (holes). There may also be a difference in the gating efficiency for ± Vg.
FIG. 4.
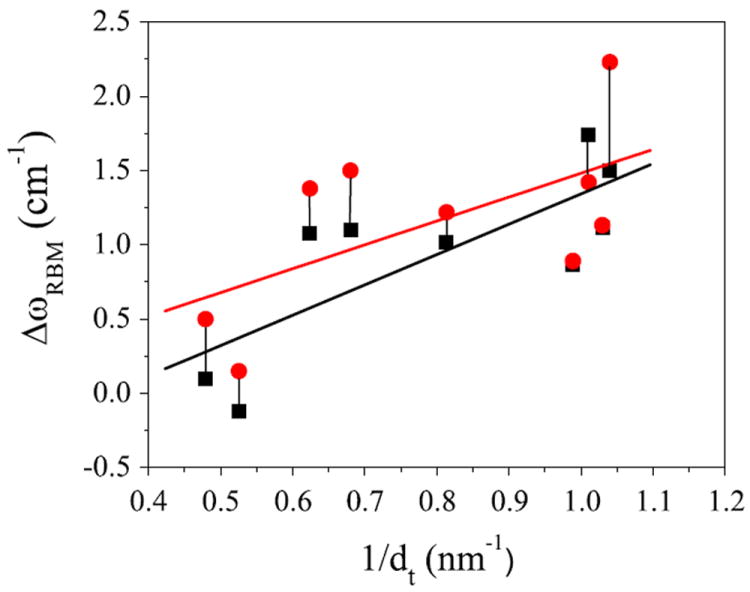
(color online). The down-shift ΔωRBM in ωRBM vs 1/dt. Red circles indicate the shift relative to Vg = V0 − 1V (hole doping) and black squares indicate the shift relative to Vg = V0 + 1V (electron doping). Solid lines represent linear fits to the experimental data points.
To further explore the θ dependence of ωRBM we have measured the Vg dependence of three consecutive m-SWNTs from the 2n + m = 24 family, namely, (11,2), (10,4), and (9,6) as shown in Fig. 5. For a given Vg, the magnitude of the measured ΔωRBM decreases from the (11,2) to the (9,6) nanotube. This is in agreement with the predicted θ dependence of the down-shift in ωRBM [7]. The e-ph matrix element, given approximately by ⟨e-h|He-ph|RBM⟩ = g(|sz|/dt) cos(3θ), where g is the off-site e-ph coupling constant and sz is the radial displacement, is greatest for the zigzag m-SWNT and approaches zero for the armchair m-SWNT [7]. Consequently the zigzag RBM is expected to exhibit the largest frequency shift but no broadening, while the armchair RBM should show neither a change in ωRBM nor in γRBM. An intermediate chiral m-SWNT could be expected to exhibit both a frequency shift and a broadening. Within the 2n + m = 24 family, only the (9,6) and (8,8) tubes have a RBM phonon which is greater in energy than the curvature-induced band gap. As shown in Ref. [7], the (9,6) tube is expected to exhibit a broadening Δγ = 2 cm−1 and a negligible frequency shift at 300 K. However, we observe a small frequency shift and no change in linewidth. On the other hand, the (10,4) SWNT is not expected to exhibit any broadening, but we observe a possible small broadening of Δγ = 1 cm−1. Besides these deviations, the overall measured dt and θ dependences of the ωRBM down-shift are in good qualitative agreement with Ref. [7].
FIG. 5.
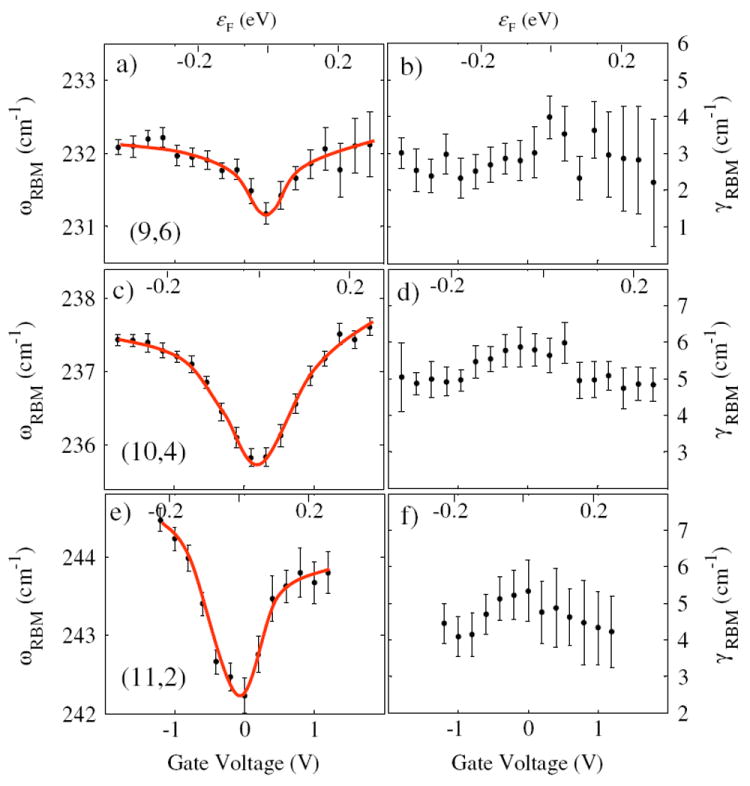
(color online). Fitted ωRBM and γRBM for three m-SWNTs from family 2n + m = 24. (a),(b) (9,6); (c), (d) (10,4); (e),(f) (11,2). The curvature-induced energy gaps for the three m-SWNTs are 19.3, 41.7, and 60.5 meV, respectively. The energy scale (top axis) is estimated for each m-SWNT as in Fig. 2. Solid red lines are curves to guide the eye.
It should be noted that the energy gaps for the (9,6) and (10,4) nanotubes are only 7 meV below and 15 meV above their RBM phonon energies, respectively. The ωRBM and γRBM of m-SWNTs are predicted to depend strongly on the position of the cutting line with respect to the K point, as well as on the size of the energy gap with respect to the ћωRBM. Small perturbations to the lattice such as strain [15], the displacement of the ALO phonon [16,17], and breaking of mirror symmetry [18] could sufficiently change the electronic structure to alter the εF dependence of the RBM peak.
In summary, we have experimentally confirmed that there is a mild softening of the ωRBM of m-SWNTs which can be removed by both positive and negative doping. The magnitude of the down-shift scales with 1/dt, and is largest for small θ. The measured ωRBM shifts agree qualitatively with the curvature-dependent softening in Ref. [7]. No gate-induced change in γRBM is found for most of the SWNTs that we studied, as is expected [7] for small (dt) SWNTs. Our result shows that chirality dependent corrections to ωRBM are required to better assign the dt and (n, m) indices for small dt m-SWNTs, and that environmental doping can be responsible for some of the variability in the observed ωRBM. This work also implies that the role of the RBM in electrical transport and other phonon assisted relaxation processes warrants further investigation.
Acknowledgments
This work is mainly supported by the Materials, Structure and Devices (MSD) Center, one of the five programs in the focus center research program (FCRP), a Semiconductor Research Corporation program. Raman measurements were carried out in the George R. Harrison Spectroscopy Laboratory supported by NSF-CHE 0111370 and NIH-RR02594. M. S.D. was supported by NSF/DMR 07-04197 and R. S. by MEXT Grants (No. 20241023 and No. 16076201).
References
- 1.Caudal N, et al. Phys Rev B. 2007;75:115423. [Google Scholar]
- 2.Sasaki K, et al. Phys Rev B. 2008;77:245441. [Google Scholar]
- 3.Yao Z, Kane CL, Dekker C. Phys Rev Lett. 2000;84:2941. doi: 10.1103/PhysRevLett.84.2941. [DOI] [PubMed] [Google Scholar]
- 4.Chou SG, et al. Phys Rev B. 2005;72:195415. [Google Scholar]
- 5.Perebeinos V, Tersoff J, Avouris P. Phys Rev Lett. 2005;94:086802. doi: 10.1103/PhysRevLett.94.086802. [DOI] [PubMed] [Google Scholar]
- 6.Farhat H, et al. Phys Rev Lett. 2007;99:145506. doi: 10.1103/PhysRevLett.99.145506. [DOI] [PubMed] [Google Scholar]
- 7.Sasaki K, et al. Phys Rev B. 2008;78:235405. [Google Scholar]
- 8.The gate potential Vg = −Ve, where Ve is the electrochemical potential, defined as the potential of the working electrode with respect to the reference electrode.
- 9.Araujo PT, et al. Phys Rev B. 2008;77:241403(R). [Google Scholar]
- 10.Yan J, Zhang Y, Kim P, Pinczuk A. Phys Rev Lett. 2007;98:166802. doi: 10.1103/PhysRevLett.98.166802. [DOI] [PubMed] [Google Scholar]; Pisana S, et al. Nature Mater. 2007;6:198. doi: 10.1038/nmat1846. [DOI] [PubMed] [Google Scholar]
- 11.Nguyen KT, Gaur A, Shim M. Phys Rev Lett. 2007;98:145504. doi: 10.1103/PhysRevLett.98.145504. [DOI] [PubMed] [Google Scholar]
- 12.Wu Y, et al. Phys Rev Lett. 2007;99:027402. [Google Scholar]
- 13.Tsang JC, et al. Nature Nanotech. 2007;2:725. doi: 10.1038/nnano.2007.321. [DOI] [PubMed] [Google Scholar]
- 14.Kalbac M, et al. Nano Lett. 2008;8:3532. doi: 10.1021/nl801637h. [DOI] [PubMed] [Google Scholar]
- 15.Huang MY, et al. Phys Rev Lett. 2008;100:136803. doi: 10.1103/PhysRevLett.100.136803. [DOI] [PubMed] [Google Scholar]
- 16.Dubay O, Kresse G, Kuzmany H. Phys Rev Lett. 2002;88:235506. doi: 10.1103/PhysRevLett.88.235506. [DOI] [PubMed] [Google Scholar]
- 17.Samsonidze GG, et al. Phys Rev B. 2007;75:155420. [Google Scholar]
- 18.Ouyang M, Huang JL, Cheung CL, Lieber CM. Science. 2001;292:702. doi: 10.1126/science.1058853. [DOI] [PubMed] [Google Scholar]


