Evaluation of genotype-specific survival using joint analysis of genetic and non-genetic subsamples of longitudinal data

Abstract

Small sample size of genetic data is often a limiting factor for desirable accuracy of estimated genetic effects on age-specific risks and survival. Longitudinal non-genetic data containing information on survival or disease onsets of study participants for whom the genetic data were not collected may provide an additional “reserve” for increasing the accuracy of respective estimates. We present a novel method for joint analyses of “genetic” (covering individuals for whom both genetic information and mortality/morbidity data are available) and “non-genetic” (covering individuals for whom only mortality/morbidity data were collected) subsamples of longitudinal data. Our simulation studies show substantial increase in the accuracy of estimates in such joint analyses compared to analyses based on genetic subsample alone. Application of this method to analysis of the effect of common apolipoprotein E (APOE) polymorphism on survival using combined genetic and non-genetic subsamples of the Framingham Heart Study original cohort data showed that female, but not male, carriers of the APOE e4 allele have significantly worse survival than non-carriers, whereas empirical analyses did not produce any significant results for either sex.

Introduction

Comparison of the age patterns of incidence or mortality rates for carriers of different alleles/genotypes can help better understand the role of genetic factors in survival or development of aging-associated diseases. Since increasing the number of genotyped individuals is still expensive, the sample size of genetic data continues to be a limiting factor of desirable accuracy of estimates of genetic effects on the age patterns of hazard rates. Therefore, the search for “indirect” approaches of increasing this accuracy is an important although challenging task. The methods for joint analyses of genetic (gene frequencies from a cross-sectional study) and demographic (mortality or incidence rates in a population) data have been suggested (Yashin et al. 1999; Yashin et al. 2000), which include parametric, semiparametric and non-parametric approaches. Ewbank (2002a) extended the relative risk approach by Yashin et al. (1999) presenting a method for combining gene frequencies from a cross-sectional study with data on mortality by genotype from cohort studies. Ewbank (2002b) further extended the method adapting it to analyzes of data on incidence and prevalence of diseases. Dato et al. (2007) implemented the algorithm for non-parametric analyses with cohort-dependent survival functions calculated from demographic life tables. Begun (2008) suggested a modification of the relative risk method by Yashin et al. (1999) that allows for modeling a cohort effect in the genotype frequencies. Yashin et al. (2007) extended the original approach by Yashin et al. (1999) suggesting a method for joint analysis of cross-sectional genetic information (gene frequencies), and longitudinal data on hazard (mortality or incidence) rates by genotype and marginal hazard rates (without genetic specification) from data collected in epidemiological, demographic, and longitudinal studies of human aging. The authors also considered correction of the method to the case of time trends in gene frequencies in subsequent birth cohorts. Arbeev et al. (2009) suggested a model for joint analyses of “genetic” (those for whom information on genetic markers is available) and “non-genetic” (those for whom information on genetic markers was not collected) subsamples of longitudinal data extending analyses to incorporate effects of age-dynamics of physiological indices measured in the study on genotype-specific hazards.

In this paper, we present a method to evaluate age patterns of allele- or genotype-specific hazard rates and survival functions from joint analyses of “genetic” and “non-genetic” subsamples of longitudinal data which is similar ideologically to that of Yashin et al. (2007) but works in a longitudinal context. We describe simulation study for a parametric model for carriers and non-carriers of some allele or genotype. The approach is applied to the Framingham Heart Study (FHS) original cohort data on mortality of female and male carriers and non-carriers of the e4 allele of the apolipoprotein E (APOE) gene.

Methods and Data

Likelihood function for genetic subsample

We assume that participants of a longitudinal study have different ages at the baseline and that genotyping is performed after some period of time since the baseline for some part of individuals from the study, which we denote the “genetic subsample.” Let $t_k^0$, k = 1…K, be ages at the start of the study (baseline) of individuals from the genetic subsample and let $t_{m,t_k^0}^{\mathit{gen}}$, m = 1…M_k, be ages at the time of collecting genetic data for such individuals. Denote by $N^{\mathit{gen}}\left(t_{m,t_k^0}^{\mathit{gen}}\right)=N_1^{\mathit{gen}}\left(t_{m,t_k^0}^{\mathit{gen}}\right)+N_0^{\mathit{gen}}\left(t_{m,t_k^0}^{\mathit{gen}}\right)$ the number of individuals in the genetic subsample who had age $t_{m,t_k^0}^{\mathit{gen}}$ at the time of collecting genetic data (and aged $t_k^0$ at the baseline). Here $N_1^{\mathit{gen}}\left(t_{m,t_k^0}^{\mathit{gen}}\right)$ and $N_0^{\mathit{gen}}\left(t_{m,t_k^0}^{\mathit{gen}}\right)$ are the numbers of carriers and non-carriers of respective allele (genotype). Let τ_i be the life span (which may be censored) of the i^th individual with a known allele (genotype) G. Denote by μ(t|G = g) the age pattern of the hazard rate for carriers (g = 1), and non-carriers (g = 0) of the respective allele (genotype), and by $\pi \left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)=P\left(G=1|\tau >t_{m,t_k^0}^{\mathit{gen}},t_k^0\right)$ the proportion of carriers at age $t_{m,t_k^0}^{\mathit{gen}}$ given that the individuals were aged $t_k^0$ at the baseline. Denote by $S_g(t)=P(\tau >t\mid G=g)=e^{-{\int }_0^t\mu (u|G=g)du}$ survival curves for carriers and non-carriers of allele/genotype G, g = 0, 1 and by P₀ = P(G=1) an initial proportion (at age 0) of carriers of allele/genotype G in a population, which is assumed here to be the same for different birth cohorts represented in the study. The total (population) survival curve is represented in terms of S_g(t) and p as S(t) = P₀S₁(t)+(1−P₀)S₀(t). Conditional survival functions for the individuals aged $t_k^0$ at the baseline are $S_g\left(t|t_k^0\right)=P(\tau >t\mid G=g,t_k^0)=e^{-{\int }_{t_k^0}^t\mu (u\mid G=g)du}$. The proportions $\pi \left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)$ are expressed in terms of conditional survival functions $S_g\left(t|t_k^0\right)$ as

$$\pi \left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)=\frac{P\left(G=1|t_k^0\right)S_1\left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)}{P\left(G=1|t_k^0\right)S_1\left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)+\left(1-P\left(G=1|t_k^0\right)\right)S_0\left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)},$$ (1)

where the proportion of carriers of allele/genotype G among those aged $t_k^0$ at the baseline is

$$P\left(G=1|t_k^0\right)=\frac{P_0{S}_1\left(t_k^0\right)}{S\left(t_k^0\right)}.$$ (2)

The likelihood function of the survival data for genotyped individuals is:

$$L^{\mathit{gen}}~\prod _{k=1}^K\prod _{m=1}^{M_k}\pi {\left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)}^{N_1^{\mathit{gen}}(t_{m,t_k^0}^{\mathit{gen}})}{\left(1-\pi \left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)\right)}^{N_0^{\mathit{gen}}(t_{m,t_k^0}^{\mathit{gen}})}\prod _{g=0}^1\prod _{i=1}^{N_g^{\mathit{gen}}(t_{m,t_k^0}^{\mathit{gen}})}{L}_i^{\mathit{gen}}(g,m,k),$$ (3)

where $\pi \left(t_{m,t_k^0}^{\mathit{gen}}|t_k^0\right)$ is given by (1) and the likelihood functions for data on i^th individual from the genetic subsample aged $t_k^0$ at the baseline and whose data on allele/genotype G = g were collected at age $t_{m,t_k^0}^{\mathit{gen}},L_i^{\mathit{gen}}(g,m,k)$, are given by

$$L_i^{\mathit{gen}}(g,m,k)=\mu {\left({\tau }_i|G=g\right)}^{{\delta }_i}exp\left(-\underset{t_{m,t_k^0}^{\mathit{gen}}}{\overset{{\tau }_i}{\int }}\mu (u|G=g)du\right).$$ (4)

Here δ_i is a censoring indicator (0 if censored, 1 otherwise).

Likelihood function for non-genetic subsample

We assume that the genetic and non-genetic subsamples (i.e., participants of the study with and without collected genetic information) are independent and that they are representative to each other, that is, carriers/non-carriers of the selected alleles/genotypes in these subsamples have the same parameters of hazard rates (note that if this is not the case but a functional relationship between the parameters in the genetic and non-genetic subsamples can be reasonably assumed, then this situation can also be modeled). It is assumed also that the initial proportion (at age 0) of carriers is P₀, as in the genetic subsample.

Denote by $N^{ng}(t_j^0)$ the number of individuals in the non-genetic subsample (i.e., for whom genetic data were not collected) aged $t_j^0$, j = 1…J, at the baseline. Since their genotypes are unknown, this group is a mixture of two sub-populations (carriers and non-carriers of the selected allele/genotype). The likelihood function of survival data in this mixture is:

$$L^{ng}=\prod _{j=1}^J\prod _{i=1}^{N^{ng}(t_j^0)}\left(P\left(G=1|t_j^0\right)L_i^{ng}(1,j)+\left(1-P\left(G=1|t_j^0\right)\right)L_i^{ng}(0,j)\right),$$ (5)

where the proportion of carriers at age $t_j^0,P\left(G=1|t_j^0\right)$, is given by (2), and

$$L_i^{ng}(g,j)=\mu {\left({\tau }_i|G=g\right)}^{{\delta }_i}exp\left(-\underset{t_j^0}{\overset{{\tau }_i}{\int }}\mu (u|G=g)du\right),g=0,1.$$ (6)

Likelihood function for combined genetic and non-genetic subsamples

Since participants of the study with and without genetic information are considered to be independent from each other, the combined likelihood function is

$$L=L^{\mathit{gen}}{L}^{ng}.$$ (7)

An important property of the likelihood functions (3) and (5) is that they are constructed from the same hazard model and, therefore, have the same unknown parameters. This property suggests that the joint analysis of data from genetic and non-genetic subsamples by maximizing the likelihood (7) will improve the accuracy of parameter estimates compared to the estimates evaluated in the analyses of data from the genetic subsample alone (i.e., maximizing the likelihood (3)).

Formulas presented above assume that both the allele/genotype frequencies and parameters of hazard rates are similar for all cohorts participating in the study. In reality, hazard rates may differ in individuals from different cohorts because of trends in endogenous and exogenous factors as well as in the effects of genetic and non-genetic factors on the rates. Initial frequencies of alleles/genotypes can be different in cohorts due to migration or other reasons. In such situations, applications of models with fixed frequencies and parameters of hazard rates in cohorts may lead to biased results. As the method essentially works in a longitudinal (cohort) context, its extension for the case of cohort-dependent parameters and/or initial proportion is straightforward (e.g., respective expressions for hazard rates and the initial proportion can be assumed as functions of the age at baseline, representing a cohort). In addition, longitudinal data typically collect various covariates which can affect mortality/morbidity risks along with genetic factors. Such covariates (e.g., race or ethnicity) can be included in the model in a similar way, i.e., expressions for hazard rates (and/or the initial proportion) can be specified as functions of these covariates (e.g., we may assume exponential hazards with covariates as in the traditional Cox proportional hazards model, or other suitable parameterizations for these relationships). However, all such extensions increase the number of parameters of the model to be estimated and, possibly, reduce the sample size due to the need to exclude individuals with non-observed covariates, which may affect the accuracy/power of estimates. It should also be noted that in cases when such covariates are not observed for a substantial subsample of participants, we can apply exactly the same approach as used for “joint analyses” of genetic and non-genetic samples to jointly analyze the “observed covariate” and “non-observed covariate” subsamples.

Framingham Heart Study data

We applied the method to estimate survival functions for carriers and non-carriers of the apolipoprotein E (APOE) e4 alleles in the Framingham Heart Study (FHS) original cohort. The FHS original cohort consists of 5209 respondents (46% male, nearly all are Caucasians) aged 28–62 years residing in Framingham, Massachusetts, between 1948 and 1951. The cohort has been followed for the occurrence of CVD, cancer, diabetes mellitus, and death through surveillance of hospital admissions, death registries, and other available sources. Examination of participants, including an interview, physical examination, and laboratory tests, has been taken biennially (Dawber et al. 1951; Dawber 1980). APOE genotyping was performed using DNA samples collected during the 19^th examination (years 1986–1987). For the present study, data on APOE polymorphisms were available for 1258 participants (802 females, 456 males) of the FHS original cohort. We will refer to this subsample as the “FHS APOE subsample.” In the FHS APOE subsample, 277 individuals (183 females, 94 males) were carriers of the e4 allele (genotypes e2/e4, e3/e4 or e4/e4) and 981 individuals (619 females, 362 males) were non-carriers of that allele (genotypes e2/e2, e2/e3 or e3/e3). Altogether, survival data on 5079 individuals (2785 females, 2294 males) from the FHS original cohort were available for this study. We will refer to this sample as the “combined APOE and non-APOE subsamples” to indicate that survival data were available for those with and without genetic information.

Results

Simulation Studies

We performed simulation studies to investigate behavior of the estimating procedures using the joint analysis of genetic and non-genetic subsamples and the analysis of genetic subsample alone, in different scenarios. We simulated longitudinal datasets structurally similar to “genetic” (APOE polymorphisms) and “non-genetic” subsamples of the FHS original cohort. For each dataset, we assumed that the total sample size equals 5000 individuals of whom 25% (1250 individuals) constitute the “genetic sample,” i.e., they have information on the genetic marker (carrier/non-carrier of a hypothetical allele) and survival data, and the rest of the sample (3750 individuals) have only data on survival status available. In each study, we simulated life spans of individuals (assuming the proportion of carriers of a hypothetical allele at birth P₀ = 0.5) using Gompertz mortality rates: ln μ(t,G)=ln a_G +bt, G = 0, 1, with ln a₁ = −9.0 (for carriers of a hypothetical allele), ln a₀ = −9.6 (for non-carriers of a hypothetical allele), in all studies. Parameter b (which is assumed the same for carriers and non-carriers) varied across the studies: b = 0.08, 0.075, 0.07, 0.065, and 0.06, in studies 1-5, respectively. Such parameters were selected to check how different proportions of censored individuals in the total sample (which range from about 25% in study 1 to about 67% in study 5) affect the estimating procedures. Hypothetical “ages at entry into the study” for each individual were simulated as a discrete random variable uniformly distributed over the interval from 30 to 60. Hypothetical “ages at collecting genetic information” were assigned as hypothetical age at entry plus 40 years. We randomly selected the individuals to form the “genetic” and “non-genetic” subsamples among those with simulated life spans exceeding ages at collecting genetic information and ages at entry into the study, respectively. Individuals with simulated life span exceeding age at entry plus 50 years were considered censored at that age. In each of the five simulation studies, this procedure was repeated 1000 times to generate 1000 datasets which were subsequently estimated using the “genetic only” likelihood L^gen (3) for the “genetic” subsamples, the “joint” likelihood L (7) for the combined “genetic” and “non-genetic” subsamples, and “genetic only” likelihood L^gen (3) assuming that the entire sample of 5000 individuals has genetic information.

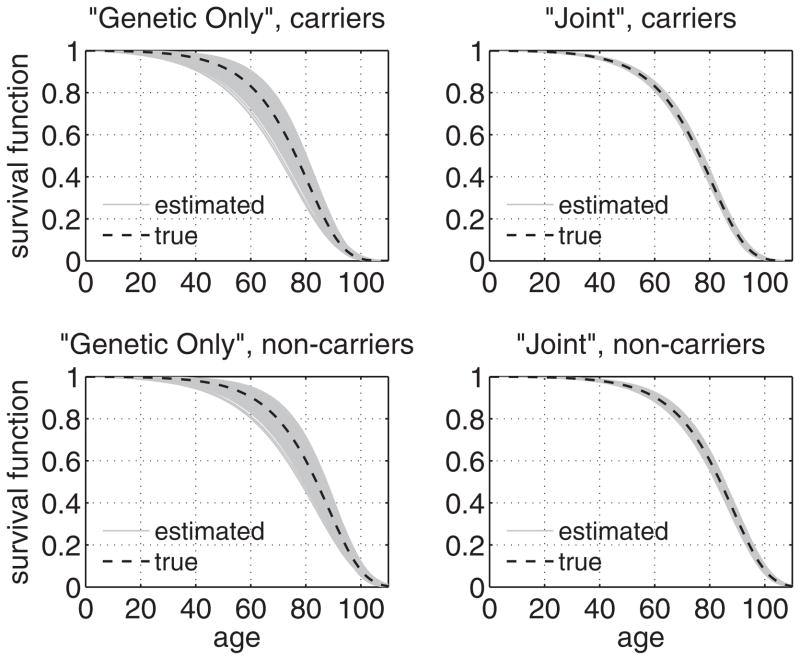
Mean values and standard deviations of parameter estimates for 1000 simulated datasets estimated by different likelihoods are given in Table 1. Estimates of survival functions for carriers and non-carriers of a hypothetical allele in 1000 simulated data sets estimated by the “genetic only” and “joint” likelihoods in study 1 are shown in Figure 1. Table 1 shows that in simulation study 1 the standard deviations of parameter estimates obtained using only “genetic” subsamples were about 3.3 to 4 times larger than those of estimates obtained using the combined “genetic” and “non-genetic” subsamples (except for the initial proportion P₀, for which the accuracy improves by about 17%). Figure 1 illustrates the respective increase in the accuracy of estimates of survival functions for carriers and non-carriers of a hypothetical allele. The standard deviations of parameter estimates (except for P₀) in the “joint analyses” are close to those obtained in analyses assuming that the entire sample (5000 individuals) has genetic information.

Table 1.

Results of simulation studies: mean values (standard deviations in parentheses) of parameter estimates for 1000 simulated datasets in different estimation procedures (“Genetic Subsample”: 1250 individuals from the genetic subsample; “Joint Analysis”: 1250 individuals from the genetic subsample + 3750 individuals from the non-genetic subsample; and “Genetic Total”: entire sample of 5000 individuals is genetic) and estimates of power in different studies

Studya	Genetic Subsample				Joint Analysis				Genetic Total				Estimates of Powerb			Avg. % Cens.c
	ln a1	b	ln a0	P0	ln a1	b	ln a0	P0	ln a1	b	ln a0	P0	wGS	wJA	wGT
1	−9.013 (0.436)	0.080 (0.005)	−9.616 (0.451)	0.500 (0.021)	−8.999 (0.109)	0.080 (0.002)	−9.600 (0.138)	0.499 (0.018)	−8.997 (0.104)	0.080 (0.001)	−9.599 (0.109)	0.500 (0.007)	0.000	0.983	1.000	24.5%
2	−9.035 (0.460)	0.075 (0.005)	−9.635 (0.471)	0.500 (0.019)	−9.013 (0.112)	0.075 (0.001)	−9.612 (0.144)	0.500 (0.016)	−9.009 (0.108)	0.075 (0.001)	−9.607 (0.113)	0.500 (0.007)	0.000	0.939	1.000	33.9%
3	−9.015 (0.506)	0.070 (0.006)	−9.612 (0.524)	0.500 (0.019)	−9.005 (0.120)	0.070 (0.002)	−9.601 (0.157)	0.499 (0.017)	−9.002 (0.116)	0.070 (0.001)	−9.603 (0.122)	0.500 (0.007)	0.000	0.807	1.000	44.8%
4	−9.007 (0.595)	0.065 (0.006)	−9.610 (0.609)	0.500 (0.018)	−9.009 (0.128)	0.065 (0.002)	−9.612 (0.169)	0.500 (0.016)	−9.005 (0.126)	0.065 (0.002)	−9.605 (0.131)	0.500 (0.007)	0.000	0.558	0.963	56.3%
5	−9.022 (0.694)	0.060 (0.007)	−9.628 (0.705)	0.501 (0.017)	−9.002 (0.147)	0.060 (0.002)	−9.607 (0.184)	0.500 (0.016)	−8.997 (0.146)	0.060 (0.002)	−9.599 (0.152)	0.500 (0.007)	0.000	0.334	0.615	67.2%

Notes:

^aParameters a₁, a₀, and P₀ are the same in all studies: ln a₁ = −9.0, ln a₀ = −9.6, P₀ = 0.5; parameter b equals 0.08, 0.075, 0.07, 0.065, and 0.06 in studies 1-5, respectively

^bPower is estimated as the proportion of the datasets with non-intersecting 95% confidence intervals for ln a₁ and ln a₀ calculated from the asymptotic covariance matrix of the maximum likelihood estimators obtained using respective estimation procedures (w_GS – genetic subsample; w_JA – joint analysis; w_GT – genetic total)

^cAverage percent of censored individuals in the datasets in respective study

Fig. 1.

Estimates of survival functions for carriers (upper row) and non-carriers (lower row) of a hypothetical allele in 1000 simulated datasets (simulation study 1) in different estimation procedures: “Genetic Only” likelihood (1250 individuals from the genetic subsample, left column) and “Joint” likelihood (1250 individuals from the genetic subsample + 3750 individuals from the non-genetic subsample, right column)

Table 1 also shows that, as the average proportion of censored individuals increases (from about 25% in study 1 to about 67% in study 5), the accuracy of estimates decreases for all parameters (except for P₀). For the likelihood procedure based on the genetic subsample only, respective standard deviations of parameter estimates increase by about 50-60 % in study 5. For the “joint likelihood” based on the genetic and non-genetic subsamples, respective standard deviations of parameter estimates also increase, but to a lesser extent (about 20-35 % in study 5). As the result of this, the ratio of standard deviations of parameters estimated by the “genetic only” likelihood to those estimated by the “joint” likelihood increases to about 3.8 – 4.7 in study 5 (the ratio is about 17-24% larger than that in study 1).

Table 1 also shows estimates of the power for detecting a difference between the survival curves for carriers and non-carriers of a genotype (i.e., for rejecting the null hypothesis on equality of parameters a₁ and a₀) at α = 0.05 in different studies and for different estimation procedures (see the column w_GS for the likelihood based on the genetic subsample of 1250 individuals, w_JA for “joint likelihood,” and w_GT for the likelihood assuming that the entire sample of 5000 individuals is genetic). The power was estimated as the proportion of the datasets for which 95% confidence intervals for ln a₁ and ln a₀ (calculated from the asymptotic covariance matrix of the maximum likelihood estimators obtained using respective estimation procedures) do not intersect. The table shows that the genetic subsample alone (column w_GS) is not sufficient to detect the difference in parameters (survival functions) in all studies for the given parametric settings. The total sample of 5000 individuals (column w_GT) generally provides the adequate power, except for study 5 with the largest proportion of censored individuals. The estimates for the “joint likelihood” (column w_JA) are between these two extremes illustrating an increase in the power when the non-genetic subsample is analyzed along with the genetic one in the “joint likelihood.” The same observation on reducing power with an increase in the proportion of censoring can be made. For the studies with relatively small proportions of censoring (studies 1-3), the estimating procedure based on the “joint likelihood” provides the adequate power. However, in studies with larger proportions of censoring (studies 4-5) the estimates of power fell below the acceptable level. Thus, in situations with larger proportions of censoring (e.g., in studies of incidence rates of diseases) even the “joint likelihood” may have a limited power compared to the similar situations when the proportion of censoring is smaller (as, for example, in mortality studies, which may be close to study 1).

Application to the FHS data

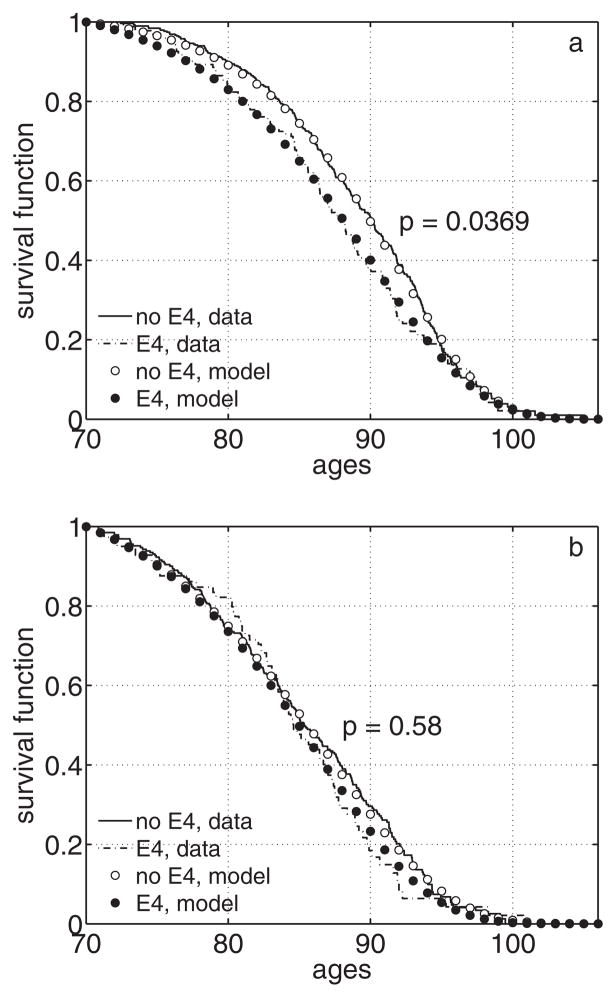
We applied the method to estimate survival functions for carriers and non-carriers of the APOE e4 allele in the FHS original cohort. First, we estimated empirical survival functions for female and male carriers and non-carriers of the e4 allele from the FHS APOE subsample using the product-limit estimator for left-truncated data (Tsai et al. 1987). The estimates for females are shown in Figure 2a. Empirical analyses do not provide statistically significant results (95% confidence intervals for carriers and non-carriers of the e4 allele intersect for almost all ages, data not shown), although female carriers of the e4 allele tend to have worse survival at ages 70+ compared to non-carriers of that allele. Results for males are non-significant, with the survival curve for carriers of the e4 allele intersecting that of non-carriers at different ages (Figure 2b).

Fig. 2.

Survival functions (conditional at age 70) for carriers and non-carriers of the APOE e4 allele in the FHS APOE subsample calculated empirically from the data and estimated using the “genetic only” likelihood with Gompertz mortality rates: a) females; b) males. Note: p denotes p-value for the likelihood ratio test for the “genetic only” likelihood for testing the null-hypothesis about equality of survival curves for carriers and non-carriers of the e4 allele

Figure 2 also shows estimates of respective survival curves from the FHS APOE subsample using the “genetic only” likelihood (3) with Gompertz mortality rates. The likelihood ratio test indicated marginal significance for the null hypothesis about equality of survival curves for female carriers and non-carriers of the e4 allele (p = 0.037). Results for males remained non-significant (p = 0.58).

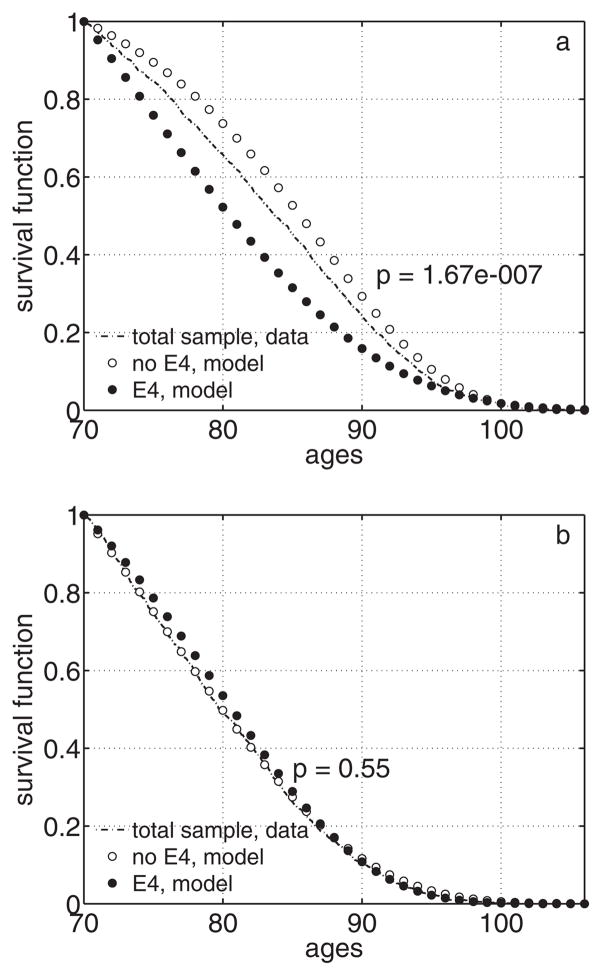
Estimates of survival functions for carriers and non-carriers of the e4 allele estimated from the entire FHS sample using the “joint” likelihood (7) with Gompertz mortality rates are given in Figure 3. Application of the “joint” likelihood to the combined FHS APOE and non-APOE subsamples substantially improved significance for females (the likelihood ratio test p-value is 1.7 · 10⁻⁷). Results for males were still non-significant in “joint” analyses (p = 0.55).

Fig. 3.

Empirical survival function (conditional at age 70) for the entire FHS sample (APOE and non-APOE subsamples) and survival functions (conditional at age 70) for carriers and non-carriers of the APOE e4 allele estimated from the entire FHS sample using the “joint” likelihood with Gompertz mortality rates: a) females; b) males. Note: p denotes p-value for the likelihood ratio test for the “joint” likelihood for testing the null-hypothesis about equality of survival curves for carriers and non-carriers of the e4 allele

Discussion

This paper, as well as those by Yashin et al. (2007) and Arbeev et al. (2009), provide methods that combine data from “genetic” and “non-genetic” subsamples of a longitudinal study. This joint analysis results in substantial improvements in the accuracy of estimates of genotype-specific hazard rates compared to analyses of “genetic” subsamples alone. Such situations when information on genetic markers cannot be collected for all participants of the study typically arise because of several reasons: 1) genotyping may be performed at some time point after beginning of the study when some initially participating individuals dropped out of it (deceased or were lost to follow-up) by the time of genetic data collection; 2) budget limitations prohibited obtaining genetic information for the entire sample; 3) some study participants refused to provide samples for genetic analyses. Thus, such methods can find applications in analyses of different studies to extract genetic information from the entire sample of participants and increase the accuracy of estimates. Note that the method presented here works in a longitudinal context that requires collecting follow-up information on participants. In case of cross-sectional studies, when such information is not available, the methods by Yashin et al. (2007) can be used for joint analyses of genetic and non-genetic data.

Application of the approach to evaluation of survival functions for female and male carriers and non-carriers of the APOE e4 allele in the FHS data revealed significantly worse survival at old ages for females, but not for males, whereas empirical analyses did not prove any significant differences. Several other longitudinal studies examined sex-specific effect of APOE on mortality with different results (Ewbank 2002a; Hayden et al. 2005; Kulminski et al. 2008; Rosvall et al. 2009). Ewbank (2002a) did not find any sex differences in the relative risk (RR) of death for carriers of the APOE e3/e4 and e4/e4 genotypes. Kulminski et al. (2008) observed that the sex-specific RR showed the opposite behavior for the APOE e2/e4 and e3/e4 genotypes (although being non-significant) in the representative sample of the elderly (65+) US population. Rosvall et al. (2009) reported a significant increase in the RR of death for male carriers of the e4 allele in the elderly (75+) Swedish cohort. Dato et al. (2007) applied the method by Yashin et al. (1999) to evaluate survival functions for carriers and non-carriers of the APOE allele e4 in the Italian population and found different age-patterns of these curves for females and males (for females, they intersect at the age about 63 years and for males the curve for carriers is uniformly lower). Hayden et al. (2005) studied an elderly (65+) predominantly white US cohort and revealed that female e3/e4 and e4/e4 carriers have significantly higher RR of death, whereas males do not, which is similar to our observations. Little et al. (2009) revealed that hazard ratios for death were significantly higher for female carriers of the APOE e4 allele (compared to those with the e3/e3 genotype) in a cohort of elderly (75+) white women in the US. The last two studies which showed results similar to our observations have cohorts generally similar to that analyzed in this study (the FHS cohort consists of predominantly white Americans aged 65+ at the time of APOE genotyping). Differences between populations under study (Ewbank 2007), such as ethnicity, environmental exposures, age distributions, and study designs (length of follow-up periods, sample sizes, etc.) may partly explain the observed differences in results. Other factors which were not available for this study, e.g., dementia, may also mediate the observed results (Little et al. 2009; Rosvall et al. 2009).

Application of different analytic methods can help reveal different patterns of genotype-specific hazards or survival functions such as intersection of survival curves (Dato et al. 2007) or decline in the relative risk of deaths with age (Ewbank 2002a), which cannot be observed in traditional analyses that use the Cox proportional hazards model. In our analyses, we observed that the effect of the e4 allele on survival diminishes with age which is in line with observations by Ewbank (2002a) and the lack of association of APOE alleles with survival of centenarians (Louhija et al. 2001).

Finally, we should note that the approach presented in this paper has certain limitations which should be taken into account in practical applications. First of all, its application does not undermine the need for collecting large genetic samples. The method does provide an increase in the accuracy/power compared to analyses of smaller genetic subsamples but the “best case” (often unrealistic) scenario is to collect genetic information for a larger sample, as Table 1 illustrates: the best accuracy and power is reached when the genetic information is available for the entire sample. We also note that in the simulation studies presented in the paper, 25% of the entire sample constituted the “genetic subsample” (this proportion was selected to resemble the FHS data). Clearly, the results for the accuracy and power would be different for other proportions of genetic subsample or different total sample sizes (same may also be true for different values of an initial proportion P₀). For example, in situations when the non-genetic subsample is a small part of the entire sample, the improvement in the accuracy/power in the “joint analyses” may be negligible. On the other hand, if the genetic subsample (or the entire sample) is too small then the resulting accuracy/power will likely not be adequate in both “genetic only” and “joint” analyses. As our simulations illustrate, applications of the method are most effective in case of intermediate values of the proportion of genetic subsample (say, 25%, as in our simulation studies).

Several possible generalizations of the method can be mentioned. The method described in the paper specifies survival functions for carriers/non-carriers of allele or genotype. Its generalization for the case of multiple genotypes is straightforward. We note also that the method described in this paper uses parametric specifications of allele- or genotype-specific survival functions. Other more flexible specifications of allele- or genotype-specific hazards (in terms of assumptions on their functional forms), such as semiparametric and non-parametric models, can be formulated (Yashin et al. 1999). Various unobserved factors (of genetic or non-genetic origin) may affect mortality risks and they may introduce bias in the results of survival analyses when they are ignored in the estimation algorithm (Vaupel and Yashin 1985). Approaches to correct for heterogeneity effects can be formulated (Yashin et al. 1999). Analysis of such models requires additional studies which are beyond the scope of this paper.