Abstract
We investigated the relationships among landscape quality, gene flow, and population genetic structure of fishers (Martes pennanti) in ON, Canada. We used graph theory as an analytical framework considering each landscape as a network node. The 34 nodes were connected by 93 edges. Network structure was characterized by a higher level of clustering than expected by chance, a short mean path length connecting all pairs of nodes, and a resiliency to the loss of highly connected nodes. This suggests that alleles can be efficiently spread through the system and that extirpations and conservative harvest are not likely to affect their spread. Two measures of node centrality were negatively related to both the proportion of immigrants in a node and node snow depth. This suggests that central nodes are producers of emigrants, contain high-quality habitat (i.e., deep snow can make locomotion energetically costly) and that fishers were migrating from high to low quality habitat. A method of community detection on networks delineated five genetic clusters of nodes suggesting cryptic population structure. Our analyses showed that network models can provide system-level insight into the process of gene flow with implications for understanding how landscape alterations might affect population fitness and evolutionary potential.
Keywords: gene flow, graph theory, landscape genetics, Martes pennanti, network, small-world
Introduction
Key goals of the emerging field of landscape genetics are to gain an understanding of how processes such as migration, genetic drift, and the distribution and connectivity of populations affect genetic structure (Manel et al. 2003; Storfer et al. 2007). Less attention has been paid to identifying general system-level features that arise from patterns of connectivity. In many complex systems, patterns of connectivity give rise to system-level properties that are not apparent from analysis of pairwise relationships between components. The ability to characterize these system-level properties, along with the local properties of individual landscapes, could improve resource management in complex, natural ecosystems. Valid inference at this level of analysis requires genetic samples from multiple populations and an analytical framework within which the influence of landscape variables on genetic variation can be determined.
We were interested in investigating the link between landscape quality and genetic connectivity among fishers (Martes pennanti) sampled from 34 landscapes in the Great Lakes Region of ON, Canada (Carr et al. 2007a). We used graph theory to model gene flow within the resulting network of genetic connectivity among fishers in order to relate system- and node-level biological characteristics to landscape quality.
Graph theory (see Table 1 for a glossary of terms) has provided a powerful framework for characterizing processes that take place in complex interconnected systems in such diverse disciplines as physics, mathematics, and sociology (Newman 2003), as well as in biology where protein–protein interactions, social structure, and food webs have been modeled (Proulx et al. 2005; May 2006). The distribution of genetic variation can also be intuitively conceptualized as a network of genetically interconnected nodes representing individuals from sampled sites connected by gene flow (Dyer and Nason 2004; Dyer 2007). We employed a recently developed technique to construct our network based solely upon genotypes of individuals sampled from multiple landscapes, avoiding the need for a priori assignment of barriers to gene flow (Dyer and Nason 2004). We considered the fishers sampled within each landscape as a node in the network.
Table 1.
A short glossary of terms and concepts in graph theory
| Betweenness: the number of shortest paths that a particular node or edge lies on. Assuming that interactions take place through the shortest path, then betweenness is a measure of the importance of a node or edge in terms of the bottleneck it creates. |
| Centrality: a measure of the relative position of a node or an edge in terms of connectivity or facilitation of node interaction (e.g., betweenness, degree, eigenvector centrality). |
| Characteristic path length: the mean of all pairwise graph distances connecting nodes. It can be used as a ‘fitness’ measure describing the ease of node communication. |
| Clustering coefficient: a measure of the probability that two nodes connected to a particular other node are themselves connected. |
| Degree: the number of edges connected to a node. If the edges are weighted, then edge weights are summed and this measure is generally termed ‘strength’. |
| Degree distribution: the distribution of node degree values of a network. The degree distribution is a particularly important measure of network topology and together with other metrics is diagnostic of certain classes of networks and some general properties of network topology. |
| Eigenvector centrality: a similar in concept to ‘degree’ but accounts for the fact that not all connections are equally connected. Here connections to well-connected nodes will likely be more influential than connections to less well-connected nodes and are weighted as such. |
| Graph theory: a branch of mathematics that deals with describing and understanding the properties of networks. |
| Modularity: a measure of community structure within a network. |
| Network: a set of entities (represented as nodes) that interact (represented as edges). Interactions can be represented as simple binary connections, can have direction, or weighted values representing the strength of interactions. |
| Graph distance: the sum of the shortest number of distinct edges (or edge weights) connecting a pair of nodes. |
There are three particularly well-described classes of networks that may be of general interest to landscape geneticists: small-world, scale-free, and random (described in Table 2; Barabasi and Albert 1999; Erdos and Renyi 1959; Watts and Strogatz 1998). These classes are of interest because they each imply characteristic dynamic features that can be interpreted in the context of dispersal, gene flow, resilience to extirpations, and genetic structure (Table 2). Generally, small-world networks are characterized by highly clustered nodes, suggesting efficient transfer of information (in our case alleles) and a decentralized network structure. Scale-free networks are characterized by a few highly connected nodes that have disproportionate importance in maintaining network connectivity. These connected ‘hubs’ are also points of vulnerability for the network if removed. Finally, random networks are useful ‘straw-men’. When constructed with similar node and edge properties as empirical networks, random networks can aid in determining whether observed properties of a network are a consequence of some nonrandom process or simply a byproduct of random linkages among nodes.
Table 2.
A description of the characteristics of random, small-world, and scale-free networks with possible biological interpretations in terms of landscape connectivity
| Random networks: A class of networks characterized by a short characteristic path length, binomial degree distribution, and a small average clustering coefficient. Because each node is approximately equally well connected, the characteristic path length increases monotonically after random or targeted node removal. If the genetic connectivity among populations displays random graph properties, this would suggest that dispersal among populations was entirely random and unstructured and that populations are separated by short paths (direct or through intermediate populations). Extirpations of populations would steadily decrease the ease through which genes were exchanged among populations. |
| Small-world networks: A class of networks characterized by a short characteristic path length, binomial degree distribution, and a large mean clustering coefficient. Small-world networks are similar to random networks in that each node has approximately the same influence on the characteristic path length if removed, however the added feature of clustering might create alternate paths between nodes such that impact of node removal could be less than on random networks. If genetic connectivity has these characteristics genes can be efficiently exchanged among populations ‘locally’ and ‘globally’. Given that there will likely be increasing fitness costs of dispersal with increasing geographic distances and greater robustness to losses of populations, we might predict the small-world network characteristics to be common to well connected populations. |
| Scale-free networks: A class of networks characterized by a short characteristic path length and a power-law degree distribution. The average clustering coefficient can vary. Most nodes have relatively few connections while a few nodes are highly connected hubs Because most nodes are not particularly well connected, the random removal of even a high proportion of nodes tends to have little impact on the network characteristic path length. However, the targeted removal of the most connected nodes leads to a rapid increase in the characteristic path length and network fragmentation. From a biological perspective, the random removal of population nodes could be considered analogous to stochastic extirpation perhaps due to severe weather events, whereas removal of the most connected nodes might occur, for example, due to over harvest of populations in high quality habitats. In this case ‘hub’ populations would warrant considerable concern within management and conservation strategies. |
Previous research has demonstrated that fishers are territorial and relatively philopatric, exhibiting short dispersal distances for a carnivore of their size (Arthur et al. 1993; Kyle et al. 2001; Koen et al. 2007). We hypothesized that this would lead to a highly clustered network of genetic connectivity, with either small-world or scale-free properties. A tendency for philopatry could lead to the clustered nodes of a small-world network. A few important source populations in high quality habitat, however, could act as the hubs of a scale-free network. We also simulated the effect of local extirpation (i.e., node removal) on network structure. A small-world network should be more resilient than a scale-free network to node removal.
Aside from system-level properties of the network, we were also interested in how the topological positions of individual nodes on the network characterized their influence on the network's dynamic processes. There are numerous metrics of node and edge position (Costa et al. 2007). Three particularly relevant measures of node centrality are degree, eigenvector centrality, and betweenness (Table 1). The degree of a node is a measure of its connectivity (number of connections); eigenvector centrality incorporates both direct and indirect connectivity (how connected a node's immediate connections are); and betweenness is a measure of the bottleneck a particular node forms in the network. Assessing the effects of targeted removal of nodes with high values for these measures on the characteristic path length should help identify nodes that are particularly important for maintaining genetic connectivity.
Metrics of node position may also be valuable for understanding the ecological properties of the network. To investigate this, we related indices of node centrality (degree and eigenvector centrality; Table 1) to the proportion of genetically identified immigrants in each node and to other measures of habitat suitability so as to identify biologically meaningful traits of the topological position of nodes. The fisher population that we studied was increasing (Bowman et al. 2006) and fishers appear to exhibit density-dependent dispersal such that, during a population increase, the proportion of immigrants into each landscape is negatively related to habitat suitability (Carr et al. 2007b). In this ecological context, central nodes should be productive and well connected. Thus, we hypothesized that node centrality should be inversely related to the proportion of immigrants to each node, and therefore directly related to habitat suitability.
Finally, a network approach to the analysis of gene flow among nodes may provide an informative method for identifying genetic structure. Many other naturally occurring networks including biological networks of social interactions (Lusseau et al. 2006) and metabolic pathways (Guimera and Amaral 2005) display structure within networks. These networks are characterized by communities of nodes with dense node connectivity within groups and relatively more sparse connections among groups. Thus, existing graph-theoretic methods for clustering based upon network topology may also be useful for clustering genetically well-connected nodes and identifying cryptic population structure. An effective method for detecting structure within networks is ‘modularity’ optimization (Danon et al. 2005; Gustafsson et al. 2006) as characterized by eigenvectors of the network matrix (Newman 2006). This method searches for natural divisions such that there are more connections within clusters or fewer connections among clusters than expected at random.
In our analyses we have compared the network's characteristic path length and clustering to that of similarly structured random networks to determine whether network clustering was a feature of the number of nodes and edges or a result of some other potentially non-random process (i.e., we tested whether the network had small-world properties). We then assessed the distribution of node connectivity to determine whether the network was characterized by a few hubs of particularly well-connected nodes (was the network scale-free?). We examined the effects of the sequential removal of the most central nodes on the network's characteristic path length to gain an understanding of possible effects of node extirpation on gene flow. Measures of node centrality were related to the proportion of immigrants in each node, as well as the show depth and proportion of coniferous forest cover within the area encompassed by the node. Finally, we assessed the ability of a network clustering technique, modularity optimization, to identify population genetic structure.
Methods
Our data set consisted of 722 fishers genotyped at 16 microsatellite loci (See Carr et al. 2007a,b for a complete description of molecular techniques). Samples were obtained from an ordered lattice of 34 landscapes, each approximately 300 km2 and selected such that daily fisher movements and home ranges did not connect the landscapes (Fig. 1; Arthur et al. 1993; Bowman et al. 2002). The mean number of fishers sampled per landscape was 21.2. For the purposes of our network analysis, a sample of fishers from a landscape was considered a network node.
Figure 1.
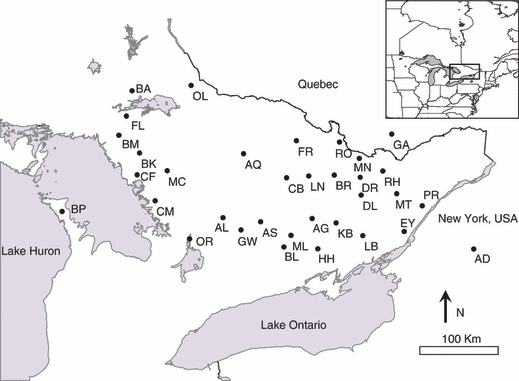
Location of fisher (Martes pennanti) sample sites from the Great Lakes region of ON, Canada. Samples were taken between 2000 and 2003. Two-letter codes refer to sample site geographic names, which are given in Appendix A. The inset map shows a section of eastern North America.
We constructed our network following Dyer and Nason (2004). Individuals within n nodes defined the nodes’ multidimensional centroid. Based upon among-node genetic covariance structure, centroids were assigned a coordinate in n dimensional space. Pairwise distances among node centroids were written as a genetic distance matrix with the off diagonal values representing network edges, which were weighted as the statistical distance between nodes. This distance matrix can be represented as a saturated network where all nodes are connected. A more informative topology is the minimal edge set that describes among-node genetic covariance. The edge set is selected based upon the statistical concept of conditional independence, where network edges are analogous to predictor variables. We retained edges between nodes that contributed most to genetic covariance structure after taking into account the genetic covariance among all nodes. The alpha level for the fit of the network after edge removal is 0.05. The values for this matrix defined genetic distances between connected nodes. For some measures described below however, we either considered the network as unweighted (each node either connected or not) or as a similarity matrix (the inverse of the distances measures). For a full statistical description of this method for constructing networks and how fit is calculated see Dyer and Nason (2004) and references therein. The network was constructed using the software GENETIC STUDIO (Dyer 2008).
Network properties
There are numerous metrics to describe network topology that could provide insight into gene flow dynamics. We calculated node degree, eigenvector centrality, and betweenness as measures of node centrality and connectivity (Table 1). Degree is simply the number of connections a node has (Freeman 1979). Eigenvector centrality is based on the leading eigenvector of a network's matrix and measures both how well a node is connected and how well its immediate connections are connected (Newman 2004). Betweenness is a measure of the bottleneck a particular node creates on a network, calculated as the number of times a particular node falls on the shortest path between any two other nodes with edges weighted, in our case as genetic distances.
The shortest path length between pairs of nodes on the network was assessed in relation to pairwise measures of geographic distance and FST (Weir and Cockerham 1984; Goudet 2001) to test for isolation by distance. Correlations between distance measures were determined using Mantel tests and considered significant at P < 0.05 after 9999 randomizations.
A characteristic path length that is similar to a random network and a clustering coefficient that is high relative to a random network indicate that a network has small-world characteristics (Watts and Strogatz 1998). The clustering coefficient varies between 0 and 1 and measures how well the connections of a node are themselves connected (Holme et al. 2007). To test for these small-world properties, we generated 1000 random networks with the same number of nodes, edges, and edge weight distribution as the fisher network and calculated the clustering coefficient and characteristic path for each network. If the clustering coefficient of the fisher network was greater than 95% of those from random networks and characteristic path length was similar to the random networks, then we considered the network to display small-world characteristics (Watts and Strogatz 1998).
We then examined the node degree distribution. If node degree has a binomial distribution around an average, then a network has a connectivity pattern similar to that expected in both random and small-world networks and all nodes are relatively equally well connected. Alternatively, if the distribution decays as a power-law then the network has scale-free properties and is characterized by a few highly connected hubs (Barabasi and Albert 1999).
We conducted node removal experiments to examine the network's resilience to node loss. The characteristic path length is an indicator of network resilience, in that connectivity decreases with increasing path length. We sequentially removed the eight nodes with the highest degree (most connected) and then highest betweenness (largest network bottleneck) values. If the characteristic path length increased or the network fractured after the removal of those nodes, then they were particularly important for maintaining network connectivity.
Node properties
We used linear regressions to test our predicted relationships between node centrality and the proportion of immigrants in each node. We considered each of the node centrality measures, degree and eigenvector centrality, as independent variables, and the proportion of immigrants in each node as the dependent variable. Immigrants were identified as individuals assigned to a genetically identifiable population other than the one they were sampled in with ≥0.60 probability based upon Bayesian clustering with the program STRUCTURE (Pritchard et al. 2000; Carr et al. 2007b). The proportion of immigrants is related to habitat suitability (Carr et al. 2007b), so we were also interested in assessing whether network topology could be related to the habitat features previously shown to be important (snow depth and coniferous forest cover). We used two criteria to determine whether model effects were likely to have occurred by chance. First, the dependent variable in each of the above-mentioned linear regressions was permuted 9999 times. If variable parameter estimates from the real data were greater or less than 95% of randomly generated values, we considered the effects as statistically significant. Second, if 95% confidence intervals around beta values did not overlap 0, then the effects were considered biologically meaningful. Spatial autocorrelation of centrality measures was assessed with Moran's I at eight Euclidean distance classes. Distance classes were selected such that samples sizes were approximately equal and large enough for tests across each class.
Network community structure
Network communities are defined as groups of nodes with either a higher density of connections between nodes than that expected by chance or fewer connections between communities than that expected by chance. Maximization of network modularity [Q; number of edges within groups minus the expected number in a similar network with edges placed at random (Newman 2004)] over possible network divisions has been shown to be an effective method for detecting such community structure in networks (Danon et al. 2005; Gustafsson et al. 2006). Modularity can have positive or negative values with positive [greater than 0.3 as a rule of thumb (Newman 2004)] values indicating that the network can be reasonably subdivided. Communities are detected by searching for divisions that yield peak values for Q. The network (or subsequent subdivision) is indivisible if there is no division that increases modularity. We calculated modularity by using eigenvectors of the network's characteristic matrix of genetic similarity (Newman 2006). Eigenvalues for nodes indicate the certainty of node assignment to a community with values farthest from 0 indicating the greatest certainty. We then heuristically compared community divisions to a previously published individual Bayesian clustering of the same genotypes (Carr et al. 2007b) undertaken with STRUCTURE.
Modularity was calculated in SOCPROG MATLAB modules written by Whitehead and Lusseau (Whitehead 2005). SOCPROG was written for the analysis of social structures and so we imported the matrix of genetic similarity among nodes as an association matrix for our analysis. All other standard and graph-theoretic analyses were conducted using igraph (Csárdi and Nepusz 2006) for R statistical software (R Development Core Team 2008).
Results
Network properties
The network that best fit the data contained 93 edges connecting the 34 nodes (Fig. 2). Mantel tests indicated that graph distance between nodes was correlated with geographic distance (R2 = 0.44, P = 0.001; Fig. 3A) and FST (R2 = 0.50, P < 0.001; Fig. 3B). The distribution of the genetic-distance-weighted edges was skewed toward shorter distances (Fig. 4A). The characteristic path length was 11.1 for the distance-weighted network and 2.26 for the binary network. Node degree was binomially distributed (Fig. 4B) indicating that the network was not scale-free. The clustering coefficient of the network was 0.254. The average clustering coefficient of 999 generated Erdos-Renyi random networks containing the same number of nodes, edges and edge-weight distribution was 0.16 (SD 0.027). The clustering coefficient of the fisher network was greater than those from all but one of the random networks (P = 0.999). The average characteristic path length from the random networks was 13.2 (SD 3.1) for weighted randomizations and 2.22 (SD 0.033) for binary calculations on the same networks. Taken together, the significantly high clustering coefficient and similar characteristic path length in the fisher network relative to the random networks as well as the binomial degree distribution suggest that this network had small-world but not scale-free characteristics. The sequential removal of the eight nodes with the highest degree (24% of nodes) had little effect on the characteristic path in either the weighted or binary network. The characteristic path length of the weighted network changed from 11.1 (SD 3.6) before removal to 12.1 (SD 4.8; Fig. 5) and from 2.26 to 2.60 in the binary network after these nodes were removed. The sequential removal of the eight nodes with the highest betweenness resulted in an increase in the characteristic path length from 11.1 to 15.0 (Fig. 5).
Figure 2.
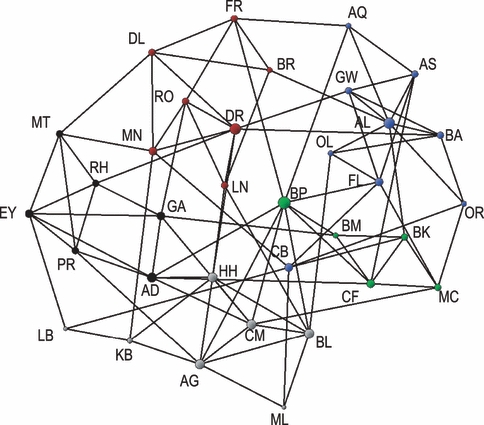
A two-dimensional projection representing the genetic relationship among fishers (Martes pennanti) sampled from 34 locations in ON, Canada during 2000–2003 and profiled at 16 microsatellite loci. Node size is proportional to increasing connectivity (degree) and edge length is proportional to the genetic distance between populations.
Figure 3.
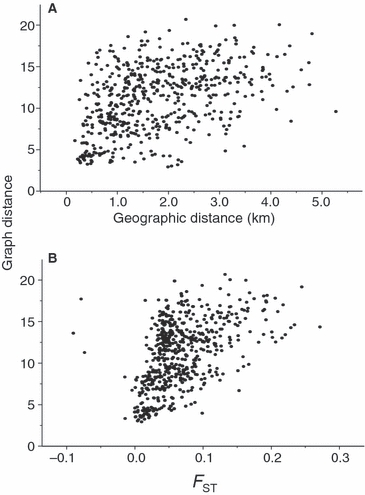
(A) The relationship between graph distance (shortest distance between pairs of nodes) and geographic distance among 34 nodes demonstrating the detection of isolation by distance within the graph structure. (B) The relationship between graph distance and FST among 34 nodes. Fishers were sampled from 34 different landscapes (nodes) in and around ON, Canada during 2000–2003 and profiled at 16 microsatellite loci.
Figure 4.
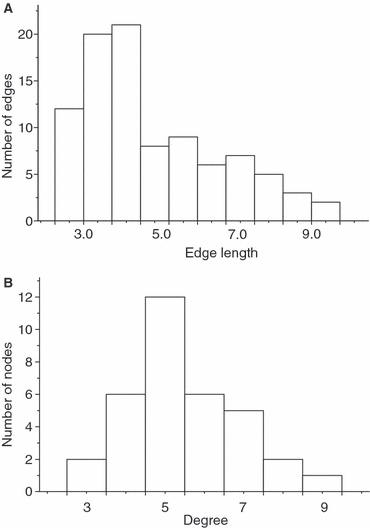
Histograms of the distribution of (A) the distance weighted network edges (connections between nodes) representing the genetic distance between connected nodes on the graph; (B) the Poisson-distributed degree distribution of a fisher, Martes pennanti, gene flow network, consistent with a small-world network. Fishers were sampled from 34 different landscapes in and around ON, Canada during 2000–2003 and profiled at 16 microsatellite loci.
Figure 5.
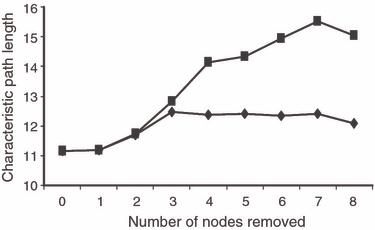
The effects of the sequential removal of nodes with the highest degree (diamond shaped points) and betweenness (square shaped points) on the network characteristic path length (measure of ease of gene flow through the network). Fishers were sampled from 34 different landscapes in and around ON, Canada during 2000–2003 and profiled at 16 microsatellite loci.
Node properties
Moran's I tests for spatial autocorrelation after Bonferroni corrections for simultaneous inference (Legendre and Fortin 1989) demonstrated that node degree was not spatially autocorrelated at any distance class (all P-values >0.00625). Eigenvector centrality was spatially autocorrelated (n = 43, r = 0.53, t = 3.94, df = 41, P = 0.0003) at the first distance class of approximately 4 km. Permutation tests on linear regression models and 95% confidence intervals around parameter estimates indicated that node degree and eigenvector centrality were negatively related to the proportion of immigrants in a node (Table 3). Similarly, the models relating degree and eigenvector centrality to snow depth and the proportion of dense coniferous forest suggested that only snow depth had a relationship with these measures of node centrality as the 95% confidence interval around parameter estimates for the term for proportion of dense coniferous forest overlapped 0, and permutation tests were not significant (Table 3). Snow depth was negatively related to both degree and eigenvector centrality.
Table 3.
Regression relationships for node properties of a fisher (Martes pennanti) genetic network in ON, Canada
| Model | Constant | Parameter estimate | r2 | P |
|---|---|---|---|---|
| Degree | ||||
| Prop. immigrants | 6.4 (0.94) | −5.0 (4.3) | 0.11 | 0.033 |
| Snow depth | 9.1 (3.4) | −0.09 (0.08) | 0.15 | 0.021 |
| Coniferous forest | – | −8.0 (13) | – | – |
| Eigenvector centrality | ||||
| Prop. immigrants | 0.20 (0.037) | −0.27 (0.17) | 0.24 | 0.004 |
| Snow depth | 0.31 (0.14) | −0.004 (0.0003) | 0.16 | 0.010 |
| Coniferous forest | – | −0.23 (0.53) | – | – |
Linear regression models relate degree and eigenvector centrality to the proportion of genetically identified immigrants as well as snow depth and coniferous forest cover. P-values were generated by randomly permuting the dependent variable and are the proportion randomly generated parameter estimates that were more extreme than those generated from the data.
Network community structure
Modularity optimization divided the network into five communities (Fig. 2, Appendix A). Modularity for this division was greater than 0.3 (Q = 0.457) suggesting that this was a useful division of the network. Previous clustering using the program STRUCTURE also identified five genetic populations (Carr et al. 2007a). Modularity optimization clustered 26 of the 34 (76.4%) populations similarly to STRUCTURE (Appendix A).
Discussion
It is difficult to predict system-level processes based solely on processes occurring within a system's component parts. We found that characterization of the fisher genetic structure as a network provided understanding of gene flow and resiliency in the system that we could not obtain from traditional population genetic measures. In the fisher network, nodes were more clustered than would be expected if they were randomly connected and the characteristic path length was short. In fact, nodes were connected by a mean of just over two edges (2 degrees of separation). This high degree of clustering in the network was not surprising given that there are likely fitness costs associated with longer distance dispersals and previous research has suggested relative philopatry in fishers (Arthur et al. 1993; Kyle et al. 2001). The clustering of nodes within the network explains the small observed effects of removing high-degree nodes on the network characteristic path length. A higher number of triangles (clusters) in a network leads to redundancy in paths between nodes such that there were alternate short paths through the network connecting nodes even after the removal of highly connected nodes. This suggests that genetic connectivity may not be particularly affected by the loss of even well-connected nodes. The characteristic path length between any two nodes remained approximately 2 after the removal of just over 24% of the most connected nodes. This is a stark contrast with scale-free networks such as the internet and the world-wide web where the removal of only the top 2% of best connected nodes leads to a more than doubling of the network's characteristic path length (Albert et al. 2000). The robustness of the fisher network to the loss of nodes has important implications for management and conservation. Fishers are harvested in most nodes and our removal experiments suggest that conservative harvest regimes are unlikely to affect genetic connectivity or induce harvest-related genetic differentiation, at least under current conditions.
Taken together, the small characteristic path length and high level of clustering are consistent with the well-characterized class of networks known as ‘small-world networks’. This network structure facilitates the efficient spread of information, disease, and indeed many network processes through ‘short-cuts’ among clusters (Watts and Strogatz 1998). The classic example of this phenomenon is the sociological concept of six degrees of separation which suggests that the average number of links between any two people in a social network of over six billion nodes (i.e., people) is approximately six (Milgram 1967). Small-world characteristics suggest that the fisher network is well connected such that information, in this case alleles, can be efficiently transferred among nodes with minimal restrictions on gene flow. Some biological examples of similar structures to the small-world fisher network can be found in animal social structures (Lusseau et al. 2006), food webs (Williams et al. 2002), neural connectivity (Achard et al. 2006), and cellular and metabolic networks (Wagner and Fell 2001) among others. It is easy to see the value of short cuts between nodes and robustness in network connectivity to loss of nodes for maintaining network function in many if these settings. In the fisher example, it seems likely that small-world patterns of connectivity among nodes are an emergent property of the spatial relationship between populations, the distribution of habitat, and the costs of dispersal.
Nodes with high betweenness values tend to be on the edge of clusters and act as bridges between different parts of the network and so their removal can have nonlocal impacts on network flow. Perhaps not surprisingly then, the removal of nodes with high betweenness did increase the network's characteristic path length relative to the removal of the same number of high-degree nodes, likely reducing genetic connectivity although in this case the network did not fragment and the increase was not drastic. This underscores that nodes that are not well connected can still play an important role in maintaining genetic connectivity. To avoid isolation of populations and maintain the potential for system wide gene flow, nodes with high betweenness appear to warrant particular management concern.
Our results demonstrate a negative relationship between the two measures of node connectivity (degree and eigenvector centrality) and the proportion of immigrants in a node. This suggests that well-connected nodes are important producers of emigrants both locally through direct connections (degree) and more broadly and indirectly through nodes connected to direct connections (eigenvector centrality). Therefore, although the characteristic path length between nodes increased very little with sequential removal of the most connected nodes, these nodes were likely important contributors of individuals to other nodes. Further, node connectivity (degree and eigenvector centrality) was also negatively related to snow depth suggesting that measures of node centrality are related to habitat suitability, and ultimately to individual fitness. Deep snow is thought to be a component of poor habitat suitability for fishers, as it impedes movement and induces higher energetic costs (Krohn et al. 1995). Fishers disperse during winter and may assess habitat suitability based in part on snow depth (Krohn et al. 1995). Our samples were from a period of population expansion in the region, where density-dependant dispersal may have led to the negative relationship between the proportion of immigrants and node centrality (e.g., Morris et al. 2004; Carr et al. 2007b).
Our heuristic look at the potential utility of modularity maximization for identifying genetically similar populations suggests that this method could be a valuable tool. We observed concordance between the popular program STRUCTURE, which takes a Bayesian approach to clustering individuals, and our estimated network communities such that both produced five genetic groupings. In addition, general patterns of node assignment were concordant; however, eight nodes assigned differently. This can be attributed to the differences in criteria for assigning sites to clusters or communities. STRUCTURE identified the highest mean ancestry and the highest proportion of highly assigned residents to provide a conservative estimate of effective migrants (Carr et al. 2007a,b). This Bayesian approach does not include a measure of genetic distance among nodes however, whereas the network approach includes genetic distance in the estimation of the mean genetic individual at a given site. As a result, the contribution of ancestries from other genetic clusters, whether through admixture or migrants, is incorporated in this mean ‘individual’ in the network approach but not in STRUCTURE. The network approach to identifying genetically similar clusters of nodes warrants further investigation and may be a valuable intermediate and complementary method between indirect estimates such as FST and individual-based Bayesian assignment tests. FST provides pairwise estimates of gene flow among sampled sites, whereas Bayesian models can estimate the number of subpopulations or genetic clusters and the ancestral contribution of each individual, but not genetic distance among populations.
Our results empirically support previous theoretical work demonstrating that population structure and processes can be modeled and visualized with biologically meaningful interpretations of network structures built solely upon genetic data (Dyer 2007). Graph theoretic approaches to understanding genetic connectivity are still relatively novel but the potential applications are exciting. From a landscape ecology perspective concepts in graph theory combined with knowledge of species habitat use and species life history have been used to model patch connectivity (Urban and Keitt 2001; O'Brien et al. 2006) and as a basis for reserve design (James et al. 2005). McRae (2006) and Brooks (2006) incorporated genetics and graph theory into analyses of isolation by distance that incorporate landscape heterogeneity and understanding scales of population organization and movement among patches, respectively. Dyer and Nason (2004) and Dyer (2007) have demonstrated through simulations that many traditional population genetic parameters can be derived from their approach to the construction of networks (which we have used here). Finally, and beyond the scope of this paper, our general approach to assessing network topology can be similarly applied to network edges. Analogous to node centrality there are measures of edge centrality that could be related to features thought to inhibit or promote connections between nodes such as road density, human settlement, and forest loss. An advantage of this approach would be that genetic connectivity could be used to identify important habitat linking nodes rather than using habitat models to infer genetic connectivity. Similarly, edge removal experiments similar to the node removal experiments conducted here may identify connections important for maintaining gene flow within a system. In summary, we found that graph theoretic measures of a node's position on a network and system-level models of network connectivity could be used to derive novel population-genetic measures. These measures provided novel insight into the gene flow and resiliency of a fisher genetic network. Our network approach to landscape genetics can be used where replicated, landscape-scale or system-level inference are desired.
Acknowledgments
This research was funded by an Ontario Living Legacy Trust grant to JB and PJW, by the Ontario Ministry of Natural Resources, and by Natural Resources Engineering and Research Council grants to JB, PJW, and CJG. We thank E.L. Koen, C.J. Kyle, C.Pilon, J.-F. Robitaille, S.M. Tully, OMNR Districts, and participating trappers for fisher tissue samples. We also are grateful to J.A.G. Jaeger, H.G. Broders, and the Geomatics and Landscape Ecology Laboratory at Carlton University for valuable comments on earlier drafts and helpful discussions.
Appendix A
Clustering results from eigenvector-based modularity maximization for a fisher (Martes pennanti) genetic network in ON, Canada. Network nodes were samples for fisher DNA during 2000–2003. Numbers under the heading Network Community represent node clustering based upon modularity maximization and letters in brackets represent population clustering from Carr et al. 2007b. Eigenvalues close to 0 indicate uncertainty in assignment of a population to its cluster.
| Site | Site ID | Sample size | Network community | Eigenvalues |
|---|---|---|---|---|
| Adirondack, NY | AD | 22 | l (a) | −0.08 |
| Escott-Yonge | EY | 20 | l (a) | −0.29 |
| Montague | MT | 21 | l (a) | −0.42 |
| Prescott | PR | 48 | l (a) | −0.24 |
| Ramsey-Huntley | RH | 20 | l (a) | −0.37 |
| Gatineau, Que. | GA | 18 | l (c) | −0.22 |
| Anson-Lutterworth | AL | 25 | 2 (b) | −0.23 |
| Algonquin | AQ | 20 | 2 (b) | 0.07 |
| Anstruther | AS | 24 | 2 (b) | −0.06 |
| Badgerow | BA | 22 | 2 (b) | −0.37 |
| Falconer | FL | 22 | 2 (b) | −0.05 |
| Galway | GW | 20 | 2 (b) | −0.26 |
| Olrig Cluster | OL | 14 | 2 (b) | −0.29 |
| Carlow-Bangor | CB | 20 | 2 (d) | −0.09 |
| Orillia-Ramara | OR | 17 | 2 (e) | −0.29 |
| Broughman | BR | 23 | 3 (c) | 0.34 |
| Dalhousie | DL | 20 | 3 (c) | 0.32 |
| Darling | DR | 22 | 3 (c) | 0.23 |
| Fraser-Richards | FR | 21 | 3 (c) | 0.42 |
| Lyndoch | LN | 19 | 3 (c) | 0.11 |
| McNab | MN | 24 | 3 (c) | 0.23 |
| Ross | RO | 19 | 3 (c) | 0.22 |
| Hungerford-Huntington | HH | 14 | 4 (b) | 0.28 |
| Angelsea-Grimsthorpe | AG | 16 | 4 (c) | 0.25 |
| Kennebec | KB | 23 | 4 (c) | 0.19 |
| Loughborough-Bedford | LB | 31 | 4 (c) | −0.03 |
| Belmont | BL | 7 | 4 (d) | 0.40 |
| Marmora-Lake | ML | 32 | 4 (d) | −0.03 |
| Conger-Freeman | CM | 15 | 4 (e) | 0.18 |
| Burton-McKenzie | BK | 16 | 5 (e) | 0.13 |
| Blair-Mowat | BM | 26 | 5 (e) | 0.43 |
| Bruce Peninsula | BP | 25 | 5 (e) | 0.55 |
| Carling-Ferguson | CF | 8 | 5 (e) | 0.31 |
| Monteith-Christie | MC | 26 | 5 (e) | 0.07 |
Literature cited
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. Journal of Neuroscience. 2006;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert R, Jeong H, Barabasi AL. Error and attack tolerance of complex networks. Nature. 2000;406:378–382. doi: 10.1038/35019019. [DOI] [PubMed] [Google Scholar]
- Arthur SM, Paragi TF, Krohn WB. Dispersal of Juvenile Fishers in Maine. Journal of Wildlife Management. 1993;57:868–874. [Google Scholar]
- Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Bowman J, Jaeger JAG, Fahrig L. Dispersal distance of mammals is proportional to home range size. Ecology. 2002;83:2049–2055. [Google Scholar]
- Bowman J, Donovan D, Rosatte RC. Numerical response of fishers to synchronous prey dynamics. Journal of Mammalogy. 2006;87:480–484. [Google Scholar]
- Brooks CP. Quantifying population substructure: extending the graph-theoretic approach. Ecology. 2006;87:864–872. doi: 10.1890/05-0860. [DOI] [PubMed] [Google Scholar]
- Carr D, Bowman J, Kyle CJ, Tully SM, Koen EL, Robitaille J-F, Wilson PJ. Rapid homogenization of multiple sources: genetic structure of a recolonizing population of fishers. Journal of Wildlife Management. 2007a;71:1214–1219. [Google Scholar]
- Carr D, Bowman J, Wilson PJ. Density-dependent dispersal suggests a genetic measure of habitat suitability. Oikos. 2007b;116:629–635. [Google Scholar]
- Costa LD, Rodrigues FA, Travieso G, Boas PRV. Characterization of complex networks: A survey of measurements. Advances in Physics. 2007;56:167–242. [Google Scholar]
- Csárdi G, Nepusz T. The igraph software package for complex network research. InterJournal Complex Systems. 2006 http://necsi.org/events/iccs6/viewabstract.php?id=88 (accessed on 11 September 2008) [Google Scholar]
- Danon L, Diaz-Guilera A, Duch J, Arenas A. Comparing community structure identification. Journal of Statistical Mechanics. Theory and Experiment. 2005 doi: 10.1088/1742-5468/2005/09/P09008. [Google Scholar]
- Dyer RJ. The evolution of genetic topologies. Theoretical Population Biology. 2007;71:71–79. doi: 10.1016/j.tpb.2006.07.001. [DOI] [PubMed] [Google Scholar]
- Dyer RJ. Genetic Studio: A suite of programs for spatial analysis of genetic-marker data. Molecular Ecology Resources. 2008 doi: 10.1111/j.1755-0998.2008.02384.x. in press. [DOI] [PubMed] [Google Scholar]
- Dyer RJ, Nason JD. Population graphs: the graph theoretic shape of genetic structure. Molecular Ecology. 2004;13:1713–1727. doi: 10.1111/j.1365-294X.2004.02177.x. [DOI] [PubMed] [Google Scholar]
- Erdos P, Renyi A. On random graphs. Publicationes Mathematicae. 1959;6:290–297. [Google Scholar]
- Freeman LC. Centrality in Social Networks: Conceptual Clarification. 1979;1:215–239. Social Networks. [Google Scholar]
- Goudet J. FSTAT, A program to estimate and test gene diversities and fixation indices. 2001. Version 2.9.3. http://www.unil.ch/popgen/softwares/fstat.htm (accessed on 11 September 2008) [Google Scholar]
- Guimera R, Amaral LAN. Functional cartography of complex metabolic networks. Nature. 2005;433:895–900. doi: 10.1038/nature03288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustafsson M, Hornquist M, Lombardi A. Comparison and validation of community structures in complex networks. Physica A: Statistical Mechanics and Its Applications. 2006;367:559–576. [Google Scholar]
- Holme P, Park SM, Kim BJ, Edling CR. Korean university life in a network perspective: dynamics of a large affiliation network. Physica A: Statistical Mechanics and Its Applications. 2007;373:821–830. [Google Scholar]
- James P, Rayfield B, Fortin MJ, Fall A, Farley G. Reserve network design combining spatial graph theory and species’ spatial requirements. Geomatica. 2005;59:323–333. [Google Scholar]
- Koen EL, Bowman J, Findlay CS, Zheng L. Home range and population density of fishers in eastern Ontario. Journal of Wildlife Management. 2007;71:1484–1493. [Google Scholar]
- Krohn WB, Elowe KD, Boone RB. Relations among fishers, snow, and martens – development and evaluation of 2 hypotheses. Forestry Chronicle. 1995;71:97–105. [Google Scholar]
- Kyle CJ, Robitaille JF, Strobeck C. Genetic variation and structure of fisher (Martes pennanti) populations across North America. Molecular Ecology. 2001;10:2341–2347. doi: 10.1046/j.1365-294x.2001.01351.x. [DOI] [PubMed] [Google Scholar]
- Legendre P, Fortin MJ. Spatial pattern and ecological analysis. Vegetation. 1989;80:107–138. [Google Scholar]
- Lusseau D, Wilson BEN, Hammond PS, Grellier K, Durban JW, Parsons KM, Barton TR, et al. Quantifying the influence of sociality on population structure in bottlenose dolphins. Journal of Animal Ecology. 2006;75:14–24. doi: 10.1111/j.1365-2656.2005.01013.x. [DOI] [PubMed] [Google Scholar]
- Manel S, Schwartz MK, Luikart G, Taberlet P. Landscape genetics: combining landscape ecology and population genetics. Trends in Ecology & Evolution. 2003;18:189–197. [Google Scholar]
- May RM. Network structure and the biology of populations. Trends in Ecology & Evolution. 2006;21:394–399. doi: 10.1016/j.tree.2006.03.013. [DOI] [PubMed] [Google Scholar]
- McRae BH. Isolation by resistance. Evolution. 2006;60:1551–1561. [PubMed] [Google Scholar]
- Milgram S. The small world problem. Psychology Today. 1967;1:60–67. [Google Scholar]
- Morris DW, Diffendorfer JE, Lundberg P. Dispersal among habitats varying in fitness: reciprocating migration through ideal habitat selection. Oikos. 2004;107:559–575. [Google Scholar]
- Newman MEJ. The structure and function of complex networks. Siam Review. 2003;45:167–256. [Google Scholar]
- Newman MEJ. Detecting community structure in networks. European Physical Journal B. 2004;38:321–330. [Google Scholar]
- Newman MEJ. Modularity and community structure in networks. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Brien D, Manseau M, Fall A, Fortin MJ. Testing the importance of spatial configuration of winter habitat for woodland caribou: An application of graph theory. Biological Conservation. 2006;130:70–83. [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proulx SR, Promislow DEL, Phillips PC. Network thinking in ecology and evolution. Trends in Ecology & Evolution. 2005;20:345–353. doi: 10.1016/j.tree.2005.04.004. [DOI] [PubMed] [Google Scholar]
- Storfer A, Murphy MA, Evans JS, Goldberg CS, Robinson S, Spear SF, Dezzani R, et al. Putting the ‘landscape’ in landscape genetics. Heredity. 2007;98:128–142. doi: 10.1038/sj.hdy.6800917. [DOI] [PubMed] [Google Scholar]
- Urban D, Keitt T. Landscape connectivity: A graph-theoretic perspective. Ecology. 2001;82:1205–1218. [Google Scholar]
- Wagner A, Fell DA. The small world inside large metabolic networks. Proceedings of the Royal Society of London Series B-Biological Sciences. 2001;268:1803–1810. doi: 10.1098/rspb.2001.1711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Weir BS, Cockerham CC. Estimating F-satistics for the analysis of population structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
- Whitehead H. Programs for analysing social structure. 2005. SOCPROG 2.2. http://myweb.dal.ca/hwhitehe/social.htm (accessed on 11 September 2008) [Google Scholar]
- Williams RJ, Berlow EL, Dunne JA, Barabasi AL, Martinez ND. Two degrees of separation in complex food webs. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:12913–12916. doi: 10.1073/pnas.192448799. [DOI] [PMC free article] [PubMed] [Google Scholar]


