Abstract
The enterprise of virulence management attempts to predict how social practices and other factors affect the evolution of parasite virulence. These predictions are often based on parasite optima or evolutionary equilibria derived from models of host-parasite dynamics. Yet even when such models accurately capture the parasite optima, newly invading parasites will typically not be at their optima. Here we show that parasite invasion of a host population can occur despite highly nonoptimal virulence. Fitness improvements soon after invasion may proceed through many steps with wide changes in virulence, because fitness depends on transmission as well as virulence, and transmission improvements can overwhelm nonoptimal virulence. This process is highly sensitive to mutation supply and the strength of selection. Importantly, the same invasion principle applies to the evolution of established parasites, whenever mutants arise that overcome host immunity/resistance. A host population may consequently experience repeated invasions of new parasite variants and possible large shifts in virulence as it evolves in an arms race with the parasite. An experimental study of phage lysis time and examples of mammalian viruses matching some of these characteristics are reviewed.
Keywords: antigenic drift, disease, dynamics, escape mutants, evolution, optimality, virulence
Virulence management is a modern field whose goal is to predict the consequences of social practices on the evolution of parasite virulence (Dieckmann et al. 2002). By understanding how virulence is expected to evolve, it may be possible to encourage social practices that indirectly select lower virulence. Of special concern in virulence management are environments that might favor evolutionary increases in virulence, such as leaky vaccines and high host densities (Ewald 1994; Gandon et al. 2001, 2003).
Typically, the models of virulence management are evolutionary. They consider how natural selection of parasites is expected to shape the evolution of virulence and other traits toward states that maximize fitness and the parasite optima. The argument put forth here is that this ‘optimality’ approach is not always suitable, because it assumes equilibrium conditions that some types of parasites may be slow to attain. Even for parasites that are able to evolve an optimum virulence, once a host population has a high density of immune or recovered individuals, then that host population remains vulnerable to invasion by parasite genotypes that escape immunity. During invasion, a much wider range of virulence can spread, at least temporarily, than is evident from evolutionary optima. The frequency of new invasions and the rapidity with which parasites evolve to their optima will dictate how often the host experiences nonoptimal parasite virulence.
We develop this argument in the context and framework of the standard models for the evolution of virulence, models that address virulence optima. Two standard models are reviewed. They differ in the state of host-parasite dynamics when the virulence optimum is calculated, but they both illustrate the same general approach. Those models are then extended to nonequilibrium conditions. Our use of those simplistic models is for ease of illustration in a familiar context. Our neglect of more complicated processes, such as within-host dynamics (Ball et al. 2007), within-host combined with between-host dynamics (Gilchrist and Coombs 2006), or of virulence models that lack optima (Dieckmann 2002) is not to deny the importance of those alternatives. Indeed, the concept of a delayed approach to equilibrium conditions can be applied to many of those and other types of models. Furthermore, the process we describe is fully and properly encompassed in the new formalism of Day and Gandon (2006, 2007) and Day and Proulx (2004), albeit that their formalism encompasses a far wider range of possibilities than the ones we emphasize.
Optimal virulence theories
R0 perspective
The now conventional method for considering the evolution of virulence is about three decades old (Anderson and May 1979, 1982). It assumes that the parasite population has gone to its dynamic equilibrium (the endemic phase), such that the parasite population is no longer spreading in the host population. This model identifies the combination of transmission and virulence that leads to highest parasite fitness. The result is that selection maximizes the parasite reproductive number, R0 (or more properly, maximizes R; Day and Gandon 2007). R0 is a dimensionless number that equals the number of new infections started during the lifetime of the first infected individual in a susceptible population (R is the number of new infections from an infected individual once the parasite has established itself in the host population.) The formula for R0 is simply the parasite fecundity rate times the average lifetime of the infection. Although R0 is defined for the first infected host in a naive population, what maximizes R0 also maximizes R because the only difference between them lies in the value of S (Ebert and Herre 1996; Day and Gandon 2006; Gilchrist and Coombs 2006). The result that selection at the dynamic equilibrium favors maximization of R0 parallels the usual demographic result that selection favors maximal lifetime reproductive output in a stable population (Wilson and Bossert 1971; Charlesworth 1994). We will expand on the implications of R0 maximization below, but it is most informative to do so in the broader context of the second virulence evolution model, considered next.
Epidemic perspective
Lenski and May (1994) pointed out that selection on parasite parameters was different during the epidemic phase than at dynamic equilibrium: maximizing R0 no longer maximized fitness if the parasite population was expanding. Again from demography, selection favors early births over late ones in a growing population, so during the epidemic phase, there is a benefit to early transmission and its consequent shorter generation time even when it lowers life-time reproductive success of the infection. In the model, earlier reproduction is achieved by a higher transmission rate, which in most models also results in higher virulence because of an assumed trade-off between transmission and virulence.
The Lenski and May model lays the foundation for the argument we develop here, so we offer a simple version in the form of an ‘SI’ model. For a constant density of susceptible hosts, S, and an absence of genetic variation in parasite and host parameters, the epidemic is characterized by one equation for the change in abundance of infected individuals, I:
| (1a) |
where β is the transmission rate, and δ is the combined death rate of infected individuals [δ is the sum of an intrinsic host mortality rate and a virulence, or parasite-induced mortality, and aside from this difference, equation (1a) is otherwise the same as equation (2) in Lenski and May (1994) and Gilchrist and Coombs (2006)]. The total host population is simply N = S + I. A constant density of susceptible hosts is reasonable whenever the infection is so rare that most hosts have not yet been infected. The per capita rate of pathogen spread is then:
| (1b) |
This quantity is a measure of parasite fitness in the epidemic (a type of invasion fitness, Metz et al. 1992), because it defines how rapidly the parasite spreads; indeed, the quantity on the right of equality (1b) is the intrinsic rate of increase of I.
The rate of spread is a function of parasite transmission (β) and the death rate of infected individuals (δ), two parameters that are typically assumed to be subject to a trade-off boundary (Fig. 1 top; Ebert and Bull 2003) . A trade-off means that the parasite cannot increase β without incurring increasing death rates (δ), although a more stringent criterion on the trade-off, such as the concavity used here, is required to select intermediate levels of virulence (Sasaki and Iwasa 1991). Following Lenski and May (1994) for now, we let δ be the sum of a constant host mortality plus virulence; we will refer to δ as simply virulence without loss of generality. Given that the parasite is confined to a trade-off but is allowed to evolve along the trade-off, the combination of β and δ maximizing parasite fitness during invasion is given by
Figure 1.
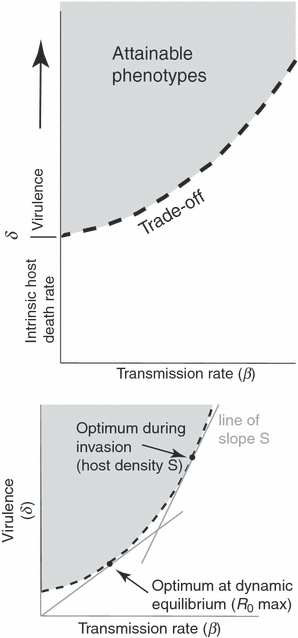
(Top) Death rate of infected hosts (δ) in relation to transmission (β). Death rate is divided into intrinsic host death rate and virulence – parasite-induced host death rate. The intrinsic host death rate is assumed to be constant, so the virulence-transmission trade-off (dashed curve) emanates from the axis at this value and increases as transmission increases. The trade-off gives the minimum total parasite death rate (δ) that could be achieved for a given transmission rate (β), so only points on and above the trade-off boundary are attainable by the parasite (shaded). For simplicity, we henceforth refer to δ as virulence, but acknowledge that it is the sum of a constant mortality plus virulence. (Bottom) Optimum for a parasite invading a host population, when the susceptible host density remains constant at S. During the epidemic phase, the parasite’s optimum lies on the dashed trade-off function and satisfies the condition that the slope of the tangent along the trade-off function equals the current density of hosts, S (upper arrow). As the parasite epidemic reduces the density of susceptible hosts, the optimum shifts progressively further down the trade-off curve, until dynamic equilibrium is reached, whereby parasite and host densities remain constant. In this state, the parasite optimum maximizes R0 = β/δ, given by the point at which a line through the origin is tangent to the trade-off function (lower arrow). In this paper, we are concerned chiefly with conditions at and shortly after the time of invasion, before the population has reached dynamic equilibrium.
| 2 |
which is graphically represented as the dot along the trade-off function whose slope is S (Fig. 1, bottom; shown in comparison to the R0 maximum). In prior work, the fitness ‘optimum’ found in this way is usually regarded as the phenotype that the parasite will evolve toward (and will ultimately attain, if the environment does not change). As demonstrated by Lenski and May (1994), this optimum changes as the density of susceptible hosts is reduced by the parasite, ultimately coinciding with the R0 maximization (Fig. 1). Thus, the optimum stops changing when the epidemic is over and the population has reached dynamic equilibrium between host and parasite (and parasite virulence is optimal).
Both prior perspectives essentially restrict evolution to the trade-off function, with an emphasis on optima. In the Lenski–May model, the optima are temporary, changing as the density of susceptible hosts changes. Both prior perspectives differ from a new approach that incorporates dynamics, selection and genetics simultaneously (Day and Proulx 2004; Day and Gandon 2006, 2007). This latter approach allows the virulence and transmission parameters to vary anywhere within the zone of attainable phenotypes, and it maps changes in the mean phenotypes as a function of selection and of genetic covariances between the two traits. The optima in this new approach are not altered, but the model is extended to include the evolutionary and population dynamics. This newer method thus subsumes the former ones.
Our goal is to recognize a possible feature of virulence evolution in parasites that newly invade a host species. More importantly, the same feature may apply when an established-parasite evolves to overcome host resistance or immunity. The method we use in developing this argument is compatible with that of Day and Gandon (2006), although our arguments are presented as if evolution proceeds via a succession of successful mutants rather than by obeying covariances of variation that is already present. Either type of model can be used to make the same point, however.
Invasion perspective
Invasion criteria are permissive
An optimum is best regarded as a long-term endpoint of evolution. Prior to attaining an optimum, however, the evolutionary dynamics apply (as codified by Day and Gandon 2006, for example). Even before dynamics are relevant, the issue is merely what range of parasite phenotypes/genotypes can invade the host population. The invasion threshold provides the boundary to the range of parameters that allows invasion. It is the set of all (mutant) parameter combinations for which the parasite neither invades nor goes extinct. Thus, parameter values on one side of the invasion threshold will allow invasion, whereas those on the other side will lead to loss/extinction.
The invasion threshold is easily found in our model. Extending result (1b) above, the pathogen invades if dI/dt > 0, or
| 3 |
The invasion threshold is thus found by replacing the inequality in equation (3) with equality. The set of parameters for invasion of a host population whose density is S* can be represented in a two-dimensional coordinate system as the points falling below a line of slope S* passing through the origin (Fig. 2, top) and above the trade-off boundary. This graph illustrates why the transmission and virulence state (β, δ) that maximizes fitness gives an inadequate picture of the levels of virulence that can invade the population. Any point inside the region between the invasion boundary line and the trade-off boundary represents a pair of parasite values (β, δ) that can invade. Thus, the population is susceptible to invasion by far more virulent parasites and by far less virulent parasites than those at the optimum, a point made by Andre and Hochberg (2005). Although all values below the line can invade, not all have the same fitness, so further evolution is expected whenever the invading genotype is not at the optimum.
Figure 2.
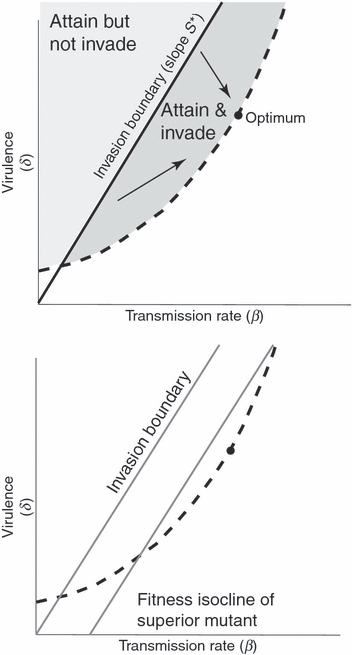
Invasion criteria. (Top) Highly virulent parasites can invade high host densities even though their virulence is far from optimal. Conditions for the invasion of a host population of density S* by a parasite with parameters (δ, β) are S* > δ/β, where δ is virulence and β is the transmission rate. Points satisfying S* = δ/β lie a line radiating from the origin (of slope S*), so radii with progressively higher slopes represent parasite parameters that can invade only at progressively higher host densities. All parasites whose values fall in the darker shaded region below the line of slope S* and above the dashed trade-off boundary are attainable and can invade, whereas the light-shaded region above the invasion boundary represents values that the parasite can attain but do not allow invasion (for host density S*). The parasite population would eventually evolve toward the dot on the trade-off boundary (arrows), but it could create a potentially highly virulent epidemic from the start of the invasion until the evolutionarily equilibrium virulence was attained. (Bottom) Evolution following invasion may be slow to approach optimal virulence. The rightmost oblique line is a fitness isocline (of slope S*), and all points on it have equal fitness, superior to the fitnesses of all points to its left. Evolution would tend to move parasites progressively toward right-most isoclines, but as a mutant’s relative position on the fitness isocline does not affect its fitness, evolution at each step could move virulence further or closer to the optimum (solid point) until the optimum was approached closely. The input of mutations (or genetic covariance between transmission and virulence) thus has a major impact on the evolution of virulence in these early stages (Day and Gandon 2007). Improved fitness need not greatly restrict the range of virulence values allowed, and indeed, virulence could evolve to deviate further from its optimum during intermediate stages of the adaptation. These arguments apply to constant host density, and if susceptible host density is declining, the fitness isoclines will have progressively shallower slopes.
Evolution following invasion may be slow to attain the optimum
Following Day and Proulx (2004), if the invading parasite persists and becomes established, it is expected that virulence and transmission will begin to evolve toward values that improve parasite fitness. Indeed, if evolution to the optimum is fast enough, the duration of nonoptimal parasite behavior could be ignored. Yet, the approach to optimum virulence may be slow for a few reasons: (i) the optimum may be changing (Lenski and May 1994), (ii) virulence evolution will be influenced by the genetic covariance or mutational properties between virulence and transmission (Day and Gandon 2006), and (iii) there may simply be little genetic variation (see also Day and Proulx 2004). As Lenski and May (1994) pointed out, (i) the optimum will shift toward progressively lower virulence values as the density of the susceptible hosts is reduced by the epidemic. Thus the optimum will not be static, and the parasite can do no better than adapt toward the current optimum. Even in the absence of this effect, parasite evolution may be slow to reach the optimum because of (ii), pleiotropy or genetic covariances. Selection favors mutations with a higher fitness than the currently dominant strains. These mutations may improve transmission but may result in virulence further away from its optimum. Fig. 2 (bottom) shows that fitness isoclines run parallel to the invasion boundary, so all points on a fitness isocline have the same fitness, assuming that S remains constant. As can be seen for the trade-off boundary drawn, there is a wide range of virulence associated with each step of evolution toward the optimum, until the optimum is neared (depending on the shape of the trade-off). Thus, particularly during the initial phases of invasion, evolution of higher parasite fitness need not be accompanied by a change in virulence. Of course, other factors may also slow the approach to equilibrium, but these two follow directly from our model.
Host recovery and repeated invasions
The invasion threshold model has been presented as though the only outcome of host infection is death. In such a system, the initial parasite invasion would be followed by a reduction in host density to the dynamic equilibrium, and the resulting low absolute host density would greatly limit opportunities for the re-invasion of any parasite mutants that had an even more devastating impact on the host. Yet, host death is not the only outcome of infection. Recovery and consequent immunity is typical of many parasites (not necessarily precluding the death of some infected hosts). How does recovery affect our model? Here, we restrict ourselves to the extreme case that recovery is complete, so that a recovered individual cannot be re-infected by the same strain (see van Baalen 1998 for models of virulence evolution with partial recovery).
Most basically, if a large fraction of the host population is immune, a large advantage can be gained by parasite mutants that can overcome the host immunity but also retain the ability to infect susceptible hosts (S). Those mutants have their own invasion threshold, and depending on their parameters, those constraints may be much more lenient than the constraints applying to parasites unable to escape host immunity (Fig. 3). Thus, parasites that engender host immunity have the potential to cause repeated invasions, with potential high and devastating virulence each time. The dynamics of this process are sensitive to the nature of host recovery and virulence, however. A highly virulent parasite (most infections lethal) that reaches high abundance in the host population will crash the host population and not leave many recovered hosts, at least in the short term. Until host numbers rebound, there would be little opportunity for new parasite invasions because of the low absolute density of hosts. If recovery rate from infection is instead high, virulence (host mortality) is necessarily low, and the parasite impact on host density will be slight. In this latter case, the host population is soon prone to invasion of mutants that escape immunity. Thus epidemics that kill large numbers of hosts will experience longer lags before possible reinvasion than epidemics that do not kill many hosts.
Figure 3.
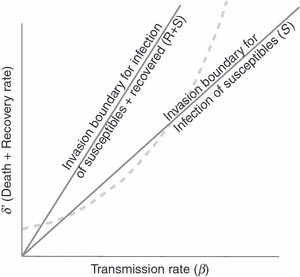
A population with a high density of recovered hosts is susceptible to invasion by highly virulent mutants. Once a parasite has evolved close to its optimum along the trade-off boundary, there will be only a small set of mutants that can invade, because they are all subject to the same constraints, provided they can infect only the susceptible hosts; the invasion threshold for those mutants is a line of slope S (the rightmost line). A mutant capable of infecting both susceptible and recovered hosts will have a much larger set of possible mutants that can invade (the invasion threshold is a line of slope S+R, where R is the density of recovered hosts, hence lies to the left of the line of slope S) and thus have greater potential to evolve nonoptimal virulence. The graph is the same as in previous figures, except that the vertical axis (δ′) now includes the recovery rate of infected hosts as well as mortality rate (the δ in previous figures was just mortality rate).
The addition of recovery does change the interpretation of the preceding model somewhat. The derivations above remain the same, but the δ term (now denoted δ′) is no longer just host mortality. Instead, the δ terms are replaced by δ′, where
and ρ is the recovery rate of infected hosts (to a state in which they can no longer be infected). Thus, if recovery from infection is allowed, the derivations and figures above merely substitute δ′ for δ, and the trade-off functions now combine recovery with virulence, as shown in Fig. 3. On intuitive grounds, parasite dynamics are sensitive to the loss of infected hosts, but it does not matter whether those infections are lost because the host died or because it recovered.
The main implication of this change for evolution of virulence theories is that evolution of higher δ′ no longer implies evolution of higher virulence. Without specifying the relationship between virulence and recovery, higher δ′ could mean a higher recovery rate, with no change in virulence or even a decline in virulence (Fig. 4). This indeterminacy applies to all evolution of virulence theories, and it is not otherwise possible to predict an optimum virulence per se when recovery is involved in the trade-off with virulence. The indeterminacy poses little problem for the invasion threshold perspective, however: the invasion threshold perspective merely specifies a range of possible virulence levels that can potentially invade. This range may be reduced by the inclusion of recovery, but it will always be wider than the range spanned by the optima.
Figure 4.
Indeterminacy of virulence (host mortality rate) when hosts recover and are immune to subsequent infection. When recovery is allowed as a component of δ in equation (1), such that δ′ = δ + ρ is substituted for δ, the evolution of higher δ′ no longer implies the evolution of higher virulence. The trade-off boundary (between δ′ and transmission) is given by the black line at the upper boundary of the gray area, and it can be seen in the shift from left to right graphs that δ′ increases somewhat but host mortality rate decreases. The sizes of the gray and clear areas are drawn for illustration and are not based on data.
Contrasting the models
Before proceeding to empirical examples, it is useful to consider the distinction between the standard R0 maximization model, the Lenski and May’s (1994) dynamic optimum model, and invasion threshold as alternative perspectives on the evolution of virulence. There is obvious overlap among these models (and both are nicely subsumed in the covariance method of Day and Gandon 2006), but the emphases from them have differed. The R0 maximization model offers a single optimum, albeit one that may be sensitive to environmental conditions. It assumes dynamic equilibrium exists between host and parasite, hence does not apply when new parasite mutants invade. The other two models, Lenski–May dynamic optimum and the invasion threshold, are similar in that both apply to invasions. The only difference is that one emphasizes the change of virulence optima during the invasion, the other addresses the range of virulence values that can invade and the nonequilibrium states that may persist after invasion. Without knowing the optima, the Lenski–May and invasion threshold perspectives are difficult to distinguish, as either or both could obtain across repeated invasions. However, observing the evolution of an increase in virulence (instead of a decrease) as the epidemic matures would support the invasion threshold model for the initial virulence, because the Lenski–May optima shift toward decreasing virulence as the epidemic matures. Likewise, if hosts merely die from the infection and do not recover (and are not resistant), then the invasion threshold model cannot possibly apply after dynamical equilibrium has been reached, because there is no reservoir of immune or resistant hosts to be exploited by a mutant parasite.
For many parasites, evolvability to escape existing immune and resistance profiles is highly adaptive. Long-term parasite success may depend not so much on the ability to achieve evolutionary equilibrium, as in the classic virulence evolution models, but rather to keep changing, staying ahead of host defenses and continually jumping outside the parameter space confining the parasite’s recent ancestors. Such a process would ensure that the invasion threshold model is relevant at many episodes in the parasite’s history. The applicability of the invasion threshold model at some times does not exclude attainment of optima at other times. Thus, over the course of history, there can be a cycling between invasion, evolution toward an optimum (perhaps indirectly), and maintenance of an optimal state. The relative importance of each phase will depend on details of the parasite and host.
We offer the caveat that the invasion threshold model is not the only model for nonoptimal virulence (Dieckmann 2002). If host and parasite populations cycle, or if environmental factors cause host populations to fluctuate profoundly, there will be no single virulence optimum, and the best the parasite might do is to track a moving optimum [Day and Gandon 2006, 2007]. Likewise, if hosts are infected by multiple strains of parasites, parasite–parasite competition within hosts will often lead to nonequilibrium evolutionary dynamics (Frank 1996; Bull et al. 2006). It should also be noted that different mathematical definitions of virulence have different evolutionary consequences (Day 2002), but again, our point about nonequilibrium dynamics should hold under many of those alternatives.
Tests and candidate viruses
The general point of the nonequilibrium model is that optimality of a phenotype involved in a trade-off may be evolved only slowly; our specific context is virulence. There is no absolute threshold for rejection of this model, only a subjective one of whether evolution to the optimum is fast enough that the period of meaningful deviation can be neglected. A quantification of nonoptimality could be provided by the experimental adaptation of a parasite with a known optimum, with the approach to that optimum measured over time.
A test satisfying several of these criteria was carried out for bacteriophage lysis time, analogous to phage virulence (Heineman and Bull 2007). The optimum was predicted when assuming a linear trade-off between lysis time and number of progeny at lysis and that the linearity extended well beyond the normal lysis time. Adaptation of phage T7 was performed under constant environmental conditions of both high and low host density; this constant host density provided for a fixed optimum and matches the models in this paper. At high host density, T7 attained a lysis time close to the optimum within 150 generations of adaptation, but the phage failed to approach the optimum at low host density in two separate adaptations of ∼300 generations each. One failure stemmed from a lack of evolution, likely because of small population size. In the other case, molecular evolution was observed, and the failure to attain the optimum was interpreted as a failure of the model used to calculate the optimum (that the assumed trade-off did not match the T7 trade-off). The failure to evolve is a special case of our nonequilibrium model, and presumably, the virus would have evolved after sufficient time. The failure to attain the optimum despite evolution in the other replicate is presumably a failure to calculate the true optimum, and thus not an illustration of nonequilibrium dynamics, unless it could be shown that the predicted equilibrium would eventually be obtained given sufficient time. Overall, this experimental study illustrates how the measurement of deviation from optimality reflects on the nonequilibrium model, but only when the basis for nonoptimality is understood.
It is no doubt rare that a parasite optimum is known and that evolution toward the optimum can be observed; repetition of this phage experiment seems especially difficult for parasites of multicellular hosts. The bacteriophage study benefited from the fact that the optimality model required only linearity of the trade-off, and that the slope of the trade-off did not affect the optimum (and even the assumption of this generality appears to have been wrong). Such generality may be rare, and quantitative knowledge of the trade-off may be necessary to predict the optimum in most systems. Even if an optimum cannot be calculated a priori, it may be determined empirically in an experiment, as a long-term equilibrium that is attained and maintained. The evolutionary approach to this optimum from different starting points then provides insight to the dynamical behavior relevant to the perspective given here.
Insight may also be gained from observations of parasites under natural conditions. Some basic characteristics predispose a parasite toward delayed-equilibrium virulence, and the following examples of vertebrate parasites (all viruses) illustrate how one may begin looking for candidates. These examples illustrate that not all parasites exhibit nonequilibrium dynamics, and even among those that do, the frequency of the phenomenon varies considerably. The primary criterion that can be used in considering the invasion threshold perspective is that a host experiences periodic invasion by new parasite mutants. As noted above, this criterion does not rule out the Lenski and May (1994) model. Thus, a second important question, but one that can rarely be answered, is whether the parasites are far off the optimum.
Polio and measles viruses
We start with two pathogens that elicit host immunity but clearly do not exhibit repeated invasions by mutants that escape immunity. Humans are the only known natural hosts for measles and polio viruses. Successful vaccines have greatly reduced the incidence of both infections, and the vaccines derived from decades-old isolates have remained effective without apparent evolution of novel antigens that escape vaccine-induced immunity (Schrag et al. 1999; Macadam et al. 2006). Both viruses, therefore, are good candidates for the R0 maximization model, but their virulence optima are difficult to establish, and alternatives to the R0 model have been proposed at least for polio (Levin and Bull 1994; Frank 1996). In addition, the virulence of measles is notoriously sensitive to host nutritional status, so it is not clear what level of virulence to apply to the model. Even without knowing whether these viruses have achieved an optimum level of virulence, both viruses appear to be good candidates for viruses that violate the invasion threshold model (at least in contemporary populations) by virtue of their failure to generate escape mutants.
As an aside, the lack of ‘escape’ mutants capable of infecting immune hosts is puzzling, as both viruses have RNA genomes, which are thought to be prone to rapid evolution. Furthermore, three antigenically distinct polioviruses are known (and each is included in the vaccine), yet no others have evolved in response to vaccine pressure (Macadam et al. 2006). These two viruses highlight the point that, contrary to common perception, some parasites may not be able to adapt to altered environmental conditions.
Human influenza A
The flu virus is notorious for its recurrent epidemics in humans, and these epidemics arise from various forms of viral evolution to escape host immunity. Flu thus exhibits one of the main features of the invasion threshold model. There is also documented variation in virulence, with the highest virulence associated with some of the new mutants (see below).
Flu dynamics are governed largely by the interaction of host immunity and viral surface antigens as well as evolution of the viral antigens (Webster et al. 1992). Influenza is typed according to two viral antigens, the hemagglutinin (‘H’ type) and neuraminidase (‘N’ type); we will limit ourselves here to the different H types. There is a wide variety of H types in nature, due partly to the fact that different influenza A strains span a wide variety of warm-blooded hosts. Currently, H1 and H3 are circulating in humans, but H2 was abundant in the past.
There are two classes of H mutants that invade humans. One class consists of simple point mutants of existing H types (referred to as subtypes, because of a process known as ‘antigenic drift’). Most annual epidemics consist of these subtype mutants, and subtype evolution is substantial enough to largely overcome immunity to the same ancestral type from several years in the past (Ferguson et al. 2003). The other class consists of H types introduced from other species (a process of ‘antigenic shift’). Flu virus with novel H types have a profound advantage because there is no prevailing immunity in humans against those types. Three world-wide flu pandemics of the 1900s were notorious for causing large numbers of infections and thus large numbers of deaths; all were due to viruses that had acquired H types that humans had not previously experienced. Not all viruses with novel H types readily spread in humans, however, and many of these introductions have simply died out. We thus have a reasonable understanding of what types of molecular variation enable a flu virus to escape prevailing immunity, although this advantage by itself is not sufficient to enable spread in the human population.
The virulence of influenza variants varies somewhat, although it is difficult to apportion mortality between the virus (its intrinsic virulence) and the host (whether it has any prevailing immunity to the strain). The case mortality rate of the H1N1 1918 flu that killed 20–40 million people worldwide was reported to be about 1%, somewhat more than a 10-fold excess of the typical mortality rate per infection of the viruses of today (Taubenberger and Morens 2006). The virulence of this strain appeared to wane over a few years. H1N1 disappeared in the 1950s, and its accidental reintroduction in 1977 to naive hosts did not lead to the high mortality rate of 1918, so it appears that the virulence per se evolved downward (Kilbourne 2006). Although mortality rates of the usual antigenic shift strains remain relatively constant, some high virulence exceptions are known (e.g., an H3N2 strain from 1997; O’Donnell et al. 2003), and there may well be many low-virulence variants that go unnoticed. However, the H5N1 strain (bird flu) that is circulating widely in birds has a case mortality rate exceeding 50% in humans, far in excess of the mortality rate observed in any strain that established itself in humans (Webster et al. 2006).
H5N1 has not established itself in the human population, but the obvious fear is that it can do so and maintain its high mortality rate, at least during its first round of global spread. The invasion threshold perspective is thus especially relevant here. Ewald has used the public media to argue that the virulence of H5N1 will quickly evolve to low levels, should it invade (Orent 2005); this view has not been widely accepted (Normile 2005), and the perspective of this paper is that, even if the H5N1 optimum in humans is low virulence, the epidemic could have devastating effects before it neared the viral optimum.
Feline calicivirus
Feline calicivirus (FCV) is an RNA virus of domestic cats. A large variety of FCV strains is known to circulate concurrently, with sequence divergence in the variable region of the capsid protein gene ranging as much as 50% between strains (Coyne et al. 2007). Virulence varies among isolates, from asymptomatic to highly virulent, the latter being as high as 50% mortality (termed VSD strains, for ‘virulent systemic disease’). Multiple strains often circulate within a local cat population. Vaccines are available, but vaccination neither prevents viral infection nor prevents viral replication within a cat, so it appears that cross immunity among strains is only partial (Coyne et al. 2007).
Consistent with the invasion threshold model, nearly a dozen separate outbreaks of VSD have been reported. When subjected to a phylogenetic analysis, the different VSD strains appear to have independent origins from less virulent ancestors. Additionally, the VSD outbreaks appear to have been terminated by viral extinctions, possibly from reducing the local cat density (Radford et al. 2007). The die-outs could be interpreted as the failure to evolve optimal virulence (consistent with the invasion threshold model), or as evidence that near-optimal strains are replacing the VSD strains as host density wanes (consistent with the Lenski–May model).
Livestock viruses: TGEV and MDV
Most agricultural animals used as food sources, such as pigs, chickens, and cattle are housed at high densities and in conditions of stress that facilitate the spread of infectious diseases. Even if a farm’s livestock is wiped out by an infection, new animals may be brought in and maintained at high densities again. This artificial maintenance of high host density is in contrast to the usual pattern in epidemiological models that parasites regulate the densities of their hosts. These enforced high host densities have been suggested to be especially prone to the evolution of highly virulent parasites, because virulent parasites do not die out even when their hosts do. Although cleanups following an outbreak are usually attempted, the same buildings and grounds are often used for restocking, allowing any remaining environmental source of parasite to reinvade.
The difficulty of applying equilibrium theory to these situations is illustrated by the pig virus transmissible gastroenteritis coronavirus (TGEV). Historically, a highly lethal gut infection of piglets in pig farms, a mutant form evolved (porcine respiratory coronavirus, or PRCV) that not only had altered tissue tropism but also apparently lower virulence (Kim et al. 2000). PRCV differs from TGEV by a small deletion and a couple point mutations, yet it infects the pig respiratory system and is often much less virulent than TGEV. There is some antibody cross reactivity between TGEV and PRCV, thus the population of one form of the virus interferes with the other, and it is suspected that a low virulence PRCV was responsible for the disappearance of TGEV in some pig farm areas. PRCV now exists in forms of high and low virulence. This example thus represents what may be a single mutant invasion in the recent history of TGEV. To what extent PRCV spread because it could overcome prevailing immunity (as assumed by the invasion threshold model) or because it had other advantages, is not clear.
Another viral scourge of agriculture is Marek’s disease virus (MDV) of chickens (Hirai 2001; Davison and Nair 2004). MDV has shown a progressive evolution toward increasing virulence over four decades, but again, many strains circulate and some have low virulence. Live vaccines have been used for three decades, the virus used in them having been changed twice. As with FCV, the vaccines do not prevent infection and replication by other strains, and it is widely suspected that the vaccines may have fostered the evolution of progressively higher virulence (references within Davison and Nair 2004; Hirai 2001). (We lack the control of viral evolution at high chicken density in the absence of the vaccine to have any confidence that the vaccine was the cause in the higher virulence evolution.) With MDV, there is considerable ambiguity in the causes of virulence evolution as well as in the spectrum of virulence evolution itself. It may well be that vaccines have selected escape mutants time and again. Whether escape mutants retained near-optimal virulence or not is difficult to establish, because there is a strong ascertainment bias – avirulent viruses are not noticed by chicken farmers. Thus, without understanding the range of virulence levels that have evolved, it is not practical to discriminate among the models. Such a system seems ripe for testing the models, however.
Future efforts
There is sufficient evidence to suggest that the invasion threshold model is relevant to the evolution of many infectious agents, but little evidence to suggest how often it is important. Recommendations for use of this perspective are thus accordingly muted. Certainly, it seems wise in virulence management efforts to be aware that a broader range of virulence might invade than is optimal and that evolution to an optimum may not be rapid. It would be obvious folly to ignore a case in which the predicted optimum was low virulence but in which a highly virulent parasite could invade and persist. If the perspective offered here proves to be broadly relevant, then its impact is to support and even bolster any concerns about the evolution of high virulence but also to raise the specter of temporary high virulence in parasites expected to equilibrate at low virulence.
The most useful work at this stage would be to contrast predicted virulence optima with actual virulence levels over time. Calculating virulence optima has not met with much success, however, likely because the optimum invariably depends on an unknown trade-off and potentially on many environmental factors. Thus, most tests of virulence evolution models have been relative, i.e., correlating virulence level with some environmental characteristic and determining if the correlation is in the right direction. Direct, quantitative tests of virulence optima are rare, nonexistent for human pathogens. If optima cannot be calculated, then it is of course difficult to test any nonequilibrium model against an optimality model. But an alternative to testing whether virulence is optimal is to observe the dynamics of virulence evolution. If virulence does not change over long periods after invasion, despite a dropping susceptible host density, then it would seem that virulence has been nonoptimal during much of the time.
Acknowledgments
We thank Troy Day, Carl Bergstrom, and Robin Bush for comments. Two reviewers essentially did the literature work for this paper. Our choice for some of the examples reviewed above was inspired by a seminar of A. Read. This work was supported by NIH GM57756 to JB. JB also receives support as the Miescher Regents Professor at the University of Texas. DE was supported by the Swiss National Fonds.
Literature cited
- Anderson RM, May RM. Coevolution of hosts and parasites. Parasitology. 1982;85(Pt 2):411–426. doi: 10.1017/s0031182000055360. [DOI] [PubMed] [Google Scholar]
- Anderson RM, May RM. Population biology of infectious diseases: part I. Nature. 1979;280:361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- Andre JB, Hochberg ME. Virulence evolution in emerging infectious diseases. Evolution; International Journal of Organic Evolution. 2005;59:1406–1412. [PubMed] [Google Scholar]
- Van Baalen M. Coevolution of recovery ability and virulence. Proceedings. Biological sciences. 1998;265:317–325. doi: 10.1098/rspb.1998.0298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball CL, Gilchrist MA, Coombs D. Modeling within-host evolution of HIV: mutation, competition and strain replacement. Bulletin of Mathematical Biology. 2007;69:2361–2385. doi: 10.1007/s11538-007-9223-z. [DOI] [PubMed] [Google Scholar]
- Bull JJ, Millstein J, Orcutt J, Wichman HA. Evolutionary feedback mediated through population density, illustrated with viruses in chemostats. The American Naturalist. 2006;167:E39–E51. doi: 10.1086/499374. [DOI] [PubMed] [Google Scholar]
- Charlesworth B. Evolution in Age-Structured Populations: Cambridge Studies in Mathematical Biology. Cambridge: Cambridge University Press; 1994. No. 14. [Google Scholar]
- Coyne KP, Edwards D, Radford AD, Cripps P, Jones D, Wood JL, Gaskell RM, et al. A longitudinal molecular epidemiological analysis of feline calicivirus infection in an animal shelter: a model for investigating calicivirus transmission within high density, high turnover populations. Journal of Clinical Microbiology. 2007;45:3239–44. doi: 10.1128/JCM.01226-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison F, Nair V. Marek’s Disease: An Evolving Problem: Biology of Animal Infections. Amsterdam: Elsevier; 2004. [Google Scholar]
- Day T. On the evolution of virulence and the relationship between various measures of mortality. Proceedings. Biological sciences. 2002;269:1317–1323. doi: 10.1098/rspb.2002.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day T, Gandon S. Applying population-genetic models in theoretical evolutionary epidemiology. Ecological Letters. 2007;10:876–888. doi: 10.1111/j.1461-0248.2007.01091.x. [DOI] [PubMed] [Google Scholar]
- Day T, Gandon S. Insights from Price’s equation into evolutionary epidemiology. In: Feng Z, Dieckmann U, Levin SA, editors. Disease Evolution: Models, Concepts, and Data Analyses. Providence, RI: American Mathematical Society; 2006. pp. 23–44. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, Vol. 71. [Google Scholar]
- Day T, Proulx SR. A general theory for the evolutionary dynamics of virulence. The American Naturalist. 2004;163:E40–E63. doi: 10.1086/382548. [DOI] [PubMed] [Google Scholar]
- Dieckmann U. Adaptive dynamics of pathogen-host interactions. In: Dieckmann U, Metz JAJ, Sabelis MW, Sigmund K, editors. Adaptive Dynamics of Infectious Diseases: In Pursuit of Virulence Management. Cambridge: Cambridge University Press; 2002. pp. 39–59. [Google Scholar]
- Dieckmann U, Metz JAJ, Sabelis MW, Sigmund K. Adaptive dynamics of infectious diseases: in pursuit of virulence management. In: Dieckmann U, Metz JAJ, editors. Cambridge Studies in Adaptive Dynamics. Cambridge: Cambridge University Press; 2002. Vol. 2, pp. xviii, 532. [Google Scholar]
- Ebert D, Bull JJ. Challenging the trade-off model for the evolution of virulence: is virulence management feasible? Trends in Microbiology. 2003;11:15–20. doi: 10.1016/s0966-842x(02)00003-3. [DOI] [PubMed] [Google Scholar]
- Ebert D, Herre EA. The evolution of parasitic diseases. Parasitology Today. 1996;12:96–101. doi: 10.1016/0169-4758(96)80668-5. [DOI] [PubMed] [Google Scholar]
- Ewald PW. Evolution of Infectious Disease. Oxford: Oxford University Press; 1994. [Google Scholar]
- Ferguson NM, Galvani AP, Bush RM. Ecological and immunological determinants of influenza evolution. Nature. 2003;422:428–433. doi: 10.1038/nature01509. [DOI] [PubMed] [Google Scholar]
- Frank SA. Models of parasite virulence. Quarterly Review of Biology. 1996;71:37–78. doi: 10.1086/419267. [DOI] [PubMed] [Google Scholar]
- Gandon S, Mackinnon MJ, Nee S, Read AF. Imperfect vaccines and the evolution of pathogen virulence. Nature. 2001;414:751–756. doi: 10.1038/414751a. [DOI] [PubMed] [Google Scholar]
- Gandon S, Mackinnon M, Nee S, Read A. Imperfect vaccination: some epidemiological and evolutionary consequences. Proceedings. Biological sciences. 2003;270:1129–1136. doi: 10.1098/rspb.2003.2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist MA, Coombs D. Evolution of virulence: interdependence, constraints, and selection using nested models. Theoretical Population Biology. 2006;69:145–153. doi: 10.1016/j.tpb.2005.07.002. [DOI] [PubMed] [Google Scholar]
- Heineman RH, Bull JJ. Testing optimality with experimental evolution: lysis time in a bacteriophage. Evolution; International Journal of Organic Evolution. 2007;61:1695–1709. doi: 10.1111/j.1558-5646.2007.00132.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirai K. Marek’s Disease: Current Topics in Microbiology and Immunology. Berlin: Springer; 2001. 255. [DOI] [PubMed] [Google Scholar]
- Kilbourne ED. Influenza pandemics of the 20th century. Emerging Infectious Diseases. 2006;12:9–14. doi: 10.3201/eid1201.051254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim L, Hayes J, Lewis P, Parwani AV, Chang KO, Saif LJ. Molecular characterization and pathogenesis of transmissible gastroenteritis coronavirus (TGEV) and porcine respiratory coronavirus (PRCV) field isolates co-circulating in a swine herd. Archives of Virology. 2000;145:1133–1147. doi: 10.1007/s007050070114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski RE, May RM. The evolution of virulence in parasites and pathogens: reconciliation between two competing hypotheses. Journal of Theoretical Biology. 1994;169:253–265. doi: 10.1006/jtbi.1994.1146. [DOI] [PubMed] [Google Scholar]
- Levin BR, Bull JJ. Short-sighted evolution and the virulence of pathogenic microorganisms. Trends in Microbiology. 1994;2:76–81. doi: 10.1016/0966-842x(94)90538-x. [DOI] [PubMed] [Google Scholar]
- Macadam AJ, Ferguson G, Stone DM, Meredith J, Knowlson S, Auda G, Almond JW, et al. Rational design of genetically stable, live-attenuated poliovirus vaccines of all three serotypes: relevance to poliomyelitis eradication. Journal of Virology. 2006;80:8653–8663. doi: 10.1128/JVI.00370-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metz JAJ, Nisbet RM, Geritz SAH. How should we define ‘fitness’ for general ecological scenarios. Trends in Ecology and Evolution. 1992;7:198–202. doi: 10.1016/0169-5347(92)90073-K. [DOI] [PubMed] [Google Scholar]
- Normile D. Avian influenza. Pandemic skeptics warn against crying wolf. Science. 2005;310:1112–1113. doi: 10.1126/science.310.5751.1112. [DOI] [PubMed] [Google Scholar]
- O’Donnell FT, Munoz FM, Atmar RL, Hwang LY, Demmler GJ, Glezen WP. Epidemiology and molecular characterization of co-circulating influenza A/H3N2 virus variants in children: Houston, Texas, 1997–8. Epidemiology and Infection. 2003;130:521–531. [PMC free article] [PubMed] [Google Scholar]
- Orent W. Chicken little. The New Republic. 2005:13–15. Sept. 12. [Google Scholar]
- Radford AD, Coyne KP, Dawson S, Porter CJ, Gaskell RM. Feline calicivirus. Veterinary Research. 2007;38:319–335. doi: 10.1051/vetres:2006056. [DOI] [PubMed] [Google Scholar]
- Sasaki A, Iwasa Y. Optimal growth schedule of pathogens within a host: switching between lytic and latent cycles. Theoretical Population Biology. 1991;39:201–239. doi: 10.1016/0040-5809(91)90036-f. [DOI] [PubMed] [Google Scholar]
- Schrag SJ, Rota PA, Bellini WJ. Spontaneous mutation rate of measles virus: direct estimation based on mutations conferring monoclonal antibody resistance. Journal of Virology. 1999;73:51–54. doi: 10.1128/jvi.73.1.51-54.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taubenberger JK, Morens DM. 1918 Influenza: the mother of all pandemics. Emerging Infectious Diseases. 2006;12:15–22. doi: 10.3201/eid1201.050979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster RG, Bean WJ, Gorman OT, Chambers TM, Kawaoka Y. Evolution and ecology of influenza A viruses. Microbiological Reviews. 1992;56:152–179. doi: 10.1128/mr.56.1.152-179.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster RG, Peiris M, Chen H, Guan Y. H5N1 outbreaks and enzootic influenza. Emerging Infectious Diseases. 2006;12:3–8. doi: 10.3201/eid1201.051024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson EO, Bossert WH. A Primer of Population Biology. Stamford, CT: Sinauer Associates; 1971. [Google Scholar]


