Towards evolution-proof malaria control with insecticides

Abstract

As many strategies to control malaria use insecticides against adult mosquitoes, control is undermined by the continual evolution of resistant mosquitoes. Here we suggest that using alternative insecticides, or conventional insecticides in alternative ways might enable effective control, but delay considerably or prevent the evolution of resistance. Our reasoning relies on an epidemiological and an evolutionary principle: (i) the epidemiology of malaria is strongly influenced by the life-span of mosquitoes, as most infected mosquitoes die before the malaria parasite has completed its development; and (ii) evolutionary pressure is strongest in young individuals, for selection on individuals that have completed most of their reproduction has little evolutionary effect. It follows from these principles, first, that insecticides that kill mosquitoes several days after exposure can delay considerably the evolution of resistance and, second, that the evolution of resistance against larvicides can actually benefit control, if it is associated with shorter life-span or reduced biting in adults. If a late-acting insecticide and a larvicide are combined, the evolution of resistance against larvicides can in some circumstances prevent the evolution of resistance against the more effective, late-acting insecticide, leading to sustainable, effective control. We discuss several potential options to create such insecticides, focussing on biopesticides.

Introduction

Since the discovery of the insecticidal action of DDT by Paul Muller in 1939, insecticides have been a key component in the control of malaria. Indoor residual spraying has contributed to the elimination of malaria from many countries, including the USA and several European countries (Trigg and Kondrachine 1998; Shiff 2002; Mabaso et al. 2004). More recently, insecticide-treated bednets have become a leading tool for malaria control (WHO 2008a) and are making an invaluable contribution to the health of people in malarious areas, cutting, for example, the malaria burden by as much as half in several African countries (WHO 2008b). Because of these successes, recent suggestions to eradicate malaria (e.g. Roll Back Malaria 2008) include substantial increases in the deployment of indoor residual spraying and insecticide-treated bednets.

One of the reasons for the success of insecticides is that they interfere with the main determinants of the intensity of transmission of malaria. They kill mosquitoes rapidly and therefore prevent infected mosquitoes from surviving the parasite's development and becoming infectious. Some insecticides (notably pyrethroids, which are used on insecticide-treated bednets) also repel mosquitoes and thereby decrease the mosquito's biting rate. The importance of these parameters can be seen in the Macdonald–Ross equation of malaria transmission (Macdonald 1957): 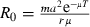, where the basic reproductive number R₀ is a measure of the intensity of transmission, m is the number of adult, female mosquitoes per human, a is the mosquito's biting rate (on humans), μ is the daily mortality of the mosquito, T is the parasite's developmental period in the mosquito, and r is the recovery rate of humans. A sensitivity analysis of R₀ (Bailey and Duppenthaler 1980) shows that adult mortality and biting rate are the two parameters that are most effective at reducing malaria transmission. While, for example, halving mosquito density halves R₀ (as m is a linear parameter), halving biting rate (which enters R₀ quadratically) reduces R₀ by 75% and doubling adult mortality decreases R₀ by about 80% (because it enters R₀ through an exponential term).

However, the efficacy of insecticides is constantly eroded by the evolution of insecticide resistance in Anopheles populations, and resistant mosquitoes can lead to sharp rises in malaria case loads. In Kwazulu-Natal, South Africa, for example, a switch from DDT to deltamethrin for indoor residual spraying led to the invasion of deltamethrin-resistant Anopheles funestus and to a surge of malaria from about 600–2000 cases per month (Hargreaves et al. 2000). Much resistance appears to be a consequence of using antimalarial insecticides for agricultural purposes (Curtis et al. 1998; Diabate et al. 2002), but insecticide resistance has evolved as a consequence of indoor residual spraying in some areas as well (Lines 1988). In a recent controlled field trial in Mexico, Anopheles populations went from 0% to 20% resistance in 3 years of indoor residual spraying (Penilla et al. 2007). There are also concerns and some evidence that insecticides on bednets will drive resistance evolution (Curtis et al. 1998; Kolaczinski et al. 2000; Hemingway et al. 2002). Indeed, intense selection for resistance is inevitable when insecticides are applied at the coverages required to provide significant public health gains, particularly for highly anthrophilic species: insecticides prevent malaria by killing the female Anopheles or by preventing them taking the blood meals needed to produce offspring. The WHO experience after the Second World War was that the operational life-span of insecticides in widespread deployment was about 5 years (Harrison 1978).

Current strategies for dealing with resistant mosquitoes boil down to three approaches: delaying the origin of resistance, resistance management and novel chemistry. These approaches could be valuable, but are no panacea. Delaying tactics, such as the use of combinations of insecticide (e.g. Pennetier et al. 2008), have no impact once resistance has arisen, as it already has. Resistance management strategies involve the use of different classes of insecticide in rotation or spatial mosaics (Curtis 1985; Hougard et al. 2003; Penilla et al. 2007). Making these approaches work requires on-going surveillance (Brogdon and McAllister 1998; Kelly-Hope et al. 2008) and a level of application management that is frequently problematic in regions where the malaria problem is most severe. But even were money and logistics no limitation, resistance management is challenged by extensive cross-resistance against the very limited insecticide arsenal currently approved by WHO for house spraying (just four classes). For bednets, resistance management is currently impossible, because only one class of insecticide is approved for use (WHO 2005a,b). Novel chemistry that simply does more of the same is not the answer either: all existing insecticides were once new. With the Global Malaria Action Plan putting the R&D costs of bringing a new public health insecticide to market at $US 175 million over 12 years (Roll Back Malaria 2008), indefinitely rolling out insecticides, each one doomed to failure by mosquito evolution, is not a sustainable option. Insecticide treadmills have proven immensely difficult to sustain, even in Western agriculture, where there are strong commercial drivers.

Here we use evolutionary ideas to discuss three alternative possibilities that could enable effective control that is less readily undermined by the evolution of resistance. These are based on two fundamental aspects of evolutionary biology. First, evolutionary pressure decreases with an individual's age (Hamilton 1966); beneficial mutations that act only when an individual has achieved most of its reproductive success increase fitness much less than similar mutations acting at a young age (Fisher 1930; Haldane 1941). The decrease of evolutionary pressure is evident for a comparison of two extreme ages. On the one hand, once individuals have achieved all of their reproduction, they have no residual reproductive success (or residual ‘fitness’), so there is no evolutionary pressure to keep them alive. On the other hand, young individuals that are about to become reproductively mature have their whole reproductive life ahead of them, so that any change in survival will have a large impact on their total reproductive success. Second, beneficial mutations at old age can be associated with detrimental effects in young individuals (antagonistic pleiotropy). Both aspects are well acknowledged in evolutionary biology, and indeed form the basis of current evolutionary theories of ageing and senescence (Williams 1957; see Ricklefs and Finch 1995 for a lucid introduction).

Much of the argumentation we present here is based on ideas we have separately presented elsewhere (Thomas and Read 2007; Koella et al. 2009; Read et al. 2009). Here, we review those ideas, demonstrate their complementarity and common themes, and bolster the arguments with novel mathematical modelling. The argument in our final section below is speculative, but underlines the potential power of utilizing evolutionary trade-offs to control the evolution of resistance.

Our arguments rely on several aspects of the biology of mosquitoes (specifically, Anopheles gambiae, the main vector of malaria in sub-Saharan Africa) and malaria. First, after taking a blood meal, mosquitoes develop and then lay their eggs into appropriate water bodies before seeking out a next blood meal. This gonotrophic cycle takes 2–4 days [and this duration is not affected by the use of insecticide-treated bednets (Quinones et al. 1997)]. Second, females are exposed to, and contact, the insecticide either on bednets during their feeding attempts or on house walls while resting immediately after the feed. Third, extrinsic mortality rates for the key vector species, even in the absence of any public health measures, are very high – on average about 10% per day (i.e. 20–40% per gonotrophic cycle), and ranging from 5% daily mortality in some areas to 20% in others (Costantini et al. 1996; Charlwood et al. 1997; Takken et al. 1998; Killeen et al. 2000; Midega et al. 2007; Okech et al. 2007). Therefore, most females go through only a few gonotrophic cycles before they die. Fourth, the malaria parasite develops over a long period (relative to the mosquito's expected life-span) before it produces the sporozoites that can infect humans. The duration of this development depends on host, parasite and environmental factors, but it is on the order of 10–14 days (or three to six gonotrophic cycles) in areas of high malaria transmission (Bradley et al. 1987; Killeen et al. 2000). Therefore, most mosquitoes do not live long enough to transmit the disease. This aspect of the mosquito–malaria interaction is the basis for the critical importance of the term e^−μT in the Ross–Macdonald equation mentioned above.

Conventional insecticides: efficacy and evolution

Current approved insecticides kill mosquitoes very rapidly after exposure. This reduces the transmission of malaria, first, by killing mosquitoes that have not yet become infected, and, second, by killing infected mosquitoes before the parasite's development is finished and thus before the mosquitoes become infectious. This combination of effects reduces the number of infectious mosquitoes (Fig. 1A), which can reduce the intensity of transmission R₀ by several orders of magnitude at high coverage. Basic epidemiological theory shows that malaria can be eliminated from a population if the intensity of transmission is decreased by the factor R₀ (Macdonald 1957). With sufficient coverage, conventional insecticides can therefore eliminate malaria even from the most endemic areas [where R₀ is on the order of 1000 (Smith et al. 2007)] (Fig. 2A). However, the high lethality also imposes strong selection for resistance, so that population genetic models predict very rapid spread of insecticide resistance (Fig. 1B), once a resistant mutant has appeared. This is particularly so for coverage that has an appreciable impact on malaria transmission. Indeed, it is clear that, if coverage were 100% (i.e. all sensitive mosquitoes were killed after one bite), only resistant mosquitoes could survive so that resistance would be 100% after one generation. If the coverage of insecticides is high enough eliminate malaria from areas with low intensities of transmission (R₀ < 10), it follows from our assumptions that resistance evolves to reach 50% within about 100 gonotrophic cycles (Fig. 1A,B). [Note that these models assume that a resistant mutant is already present at a low frequency (10⁻⁴ in our simulations). As high coverage reduces the population size, it also reduces the probability that such a mutation appears. Estimating such probabilities – through mutation or immigration – is beyond the scope of this study.] Some insecticides also repel mosquitoes (e.g. pyrethroids); for anthrophilic mosquitoes, such as Anopheles gambiae, this reduces their biting rate and hence their fecundity, imposing similarly strong selection for resistance.

Figure 1.

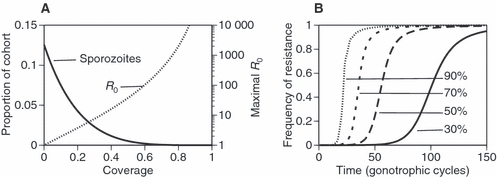
Conventional insecticides, that kill exposed mosquitoes shortly after exposure. (A) Measures of the effectiveness of control with a conventional insecticide as a function of the coverage (i.e. the probability that a mosquito is exposed to an insecticide during a bite and assuming that daily mortality is 10% and the probability of infection is 0.3 per bite). The solid line shows the proportion of the emerging mosquitoes that survive to harbour sporozoites and thus become infectious (see Appendix). The dotted line shows the intensity of transmission (expressed as R₀) up to which malaria is eliminated from the population for a given coverage. This takes into account the two parameters affected by the insecticide: the proportion of infectious mosquitoes and the expected longevity (the term 1/μ in the equation for R₀) of infectious mosquitoes (Macdonald 1957). The calculation of both terms is described in the Appendix. (B) The evolutionary trajectories of the proportion of resistant individuals in a population with four levels of coverage of the insecticide (shown by the four lines). Note that time is given in the equivalent of gonotrophic cycles (i.e. as a multiple of 3 days). Resistance is assumed to be governed by a single gene, with resistance determined by a dominant allele (i.e. heterozygotes are identical to homozygous resistants). The initial frequency of the resistance-allele was 10⁻⁴.

Figure 2.

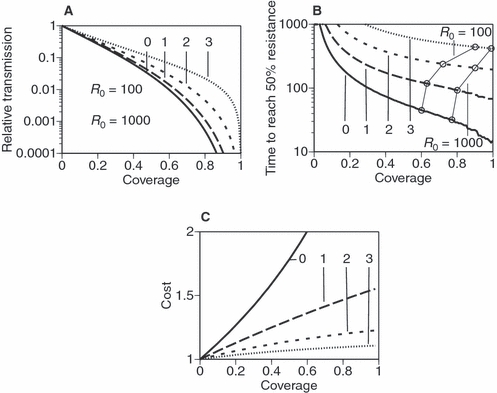
Comparison of late-acting insecticides (with a delay of one to three gonotrophic cycles) and conventional insecticides (with a delay of 0). (A) A measure of the effectiveness of control with a conventional insecticide (solid line) and insecticides that delay their action by one to three gonotrophic cycles as a function of coverage by the insecticide. The y-axis shows the intensity of transmission, R₀, relative to the intensity in the absence of any control. [This is the inverse of the intensity of transmission (expressed as R₀) up to which malaria is eliminated from the population, see Fig. 1A. Thus the solid curve (for a conventional insecticide) is the inverse of the dotted line of Fig. 1A.] The horizontal lines represent the level of control necessary to eliminate malaria in an area with moderate transmission (R₀ = 100) and extremely intense transmission (R₀ = 1000). (B) Evolution of resistance against late-acting insecticides. The circles, connected with thin lines and labelled with R₀ = 100 and R₀ = 1000, show the time (as a multiple of gonotrophic cycles) required for resistance to reach 50% of the population at the coverages that would eliminate malaria in areas with moderate and intensive transmission (see panel A). (C) Evolutionary cost of resistance required to block the evolution of resistance. The equations of Fig. 2B are used, except that in resistant mosquitoes fecundity is decreased to F/γ and adult mortality rate is increased to δγ where γ is the cost of resistance (i.e. γ = 1 implies no cost; γ = 2 implies a twofold cost so that fecundity is halved and mortality is doubled). See Appendix for model details.

An important, but under-appreciated operational implication of this analysis is that maximal coverage is not optimal. While it appears that control strategies generally aim for very high coverage, Fig. 1A shows that it should be possible to eliminate malaria even from areas with very intense transmission, say R₀ = 1000, with a coverage of about 80%; in an area with R₀ = 100, a coverage of about 60% would be enough. Thus, in some areas elimination could be achieved with just modest adoption of interventions, whereas expensive efforts to maximize coverage would give no benefit to the population. Indeed, such efforts would be detrimental in the long-term, as exceeding the minimum target coverage imposes stronger selection for resistance, thus shortening the useful life-span of a product unnecessarily (Fig. 1B).

Delayed resistance: late-acting insecticides

It is possible to change this evolutionary-epidemiological pattern of insecticides in a way that enables them to be effective, but does not impose strong selection for resistance. One option is to use late-acting insecticides (Thomas and Read 2007). The details of the underlying theory are presented elsewhere (Read et al. 2009); here we present simplified models to review the main ideas about their efficacy and about the evolution of resistance.

As transmission depends on the survival of the mosquito throughout the developmental period of malaria of 10 days or more, effective control does not require an insecticide that kills mosquitoes shortly after biting. Rather, all that is required is an insecticide that kills mosquitoes at some point before the malaria parasite has developed its infectious sporozoites. There are two ways to do this. The insecticide could be disproportionately efficacious against older mosquitoes, or it could act sometime after first exposure (as, for example, if the insecticide was based on an infectious agent). For simplicity, and consistency with our arguments below, we here consider the latter, delayed-action case. Read et al. (2009) primarily considered age-specific killing, but show that the net effect is the same.

If coverage was complete (i.e. if all mosquitoes were exposed to the insecticide when they first bite), an insecticide that kills mosquitoes several days after exposure would be as effective at control as conventional insecticides. However, as coverage is generally not complete, some mosquitoes are exposed to the insecticides only after they have been infected by malaria. Therefore, the late-acting insecticide may not kill all infected mosquitoes before they start transmitting malaria, so that its efficacy of control is necessarily lower than that of a conventional one (Fig. 2A). However, the goal of a control program is not to prevent transmission, but to reduce it to a satisfactory degree; indeed, as mentioned above, reducing the intensity of transmission by a factor of R₀ is enough to eliminate malaria from the population (Macdonald 1957). Figure 2A shows that, if coverage is sufficiently high, insecticides that kill mosquitoes shortly before they become infectious (three gonotrophic cycles after exposure) can eliminate malaria from areas with moderate intensities transmission (R₀ = 100, indicated by the upper horizontal line). Even in the most endemic areas [where R₀ can be on the order of 1000 (Smith et al. 2007), indicated by the lower horizontal line], insecticides that delay their action several days after exposure can eliminate malaria. It is only as the delay of action approaches the duration of the parasite's development that the insecticide's efficacy (for <100% coverage) decreases to values that are too low to eliminate malaria in very high transmission situations (Fig. 2A).

However, in contrast to conventional insecticides, the efficacy of which is rapidly compromised by resistance evolution, late-life acting insecticides can provide evolutionarily sustainable control. As argued above, control efficacy is sensitive to the survival of the oldest mosquitoes, but evolutionary pressure decreases with an individual's age (Hamilton 1966), as beneficial mutations that act only when an individual has achieved most of its reproductive success increase fitness much less than mutations acting at a young age (Fisher 1930; Haldane 1941). Therefore, the pressure imposed by late-acting insecticides on mosquitoes to evolve resistance is lower than that imposed by conventional ones, delaying the evolution of resistance considerably (Fig. 2B). For example, delaying the lethal action of an insecticide with a coverage of 80% by 6 days (two gonotrophic cycles) increases the time until 50% of mosquitoes become resistant more than sevenfold. Thus, where the WHO experience was that DDT control worked very well for 5 years in areas of high and continual coverage, a two-cycle delayed action insecticide would provide continuous control for 35 years. Note that, as effectiveness decreases with the age at which the insecticide becomes active, for any given R₀, higher coverage is required for elimination for a late-acting insecticide than for a conventional one (indicated by the circles in Fig. 2B). However, even at this higher coverage, mosquito resistance erodes efficacy much more slowly for a late-acting insecticide (Fig. 2B), so that the insecticide is more likely to work long enough to ensure elimination.

Resistance frequently comes with an evolutionary cost. In Culex and other insects, for example, resistant individuals have shorter life-spans (Gazave et al. 2001), have longer development times (Bourguet et al. 2004) or are smaller as adults (Bourguet et al. 2004) than sensitive ones. Such costs generally impede or, if the costs are sufficiently high, block the evolution of resistance. If we assume that resistance decreases fecundity [as observed in, for example, insecticide-resistant moths (Boivin et al. 2001)] and longevity strongly enough [as observed in mosquitoes (Gazave et al. 2001)], the evolution of resistance is blocked for conventional insecticides; the cost required to block resistance decreases considerably as the delay of their action increases (Fig. 2C). Thus, if a late-acting insecticide kills mosquitoes 9 days (three gonotrophic cycles) after exposure, resistance is prevented if fecundity and longevity are reduced by 10%. The low cost required to prevent resistance against late-acting insecticides is because evolutionary pressure on old mosquitoes is low: as there is only weak selection pressure to evolve resistance, a low cost can block evolution. Read et al. (2009) show that the resistance costs required to prevent resistance evolving against late-acting insecticides are further lowered if the insecticides are disproportionately efficacious against malaria-infected mosquitoes, as is likely if malaria-stressed mosquitoes are more vulnerable than uninfected ones.

There are several plausible options for late-acting insecticides. The simplest would change the way that conventional insecticides are used. Using a lower dose might delay their action in two ways. First, old mosquitoes are more sensitive to some insecticides (DDT, malathion and pyrethroids) than young ones (Lines and Nassor 1991; Hodjati and Curtis 1999; Hunt et al. 2005), although in one study the age-dependent resistance was observed only for sugar-fed, but not for blood-fed mosquitoes (Hunt et al. 2005). A possible reason for this decline in resistance with age is that key enzymes associated with resistance, e.g. acetylcholinesterase, decline with age (Mourya et al. 1993). Therefore, it may be possible to find a dose that does not kill young adults, but is lethal for older ones. Second, the accumulation of sublethal doses over several bites could kill the older mosquitoes. Alternatively, slow-release formulations, e.g. microencapsulation of the insecticide, could delay the insecticide's lethal concentration.

Biopesticides, a viable alternative to chemicals (e.g. Thomas and Read 2007), could also produce the required mode of action. As many parasites of mosquitoes develop over a considerable period of the mosquito's life-cycle before they can kill their host, they may be used as insecticides with the required property of late action. Certain isolates of the fungi Beauveria bassiana and Metarhizium anisopliae, for example, infect mosquitoes. Their spores germinate on the insect's cuticle, then penetrate the insect and grow throughout the haemolymph to kill the mosquito in 7–14 days, depending on dose, formulation and fungal strain (Scholte et al. 2004, 2005; Blanford et al. 2005). The fungal infection completely blocked the production of malaria sporozoites in one experiment (Blanford et al. 2005), stimulating the suggestion of using it as an evolution-proof late-acting insecticide (Thomas and Read 2007). The microsporidian parasite Vavraia culicis, as another example, infects mosquito larvae when they ingest its spores, and then replicates extensively before developing a new generation of spores (Andreadis 2007). In some cases these kill the larvae and are released for transmission. In other cases, infected larvae survive to emerge as adults (Bedhomme et al. 2004) and the microsporidian kills the adult after about 2 weeks (Koella et al. 2009). As there appears to be a trade-off between the two strategies (L. Lorenz, PhD thesis) (some isolates of V. culicis are virulent in larvae but have almost no impact on emerging adults; the isolates that kill adults earliest have negligible effect on larvae), isolates with the desired phenotype could be used as late-acting insecticides.

Beneficial resistance: larval insecticides

Another possibility to maintain long-term efficacy of control follows the contrasting approach of using insecticides that target larval stages (Koella et al. 2009). We argue that, although they are not as effective as adulticides, larvicides can be effective in the field and, importantly, that the rapid resistance evolution they prompt can actually benefit control.

The epidemiological effect of larval insecticides is to decrease the number of adult mosquitoes. This is less effective at reducing R₀ than decreasing biting rate or adult longevity (Macdonald 1957). Indeed, to reduce R₀ by a factor of 100 (i.e. to eliminate malaria from regions with moderate transmission), at least 99% of the mosquitoes must be killed. Despite this apparent inefficacy, larviciding dramatically reduced malaria transmission in sub-Saharan Africa (Utzinger et al. 2001), showing that targeted effort can compensate for the low efficacy. The transmission-reducing efficacy of larval insecticides may be enhanced if mosquitoes exposed to sublethal doses survive to emerge as low-quality adults that are ineffective at transmitting malaria. Chemical insecticides could have this effect, but to focus the argument, consider again the microsporidian V. culicis. Although infected individuals often survive when they are exposed to a low dose, these develop into adults with a shorter life-span than uninfected individuals (Koella et al. 2009) and in which malaria parasites develop more slowly, resulting in lower infection rate (Bargielowski and Koella 2009). Vavraia-infected mosquitoes may also bite less frequently than uninfected individuals, as other microsporidians can completely block biting (Koella and Agnew 1997). Even if each of these four parameters – the number of mosquitoes, their biting rate, their survival rate as adults and the probability of infection – is reduced by only 50%, R₀ is reduced by more than 95%. Thus, a microsporidian biopesticide could be an effective agent of malaria control, as it targets critical adult traits in addition to larval survival.

As larval insecticides kill exposed mosquitoes before they reproduce, they exert strong selection pressure on mosquitoes to evolve resistance. Indeed, intensive agricultural use of insecticides, which is probably responsible for the evolution of resistance (Curtis et al. 1998; Diabate et al. 2002), is likely to have most of its inadvertent impact on Anopheles in larval habitats. There is therefore little doubt that intensive larviciding will lead to the rapid evolution of resistance. However, we suggest that such evolution does not necessarily undermine control, and may indeed enhance its efficacy. The basis of this suggestion is that insecticide resistance in larvae has an impact on adult traits, and in particular, reduces life-span (Gazave et al. 2001), the most important trait affecting the transmission of malaria (Macdonald 1957). Impaired adult performance as a consequence of larval resistance has been observed in mosquitoes (Rodcharoen and Mulla 1997; Gazave et al. 2001; Bourguet et al. 2004) and other insects (e.g. Groeters et al. 1993; Boivin et al. 2001).

As an example, consider again the use of microsporidians as a biopesticide. Although mosquitoes do not appear to have mechanisms to clear a microsporidian infection, they can tolerate infection so that, despite being infected, they are less affected by the parasite. One way of being tolerant is pupate earlier (Koella and Agnew 1999; Agnew et al. 1999). In a mosquito with a short larval period, the microsporidian does not have sufficient time to produce a lethal number of spores. Therefore, the intensive microsporidian pressure associated with a control program would be likely to lead to the evolution of earlier pupation. As age at pupation is usually traded off with adult size (Koella and Offenberg 1999), the evolution of earlier pupation should lead to smaller adults. Adult size is, in turn, correlated with longevity (e.g. Hawley 1985; Lehmann et al. 2006). Adult size is also correlated with biting rate (Koella et al. 2002). It follows from this series of correlations that the evolution of resistance to the microsporidian would lead to adults that bite less frequently and die younger than sensitive mosquitoes. A genetic basis to some of these correlations has yet to be proven, and several of the observations concern nonanopheline species, but the implication is that the direct response of evolution – resistance to the microsporidian – will increase malaria transmission because more larvae will survive, but the correlated responses – less frequent biting and shorter life – will decrease transmission. The overall effect of evolution depends on the quantitative details of these responses (Fig. 3A).

Figure 3.

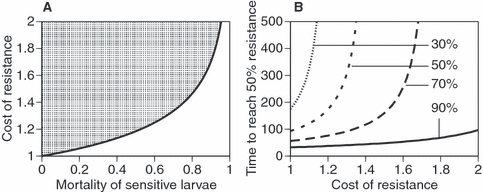
Larval insecticides. (A) The epidemiological consequence of the evolution of resistance, if resistance is evolutionarily costly. The cost is reflected as a factor γ by which the biting rate of resistant mosquitoes is divided and the adult mortality rate of resistant mosquitoes is multiplied. (Note that a cost with respect to fecundity is not considered, as fecundity has no epidemiological relevance.) The effect of the insecticide in sensitive mosquitoes is given as the proportion of juvenile mosquitoes that are killed by the insecticide. The line shows the combination of the mortality of sensitive larvae and the cost of resistance where R₀, calculated from the Ross–Macdonald equation, is equal for sensitive (with increased juvenile mortality but no cost) and resistant mosquitoes (with no juvenile mortality but reduced biting rate and increased mortality rate), and the shaded area shows parameters where evolution of resistance increases the effectiveness of control. (B) Evolution of resistance for four levels of insecticide-induced juvenile mortality (shown by the four lines) as a function of the cost of resistance for fecundity and mortality rate. The equations used to calculate the evolutionary response are identical to the ones in Fig. 1, except that (i) juvenile survival of sensitive mosquitoes is decreased by the use of the insecticide, (ii) the mortality rate and fecundity of adult mosquitoes are independent of the insecticide, but in resistant mosquitoes mortality is increased and fecundity decreased by a factor identical to the cost of resistance. (Note that the effect of resistance on biting rate is ignored, for it has no direct effect on evolution.)

In Fig. 3A, we assumed that the insecticide has an effect only on juvenile mortality and compared the Ross–Macdonald equation for sensitive mosquitoes (that are killed by the insecticide) with that of resistant mosquitoes (for which biting rate is divided and daily mortality rate is multiplied by the cost of resistance). [Note that we ignore the cost of resistance expressed as a reduction of fecundity (Fig. 2C), as fecundity does not affect the epidemiological dynamics.] The figure shows that a sufficiently high cost of resistance can more than compensate for the loss of the insecticide's efficacy due to the evolution of resistance. For example, if an insecticide kills half of the larvae in a population, the evolution of resistance against this insecticide leads to more effective control if adult mortality rate and biting rate are changed by more than about 20%.

As mentioned above, the evolution of resistance against larval insecticides can be rapid (Fig. 3B), with cost-free resistance evolving in <100 gonotrophic cycles if the insecticide kills 90% of the larvae. As in Fig. 2A, we consider a cost that decreases longevity and fecundity. Then, as the costs increase, the time required for resistance to reach a frequency of 50% increases, but this increase is slight if the insecticide is very lethal (i.e. coverage is high). Again, this pattern of evolution arises because the evolutionary pressure is stronger in young individuals (which experience the lethal effects of the insecticide) than it is in older ones (which experience the cost of resistance). Unless the effect of the insecticide is low or the cost is very high, evolution is not blocked (not shown).

Thus, despite an evolutionary cost, resistance can evolve rapidly if a larval insecticide is used intensively, and this rapid evolution may well be desirable; rather than undermining control, the evolution of resistance can lead to greater reduction of transmission than is due to the lethal effects of the insecticide. However, the effects on transmission will be moderate, whether resistance has evolved or not. While mosquitoes are sensitive, R₀ is decreased proportionally to the effect of the insecticide. With, say, 50% coverage, the insecticide kills 50% of the juveniles and therefore decreases the number of adults and thus R₀ by 50%. When mosquitoes have become resistant, R₀ is decreased by about 60% if resistance decreases biting-rate and longevity by 25%.

Preventing resistance by combining larval and late-acting insecticides

The arguments above can be used to discuss combinations of insecticides that force evolution in a way that prevents resistance against the effective one. An underlying assumption of this idea is that resistance in larvae and in adults is constrained via genetic trade-offs, so that resistance can only evolve in larvae or in adults, but not in both. Let us consider how such a negative correlation could come about using as an example, the use of several strains of microsporidians as a biopesticide.

On the one hand, as mentioned above, late-acting strains, which reduce longevity, can give very effective control. Although there is little selection pressure for resistance, antimicrosporidian resistance is likely to evolve, albeit slowly. Such resistance may be associated with adult size [which is genetically correlated with the immune response (Voordouw et al. 2008)], for the longevity of microsporidian-infected mosquitoes increases with their size (L. Lorenz, unpublished PhD). Thus, resistance will evolve together with larger adults that have more effective immune responses.

On the other hand, larval-killing strains of microsporidians will lead to the rapid evolution of resistance of the mosquitoes, which is likely to be associated with earlier pupation. This will, in turn, lead not only to smaller adults (see above), but also to adults with less effective immune responses (Koella and Boëte 2003).

Thus, selection for resistance against the larvicide and selection against the late-acting adulticide are in opposition: the former leads to smaller adults with a less effective immune response, and the latter to larger adults with an effective immune response. As the evolutionary pressure on the larvae is stronger than that on the old adults (Hamilton 1966), the evolutionary outcome is most likely to be resistance against the larval insecticide, even if this means that the adults will be small and have ineffective immunity, and thus remain sensitive to the late-acting one. In other words, the use of a larval-killing insecticide forces evolution in a direction that does not allow the evolution of resistance against simultaneously used late-acting insecticides.

Although the trade-offs necessary for this argument are plausible, we are unaware of any direct evidence of their existence. Thus, while the suggested mechanism is highly speculative, the principle is clear. We might be able to use one insecticide to force evolution in a way that maintains the sensitivity of mosquitoes to a second insecticide, and thus enables sustainable and effective control.

Discussion and conclusion

The ideas discussed here yield a pessimistic conclusion about current insecticides. The WHO Pesticide Evaluation Scheme for Phase 1 (laboratory) testing, for example, requires that potential insecticides for impregnated bednets and for indoor residual spraying must kill 80% of 2- to 5-day-old female Anopheles within 24 h after exposure (WHO 2005a,b). These criteria will lead to the discovery of not only very effective insecticides, but also insecticides that will generate near maximal selection for resistance.

More optimistically, our suggestions give several potential ways around the problem of resistance. First, late-acting insecticides can be very effective at controlling malaria, but will delay considerably the evolution of resistance, particularly if resistance is costly. Second, larvicides will usually lead to the rapid evolution of resistance, but the evolution of resistance against larvicides need not undermine control, and can indeed enhance it. Third, if we combine a larvicide and a late-acting adulticide, resistance to the two insecticides might involve opposite changes in the traits associated with resistance. Evolution will generally solve this conflict by favouring resistance of the larvae, thereby preventing the resistance against late-acting insecticide.

The key arguments underpinning our optimism are that (i) selection pressure decreases with age, (ii) the epidemiological importance of mosquitoes increases with age, and (iii) traits like resistance are genetically correlated in the right sort of way at different ages. The first two of these are a theoretical necessity, and indeed form the basis for many aspects of evolutionary biology (Charlesworth 1980), particularly the evolution of senescence (Williams 1957), and for ideas about malaria control (Macdonald 1957). The third is an open empirical issue. In particular, the lack of data on the cost of resistance in Anopheles mosquitoes is in striking contrast with work on Culex pipiens around Montpellier in France, where costs of resistance have been estimated in the field (Labbé et al. 2007). While some studies have estimated trade-offs among traits, these have generally been done in the laboratory, whereas reliable data must be obtained in natural situations.

Our models are caricatures of reality, and are designed to evaluate general principles rather than explore specific management strategies. They do not, for example, include any spatial structure or variability of coverage [which can give nonintuitive predictions, at least for the evolution of antimalarial resistance (Koella and Antia 2003)], variability in mosquito densities (which can increase the role of random genetic drift during the seasons with low densities), any effect of the insecticide on the future density of the mosquitoes, or any effect of the insecticide on fecundity (which could impose considerable selection pressure, even if the insecticide does not kill mosquitoes). To model a specific situation, analyses of such complexities would be necessary. Perhaps an assumption more relevant to evaluate the concepts we lay out here is the potential evolutionary response of the malaria parasite to a shorter life of the mosquito. Indeed, why should it not shorten its own development and release sporozoites earlier to compensate for the effect of a late-acting insecticide? This possibility is intriguing, but ideas about the evolutionary pressures underlying the developmental period of malaria are sketchy (Koella 1999). The very high rates of mortality due to natural causes and conventional insecticides must already impose very strong selection for more rapid development. Without understanding the counterbalancing forces which currently maintain long development times, it is difficult to evaluate the epidemiological consequences of any malaria evolution which might be prompted by the strategies we outline here. We plan theoretical and empirical studies to evaluate this issue.

Despite the historical experience, the problem insecticide resistance poses for new plans to control and eradicate malaria (Roll Back Malaria 2008) has received remarkably little attention. What planning there is revolves around traditional resistance management strategies and reliance on an insecticide R&D pipeline. Both ideas borrow heavily on the agricultural experience. However, in agriculture, reductions in pest densities are necessarily the sole aim of the game. In malaria, the situation is different: malaria control, not mosquito control, is the aim. If this can be accepted by the vector control community, new and sustainable strategies can be envisaged. We have argued that exploiting the difference between what is important for epidemiology (old mosquitoes) and for evolution (young mosquitoes) makes possible insecticidal products that themselves manage resistance. Our more general conclusion is that we may find novel solutions to evolutionary problems for the control of malaria and other infectious diseases by merging evolutionary ecology and epidemiology.

Appendix

Effectiveness of control with a conventional insecticide

Two aspects of the mosquito's life-cycle determine the effectiveness of control: the probability that an emerging mosquito survives to become infectious (i.e. harbor sporozoites) and the mosquito's longevity once it is infectious. (i) Survival. If coverage (and, as death follows shortly after exposure, insecticide-related death rate) are c and the mortality per gonotrophic cycle of unexposed mosquitoes is δ [where δ = 1 − e^−μx and x is the duration of the gonotrophic cycle (assumed to be 3 in our simulations)], a mosquito infected at its, say, z-th bite survives the developmental period to transmit malaria with probability 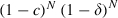, where N is the duration of the parasite's development, as measured in gonotrophic cycles. The probability that a mosquito becomes infected at bite z (but not before) is 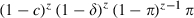, where π is the probability per bite that a mosquito is infected, so the probability that an emerging mosquito survives to transmit malaria is 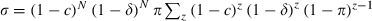. (ii) Longevity once infectious. Longevity is calculated as the sum of the survival terms l_z, starting at the time z = T when mosquitoes become infectious: 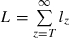, where l_T = 1, l_z = sl_z−1 is survival up to age z and s is the probability that a mosquito survives during a gonotrophic cycle: 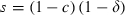(for sensitive mosquitoes). Malaria can be eliminated if the insecticide decreases the intensity of transmission from the insecticide-free level R₀ to a level R₀′ < 1, i.e. if .

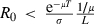Effectiveness of control with a late-acting insecticide

The calculation of effectiveness follows the ideas above. As we assume that for a late-acting insecticide death follows τ gonotrophic cycles after exposure, the equations must be changed as follows. Mosquitoes infected at their z-th bite survive to become infectious after N gonotrophic cycles if they are not exposed to the insecticide between the ages z − τ and z + N − τ and they survive the natural mortality. The probability of surviving is thus 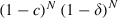if z ≥ τ and 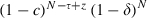if z < τ. Mosquitoes survive up to their z-th bite if they are not exposed before z − τ and do not die of natural causes. Thus, the probability of infection at the z-th bite is 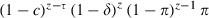if z ≥ τ and 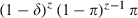if z < τ. The probability that an emerging mosquito survives to transmit malaria is 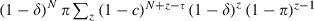. Note that for τ = 0, this equation is equal to the one given for conventional insecticides.

Evolution of resistance

We predicted the evolutionary spread of resistance by calculating the allele frequencies every generation in a simulation of an explicit age-structured model that keeps track of the number of sensitive, resistant homozygous and resistant heterozygous individuals at each age-class. Resistance is assumed to be governed by a single gene, with resistance determined by a dominant allele (i.e. heterozygotes are identical to homozygous resistants). Briefly, at each time step (which is the equivalent of a gonotrophic cycle), the number of individuals surviving to the next gonotrophic cycle is calculated with the survival probability s (for resistant mosquitoes: 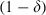; for sensitive mosquitoes exposed to a conventional insecticide (which kills mosquitoes immediately): 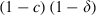; for sensitive mosquitoes exposed to a late-acting insecticide (which kills mosquitoes τ gonotrophic cycles after exposure: 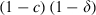if z ≥ τ and 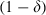if z < τ. The last case assumes that mosquitoes die if they were exposed to the insecticide τ gonotrophic cycles before the current cycle, but that they are unaffected by the insecticide if their exposure was less than τ cycles earlier). Mating is random with respect to resistance, and each individual lays 10 (female) eggs (i.e. we assumed that fecundity is independent of age and resistance). The larvae hatch and take the equivalent of four gonotrophic cycles to reach adulthood. We assumed that 36% of the eggs survive their development, i.e. that about 10% of the larvae die per day. In all simulations, the initial frequency of resistance was set to 10⁻⁴. (Note that, as the evolutionary predictions depend on fecundity and larval survival, the choice of our parameters will not generally give quantitatively correct predictions for the rate at which resistance evolves. Rather, our intention is to compare the evolution of resistance for different scenarios. Such a comparison gave similar results for all of the parameters that we tested.)