Abstract
Salmonid fishes exhibit high levels of population differentiation. In particular, the brown trout (Salmo trutta L.) demonstrates complex within river drainage genetic structure. Increasingly, these patterns can be related to the underlying evolutionary models, of which three scenarios (member-vagrant hypothesis, metapopulation model and panmixia) facilitate testable predictions for investigations into population structure. We analysed 1225 trout collected from the River Dart, a 75 km long river located in southwest England. Specimens were collected from 22 sample sites across three consecutive summers (2001–2003) and genetic variation was examined at nine microsatellite loci. A hierarchical analysis of molecular variance revealed that negligible genetic variation was attributed among temporal samples. The highest levels of differentiation occurred among samples isolated above barriers to fish movement, and once these samples were removed, a significant effect of isolation-by-distance was observed. These results suggest that, at least in the short-term, ecological events are more important in shaping the population structure of Dart trout than stochastic extinction events, and certainly do not contradict the expectations of a member-vagrant hypothesis. Furthermore, individual-level spatial autocorrelation analyses support previous recommendations for the preservation of a number of spawning sites spaced throughout the tributary system to conserve the high levels of genetic variation identified in salmonid species.
Keywords: genetic differentiation, member-vagrant hypothesis, metapopulation model, microsatellite, population genetics
Introduction
The discovery of microsatellites, and other hypervariable genetic markers, has enabled the study of genetic differentiation and population subdivision at small scales (e.g. Reisch and Kellermeier 2007), even down to the level of the individual (e.g. Carlsson and Carlsson 2002; Peakall et al. 2003; Pemberton et al. 2007). The information gathered can have important implications for conservation work intended to preserve genetic variation. The significance of this objective increased following the World Summit on Sustainable Development and the publication of the framework for action on biodiversity and ecosystem management, which identifies genetic variation as one of the three levels of biodiversity recommended for conservation (WEHAB 2002). Information on the scale over which genetic differentiation occurs also has important implications for the management of natural resources and the potential for local adaptation.
Studies into freshwater salmonid fishes have revealed that genetic differentiation can occur over very short distances within river catchments. This can be associated with physical barriers to movement, which can isolate populations that then differentiate by genetic drift (Hindar et al. 1991). In addition, differentiation has also been noted where salmonids exist without such barriers, including populations of the many anadromous species that could potentially be linked by gene flow (Stahl 1987; Small et al. 1998; Beacham et al. 2000; Primmer et al. 2006). As such, these species represent an interesting case for studying processes of population differentiation. Specifically, the propensity towards population subdivision appears linked to two key factors: (a) the well-known ability of salmonids to home back to specific natal rivers (Stabell 1984) and (b) the patchy distribution of spawning areas within rivers (Neville et al. 2006) that may act to restrict gene flow among fish in different areas of a river (although other processes e.g. extinction-recolonization dynamics have also been described; Ostergaard et al. 2003).
Amongst salmonid species, the brown trout (Salmo trutta) is typified by having a particularly complex within catchment genetic structure, with high levels of genetic differentiation and an apparent lack of correlation between genetic and geographic distance (Bouza et al. 1999; Crozier and Ferguson 1986; Ferguson 1989; Moran et al. 1995; Ruzzante et al. 2001; Ryman 1983; but also see Carlsson and Nilsson 2000; Estoup et al. 1998). Recently there has been an increasing emphasis placed on understanding the deeper biological significance of this complex population structure and there is a need to understand the underlying evolutionary models that may explain the observed patterns of genetic differentiation, which also have important implications for the ecology of brown trout, as well as the conservation of genetic diversity and management of the species. However, brown trout are under pressure from habitat destruction, pollution, over-exploitation and stocking with non-native fish, i.e. local factors that may erode the high levels of genetic variation observed and cause the extinction of unique varieties and loss of unique traits (Ferguson 1989).
Although the River Dart is no exception to the pressures that threaten the persistence of brown trout at a local scale, it does drain a National Park and so benefits from a relatively high level of statutory protection. Regular electrofishing surveys undertaken by the Environment Agency (EA; the national regulatory body in England and Wales) suggest that numbers of brown trout within the River Dart are significant and stable, although there has been a negative trend since records began in the 1960s (Steele 1996; EA 2001). Changes in land use have led to habitat degradation in the headwaters, although a major threat facing trout in the River Dart arises from both human mediated and natural acidification. The low pH values which characterize the River Dart, combined with the fact that brown trout may spawn in small rivers (Elliott 1994), may make Dart trout more susceptible to catastrophic events. In turn, this may lead to localized extinctions and recolonizations, with important implications for patterns of genetic differentiation among groups of brown trout (Hansen and Mensberg 1996; Ostergaard et al. 2003). Alternatively, the naturally low pH of rivers on Dartmoor may actually have promoted the tolerance of high acidity in indigenous populations of trout, generating the potential for local adaptation (Taylor 1991).
The purpose of this study was to investigate the population genetic structure of brown trout at the scale of a single river catchment and to reconcile the potential for environmental instability to cause localized extinction events (e.g. Ostergaard et al. 2003; Koizumi et al. 2006; Neville et al. 2006) with the apparently stable trout numbers present in the River Dart. Garant et al. (2000) have previously proposed three scenarios that form an appropriate framework for addressing this question. Under the member-vagrant model, nursery areas play a vital role in determining population structure and selection favours individuals that return to their natal spawning grounds to reproduce, which maximizes survival of the young and promotes the development of locally adapted gene pools. Thus, fish that complete this process of homing are considered ‘members’, contributing to local adaptation and those that do not return to natal areas are known as ‘vagrants’ (Iles and Sinclair 1982; Garant et al. 2000). This model predicts temporal stability of population structure, a significant effect of isolation-by-distance and strong genetic differentiation among populations. Under the second model, the metapopulation model, the degree of genetic structuring depends on the temporal stability of habitats, so in an unstable environment the occurrence of locally adapted gene pools can be curtailed because of local extinctions (and subsequent recolonizations, reviewed in Beebee and Rowe 2004; McQuinn 1997; Rieman and Dunham 2000). The key features of this model are that local populations (or subpopulations) are interconnected not only by migration but also recolonization and empty/unoccupied patches have an important role in metapopulaton dynamics. This model predicts that there would be lower levels of temporal stability in population structure, no significant effect of isolation-by-distance and lower genetic divergence between subpopulations (but still statistically significant because of founder effects, Garant et al. 2000; McQuinn 1997; Rieman and Dunham 2000). The third scenario is panmixia, where gene flow is unrestricted across the catchment and suggests the absence of genetic differentiation, such that neither of the previous two models applies. Elucidation of the evolutionary model appropriate to Dart trout offers the potential not only to aid local management and conservation, but also to begin to address the relative scarcity of population genetics research completed on salmonids in England and Wales.
The present study examined the variability at nine microsatellite loci in brown trout sampled from the River Dart over a 3-year period, with the specific aim of ascertaining the pattern of genetic differentiation within a river system that is particularly vulnerable to severe pH depressions. The results from this analysis, which included application of the decomposed pairwise regression (DPR) method that allowed the relative strengths of genetic drift and gene flow to be accessed in each sample, were then used to consider which evolutionary model (member-vagrant, metapopulation or panmixia) best fitted the data. In addition, spatial autocorrelation was also employed to determine the geographic scale over which genetic differentiation occurred in Dart trout: the conservation implications of these results are discussed.
Methods
The study area
The River Dart catchment is located in Devon, southwest England (Fig. 1). It is approximately 75 km long, covers an area of 475 km2 and flows into the English Channel through the Dart Estuary and into Start Bay. The river rises on Dartmoor National Park, an upland granite mass that reaches over 600 m high. The catchment is a typical moorland system, characterized by high rainfall and a peaty, acidic soil. The area represents the largest unglaciated expanse of upland in Great Britain and the largest granite surface in England. There are no real aquifers on Dartmoor and water is primarily stored in wetlands and bogs. The river is formed from two main tributaries, the East and West Dart. The upper reaches support small-scale livestock farming, which becomes more intensive and incorporates arable farming once it flows off the moor.
Figure 1.
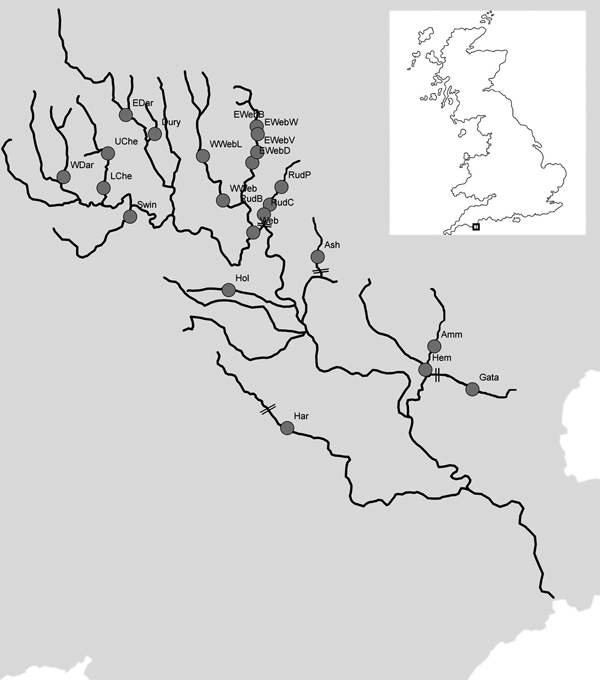
Map of the River Dart. Grey dots indicate sampling sites, which are accompanied by abbreviated sample names that match those in Table 1. Significant barriers to fish movement are indicated by double lines perpendicular to the river.
The catchment supports a locally important stock of resident and anadromous trout (see rod-catch data below), with all the tributaries and several stretches of the main river containing excellent spawning and nursery areas. In particular, many of the headwaters provide valuable spawning grounds, not only for brown trout, but also Atlantic salmon (Salmo salar L.). The river also supports a rod/game fishery, as well as a limited commercial estuary (seine) net fishery. Catches of sea trout in 2002, the year this study began, were 712 for rod catches and 727 for net catches (EA 2002).
Formal records of brown trout stocking in the UK were first collected by the national river boards during the 1950s and show that in the period up to 2005, 145 212 individual ova, fry or smolt were stocked into the River Dart. These comprised 65 separate stocking events at a minimum of 18 discrete locations within the river. The largest single stocking incident was of 96 000 eyed ova into the headwaters of the East Dart in 1961 (this single event accounts for the majority of all recorded stocking on the River Dart). The source of most stocked trout is thought to be various local hatcheries from southwest England, but the ultimate origin of hatchery stocks has been impossible to uncover (Finnegan and Stevens 2005). In the last decade local fisheries groups have taken to stocking the lower reaches of the River Dart with much smaller numbers (in the hundreds) of hatchery reared smolt which are typically bred from trout of Dart origin.
Sample collection
A total of l1225 brown trout of multiple year classes, but predominantly parr and excluding fry (to avoid collecting siblings; Hansen et al. 1997), were collected by electrofishing from 22 sites spread across 14 tributaries within the River Dart catchment. Five of these sites were isolated above barriers; the Gata and the Ash above man-made weirs and the Rud group of samples above a natural waterfall (Fig. 1). The average in-water distance among sample sites was 22.7 km, with a range of 0.8–64.4 km. Sampling was carried out each summer (July–September), from 2002 to 2004 (Table 1; Fig. 1). The adipose fin was removed from each fish and preserved in 98% ethanol, after which the fish was released; removal of the adipose fin provided a permanent mark so the same individuals were not sampled again in subsequent years.
Table 11.
Sample site abbreviations
| Abbreviation | Latitude | Longitude | Details | Year | n |
|---|---|---|---|---|---|
| Amm | 50°28′27″N | 3°39:44″W | Amm Brook, Amm house weir | 2002 | 32 |
| Ash | 50°31′50″N | 3°45′26″W | Ashburn, Belford Hill | 2002 | 36 |
| Dury | 50°35′06″N | 3°53′26″W | Dury Brook, Dury Farm | 2002 | 33 |
| EDar | 50°35′44″N | 3°54′49″W | East Dart, Postbridge | 2002 | 21 |
| EWebB | 50°35′21″N | 3°48′27″W | East Webburn, Bagpark Estate | 2003 | 28 |
| EWebD | 50°34′12″N | 3°48′40″W | East Webburn, Dunstone Bridge | 2004 | 57 |
| EWebV | 50°34′32″N | 3°48′25″W | East Webburn, Veton Bridge | 2003 | 49 |
| EWebW | 50°35′08″N | 3°48′26″W | East Webburn, Wooder Manor | 2002 | 25 |
| EWebW | 50°35′08″N | 3°48′26″W | East Webburn, Wooder Manor | 2003 | 52 |
| Gata | 50°27′08″N | 3°37′49″W | Gatacombe River | 2002 | 34 |
| Har | 50°25′55″N | 3°46′54″W | Harbourne, Hatcheries Fish Farm | 2002 | 41 |
| Hem | 50°27′45″N | 3°40′08″W | River Hems | 2002 | 40 |
| Hol | 50°30′15″N | 3°49′47″W | Holly Brook | 2002 | 29 |
| LChe | 50°33′27″N | 3°55′55″W | Cherry Brook, Lower Bridge | 2002 | 32 |
| LChe | 50°33′27″N | 3°55′55″W | Cherry Brook, Lower Bridge | 2003 | 27 |
| RudB | 50°32′55″N | 3°47′46″W | Ruddycleave, Bowden Farm | 2003 | 42 |
| RudB | 50°32′55″N | 3°47′46″W | Ruddycleave, Bowden Farm | 2004 | 54 |
| RudC | 50°32′39″N | 3°48′05″W | Ruddycleave, Ruddycleave Cottage | 2003 | 36 |
| RudP | 50°33′28″N | 3°47′11″W | Ruddycleave, Pudsham Down | 2002 | 21 |
| RudP | 50°33′28″N | 3°47′11″W | Ruddycleave, Pudsham Down | 2003 | 38 |
| RudP | 50°33′28″N | 3°47′11″W | Ruddycleave, Pudsham Down | 2004 | 39 |
| Swin | 50°32′33″N | 3°54′36″W | River Swincombe, Wydemeet | 2002 | 32 |
| Swin | 50°32′33″N | 3°54′36″W | River Swincombe, Wydemeet | 2004 | 48 |
| UChe | 50°34′38″N | 3°55′58″W | Cherry Brook, Upper Bridge | 2003 | 29 |
| UChe | 50°34′38″N | 3°55′58″W | Cherry Brook, Upper Bridge | 2004 | 41 |
| WDar | 50°33′47″N | 3°57′53″W | West Dart, Cockern Tor | 2002 | 39 |
| WDar | 50°33′47″N | 3°57′53″W | West Dart, Cockern Tor | 2003 | 32 |
| WDar | 50°33′47″N | 3°57′53″W | West Dart, Cockern Tor | 2004 | 48 |
| Web | 50°31′35″N | 3°47′43″W | River Webburn, Mistresses Piece | 2002 | 32 |
| WWeb | 50°33′03″N | 3°50′03″W | West Webburn, Pondsworthy Bridge | 2002 | 47 |
| WWeb | 50°33′03″N | 3°50′03″W | West Webburn, Pondsworthy Bridge | 2003 | 32 |
| WWeb | 50°33′03″N | 3°50′03″W | West Webburn, Pondsworthy Bridge | 2004 | 46 |
| WWebL | 50°34′26″N | 3°51′02″W | West Webburn, Lower Cator Bridge | 2002 | 33 |
Location details, year of sample collection and numbers of fish sampled (n). See Fig. 1 for locations.
Microsatellites
DNA was extracted from the fin tissue according to an ammonium acetate precipitation method, similar to that described in Bruford et al. (1998). Genetic variation was determined at nine di-nucleotide microsatellite loci: Str15, Str60, Str73 (Estoup et al. 1993), Str85 (Presa and Guyomard 1996), SsoSL417, SsoSL25 (Slettan et al. 1995), Strutta58 (Poteaux 1995), SsoSL438 (A. Slettan, unpublished data, GenBank accession no. Z49134) and SsHaeIII.14.20 (J. L. Goodier unpublished, GenBank accession no. U10050). Genotypes were assayed through polymerase chain reaction (PCR) and polyacrylamide gel electrophoresis with fluorescently labelled primers. PCR reactions were carried out in 10 μL reaction volumes and standard PCR reagents were used in a mixture containing 10–100 ng DNA, 0.5 μm of each primer, 1–1.5 mm MgCl2, 200 μm of each dNTP, 1× reaction buffer and 0.5 U of Taq DNA polymerase (Bioline, London, UK). The PCR profile consisted of: a single denaturing set lasting 3 min at 94°C, 30 iterations of 94°C for 30 s, annealing temperatures 51°C (Str85), 52°C (Str15 & Sso417), 54°C (Sso25 & Strutta58), 58°C (SsHae), 60°C (Str 73) or 65°C (Str60) for 30 s and 72°C for 30 s with a single elongation step of 72°C for 10 min. However, the Sso438PCR profile was a stepwise program, with the annealing stage made up of six iterations at 1° intervals between 54°C and 48°C. For those loci producing weak products (SsHae, Str15 and Str73) 40 iterations were generally used.
Size determination of the labelled PCR products was performed using a Beckman-Coulter (Fullerton, California, USA) CEQ8000 automated DNA sequencer with an internal size standard, according to the manufacturer's instructions. The raw data were analysed with the platform's-associated fragment analysis software (Beckman-Coulter).
Genetic diversity analysis
ARLEQUIN version 3 (Schneider et al. 2000) was used to estimate the variance components in allele frequencies among years (Excoffier et al. 1992) and all samples were found to exhibit temporal stability (see Results). Therefore, in subsequent analyses temporal samples from a location were combined to estimate population allele frequencies, as recommended by Waples (1989). Each sample at each locus was tested for conformity to Hardy–Weinberg equilibrium (HWE; Guo and Thompson 1992) using GENEPOP 3.4 (Raymond and Rousset 1995) and any deviations were further investigated with Microchecker (Oosterhout et al. 2004). Critical levels of significance for simultaneous tests were adjusted using the sequential Bonferroni procedure for multiple tests (Rice 1989). In addition, Powermarker version 3.25 (Liu and Muse 2005) was used to calculate expected and observed heterozygosity, and FSTAT version 2.9 (Goudet 2002) was used to calculate allelic richness (allele number corrected for sample size using the rarefaction method of El Mousadik and Petit 1996) and the inbreeding coefficient.
To examine the levels of genetic differentiation between pairs of samples a test of the homogeneity of allele frequency distributions (the so-called test of ‘genic differentiation’) was run in GENPOP (Raymond and Rousset 1995) and FST values were calculated (Weir and Cockerham 1984) in ARLEQUIN. Critical levels of significance for simultaneous tests were adjusted using the sequential Bonferroni procedure for multiple tests (Rice 1989). The chord distance (DCE,Cavalli-Sforza and Edwards 1967) was also used to quantify genetic differentiation between samples. This measure was chosen because the close proximity of samples included in the study means mutation is unlikely to have contributed to population divergence and the DCE distance is based on geometric distances, which are independent of models of microsatellite mutation (Liu and Muse 2005). It has also been shown to be one of the most efficient methods for obtaining correct tree topology using microsatellite data (Takezaki and Nei 1996). Neighbour-joining (NJ) phylograms were constructed and confidence intervals on tree topology were estimated by bootstrap resampling of loci 1000 times utilizing the programs Powermarker version 3.23 (Liu and Muse 2005), Consense (from Phylip 3.6; Felsenstein 1995) and Tree View version 1.6 (Page 1996).
Decomposed pairwise regression analysis
To detect outlier populations and accurately elucidate patterns of isolation-by-distance, the DPR (Koizumi et al. 2006) was applied. The DPR can also estimate the relative strengths of genetic drift and gene flow for each sample, by decomposing the regression of the pairwise genetic and geographic distances (Rousset 1997). Briefly, genetic distance [FST/(1 − FST)] is plotted against geographic distance for all pairwise comparisons. Outlier analysis then determines which samples have exceptional characteristics that may falsely influence the pattern of IBD (e.g. founder effects, bottlenecks, physical barriers, all of which can strongly affect the overall pattern). These outlying samples were determined based on the systematic bias of the regression residuals (process one, which identifies ‘putative’ outliers). The outliers were then sequentially removed from the analysis and the best model was selected based on the AIC (Akaike's information criteria) value (process two, which identifies ‘true’ outliers); the smallest values indicate the most plausible model (Burnham and Anderson 2002). Because of the small sample sizes, the corrected AIC (AICC) was used.
Finally, after determining the best model and the ‘true’ outliers, the pairwise genetic and geographic distances were regressed separately for each sample (including the outlier samples) against the nonoutlier samples, to investigate the different patterns of geneflow and drift. The significance of the relationship was assessed by ordinary least-squares regression.
Spatial autocorrelation analysis
Spatial genetic structure was tested with the software package genalex version 6.1 (Peakall and Smouse 2006 and according to Primmer et al. 2006). A Mantel test of matrix correspondence was used to examine the association between pairwise FST values and the in-water distance between sampling sites by estimating the rxy measure that is analogous to an autocorrelation coefficient (Smouse et al. 1986), with 999 permutations used to test the statistical significance of the values. At the scale of individual specimens, a multivariate microspatial autocorrelation approach was also employed (Smouse and Peakall 1999; Peakall et al. 2003). This test employed the squared distances measure (PhiPT; Peakall et al. 2003) to estimate individual genetic distance, and the same in-water distances between sample sites used in the Mantel test for distance between individual specimens (with the exception that all individuals caught from the same sample site were assigned a distance value of zero). To assess the extent of nonrandom genetic structure among individuals (Peakall et al. 2003), a correlogram of the autocorrelation coefficient (r) was plotted as a function of distance, specifically five distance classes: 0–5, 6–15, 16–25, 26–45, 46–65 km; a range of alternate distance classes from 5 to 25 km were also analysed. A multi-distance class (MDC) analysis was also used to give a more accurate estimate of the scale over which genetic structure was detected (Peakall et al. 2003). In this approach the same classes as above were utilized, except that multiple analyses were performed with automatically increasing distance size classes, such that individuals from more distant classes were added to the previous groups (Peakall et al. 2003). One thousand bootstrap replicates were used to ascertain the 95% confidence interval (CI) of the r estimates, and 999 permutations were used to resolve the 95% CI about the null hypothesis of no spatial genetic structure. Significant genetic autocorrelation was concluded when the CI of r and those of the null hypothesis did not overlap (Peakall et al. 2003).
Results
Genetic diversity
Pairwise testing of temporal samples revealed only one case of significant genetic heterogeneity between 2003 and 2004 samples at the RudB site in locus Strutta58 (P < 0.05, corrected across loci; k = 9). Furthermore, quantitative estimates of hierarchical gene diversity across the whole dataset showed that while a significant amount of genetic variation (P < 0.00001) was identified both within samples and among different sample sites (96% within samples and 4% between sites), a nonsignificant estimate of 0% variation was attributed to variation among temporal samples. Therefore, all temporal samples collected at individual sites were pooled in subsequent analyses.
Genetic diversity indices for each locus and population are presented in Table 2. Significant deviations from HWE (P < 0.05, corrected across loci; k = 9) for pooled samples were detected in two cases (EDar at SsoSL25 and EWebW at Str73). Further analysis of these cases with Microchecker did not reveal any evidence of null alleles or scoring errors, although the EDar case was associated with a significantly positive Fis value (Table 2), which could result from the nonrepresentative sampling of juveniles fish (‘family sampling’; Allendorf and Phelps 1981; Hansen et al. 1997; Wenburg et al. 1998). The mean number of alleles at a locus, across the whole dataset was 10.7 and ranged from 3 (Str60) to 27 (Str58). The mean number of alleles per locus within samples had an average of 6.6 and ranged from 4.4 (RudB) to 8.0 (Har). The allelic richness (the average allele number within samples, corrected for a minimum sample size of 16 in this case) was smaller, with an average of 5.5 and ranged between 4.0 (RudB) and 6.6 (Har). The average observed heterozygosity (HO) across all samples was 0.6 and varied from 0.55 (RudP) to 0.74 (Amm).
Table 22.
Microsatellite diversity indices of the samples collected from 22 sites and results of the Hardy–Weinberg equilibrium test
| Sample | Indices | SsHae | Str15 | Str58 | Str60 | Sso25 | Sso438 | Str73 | Sso417 | Str85 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Amm | N | 32 | 32 | 32 | 32 | 32 | 27 | 32 | 32 | 31 | |
| A | 10 | 5 | 13 | 2 | 10 | 4 | 4 | 8 | 6 | 6.889 | |
| AR | 8.616 | 4.488 | 10.919 | 2 | 8.32 | 3.83 | 3.5 | 7.632 | 5.389 | 6.077 | |
| HE | 0.843 | 0.695 | 0.88 | 0.482 | 0.812 | 0.582 | 0.604 | 0.829 | 0.64 | 0.708 | |
| HO | 0.875 | 0.844 | 0.969 | 0.438 | 0.844 | 0.593 | 0.625 | 0.813 | 0.677 | 0.742 | |
| Fis | 0.294 | −0.198 | −0.085 | 0.109 | −0.024 | 0.001 | −0.018 | 0.036 | −0.041 | −0.032 | |
| HWE | −0.22 | 0.142 | 0.112 | 0.744 | 0.567 | 0.761 | 0.61 | 0.161 | 0.96 | ||
| Ash | N | 36 | 33 | 35 | 36 | 36 | 36 | 34 | 35 | 36 | |
| A | 9 | 5 | 11 | 2 | 8 | 3 | 5 | 9 | 5 | 5.889 | |
| AR | 7.51 | 4.223 | 8.22 | 2 | 6.494 | 2.606 | 4.955 | 6.997 | 4.138 | 5.238 | |
| HE | 0.824 | 0.671 | 0.644 | 0.277 | 0.766 | 0.155 | 0.74 | 0.782 | 0.639 | 0.611 | |
| HO | 0.916 | 0.667 | 0.657 | 0.277 | 0.805 | 0.111 | 0.823 | 0.828 | 0.722 | 0.645 | |
| Fis | −0.098 | 0.022 | −0.006 | 0.014 | −0.037 | 0.3 | −0.099 | −0.045 | −0.116 | −0.042 | |
| HWE | 0.453 | 0.986 | 0.708 | 1 | 0.858 | 0.858 | 0.094 | 0.363 | 0.374 | ||
| Dury | N | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 32 | |
| A | 7 | 5 | 10 | 2 | 8 | 4 | 3 | 9 | 5 | 6.222 | |
| AR | 5.931 | 4.608 | 8.451 | 2 | 6.828 | 3.738 | 3 | 6.925 | 4.827 | 5.145 | |
| HE | 0.74 | 0.695 | 0.817 | 0.5 00 | 0.733 | 0.639 | 0.633 | 0.777 | 0.535 | 0.674 | |
| HO | 0.909 | 0.757 | 0.787 | 0.575 | 0.727 | 0.696 | 0.636 | 0.727 | 0.593 | 0.712 | |
| Fis | −0.214 | −0.075 | 0.052 | −0.136 | 0.024 | −0.074 | 0.01 | 0.08 | −0.094 | −0.041 | |
| HWE | 0.31 | 0.459 | 0.454 | 0.489 | 0.121 | 0.058 | 0.987 | 0.093 | 0.361 | ||
| EDar | N | 21 | 21 | 20 | 21 | 21 | 21 | 16 | 21 | 21 | |
| A | 6 | 6 | 11 | 2 | 8 | 4 | 3 | 8 | 6 | 6 | |
| AR | 5.699 | 5.522 | 9.963 | 2 | 7.233 | 3.946 | 3 | 7.471 | 5.472 | 5.59 | |
| HE | 0.732 | 0.68 | 0.837 | 0.495 | 0.783 | 0.620 | 0.646 | 0.781 | 0.594 | 0.685 | |
| HO | 0.619 | 0.666 | 0.85 | 0.619 | 0.619 | 0.571 | 0.437 | 0.857 | 0.666 | 0.656 | |
| Fis | 0.179 | 0.044 | 0.011 | −0.226 | 0.233 | 0.103 | 0.352 | −0.073 | −0.098 | −0.098 | |
| HWE | 0.144 | 0.822 | 0.549 | 0.384 | 0.002 | 0.279 | 0.065 | 0.945 | 0.904 | ||
| EWebB | N | 25 | 26 | 27 | 28 | 28 | 28 | 27 | 28 | 28 | |
| A | 7 | 5 | 13 | 2 | 8 | 4 | 4 | 5 | 6 | 6 | |
| AR | 6.142 | 4.942 | 10.906 | 2 | 6.994 | 3.809 | 3.592 | 4.792 | 5.103 | 5.364 | |
| HE | 0.712 | 0.686 | 0.872 | 0.492 | 0.686 | 0.447 | 0.59 | 0.689 | 0.582 | 0.639 | |
| HO | 0.72 | 0.692 | 0.851 | 0.571 | 0.821 | 0.5 | 0.629 | 0.821 | 0.607 | 0.69 | |
| Fis | 0.03 | 0.031 | 0.061 | −0.125 | −0.161 | −0.082 | −0.028 | −0.156 | −0.005 | −0.041 | |
| HWE | 0.969 | 0.516 | 0.265 | 0.705 | 0.845 | 0.332 | 0.965 | 0.763 | 0.632 | ||
| EWebD | N | 53 | 56 | 57 | 57 | 57 | 52 | 56 | 57 | 52 | |
| A | 8 | 5 | 16 | 2 | 9 | 4 | 5 | 10 | 5 | 7.111 | |
| AR | 6.618 | 4.805 | 11.322 | 2 | 6.829 | 3.957 | 3.569 | 8.182 | 4.259 | 5.727 | |
| HE | 0.769 | 0.687 | 0.862 | 0.49 | 0.683 | 0.526 | 0.605 | 0.805 | 0.617 | 0.671 | |
| HO | 0.811 | 0.642 | 0.877 | 0.508 | 0.701 | 0.634 | 0.535 | 0.754 | 0.634 | 0.677 | |
| Fis | −0.036 | 0.083 | 0 | −0.02 | −0.008 | −0.187 | 0.132 | 0.081 | −0.007 | 0.009 | |
| HWE | 0.553 | 0.28 | 0.1 | 1 | 0.769 | 0.51 | 0.336 | 0.237 | 0.078 | ||
| EWebV | N | 48 | 48 | 49 | 48 | 49 | 48 | 48 | 49 | 47 | |
| A | 8 | 5 | 17 | 2 | 9 | 4 | 4 | 11 | 6 | 7.333 | |
| AR | 7.165 | 4.795 | 12.381 | 2 | 6.752 | 3.838 | 3.333 | 8.405 | 5.521 | 6.021 | |
| HE | 0.809 | 0.722 | 0.875 | 0.477 | 0.691 | 0.457 | 0.603 | 0.8 | 0.612 | 0.672 | |
| HO | 0.75 | 0.75 | 0.918 | 0.479 | 0.653 | 0.458 | 0.667 | 0.877 | 0.489 | 0.671 | |
| Fis | 0.095 | −0.017 | −0.028 | 0.017 | 0.076 | 0.02 | −0.084 | −0.075 | 0.222 | 0.023 | |
| HWE | 0.079 | 0.476 | 0.858 | 1 | 0.485 | 0.677 | 0.209 | 0.651 | 0.045 | ||
| EWebW | N | 77 | 77 | 77 | 77 | 77 | 77 | 77 | 77 | 77 | |
| A | 7 | 5 | 17 | 2 | 9 | 5 | 4 | 11 | 6 | 7.333 | |
| AR | 6.245 | 4.34 | 11.712 | 2 | 6.496 | 3.608 | 3.738 | 8.059 | 4.227 | 5.603 | |
| HE | 0.749 | 0.688 | 0.882 | 0.494 | 0.668 | 0.455 | 0.628 | 0.77 | 0.414 | 0.639 | |
| HO | 0.853 | 0.727 | 0.868 | 0.467 | 0.71 | 0.447 | 0.608 | 0.84 | 0.446 | 0.663 | |
| Fis | −0.125 | −0.044 | 0.029 | 0.067 | −0.05 | 0.031 | 0.046 | −0.076 | −0.06 | −0.024 | |
| HWE | 0.337 | 0.649 | 0.115 | 0.648 | 0.097 | 0.27 | 0.001 | 0.13 | 0.142 | ||
| Gata | N | 34 | 34 | 34 | 34 | 34 | 32 | 32 | 34 | 34 | |
| A | 6 | 4 | 7 | 2 | 7 | 3 | 3 | 5 | 4 | 4.556 | |
| AR | 5.925 | 3.991 | 6.185 | 2 | 6.579 | 2.5 | 3 | 3.94 | 2.941 | 4.118 | |
| HE | 0.803 | 0.711 | 0.805 | 0.389 | 0.82 | 0.494 | 0.642 | 0.638 | 0.517 | 0.647 | |
| HO | 0.823 | 0.764 | 0.823 | 0.411 | 0.764 | 0.468 | 0.656 | 0.647 | 0.47 | 0.647 | |
| Fis | −0.01 | −0.059 | −0.008 | −0.043 | 0.083 | 0.068 | −0.006 | 0.001 | 0.106 | 0.014 | |
| HWE | 0.036 | 0.76 | 0.182 | 1 | 0.994 | 0.572 | 0.485 | 0.372 | 0.866 | ||
| Har | N | 35 | 39 | 39 | 40 | 41 | 39 | 26 | 38 | 37 | |
| A | 9 | 6 | 19 | 2 | 11 | 4 | 4 | 10 | 7 | 8 | |
| AR | 7.81 | 5.649 | 13.924 | 2 | 7.815 | 3.635 | 3.615 | 8.712 | 6.364 | 6.614 | |
| HE | 0.843 | 0.798 | 0.912 | 0.488 | 0.775 | 0.487 | 0.633 | 0.845 | 0.812 | 0.733 | |
| HO | 0.8 | 0.794 | 0.82 | 0.45 | 0.658 | 0.41 | 0.615 | 0.868 | 0.891 | 0.701 | |
| Fis | 0.066 | 0.018 | 0.114 | 0.092 | 0.162 | 0.171 | 0.049 | −0.014 | −0.084 | 0.057 | |
| HWE | 0.353 | 0.552 | 0.145 | 0.752 | 0.351 | 0.294 | 0.783 | 0.394 | 0.888 | ||
| Hem | N | 40 | 39 | 31 | 40 | 40 | 40 | 40 | 40 | 40 | |
| A | 9 | 5 | 18 | 2 | 11 | 4 | 4 | 9 | 7 | 7.667 | |
| AR | 7.466 | 4.655 | 14.027 | 2 | 9.235 | 3.858 | 3.877 | 8.033 | 5.785 | 6.548 | |
| HE | 0.824 | 0.751 | 0.907 | 0.474 | 0.858 | 0.556 | 0.674 | 0.825 | 0.609 | 0.72 | |
| HO | 0.75 | 0.794 | 0.935 | 0.375 | 0.875 | 0.575 | 0.65 | 0.85 | 0.6 | 0.711 | |
| Fis | 0.103 | −0.045 | −0.014 | 0.222 | −0.006 | −0.02 | 0.048 | −0.018 | 0.028 | 0.025 | |
| HWE | 0.281 | 0.831 | 0.616 | 0.185 | 0.735 | 0.808 | 0.371 | 0.845 | 0.323 | ||
| Hol | N | 26 | 29 | 29 | 29 | 29 | 17 | 24 | 25 | 28 | |
| A | 10 | 6 | 13 | 3 | 9 | 4 | 3 | 9 | 6 | 7 | |
| AR | 9.109 | 5.535 | 10.373 | 2.552 | 7.718 | 3.998 | 3 | 8.017 | 5.806 | 6.234 | |
| HE | 0.826 | 0.775 | 0.848 | 0.463 | 0.717 | 0.624 | 0.6 | 0.752 | 0.718 | 0.703 | |
| HO | 0.807 | 0.724 | 0.862 | 0.482 | 0.758 | 0.47 | 0.541 | 0.8 | 0.714 | 0.684 | |
| Fis | 0.043 | 0.083 | 0.002 | −0.025 | −0.04 | 0.275 | 0.119 | −0.042 | 0.024 | 0.046 | |
| HWE | 0.353 | 0.309 | 0.191 | 1 | 0.898 | 0.08 | 0.308 | 0.588 | 0.735 | ||
| LChe | N | 58 | 59 | 57 | 55 | 58 | 58 | 52 | 59 | 57 | |
| A | 8 | 5 | 16 | 2 | 9 | 5 | 4 | 10 | 5 | 7.111 | |
| AR | 6.95 | 4.555 | 10.839 | 2 | 6.37 | 4.155 | 3.846 | 8.651 | 4.677 | 5.783 | |
| HE | 0.789 | 0.625 | 0.872 | 0.495 | 0.745 | 0.622 | 0.629 | 0.851 | 0.571 | 0.689 | |
| HO | 0.741 | 0.627 | 0.807 | 0.472 | 0.793 | 0.724 | 0.73 | 0.949 | 0.578 | 0.713 | |
| Fis | 0.078 | 0.014 | 0.093 | 0.063 | −0.047 | −0.147 | −0.141 | −0.098 | 0.004 | −0.018 | |
| HWE | 0.403 | 0.686 | 0.171 | 0.787 | 0.488 | 0.107 | 0.719 | 0.364 | 0.372 | ||
| RudB | N | 90 | 92 | 94 | 96 | 93 | 92 | 90 | 94 | 92 | |
| A | 5 | 5 | 8 | 2 | 3 | 3 | 4 | 6 | 4 | 4.444 | |
| AR | 4.508 | 4.679 | 7.681 | 2 | 2.994 | 2.744 | 3.069 | 5.137 | 3.615 | 4.047 | |
| HE | 0.677 | 0.704 | 0.828 | 0.496 | 0.554 | 0.426 | 0.524 | 0.687 | 0.555 | 0.606 | |
| HO | 0.722 | 0.75 | 0.787 | 0.479 | 0.58 | 0.326 | 0.422 | 0.659 | 0.543 | 0.585 | |
| Fis | −0.055 | −0.053 | 0.061 | 0.045 | −0.037 | 0.245 | 0.206 | 0.052 | 0.033 | 0.045 | |
| HWE | 0.334 | 0.58 | 0.434 | 0.686 | 0.453 | 0.014 | 0.021 | 0.022 | 0.927 | ||
| RudC | N | 35 | 36 | 36 | 36 | 36 | 36 | 35 | 34 | 36 | |
| A | 6 | 6 | 9 | 2 | 4 | 3 | 4 | 6 | 4 | 4.889 | |
| AR | 5.332 | 5.262 | 7.957 | 2 | 3.693 | 2.953 | 3.825 | 5.839 | 3.953 | 4.535 | |
| HE | 0.625 | 0.576 | 0.832 | 0.475 | 0.569 | 0.519 | 0.591 | 0.781 | 0.664 | 0.626 | |
| HO | 0.628 | 0.556 | 0.972 | 0.583 | 0.583 | 0.472 | 0.685 | 0.852 | 0.778 | 0.679 | |
| Fis | 0.025 | 0.065 | −0.14 | −0.199 | 0.003 | 0.119 | −0.131 | −0.061 | −0.144 | −0.056 | |
| HWE | 0.093 | 0.172 | 0.754 | 0.305 | 0.11 | 0.685 | 0.122 | 0.578 | 0.312 | ||
| RudP | N | 96 | 94 | 94 | 98 | 95 | 92 | 96 | 96 | 95 | |
| A | 5 | 5 | 10 | 2 | 3 | 3 | 4 | 8 | 4 | 4.889 | |
| AR | 4.904 | 4.67 | 7.256 | 2 | 2.817 | 2.538 | 3.852 | 5.251 | 3.27 | 4.062 | |
| HE | 0.706 | 0.644 | 0.802 | 0.462 | 0.467 | 0.428 | 0.595 | 0.64 | 0.246 | 0.554 | |
| HO | 0.708 | 0.595 | 0.787 | 0.489 | 0.505 | 0.445 | 0.5 | 0.645 | 0.242 | 0.546 | |
| Fis | 0.008 | 0.086 | 0.03 | −0.049 | −0.069 | −0.028 | 0.17 | 0.003 | 0.027 | 0.026 | |
| HWE | 0.745 | 0.007 | 0.106 | 0.669 | 0.136 | 0.768 | 0.109 | 0.174 | 0.097 | ||
| Swin | N | 76 | 80 | 80 | 80 | 80 | 74 | 80 | 80 | 74 | |
| A | 9 | 5 | 17 | 2 | 11 | 4 | 5 | 10 | 8 | 7.889 | |
| AR | 6.327 | 4.667 | 11.744 | 2 | 7.182 | 3.858 | 3.688 | 9.061 | 6.225 | 6.084 | |
| HE | 0.753 | 0.707 | 0.886 | 0.471 | 0.786 | 0.558 | 0.636 | 0.849 | 0.707 | 0.706 | |
| HO | 0.802 | 0.737 | 0.912 | 0.425 | 0.837 | 0.621 | 0.7 | 0.85 | 0.783 | 0.741 | |
| Fis | −0.052 | −0.03 | −0.017 | 0.111 | −0.052 | −0.099 | −0.088 | 0.012 | −0.094 | −0.036 | |
| HWE | 0.292 | 0.335 | 0.428 | 0.352 | 0.133 | 0.594 | 0.217 | 0.186 | 0.445 | ||
| UChe | N | 68 | 70 | 69 | 68 | 67 | 66 | 68 | 64 | 67 | |
| A | 7 | 5 | 15 | 2 | 9 | 5 | 4 | 10 | 7 | 7.111 | |
| AR | 6.01 | 4.86 | 11.507 | 2 | 7.525 | 3.921 | 3.417 | 8.267 | 5.35 | 5.837 | |
| HE | 0.773 | 0.684 | 0.891 | 0.492 | 0.796 | 0.588 | 0.659 | 0.814 | 0.599 | 0.699 | |
| HO | 0.735 | 0.657 | 0.898 | 0.441 | 0.716 | 0.651 | 0.691 | 0.796 | 0.641 | 0.692 | |
| Fis | 0.064 | 0.054 | 0.007 | 0.118 | 0.116 | −0.093 | −0.033 | 0.038 | −0.056 | 0.026 | |
| HWE | 0.765 | 0.086 | 0.244 | 0.462 | 0.17 | 0.592 | 0.735 | 0.535 | 0.865 | ||
| WDar | N | 114 | 112 | 116 | 119 | 118 | 103 | 112 | 118 | 117 | |
| A | 8 | 6 | 15 | 2 | 9 | 5 | 5 | 11 | 7 | 7.556 | |
| AR | 5.884 | 4.62 | 11.142 | 2 | 6.042 | 3.426 | 3.286 | 8.167 | 4.754 | 5.48 | |
| HE | 0.746 | 0.695 | 0.89 | 0.495 | 0.755 | 0.544 | 0.654 | 0.829 | 0.579 | 0.688 | |
| HO | 0.78 | 0.687 | 0.922 | 0.512 | 0.779 | 0.514 | 0.687 | 0.813 | 0.572 | 0.696 | |
| Fis | −0.036 | 0.02 | −0.027 | −0.026 | −0.023 | 0.065 | −0.041 | 0.027 | 0.021 | −0.004 | |
| HWE | 0.736 | 0.271 | 0.939 | 0.854 | 0.427 | 0.703 | 0.991 | 0.279 | 0.099 | ||
| Web | N | 32 | 32 | 32 | 31 | 32 | 21 | 29 | 28 | 31 | |
| A | 10 | 2 | 12 | 2 | 9 | 4 | 4 | 8 | 6 | 6.333 | |
| AR | 8.276 | 4.994 | 9.874 | 2 | 7.129 | 3.751 | 3.551 | 7.341 | 5.009 | 5.769 | |
| HE | 0.788 | 0.758 | 0.871 | 0.481 | 0.68 | 0.447 | 0.618 | 0.785 | 0.53 | 0.662 | |
| HO | 0.75 | 0.781 | 0.875 | 0.483 | 0.656 | 0.285 | 0.758 | 0.785 | 0.516 | 0.654 | |
| Fis | 0.064 | −0.014 | 0.011 | 0.011 | 0.052 | 0.383 | −0.21 | 0.017 | 0.044 | 0.029 | |
| HWE | 0.706 | 0.493 | 0.474 | 1 | 0.029 | 0.045 | 0.417 | 0.11 | 0.492 | ||
| WWeb | N | 122 | 122 | 114 | 125 | 125 | 115 | 120 | 125 | 112 | |
| A | 11 | 5 | 18 | 2 | 9 | 4 | 4 | 10 | 7 | 7.778 | |
| AR | 7.546 | 4.732 | 11.109 | 2 | 6.298 | 3.875 | 3.58 | 8.011 | 4.844 | 5.777 | |
| HE | 0.775 | 0.728 | 0.88 | 0.497 | 0.681 | 0.544 | 0.632 | 0.838 | 0.595 | 0.686 | |
| HO | 0.778 | 0.721 | 0.877 | 0.44 | 0.728 | 0.547 | 0.633 | 0.864 | 0.642 | 0.692 | |
| Fis | 0.005 | 0.019 | 0.013 | 0.124 | −0.06 | 0.002 | 0.007 | −0.022 | −0.07 | −0.001 | |
| HWE | 0.276 | 0.07 | 0.742 | 0.221 | 0.646 | 0.709 | 0.191 | 0.489 | 0.668 | ||
| WWebL | N | 29 | 24 | 33 | 33 | 33 | 31 | 31 | 31 | 26 | |
| A | 8 | 5 | 15 | 2 | 8 | 4 | 3 | 11 | 5 | 6.778 | |
| AR | 6.675 | 4.968 | 11.846 | 2 | 6.531 | 3.76 | 3 | 9.709 | 4.546 | 5.893 | |
| HE | 0.763 | 0.749 | 0.891 | 0.477 | 0.64 | 0.493 | 0.608 | 0.868 | 0.507 | 0.666 | |
| HO | 0.827 | 0.75 | 0.939 | 0.545 | 0.515 | 0.387 | 0.741 | 0.87 | 0.461 | 0.671 | |
| Fis | −0.067 | 0.02 | −0.039 | −0.127 | 0.21 | 0.231 | −0.204 | 0.014 | 0.11 | 0.01 | |
| HWE | 0.176 | 0.024 | 0.337 | 0.711 | 0.14 | 0.155 | 0.406 | 0.161 | 0.176 | ||
| Mean | N | 1178 | 1188 | 1187 | 1216 | 1213 | 1137 | 1150 | 1196 | 1158 | |
| A | 13 | 7 | 27 | 3 | 13 | 6 | 5 | 13 | 10 | ||
| AR | 6.666 | 4.798 | 10.424 | 2.025 | 6.54 | 3.559 | 3.513 | 7.39 | 4.822 | ||
| HE | 0.795 | 0.734 | 0.902 | 0.499 | 0.741 | 0.533 | 0.676 | 0.836 | 0.6 | ||
| HO | 0.775 | 0.705 | 0.863 | 0.473 | 0.707 | 0.504 | 0.628 | 0.802 | 0.585 |
n, number of individuals; A, number of alleles; AR, allelic richness; HO, observed heterozygosity; HE, expected heterozygosity; Fis, inbreeding coefficient (values in bold differ significantly from zero at the 5% level, although none remained significant after table-wide Bonferroni correction); HWE, P-value of the Hardy–Weinberg equilibrium test.
Tests for the homogeneity of allele frequency distributions revealed significant genetic differentiation occurred between the majority of the 231 pairwise comparisons, except in nine cases (upper diagonal, Table 3), of which approximately half involved samples collected from within the same tributary. Quantification of genetic differentiation with FST values (lower diagonal, Table 3), demonstrated a range of 0.00–0.16, with a global FST of 0.04. The highest FST occurred between samples above significant barriers to fish movement, whereas the lowest, and nonsignificant FST values, tended to occur between (but not exclusively between) proximate samples from the same or neighbouring tributaries.
Table 3.
Tests for genetic differentiation between pairs of samples
| Amm | Ash | Dury | EDar | EWebB | EWebD | EWebV | EWebW | Gata | Har | Hem | Hol | LChe | RudB | RudC | RudP | Swin | UChe | WDar | Web | WWeb | WWebL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Amm | – | * | * | * | * | * | * | * | * | * | NS | * | * | * | * | * | * | * | * | * | * | * |
| Ash | 0.050 | – | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| Dury | 0.021 | 0.091 | – | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| EDar | 0.016 | 0.068 | 0.021 | – | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| EWebB | 0.023 | 0.085 | 0.017 | 0.023 | – | * | NS | NS | * | * | * | * | * | * | * | * | * | * | * | NS | * | * |
| EWebD | 0.025 | 0.068 | 0.021 | 0.016 | 0.005 | – | NS | * | * | * | * | * | * | * | * | * | * | * | * | NS | * | * |
| EWebV | 0.021 | 0.054 | 0.020 | 0.013 | 0.007 | 0.007 | – | * | * | * | * | * | * | * | * | * | * | * | * | NS | * | * |
| EWebW | 0.023 | 0.077 | 0.012 | 0.021 | 0.000 | 0.004 | 0.004 | – | * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| Gata | 0.050 | 0.067 | 0.086 | 0.073 | 0.087 | 0.079 | 0.058 | 0.076 | – | * | * | * | * | * | * | * | * | * | * | * | * | * |
| Har | 0.013 | 0.068 | 0.042 | 0.040 | 0.040 | 0.032 | 0.028 | 0.045 | 0.079 | – | * | * | * | * | * | * | * | * | * | * | * | * |
| Hem | 0.000 | 0.041 | 0.021 | 0.020 | 0.020 | 0.018 | 0.018 | 0.017 | 0.031 | 0.011 | – | * | * | * | * | * | * | * | * | * | * | * |
| Hol | 0.014 | 0.050 | 0.028 | 0.016 | 0.029 | 0.019 | 0.005 | 0.020 | 0.053 | 0.018 | 0.007 | – | * | * | * | * | * | * | * | * | * | * |
| LChe | 0.019 | 0.077 | 0.013 | 0.007 | 0.024 | 0.019 | 0.020 | 0.019 | 0.077 | 0.043 | 0.023 | 0.026 | – | * | * | * | * | * | * | * | * | * |
| RudB | 0.076 | 0.119 | 0.056 | 0.072 | 0.039 | 0.045 | 0.046 | 0.044 | 0.140 | 0.073 | 0.071 | 0.067 | 0.054 | – | * | * | * | * | * | * | * | * |
| RudC | 0.068 | 0.122 | 0.056 | 0.061 | 0.026 | 0.027 | 0.045 | 0.031 | 0.129 | 0.067 | 0.066 | 0.065 | 0.048 | 0.021 | – | * | * | * | * | * | * | * |
| RudP | 0.092 | 0.153 | 0.053 | 0.095 | 0.059 | 0.078 | 0.064 | 0.053 | 0.160 | 0.112 | 0.090 | 0.090 | 0.071 | 0.033 | 0.061 | – | * | * | * | * | * | * |
| Swin | 0.016 | 0.079 | 0.015 | 0.013 | 0.024 | 0.021 | 0.026 | 0.029 | 0.083 | 0.027 | 0.018 | 0.029 | 0.011 | 0.060 | 0.050 | 0.090 | – | * | * | * | * | * |
| UChe | 0.016 | 0.081 | 0.012 | 0.008 | 0.020 | 0.017 | 0.021 | 0.019 | 0.072 | 0.036 | 0.013 | 0.027 | 0.000 | 0.050 | 0.044 | 0.071 | 0.006 | – | * | * | * | * |
| WDar | 0.021 | 0.065 | 0.024 | 0.013 | 0.034 | 0.031 | 0.023 | 0.034 | 0.075 | 0.041 | 0.018 | 0.026 | 0.009 | 0.063 | 0.076 | 0.088 | 0.014 | 0.011 | – | * | * | * |
| Web | 0.029 | 0.091 | 0.013 | 0.023 | 0.000 | 0.000 | 0.008 | 0.002 | 0.086 | 0.036 | 0.017 | 0.022 | 0.020 | 0.025 | 0.018 | 0.050 | 0.021 | 0.014 | 0.030 | – | * | NS |
| WWeb | 0.021 | 0.077 | 0.013 | 0.033 | 0.011 | 0.012 | 0.012 | 0.011 | 0.081 | 0.023 | 0.019 | 0.024 | 0.029 | 0.040 | 0.039 | 0.060 | 0.025 | 0.025 | 0.034 | 0.005 | – | NS |
| WWebL | 0.021 | 0.099 | 0.013 | 0.026 | 0.015 | 0.009 | 0.010 | 0.013 | 0.086 | 0.027 | 0.016 | 0.025 | 0.024 | 0.037 | 0.034 | 0.063 | 0.013 | 0.016 | 0.025 | 0.000 | 0.000 | – |
The upper diagonal shows pairwise FST values; all significant values (P < 0.05) are highlighted in bold. The lower diagonal shows the result of tests for homogeneity of allele frequencies: NS, not significant; *significant at the 5% level. Table-wide significance levels were applied using the sequential Bonferroni procedure (k = 231) for all tests.
The NJ DCE phylogram (Fig. 2) reveals several samples that have high bootstrap support and relatively long branch lengths, namely the Rud group of samples and the Gata and Ash; this relates well to their positions above significant barriers to fish movement (Fig. 1) that may have acted to isolate these samples from the rest of the catchment. Moderate support is also noted on the phylogram among groups of samples from the upper west (Che, WDar, Swin, Dury and EDar), upper east (Web, EWeb and WWeb) and lower (Amm, Har, Hol and Hem) areas of the catchment. In addition, there is some support for proximate groups of samples, especially those collected within the same tributary, e.g. within the West and the East Webburn. A principal component analysis (PCA) was also performed on these data using the default settings in genalex 6 (Peakall and Smouse 2006), the findings of which support the main conclusions of the phylogram; the PCA plot in Fig. S1.
Figure 2.
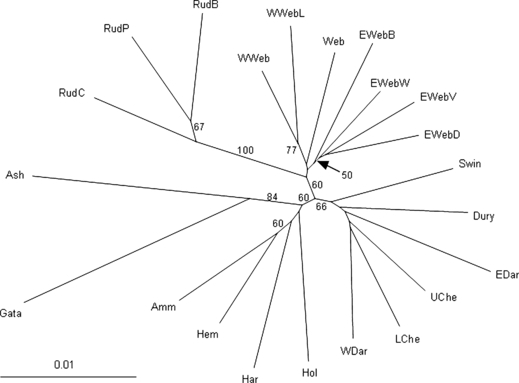
Neighbour-joining phylogram based on pairwise DCE distances between samples. Numbers next to branch nodes represent bootstrap support (%) based on 1000 replicates, only values over 50% are shown. Sample abbreviations match Table 1.
Decomposed pairwise regression
Genetic distance was positively correlated with geographic distance when comparing all pairwise sample combinations, but the correlation was weak and nonsignificant (P = 0.137, r2 = 0.036; Fig. 3). Based on the systematic bias of the regression residuals (process one) nine putative outlier samples were detected; RudP, Ash, Gata, RudB, RudC, Hem, Amm, WDar and UChe. The AIC values were compared for models with and without putative outliers (process two) and the best model included 17 samples (indicating RudP, Ash, Gata, RudB and RudC were true outliers; Table 4). This result is consistent with a priori predictions as all these samples originated from sites above significant barriers to fish movement. The exclusion of these samples strengthened the positive correlation between genetic and geographic distance, which also become statistically significant (P < 0.001, r2 = 0.476; Fig. 3). Each of the outlier samples was individually regressed with the nonoutlier samples, which indicated that the majority of outlier samples were significantly diverged from adjacent populations but exhibited strong and significant correlations between genetic and geographic distance (Fig. 4). This suggests that despite of a strong effect of genetic drift acting on the isolated samples (either through small effective population size or founder effects or bottleneck) evidence of gene-flow still remains. The Ash sample was the exception; while significantly divergent from the other samples, it showed no correlation between genetic and geographic distance, suggesting that the effect of genetic drift far outweighs that of gene flow. The decomposed regressions of the 17 nonoutlier samples showed similar regression lines with significant relationships between genetic and geographic distance, except for the Amm, Hol and Swin (Fig. 4). This suggests that these samples are close to, or at, equilibrium between drift and gene flow.
Figure 3.
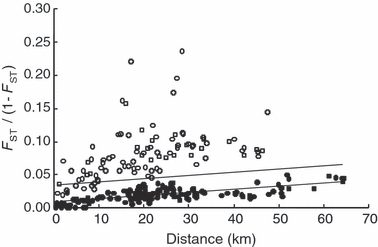
Relationship between genetic distance [FST/(1 − FST)] and geographic distance (km) for all 22 samples (open and closed diamonds combined; rxy = 0.191, P = 0.137, r2 = 0.036, upper line) and excluding the five outlier samples (filled diamonds only; rxy = 0.690, P < 0.001, r2 = 0.476, lower line).
Table 4.
Fit of alternative models with and without the putative outlier samples
| Samples excluded | n | k | r2 | P value | AICC | ΔAICC |
|---|---|---|---|---|---|---|
| RudP, Ash, Gata, RudB, RudC | 17 | 1 | 0.4768 | <0.001 | −108.49 | 0.00 |
| RudP, Ash, Gata, RudB, RudC, Hem | 16 | 1 | 0.5281 | <0.001 | −103.26 | 5.23 |
| RudP, Ash, Gata, RudB, RudC, Hem, Amm | 15 | 1 | 0.6292 | <0.001 | −99.37 | 9.12 |
| RudP, Ash, Gata, RudB, RudC, Hem, Amm, WDar | 14 | 1 | 0.6504 | <0.001 | −94.50 | 13.98 |
| RudP, Ash, Gata, RudB | 18 | 1 | 0.1353 | 0.064 | −90.73 | 17.76 |
| RudP, Ash, Gata, RudB, RudC, Hem, Amm, WDar, UChe | 13 | 1 | 0.6459 | <0.001 | −87.68 | 20.81 |
| RudP, Ash, Gata | 19 | 1 | 0.0612 | 0.1099 | −86.11 | 22.38 |
| RudP, Ash | 20 | 1 | 0.0880 | 0.066 | −75.52 | 32.97 |
| RudP | 21 | 1 | 0.0589 | 0.076 | −72.33 | 36.16 |
| None | 22 | 1 | 0.0335 | 0.142 | −68.86 | 39.63 |
n refers to the number of samples and k the number of parameters.
Figure 4.
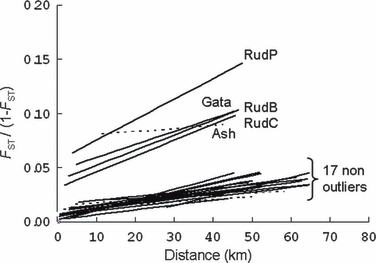
Decomposed pairwise regression of genetic distance [FST/(1 − FST)] and geographic (km) distances for the 22 samples. Each of the five outlier samples was regressed with the 17 nonoutlier samples, whilst each of the 15 nonoutliers was regressed with the other 14 samples. Solid and dashed lines represent statistically significant or nonsignificant regressions respectively.
Spatial autocorrelation
Tests of microspatial autocorrelation at the level of the individual were carried out on samples not isolated above barriers to fish movement (this included all 17 samples not identified in the DPR as true outliers). The results showed that the genetic autocorrelation coefficient (r) was significantly positive at the 0–5 and 5–15 km size classes, and intercepted the x-axis at 20 km (Fig. 5A); results from the analysis of alternative classes produced broadly similar results, with intercepts ranging from 15 to 20 km (results not shown). In all size classes above 15 km, r was significantly negative, meaning that proximal individuals showed greater genetic divergence than that expected for a random distribution of genotypes, although in the largest size classes r approached the null hypothesis of no significant structure. The MDC analysis with increasing distance size classes revealed that r was significantly positive for distance classes up to and including 25 km (Fig. 5B). The inclusion of specimens separated by >45 km meant that significant positive genetic autocorrelation was no longer observed. The addition of samples collected above barriers did not radically alter the results of the spatial autocorrelation (analysis not shown), except in the correlogram (Fig. 5A), in which case r was not as strongly negative (r = −0.015 in the 25 km class) and at the largest distance class the null hypothesis could not be rejected. However, because of the uncertainties of applying an individual-based test to samples collected at specific sample sites (where separation between individuals is assumed to be zero), these findings should be interpreted with some caution.
Figure 5.
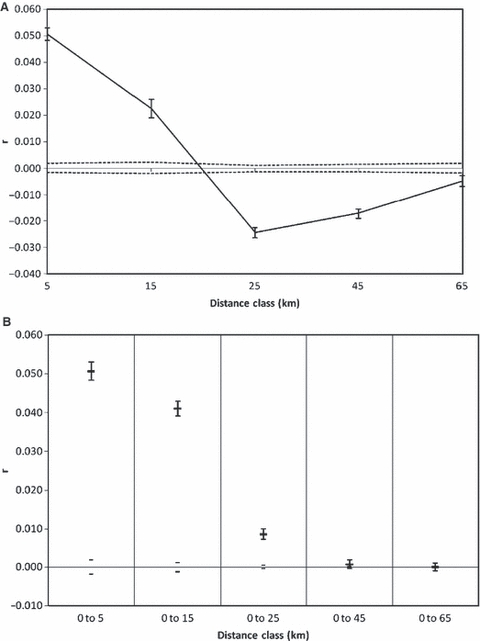
Spatial autocorrelation analyses with samples isolated above barriers removed. (A) correlogram of the genetic correlation (r) as a function of distance. (B) The genetic correlation (r) as a function of increasing distance classes. Dotted lines (A) and grey bars (B) indicate the 95% confidence interval (CI) about the null hypothesis and error bars about r indicate the 95% CI.
Discussion
The purpose of this study was to examine, within-catchment population structure of brown trout in a region that despite being a focus for salmonid fishing and conservation, has until now, received relatively little attention. The results revealed significant differentiation among samples collected within a single river catchment and, in the case of the Ruddycleave and Cherry Brook, even between sample sites within a tributary. These results demonstrate that Dart trout do not represent a single panmictic population in which gene flow is unrestricted across the catchment. The global FST across all 22 samples sites was 0.04, with a range of 0.000–0.160 for pairwise FST estimates, which accords with previous work on brown trout employing microsatellites (e.g. Carlsson et al. 1999, FST = 0.00–0.114; Jensen et al. 2005, 0.009–0.065; Hansen et al. 2002, 0.010–0.071; Ostergaard et al. 2003, 0.004–0.154).
Effect of barriers
What is particularly striking from the phylogram (Fig. 2) and pairwise FST estimates (Table 3) is the effect barriers have on population structure; the largest values all occur between comparisons involving samples isolated above a barrier to fish movement. The significant effect of barriers on population structure has been previously documented and has been associated with reductions in population size, bottlenecks and genetic drift (Hindar et al. 1991; Montgomery et al. 2000; Palm et al. 2003; Van Houdt et al. 2005). Such processes may also have been in operation in these isolated samples identified within the River Dart, as the levels of heterozygosity and allelic richness were also depressed (Couvet 2002). The results of the DPR analysis also afford some further insight into the demographic processes occurring within these samples. In the case of the Ash sample, genetic drift has acted to obscure any correlation between genetic and geographic distance between samples; as the barrier to migration on this tributary is man-made (and therefore not ancient), small effective population size and founder effects appear to be the most likely explanation for the patterns of genetic divergence observed. In the case of the other highly diverged and isolated samples (RudC, RudB, RudP and Gata) a relatively strong correlation between genetic and geographic distance remains, suggesting that effective population sizes have not been reduced to the level that genetic drift is strong enough to obscure the correlation. Alternatively, some form of gene flow could be occurring, perhaps associated with barriers being by-passed in high flows. However, it is interesting to postulate that unidirectional, downstream migration from the isolated areas could act to partially restore the correlation between genetic and geographic distance.
The importance of identifying barriers to fish movement has been highlighted for a number of conservation issues, in particular, the negative effects of genetic drift in small populations and the isolation of indigenous stocks from the effects of stocking undertaken below barriers (Yamamoto et al. 2004; Van Houdt et al. 2005), both topics that appear to warrant further investigation within the River Dart.
Population structure and evolutionary models
The phylogram (Fig. 2) shows that genetic structuring among samples within the catchment is present; moderate levels of bootstrap support occurred between three groups of proximate samples from the upper east, upper west and lower Dart. This association between genetic and geographic distance is further supported by a significant effect of isolation-by-distance, as demonstrated by DPR analysis (Fig. 4). However, a strongly negative genetic correlation (r) was identified at the 25 and 45 km size classes used in the spatial autocorrelation on Dart trout (Fig. 5A), meaning that proximal individuals showed greater genetic divergence than that expected for a random distribution of genotypes. Such a finding may be the result of a discontinuity in gene flow between trout in different tributaries or could reflect the fact that some sampling was completed outside of the spawning season, and therefore, may include adult specimens of trout that may have moved away from nursery areas.
The observation of isolation-by-distance at the intra-catchment level is somewhat at odds with many of previous studies describing the population structure of brown trout (Crozier and Ferguson 1986; Ferguson 1989; Moran et al. 1995; Bouza et al. 1999; Ruzzante et al. 2001), although, it is not unique (Estoup et al. 1998; Carlsson and Nilsson 2000). Recent studies of anadromous brown trout inhabiting relatively small rivers in Denmark and the Baltic Sea (Laikre et al. 2002; Ostergaard et al. 2003; Jensen et al. 2005) suggested a population structure consisting of a system of highly interconnected, small and unstable populations where, in accordance with the metapopulation model, there was no significant effect of isolation-by-distance and a lack of temporal stability (even over the short-term). This pattern was generally linked to high levels of gene flow and occasional extinction–recolonization events caused by environmental instability, e.g. low summer water levels (Ostergaard et al. 2003). These results sharply contrast with the population structure described in this study, where a significant effect of isolation-by-distance (once outliers have been excluded) and at least short-term temporal stability of population structure was observed. Therefore, it appears that, despite the potential for low pH to perturb the environment, the population structure of brown trout inhabiting the tributaries of the River Dart is determined more by ecological events and natal homing, than by rare stochastic extinction events, with migration occurring mostly between neighbouring groups. The key to reconciling these contrasting results among studies appears to be catchment size, whereby larger population systems appear to be stable and smaller systems tend to undergo localized extinction–recolonization events (Hansen et al. 2002; Ostergaard et al. 2003; Jensen et al. 2005; Neville et al. 2006; Primmer et al. 2006).
Historical and temporal effects
There are some limitations to this study; in particular, the effects of postglacial recolonization and stocking on population structure of Dart trout still await assessment. Although, the results of the DPR analysis suggests the majority of the samples are at, or close to, drift–migration equilibrium following such perturbation (Fig. 4). In particular, these processes (especially artificial stocking), would generally have acted to obscure the strong pattern of isolation-by-distance identified in this study (Koljonen et al. 1999; Nielsen et al. 1999), suggesting they are not the strongest determinants of population structure in this case. In addition, the temporal samples collected in the study represent only a subset of sites from across the catchment and cover a relatively short period: 2002–2004. Palm et al. (2003) found that the probability of detecting significant allele frequency differences between temporal samples taken from the same population, but spaced only a few years apart, could be small. Indeed, if extinction events happen infrequently, i.e. over the scale of decades, then this instability may not become evident in samples taken only a few years apart (although the strong pattern of isolation-by-distance identified suggests longer term temporal stability, at least as long as it takes for drift–migration equilibrium to be established after perturbation).
Evolutionary hypotheses
The hypotheses proposed by Garant et al. (2000) provide a useful framework within which to analyse population structure; however, they remain quite general and any situation in which gene flow is limited by geographic distance may yield similar results. Indeed, work on genetic population structure of Dolly Varden charr (Salvelinus malma; Koizumi et al. 2006) yielded analogous results to the present study, but the authors suggested that a source-sink metapopulation structure best fitted their results. In that case, outlier samples were identified in the absence of barriers to migration, suggesting founder effects or bottlenecks had occurred; such factors have not been identified within the current study of the River Dart (where the results of the DPR actually suggest relatively stable population structure). Additionally, many of the predictions of the proposed models are quite simplistic, e.g. the prediction that that there would be no significant pattern of isolation by distance in a metapopulation may not hold true if recolonization and gene flow occurred predominantly between neighbouring populations (a scenario made more likely by the linear nature of a river). Another prediction, that the level of genetic structuring would be expected to be lower under a metapopulation model, can also be questioned. It has been shown that the range of FST estimates in this study is similar to that used previously to describe both small temporally unstable populations (Jensen et al. 2005) and large stable populations (Hansen et al. 2002). It appears that levels of differentiation, especially FST values, may not differ under the two evolutionary models summarized by Garant et al. (2000) and are dependant on the complex mechanics of recolonization (Hedrick 1999; Neville et al. 2006). Indeed, extinction–recolonization events may act to increase levels of genetic differentiation (Hansen and Mensberg 1996; Haag et al. 2005).
Delineating demographic units
Spatial autocorrelation analyses were used to determine the geographic scale of genetic structuring within the River Dart. Figure 4B illustrates the tendency for genetic distance between individuals to decrease with increasing distance, such that at in-water distances of >45 km gene flow is minimal. It has also been proposed that the x-axis intercept of the correlogram (Fig. 5A) be considered as a minimum distance that can conserve genetic diversity at a lower cost (Diniz-Filho and De Campos Telles 2002), resulting in a management unit size of approximately 15–20 km for the River Dart.
The results from spatial autocorrelation analyses bear some similarities to work on Atlantic salmon in the Varzuga River in Russia (Primmer et al. 2006), which also highlighted the importance of conserving multiple spawning and nursery areas for the long-term preservation of fish populations. However, most striking difference is the distance across which gene flow was observed within the Varzuga; the genetic correlation remained positive at distances up to 120 km and the x-axis intercept of the correlogram occurred at 34 km. This may reflect the larger size of the Varzuga River (when compared with the River Dart), and the fact that samples were separated by greater average in-water distances (Vekemans and Hardy 2004). Alternatively, it is interesting to hypothesize that the lower distance over which gene flow occurs in brown trout may reflect their resident life history, resulting in more restricted gene flow and greater genetic differentiation (Hansen and Mensberg 1998; Knutsen et al. 2001; Neville et al. 2006).
Conclusions
Brown trout inhabiting the River Dart demonstrate significant within-river population differentiation; this differentiation is most significant when associated with barriers to movement, but otherwise demonstrates a pattern of isolation-by-distance and at least short-term temporal stability. These results are taken as evidence that ecological events are more important in shaping the population structure of Dart trout than stochastic extinction events, and certainly do not contradict the expectations of a member-vagrant evolutionary model of population structure for Dart trout (Garant et al. 2000). However, the results of the spatial autocorrelation demonstrate gene flow does occur between neighbouring samples, suggesting the need to conserve not only different spawning areas within the basin (particularly in different tributaries), but links between them as well.
Acknowledgments
This research was supported by funding from the Natural Environment Research Council (NERC), UK through the award of a CASE studentship (NER/S/A/2001/06178) with the Westcountry Rivers Trust (CASE partner) and the award of a NERC training grant to work at the Sheffield Molecular Genetics Facility (SMGF/047). The EA is acknowledged for assistance in sample collection, in particular Fisheries Officers Dave Hoskin and Adam Bailey, without whom the project would not have been possible. Further acknowledgement is also due to all those who helped with fieldwork, especially Jan Shears and Phil Shears, and to Anna Finnegan for provision of stocking data and GIS support. This study also benefited from technical training by members of the Sheffield Molecular Genetics Facility: Terry Burke, Deborah Dawson and Andy Krupa.
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Figure S1. Principal componentanalysis plotted from a matrix of pairwise Nei's geneticdistances between all populations and computed using the programgenalex (Peakall andSmouse 2006). Axis 1 explains 36% of the variation and axis 2, 22%of the variation. Populations analysed are the same as thoseanalysed in the phylogram (Fig. 2); sample abbreviationsmatch Table 1.
Please note: Wiley-Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
Literature cited
- Allendorf FW, Phelps SR. Use of allelic frequencies to describe population-structure. Canadian Journal of Fisheries and Aquatic Sciences. 1981;38:1507–1514. [Google Scholar]
- Beacham TD, Pollard S, Le KD. Microsatellite DNA population structure and stock identification of steelhead trout (Oncorhynchus mykiss) in the Nass and Skeena Rivers in northern British Columbia. Marine Biotechnology. 2000;2:587–600. doi: 10.1007/s101260000045. [DOI] [PubMed] [Google Scholar]
- Beebee TJC, Rowe G. An Introduction to Molecular Ecology. Oxford: Oxford University Press; 2004. [Google Scholar]
- Bouza C, Arias J, Castro J, Sanchez L, Martinez P. Genetic structure of brown trout, Salmo trutta L., at the southern limit of the distribution range of the anadromous form. Molecular Ecology. 1999;8:1991–2001. doi: 10.1046/j.1365-294x.1999.00794.x. [DOI] [PubMed] [Google Scholar]
- Bruford MW, Hanotte O, Brookfield JFY, Burke T. Multilocus and single-locus DNA fingerprinting. In: Hoelzel AR, editor. Molecular Genetic Analysis of Populations: A practical Approach. 2nd edn. Oxford: IRL Press; 1998. pp. 287–336. [Google Scholar]
- Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. New York: Springer; 2002. [Google Scholar]
- Carlsson J, Carlsson JEL. Micro-scale distribution of brown trout: an opportunity for kin selection? Ecology of Freshwater Fish. 2002;11:234–239. [Google Scholar]
- Carlsson J, Nilsson J. Population genetic structure of brown trout (Salmo trutta L.) within a northern boreal forest stream. Hereditas. 2000;132:173–181. doi: 10.1111/j.1601-5223.2000.00173.x. [DOI] [PubMed] [Google Scholar]
- Carlsson J, Olsen KH, Nilsson J, Overli O, Stabell OB. Microsatellites reveal fine-scale genetic structure in stream-living brown trout. Journal of Fish Biology. 1999;55:1290–1303. [Google Scholar]
- Cavalli-Sforza LL, Edwards A. Phylogenetic analysis: models and estimation procedures. American Journal of Human Genetics. 1967;19:233–257. [PMC free article] [PubMed] [Google Scholar]
- Couvet D. Deleterious effects of restricted gene flow in fragmented populations. Conservation Biology. 2002;16:369–376. [Google Scholar]
- Crozier WW, Ferguson A. Electrophoretic examination of the population-structure of brown trout, Salmo Trutta L., from the Lough Neagh catchment, Northern-Ireland. Journal of Fish Biology. 1986;28:459–477. [Google Scholar]
- Diniz-Filho JAF, De Campos Telles MP. Spatial autocorrelation analysis and the identification of operational units for conservation in continuous populations. Conservation Biology. 2002;16:924–935. [Google Scholar]
- EA. Local Environment Agency Plan; Dart Third Annual Review. Exeter: Environment Agency; 2001. [Google Scholar]
- EA. Salmonid and Freshwater Fisheries Statistics for England and Wales, 2002. Bristol: Environment Agency; 2002. [Google Scholar]
- El Mousadik A, Petit RJ. High level of genetic differentiation for allelic richness among populations of the argan tree Argania spinosa (L.) Skeels endemic to Morocco. Theoretical and Applied Genetics. 1996;92:832–839. doi: 10.1007/BF00221895. [DOI] [PubMed] [Google Scholar]
- Elliott JM. Quantitative Ecology and the Brown Trout. Oxford: Oxford University Press; 1994. [Google Scholar]
- Estoup A, Presa P, Krieg F, Vaiman D, Guyomard R. (CT)(N) and (GT)(N) microsatellites – a new class of genetic-markers for Salmo trutta L. (brown trout) Heredity. 1993;71:488–496. doi: 10.1038/hdy.1993.167. [DOI] [PubMed] [Google Scholar]
- Estoup A, Rousset F, Michalakis Y, Cornuet JM, Adriamanga M, Guyomard R. Comparative analysis of microsatellite and allozyme markers: a case study investigating microgeographic differentiation in brown trout (Salmo trutta. Molecular Ecology. 1998;7:339–353. doi: 10.1046/j.1365-294x.1998.00362.x. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Smouse PE, Quattro JM. Analysis of molecular variance inferred from metric distances among DNA haplotypes – application to human mitochondrial-DNA restriction data. Genetics. 1992;131:479–491. doi: 10.1093/genetics/131.2.479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Phylip (Phylogeny Inference Package) Seattle, WA: Department of Genetics, University of Washington; 1995. [Google Scholar]
- Ferguson A. Genetic-differences among brown trout, Salmo trutta, stocks and their importance for the conservation and management of the species. Freshwater Biology. 1989;21:35–46. [Google Scholar]
- Finnegan AK, Stevens JR. 2005. Population structuring of brown trout and Atlantic Salmon on Dartmoor: unravelling the influence of historical stocking on current structuring through exploration with GIS, University of Exeter, Report for Dartmoor National Park Authority.
- Garant D, Dodson JJ, Bernatchez L. Ecological determinants and temporal stability of the within-river population structure in Atlantic salmon (Salmo salar L.) Molecular Ecology. 2000;9:615–628. doi: 10.1046/j.1365-294x.2000.00909.x. [DOI] [PubMed] [Google Scholar]
- Goudet J. FSTAT, a program to estimate and test gene diversities and fixation indices (version 2.9.3) 2002. http://www2.unil.ch/popgen/softwares/fstat.htm (accessed 03/07/09)
- Guo SW, Thompson EA. Performing the exact test of Hardy–Weinberg proportion for multiple alleles. Biometrics. 1992;48:361–372. [PubMed] [Google Scholar]
- Haag CR, Riek M, Hottinger JW, Pajunen VI, Ebert D. Genetic diversity and genetic differentiation in Daphnia metapopulations with subpopulations of known age. Genetics. 2005;170:1809–1820. doi: 10.1534/genetics.104.036814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen MH, Mensberg KLD. Founder effects and genetic population structure of brown trout (Salmo trutta) in a Danish river system. Canadian Journal of Fisheries and Aquatic Sciences. 1996;53:2229–2237. [Google Scholar]
- Hansen MM, Mensberg KLD. Genetic differentiation and relationship between genetic and geographical distance in Danish sea trout (Salmo trutta L.) populations. Heredity. 1998;81:493–504. [Google Scholar]
- Hansen MM, Nielsen EE, Mensberg KLD. The problem of sampling families rather than populations: relatedness among individuals in samples of juvenile brown trout Salmo trutta L. Molecular Ecology. 1997;6:469–474. [Google Scholar]
- Hansen MM, Ruzzante DE, Nielsen EE, Bekkevold D, Mensberg KLD. Long-term effective population sizes, temporal stability of genetic composition and potential for local adaptation in anadromous brown trout (Salmo trutta) populations. Molecular Ecology. 2002;11:2523–2535. doi: 10.1046/j.1365-294x.2002.01634.x. [DOI] [PubMed] [Google Scholar]
- Hedrick PW. Highly variable loci and their interpretation in evolution and conservation. Evolution. 1999;53:313–318. doi: 10.1111/j.1558-5646.1999.tb03767.x. [DOI] [PubMed] [Google Scholar]
- Hindar K, Jonsson B, Ryman N, Stahl G. Genetic-relationships among landlocked, resident, and anadromous brown Trout, Salmo trutta L. Heredity. 1991;66:83–91. [Google Scholar]
- Iles TD, Sinclair M. Atlantic herring: stock discreteness and abundance. Science. 1982;215:627–633. doi: 10.1126/science.215.4533.627. [DOI] [PubMed] [Google Scholar]
- Jensen LF, Hansen MM, Carlsson J, Loeschcke V, Mensberg KLD. Spatial and temporal genetic differentiation and effective population size of brown trout (Salmo trutta, L.) in small Danish rivers. Conservation Genetics. 2005;6:615–621. [Google Scholar]
- Knutsen H, Knutsen JA, Jorde PE. Genetic evidence for mixed origin of recolonized sea trout populations. Heredity. 2001;87:207–214. doi: 10.1046/j.1365-2540.2001.00907.x. [DOI] [PubMed] [Google Scholar]
- Koizumi I, Yamamoto S, Maekawa K. Decomposed pairwise regression analysis of genetic and geographic distances reveals a metapopulation structure of stream-dwelling Dolly Varden charr. Molecular Ecology. 2006;15:3175–3189. doi: 10.1111/j.1365-294X.2006.03019.x. [DOI] [PubMed] [Google Scholar]
- Koljonen ML, Jansson H, Paaver T, Vasin O, Koskiniemi J. Phylogeographic lineages and differentiation pattern of Atlantic salmon (Salmo salar) in the Baltic Sea with management implications. Canadian Journal of Fisheries and Aquatic Sciences. 1999;56:1766–1780. [Google Scholar]
- Laikre L, Jarvi T, Johansson L, Palm S, Rubin JF, Glimsater CE, Landergren P, et al. Spatial and temporal population structure of sea trout at the Island of Gotland, Sweden, delineated from mitochondrial DNA. Journal of Fish Biology. 2002;60:49–71. [Google Scholar]
- Liu K, Muse S. PowerMarker: An integrated analysis environment for genetic marker analysis. Bioinformatics. 2005;21:2128–2129. doi: 10.1093/bioinformatics/bti282. [DOI] [PubMed] [Google Scholar]
- McQuinn IH. Metapopulations and the Atlantic herring. Reviews in Fish Biology and Fisheries. 1997;7:297–329. [Google Scholar]
- Montgomery ME, Woodworth LM, Nurthen RK, Gilligan DM, Briscoe DA, Frankham R. Relationships between population size and loss of genetic diversity: comparisons of experimental results with theoretical predictions. Conservation Genetics. 2000;1:33–43. [Google Scholar]
- Moran P, Pendas AM, Garciavazquez E, Izquierdo JI, Loboncervia J. Estimates of gene flow among neighboring populations of brown trout. Journal of Fish Biology. 1995;46:593–602. [Google Scholar]
- Neville HM, Dunham JB, Peacock MM. Landscape attributes and life history variability shape genetic structure of trout populations in a stream network. Landscape Ecology. 2006;21:901–916. [Google Scholar]
- Nielsen EE, Hansen MM, Loeschcke V. Genetic variation in time and space: microsatellite analysis of extinct and extant populations of Atlantic salmon. Evolution. 1999;53:261–268. doi: 10.1111/j.1558-5646.1999.tb05351.x. [DOI] [PubMed] [Google Scholar]
- Oosterhout CV, Hutchinson WF, Willis DPM. MICRO-CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Molecular Ecology Notes. 2004;4:535–565. [Google Scholar]
- Ostergaard S, Hansen MM, Loeschcke V, Nielsen EE. Long-term temporal changes of genetic composition in brown trout (Salmo trutta L.) populations inhabiting an unstable environment. Molecular Ecology. 2003;12:3123–3135. doi: 10.1046/j.1365-294x.2003.01976.x. [DOI] [PubMed] [Google Scholar]
- Page RDM. TREEVIEW: an application to display phylogenetic trees on personal computers. Computer Applications in the Biosciences. 1996;12:357–358. doi: 10.1093/bioinformatics/12.4.357. [DOI] [PubMed] [Google Scholar]
- Palm S, Laikre L, Jorde PE, Ryman N. Effective population size and temporal genetic change in stream resident brown trout (Salmo trutta, L.) Conservation Genetics. 2003;4:249–264. [Google Scholar]
- Peakall R, Smouse PE. GENALEX 6: genetic analysis in Excel. Population genetic software for teaching and research. Molecular Ecology Notes. 2006;6:288–295. doi: 10.1093/bioinformatics/bts460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peakall R, Ruibal M, Lindenmayer DB. Spatial autocorrelation offers new insights into gene flow in the Australian bush rat, Rattus fuscipes. Evolution. 2003;57:1182–1195. doi: 10.1111/j.0014-3820.2003.tb00327.x. [DOI] [PubMed] [Google Scholar]
- Pemberton AJ, Hansson LJ, Craig SF, Hughes RN, Bishop JDD. Microscale genetic differentiation in a sessile invertebrate with cloned larvae: investigating the role of polyembryony. Marine Biology. 2007;153:71–82. [Google Scholar]
- Poteaux C. Interactions genetiques entre formes sauvages et formes domestique chez la truite commune (Salmo trutta fario L.) Montpellier: Universite Montpellier II; 1995. [Google Scholar]
- Presa P, Guyomard R. Conservation of microsatellites in three species of salmonids. Journal of Fish Biology. 1996;49:1326–1329. [Google Scholar]
- Primmer CR, Veselov AJ, Zubchenko A, Poututkin A, Bakhmet I, Koskinen MT. Isolation by distance within a river system: genetic population structuring of Atlantic salmon, Salmo salar, in tributaries of the Varzuga River in northwest Russia. Molecular Ecology. 2006;15:653–666. doi: 10.1111/j.1365-294X.2005.02844.x. [DOI] [PubMed] [Google Scholar]
- Raymond M, Rousset F. GENEPOP (version 1.2): population genetics software for exact tests and ecumenicism. Journal of Heredity. 1995;86:248–249. [Google Scholar]
- Reisch C, Kellermeier J. Microscale variation in alpine grasslands: AFLPs reveal a high level of genotypic diversity in Primula minima (Primulaceae) Botanical Journal of the Linnean Society. 2007;155:549–556. [Google Scholar]
- Rice WR. Analyzing tables of statistical tests. Evolution. 1989;43:223–225. doi: 10.1111/j.1558-5646.1989.tb04220.x. [DOI] [PubMed] [Google Scholar]
- Rieman BE, Dunham JB. Metapopulations and salmonids: a synthesis of life history patterns and empirical observations. Ecology of Freshwater Fish. 2000;9:51–64. [Google Scholar]
- Rousset F. Genetic differentiation and estimation of gene flow from F-Statistics under isolation by distance. Genetics. 1997;145:1219–1228. doi: 10.1093/genetics/145.4.1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruzzante DE, Hansen MM, Meldrup D. Distribution of individual inbreeding coefficients, relatedness and influence of stocking on native anadromous brown trout (Salmo trutta) population structure. Molecular Ecology. 2001;10:2107–2128. doi: 10.1046/j.1365-294x.2001.01352.x. [DOI] [PubMed] [Google Scholar]
- Ryman N. Patterns of distribution of biochemical genetic-variation in salmonids – differences between species. Aquaculture. 1983;33:1–21. [Google Scholar]
- Schneider S, Roessli D, Excoffier L. ARLEQUIN: A Software for Population Genetics Data Analysis, Version 2. Geneva: University of Geneva; 2000. [Google Scholar]
- Slettan A, Olsaker I, Lie O. Atlantic salmon, Salmo salar, microsatellites at the Ssosl25, Ssosl85, Ssosl311, Ssosl417 Loci. Animal Genetics. 1995;26:281–282. doi: 10.1111/j.1365-2052.1995.tb03262.x. [DOI] [PubMed] [Google Scholar]
- Small MP, Beacham TD, Withler RE, Nelson RJ. Discriminating coho salmon (Oncorhynchus kisutch) populations within the Fraser River, British Columbia, using microsatellite DNA markers. Molecular Ecology. 1998;7:141–155. [Google Scholar]
- Smouse PE, Peakall R. Spatial autocorrelation analysis of individual multiallele and multilocus genetic structure. Heredity. 1999;82:561–573. doi: 10.1038/sj.hdy.6885180. [DOI] [PubMed] [Google Scholar]
- Smouse PE, Long JC, Sokal RR. Multiple regression and correlation extensions of the Mantel test of matrix correspondence. Systematic Zoology. 1986;35:627–632. [Google Scholar]
- Stabell OB. Homing and olfaction in salmonids – a critical-review with special reference to the Atlantic salmon. Biological Reviews of the Cambridge Philosophical Society. 1984;59:333–388. [Google Scholar]
- Stahl G. Genetic population structure of Atlantic salmon. In: Ryman N, Utter F, editors. Population Genetics and Fisheries Management. Washington: University of Washington Press; 1987. pp. 112–140. [Google Scholar]
- Steele S. Devon Area Report River Dart Fisheries Survey 1996. Exeter: Environment Agency; 1996. [Google Scholar]
- Takezaki N, Nei M. Genetic distances and reconstruction of phylogenetic trees from microsatellite DNA. Genetics. 1996;144:389–399. doi: 10.1093/genetics/144.1.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor EB. A review of local adaptation in salmonidae, with particular reference to Pacific and Atlantic salmon. Aquaculture. 1991;98:185–207. [Google Scholar]
- Van Houdt JKJ, Pinceel J, Flamand MC, Briquet M, Dupont E, Volckaert FAM, Baret PV. Migration barriers protect indigenous brown trout (Salmo trutta) populations from introgression with stocked hatchery fish. Conservation Genetics. 2005;6:175–191. [Google Scholar]
- Vekemans X, Hardy OJ. New insights from fine-scale spatial genetic structure analyses in plant populations. Molecular Ecology. 2004;13:921–935. doi: 10.1046/j.1365-294x.2004.02076.x. [DOI] [PubMed] [Google Scholar]
- Waples RS. Temporal variation in allele frequencies – testing the right hypothesis. Evolution. 1989;43:1236–1251. doi: 10.1111/j.1558-5646.1989.tb02571.x. [DOI] [PubMed] [Google Scholar]
- WEHAB. 2002. A framework for action on biodiversity and ecosystem management. http://www.un.org/jsummit/html/documents/summit_docs/wehab_papers/wehab_biodiversity.pdf. Water, Energy, Health, Agriculture and Biodiversity Working Group Report, August 2002 (accessed 03/07/09)
- Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
- Wenburg JK, Bentzen P, Foote CJ. Microsatellite analysis of genetic population structure in an endangered salmonid: the coastal cutthroat trout (Oncorhynchus clarki clarki) Molecular Ecology. 1998;7:733–749. [PubMed] [Google Scholar]
- Yamamoto S, Morita K, Koizumi I, Maekawa K. Genetic differentiation of white-spotted charr (Salvelinus leucomaenis) populations after habitat fragmentation: Spatial–temporal changes in gene frequencies. Conservation Genetics. 2004;5:529–538. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


