High-throughput DNA methylation datasets for evaluating false discovery rate methodologies

Abstract

When analyzing high-throughput genomic data, the multiple comparison problem is most often addressed through estimation of the false discovery rate (FDR), using methods such as the Benjamini & Hochberg, Benjamini & Yekutieli, the q-value method, or in controlling the family-wise error rate (FWER) using Holm’s step down method. To date, research studies that have compared various FDR/FWER methodologies have made use of limited simulation studies and/or have applied the methods to one or more microarray gene expression dataset(s). However, for microarray datasets the veracity of each null hypothesis tested is unknown so that an objective evaluation of performance cannot be rendered for application data. Due to the role of methylation in X-chromosome inactivation, we postulate that high-throughput methylation datasets may provide an appropriate forum for assessing the performance of commonly used FDR methodologies. These datasets preserve the complex correlation structure between probes, offering an advantage over simulated datasets. Using several methylation datasets, commonly used FDR methods including the q-value, Benjamini & Hochberg, and Benjamini & Yekutieli procedures as well as Holm’s step down method were applied to identify CpG sites that are differentially methylated when comparing healthy males to healthy females. The methods were compared with respect to their ability to identify CpG sites located on sex chromosomes as significant, by reporting the sensitivity, specificity, and observed FDR. These datasets are useful for characterizing the performance of multiple comparison procedures, and may find further utility in other tasks such as comparing variable selection capabilities of classification methods and evaluating the performance of meta-analytic methods for microarray data.

1. Introduction

The p-value is the probability of obtaining a test statistic as or more extreme as the one observed under the conditions of the null hypothesis. In most scientific endeavors, an α = 0.05 threshold is customarily applied so that a p-value < 0.05 is considered as evidence for the alternative hypothesis, that is, p < 0.05 typically indicates a significant finding. However, application of an α = 0.05 threshold to univariable tests of significance in high-throughput genomic settings will yield a large number of Type I errors simply by chance. The statistical literature includes various methods for adjusting for multiple comparisons by controlling the family wise error rate (FWER). The FWER is the probability of making one or more false discoveries, or type I errors, among all null hypotheses being tested (Dudoit et al., 2003). Controlling for multiple comparisons using the false discovery rate (FDR) was later suggested by Benjamini and Hochberg (1995) and has received a great deal of attention in the statistical analysis of DNA microarray experiments for detecting differential gene expression. Briefly, the FDR can be used in place of the traditional α = 0.05 threshold to control the expected proportion of incorrectly rejected null hypotheses. Because the FDR method is less conservative than controlling the FWER, it has increased power. Additionally, if all tested null hypotheses are true, controlling the FDR controls the family wise error rate (Benjamini and Yekutieli, 2001). Various methods for controlling the FDR have been developed, including the Benjamini & Hochberg method (Benjamini and Hochberg, 1995), the Benjamini & Yekutieli method (Benjamini and Yekutieli, 2001), and more recently the q-value method (Storey and Tibshirani, 2003).

To date, research studies that have been performed comparing FDR/FWER methodologies have included limited simulation studies and/or application of the methods to one or more microarray gene expression dataset(s) (Dudoit et al., 2002, 2003; Korn et al., 2004). A limitation of simulation studies is that the simulated datasets usually include a limited number of variables, so they do not properly mimic a high-throughput genomic dataset. Moreover, often the simulated data are not generated to have the complex correlation structure that is seen in high-throughput genomic datasets such as in gene expression microarray data, so that the observed performance in a simulation study may not be sustained in a high-throughput genomic setting. Another limitation is that for the application datasets, no one really knows which genes on the microarray should be identified as statistically significant so that performance cannot be objectively evaluated.

In mammals, normal females have two X chromosomes while males have one X chromosome. Through observations of mouse coat color and the knowledge that only one active X is required for normal development, it was suggested that in females, one X chromosome is inactivated (Lyon, 1961). Shortly thereafter, an expanded hypothesis advocated that X-chromosome inactivation was the method of gene dosage compensation for X-linked genes in all mammals (Lyon, 1962). Later, a cytogenetic study identified a single center responsible for X-chromosome inactivation (Rastan and Robertson, 1985). The X-inactive specific transcript (XIST) is a gene in the X-inactivation center (XIC) that is expressed exclusively from the inactive X chromosome. The process of X-inactivation begins at the XIC and spreads to result in chromosome-wide transcriptional silencing (Li, 2002). It was found that XIST is completely methylated in males and partially methylated in females (McDonald et al., 1998). These researchers concluded that the partial methylation of XIST observed in females was likely due to the presence of methylated XIST on the unexpressed allele, and unmethylated XIST on the expressed allele within a given cell (McDonald et al., 1998). On the active X chromosome, most genes are unmethylated with the exception of XIST, whereas on the inactive X chromosome most genes are methylated with the exception of XIST (Gartler and Goldman, 2005). Although it is not known whether DNA methylation of XIST is the initiating factor in determining which X chromosome is active or inactive, certainly DNA methylation maintains the X-inactivation pattern (Gartler and Goldman, 2005).

DNA methylation in mammals mainly occurs at the 5′ carbon of CpG dinucleotides. Although DNA methylation does not alter the DNA sequence, it can be inherited by propagation during cell division. Dense methylation of CpG islands in the promoter regions of genes can affect gene transcription, and is often termed epigenetic silencing (Laird, 2003). Therefore methylated genes on the inactive X chromosome are not expressed (Li, 2002). Due to the role of methylation in X-chromosome inactivation, differential methylation patterns between males and females have been observed for CpG sites of genes located on the X chromosome (McDonald et al., 1998; Bell et al., 2011). In fact, 19 CpG sites for six X-linked genes (EFNB1, ELK1, FMR1, G6PD, GPC3, GLA) serve as controls on Illumina’s GoldenGate Methylation BeadArray. For these six genes, the percent methylation should demonstrate little to no methylation for males and methylation of half the alleles for females (Bibikova et al., 2006). In addition, the Illumina technology has been described as being capable of detecting a difference in the proportion of methylated alleles of 0.17 or greater (Bibikova et al., 2006), based on a dilution study performed using ratios of 100:0, 50:50, 20:80, 10:90, 5:95, and 0:100 female to male genomic DNA.

Due to the role of methylation in X-chromosome inactivation and observed DNA methylation difference in males and females, we postulate that high-throughput methylation datasets that include normal healthy subjects and having gender annotated may provide an appropriate forum for evaluating FDR/FWER methodologies. Illumina’s Golden Gate Methylation Cancer Panel I and Infinium HumanMethylation27 assays enable high-throughput profiling of DNA methylation. We identified several DNA methylation datasets through Gene Expression Omnibus and PubMed that included normal healthy subjects and had gender annotated as a phenotypic variable. In this study, these datasets were used to compare FDR/FWER methods with respect to their ability to identify CpG sites that are significantly different when comparing normal subjects by gender.

2. Review of Methods for Controlling False Discoveries

A test of statistical hypothesis is a rule or procedure for deciding whether to reject the null hypothesis, H₀. We typically seek to control the probability of committing a Type I error, that is, rejecting H₀ when in fact H₀ is true, by fixing a threshold α. A hypothesis test resulting in a p-value that falls below the pre-specified α level is rejected. However, when many hypotheses are tested, each test with a specified Type I error probability, the probability that at least some Type I errors are committed increases sharply with the number of hypotheses tested. For example, when testing 10,000 H₀’s simultaneously, the family-wise error rate (FWER) is the probability of at least one Type I error in the family. At the α = 0.05 level, 500 genes are expected to be called significant by chance. Various methods for controlling the FWER have been described including Bonferroni, Šidák single step, Šidák step down, Holm step-down, and Hochberg step-up procedures. A thorough review of these procedures has been published previously (Dudoit et al., 2003). Because the Holm step-down FWER is less conservative than single step procedures such as the Bonferroni and Šidák single step and results using Holm’s step down do not differ materially from the Šidák step down and Hochberg step-up procedures, we describe it here and compare its performance to the FDR procedures.

Holm step-down FWER procedure

When testing g null hypotheses

1. Order the p-values and hypotheses P₍₁₎ ≥ … ≥ P_(g) corresponding to H₍₁₎, …, H_(g)

2. Let i = 1.

3. If P_(g−i+1) > α/(g − i + 1) then accept all remaining hypotheses H_(g−i+1) and STOP.

4. If P_(g−i+1) ≤ α/(g − i + 1) then reject H_(g−i+1) and increment i, then return to step 3.

Benjamini & Hochberg method

Rather than controlling the FWER which is conservative, in high-throughput genomic settings it may be more appropriate to control the proportion of false positives among the differentially expressed genes. Given the cross-tabulation of results from m tests of significance by veracity of H₀ (Table 1), the FDR is defined as the expected proportion of false discoveries, or FDR = E (F/(S ∨ 1)), where S ∨ 1 = max(S, 1) to avoid division by 0 (Benjamini and Hochberg, 1995). Controlling for the False Discovery Rate (FDR) allows one to identify as many genes with significant differences as possible, while incurring a relatively low proportion of false positives. Assuming the p-values from the null distribution are independent and uniformly distributed, the Benjamini & Hochberg method for controlling the FDR is as follows:

1. Let p₍₁₎ ≤ … ≤ p_(g) be the ordered p-values from the g tests.

2. Calculate $\widehat{k}=\text{max}(k:p_{(k)}\le \frac{\alpha k}{g})$

3. If k̂ exists, the reject the null hypotheses corresponding to p₍₁₎ ≤ … ≤ p_(k̂); otherwise, reject nothing.

Table 1.

Cross-tabulation m tests of significance by true underlying condition of the null hypotheses.

	Reject H0	Fail to reject H0	Total
H0 True	F	m0 − F	m0
H0 False	T	m1 − T	m1
Total	S = F + T	m − S	m

Benjamini & Yekutieli method

The Benjamini & Yekutieli method controls the false discovery rate under dependence assumptions and is similar to the Benjamini & Hochberg method with exception that step 2 is replaced by finding the largest k such that $\widehat{k}=\text{max}(k:p_{(k)}\le \frac{\alpha k}{g\times c(g)})$, where c(g) = 1 if the tests are independent and $c(g)={\displaystyle {\sum }_{i=1}^g}1/i$ if the tests are correlated (Benjamini and Yekutieli, 2001).

q-value method

The q-value of a particular feature is the expected proportion of false positives among all features as or more extreme than the one observed (Storey and Tibshirani, 2003). For a given p-value threshold t where 0 ≤ t ≤ 1, we want to estimate FDR(t) = E (F(t)/S (t)) ≈ E(F(t))/E(S (t)). Following the notation from Table 1, here F(t) represents the number of false discoveries at threshold t while S (t) represents the number of null hypotheses considered significant at threshold t. Formally, FDR(t) is estimated as

$$\widehat{\mathit{\text{FDR}}(t)}=\frac{{\pi }_0\mathit{\text{mt}}}{S(t)}=\frac{{\pi }_0\mathit{\text{mt}}}{{\displaystyle {\sum }_{g=1}^{m}I(p_g\le t)}},$$ (1)

where π₀ represents the proportion of hypotheses for which the null is true. For application datasets, π₀ is typically unknown and so is estimated using the distribution of raw p-values using either a smoothing or bootstrap method.

3. Methods

3.1. Data

Three datasets produced using the Illumina Golden Gate Methylation assay and three datasets produced using the Illumina Infinium HumanMethylation27 assay were analyzed in this study. Each dataset is briefly described in sections 3.1.1 and 3.1.2. The Golden Gate assay assesses methylation of 1,505 CpG sites including 84 CpG sites from the X chromosome. The Infinium assay assesses 27,578 CpG sites including 1,085 CpG sites from the X chromosome and seven from the Y chromosome.

3.1.1. Illumina Golden Gate Methylation assay

Boks et al. (2009). The heritability of DNA methylation as well as the effects of age and gender were studied using DNA extracted from peripheral blood samples taken from 23 monozygotic and 23 dizygotic healthy twin-pairs as well as in 96 healthy singletons (Boks et al., 2009). Using the Illumina Golden Gate Methylation assay, DNA methylation for 1505 CpG sites representing 807 unique genes in the human genome were interrogated. Upon request the authors supplied the methylation and phenotypic data for 95 healthy singletons, which included 47 males and 48 females.

Javierre et al. (2010). To identify aberrant DNA methylation associated with autoimmune disorders, monozygous twins discordant for systemic lupus erythrmatosus (N=5), rheumatoid arthritis (N=5), and dermatomyositis (N=5) and healthy controls where studied using the Illumina Golden Gate Methylation Cancer Panel I (Javierre et al., 2010), which interrogates 1505 CpG sites representing 807 unique genes. The data were downloaded from Gene Expression Omnibus accession number GSE19033. For this study, two separate analyses comparing gender were performed: one in which the 29 control subjects were included (Javierre Controls: 8 males, 21 females) and another in which the 15 healthy twins were included (Javierre Healthy Twins: 4 males, 11 females).

Stein et al. (2010). Silencing of transgene expression due to methylation in X-linked chronic granulomatous disease was studied in 2 cases and 25 control subjects using the Illumina Golden Gate Methylation Cancer Panel I (Stein et al., 2010). The data were downloaded from Gene Expression Omnibus accession number GSE19515. For this study, we restricted attention to the 25 controls which included 12 males and 13 females.

3.1.2. Illumina Infinium HumanMethylation27 assay

Rakyan et al. (2010). To identify aging-associated differentially methylated regions (aDMRs), samples from female twin pairs, singletons, and an independent cohort were profiled using Illumina’s HumanMethylation27 array, which interrogates 27,578 CpG sites (Rakyan et al., 2010). The independent cohort was downloaded from Gene Expression Omnibus accession number GSE20242. This cohort consisted of healthy singletons for which CD14⁺ monocytes and CD4⁺ T-cells were both examined. Therefore, in this study two different comparisons were performed, one for CD14⁺ monocytes (7 males, 19 females) and another for CD4⁺ T-cells (6 males, 18 females).

Bell et al. (2011). Methylation levels for 27,578 CpG sites were measured using Illumina’s Infinium HumanMethylation27 assay in 77 Yoruba individuals (34 males, 43 females) from the HapMap project (Bell et al., 2011). For each subject, the bisulphite converted DNA was hybridized to at least two arrays. The data were downloaded from Gene Expression Omnibus accession number GSE26133. In this study we performed two independent analyses: the first for the 77 replicate 1 samples (Yoruba 1); and the second for the 77 replicate 2 samples (Yoruba 2).

Liu et al. (2010). To identify epigenetic modulation associated with Cornelia de Lange syndrome, lymphoblastoid cells lines from Cornelia de Lange syndrome and Roberts syndrome probands along with 22 healthy controls were assayed using Illumina’s Infinium HumanMethylation27 assay, which interrogates 27,578 CpG sites (Liu et al., 2010). These data were downloaded from Gene Expression Omnibus accession number GSE18458. In this study we restricted attention to the 22 healthy controls (12 males, 10 females).

3.2. Statistical Methods

For each dataset, we downloaded the phenotypic and gene expression data using the GEOquery package in the R programming environment (R Development Core Team, 2011). Each dataset was restricted to include samples from only normal healthy subjects as described in section 3.1. For datasets that included CpG sites having missing values, k-nearest neighbors averaging was used for imputation using the impute R package (Hastie et al., 2011). Because the expression value, β, reported for each CpG site represents “proportion methylated” which is in the [0, 1] interval, we transformed the expression values using the log₂(β/(1 − β)) transformation. There-after, for each CpG site a moderated t-test was applied to test for differential methylation between males and females using the limma package in R (Smyth, 2004). We used the raw p-value, Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm’s step down, the default q-value method which estimates π₀ using a smoothing method, and the q-value method where π₀ is estimated using the bootstrap to identify significant CpG sites using a 0.05 threshold. For each FDR/FWER method we reported the sensitivity, specificity, and observed false discovery rate. Sensitivity was defined as the percent of CpG sites located on either the X or Y chromosome declared significant (a/(a + b) × 100 from Table 2). Specificity was defined as the percent of CpG sites on autosomes that were not significant (d/(c + d) × 100 from Table 2). Finally the observed false discovery rate was defined as the proportion of CpG sites on autosomes identified as significant among the total number of CpG sites declared significant (c/(a + c) from Table 2)

Table 2.

Cross-tabulation of the results of g tests of significance comparing gender by chromosomal location of CpG site for methylation array data.

	X or Y CpG site (Truly significant)	Autosomal CpG site (Truly Not significant)	Total
Rejected	a	c	a + c
Not rejected	b	d	b + d
Total	a + b	c + d	g = a + b + c + d

4. Results

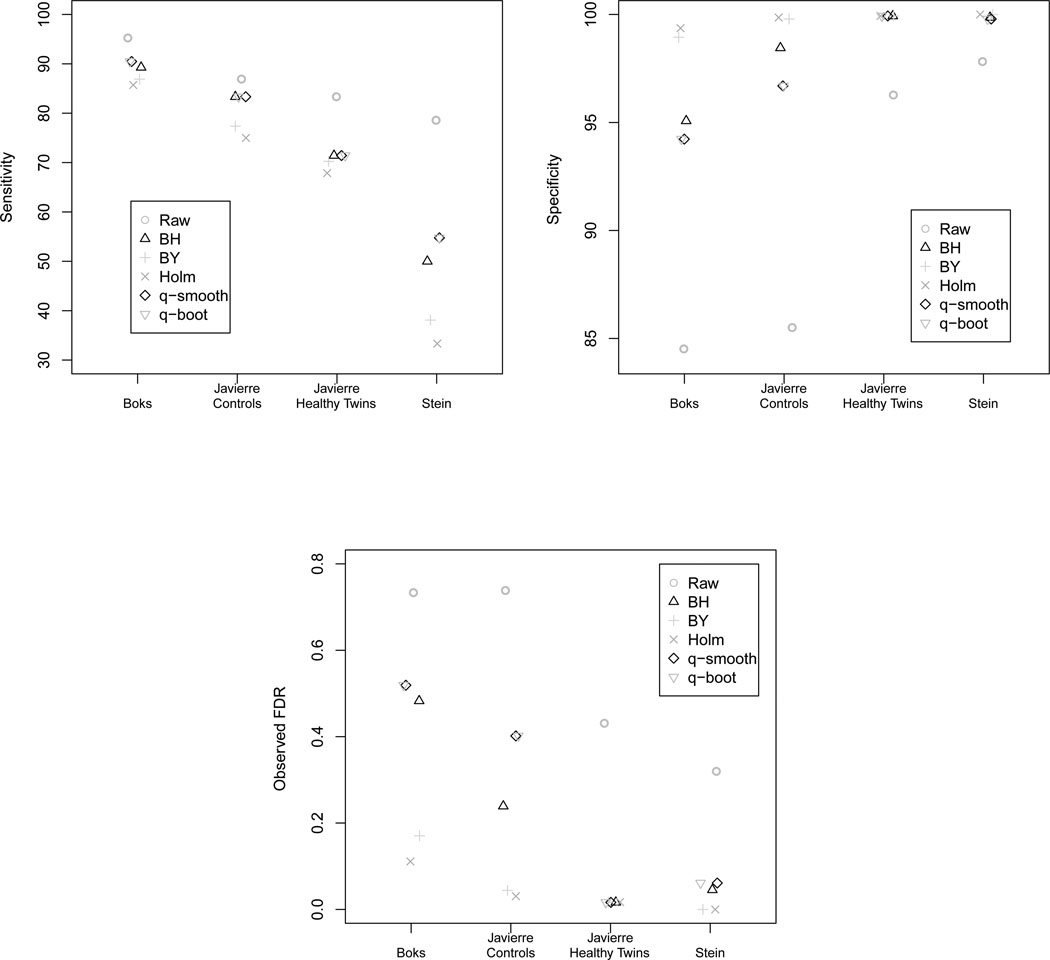
The two platforms differ with respect to the number of CpG sites interrogated, therefore, results are summarized by platform. For the Golden Gate Methylation Cancer Panel I platform, although the raw p-value method always yielded the highest sensitivity (Table 3), the specificity was much lower (Table 4) leading to an observed FDR that was quite high (Figure 1, Table 5). Holm’s step down procedure consistently yielded the lowest sensitivity, but because its specificity was the highest, Holm’s step down procedure yielded the lowest observed FDR. The Benjamini & Yeuketili method performed similarly to Holm’s step down procedure (Table 3, 4, 5). There was no discernible difference between the q-value method when using either the default smoothing method or the bootstrap method to estimate π₀. The Benjamini & Hochberg and both q-value methods had variable performance, as the observed FDRs were close to the nominal 0.05 level for the Javierre Healthy Twins and Stein datasets but far from the nominal level for the Javierre Controls and Boks datasets (Table 5). The variable performance of the q-value method with respect to the observed FDR may be attributed to difficulties introduced by estimating the proportion of truly null hypotheses, π₀, using the small number of CpG sites interrogated by the Golden Gate Methylation Cancer Panel I, only 1,505.

Table 3.

Sensitivity for the Golden Gate Methylation Cancer Panel I platform when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smoother), and the q-value method where π₀ is estimated using the bootstrap (q-bootstrap).

Dataset	Raw	BH	BY	Holm	q-smoother	q-bootstrap
Boks	95.2	89.3	86.9	85.7	90.5	90.5
Javierre Controls	86.9	83.3	77.4	75.0	83.3	83.3
Javierre Healthy Twins	83.3	71.4	70.2	67.9	71.4	71.4
Stein	78.6	50.0	38.1	33.3	54.8	54.8

Table 4.

Specificity for the Golden Gate Methylation Cancer Panel I platform when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smoother), and the q-value method where π₀ is estimated using the bootstrap (q-bootstrap).

Dataset	Raw	BH	BY	Holm	q-smoother	q-bootstrap
Boks	84.5	95.1	98.9	99.4	94.2	94.2
Javierre Controls	85.5	98.5	99.8	99.9	96.7	96.7
Javierre Healthy Twins	96.3	99.9	99.9	99.9	99.9	99.9
Stein	97.8	99.9	100.0	100.0	99.8	99.8

Figure 1.

Sensitivity, specificity, and observed FDR for the Golden Gate Methylation Cancer Panel I platform (1,505 CpG sites) when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smooth), and the q-value method where π₀ is estimated using the bootstrap (q-boot).

Table 5.

Observed FDR for the GoldenGate Methylation Cancer Panel I platform when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smoother), and the q-value method where π₀ is estimated using the bootstrap (q-bootstrap).

Dataset	Raw	BH	BY	Holm	q-smoother	q-bootstrap
Boks	0.733	0.483	0.170	0.111	0.519	0.519
Javierre Controls	0.738	0.239	0.044	0.031	0.402	0.402
Javierre Healthy Twins	0.431	0.016	0.017	0.017	0.016	0.016
Stein	0.320	0.045	0	0	0.061	0.061

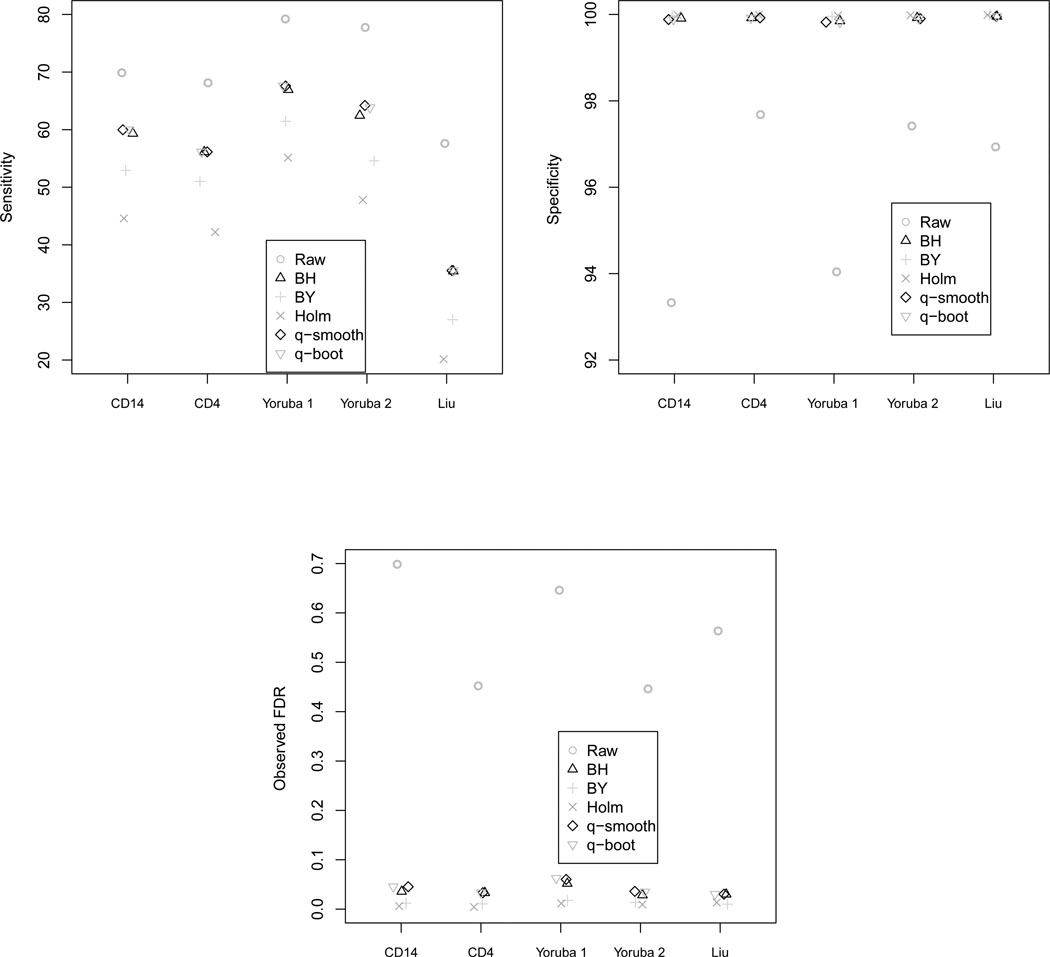
For the Infinium HumanMethylation27 assay, although the raw p-value method always yielded the highest sensitivity (Table 6), the specificity was much lower (Table 7) leading to an observed FDR that was quite high (Figure 2, Table 8). Holm’s step down procedure consistently yielded the lowest sensitivity, but because its specificity is highest, Holm’s step down procedure yielded the lowest observed FDR (Table 6, 7, 8). However, the observed FDR for Holm’s step down procedure was well below the nominal 0.05 threshold (Table 8). The Benjamini & Yeuketili method performed similarly to Holm’s step down procedure (Table 6, 7, 8). The Benjamini & Hochberg and both q-value methods yielded observed FDRs closest to the nominal 0.05 level while maintaining relatively high sensitivities. Again there was no discernible difference between the q-value method when using either the default smoothing method or the bootstrap method to estimate π₀.

Table 6.

Sensitivity for the Infinium HumanMethylation27 array when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smoother), and the q-value method where π₀ is estimated using the bootstrap (q-bootstrap).

Dataset	Raw	BH	BY	Holm	q-smoother	q-bootstrap
Rakyan CD14+	69.9	59.3	52.9	44.6	60.0	60.0
Rakyan CD4	68.1	56.1	51.0	42.2	56.1	56.1
Bell Yoruba 1	79.2	66.9	61.4	55.1	67.6	67.6
Bell Yoruba 2	77.7	62.5	54.6	47.8	64.2	63.8
Liu	57.6	35.4	27.0	20.1	35.5	35.5

Table 7.

Specificity for the Infinium HumanMethylation27 array when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smoother), and the q-value method where π₀ is estimated using the bootstrap (q-bootstrap).

Dataset	Raw	BH	BY	Holm	q-smoother	q-bootstrap
Rakyan CD14+	93.3	99.9	100	100	99.9	99.9
Rakyan CD4	97.7	99.9	100	100	99.9	99.9
Bell Yoruba 1	94.0	99.8	100	100	99.8	99.8
Bell Yoruba 2	97.4	99.9	100	100	99.9	99.9
Liu	96.9	100.0	100	100	100.0	100.0

Figure 2.

Sensitivity, specificity, and observed FDR for the Infinium HumanMethylation27 platform (27,568 CpG sites) when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smooth), and the q-value method where π₀ is estimated using the bootstrap (q-boot).

Table 8.

Observed FDR for the Infinium HumanMethylation27 array when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smoother), and the q-value method where π₀ is estimated using the bootstrap (q-bootstrap).

Dataset	Raw	BH	BY	Holm	q-smoother	q-bootstrap
Rakyan CD14+	0.698	0.036	0.012	0.006	0.045	0.045
Rakyan CD4	0.452	0.033	0.011	0.004	0.033	0.033
Bell Yoruba 1	0.646	0.052	0.018	0.011	0.060	0.063
Bell Yoruba 2	0.446	0.028	0.013	0.009	0.036	0.035
Liu	0.563	0.030	0.010	0.013	0.030	0.030

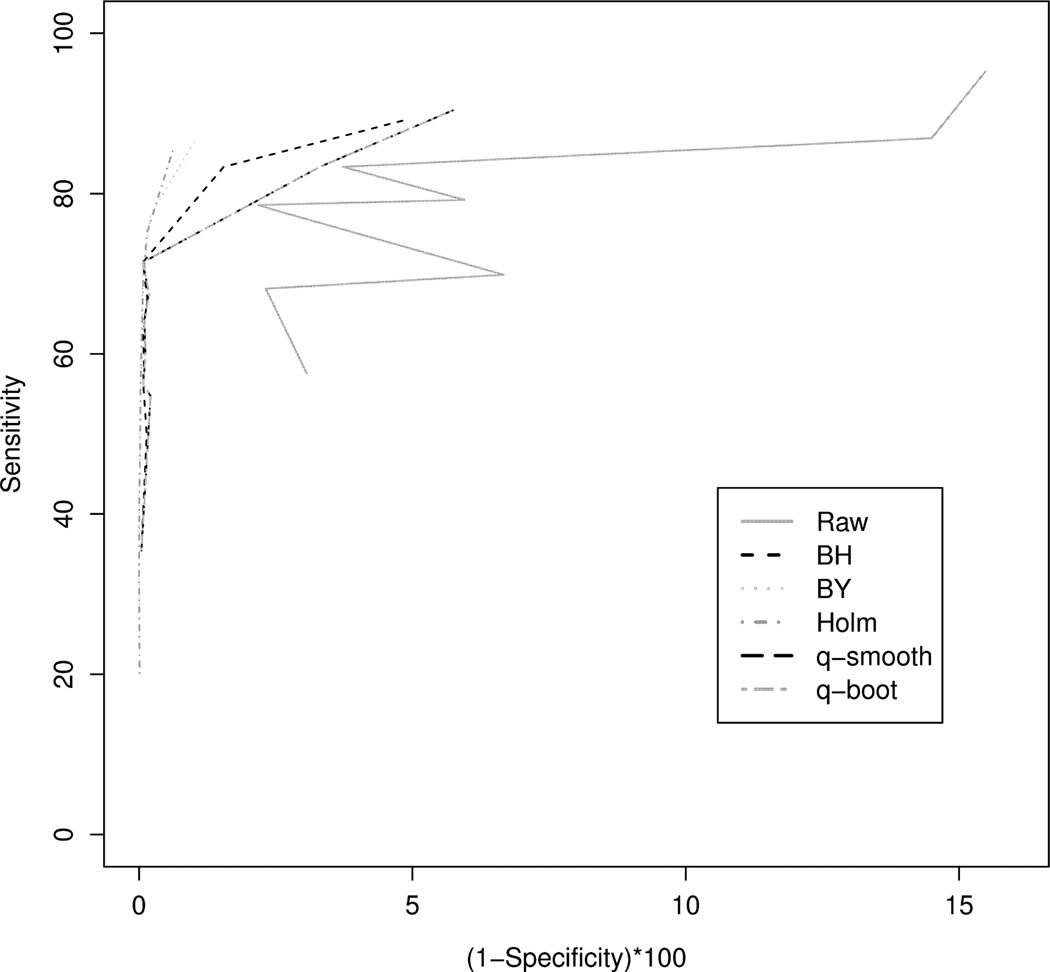
The sensitivities and specificities from the two different DNA methylation platforms were then combined and the receiver operating characteristic curves were plotted for each FDR method (Figure 3). From the ROC curve we observed that Holm’s procedure followed closely by the Benjamini & Yeuketili method and subsequently the Benjamini & Hochberg method yield the best performance.

Figure 3.

Receiver operating characteristic curve when using the raw p-value (Raw), Benjamini & Hochberg (BH), Benjamini & Yekutieli (BY), Holm step down (Holm), the default q-value method which estimates π₀ using a smoothing method (q-smooth), and the q-value method where π₀ is estimated using the bootstrap (q-boot).

5. Discussion & Conclusion

The raw p-value method had the highest sensitivity, regardless of the platform analyzed. However, the drawback in using raw p-values is that its lower specificity results in a very high observed FDR. In fact, the observed FDR for the raw p-value method is typically ≥ 0.50, much higher than the desired nominal level of 0.05. Therefore because researchers typically have limited resources for following up significant results, raw p-values are not recommended for use in high-throughput genomic experiments. As expected, the Holm step down method, which adjusts for the FWER, is the most conservative and therefore has the lowest sensitivity and an observed FDR much lower than the nominal level. Therefore, when researchers have limited resources for following up on significant findings, controlling the FWER may be a better option than controlling the FDR in high-throughput genomic studies. For both platforms, there was no discernible difference between the q-value method when using either the default smoothing method or the bootstrap method to estimate π₀. However, the q-value method suffered from variable performance with respect to the observed FDR for the Golden Gate Methylation Cancer Panel I platform. The Golden Gate Methylation Cancer Panel I platform only interrogates 1,505 CpG sites. This may cause difficulties in estimating the proportion of truly null hypotheses, π₀, as the distribution of p-values may not be very refined, implying the q-value method may not be the most appropriate choice when small boutique arrays are being analyzed. Nevertheless, for the larger Infinium HumanMethylation27 array, the Benjamini & Hochberg and q-value method have the higher sensitivities, higher specificities, and observed FDRs closer to the nominal 0.05 level compared to the other methods compared. Although the nominal FDR level differed among the studies, the methods consistently ranked in the same order of performance. This is in spite of the datasets differing by platform (Golden Gate versus Infinium) and biological source from which the genomic DNA was extracted (peripheral blood (Boks et al., 2009; Stein et al., 2010), white blood cells (Javierre et al., 2010), CD14⁺ monocytes and CD4⁺ T-cells (Rakyan et al., 2010), and lymphoblastoid cell lines (Liu et al., 2010; Bell et al., 2011)), and different numbers of normal healthy males and normal healthy females analyzed in each study.

We have posited that high-throughput DNA methylation datasets are useful for assessing the performance of FDR and FWER methodologies. This is due to the role that DNA methylation plays in maintaining the inactive state on one X-chromosome in females (Gartler and Goldman, 2005). To formalize this argument, the Illumina technology is a two channel array that measures the proportion methylated for each CpG site, defined as β = M/(M + U) where M represents the signal intensity from the methylated allele and U represents the signal intensity from the unmethylated allele. Therefore β takes on values in the [0, 1] interval with 0 representing an unmethylated CpG site and 1 representing a methylated CpG site. Next consider DNA methylation in normal females expressed as a mixture distribution, with π = 0.5 representing the proportion of X chromosomes inactivated and 1 −π representing the proportion of X chromosomes that are active. Therefore in females the proportion methylated can be expressed as β_female = π × 1 + (1 − π) * 0 = 0.5. Because this proportion is 0.5, the X chromosome in normal females is said to be hemi-methylated (Bibikova et al., 2006). As previously mentioned, males should have little to no X chromosome methylation (except for XIST) because normal males have only one X chromosome, so for normal males π = 0 such that in males the proportion methylated can be expressed β_male = π × 1 + (1 − π) * 0 = 0. For CpG sites on the X chromosome, the expected difference in proportion methylated between females and males is 0.5. Therefore DNA methylation datasets can serve as a biological gold standard for assessing the performance of FDR and FWER methodologies. However, because X chromosome inactivation serves as a dosage compensator of X chromosome genes in females (Avner and Heard, 2001), gene expression datasets cannot necessarily be used for the same purpose.

High-throughput methylation data may additionally be useful for comparing classification methods. Similar to the FDR literature, performance of classifiers for microarray data has often been assessed using limited simulation studies and/or by application of the classifiers to applied microarray datasets. When using applied microarray datasets, the assessment of the method’s variable selection performance can only be made by subjectively interpreting the biological function of the genes selected by each model in relation to the modeled disease process. For example, in a study comparing various penalized classification models, the investigators generated p variables and n samples using three simulation scenarios (Garcia-Magariños et al., 2010). For simulation scenario 1, p = 9 and n = 200 or 400; for simulation scenario 2, p = 12 and n = 200; and for simulation scenario 3, p = 1, 000 and n = 100, 200, or 400. The number of variables which had nonzero coefficients (s), i.e. true predictors, was s = 3 for scenarios 1 and 2 and s = 10 for scenario 3. These simulation scenarios are unlike data that result from high-throughput genomic experiments, where typically p > 20, 000 and n < 100. The authors also compared the performance of the classifiers by applying the methods to two well-known gene expression datasets, namely the leukemia (Golub et al., 1999) and colon datasets (Alon et al., 1999). A limitation is that for these application datasets, the veracity of each null hypothesis tested is unknown so that an objective evaluation of performance of variable selection capabilities cannot be rendered for application data. Therefore, in addition to assessing the performance of FDR and FWER methodologies, high-throughput methylation datasets that include normal healthy subjects with gender annotated presents useful data for comparing classifier performance and appropriateness of classifiers’ variable selection capabilities because CpG sites on sex chromosomes are known to be truly differentially methylated between males and females.

Because identifying differentially expressed genes is a common goal among high-throughput genomic studies, methylation datasets in which the CpG sites that are differentially expressed are known presents a useful means to assess FDR/FWER techniques. Moreover, these datasets may prove useful for characterizing the performance of multiple comparison procedures, and may find further utility in other tasks such as comparing classifiers and evaluating the performance of meta-analytic methods for microarray data.