The Power of Hard-Sphere Models: Explaining Side-Chain Dihedral Angle Distributions of Thr and Val

Abstract

The energy functions used to predict protein structures typically include both molecular-mechanics and knowledge-based terms. In contrast, our approach is to develop robust physics- and geometry-based methods. Here, we investigate to what extent simple hard-sphere models can be used to predict side-chain conformations. The distributions of the side-chain dihedral angle χ₁ of Val and Thr in proteins of known structure show distinctive features: Val side chains predominantly adopt χ₁ = 180°, whereas Thr side chains typically adopt χ₁ = 60° and 300° (i.e., χ₁ = ±60° or g− and g⁺ configurations). Several hypotheses have been proposed to explain these differences, including interresidue steric clashes and hydrogen-bonding interactions. In contrast, we show that the observed side-chain dihedral angle distributions for both Val and Thr can be explained using only local steric interactions in a dipeptide mimetic. Our results emphasize the power of simple physical approaches and their importance for future advances in protein engineering and design.

Introduction

Ramachandran and Ramachandran (1) calculated the sterically allowed combinations of protein backbone dihedral angles (ϕ and ψ) using hard-sphere models of dipeptides. They found excellent agreement between the allowed ϕ- and ψ-angles they calculated and reported in the Ramachandran plot, and those found in the first crystal structures of peptides and small proteins (2). Since then, researchers have found that the ϕ- and ψ-angles for all amino acids in thousands of proteins fall within the allowed regions of the Ramachandran plot. Indeed, a comparison of the ϕ- and ψ-angles for all amino acids in a protein with the Ramachandran plot is now a routine quality test for new protein structures (3,4).

Surprisingly, few similar calculations have been performed to predict sterically allowed conformations of amino-acid side-chain dihedral angles (5,6). Some studies have employed quantum mechanical calculations to predict side-chain dihedral angle distributions for dipeptides (7,8). However, such calculations are too computationally intensive to be routinely applied to proteins. As of this writing, most structure prediction software employs the statistics of side-chain dihedral angles that occur in proteins of known structure to construct knowledge-based side-chain dihedral angle energy functions (9–11) or rotamer libraries (12–20).

We present the results of our calculations on the side-chain dihedral angle distributions of Val and Thr using a simple hard-sphere model for a dipeptide mimetic analogous to that of Ramachandran and colleagues (Fig. 1). It is essential to include all hydrogen atoms in the model; indeed interatomic clashes that arise from rotations of the hydroxyl and methyl hydrogens within the dipeptide mimetic determine the form of the side-chain dihedral angle distributions. Our predictions for the side-chain dihedral angle distributions for Val and Thr match those observed in proteins of known structure. We chose Val and Thr for the following reasons: 1), both possess a single side-chain dihedral angle, χ₁; 2), Val has an exclusively nonpolar, aliphatic side chain, whereas there is a polar, hydroxyl group on the Thr side chain; and 3), both Val and Thr are β-branched, but their side-chain dihedral angle distributions are distinct (Fig. 2). In particular, the major peak in the side-chain dihedral angle distribution for Val in an α-helix backbone conformation is at χ₁ = 180°, whereas the major peak for Thr in an α-helix conformation is at χ₁ = 300° (g⁺ or −60°). Note that our results provide an alternative explanation for the dihedral angle distribution of Thr in the α-helix conformation. Previous hypotheses invoked interresidue hydrogen-bonding and steric clashes between the Thr side-chain and main-chain atoms on neighboring residues (21–23).

Figure 1.

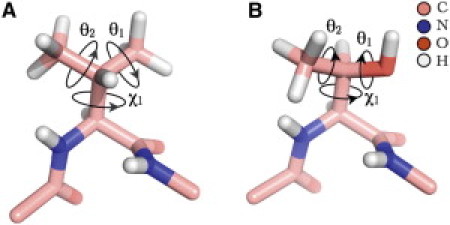
Stick representation of (A) Val and (B) Thr dipeptide mimetics. Both Val and Thr are shown in an α-helix backbone conformation (ϕ = −57°, ψ = −47°). The side-chain dihedral angle χ₁ (N-C_α-C_β-C_γ1) for both Val (χ₁ = 179.5°) and Thr (χ₁ = 117.7°), hydrogen dihedral angles θ₁ = 180° (C_α-C_β-C_γ1-${\text{H}}_{C_{\gamma 1}}^1$ on C_γ1) and θ₂ = 0° (C_α-C_β-C_γ2-${\text{H}}_{C_{\gamma 2}}^1$ on C_γ2) for Val and θ₁ = 180° (C_α-C_β-O_γ1-${\text{H}}_{C_{\gamma 1}}^1$) and θ₂ = 30° (C_α-C_β-C_γ2-${\text{H}}_{C_{\gamma 2}}^1$) for Thr are indicated.

Figure 2.

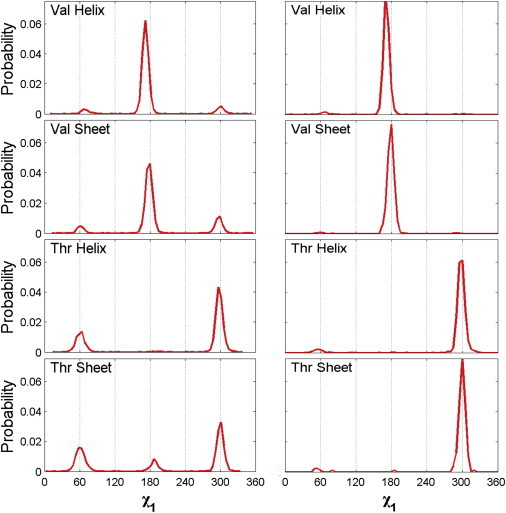
Probability distributions of side-chain dihedral angles for Val and Thr. (Left panel) Side-chain χ₁ distributions for Thr and Val averaged over all α-helix (or β-sheet) conformations with ϕ- and ψ-angles within the Dunbrack secondary structure classification scheme. (Right panel) Side-chain χ₁ distributions for conformations of Thr and Val in the Dunbrack database with ϕ- and ψ-values over narrow ranges (±10°) that are centered on the canonical α-helix and β-sheet ϕ- and ψ-angles (ϕ = −57°, ψ = −47° for α-helix and ϕ = −119°, ψ = −113° for β-sheet).

Materials and Methods

Database of protein crystal structures

We compare our predictions of the side-chain dihedral angle distributions for Val and Thr to the distributions obtained from the Dunbrack database (20). This database is composed of 850 high-resolution nonhomologous protein structures (sequence identity <50%) solved by x-ray crystallography and deposited in the Protein Data Bank. Only structures with resolution ≤1.7 Å, side chain B-factors <30 Å², and R-factors ≤0.25 are included.

We calculated two sets of probability distributions for Val and Thr in both α-helix and β-sheet backbone conformations from the Dunbrack database (Fig. 2). (The probability distribution of ϕ- and ψ-angles for Thr and Val in the Dunbrack distribution are shown in Fig. S6 in the Supporting Material.) The left panel of Fig. 2 provides the side-chain χ₁ distributions for Thr and Val averaged over all α-helix (or β-sheet) conformations, where the secondary structure classification was deposited into the Protein Data Bank. This first data set includes 3418 examples of Val in an α-helix, 5020 examples of Val in a β-sheet, 2598 examples of Thr in an α-helix, and 2727 examples of Thr in a β-sheet. The right panel shows the side-chain χ₁ distributions for Thr and Val for conformations with ϕ- and ψ-values over narrow ranges (±10°) that are centered on the canonical α-helix and β-sheet ϕ- and ψ-angles (ϕ = −57°, ψ = −47° for α-helix and ϕ = −119°, ψ = −113° for β-sheet). The second data set includes 2149 examples of Val in an α-helix, 681 examples of Val in a β-sheet, 1453 examples of Thr in an α-helix, and 189 examples of Thr in a β-sheet. The probability distributions for the side-chain dihedral angle χ₁ were calculated using a bin size of 5° and normalized so that the area under the curve equals 1.

Hard-sphere model

The χ₁ dihedral angles of Val and Thr are defined by the clockwise rotation around the C_α-C_β bond (viewed from C_α to C_β) of the backbone atoms N-C_α-C_β-C_γ1. Note that we use the standard IUPAC-IUB (24) chemistry conventions for the atomic labeling order. Thus, χ₁ = 180° for Val puts its two C_γ atoms in the same position that the β-branch of Thr would occupy for χ₁ = 60°. Thus, O_γ1 in Thr is equivalent to C_γ2 in Val. In Val, the dihedral angle is defined by the clockwise rotation about the C_β-C_γ1 bond (viewed from C_β to C_γ1) involving the side-chain atoms C_α-C_β- C_γ1-${\text{H}}_{O_{\gamma 1}}^1$, and the θ₂ dihedral angle is defined by the clockwise rotation about the C_β-C_γ2 bond (viewed from C_β to C_γ2) involving the side-chain atoms C_α-C_β-C_γ2-${\text{H}}_{C_{\gamma 2}}^1$. In Thr, the θ₁ dihedral angle is defined by the clockwise rotation about the C_β-O_γ1 bond (viewed from C_β to O_γ1) involving the side-chain atoms C_α-C_β-O_γ1-${\text{H}}_{O_{\gamma 1}}^1$, and the θ₂ dihedral angle is defined in the same way as θ₂ for Val. (See Fig. 1 and Fig. S1.)

We built the Val and Thr dipeptide mimetics (n-acetyl-L-Val-methylester and n-acetyl-L-Thr-methylester) starting from randomly chosen Val and Thr residues from the Dunbrack database, with all hydrogens added using the REDUCE program (25). (See Fig. 1.) The bond lengths and bond angles of the dipeptide mimetics were set to the mean bond length and angles associated with Val and Thr residues in Dunbrack database. (See Tables 1 and 2, and see Table S1, Table S2, Table S3, and Table S4 and Fig. S2 in the Supporting Material). The backbone conformations were set to canonical α-helix (ϕ = −57°, ψ = −47°) and β-sheet (ϕ = −119°, ψ = −113°) values.

Table 1.

Mean bond lengths for the seven bond types in Val and Thr from the Dunbrack database

Bond type	Mean bond length (Å)
	Val	Thr
C′–O	1.23	1.23
C′–N	1.33	1.33
Cα–C′	1.53	1.53
Cα–N	1.46	1.46
Cα–Cβ	1.55	1.54
Cβ–Cγ1	1.52	—
Cβ–Oγ1	—	1.43
Cβ–Cγ2	1.52	1.52

C′ indicates the backbone carbonyl carbon. (See the top panel of Fig. S2 for the bond length distributions.)

Table 2.

Mean bond angle for the 10 bond angles in Val and Thr from the Dunbrack database

Bond angle	Mean bond angle (°)
	Val	Thr
C′(i − 1)–N–Cα	121.7	121.0
N–Cα–C′	110.2	111.2
N–Cα–Cβ	111.2	109.4
C′–Cα–Cβ	109.3	111.0
Cα–C′–O	120.7	120.7
Cα–C′–N(i + 1)	116.2	116.5
O–C′–N(i + 1)	122.9	122.7
Cγ1–Cβ–Cγ2	110.2	—
Oγ1–Cβ–Cγ2	—	109.2
Cγ1–Cβ–Cα	110.2	—
Oγ1–Cβ–Cα	—	109.5
Cγ2–Cβ–Cα	110.0	110.6

C′ indicates the backbone carbonyl carbon; C′(i – 1) is the carbonyl carbon in the residue preceding Val or Thr; N(i + 1) is the nitrogen atom in the residue following Val or Thr. (See the bottom panel of Fig. S2 for the bond angle distributions.)

All bond lengths, bond angles, and backbone dihedral angles are fixed whereas χ₁, θ₁, and θ₂ are varied. The side-chain dihedral angle χ₁ was sampled from 0° to 360° in 5° increments, whereas θ₁ and θ₂ in Val and θ₂ in Thr were sampled from 0° to 120° in 5° increments because of the threefold symmetry of the methyl group. The value θ₁ for the OH group in Thr is sampled from 0° to 360° in 5° increments. Thus, we sampled 41, 472 (72 × 24 × 24) and 124, 416 (72 × 24 × 72) combinations of χ₁, θ₁, and θ₂ in Val and Thr, respectively. The positions of the nonrotatable hydrogens, including those in the NH group and on C_α and C_β, are determined by chemistry.

The set of conformations that arise from the dihedral angle rotations, χ₁, θ₁, and θ₂, are obtained using the following computational technique. The new position ${\overrightarrow{r}}^{\prime }=\left(x^{\prime },y^{\prime },z^{\prime }\right)$ of an atom originally located at $\overrightarrow{r}=\left(x,y,z\right)$ following a rotation by an angle w (where w can be χ₁, θ₁, or θ₂) about a unit vector $\hat{n}=\left(n_x,n_y,n_z\right)$ (i.e., from C_α to C_β for χ₁ in both Val and Thr, from C_β to C_γ1 for θ₁ in Val, from C_β to O_γ1 for θ₁ in Thr, and from C_β to C_γ2 for θ₂ in both Val and Thr) is given by

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)=\mathbf{Q}\left(\begin{array}{c}x\\ y\\ z\end{array}\right),$$ (1)

where

$$\mathbf{Q}=\left(\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2\left(q_1{q}_2-q_0{q}_3\right)& 2\left(q_0{q}_2+q_1{q}_3\right)\\ 2\left(q_1{q}_2+q_0{q}_3\right)& \left(q_0^2-q_1^2+q_2^2-q_3^2\right)& 2\left(-q_0{q}_1+q_2{q}_3\right)\\ 2\left(-q_0{q}_2+q_1{q}_3\right)& 2\left(q_0{q}_1+q_2{q}_3\right)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right),$$ (2)

and where $q_0=\text{cos}w/2$, $q_1=n_x\text{sin}w/2$, $q_2=n_y\text{sin}w/2$, and $q_3=n_z\text{sin}w/2$. The unit vectors $\hat{n}$ are $\left({\overrightarrow{r}}_{C_{\alpha }}-{\overrightarrow{r}}_{C_{\beta }}\right)/\left|{\overrightarrow{r}}_{C_{\alpha }}-{\overrightarrow{r}}_{C_{\beta }}\right|$ for χ₁ in both Val and Thr, $\left({\overrightarrow{r}}_{C_{\beta }}-{\overrightarrow{r}}_{C_{\gamma 1}}\right)/\left|{\overrightarrow{r}}_{C_{\beta }}-{\overrightarrow{r}}_{C_{\gamma 1}}\right|$ for θ₁ in Val, $\left({\overrightarrow{r}}_{C_{\beta }}-{\overrightarrow{r}}_{O_{\gamma 1}}\right)/\left|{\overrightarrow{r}}_{C_{\beta }}-{\overrightarrow{r}}_{O_{\gamma 1}}\right|$ for θ₁ in Thr, and $\left({\overrightarrow{r}}_{C_{\beta }}-{\overrightarrow{r}}_{C_{\gamma 2}}\right)/\left|{\overrightarrow{r}}_{C_{\beta }}-{\overrightarrow{r}}_{C_{\gamma 2}}\right|$ for θ₂ in both Val and Thr. Because the dihedral angle rotations about ${\hat{n}}_{{\chi }_1}$, ${\hat{n}}_{{\theta }_1}$, and ${\hat{n}}_{{\theta }_2}$ commute, the order in which the rotations are performed does not affect the final location ${\overrightarrow{r}}^{\prime }$.

We determine for each combination of χ₁, θ₁, and θ₂ the distance between all pairs of nonbonded atoms. If the distance between the centers of all nonbonded atoms satisfies

$$r_{ij}\ge d_{ij},$$ (3)

where d_ij is the sum of their radii, we consider the conformation with this particular χ₁, θ₁, and θ₂ as “allowed”. The proportion of θ₁ and θ₂ combinations that yield allowed conformations was tabulated for each χ₁ sampled. From this fraction, we calculate the probability distribution of allowed side-chain dihedral angles for Val and Thr.

We varied the five atom sizes in increments of 0.05 Å over the ranges indicated in Table 3. Thus, 6 × 10⁴ different combinations of atomic radii were tested. For each combination of atom sizes and dipeptide model (Val in α-helix, Val in β-sheet, Thr in α-helix, and Thr in β-sheet), we scored the predicted χ₁ probability distributions to determine how well they match the observed distributions in the right panel of Fig. 2.

Table 3.

Atom sizes screened in the hard-sphere model of Val and Thr dipeptide mimetics

Atom	Range of radii (Å)	Number of sizes tested
H	0.90–1.10	5
N	1.25–1.60	8
O	1.10–1.55	10
C	1.30–2.00	15
C′	1.30–1.75	10

For each combination of atom sizes (using increments of 0.05 Å), we calculated the interatomic distances of nonbonded atoms to determine steric clashes.

We considered a spectrum of scoring functions to determine the optimal values for the five atomic radii. For example, we considered the scoring function

$$S_1=\stackrel{{360}^{°}}{\sum _{{\chi }_1=0^{°}}}{\left(P_{\text{obs}}\left({\chi }_1\right)-P_{\text{calc}}\left({\chi }_1\right)\right)}^2,$$ (4)

where P_obs (χ₁) is the observed probability distribution of χ₁ from the Dunbrack database in the right panel of Fig. 2, and P_calc (χ₁) is our prediction. Smaller scores indicate closer correspondence between P_obs and P_calc. However, S₁ over-weights matches of the highest peaks.

We also considered the Matthew's correlation coefficient S₂ (26). We first convert the probabilities at each χ₁ to binary numbers p(χ₁) = 1 (for P(χ₁) > ε) and p(χ₁) = 0 (for P(χ₁) < ε), where ε = 6 × 10⁻⁵ is the smallest nonzero value for the probability in the Dunbrack database. We define

$$S_2=\frac{\left(TP\right)\left(TN\right)-\left(FP\right)\left(FN\right)}{\sqrt{\left(TP+FN\right)\left(TN+FP\right)\left(TP+FP\right)\left(TN+FN\right)}},$$ (5)

where $TP={\sum }_{{\chi }_1}{p}_{\text{obs}}{p}_{\text{calc}}$ is the total number of true-positive events, $TN={\sum }_{{\chi }_1}{\overline{p}}_{\text{obs}}{\overline{p}}_{\text{calc}}$ is the total number of true-negative events, $FP={\sum }_{{\chi }_1}{\overline{p}}_{\text{obs}}{p}_{\text{calc}}$ is the total number of false-positive events, and $FN={\sum }_{{\chi }_1}{p}_{\text{obs}}{\overline{p}}_{\text{calc}}$ is the total number of false-negative events. The value $\overline{p}$ is the logical NOT operator that changes the zero bit to 1 and the one bit to zero. S₂ = 1 represents a perfect prediction and S₂ = 0 represents a random prediction. We find that S₂ over-weights matches between the smallest peaks, which are subject to large statistical fluctuations due to limited data.

We found that using a third scoring function S₃ ameliorates the problems associated with the first two scoring functions. We define

$$S_3=\sum _{{\chi }_1=0^{\circ }}^{{360}^{\circ }}\frac{P_{\text{obs}}\left({\chi }_1\right)+P_{\text{calc}}\left({\chi }_1\right)}{2}{e}^{-\frac{{\left(P_{\text{obs}}\left({\chi }_1\right)-P_{\text{calc}}\left({\chi }_1\right)\right)}^2}{8{\sigma }^2}}.$$ (6)

The maximum score for a perfect match between the observed and calculated distributions is 1. The minimum score $\left(S_3^{\text{min}}\approx e^{-1/\left(8{\sigma }^2\right)}\approx 0\right)$ occurs when there is no overlap between P_obs and P_calc. The prefactor P_obs + P_calc of the scoring function weights the matches between the high probability peaks more than matches between lower probability subpeaks. The Gaussian factor with σ = 0.04 was included to appropriately weight matches of peaks of differing heights.

By applying the scoring function S₃, we obtain the best overall match between the observed and calculated side-chain probability distributions for Val and Thr (in α-helix and β-sheet backbone conformations) with the following radii: 1.05 Å for hydrogen, 1.5 Å for sp³ carbon, 1.4 Å for sp² carbon, 1.4 Å for nitrogen, and 1.45 Å for oxygen (Fig. 3). We optimized over all four distributions at once because we sought a generally applicable result rather than multiple, optimal atom sizes that depend on amino-acid type and backbone conformation. In Fig. 5, we show a comparison of P_calc and P_obs for the optimal set of atom sizes. In contrast, we show P_calc for typical nonoptimized sets of atom sizes in Fig. S3.

Figure 3.

Reported values of atomic radii from the literature. Atomic radii from 12 different sources are indicated for hydrogen, nitrogen, oxygen, carbon (sp³ and sp²), and sulfur. (Stars) The atom sizes that yield the best match between our calculated and the observed distributions of side-chain dihedral angles for Val and Thr. In our model, all carbons are sp³ except for the main chain carbonyl carbon (C′), which is sp². Note references (1,33–43) in the right panel.

Figure 5.

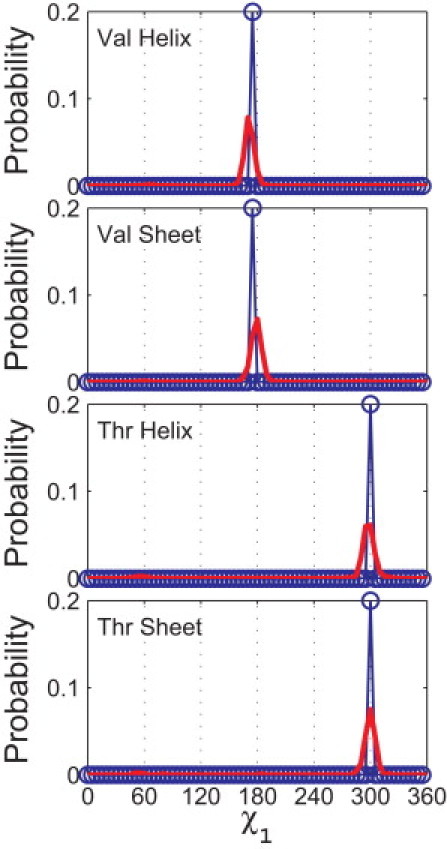
Comparison of the probability distributions of the observed and calculated side-chain dihedral angles for Val and Thr. Probability distributions of the side-chain dihedral angle χ₁ from the Dunbrack distribution (20) (red lines) are compared to predictions from our hard-sphere model (blue circles) for Val (α-helix and β-sheet) and Thr (α-helix and β-sheet). The calculation of the probability distribution for χ₁ for the hard-sphere model is described in the caption to Fig. 4. Both P_calc and P_obs are normalized so that the area below the curve is 1. (The set of atom sizes used to calculate P_calc is indicated by the star symbols in Fig. 3.)

The sensitivity of the score S₃ to variations in the atomic sizes is shown in Fig. S4 and Fig. S5. In all cases, the values selected for the atomic radii correspond to minima in S₃. The score S₃ is most sensitive to the size of the Csp² and Csp³ atom sizes. We also confirmed that our hard-sphere model with the optimized set of atomic radii captures the essential features of the Ramachandran map of backbone dihedral angles ϕ and ψ of the alanyl dipeptide mimetic (n-acetyl-L-Ala-methylester).

Results

We investigated the extent to which simple hard-sphere models for dipeptide mimetics can predict the allowed conformations of amino-acid side chains. Specifically, we calculate the side-chain dihedral angle distribution P(χ₁) for Val and Thr in canonical α-helix and β-sheet backbone conformations. We compare the results of our calculations with the distributions of the side-chain dihedral angle χ₁ for Val and Thr observed in a database of high-resolution nonhomologous protein crystal structures (20). Such comparisons are the benchmark for our calculations. The side-chain dihedral angle distributions of χ₁ for Val and Thr from the Dunbrack database are shown in Fig. 2. The left panel shows the χ₁ distributions obtained from all residues designated as either α-helix or β-sheet and the right panel shows the distribution for the canonical α-helix and β-sheet ϕ- and ψ-values (ϕ = −57°, ψ = −47° for α-helix and ϕ = −119°, ψ = 113° for β-sheet).

The fact that the two χ₁ distributions in Fig. 2 have small but significant differences indicates that the side-chain dihedral angle distributions vary to some extent with the backbone conformation. A comprehensive study of the extent of such variations will be the subject of future work. In this article, we focus on calculations of the sterically allowed side-chain dihedral angle conformations for the canonical α-helix and β-sheet ϕ- and ψ-values.

The distributions for Val in both the α-helix and β-sheet conformations possess a major peak at χ₁ = 180° and minor peaks at 60° and 300° that are ϕ- and ψ-dependent. In contrast, the χ₁ distribution for Thr displays a major peak at 300° with minor peaks at 60° and 300° that are ϕ- and ψ-dependent.

It has been suggested that the absence of the peak in the side-chain dihedral angle distribution at χ₁ = 180° for Thr in an α-helix conformation is because Thr at position i can hydrogen-bond with residues at (i − 4) when χ₁ = 60° or 300° (21). It has also been suggested that the χ₁ = 180° conformation is disallowed because it leads to steric clashes between the methyl C_γ of Thr at position i and the main-chain oxygen of residue (i − 3) (22,23). Whereas these explanations of the side-chain dihedral angle distributions emphasize interresidue constraints, our studies focus on local steric constraints.

We employ a hard-sphere representation of Val and Thr dipeptide mimetics with fixed bond lengths and angles (see Tables 1 and 2). The dipeptide mimetics possess a central amino acid whose side chain is either Val or Thr, which is flanked by “half of an amino-acid backbone” on either side (Fig. 1 and Fig. S1). To specify the geometry of the dipeptide mimetic, we set the values of the 7 bond lengths and 10 bond angles for Val and Thr to be the mean values of those bond lengths and angles observed in the Dunbrack database. For both Val and Thr dipeptide mimetics, the backbone conformations were set to either canonical α-helix or β-sheet ϕ- and ψ-angles. Our model includes explicit hydrogen atoms (10 on Val and 8 on Thr) that are initially placed using the REDUCE software package (25). The side-chain methyl and hydroxyl groups are subsequently rotated by the dihedral angles θ₁ and θ₂ to sample different conformations (Fig. 1).

We then calculate whether a particular combination of χ₁, θ₁, and θ₂ is sterically allowed (no clashes) or disallowed (one or more clashes) for each combination of sizes for all five atom types (H, N, O, C(sp³), and C(sp²)). Fig. 3 shows the ranges of radii for each atom type that have been reported in the literature. These values include measurements from gas phase experiments, small molecule and protein crystal structures, and quantum mechanics calculations, and thus represent reasonable ranges for our study. Therefore, in our calculations, we varied atom sizes in increments of 0.05Å over the following ranges: H = 0.9–1.1 Å, N = 1.25–1.6 Å, O = 1.1–1.55 Å, Csp³ = 1.3–2.0 Å, and Csp² = 1.3–1.75 Å (Table 3). For all combinations of atom sizes (6 × 10⁴ in total), we sampled χ₁, θ₁, and θ₂ in 5° increments. We considered several scoring functions and selected S₃ in Eq. 6 to evaluate our results. We describe the different scoring functions and the reason for choosing S₃ in the Materials and Methods section. We thus identified the combination of atom sizes (see star symbols in Fig. 3) that gives the best match between our predictions and the observed χ₁ distributions for Val and Thr in the α-helix and β-sheet conformations. In Fig. 4, we describe our method of calculating the χ₁ distribution using Val in an α-helix conformation as an example. For a particular combination of atom sizes, we identify the number of atomic clashes for each combination of χ₁, θ₁, and θ₂. For each 5° χ₁ increment, we calculate the fraction of θ₁, and θ₂ combinations that have no steric clashes (top panel of Fig. 4), and plot this fraction (as a normalized probability distribution) versus χ₁ (bottom panel of Fig. 4).

Figure 4.

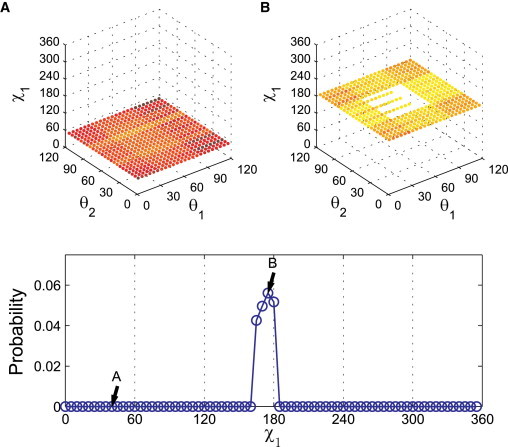
Illustration of the prediction of the χ₁ probability distribution using Val in the α-helix backbone conformation. We sampled χ₁ from 0° to 360° and θ₁ and θ₂ from 0° to 120° every 5°. Each data point is colored from white (no clashes) to dark red (highest number of clashes). (A, top panel) The layer at χ₁ = 40° with no white data points corresponds to probability P_calc = 0 as indicated in the bottom panel. (B, top panel) The layer at χ₁ = 175° with approximately one-eighth of all possible θ₁ and θ₂ allowed combinations corresponds to point B in the lower panel. The same calculations are performed for all sampled values of χ₁ (and shown as the blue points in the lower panel). The probability P_calc is normalized so that the area below the curve is 1. (The set of atom sizes used to calculate P_calc is indicated by the star symbols in Fig. 3.)

In Fig. 5, we compare the predicted χ1 probability distributions for Val and Thr in the α-helix and β-sheet conformations to the corresponding χ₁ distributions for residues with the canonical α-helix and β-sheet ϕ- and ψ-values taken from the Dunbrack database. Our calculations predict the strongest peaks of the observed side-chain distributions, i.e., the strong peaks at 180° for Val in the α-helix and β-sheet conformations and at 300° for Thr in the α-helix and β-sheet conformations.

Thus, we have demonstrated that using a hard-sphere model of a dipeptide mimetic with a single set of atom sizes is sufficient to describe the major attributes of the side-chain dihedral angle distributions for Val and Thr in both α-helix and β-sheet backbone conformations. Note that no additional features are required to describe the side-chain dihedral angle distribution for Thr.

Discussion

We have shown that we can predict the key features of the side-chain dihedral angle distributions of Val and Thr in both α-helix and β-sheet backbone conformations using only steric interactions. No steric interactions other than those involving atoms in the dipeptide mimetic are considered. Also, the side-chain OH group of Thr and backbone CO and NH groups are modeled as hard spheres with no polarity and hydrogen-bonding interactions.

Val possesses a simple aliphatic side chain and thus one might not be surprised that a steric model can predict its side-chain dihedral angle distributions (Fig. 5). In contrast, Thr possesses a polar side chain, and thus one might expect that a repulsive hard-sphere model with only intradipeptide interactions would not be able to predict its side-chain dihedral angle distributions. However, the data show that we can predict the side-chain dihedral angle distributions for both Thr and Val. In particular, we predict the absence of major peaks at 180° and the presence of major peaks at 300° and subpeaks at 60° for Thr in both α-helix and β-sheet backbone conformations.

The prevailing two explanations in the literature for the observed side-chain dihedral angle distribution for Thr in the α-helix conformation are the following: 1), The 60° and 300° side-chain dihedral angles are favored because in these conformations the Thr side chain (residue i) can hydrogen bond with the backbone carbonyl oxygen at location (i − 3) or (i − 4) (21,22). Indeed, McGregor et al. (21) state, “Hydrogen bonding is almost certain to explain why these residues [Ser and Thr] show a shift toward g⁺ [300°] in the α-helix.” 2), For Thr with χ₁ = 180°, there is an interresidue clash between the methyl C_γ on the Thr side chain at residue i and the main-chain oxygen of residue (i − 3) (21,22). However, we argue that these reasons cannot be the fundamental explanations for the observed χ₁ distributions for Thr: 1), The 60° and 300° side-chain dihedral angles are highly populated in both the α-helix and β-sheet conformations. Thus, the hydrogen-bonding based explanation cannot be the fundamental reason for the observed χ₁ distributions because χ₁ = 60° and 300° do not position the side chain for hydrogen bonding in the β-sheet backbone conformation; and 2), our calculations show that we do not need to include nonlocal interresidue steric clashes (i.e., we do not include residues (i − 3) or (i − 4) in the model) to predict the observed χ₁ distributions. We believe that our conclusion that steric constraints determine the χ₁ distributions for Thr (without the necessity to include any explicit energetic contribution from side-chain H-bonding) is of fundamental importance. However, once the side chain for Thr in the α-helix conformation is in one of its sterically preferred conformations, it is well positioned to hydrogen bond.

Thus, our key finding is that only local steric constraints among atoms within a dipeptide are sufficient to predict the observed side-chain dihedral angle distributions. Having demonstrated the power of this approach (27), we will perform similar studies of all amino-acid side chains to determine which side-chain dihedral angle distributions can be predicted using simple hard-sphere models of dipeptide mimetics and which require models with additional features. We envision that our hard-sphere model will not be able to capture the behavior of the side-chain dihedral angle distributions for all polar and charged residues. Determining how far the steric model can take us, and when additional features must be included to reproduce observed behavior, is of key importance and will be the subject of future work.

Our modeling methods do not rely on knowledge-based and statistical approaches that overemphasize average properties of the side-chain dihedral angle distributions. There is ample precedent for this approach in studies of organic molecules (28–31). Instead, we will develop a fundamental understanding of the side-chain dihedral angle distributions, which will allow us to better rank and compare individual protein designs. In addition, our approach will allow us to predict the conformations of peptide foldamers (32), for which there is limited structural data.