A Physics-Based Approach of Coarse-Graining the Cytoplasm of Escherichia coli (CGCYTO)

Abstract

We have investigated protein stability in an environment of Escherichia coli cytoplasm using coarse-grained computer simulations. To coarse-grain a small slide of E. coli's cytoplasm consisting of over 16 million atoms, we have developed a self-assembled clustering algorithm (CGCYTO). CGCYTO uses the shape parameter and asphericity as well as a parameter λ (ranging from 0 to 1) that measures the covolume of a test protein and a macromolecule against the covolume of a test protein and a sphere of equal volume as that of a macromolecule for the criteria of coarse-graining a cytoplasmic model. A cutoff λ_c = 0.8 was chosen based on the size of a test protein and computational resources and it determined the resolution of a coarse-grained cytoplasm. We compared the results from a polydisperse cytoplasmic model (PD model) produced by CGCYTO with two other coarse-grained hard-sphere cytoplasmic models: 1), F70 model, macromolecules in the cytoplasm were modeled by homogeneous hard spheres with a radius of 55 Å, the size of Ficoll70 and 2), HS model, each macromolecule in the cytoplasm was modeled by a hard sphere of equal volume. It was found that the folding temperature T_f of a test protein (apoazurin) in a PD model is ∼5° greater than that in a F70 model. In addition, the deviation of T_f in a PD model is twice as much as that in a HS model when an apoazurin is randomly placed at different voids formed by particle fluctuations in PD models.

Introduction

It has been shown that the thermodynamic and kinetic properties of a protein inside a cell are different from dilute aqueous solutions (1–9) because there are macromolecules that make up to 40% of the volume of a cell (10). These macromolecules exert volume exclusion on a protein (11), which changes its dynamics and behavior. It is called the macromolecular crowding effect (12) that stabilizes the folded state by destabilization of the unfolded states. It is one of the dominant factors affecting protein stability and dynamics inside cells (13–16). To advance the knowledge of protein biophysics in vivo, it is important to quantify the excluded volume effect in a crowded milieu.

The use of nonionic synthetic crowding agents (or crowders) such as Ficoll70 and Dextran (17) in experiments has enabled a quantitative understanding of the macromolecular crowding effect on protein stability (17), protein folding and structure (18–20), and protein associations (21–23). With regard to coarse-grained computer simulations, Ficoll70 has been modeled as semirigid (24,25) hard spheres with a radius 55 Å, and dextran has been represented by aspherical hard cores (19) that capture the shape of dextran in experiments. Despite its frequent use in experiments and simulations, they are still far from the resemblance of a cellular interior (26). For example, a cellular milieu is crowded with macromolecules of various sizes and shapes, or polydisperse (27,28), whereas synthetic crowders provide a rather homogenous environment. It has been shown that the sizes and shapes of crowders can greatly affect the folding process of a protein (29,30). In addition, recent experiments have shown a sizeable range of folding kinetics at different cytoplasmic regions of a cell (31). Thus, a polydisperse model that can adequately represent the composition inside a cell is needed for understanding protein folding in vivo.

Several groups have attempted to build a polydisperse cytoplasm model (PD model) based on limited experimental data. In 1996 (32) Bicout and Field created a cytoplasm model by incorporating three different sizes of crowders (hard sphere), and each represents ribosomes, proteins, and tRNA molecules, respectively. Other groups (33,34) considered several various sizes of spherical macromolecular crowders in the cytoplasm; as a result, the heterogeneity of shapes of these crowders was not included. McGuffee and Elcock built the atomistic cytoplasm of Escherichia coli (35) using 50 different species of macromolecules based on the experiments by Link et al. (36). Interestingly, other groups such as Alber et al. (37) have built macromolecular assemblies from proteomic data and biophysical methods. In these studies, macromolecules were modeled as rigid bodies to reduce the computational costs; however, they lack the capacity for probing structural fluctuations, which is important to the folding and association processes that are meaningful to their cellular functions.

Here, we have developed a novel, to our knowledge, algorithm (CGCYTO) that coarse-grains a section of high-resolution atomistic macromolecules of E. coli cytoplasm into a low-resolution one for the purpose of studying their volume exclusion effect on protein folding by using coarse-grained computer simulations (38). Chemical details are ignored in the model, whereas the characteristics of the shape of these macromolecules are maintained for the investigation of the macromolecular crowding effect. In addition to the shape parameter and asphericity derived from an inertia tensor, we set a physical parameter λ that measures the covolume of a test protein and a macromolecule against the covolume of a test protein and a sphere with equal volume of that macromolecule, to justify the criteria for the resolution of coarse-grained macromolecules in a cytoplasm. With the consideration of λ, the level of coarse-grained cytoplasmic model depends on the size of a test protein—when the size of a test protein is smaller than a macromolecule, a higher resolution with greater structural detail of the macromolecule is needed for a cytoplasmic model.

Another consideration in CGCYTO that determines the resolution is computational resources. This is why it is still not possible to include every single atom in molecular dynamics simulations. Although we have tried to include as many coarse-grained polydisperse macromolecules as possible in the simulations, there is a practical limit on the simulation size that we could afford to study protein folding. We have introduced a cutoff on λ to set the resolution of the coarse-grained cytoplasmic model, a resolution parameter λ_c. Any macromolecule whose λ is below λ_c will be further partitioned into smaller hard cores; otherwise, it is represented by a single hard sphere.

We have started with over 16 million atoms in a slice of Elcock's E. coli cytoplasm (35) and an apoazurin as our test protein. We set λ_c = 0.8 for CGCYTO. Subsequently, CGCYTO produced a coarse-grained cytoplasmic model composed of 4189 hard spheres (some of these hard spheres are connected into polydisperse models), and they occupy the same volume fraction as their corresponding atomistic models. Despite a low resolution of such a coarse-grained PD model, we have genuinely kept at least 80% of the covolume of each macromolecule in a cytoplasm that allows us to investigate the volume exclusion effect on protein folding dynamics of a single-domain, two-state protein apoazurin (39) by using coarse-grained molecular simulations. In addition, we have compared the folding dynamics of apoazurin in the PD model with two other coarse-grained hard-sphere cytoplasmic models to investigate the impact of heterogeneity in shape and sizes of macromolecules on volume exclusion in cytoplasmic models: 1), F70 model, macromolecules were modeled as homogeneous hard spheres with a radius of 55 Å, the size of Ficoll70; and 2), HS model, each macromolecule in the cytoplasm was modeled by a spherical hard core of equal volume. An increase in the folding free energy calculated from the molecular simulations based on F70 and the HS cytoplasmic model are qualitatively in agreement with the analytical calculations based on the scaled particle theory (SPT) by Minton (14) and Zhou (40). More importantly, we have computed the folding free energy of apoazurin in a cytoplasmic environment by coarse-grained molecular simulations. The level of coarse-graining a cytoplasm model by CGCYTO is dependent on the size of a test protein as well as a resolution cutoff dictated by computational resources, and it can be generalized for any protein of interest. Our proposed polydisperse model opens a door to investigate the thermodynamics and kinetics of a protein with a high structural flexibility in the cytoplasm in silico.

Methods

Coarse-grained modeling of E. coli's cytoplasm

We have developed an algorithm that coarse-grains a slice of E. coli's cytoplasm based on the structural data compiled by McGuffee and Elcock (35). It involves the top 50 macromolecules that account for 85% of the cytoplasm's characterized protein content by weight according to a study from Church's group (36). It is called the polydisperse (PD) model: each kind of the macromolecules was modeled as a hard sphere or a set of several connected hard spheres. The size and the number of these hard spheres of a macromolecule are determined by three factors: 1), the volume sum of hard spheres that are the same as the volume of a macromolecule, 2), the covolume (12) that is the excluded volume of this macromolecule and a test protein apoazurin (PDB ID: 1E65), and 3), the shape parameter (S) and asphericity (Δ) derived from inertia tensor (41).

The algorithm to construct a coarse-grained PD model is represented in Fig. 1 A. We first justify the shape of each macromolecule by its two rotationally invariant quantities determined from an inertia tensor, asphericity (Δ) and shape parameter (S). The values of S and Δ of the 50 macromolecules are provided in Table S1 in the Supporting Material. A sphere is represented by S = 0 and Δ = 0. Δ ranges from 0 to 1, and S ranges from −0.25 to 2 where a negative S represents an oblate and a positive S represents a prolate. Any macromolecule with S ≥ 0.25 or Δ ≥ 0.25 does not suffice for a sphere and it will be partitioned into several hard spheres in later steps. For any macromolecule with S < 0.25 and Δ < 0.25 to further justify its shape, it is required that an additional step is needed for the calculation of its covolume V_co-macro, which adequately captures the impact of crowder's shape into the macromolecular crowding effect (12). V_co-macro was calculated by a rolling ball approach in which a test protein modeled as a hard sphere with a radius of R_test rolls over the surface of a macromolecule that is assigned on a cubic grid atomically (42). Here, R_test was set to the radius of gyration of the crystal structure of apoazurin (14 Å). V_co-macro is compared against V_co-sphere defined in Eq.1. V_co-sphere is the covolume between a test protein and a sphere (with a radius R_eff) that has the same volume as that macromolecules. V_co-sphere, which represents the excluded volume between a perfect sphere and a test particle is below:

$$V_{co\mathit{-}sphere}=\frac{4\pi }{3}{\left(R_{eff}+R_{test}\right)}^3,$$ (1)

V_co-sphere is always less than V_co-macro when a macromolecule is not a sphere. Thus, we set the ratio between the two as λ:

$$\mathit{\lambda }=\frac{V_{co\mathit{-}sphere}}{{\mathit{V}}_{\mathit{co-macro}}},$$ (2)

λ ranges from 0 to 1 and it measures the extent to which a macromolecule's shape deviates from a sphere. The values of V_co-macro, V_co-sphere, and λ for each macromolecule are shown in Table S1.

Figure 1.

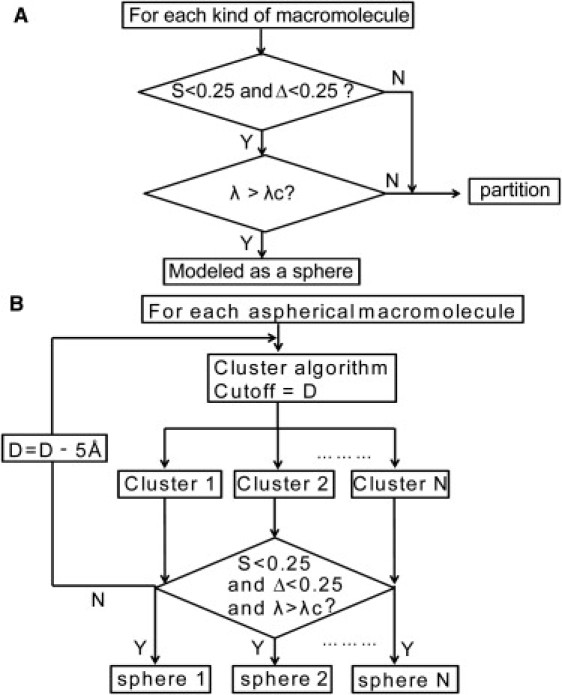
Flowchart of an algorithm to build a polydisperse PD model. (A) Decision on creating a polydisperse macromolecule for the PD cytoplasm model and (B) partition of an aspherical macromolecule into several spheres. See the definitions of S, Δ, λ, and D in the Methods section. λ_c = 0.8. The initial cutoff of a Euclidean distance D is 60 Å. N is the number of the partitioned clusters and it varies in each cycle when a new cutoff D is introduced.

To coarse-grain cytoplasm in which either a hard sphere or a number of connect hard spheres can represent a macromolecule, we set a cutoff λ_c as a resolution parameter such that any macromolecule with λ below λ_c is not a sphere and it should be further partitioned into several hard spheres in the next step. Otherwise, when λ ≥ λ_c, it can be represented by a single hard sphere and a controlled amount of shape information, which has been coarse-grained out from the model. The center of a sphere locates at the geometry center of a macromolecule with radius R_eff. In our study, we set λ_c = 0.8 and all of the macromolecules were partitioned into 1–5 beads. The covolume of a polydisperse macromolecule, V_co-PD, is computed and λ′ = V_co-PD/V_co-macro.

When a macromolecule cannot be considered as a single hard sphere, a nonhierarchical clustering method based on a self-organizing neural net algorithm (43,44) was used to automatically partition the atomic coordinates of a macromolecule into several clustered sets that can be further modeled into several smaller hard spheres without the assumption of any prior referenced structure. A detailed process of this clustering method is provided in the Supporting Material. A checkpoint for the determination of a spherical shape for each cluster is made at the end of the clustering process (S < 0.25, Δ < 0.25, and λ > 0.8). If it is not satisfied, a cutoff D (initially set at 60 Å) is then reduced by another 5 Å. This nonhierarchical clustering procedure repeats again until for every cluster a computed λ from its partitioned atoms exceeds λ_c, indicating that it is appropriate to represent a macromolecule by N connecting hard spheres. Fig. 1 B shows a flowchart of the CGCYTO algorithm. Table S3 shows the outcome of partitioning for every macromolecule for our PD model and Table S2 shows only the partitioning of macromolecules that are not considered as a single hard sphere. As a result, we have created an algorithm to produce a polydisperse coarse-grained cytoplasm that depends on the size of a test protein. A snapshot of a PD model is shown in Fig. 2, bottom left. The atomistic representation of cytoplasm is shown in Fig. 2, bottom right. The energy potential for the macromolecular crowders can be found in the Supporting Material.

Figure 2.

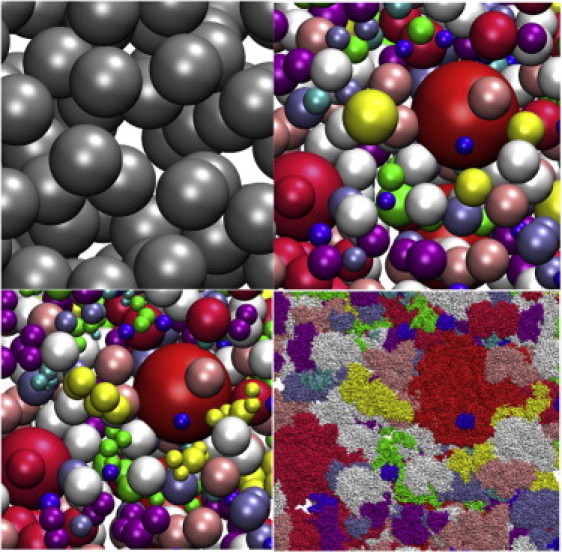
Illustration of several models that represent a portion of Escherichia coli cytoplasm. Upper left: the F70 model (φ_c = 32%); upper right: the HS model; bottom left: the PD model; and bottom right: the all-atomistic representations. See the definitions of the F70, HS, and PD models in the Methods section. Except in the F70 model, for macromolecules that are modeled as a single sphere, they are colored from red to blue according to its size; those that are partitioned into two spheres are colored in purple; those that can be partitioned into three spheres are colored in green; those that can be partitioned into four spheres are colored in cyan; and those that can be partitioned into five spheres are colored in yellow.

We have also developed another two types of coarse-grained cytoplasmic models to compare with the PD model: 1), The F70 (Ficoll70) model: the total volume fraction of macromolecules (φ_c = 32%) in the cytoplasmic model was captured by a periodic cubic box of hard spheres with a radius 55 Å (that is the size of a Ficoll70). In addition, two other volumes of fractions of Ficoll70 crowders (φ_c), φ_c = 25% and 40%, were investigated. A F70 model with φ_c = 32% is represented in Fig. 2, upper left. 2), The HS (hard sphere) model: each macromolecule with volume V_p was modeled as a hard sphere of equal volume with an effective radius $R_{eff}=\sqrt[3]{3V_p/4\pi }$ (42). The values of R_eff and V_p are provided in Table S1. For an HS model, φ_c is 32% and a snapshot of the HS model is shown in Fig. 2, upper right.

Simulation techniques

Coarse-grained molecular simulations were performed by using the Langevin equations of motion. An in-house developed version of AMBER10 (45) was used, where the Langevin equations of motion were integrated into the low-friction limit (46). The replica exchange method (47) was implemented to enhance the sampling efficiency of the simulations and details can be found in prior studies (13). There are 20 replicas and the range of simulation temperatures include 1.13, 1.17, 1.20, 1.23, 1.27, 1.30, 1.32, 1.33, 1.35, 1.36, 1.37, 1.38, 1.39, 1.4, 1.42, 1.43, 1.47, 1.50, 1.53, and 1.57 in the unit of k_BT/ε. The distribution of the potential energy is shown in Fig. S3. The integration time step is ${10}^{-3}{\tau }_L$, where ${\tau }_L={\left(m{\sigma }^2/\epsilon \right)}^{0.5}$. m is the mass of a C_α bead, ε is the solvent-mediated interaction, and σ is the van der Waals radius of a C_α bead. Each exchange was attempted at every 400 τ_L. There are a total of 48 million integration time steps per replica. Multiple initial structures have been used as initial conditions for the replica-exchange molecular dynamics. The collection of data was sampled at every 1000 integration steps. Thermodynamic properties and errors were calculated using the weighted histogram analysis method (48).

Results

Coarse-grained modeling of E. coli's cytoplasm

It is shown in Table S1 that the sizes and shapes of 50 macromolecules vary greatly. The shape of a macromolecule can be quite spherical, such as Ppa (S = 0 and Δ = 0), or it can be far from a sphere such as Frr (S = 1.18 and Δ = 0.71). To create a sound physics-based reasoning for the procedure of coarse graining, we must also take a test protein's size into account, because a larger test protein requires less detail on the coarse-grained cytoplasm. We therefore introduced another parameter λ that considers the size of a test protein model through the calculation of covolume—the volume excluded by both the test protein and a crowder. By setting λ_c = 0.8, it defines the resolution of a coarse-grained cytoplasm by setting a cutoff above which a macromolecule can be modeled as a sphere and below which it dictates the number of partitioned spheres for each macromolecule whose shape characteristics remain.

Using the criteria based on S, Δ, and λ, 50 macromolecules were divided into four groups: (group 1) S < 0.25, Δ < 0.25, and λ > 0.8, such as Ppa; (group 2) S < 0.25, Δ < 0.25, and λ < 0.8, such as AhpC; (group 3) S > 0.25, Δ > 0.25, and λ > 0.8, such as Pgk; (group 4) S > 0.25, Δ > 0.25, and λ < 0.8, such as Frr. The macromolecules in (group 1) were modeled as a single sphere. For a macromolecule in (group 2, 3, and 4), its coordinates were automatically partitioned to several smaller clusters—as described in the Methods section. Take Frr as an example, the calculations on structural characteristics are S = 1.18, Δ = 0.71, and λ = 0.74 before CGCYTO. After partitioning into three parts, all of the constituents can each be represented by a sphere with increased λ (Table S2): for the first bead, S = 0.1, Δ = 0.14, and λ = 0.9; for the second bead, S = 0.14, Δ = 0.17, and λ = 0.89; and for the third bead, S = 0.04, Δ = 0.08, and λ = 0.92. Note that λ of a 3-bead Frr macromolecule becomes 0.98 (Table S2), indicating that an aspherical Frr macromolecule can be adequately represented by three smaller spherical hard spheres, whereas the total volume of a macromolecule remains the same when a test protein is an apoazurin (Fig. S4).

For a macromolecule in (group 2), take AhpC as an example, S and Δ are close to 0 (S = −0.14 and Δ = 0.17). However, its λ = 0.75 is lower than λ_c = 0.8, indicating that the covolume made up of AhpC and a test protein (apoazurin) is far from that made of a sphere with the same volume as AhpCs and a test protein apoazurin, because AhpC is composed of 10 subunits that form a ring with a hole in the center. The radius of this hole is around 28 Å, which is larger than the radius of gyration of apoazurin in its folded state (15 Å). In other words, although the shape of AhpC is close to a sphere judged by S and Δ, the size of an apoazurin is small enough to pass through the center hole of AhpC. From an apoazurin's perspective, the shape of AhpC is closer to a ring than a sphere (Fig. S4). Thus, AphC needs to be further partitioned into a polydisperse model when an apoazurin is a test protein. Here, we emphasize that the level of a coarse-grained cytoplasm is dependent on the size of a test protein. If another protein with a size larger than 28 Å is introduced as a test protein and it cannot fit into the hole of AhpC, AhpC can then be modeled as a sphere.

For a macromolecule in (group 3), its criteria are the opposite of (group 2). For (group 3), take Pgk as an example, its λ is 0.87, indicating that the covolume made up of a Pgk and an apoazurin is similar to that made up of a sphere with the same volume as Pgk and apoazurin. However, its S and Δ are larger than 0.25, indicating that Pgk is not a sphere. Such discrepancy is a result of a cleft formed by the two domains of a pacman-shaped Pgk. The shape of Pgk is not a perfect sphere due to this cleft (Fig. S4). This cleft is still not large enough to accommodate an apoazurin such that the computation of the covolume between Pgk and a test protein apoazurin is close to that between a sphere and a test protein apoazurin. If the size of another test protein is small enough to be inserted into the cleft of Pgk, λ will then decrease and it should be further partitioned by CGCYTO, which will be the case for group 4.

The overall partitioned information for the cytoplasm based on λ_c = 0.8 is shown in Table S3. The distribution of radii of the spheres in the PD cytoplasm models, as well as the HS model for comparison, was represented in Fig. 3. For the HS model, the radii range from 14 Å to 86 Å and for the PD model, the radii range from 9 Å to 86 Å, indicating that the cytoplasm is a highly heterogeneous environment. The radii of most spheres are larger than the size of the apoazurin in the folded state. Interestingly, the radius of Ficoll70 (55 Å), which is frequently used in in vitro experiments, is must larger than the radii of most spheres in either the HS or PD cytoplasm model.

Figure 3.

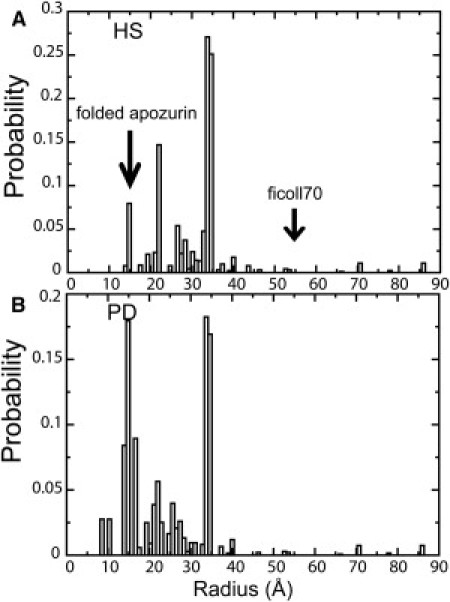
Radius distribution of the spheres of (A) HS model and (B) PD model for the cytoplasm. The size of the folded apoazurin and Ficoll70 is marked by black arrows.

Thermodynamics of apoazurin under the bulk condition and in a cytoplasmic F70 model

The radius of gyration (R_g) of an apoazurin as a function of temperature is shown in Fig. 4 for the bulk condition and the coarse-grained cytoplasm made by the F70 model. All curves follow a two-state folding behavior. These curves shift to the right when apoazurin is immersed by crowders compared to that in the bulk; the folding stability of apoazurin is enhanced by the macromolecular crowding effect. At a high temperature 1.37 k_BT/ε, R_g (bulk) is 35.7 Å, R_g (φ_c = 25%) is 34.3 Å, R_g (φ_c = 32%) is 33.5 Å, and R_g (φ_c = 40%) is 30.8 Å. R_g lowers at a high crowding level, indicating that the unfolded state of apoazurin is statistically more compact in the presence of crowders.

Figure 4.

Radius of gyration R_g of apoazurin as a function of temperature under bulk and several crowding conditions. Error bars are included.

To investigate the folding stability of apoazurin in the coarse-grained cytoplasmic F70 model, we have produced the free energy versus the fraction of the native contact formation (Q) in Fig. 5. The unfolded state Q_u of apoazurin was defined as 0.15 < Q < 0.2 and the folded state Q_f of apoazurin was defined as 0.78 < Q < 0.82. For the folded state, the position of Q_f remains the same in the bulk and in the cytoplasmic F70 model. This indicates that the structure of apoazurin in the native is not significantly altered by the macromolecular crowding effect. However, the free energy difference between the folded state and the unfolded state ΔG_uf is greatly affected by the volume fraction of crowders φ_c. For example, in the bulk case ΔG_uf is 0 kcal/mol at T_f = 1.32 k_BT/ε. We defined the impact of crowding on folding stability ΔG_uf as ΔΔG_uf = ΔG_uf (φ_c ≠0) – ΔG_uf (bulk, φ_c = 0). The value of ΔΔG_uf ranges from −1.34 ± 0.08 kcal/mol (F70 model, φ_c = 25%) to −3.25 ± 0.07 kcal/mol (F70 model, φ_c = 40%), indicating that the stability of apoazurin in the folded state is greatly enhanced by the macromolecular crowding effect (Table S4).

Figure 5.

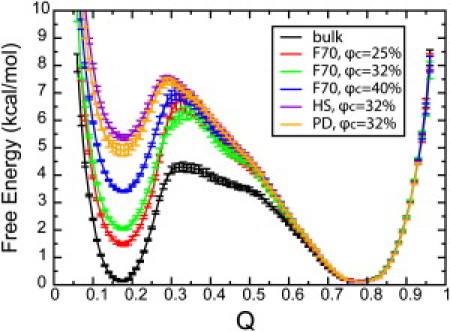
Free energy landscape of apoazurin as a function of the fraction of the native contact formation (Q) under bulk and several crowding conditions at 1.32 k_BT/ε. Error bars are included.

Thermodynamics of apoazurin in either a coarse-grained HS cytoplasmic model or a PD cytoplasmic model

Apoazurin statistically adopts a much more compact structure in the unfolded state in the HS cytoplasmic model over the F70 model at the same φ_c. At φ_c = 32%, in the HS model, R_g of apoazurin is 22.0 Å around the transition temperature 1.37 k_BT/ε, 11.5 Å less than that in the F70 model (Fig. 4), whereas it is about the same as the R_g of apoazurin in the PD model. In addition, the folding stability of apoazurin is greater in the HS model than the F70 model, given ΔΔG_uf of apoazurin from the HS model is 3.35 kcal/mol lower than that from the F70 model at φ_c = 32% from our computer simulations (Table S4). We have sorted the conditions of the weakest crowding effect to the strongest crowding effect based on ΔΔG_uf: F70 model (φ_c = 25%) < F70 model (φ_c = 32%) < F70 model (φ_c = 40%) < HS model (φ_c = 32%) ∼ PD model (φ_c = 32%).

Our simulation results were compared with the SPT calculation for mixed crowders (Table S4) using Minton's formula in Eq. S4 and Zhou's formula in Eq. S7. The simulation results qualitatively agree with the SPT calculation, except for the PD model where the SPT formula is inadequate for a nonconvex polydisperse medium (49,50). The values of ΔΔG_uf from our simulations lie between the two calculated SPT values. It was reported that Minton's formula may overestimate the stability of a protein in the presence of crowders and Zhou's formula may underestimate with regard to the folding stability of cytochrome c, whereas the coarse-grained molecular simulations have produced the same order of magnitude on the folding stability as the experimental measurement (29). In this work, our results perhaps are in the ballpark of the folding stability induced by a macromolecular crowding effect inside cells if only the excluded volume effect of polydisperse macromolecules is considered and these predictions have yet to be validated by experiments.

In contrast to the F70 model, the HS and PD models are heterogeneous systems. ΔΔG_uf in both HS and PD models is similar regarding its average value (Table S4). However, the standard deviations of ΔΔG_uf from two models are noticeably different. For the HS model, the standard deviation is 0.41 kcal/mol, whereas the standard deviation of ΔΔG_uf for the PD model is 0.76 kcal/mol, almost twice as much as the HS model. In addition, the radius of gyration R_g as a function of temperature for 10 independent simulations was plotted in Fig. S2. For the HS model, the range of transition temperature T_f, defined as the turning point of a sigmoidal curve in Fig. S2 is from 1.37 to 1.38 k_BT/ε, which corresponds to 2 Kelvin. For the PD model, the range of T_f is from 1.36 to 1.38 k_BT/ε, which corresponds to 5 Kelvin. The deviation of T_f for the PD model is 1.7 Kelvin, which is 0.7 Kelvin greater than that for the HS model.

To fully understand the reason for such a large deviation on the thermodynamic properties of apoazurin raised from the heterogeneity of the macromolecule's shapes and sizes in the coarse-grained HS and PD cytoplasmic models, we further investigated the local crowding environment surrounding apoazurin by measuring its local accessible free volume 〈LV_free〉, by using a particle insertion method as described in the Supporting Material. As heterogeneity increases in cytoplasmic models, the distribution on local free volume broadens. We have 10 independent folding simulations where in each simulation an apoazurin was placed at a randomly selected void as an initial condition. We have computed 〈LV_free〉 for apoazurin at several crowding conditions and plotted against the folding transition temperature T_f of azurin at that environment in Fig. 6. The coefficient of linear regression between 〈LV_free〉 and kT_f/ε is 0.87 indicates that the correlation between the two is strong. Under a high volume fraction of crowders, the stability of folded apoazurin is subtly sensitive to its local crowding environment varied by shapes and sizes of the crowders. When 〈LV_free〉 is lower, there is less free space for apoazurin, the crowding or confining effect is stronger, and that results in a slightly greater transition temperature T_f. It was also addressed in our prior study on the impact of the shape of crowders on folding stability and folding routes at a high volume fraction of crowders (51).

Figure 6.

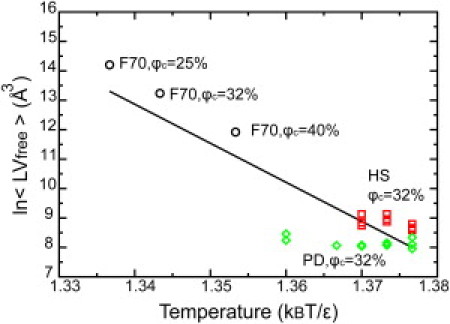
Natural logarithm of local free volume 〈LV_free〉 (see the definition in the Supporting Material, Methods section) of apoazurin as a function of the folding temperature T_f. The error bar is smaller than the size of a symbol. Data from the F70 model are shown in circles, data from the HS model are shown in red squares, and data from the PD model are shown in green diamonds. The solid line is from linear regression with R = 0.87.

Discussion

An analytical study based on the SPT (52) has been used to investigate the excluded volume effect on protein stability (14,40) and protein association (53). By mimicking a folded protein as a hard core, these studies provide an estimate on the thermodynamics of selected proteins in the presence of crowders over the bulk solution. However, SPT-based analytical calculations lack molecular details on the systems. There are several other methods that have been developed where a folded protein is not a simple hard sphere. For example, a coarse-grained molecular simulation approach has been implemented to explore the full folding energy landscape of protein folding under confinement and crowding (13,44). Recently, there are methods that reserve an atomistic protein representation in the calculations based on Widom's particle insertion method (54). In these studies, proteins are modeled as two-state folders and the configurations of their folded states and unfolded states are randomly inserted into the crowded media. The free energy of the folded states is thus computed by the success of insertion compared to the unfolded ones (35,55). These simulations involve a large number of crowders and that demands great computational resources. Other studies have attempted to avoid heavy computation by including the effect of crowding into pairwise interactions in the Hamiltonian of a protein system (56), as described by the Asakura-Oosawa theory (57,58), or by including the features of crowders via their number density in the expression of chemical potential (59) based on the fundamental measure theory (60).

However, so far only the approach of coarse-grained molecular simulations has been able to address the thermodynamics of a protein with high flexibility (20,61–64). It is particularly suited to sample a complex folding energy landscape on which new states are induced by the macromolecular crowding effects (20,63), where the particle insertion methods and others that assume proteins have only two states likely miss the sampling of important states induced by the mechanistic interactions between a protein and crowders. In addition, although all-atomistic protein representations of macromolecules in an E. coli cytoplasm has been available recently (35), these macromolecules are still modeled as hard cores and they lack structural flexibility because of limited computing resources.

To extend coarse-grained molecular simulations of protein inside a cell, in this work we have proposed a novel, to our knowledge, algorithm of coarse-graining the cytoplasm of E. coli that is dependent on the size of a test protein as well as the limit on computational resources. On one hand, due to the limitation of computational resources, it is practical to incorporate a reasonable coarse-grained macromolecule with fewer numbers of spheres. On the other hand, it is important to establish a physical rule that keeps the shape characteristics of macromolecules in the cytoplasm. Imagine that when a test protein is much larger than a macromolecule, the clefts or holes of this macromolecule are negligible. With respect to a test protein this macromolecule can be modeled as a sphere. Otherwise, when a test protein is small enough to probe the presence of the holes and clefts of a macromolecule, a rather detailed representation of a macromolecule from the prospective of a test protein must be considered. Conclusively, to what extent a macromolecule can be modeled as a sphere depends on the relative size and shape of this macromolecule compared to a test protein.

We have emphasized that the shape of a macromolecule (shape parameter S and anisotropy Δ) alone is not sufficient to justify the resolution of a coarse-grained cytoplasm. Following SPT, information about the covolume of a test protein that measures the excluded volume between a test protein and a macromolecule must also be included for consideration of modeling a cytoplasm. This is introduced to parameter λ, which measures the ratio of covolumes when a macromolecule is compared to a sphere with equal volume. Note that λ alone is not sufficient for coarse-graining a cytoplasm because it is insensitive to the composition of multidomain proteins. S and Δ are needed for partitioning a multidomain molecule (such as Pgk) into several smaller domains or needed for partitioning a dimer (such as UspA) into two monomers. Our protein-dependent algorithm of coarse-graining a cytoplasm (CGCYTO) is physically sound for a generalized coarse-grained cytoplasm model when all of the chemical details are neglected—each test protein should have its own coarse-grained cytoplasm model based on the volume exclusion.

One of the key factors in our algorithm is to choose a reasonable λ_c, the resolution parameter of a coarse-grained cytoplasm. If λ_c equals to 1, it will recover to the all-atomistic representation, which is very difficult for us to perform the computer simulations considering its enormous size (over 16 million) and broad timescales (millisecond to second). If λ_c approaches 0, where a coarse-grained cytoplasm has completely lost its shape characteristics, the resolution will approach a HS model. In this work, we have set the cutoff at λ_c = 0.8 so that the size of a cytoplasm is manageable with regard to our present computing resources. Despite macromolecules that made up no more than five spheres in a coarse-grained cytoplasmic model, the distribution of polydisperse macromolecules is still genuinely preserved as shown by high λ′ (Table S2), where their covolume from the coarse-grained model is almost within 90% to their counterpart all-atomistic protein model. Given the computational resources we have had, we consider this coarse-grained PD model a powerful alternative to an all-atomistic model for the investigation of the excluded volume effect on protein folding stability in a cytoplasm, although all-atomistic models are needed for the investigation of the energetics of protein interactions.

By comparing the thermodynamic properties of apoazurin in F70, HS, and PD models, we have found that although Ficoll70 is widely used for in vitro experiments to mimic a cell-like environment, the stability of the native state for a protein in the F70 cytoplasmic model is much less than that in the HS or PD models. Given the same volume of fraction of crowders (φ_c = 32%), ΔΔG_uf of apoazurin in the HS and PD models is lower by 3.35 kcal/mol than the F70 model (Table S4). Interestingly, the impact of a macromolecular crowding effect exerted from the HS and PD models at φ_c = 32% is even stronger than that of the F70 model at φ_c = 40%, because the effect of macromolecular crowding is not only dependent on φ_c but also dependent on the ratio between the size of a crowder and a test protein. Ficoll70 with a radius of 55 Å is much larger than the radii of most macromolecules in the cytoplasm (Fig. 3). Given the same φ_c, the number density of crowders in a HS or PD model is much larger than that in F70 model. The stability of an unfolded state protein reduced more in the PD model than F70 model. As a result, the transition temperature of the protein in the PD model is higher than that in the F70 model.

Another stark difference among the F70, HS, and PD models is that the HS and PD models provide a polydisperse macromolecular crowding environment, whereas the F70 model only provides a monodisperse one. The available volume of a local crowding environment surrounding a test protein fluctuates greatly in a polydisperse condition, and it leads to a subtle spread of folding temperatures for a protein at various parts of the cytoplasm. In addition, the macromolecules in the HS model vary only by their sizes, whereas the PD model includes the heterogeneity in both their sizes and shapes. Thus, between the PD model and the HS model, the former presents a slightly broader distribution of the thermodynamic properties for a protein than that with the latter. For example, although the average ΔΔG_uf (Table S4) is quite close between the HS and PD models, the standard deviations of ΔΔG_uf for the PD model are over twice as large as that for the HS model. Our result indicates that although the average value of the thermodynamic properties of a protein are similar in the HS and PD models, the HS model cannot reflect the extent of structural fluctuation accounted for by the irregular shapes of crowders. It is found by experiments that the heterogeneity inside a cancerous cell affects the folding rate of a protein (65). The spread (defined as the root of the variance for each ensemble of cells studied) of the relaxation time τ of a PGK protein was found to be three times greater in the cytoplasm than in the nucleus, indicating that the cytoplasm is a quite heterogeneous environment. In our work, the spread of the T_f of apoazurin is 1.7 Kelvin in the PD model, which is at the same order of magnitude with the experimental value at 1.1 Kelvin (65). However, we fully recognized that for a test protein, the deviation of its thermodynamic properties such as T_f or ΔΔG_uf increases when λ_c increases.

There are several factors that have not been considered in our coarse-grained cytoplasm model such as the attraction interactions between crowders and crowder proteins. Therefore, our model has yet to acknowledge several recent experimental findings. For example, it was found by experiments that protein λ_6–85 has the same stability both in vivo and in vitro (1). In addition, protein CRABP (66) and ubiquitin (67) were less stabilized in vivo over in vitro. These results are opposite to the prediction that the stability of folded protein will increase inside crowded milieu due to the exclude volume effect. It is suggested by experiments that the intermolecular interactions were found to be important and cancel off the macromolecular crowding effects (26). In addition, it has been recently shown by using molecular dynamic simulations that variable interactions between protein crowders and biomolecular solutes were important (68). Although attractive interaction in computer simulations between a test protein and its surrounding macromolecules has been fitted to match the experimental data with regard to GFP diffusion (35), the mechanism behind this attractive interaction has not been fully understood. Second, we have not included the hydrodynamics interaction (HI) in the system (69). Although HI does not affect the thermodynamic properties of the system, HI was reported to be another important factor, besides the excluded volume, that affects the kinetic behaviors of a protein in vivo and its conclusion was supported by a recent experimental study (70). These factors will be investigated in our future work.