Generalized Facilitated Diffusion Model for DNA-Binding Proteins with Search and Recognition States

Abstract

Transcription factors (TFs) such as the lac repressor find their target sequence on DNA at remarkably high rates. In the established Berg-von Hippel model for this search process, the TF alternates between three-dimensional diffusion in the bulk solution and one-dimensional sliding along the DNA chain. To overcome the so-called speed-stability paradox, in similar models the TF was considered as being present in two conformations (search state and recognition state) between which it switches stochastically. Combining both the facilitated diffusion model and alternating states, we obtain a generalized model. We explicitly treat bulk excursions for rodlike chains arranged in parallel and consider a simplified model for coiled DNA. Compared to previously considered facilitated diffusion models, corresponding to limiting cases of our generalized model, we surprisingly find a reduced target search rate. Moreover, at optimal conditions there is no longer an equipartition between the time spent by the protein on and off the DNA chain.

Introduction

The survival of cells relies crucially on their ability to efficiently control their metabolism. For example, the bacterium Escherichia coli is able to digest both glucose and lactose. However, the use of lactose as an energy source is disadvantageous if both substances are available. Hence, in this situation the production of lactose-digesting enzymes is inhibited. This task is accomplished by a transcription factor (TF) named the lac repressor that binds specifically to the respective operator region on the DNA.

More than four decades ago, Riggs et al. (1) observed in vitro that the association rate k_a of the repressor to the operator in this system was k_a = 7 × 10⁹ M⁻¹ s⁻¹. The occurrence of this high rate came as a surprise, because an application of the classical Smoluchowski formula for diffusion-controlled reactions (2) yields a rate of ∼10⁸ M⁻¹ s⁻¹, i.e., a result that is nearly two orders of magnitude smaller.

Riggs et al. attempted to explain this discrepancy and the observed dependence on ionic strength with the “electrostatic attraction between a positively charged site on the repressor and the negatively charged phosphate groups in the operator” (1). They rejected the idea that the repressor could bind to DNA and hop along it to reach the operator.

Four years later, Richter and Eigen (3) interpreted the results in the opposite way: they claimed that the electrostatic forces cannot explain the high association rate. In their model, the repressor first binds unspecifically to the DNA and then diffuses along the chain to the operator region that serves as a target for this process. This was the starting point for the formulation of the classical facilitated-diffusion model by Berg, von Hippel, and co-workers (4–8).

In their seminal work, they explain the unusually high rates as the result of the combination of different search mechanisms: because the target is part of the DNA chain, a TF combines three-dimensional diffusion in the bulk solution with one-dimensional sliding along the contour of the DNA. While bound to the chain it can dissociate from the chain and reassociate at another point on the DNA after a round of three-dimensional diffusion. Depending on the distances traveled in this manner, these processes are called hops (short distances) or jumps (long distances). This theoretical model successfully explains the experimentally observed nonmonotonic dependence of the association rate on the salt concentration (7). In some versions of the Berg-von Hippel model, another propagation mode for bound TFs exists called intersegmental transfer: if the DNA chain forms a loop, the protein can use it as a shortcut to reach another point on the DNA far away measured along the contour without dissociating. Another possibility are intersegmental jumps that are also possible for TFs with only one binding site. The interplay of these different search mechanisms was studied in Lomholt et al. (9) showing that intersegmental transfer can (partially) replace volume excursions as a mixing mechanism.

In subsequent years the target search problem for transcription factors was reformulated as a simplified version of the Berg-von Hippel model by Halford and Marko (10) and was studied starting from first principles by Klenin et al. (11). In addition to these kinetic studies, it was investigated by means of a stochastic approach by Coppey et al. (12) and by Meroz et al. (13). In a similar context, intermittent search processes were studied by Eliazar et al. (14) and by Oshanin et al. (15).

In recent years, the topic of search processes of TFs has obtained renewed interest. This has been fueled by the possibility of analyzing DNA-binding proteins on the single-molecule level (16–19), in some cases even in living cells (20).

Due to the increase in computational power over the past decades, it has also become possible to study this target search problem with computational methods, as done by Florescu and Joyeux (21,22) and by Koslover et al. (23). The main focus of the latter work was to elucidate the role of different DNA conformations following the experimental study by van den Broek et al. (24) and the related analytical approach by Lomholt et al. (25).

Even though the general form of the facilitated diffusion model is widely accepted, a conceptual problem exists as the so-called speed-stability paradox (26,27), which can be understood in the following way: the sliding along the DNA can be interpreted as a one-dimensional diffusion process through a random potential landscape. The effective diffusion constant in such a potential is proportional to exp(−σ²), where σ denotes the root-mean-squared roughness of the potential (28). As pointed out by Mirny and co-workers, the TF can only slide rapidly to the target if σ < k_BT; concurrently the protein has to stay bound to the target sequence long enough for the actual gene expression to take place, which requires σ > 5 k_BT (26,27).

The problem of these seemingly contradictory constraints can be solved by introducing two conformations of the TF: a search state and a recognition state (26,27), an idea already anticipated by Winter et al. (7). This is an assumption that is to some extent affirmed by multidimensional nuclear magnetic resonance observations (29). Similar two-state models for the target search of transcription factors have been studied by Hu et al. (30), Zhou (31), and Reingruber and Holcman (32). In a related context, Reingruber and Holcman (33) showed, analytically, for one-dimensional motion that the escape time from an interval can be reduced by introducing a second (faster-moving) state even if the particle is not allowed to leave the interval in this state.

However, a large majority of modern reinterpretations of the classical facilitated diffusion model assumes that start- and end-points of intermediate rounds of three-dimensional diffusion are completely uncorrelated, a fact already criticized by Hu et al. (34) and Kolomeisky (35). In this article, we consider the full facilitated diffusion model for rodlike DNA chains, where the correlations between dissociation and reassociation points are treated explicitly. In addition, we generalize it by including the two-state model to overcome the speed-stability paradox. The relaxed, coiled conformation is effectively included in our model. Consequently, many previous theoretical models are formed from the limiting cases of our approach. The two most important findings of this study are that: 1), the overall association rate in our generalized model is reduced in comparison to these limiting cases; and 2), at optimum, the time spent on the DNA by the TF exceeds the time spent in the bulk.

Methods

Model

Following the approach by Berg and Blomberg (4), we consider the search of a single TF on a DNA chain of contour length 2L, applying their closed-cell approach, which will be further clarified in the next section. The corresponding process of a single repressor on a rodlike DNA is schematically drawn in Fig. 1: the TF is illustrated as a U-shaped red particle and the target region on the DNA is depicted in black. The situation of a TF searching for a target on a DNA in the coiled conformation is described at the end of the following section. The TF starts its search for the target site somewhere in the bulk solution where it diffuses three-dimensionally (with diffusion constant D₃). Some exemplary three-dimensional diffusive trajectories are drawn in gray color. Even though we consider the TF as being present in two possible conformations, while it diffuses in the bulk solution, we suppose that both conformations are physically indistinguishable (31).

Figure 1.

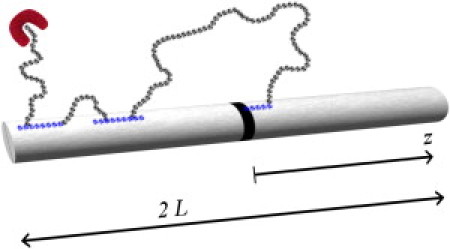
Schematic of the target search process by a transcription factor (TF, U-shape) on a rodlike DNA. The TF diffuses in the bulk and may slide one-dimensionally along the DNA while nonspecifically bound. Eventually it reaches its target, the specific binding site placed at z = 0.

On an encounter with some part of the DNA the protein can bind to it (with rate k_on) and subsequently it will be able to slide along the DNA contour one-dimensionally (with diffusion constant D_s). After such an association, the protein is at first in the search mode, but it can change its conformation to the recognition mode (26) (with rate k_sr). At the same time, there is the possibility to leave the search mode by dissociation to the bulk solution (with rate k_off). The corresponding one-dimensional diffusive trajectories are depicted in blue in Fig. 1.

After leaving the chain, the TF will start a round of three-dimensional diffusion and will eventually return to some point on the DNA chain. Before such a dissociation event, however, the TF could change to the recognition-mode. It may still diffuse along the DNA contour, but now with the much smaller diffusion constant D_r. With rate k_rs it switches back to the search state.

The reason for the reduced diffusivity D_r in the recognition mode is that the protein-DNA binding energy is not constant along the chain. Thus, effectively, the motion can be described as diffusion in a rugged potential landscape, such that

$$D_i\propto \text{exp}\left(-{\sigma }_i^2\right).$$ (1)

Here σ_i denotes the variance of the TF-DNA binding potential where i stands for either recognition or search mode (26,28). Whereas in the search mode the protein is only loosely bound to the DNA, in the recognition mode it interacts strongly with the DNA, such that σ_r ≫ σ_s and thus the difference in the diffusivities, D_s ≫ D_r. It is assumed that the operator can only recognize its specific binding site and bind tightly in the recognition mode.

The dynamical quantities that we study in the following are the densities per length n_i(z,t) of the transcription factor on the DNA, where again i denotes either recognition or search mode and z stands for the distance along the DNA contour. These two densities obey the two coupled diffusion equations

$$\frac{\partial n_r\left(z,t\right)}{\partial t}=D_r\frac{{\partial }^2{n}_r\left(z,t\right)}{\partial z^2}-k_{\text{rs}}{n}_r\left(z,t\right)+k_{\text{sr}}{n}_s\left(z,t\right),$$ (2)

and

$$\frac{\partial n_s\left(z,t\right)}{\partial t}=D_s\frac{{\partial }^2{n}_s\left(z,t\right)}{\partial z^2}+k_{\text{rs}}{n}_r\left(z,t\right)-k_{\text{sr}}{n}_s\left(z,t\right)+G\left(z,t\right)-k_{\text{off}}{n}_s\left(z,t\right)+k_{\text{off}}\underset{0}{\overset{L}{\int }}d{z}^{\prime }\underset{0}{\overset{t}{\int }}d\tau F\left(z,z^{\prime },t-\tau \right)n_s\left(z^{\prime },\tau \right).$$ (3)

For symmetry reasons, it suffices to consider only half of the DNA with positive values of z: $0\le z\le L$. Equation 2 describes the change of the density n_r(z,t) of proteins in the recognition mode at position z and time t. The first term on the right-hand side corresponds to the one-dimensional (sliding) motion. The two other terms represent variations in the distribution resulting from the conformational change to and from the search mode.

In Eq. 3 for the distribution n_s(z,t) of proteins in the search mode, the first three terms on the right-hand side are equivalent to the ones in Eq. 2. The term G denotes the virgin flux, i.e., the influx of TFs that have not been bound to the chain previously. The term proportional to k_off describes particles dissociating from the chain into the bulk. The last term represents proteins that have dissociated at position z′ at an earlier time and now return to the DNA at z.

As already stated, we assume that in the beginning the repressor molecule is delocalized in the bulk that corresponds to vanishing initial concentrations n_i on the chain,

$$n_r\left(z,t=0\right)=n_s\left(z,t=0\right)=0.$$ (4)

We assume that for the TF in the recognition mode any encounter with the operator region at z = 0 leads to a specific association that is equivalent to the boundary condition

$$n_r\left(z=0,t\right)=0.$$ (5)

We assume that the extremity of the DNA at z = L acts as a reflecting boundary for the protein in the recognition mode. Reflection off the end of the DNA was indeed observed experimentally for the endonuclease EcoRV (36). Because the TF cannot see the operator while being in the search mode, for the corresponding density n_s(z,t) both boundaries are reflecting

$${\frac{\partial n_s}{\partial z}|}_{z=0}={\frac{\partial n_s}{\partial z}|}_{z=L}={\frac{\partial n_r}{\partial z}|}_{z=L}=0.$$ (6)

To convert the partial differential equations, Eq. 2 and Eq. 3 to ordinary differential equations, we apply a Laplace transformation, yielding

$$\left(u+k_{\text{rs}}-D_r\frac{{\partial }^2}{\partial z^2}\right){\tilde{n}}_r\left(z,u\right)=k_{\text{sr}}{\tilde{n}}_s\left(z,u\right)$$ (7)

and

$$\left(u+k_{\text{sr}}+k_{\text{off}}-D_s\frac{{\partial }^2}{\partial z^2}\right){\tilde{n}}_s\left(z,u\right)=k_{\text{rs}}{\tilde{n}}_r\left(z,u\right)+k_{\text{off}}\underset{0}{\overset{L}{\int }}d{z}^{\prime }\tilde{F}\left(z,z^{\prime },u\right){\tilde{n}}_s\left(z^{\prime },u\right)+\tilde{G}\left(z,u\right).$$ (8)

Here the tilde denotes a Laplace transform with respect to time,

$${\tilde{n}}_i\left(z,u\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{n}_i\left(z,t\right)\text{exp}\left(-ut\right)dt,$$

where u is the corresponding variable with the physical dimension of a frequency. The mean specific association time τ of the TF can be then derived from the Laplace transform of the flux to the target,

$$j\left(t\right)={D_r\frac{\partial n_r\left(z,t\right)}{\partial z}|}_{z=0},$$ (9)

in the following way:

$$\tau =-{\frac{\partial \tilde{j}\left(u\right)}{\partial u}|}_{u=0}.$$ (10)

From this mean first-passage time, the association rate k_a becomes (4)

$$k_a=\frac{1}{\tau n_0},$$ (11)

where n₀ denotes the density of operators placed on the DNA. To proceed, we determine the kernel $\tilde{F}$ and the virgin flux $\tilde{G}$ from first principles.

(Re)association process and closed-cell approach

The two functions $\tilde{G}\left(u,z\right)$ and $\tilde{F}\left(u,z\right)$ describe the association of previously unbound proteins and the reassociation of particles that dissociated earlier. To obtain these functions, it is necessary to study the diffusive motion of the transcription factors in the bulk.

We first consider the case of a rodlike chain to mimic chains that are arranged in parallel. If they are distributed homogeneously, it is possible to apply the closed-cell approach as described by Berg and Blomberg (4). We enclose every DNA with a parallel cylinder (of length 2L) with a radius of R₂ that is equal to half the distance to the nearest DNA chains. Thus, this radius is an effective measure of the density of DNA chains and determines at which distance the sector of a neighboring chain begins. Because we assume an initially homogeneous distribution of chains, for TFs diffusing in the bulk, the point at which it attempts to enter its neighbor's sector is equivalent to the point at which it attempts to leave its own sector. Consequently, it is in order to consider a single particle in a single sector that is reflected at the boundaries of the sector instead of analyzing multiple particles that are allowed to leave their sectors.

For $\tilde{F}$ as well as for $\tilde{G}$, we solve the cylindrical diffusion equation

$$\frac{\partial P\left(r,z,t\right)}{\partial t}=D_3\left(\frac{{\partial }^2}{\partial z^2}+\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}\right)P\left(r,z,t\right)$$ (12)

for the probability density P(r,z,t) to find the particle at position (r, z) at time t. Because of the closed-cell approach, we consider the boundary conditions,

$${\frac{\partial P\left(r,z,t\right)}{\partial z}|}_{z=0,L}={\frac{\partial P\left(r,z,t\right)}{\partial r}|}_{r=R_2}=0,$$ (13)

where, again, due to symmetry, we only consider positive values of z.

In the case of $\tilde{F}$, initially there is no TF in the space between the two cylinders and the protein that has just dissociated from the DNA chain of radius R₁. This is introduced in terms of a δ-function in the reactive boundary condition at r = R₁,

$$P\left(r,z,t=0\right)=0\text{and}{D}_3{\frac{\partial P\left(r,z,t\right)}{\partial r}|}_{r=R_1}=\frac{\delta \left(t\right)\delta \left(z-z^{\prime }\right)}{2\pi R_1}+k_{\text{on}}P{|}_{r=R_1}.$$ (14)

Here and in the following formulas, 2πR₁ denotes the effective circumference of the DNA chain and has to be included as rotational symmetry is assumed throughout. After solving for P(r,z,t) and calculating its Laplace transform, $\tilde{F}\left(z,z^{\prime },u\right)$ is obtained via

$$\tilde{F}\left(z,z^{\prime },u\right)=2\pi R_1{k}_{\text{on}}\tilde{P}\left(r=R_1,z,u\right),$$ (15)

where k_on denotes a phenomenological binding rate to the DNA.

In the case of $\tilde{G}$, initially the starting position of the TF is uniformly distributed outside the DNA and we have a reactive boundary condition at r = R₁,

$$P\left(r,z,t=0\right)=\frac{1}{\pi L\left(R_2^2-R_1^2\right)}\text{and}{D}_3{\frac{\partial P\left(r,z,t\right)}{\partial r}|}_{r=R_1}=k_{\text{on}}P{|}_{r=R_1}.$$ (16)

The denominator includes the cross-section $\pi \left(R_2^2-R_1^2\right)$ between inner and outer cylinders. $\tilde{G}\left(z,u\right)$ is calculated in the form

$$\tilde{G}\left(z,u\right)=2\pi R_1{k}_{\text{on}}\tilde{P}\left(r=R_1,z,u\right).$$ (17)

The results for the cylindrical geometry are identical to the ones for Berg and Blomberg (4) (note that their definition of the binding rate k slightly differs from the one used here for k_on). We obtain

$$\tilde{F}\left(z,z^{\prime },u\right)=\sum _{m=0}^{\infty }{g}_m\left(u\right)\text{cos}\left(\frac{m\pi z}{L}\right)\text{cos}\left(\frac{m\pi z^{\prime }}{L}\right),$$ (18)

where

$$g_m\left(u\right)=\frac{2-{\delta }_{m,0}}{L}\frac{k_{\text{on}}{\Delta }_{01}\left(\sqrt{a_m}{R}_1\right)}{k_{\text{on}}{\Delta }_{01}\left(\sqrt{a_m}{R}_1\right)-D_3\sqrt{a_m}{\Delta }_{11}\left(\sqrt{a_m}{R}_1\right)}$$

with

$$a_m=\frac{u}{D_3}+\frac{m^2{\pi }^2}{L^2},$$

and where we introduced the auxiliary functions

$${\Delta }_{01}\left(\sqrt{a_m}r\right)=I_0\left(\sqrt{a_m}r\right)K_1\left(\sqrt{a_m}{R}_2\right)+I_1\left(\sqrt{a_m}{R}_2\right)K_0\left(\sqrt{a_m}r\right),$$ (19)

$${\Delta }_{11}\left(\sqrt{a_m}r\right)=I_1\left(\sqrt{a_m}r\right)K_1\left(\sqrt{a_m}{R}_2\right)-I_1\left(\sqrt{a_m}{R}_2\right)K_1\left(\sqrt{a_m}r\right).$$ (20)

Here I_i and K_i represent modified Bessel functions of order i. The occurrence of the term $\tilde{F}$ in fact leads to a short-time superdiffusive motion along the cylinder that was studied for infinitely long cylinders by Chechkin et al. (37,38).

In an analogous way, we obtain

$$\tilde{G}\left(u\right)=\frac{2R_1}{L\left(R_2^2-R_1^2\right)}\frac{k_{\text{on}}}{u}\frac{D_3\sqrt{a_0}{\Delta }_{11}\left(\sqrt{a_0}{R}_1\right)}{D_3\sqrt{a_0}{\Delta }_{11}\left(\sqrt{a_0}{R}_1\right)-k_{\text{on}}{\Delta }_{01}\left(\sqrt{a_0}{R}_1\right)}.$$ (21)

Note that because we assume that the protein initially is homogeneously distributed outside the DNA chain, the function $\tilde{G}\left(u\right)$ does not depend on z.

For DNA in the relaxed, coiled conformation, the situation is slightly different (see Fig. 2). Here segments of the same DNA chain can be very close to each other. For instance, for the TF in Fig. 2, which has just dissociated from the lower part of the chain, the probability to be captured by the upper part (close in real-space, but distant measured along the contour of the chain) is very high. In a rather simplified model for such coiled DNA, it is common to assume that, after dissociating from the chain, the TF immediately loses track of its z coordinate and that it reassociates with equal probability to any position on the chain. In terms of our model, this assumption corresponds to putting g_m(u) = 0 for all m ≥ 1 in Eq. 18.

Figure 2.

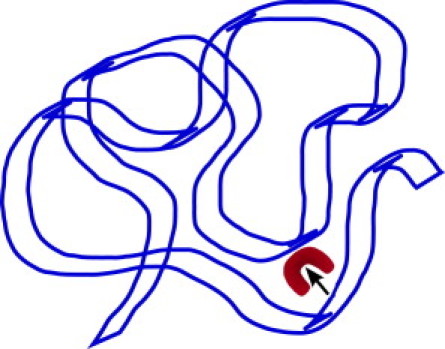
Schematic of the search process on coiled DNA.

Results and Discussion

Mean association time

We first concentrate on the case of rodlike DNA: once $\tilde{F}\left(z,z^{\prime },u\right)$ and $\tilde{G}\left(u\right)$ are known, it is possible to determine the mean association time, τ, by solving the coupled Eqs. 7 and 8. The corresponding calculations are presented in the Appendix. We obtain

$$\tau ={\tau }_1+N\left({\tau }_2+{\tau }_3\right)-{\tau }_4.$$ (22)

The result is in its form similar to the classical result of Berg and Blomberg (4) for only one bound state, and the two terms τ₁ and τ₂ are, in fact, identical in both models. The various entries of Eq. 22 can be interpreted in the following way.

The value τ₁ is the mean time for the first encounter with the DNA chain that results in successful binding of the TF to the DNA,

$${\tau }_1=-L\dot{\tilde{G}}\left(0\right)=\frac{R_2^2}{2D_3}\left\{\frac{1-R_1^2/R_2^2}{k_{\text{on}}{R}_1/D_3}+\frac{\text{ln}\left(R_2/R_1\right)}{1-R_1^2/R_2^2}\right\}-\frac{R_2^2}{8D_3}\left\{3-R_1^2/R_2^2\right\},$$ (23)

where we abbreviated $\dot{\tilde{G}}\left(u\right)=d\tilde{G}\left(u\right)/du$. The value τ₂ is the mean time the TF spends in the bulk after a dissociation from the chain,

$${\tau }_2=-L{\dot{g}}_0\left(0\right)=\frac{R_2^2-R_1^2}{2k_{\text{on}}{R}_1}.$$ (24)

The value τ₃ denotes the mean time that the protein spends bound to the chain both in the recognition and in the search mode,

$${\tau }_3=\frac{1}{\vartheta }\left(\frac{1}{k_{\text{rs}}}+\frac{1}{k_{\text{sr}}}\right).$$ (25)

Here, ϑ = k_off/k_sr is a measure for proteins in the search state describing how likely the occurrence of a dissociation event is in comparison to a prior conformational change to the recognition state.

The term N denotes the number of rounds of three-dimensional excursions followed by reassociation events and the subsequent sliding along the DNA needed to reach the target. All the information about the spatial organization of the chain is stored in this term, or, more precisely, in the functions g_m(u). We find

$$N=\frac{\vartheta }{x_r}\text{coth}\left(\frac{1}{x_r}\right)+2\vartheta \sum _{m=1}^{\infty }{\left[p_r\left(m\right)\left(p_r\left(m\right)\left(p_s\left(m\right)+\vartheta \left(1-\frac{L{g}_m\left(0\right)}{2}\right)\right)-1\right)\right]}^{-1}$$ (26)

where p_i(m) = 1 + m²π²x_i² and i stands for either recognition or search mode. The terms

$$x_r=\sqrt{\frac{D_r}{\left(k_{\text{rs}}{L}^2\right)}}\text{and}{x}_s=\sqrt{\frac{D_s}{\left(k_{\text{sr}}{L}^2\right)}}$$

are dimensionless quantities measuring the fraction of the whole contour length that a protein in the corresponding conformation can slide along before changing to the other state (neglecting dissociation events).

Finally, τ₄ = 1/k_rs is a correction term accounting for the fact that, in contrast to the first N−1 rounds of consecutive three-dimensional and one-dimensional diffusion, in the final round the last conformational change to the search state is not performed and the TF therefore reaches the target in the recognition mode.

Connection to previous models

Before we consider the result in more detail, it is in order to relate it to previous results. We first consider the case when the conformational changes between search and recognition mode occur very rapidly, that is, before a considerable fraction of the DNA was scanned. Mathematically this corresponds to k_rs ≫ D_r/L² and k_sr ≫ D_s/L² or x_r/s ≈ 0.

In this limit, N can be written as

$$N\approx \sum _{m=1}^{\mathrm{\infty }}\frac{2\vartheta }{\vartheta \left(1-L{g}_m\left(0\right)/2\right)+m^2{\pi }^2\left(x_r^2+x_s^2\right)}$$ (27)

and τ₄ ≈ 0 can be neglected. If we further assume that D_r = D_s = D₁ and k_rs = k_sr such that both states are indistinguishable apart from the fact that the search state is insensitive to the target, we get

$${\tau }_3=\frac{2}{k_{\text{off}}}$$ (28)

and

$$N\approx \frac{2k_{\text{off}}}{k_{\text{off}}\left(1-L{g}_m\left(0\right)/2\right)+2m^2{\pi }^2{D}_1^2/L^2}.$$ (29)

If we identify k_off/2 with the λ in the work of Berg and Blomberg (4), both results for the mean association time coincide. The factor of 2 between the dissociation rates stems from the fact that the protein is only able to dissociate while being in the search state that in the fast-switching limit with k_rs = k_sr amounts to half of the total time bound to the chain. Thus, to obtain matching results, the rate at which the TF dissociates must be doubled with respect to the classical model. The result of Lomholt et al. (25) for the straight-rod configuration corresponds to the limit of an infinitely long DNA chain, and different boundary conditions. Namely, instead of our finite system, Lomholt et al. (25) consider an infinite system (both longitudinally and radially) with a finite protein concentration in the vicinal bulk. Technically, the infinite chain limit replaces the Fourier series 18 with a continuous Fourier transform; compare Eqs. 4 and 12 in Lomholt et al. (25).

As a second limiting case, we consider the simplified model for coiled DNA as described in the last section; that is, we use g_m(u) = 0 for all m ≥ 1. Then it is possible to evaluate the sum in Eq. 26 explicitly, yielding

$$N=\vartheta \left(1+\frac{X+\left(x_s^2-x_r^2\left(1+\vartheta \right)\right)}{2x_r^{2}X}f\left(y_{+}\right)+\frac{X-\left(x_s^2-x_r^2\left(1+\vartheta \right)\right)}{2x_r^{2}X}f\left(y_{-}\right)\right),$$ (30)

where we use the notation of Reingruber and Holcman (33) for $f\left(x\right)=\text{coth}\left(\sqrt{\mathit{x}}\right)/\sqrt{\mathit{x}}-1/x$. In Eq. 30, we introduced the quantities

$$X=\sqrt{x_s^4-2x_r^2{x}_s^2\left(\vartheta -1\right)+x_r^4{\left(1+\vartheta \right)}^2}$$ (31)

and

$$y_{\pm }=\frac{x_r^2\left(1+\vartheta \right)+x_s^2\pm X}{2x_r^2{x}_s^2}.$$ (32)

Changing our initial condition to n_r(z,t = 0) = 1/L and G(z,t) = 0, i.e., the particle starts uniformly distributed in the recognition state and there are initially no unbound particles, we obtain

$$\tau =\left({\tau }_2+{\tau }_3\right)\left(N-\vartheta \right).$$ (33)

This coincides with the result of Reingruber and Holcman (32). Note the typo in the definition of ξ₂ in Reingruber and Holcman (32); ξ₂ should read

$$\sqrt{1-\frac{2\left(l_{23}-l_{21}\right)}{l_{12}}+\frac{{\left(l_{21}+l_{23}\right)}^2}{l_{12}^2}}.$$

Finally, their previous result (33) can be obtained by setting k_off = 0 (that is, the TF will not dissociate from the DNA at all). Then we have

$$\tau =\left(\frac{1}{k_{\text{rs}}}+\frac{1}{k_{\text{sr}}}\right)\frac{x_r^2+3x_s^{2}f\left(1/x_r^2+1/x_s^2\right)}{3x_r^2\left(x_r^2+x_s^2\right)}.$$ (34)

Performing the same approximation for coiled DNA in the original one-state model of Berg and Blomberg, we obtain for TFs starting homogeneously distributed in the bulk solution,

$$\tau ={\tau }_1+N\left({\tau }_2+{\tau }_3\right),$$ (35)

where τ₁ and τ₂ are the same as before. But in this case we have ${\tau }_3=k_{\text{off}}^{-1}$ and

$$N=\sqrt{\frac{k_{\text{off}}{L}^2}{D_1}}\text{coth}\left(\sqrt{\frac{k_{\text{off}}{L}^2}{D_1}}\right)-1=\frac{k_{\text{off}}{L}^2}{D_1}f\left(\frac{k_{\text{off}}{L}^2}{D_1}\right),$$ (36)

in accordance with the result obtained by Coppey et al. (12) and similarly by Slutsky and Mirny (26). For the latter search mechanism, it is known that the mean association time is minimized when the times spent on and off the chain are equal (12,26).

Numerical results

In the general case, it is not feasible to obtain a result in closed form for the mean association time τ, due to the complex infinite sum in Eq. 26. However, it is possible to examine τ numerically. If not stated otherwise, we consider the following parameter values that are suitable for the lac repressor in E. coli.

Following Riggs et al. (1), we consider a concentration of operators of n₀ = 1 pM. Using n₀ = (πR₂²2L)⁻¹ and 2L = 16 μm, this corresponds to R₂ ≈ 5.75 μm (4). Furthermore, we take for the effective radius of the DNA cylinder, R₁ = 6 nm, a three-dimensional diffusion constant of D₃ = 50 μm²/s and a reaction rate of k_on = 5.56 × 10⁴ μm/s (4,5). Note that the physical dimension of length/time is a matter of choice when we define the coupling constant k_on in a cylindrical geometry; see Eq. 14 and the discussion in Chechkin et al. (38).

As described in Zhou (31), the transition rate from the recognition to the search state should be much larger than the opposite one, to guarantee that the TF spends most of the time in the faster diffusing state. Consequently we use k_sr = k_rs/10 = 10⁴/s, in the range of rates known for repressor isomerizations (39). The experimentally accessible apparent diffusion constant (32)

$$D_a=\frac{D_s/k_{\text{sr}}+D_r/k_{\text{rs}}}{1/k_{\text{sr}}+1/k_{\text{rs}}}$$ (37)

in such a fast switching case approximates as

$$D_a\approx \frac{D_s}{1+k_{\text{sr}}/k_{\text{rs}}}.$$ (38)

For the one-dimensional diffusion coefficient in the search state, we employ D_s = 0.05 μm²/s (18,20). Now, according to Eq. 1, the diffusion constant in the recognition state, D_r, can be written as D_r = D_s × exp(−χ), where χ denotes the activation (32).

We consider the contributions of the characteristic terms in Eq. 22 to the mean association time for χ = 8. The corresponding values are plotted in Fig. 3 as a function of the dissociation rate k_off. Experimentally, this corresponds to different salt concentrations because increasing the salt concentration leads to an increasing dissociation frequency (6,7). The solid line represents the total mean association time, the dotted line the contribution of τ₁, and the dashed and dot-dashed lines the contributions of Nτ₂ and Nτ₃. The latter two represent the total times spent off and on the chain after the first nonspecific association with the chain. Apparently, the time it takes for this first association, τ₁, is independent of the dissociation rate and is negligible for the parameters considered here. The total time the particle spends off the chain increases with k_off, whereas the time spent on the DNA decreases. At k_off/k_sr ≈ 10⁻³, the mean association time has a minimum. For values much smaller and larger than this optimal value, one of the two terms is dominant and the other one negligible. For very small k_off, a plateau is reached (out of the range of Fig. 3).

Figure 3.

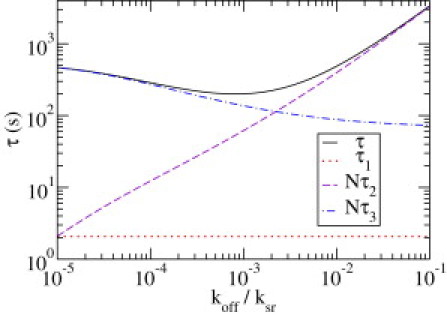
Contributions to the mean association time (solid line) as a function of the dissociation rate k_off in units of k_sr: first association time τ₁ (dotted line), total time spent off the chain, Nτ₂ (dashed line), and total time spent on the chain, Nτ₃ (dot-dashed line). For other parameters, see text.

However, unlike in the simplified one-state model for coiled DNA at the optimal value of the dissociation rate, the TF does not spend equal amounts of time bound and unbound. In fact, for the parameters used in Fig. 3, the optimal partition is that the particle spends ≈73% of the time on the DNA chain. This observation is reminiscent of the experimental findings that, in vivo, TFs seem to spend nearly 90% of the time nonspecifically bound to the DNA chain (7,20,40). The value of the optimal fraction of time spent nonspecifically bound depends obviously on the choice of the parameter values. The characteristic measure for the influence of the two-state scenario on this optimal fraction is the typical time spent in the recognition mode as quantified by 1/k_rs, or the typical sliding length in the recognition mode, ${\ell }_r=\sqrt{D_r/k_{\text{rs}}}$ (32). Increase of ℓ_r will further increase the value of the optimal fraction, and vice versa.

Next we investigate the influence of χ, measuring the difference of the diffusivities in both states, on the association rate k_a = 1/(τn₀), because this is the rate that is usually studied experimentally. The results are depicted in Fig. 4, again as a function of the dissociation rate k_off, but this time over a larger range of values. We consider the case where χ = 4 (dashed line), implying D_s/D_r ≈ 55, in more detail, because the nonmonotonic shape of the corresponding curve here is most definite. We note that, experimentally, this ratio has, to our best knowledge, not been measured, and only the apparent diffusion constant D_a from Eq. 37 is available in literature (18,20). To begin, we observe that the maximal rate k_a,max ≈ 9.2 × 10⁹ M⁻¹ s⁻¹ is close to the experimentally obtained value (1). Winter et al. (7) measured that this maximum occurred at 0.1 M KCl concentration. Moreover, the shape of the curves is similar to earlier results (7,23) typical for facilitated diffusion models where three different regimes can be distinguished.

Figure 4.

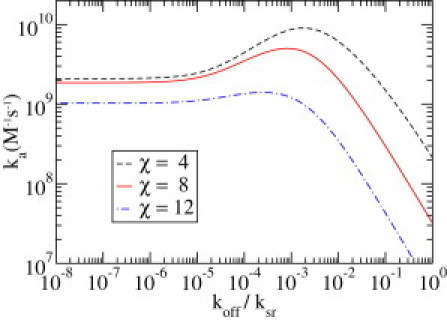
Association rate k_a as a function of the dissociation rate, k_off in units of k_sr, for three values of χ: χ = 4 (dashed line), χ = 8 (solid line), and χ = 12 (dot-dashed line). For other parameters, see text.

For k_off/k_sr ≲ 10⁻⁶, the association rate is nearly constant. In this regime, k_sr is several orders of magnitude larger than k_off; consequently, after binding to the DNA the protein will not even once leave the chain for a round of three-dimensional diffusion. Thus, the time to reach the target is determined by the time of first association, τ₁, and the time it takes to slide to the target without dissociating, but undergoing numerous conformational changes. The corresponding association rate k_a can be calculated from Eq. 34 to which τ₁ and $k_{\text{sr}}^{-1}$ have to be added to take into account the different initial conditions. However, such an essentially one-dimensional search strategy is highly redundant and thus, disadvantageous, because already scanned regions are visited repeatedly—an effect known as oversampling.

In the opposite regime, k_off/k_sr ≳ 10⁻¹, there is a substantial probability that the particle will dissociate before it could explore the neighboring region extensively in both the recognition and the search state. The larger the k_off is, the more unfavorable this effect becomes, which is revealed by the behavior $k_a\propto k_{\text{off}}^{-1}$ in this regime. In a way, with these parameters, the protein spends too much time diffusing in three dimensions, which is equally disadvantageous for the total search process.

As already seen in the discussion of the contributions to the mean association time in the intermediate regime k_off/k_sr ≈ 10⁻³, a maximum of the association rate can be found. Here the partition between the times spent on and off the chain is optimal. On the one hand, the TF leaves the chain soon enough before the redundant one-dimensional search becomes disadvantageous; but, on the other hand, it is attached long enough to the chain to efficiently search for the target.

For even lower diffusion constants in the recognition mode, χ = 8, corresponding to D_s/D_r ≈ 3000 (solid line) and χ = 12 (equivalent to D_s/D_r ≈ 160,000 (dot-dashed line)), the nonmonotonic shape of the curve is still present although less pronounced. Thus, the acceleration due to facilitated diffusion becomes less and less important, the slower the one-dimensional diffusion in the recognition mode is. We also observe that, for TFs with a lowered diffusivity, the value of k_off at which the maximal association rate is reached is shifted to lower values. This is obvious, because slower diffusing TFs should stay bound to the chain for longer times to obtain an effective search.

In Fig. 5 we compare our generalized model with the same parameters as in Fig. 3 to three of its special cases that correspond to previously studied models. The solid line corresponds to the full two-state model (with χ = 8) and is thus identical to the solid line in Fig. 4. The dotted line displays the behavior in the simplified two-state model for coiled DNA (32) in which the reassociation time τ₂ was chosen to be the same as in our model. The dashed line corresponds to the classical one-state model of Berg and Blomberg (4) and the dot-dashed line to the limiting case for coiled DNA (12). We use D₁ = 0.0455 μm²/s such that D_a = D₁ for the parameters stated in the preceding section.

Figure 5.

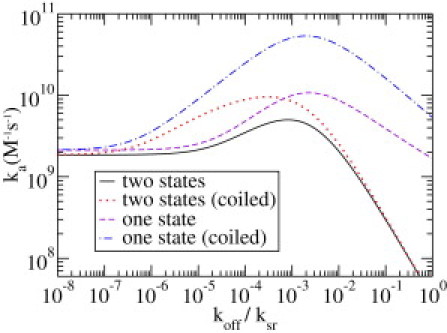
Association rate, k_a, as a function of the dissociation rate k_off in units of k_sr for four different models: the two-state model presented in this article (solid line), two-state model for coiled DNA (dotted line), original one-state model (4) (dashed line), and one-state model for coiled DNA (12) (dot-dashed line). For other parameters, see text.

In all four cases, we observe the three regimes that we mentioned before. For small values of k_off, the two-state model for coiled DNA approaches the same value as the corresponding full model. In the same regime, both one-state models approach the rate: k_a = 1/(n₀(τ₁ + τ₃)), where τ₃ is the well-known first-passage time in an interval τ₃ = L²/(3D₁) (41). Also, for very high dissociation rates the association rate obtained with the two models for coiled DNA approach their corresponding values for straight DNA. However, in the one-state models, the scaling in this regime reads $k_a\propto k_{\text{off}}^{-1/2}$. Thus, for the one-state model, a further increase of the dissociation rate in this regime is less fatal than for the two-state model, where $k_a\propto k_{\text{off}}^{-1}$.

We observe that, in both cases, the search rate for coiled DNA is larger than for rodlike DNA, and that the value at which the maximum occurs is shifted. The first point can be attributed to the fact that τ₂ that was chosen identical for both conformations is just the mean time the TF spends for a bulk excursion. In our approximation for coiled DNA it means that, on this timescale, the TF jumps to any other position on the chain, whereas for straight DNA most of the jumps lead to a nearby position, and the rare long-range jumps take more time. Thus, in some sense, the distribution of the TF equilibrates much faster and the redundant, effectively one-dimensional search on straight DNA is avoided.

Another observation that is, at first sight, disappointing is that the two-state model is always slower in target location than the corresponding one-state model. This might seem to contradict the findings of Reingruber and Holcman (33). However, they showed that the introduction of a second faster diffusing state decreases the mean first-passage time from an interval, whereas, in the context of this article, the new state is much slower than the one in the one-state model (such that D_a = D₁) and its motivation is to overcome the speed-stability paradox.

Conclusions

The generalized model for facilitated diffusion studied herein describes the specific association of a TF with its operator region on DNA, as studied in typical in vitro experiments. We generalized the classical Berg-von Hippel model of facilitated diffusion to the case when the TF is assumed to alternate between two conformational states. The protein starts the search process somewhere in the bulk solution, and binds nonspecifically to the DNA chain. Bound to the chain, it explores the DNA one-dimensionally in the search state characterized by its relatively high diffusivity. Stochastically, it switches to the recognition state in which it has a significantly reduced diffusivity but is able to recognize, and bind, to the target binding site. A key result is that, for typical parameters, the association rate to the target is reduced compared to previous models, which correspond to limiting cases of our generalized model. Although the generalized model still has a maximum of the association rate as function of the ambient salt concentration, this maximum is more pronounced when the diffusion constant of the recognition state is close to the one of the search state. However, even for nearly immobile TFs in the recognition mode, the maximum is present.

The classical Berg-von Hippel model of facilitated diffusion with only one bound state, as well as related studies that interpret the target search process as a narrow-escape problem, are presented as limiting cases of our model. Unlike many recent reformulations of the problem in which the TF spends equal amounts of time on and off the DNA, we obtain that already in the dilute in vitro situation it is advantageous for the TF to spend more time bound to the chain than in the bulk solution. The optimal partition depends on the actual values of the system parameters.

When taking typical experimentally obtained one-dimensional diffusion constants for the effective diffusion constant in the fast-switching limit of our generalized model, we obtain association rates that are actually lower than the ones obtained with the corresponding classical Berg-von Hippel model. However, our model with two conformational states reconciles tight binding to the target with fast diffusion along the chain and treats the microscopic excursions explicitly.

An important question for future studies is whether it is possible to extend the model to the in vivo situation, where molecular crowding and the resulting slow or even anomalous diffusion might play an important role. Recent simulation studies indicate that, particularly, magnitudes of the binding constants become modified (42).

Appendix A: Determination of the Mean Association Time

To obtain the mean association time, τ, we use an analogous ansatz to Berg and Blomberg (4) that satisfies the boundary conditions, Eq. 5 and Eq. 6:

$${\tilde{n}}_r\left(u,z\right)=\sum _{n=0}^{\mathrm{\infty }}{f}_n\left(u\right)\text{sin}\left(\frac{2n+1}{2L}\pi z\right),$$ (39)

$${\tilde{n}}_s\left(u,z\right)=\sum _{m=0}^{\mathrm{\infty }}{h}_m\left(u\right)\text{cos}\left(\frac{m\pi z}{L}\right).$$ (40)

According to Eq. 9, we have

$$\tilde{j}\left(u\right)=\frac{D_r\pi }{2L}\sum _{n=0}^{\mathrm{\infty }}\left(2n+1\right)f_n\left(u\right).$$ (41)

Inserting the ansatz in Eq. 7 and Eq. 8, we obtain two equations that can be complemented by multiplying Eq. 7 with cos($m^{\prime }$πz/L) and a subsequent integration over z. Omitting the argument u for a better readability, we obtain

$$\frac{2L}{\pi }{\gamma }_m{Y}_m+\tilde{j}=k_{\text{sr}}{L}_m{h}_m,$$ (42)

$$h_m{L}_m\left({\alpha }_m-k_{\text{off}}{L}_m{g}_m\right)=GL{\delta }_{m,0}+\frac{2L}{\pi }{k}_{\text{rs}}{Y}_m,$$ (43)

$$\tilde{j}=\frac{2D_r}{L}\sum _{m,n=0}^{\mathrm{\infty }}\frac{k_{\text{sr}}}{{\beta }_n}{h}_m\frac{{\left(2n+1\right)}^2}{{\left(2n+1\right)}^2-4m^2},$$ (44)

where all the functions denoted by Greek letters have the physical dimension of a frequency:

$${\alpha }_m\left(u\right)=u+k_{\text{off}}+k_{\text{sr}}+\frac{D_s{m}^2{\pi }^2}{L^2},$$

$${\beta }_n\left(u\right)=u+k_{\text{rs}}+\frac{D_r{\left(2n+1\right)}^2{\pi }^2}{\left(4L^2\right)},$$

$${\gamma }_m\left(u\right)=u+k_{\text{rs}}+\frac{D_r{m}^2{\pi }^2}{L^2},$$

$$L_m=\frac{L\left(1+{\delta }_{m,0}\right)}{2},$$

and

$$Y_m\left(u\right)=\sum _{n=0}^{\mathrm{\infty }}{f}_n\left(u\right)\frac{2n+1}{{\left(2n+1\right)}^2-4m^2}.$$

With the first two equations, Y_m(u) can be eliminated such that

$$h_m{L}_m\left[{\gamma }_m\left({\alpha }_m-k_{\text{off}}{L}_m{g}_m\right)-k_{\text{rs}}{k}_{\text{sr}}\right]=GL{\gamma }_m{\delta }_{m,0}-k_{\text{rs}}\tilde{j}.$$ (45)

Together with Eq. 44, we obtain, omitting the argument u,

$$\tilde{j}=LG/\left\{\frac{k_{\text{rs}}}{{\gamma }_0}+\frac{{\mathit{ϵ}}_0\left({\gamma }_0\left[{\alpha }_0-k_{\text{off}}L{g}_0\right]-k_{\text{rs}}{k}_{\text{sr}}\right)}{{\gamma }_0}\times \left[\frac{L^2}{2D_r{k}_{\text{sr}}}+\sum _{m=1}^{\mathrm{\infty }}\frac{2k_{\text{rs}}/{\mathit{ϵ}}_m}{{\gamma }_m\left({\alpha }_m-k_{\text{off}}\frac{L}{2}{g}_m\right)-k_{\text{rs}}{k}_{\text{sr}}}\right]\right\},$$ (46)

where

$${\mathit{ϵ}}_m\left(u\right)={\left(\sum _{n=0}^{\mathrm{\infty }}\frac{1}{{\beta }_n}\frac{{\left(2n+1\right)}^2}{{\left(2n+1\right)}^2-4m^2}\right)}^{-1}.$$

Starting from this result, we can calculate the mean association time Eq. 22 via Eq. 10.