Joint generalized models for multidimensional outcomes: A case study of neuroscience data from multimodalities

Abstract

This paper is motivated from the analysis of neuroscience data in a study of neural and muscular mechanisms of muscle fatigue. Multidimensional outcomes of different natures were obtained simultaneously from multiple modalities, including handgrip force, electromyography (EMG), and functional magnetic resonance imaging (fMRI). We first study individual modeling of the univariate response depending on its nature. A mixed-effects beta model and a mixed-effects simplex model are compared for modeling the force/EMG percentages. A mixed-effects negative-binomial model is proposed for modeling the fMRI counts. Then, I present a joint modeling approach to model the multidimensional outcomes together, which allows us to not only estimate the covariate effects but also to evaluate the strength of association among the multiple responses from different modalities. A simulation study is conducted to quantify the possible benefits by the new approaches in finite sample situations. Finally, the analysis of the fatigue data is illustrated with the use of the proposed methods.

1 Introduction

Recently, more and more studies in brain research obtain experimental data from multiple modalities simultaneously, such as from electroencephalography (EEG), electromyography (EMG), magnetoencephalography (MEG), functional magnetic resonance imaging (fMRI), or diffusion tensor imaging (DTI). The setting involves high-dimensional, multichannel and/or time-dependent data of different natures. It is of interest to make statistical inference by combining information from multiple data sources.

The analysis of high-dimensional biosignals in each modality often involves a statistical ensemble built on several data mining steps. Typically, one calculates a set of statistical features from raw signals of a single subject under each design factor and then builds up a statistical regression model for the features over multisubjects across conditions. In the first stage analysis of the studies, percentage outcomes are obtained from raw EMG, EEG, or MEG signals; count outcomes in regions of interest (ROIs) are obtained from raw fMRIs; continuous outcomes (such as mean diffusivity) in ROIs are obtained from raw DTIs. In the second stage analysis, however, those types of nonnormal outcomes are frequently modeled with standard linear regression without any transformation in medical literature. See, for example, Carlsen et al. (2007), Kofler et al. (2008), Ciccarelli et al. (2005), Kautz and Brown (1998) for the analysis of EMG percentage outcomes and Carey et al. (2002), Luft et al. (2002), Osaka et al. (2004), Benwell et al. (2005), Brodtmann et al. (2007) for the analysis of fMRI voxel counts.

Percentage data from the neuroscience studies are continuous data between zero and one. Count data from the neuroscience experiments are nonnegative integers and typically exhibit right-skewed and long-tailed distributions. Overdispersion often occurs in these percentage data and/or count data (Wang et al., 2007). Ignoring the nature of the percentage or count outcomes could cause biased estimates and might further lead to erroneous conclusions in these studies.

In this paper, I discuss a class of generalized regression models that result from the analysis of multimodality data in a study for neural and muscular mechanisms of muscle fatigue. The models can be viewed as a natural extension of conventional generalized linear mixed models (GLMMs). We first study individual modeling of the outcomes depending on their natures. A mixed-effects beta or simplex model is proposed for modeling longitudinal proportional data from handgrip force or EMG. A mixed-effects negative-binomial model is suggested for modeling longitudinal count data from fMRI. Then, I present a joint model for the multiple outcomes, which allows us to not only assess the covariate effects simultaneously, but also to evaluate the strength of association among the multiple responses from different modalities. The rest of this paper is organized as follows: Section 2 illustrates the experiment regarding the muscle fatigue study and discusses data preprocessing procedures of the raw data from the multimodalities: force, EMG, and fMRI. Section 3 discusses the individual models of the univariate responses, and then presents the joint model approach to model them together. Section 4 addresses a simulation study to explore the proposed models. Section 5 describes analysis results of the fatigue data based on the joint model and compare it with the results from univariate models. Section 6 is a discussion of the methods and their implication. The software codes for the proposed methods in this paper can be obtained on the journal's webpage.

2 The fatigue study and data

Fatigue is a common experience that increases chances of injury and reduces quality of life. It is a common psychophysiological symptom that interacts with the control mechanisms regulating task behavior. Increased fatigability occurs in every patient with muscle weakness, regardless of whether the weakness is due to a central or peripheral neurological disorder (Gandevia, 2001). Mechanisms of brain activation during muscle fatigue have been studied extensively in the last decades, including several recent studies (Liu et al., 2005a, b; Roesler et al., 2009; Wang et al., 2009). The fatigue study presented in this paper investigates (i) the time effects of the multiple responses of interest during the fatigue task performances and (ii) the strength of association among the responses from multimodalities.

2.1 Subjects and motor task

Eight healthy right-handed subjects participated in the study. The experimental procedures were approved by the Institutional Review Board at the Cleveland Clinic. All subjects gave informed consent prior to the participation. During the experiment, each subject performed about 100 intermittent handgrip contractions at 100% maximal voluntary contraction (MVC) level of the right arm while his/her brain was imaged. The task lasted about 300 s. Figure 1 gives a graphical description of the experiment. The data of handgrip force, EMG and fMRIs were collected simultaneously while the subjects performed the muscle contractions.

Figure 1.

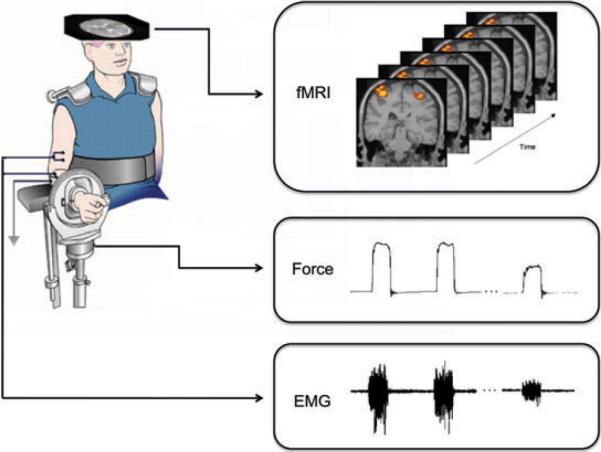
A graphical description of the fatigue experiment: the subjects performed the muscle contractions while the data of force, EMG, and fMRI images were collected simultaneously.

2.2 Data recording and preprocessing

2.2.1 Force

Handgrip force was measured by a system that was connected to a pressure transducer (EPX-N1 250 PSI, Entran Devices, Inc., Fairfield, NJ) by a nylon tube filled with distilled water (Liu et al., 2005a). The force applied by the subject was converted to a voltage signal by the pressure transducer and then directed to an amplifier. The final voltage signal was input to the channel of a Spike 2 data acquisition system (version 3.05, Cambridge Electronic Design, Ltd., Cambridge, UK) and was transferred to a computer.

The voltage signals were then processed using the Spike 2 analysis package. They were first converted to force (N) using the calibration equation (Liu et al., 2005a) and then the mean of the force was calculated over each 50-s period. So, in total, six repeated measurements were obtained over the experimental time. Finally, the mean values were normalized to the initial baseline MVC values, which were recorded at the beginning of the experiment and prior to the task performances. The final normalized force values (used for further statistical analysis) were fractional within the range (0, 1).

2.2.2 EMG

Surface EMG signals were collected using the Neurodata Amplifier System (Grass-Telefactor, West Warwick, RI) from four muscles including: flexor digitorum superficialis (FDS), flexor digitorum profundus (FDP), extensor digitorum (ED) in the right arm and FDS in the left arm. The EMG signals were amplified and recorded at a sampling rate of 1000 Hz to the computer by the Spike 2 data acquisition system.

At the beginning of each experiment, a brief MVC involving each muscle was performed and the initial baseline EMG was recorded. The EMG data of each trial for each muscle were processed in a similar manner as the force data after full-wave rectification. The mean of the EMG was calculated over each 50-s period and then normalized to the initial baseline EMG value. Therefore, the final normalized outcomes of EMG (those used for further statistical analysis) were a fraction/percentage within the range (0, 1).

2.2.3 fMRI

fMRIs were obtained at a SIEMENS VISION 1.5-T system in the same transverse planes. Each brain volume contained 20 slices that included the whole cerebrum and cerebellum. The field of view was 256 mm × 256 mm and the matrix was 128 × 128 for fMRI, hence the fMRIs were obtained with an in-plane resolution of 2 mm × 2 mm. In the experiment, the fMRIs were collected during rest (baseline) condition (OFF) and task performance (ON). Before collecting the baseline images, a “rest” audio command was given to the subject. The baseline images included 10 continuous scans while the target force was shown as a static line. With a “start” audio order, the subject began the handgrip contractions. The capture of the ON images began 5 s later due to the delay of the imaging system and included 120 scans during the task.

The analysis of fMRI images was performed using the MEDx 3.4 software package (Sensor Systems, Inc., Sterling, VA). Image data preprocessing includes: motion correction using the automated image registration algorithm programed in the MEDx software. Normalization of image intensities was implemented in order to remove fMRI signal shifts. Spatial smoothing with a Gaussian filter was also performed on the data. Then general linear models were applied to detect fMRI signal changes. Each alternate 10 scans of the 120 ON scans (11–20, 31–40, …) were compared to the 10 OFF scans in each subject. Six z-score images were then acquired. Activated voxels in each image were thresholded at p < 0.05, with Bonferroni correction for the number of regions evaluated. Brain activation for each subject was quantified by counts of the activated voxels for several cortical ROIs.

In total, six repeated measurements in each ROI from fMRIs were obtained to match the percentage outcomes from Force and EMG during the same time periods. The individual cortical regions being calculated included: primary motor cortex (PMC), primary sensory cortex (PSC), prefrontal cortex (PFC), cerebellum (CB), cingulate gyrus (CG), and supplementary motor area (SMA). The new outcomes after data preprocessing from fMRIs were count data for each subject, which were discrete and not normally distributed.

It should be remarked that quantifying brain activation by the number of activated voxels in each ROI for each subject is common in neurophysiological studies, although there are still disputes in the neuroscience literature (Poldrack, 2007). A common reason to perform ROI analysis for fMRI in medical studies is that it can be difficult to detect the pattern of activity across conditions from an overall map in a complex factorial design. Activated voxel counts give appropriate measurements/indices to measure the degree of brain activation (Luft et al., 2002; Wang et al., 2012), but one should use caution on the determination of ROIs and threshold levels. Some neuroscientists prefer to use the average intensity values instead of activated voxel counts within ROIs. Nevertheless, the proposed joint model that is presented in the next section is also applicable to the intensity outcomes.

3 Statistical models

After data preprocessing, I acquired multidimensional longitudinal outcomes from the multimodalities. Table 1 describes the 11 responses that were obtained from the experiment. There are one from force, four from EMGs, and six from fMRIs. The force and EMG percentage data are in the range (0, 1), and the fMRI count data are discrete nonnegative integers. These responses are nonnormally distributed.

Table 1.

Description and classification of the response variables of interest, of which six are count data and five are percentage data.

No.	Variable	Resource	Type	Description
1	FORCE	Force	Percentage	Normalized handgrip force
2	FDPR	EMG	Percentage	Normalized data at the flexor digitorum superficialis (right arm)
3	FDSR	EMG	Percentage	Normalized data at the flexor digitorum profundus (right arm)
4	EDR	EMG	Percentage	Normalized data at the extensor digitorum (right arm)
5	FDPL	EMG	Percentage	Normalized data at the flexor digitorum superficialis (left arm)
6	PMC	fMRI	Count	Activated voxel counts at the primary motor cortex
7	PSC	fMRI	Count	Activated voxel counts at the primary sensory cortex
8	PFC	fMRI	Count	Activated voxel counts at the pre-frontal cortex
9	CB	fMRI	Count	Activated voxel counts at the cerebellum
10	CG	fMRI	Count	Activated voxel counts at the cingulate gyrus
11	SMA	fMRI	Count	Activated voxel counts at the supplementary motor area

Typical transformations for percentage data include logistic transformation or arcsine transformation, while common transformations for count data include logarithm transformation or Box-Cox transformation. In my initial exploratory data analysis, I considered logistic transformation (log(y/(1 − y))) for percentage outcomes and logarithm transformation (log(y 0.5)) for count outcomes. Figure 2 displays the longitudinal data plots with transformations. Each+panel of Fig. 2 shows a plot of the mean with the standard deviation (SD) over the normalized time for a transformed response. The average longitudinal profile and data variation can be virtually identified through the plots. I notice the obvious downward trend for the force and the EMG percentages of FDS_R, FDP_R, and ED_R. In contrasts, there is no strong downward trend in the fMRI counts and the EMG percentage of FDP_L. The graphical method gave us intuitive and visual results, however, formal statistical models are needed to discover the relationship among the outcomes.

Figure 2.

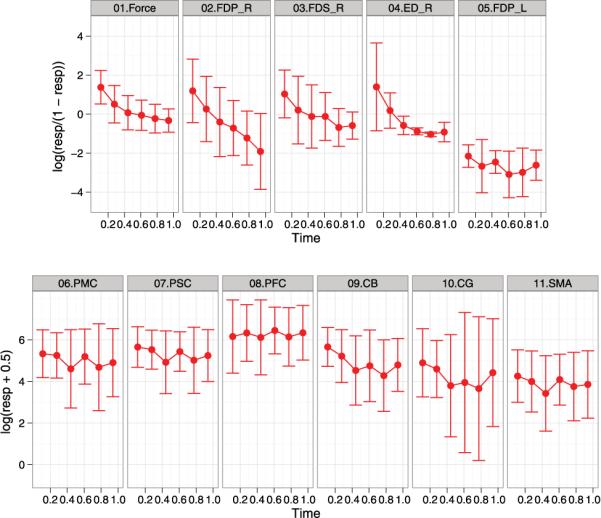
Summarized longitudinal data with transformations (logistic transformation for percentage outcomes and logarithm transformation for count outcomes). Each panel shows a plot of the mean with the standard deviation over the normalized time for a transformed response. There is the downward trend for the force and the EMG percentages of FDS_R, FDP_R, and ED_R. In contrasts, there is no strong downward trend in the fMRI counts and the EMG percentage of FDP_L.

Generalized linear models (GLMs; McCullagh and Nelder, 1989) are an extension of the conventional linear regression models, which allow a model to fit data that follow probability distributions other than the normal distribution. GLMs can be further extended to fit mixed-effect models and are referred to as GLMMs. Random effects, random coefficients, temporal, or spatial covariance patterns can be included in a GLMM in much the same way as in normal mixed-effect models (Molenberghs and Verbeke, 2005). GLMMs have received a lot of attention and have become frequently used random-effects models in the context of “nonnormal” repeated measurements. In the fatigue study, the responses from force, EMG and fMRI exhibited nonnormal feature and overdispersed behavior. Repeated measurements were obtained over time from different subjects in the study and thus random effects should be taken into account in modeling procedure. Here, I consider a class of generalized models, which can be viewed as extended models of the conventional GLMMs.

Let K be the total number of outcomes that need to be modeled. Y_{ki j} denotes the measurement taken on the i-th subject at the j-th time point, for the k-th outcome, where i = 1, …, n, j = 1, …, m, and k = 1, …, K. I further write the K sequences for the i-th subject as Y_1i = (Y_1i1, Y_1i2, …, Y_1im)^T, Y_2i = (Y_2i1, Y_2i2, …, Y_2im)^T, …, Y_Ki = (Y_Ki1, Y_Ki2, …, Y_Kim)^T. In my study, the sequence Y_ki (k = 1, …, K) can be either percentages or counts, which is the vector of m measurement taken on subject i, for outcome k. I shall first discuss individual modeling for the two types of responses and then address a joint model for the multiple responses, which allows for the estimation of the covariance matrix of the random effects and thus results in the evaluation of the association among the multiple outcomes.

3.1 Modeling of univariate percentage response from force or EMG

The responses from force and EMG were percentages/fractions, where the data represented the percentages of MVC force and EMG at the initial baseline condition. Percentages are common outcomes from raw EMGs in medical studies (Kautz and Brown, 1998; Ciccarelli et al., 2005). Because little is known about the distribution of the percentages, modeling the data with a common distribution from the exponential family is difficult. I only know that the distribution should be continuous within the range (0, 1). The data were far from normal based on my exploratory data analysis. They were not binomial proportions, because they did not represent the ratio of a count over a total number of Bernoulli trials. Indeed, two types of probability distributions can be used to model the percentage-dependent variable, in which either of them is very flexible and covers a variety of shapes restricted in (0, 1).

The first parametric distribution is the reparameterized beta distribution. The probability density function (PDF) of the conventional beta distribution is given by f (y; p, q) = y^p−1(1 − y)^q−1/B(p, q), where p, q > 0, and B(p, q) is the beta function. If I let μ = p/(p + q) and τ = p + q, the density function can be reparameterized as

$$f(y;\mu ,\tau )=\frac{1}{B(\mu \tau ,(1-\mu )\tau )}{y}^{\mu \tau -1}{(1-y)}^{(1-\mu )\tau -1},$$ (1)

where μ ∈ (0, 1), τ > 0. I denote a random variable Y that follows a beta distribution with the density form (1) by Y ~ Beta(μ, τ). It can be shown that E(Y) = μ, and Var(Y) = μ(1 − μ)/(1 + τ). The parameter τ can be interpreted as a dispersion parameter, since the dispersion of the distribution increases as τ decreases (Ferrari and Cribari-Neto, 2004).

The second parametric distribution is the simplex distribution, which was discovered by Barndorff-Nielsen and Jørgensen (1991) and extensively studied by Jørgensen (1997). Let us denote a random variable Y that follows a standard simplex distribution with parameters μ ∈ (0, 1) and τ > 0 by Y ~ S⁻(μ, τ). Its PDF is defined by

$$f(y;\mu ,\tau )=\frac{1}{\sqrt{2\pi \tau y^3{(1-y)}^3}}\exp \left\{-\frac{1}{2\tau }\cdot \frac{{(y-\mu )}^2}{y(1-y){\mu }^2{(1-\mu )}^2}\right\},$$ (2)

where the parameter μ and τ have very clear interpretations as position and dispersion parameters. It has been shown by Jørgensen (1997) that E(Y) = μ and

$$\mathrm{Var}\left(Y\right)=\mu (1-\mu )-\frac{1}{\sqrt{2\tau }}\exp \left\{\frac{1}{\tau {\mu }^2{(1-\mu )}^2}\right\}\Gamma \left\{\frac{1}{2},\frac{1}{2\tau {\mu }^2{(1-\mu )}^2}\right\},$$

where Γ(α, z) = ${\int }_z^{\infty }{t}^{\alpha -1}{e}^{-t}dt$ is the incomplete gamma function.

Both the beta distribution and the simplex distribution cover a large class of distributions confined in (0, 1), which include probability density shapes from right skewed, left skewed to very flat. A key difference of two distributions is that the beta distribution does not belong to the proper dispersion family defined by Jørgensen (1997), while the simplex distribution does. Accordingly, the technique of the analysis of deviance in conventional GLMs can be applied to regression models based on the simplex distribution, but not to regression models based on the beta distribution. I will see that using the beta model and the simplex model for percentage data results in compatible estimates in simulations from Section 4. The two models are often exchangeable for practical use.

In the fatigue study, either a mixed-effect beta regression model or a mixed-effect simplex regression model can be applied to fit the force or EMG data. For the simplicity of notation, I let k = 1 be the percentage response and k = 2 be the count response in the discussion of individual modeling. I consider the following model for the univariate percentage response:

$$\{\begin{array}{c}{Y}_{1ij}\mid u_{1i}~Beta({\mu }_{1ij},\tau )or{S}^{-}({\mu }_{1ij},\tau )\hfill \\ \mathrm{logit}\left({\mu }_{1ij}\right)={\beta }_{10}+{\beta }_{11}{t}_{1ij}+u_{1i}\hfill \\ u_{1i}\stackrel{\mathrm{iid}}{~}N(0,{\sigma }_1^2),\hfill \end{array}\phantom{\}}$$ (3)

where the normal random variables u_1i are a mechanism to account for the random cluster effects of the i-th subject. They are shared among observations with the same cluster and thus those observations are being modeled as correlated. Following Ferrari and Cribari-Neto (2004), Jørgensen (1997), the logit link function is used for either the beta model or the simplex model.

To estimate the parameters (β₁₀, β₁₁, τ, ${\sigma }_1^2$), I need to maximize the likelihood of the model (3). Conditional on the random effect u_1i, Y_1i1, …, Y_1im are independent. So, the conditional PDF of Y_1i = (Y_1i1, …, Y_1im)^T given u_1i is ${\prod }_{j=1}^{m}f(y_{1ij}\mid u_{1i};{\beta }_{10},{\beta }_{11},\tau )$. Let ϕ(·; σ²) denote the normal density with mean zero and variance σ². The joint log-likelihood based on the unconditional PDF is

$$l_1=\sum _{i=1}^n\log \left({\int }_{-\infty }^{\infty }\prod _{j=1}^{m}f(y_{1ij}\mid u_{1i};{\beta }_{10},{\beta }_{11},\tau )\varphi (u_{1i};{\sigma }_1^2)\mathrm{d}{u}_{1i}\right).$$

The above log-likelihood is the sum of independent contributions from each subject and each subject involves a single-dimensional integral. It cannot be evaluated in closed form and thus maximizing values cannot be expressed in closed form either. Nevertheless, numerical integration for calculating the log-likelihood can be evaluated accurately using adaptive Gauss–Hermite quadrature techniques. The usual large-sample tools are available for statistical inferences based on the model (Molenberghs and Verbeke, 2005). For instance,Wald tests can be formed by utilizing the large-sample normality of estimators.

3.2 Modeling of univariate count response from fMRI

In the fMRI count data, the observed variances were greater than the observed means. This situation is known as overdispersion, which is often due to the unobserved heterogeneity of count data. The Poisson distribution is commonly used in represent the distribution of count data. However, a characteristics of the Poisson distribution is that its mean is equal to its variance. The extra-Poisson variation can be modeled naturally by integrating the Poisson distribution with respect to its conjugate distribution, the Gamma distribution. The resulting marginal distribution becomes the negative-binomial distribution, where its probability mass function is given by

$$p(y;\nu ,\mu )=\frac{\Gamma (y+1∕\nu )}{\Gamma (y+1)\Gamma (1∕\nu )}\frac{{\left(\nu \mu \right)}^y}{{(1+\nu \mu )}^{y+1∕\nu }}.$$

Let us denote a random variable Y that follows a negative-binomial distribution with parameters ν and μ by Y ~ NB(μ, ν). It can be shown that E(Y) = μ and Var(Y) = μ + νμ². The dispersion parameter ν quantifies the amount of overdispersion. The distribution becomes the Poisson distribution as ν = 0.

In the fatigue study, I consider a mixed-effect negative-binomial model for the fMRI count data,

$$\{\begin{array}{c}{Y}_{2ij}\mid u_{2i}~NB({\mu }_{2ij},\nu )\hfill \\ \log \left({\mu }_{2ij}\right)={\beta }_{20}+{\beta }_{21}{t}_{2ij}+u_{2i}\hfill \\ u_{2i}\stackrel{\mathrm{iid}}{~}N(0,{\sigma }_2^2).\hfill \end{array}\phantom{\}}$$ (4)

Similarly as in model (3), u_2i are the cluster specific random effects that accounts for the random variation over subjects.

The joint log-likelihood of the model (4) is

$$l_2=\sum _{i=1}^n\log \left({\int }_{-\infty }^{\infty }\prod _{j=1}^{m}p(y_{2ij}\mid u_{2i};{\beta }_{20},{\beta }_{21},\nu )\varphi (u_{2i};{\sigma }_2^2)\mathrm{d}{u}_{2i}\right).$$

Estimating the unknown parameters based on the above marginal maximum log-likelihood method can be also achieved by numerical computations using adaptive Gauss–Hermite quadrature techniques. For example, SAS procedure NLMIXED can be used to maximize the likelihood function with the numerical approaches.

3.3 Joint modeling of multiple responses from multimodalities

I now consider extending the univariate models to a joint model for multiple responses. A key motivation for the joint model is that the association structure among the different responses is of interest. I am also interested in comparing average time trends for different responses with the correlations taken into account. My joint model assumes a GLMM for each response variable depending on its nature, and these univariate GLMMs are combined through specification of a multivariate normal distribution for all random effects.

For the K-variate response vector ${\mathit{Y}}_i={({\mathit{Y}}_{1i}^T,{\mathit{Y}}_{2i}^T,\dots ,{\mathit{Y}}_{Ki}^T)}^T$, I write the joint GLMM as a general hierarchical model

$$\{\begin{array}{c}{\mathit{Y}}_i={\mu }_i+{\epsilon }_i\hfill \\ \mathit{g}\left({\mu }_i\right)={\mathit{X}}_i{\beta }_i+{\mathit{Z}}_i{\mathit{u}}_i’\hfill \end{array}\phantom{\}}$$ (5)

where X_i and Z_i are the fixed- and random-effects design matrices and β_i and u_i are the vectors of fixed- and random-effects parameters as in the normal mixed model. g(·) denotes a function whose components are suitable link functions. For the fatigue study, the mean structure of each response in the model (5) is specified as

$${\mu }_{kij}=h_k({\beta }_{k0}+{\beta }_{k1}{t}_{ij}+u_{ki}),$$

where h_k is the k-th inverse link function. X_i and Z_i are (mK × 2K) and (mK × K)-dimensional matrices of known covariate values corresponding to subject i, and β_i is a 2K-dimensional vector of unknown fixed regression coefficients to be estimated. Moreover, the K-dimensional random effects, u_i = (u_1i, u_2i, …, u_ki)^T are assumed to follow a K-dimensional multivariate normal distribution, ui ~ N(0, Σ) and Σ is defind as

$$\Sigma =\left[\begin{array}{ccccc}\hfill {\sigma }_1^2\hfill & \hfill {\rho }_{12}{\sigma }_1{\sigma }_2\hfill & \hfill {\rho }_{13}{\sigma }_1{\sigma }_3\hfill & \hfill \cdots \hfill & \hfill {\rho }_{1K}{\sigma }_1{\sigma }_K\hfill \\ \hfill {\rho }_{12}{\sigma }_2{\sigma }_1\hfill & \hfill {\sigma }_2^2\hfill & \hfill {\rho }_{23}{\sigma }_2{\sigma }_3\hfill & \hfill \cdots \hfill & \hfill {\rho }_{2K}{\sigma }_2{\sigma }_K\hfill \\ \hfill {\rho }_{13}{\sigma }_3{\sigma }_1\hfill & \hfill {\rho }_{23}{\sigma }_3{\sigma }_2\hfill & \hfill {\sigma }_3^2\hfill & \hfill \cdots \hfill & \hfill {\rho }_{3K}{\sigma }_3{\sigma }_K\hfill \\ \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill {\rho }_{1K}{\sigma }_K{\sigma }_1\hfill & \hfill {\rho }_{2K}{\sigma }_K{\sigma }_2\hfill & \hfill {\rho }_{3K}{\sigma }_K{\sigma }_3\hfill & \hfill \cdots \hfill & \hfill {\sigma }_K^2\hfill \end{array}\right].$$

The model (5) is written in a conventional linear model way, following the notation in Molenberghs and Verbeke (2005). From this “artificial-looking” model, outcomes are decomposed in terms of the mean and an appropriate error term. The components of the error structure have the appropriate distribution with the variance depending on the mean-variance relationship of the responses. The mean μ_i and X_iβ_i + Z_iu_i are related by a “link” function, g, where the components of g(·) depend on the nature of the outcomes and take a form suitable for the distribution of the data. Following the discussion of individual modeling, I consider “log” link for the count outcomes and “logit” link for the percentage outcomes.

The joint log-likelihood for the model (5) is

$$l_3=\sum _{i=1}^n\log \left({\int }_{{\mathbb{R}}^K}\prod _{j=1}^m{p}_{ij}(y_{i1j},y_{i2j},\dots ,y_{iKj}\mid {\mathit{u}}_i;{\beta }_i,\eta )\psi ({\mathit{u}}_i;\Sigma )d{\mathit{u}}_i\right),$$ (6)

where p_{i j} denotes the conditional density of (Y_i1j, Y_i2j, …, Y_iKj) given u_i, ψ denotes the K-variate normal density with mean zero and covariance matrix Σ, η is the K-dimensional vector of dispersion parameters, where the element of η depends on its one-dimensional response distribution.

Maximizing the log-likelihood (6) involves K-dimensional integrals that do not have a closed form. Numerical integration is very difficult here since K = 11 is very large and the responses are different types. To avoid the computational complexity in maximizing (6), I follow the idea of the pairwise modeling approach discussed by Fieuws and Verbeke (2006), Faes et al. (2008). The key is to consider maximizing the following joint log pseudolikelihood instead.

$$\begin{array}{cc}\hfill p{l}_3& =\sum _{i=1}^n\log \left(\prod _{r=k+1}^K\prod _{k=1}^{K-1}{\int }_{{\mathbb{R}}^2}\prod _{j=1}^m{p}_{ij}(y_{ikj},y_{irj}\mid {\mathit{u}}_i^{kr};{\beta }_i,\eta )\psi ({\mathit{u}}_i^{kr};\Sigma )d{\mathit{u}}_i^{kr}\right)\hfill \\ \hfill & =\sum _{i=1}^n\sum _{r=k+1}^K\sum _{k=1}^{K-1}\log \left({\int }_{{\mathbb{R}}^2}\prod _{j=1}^m{p}_{ij}(y_{ikj},y_{irj}\mid {\mathit{u}}_i^{kr};{\beta }_i,\eta )\psi ({\mathit{u}}_i^{kr};\Sigma )d{\mathit{u}}_i^{kr}\right),\hfill \end{array}$$ (7)

where ${\mathit{u}}_i^{kr}=(u_i^k,u_i^r)$ denotes a bivariate random effect for the k-th and r-th outcomes of subject i. The log pseudolikelihood in (7) is contributed by all bivariate likelihood functions for all possible paired outcomes. With this approximation, I simplify the 11-dimensional integration problems to two-dimensional integration problems. I will show that, through simulations in the next section, the pseudolikelihood method does not lose the efficiency of the estimates and yields robust estimated parameters and standard errors.

In practice, the pseudolikelihood method can be programed with the flexible procedure NLMIXED in SAS. However, because of the estimation for the high-dimensional nonlinear mixed-effects model, one often needs a careful selection of starting values to make the algorithm convergence criterion satisfied. My recommendation for the selection of initial values is to use the estimates from univariate models. It should be cautioned that the pseudolikelihood method does not guarantee the estimated covariance matrix to be always positive definite, although it yields reasonable parameter estimates. I define here an unstructured covariance matrix in the joint model. Depending on the applications, one may consider a variety of covariance structures, such as compound symmetry, autoregressive covariance structures.

When the dimension of the response is very high, there are a few skills that can be applied in the model fitting. The dispersion parameters are the nuisance parameters in the joint model, since the mean and covariance parameters are of interest here. The estimated likelihood approach can help us to fit the complex model (Pawitan, 2001, chapter 10). It replaces the nuisance parameters with their reasonable estimates in the likelihood function, and then maximizes the estimated likelihood. In my study, a good choice could be plugging the dispersion parameter estimates from univariate models into the joint log pseudolikelihood. The estimated likelihood does not account for the extra uncertainty due to the nuisance parameter, however there is little practical difference between it and the likelihood with unknown nuisance parameters from my simulation experiences. It often increases stability of estimating the high-dimensional covariance parameters. Another method that helps the model fitting is to use Laplace approximation in the numerical computation, which is also beneficial to the convergence of the algorithm.

4 Simulations

I conducted simulation studies to evaluate the performance of the proposed models. The first simulation study was to compare regression models for simulated continuous percentage data. I set the mean function μ_{1i j} = β₁₀ + β₁₁t_{1i j} + u_1i with β₁₀ = 0.5, β₁₁ = 1 and u_1i ~ N(0, 0.5²), where the subject i = 1, …, n and the time point j = 1, …, m. Two left-skewed distributions were considered for generating the percentage data: y_{1i j} ~ Beta(exp{μ_{1i j}}/(1 + exp{μ_{1i j}}), 15); or y_{1i j} ~ Simplex(exp{μ_{1i j}}/(1 + exp{μ_{1i j}}), 6). I set n = 10, or 50 and m = 10, or 25. Three different regression modelswere applied to fit the simulated data: the beta mixed model (BMM), the simplex mixed model (SMM), and the normal linear mixed model with logistic transformation (i.e., log(y/(1 − y))) (LMM1). Table 2 summarized the results from 500 replicates of simulations. The means and SDs of the parameter estimates, as well as the means of the estimated standard errors (Mean$\left(\widehat{se}\right)$) are reported for each model. The results show that both BMM and SMM outperform LMM1 for the parameter estimation. Although LMM1 gives reasonable estimates, it tends to estimate the true parameters larger. It is unsurprising thatBMMis slightly better than SMM for the data from the beta mixture distribution, while SMM becomes a little better than BMMfor the data from the simplex mixture distribution. The Mean$\left(\widehat{se}\right)$s are close to the SDs of the parameter estimates, which indicates the models give reasonable estimates for standard errors. As sample size increases, the SDs and Mean$\left(\widehat{se}\right)$s became smaller for all models. In summary, BMMand SMM are compatible in modeling longitudinal percentages observed in (0, 1).

Table 2.

Simulation results for modeling univariate percentage data. The estimates of three models are compared: BMM, the beta mixed model; SMM, the simplex mixed model; LMM1, the normal linear mixed model with logistic transformation. The true parameters β₀ = 0.5, β₁ = 1.

Simulated data	n	m	Estimate	BMM		SMM		LMM1
				${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$
Beta	10	10	Mean	0.497	0.992	0.484	1.051	0.535	1.148
			SD	0.213	0.203	0.228	0.252	0.234	0.233
			Mean($\widehat{se}$)	0.190	0.198	0.223	0.249	0.229	0.231
	50	25	Mean	0.502	0.998	0.489	1.058	0.536	1.135
			SD	0.076	0.057	0.091	0.120	0.084	0.068
			Mean($\widehat{se}$)	0.077	0.056	0.088	0.076	0.089	0.065
Simplex	10	10	Mean	0.565	0.956	0.491	1.016	0.615	1.184
			SD	0.247	0.359	0.215	0.235	0.247	0.360
			Mean($\widehat{se}$)	0.280	0.343	0.203	0.236	0.281	0.343
	50	25	Mean	0.541	0.931	0.495	1.021	0.609	1.154
			SD	0.072	0.034	0.081	0.029	0.087	0.038
			Mean($\widehat{se}$)	0.069	0.032	0.073	0.027	0.081	0.032

My second simulation study evaluated the performance of different regression models for simulated overdispersed count data. Similarly, the mean function was μ_{2i j} = β₂₀ + β₂₁t_{2i j} + u_2i with β₂₀ = 1, β₂₁ = 1, and u_2i ~ N(0, 1). Two types of distributions were considered for generating the count data: y_{2i j} ~ NB(exp{μ_{2i j}}, 1/2); or y_{2i j} ~ Poisson(exp{μ_{1i j}}). Both cases generate overdispersed count data, since the mean function contents a random effect. However, the data from the negative-binomial mixture distribution are more overdispersed than the data from the Poisson mixture distribution. Three different regression models were applied to fit the simulated count data: the negative-binomial mixed model (NMM), the Poisson mixed model (PMM), and the normal linear mixed model with logarithm transformation (i.e., log(y + 0.5)) (LMM2). Table 3 summarized the results from 500 replicates. Both NMM and PMM outperform LMM2 in terms of the parameter estimation. Note that, in the case of simulated negative-binomial data, the Mean$\left(\widehat{se}\right)$s of β₁based on the PMM are much smaller than the corresponding SDs. Poisson distribution assumes that its variance equals its mean, thus the estimated $\widehat{se}\mathrm{s}$ are too low and the inference from the PMM could be mistaken. In summary, PMM seems to handle mildly overdispersed data but not to deal with moderately/severely overdispersed data.

Table 3.

Simulation results for modeling univariate count data. The estimates of three models are compared: NMM, the negative-binomial mixed model; PMM, the Poisson mixed model; LMM2, the normal linear mixed model with log transformation. The true parameters β₀ = 1, β₁ = 1.

Simulated data	n	m	Estimate	NMM		PMM		LMM2
				${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$
Negative binomial	10	10	Mean	1.008	0.997	0.980	0.995	0.922	0.863
			SD	0.371	0.309	0.401	0.368	0.319	0.296
			Mean($\widehat{se}$)	0.354	0.306	0.317	0.133	0.328	0.299
	50	25	Mean	0.998	1.004	0.986	1.003	0.908	0.872
			SD	0.149	0.085	0.155	0.117	0.126	0.085
			Mean($\widehat{se}$)	0.149	0.086	0.143	0.036	0.133	0.085
Poisson	10	10	Mean	0.986	0.997	0.986	0.996	1.068	0.923
			SD	0.335	0.138	0.335	0.137	0.310	0.187
			Mean($\widehat{se}$)	0.313	0.139	0.311	0.134	0.309	0.177
	50	25	Mean	0.988	1.002	0.987	1.002	1.064	0.931
			SD	0.141	0.038	0.142	0.037	0.128	0.054
			Mean($\widehat{se}$)	0.142	0.037	0.141	0.037	0.134	0.051

My third simulation study evaluated the performance of the joint model. Because BMM is stable for continuous percentage data and the NMM is stable for overdispersed count data from my experiences, I only considered the beta mixture distribution and the negative-binomial mixture distribution for the joint modeling in the simulation and the real data analysis. I had the following simulation design: four outcomes were simulated for the joint modeling. The first two were percentage responses and the last two were count outcomes. The mean function was μ_{ki j} = β_k0 + β_k1t_{ki j} + u_ki (k = 1, …, 4, i = 1, …, 50, j = 1, …, 10), where β₁₀ = β₂₀ = 1, β₁₁ = β₂₁ = 0.5, β₃₀ = β₄₀ = 1, β₃₁ = β₄₁ = 1, and (u_1i, u_2i, u_3i, u_4i)^T follows a multinormal distribution with σ₁ = σ₂ = σ₃ = σ₄ = 1, ρ₁₂ = ρ₂₃ = ρ₃₄ = 0.8, ρ₁₃ = ρ₁₄ = ρ₂₄ = 0.5. The percentage data were simulated from Beta(exp{μ_{ki j}}/(1 + exp{μ_{ki j}}), 10), k = 1, 2 and the count data were simulated from NB(exp{μ_{ki j}}, 1/3), k = 3, 4. Tables 4 and 5 summarize the results from 500 replicates. In Table 4, the averaged estimates of the mean parameters from the joint model using the estimated pseudo-likelihood approach are compared with those from the univariate models (i.e., the four separate individual models for the four univariate responses by ignoring the correlation). Both the joint model and the univariate models give accurate estimates for all of the mean parameters. The relative efficiencies of the estimates based on the joint model to those based on the univariate models show that the joint model seems slightly more efficient than the univariate models. However, no big improvement in terms of the estimation of mean parameters has been found from fitting the joint model. In Table 5, simulation results for the estimates of the covariance parameters based on the joint model are reported. The estimates remain accurate to the true parameters, although the estimated standard errors appear a little underestimated. In all, the pseudolikelihood or the estimated pseudolikelihood method is a feasible approach to fit the complex joint model for multiple responses.

Table 4.

Simulation results for the estimates of the mean parameters in comparison of the joint model and the univariate models. The true parameters β₁₀ = β₂₀ = 1, β₁₁ = β₂₁ = 0.5, and β₃₀ = β₄₀ = 1, β₃₁ = β₄₁ = 1.

	${\widehat{\beta }}_{10}$	${\widehat{\beta }}_{12}$	${\widehat{\beta }}_{20}$	${\widehat{\beta }}_{21}$	${\widehat{\beta }}_{30}$	${\widehat{\beta }}_{31}$	${\widehat{\beta }}_{40}$	${\widehat{\beta }}_{42}$
Mean (joint model)	1.023	0.501	1.015	0.502	1.038	0.999	1.040	0.993
Mean (univariate model)	1.006	0.507	0.999	0.510	1.015	0.992	1.010	0.996
Relative efficiency	1.021	1.032	0.953	1.027	1.055	1.020	1.002	0.979

Table 5.

Simulation results for the estimates of the covariance parameters in the joint model using the pseudolikelihood approach. The true parameters σ₁ = σ₂ = σ₃ = σ₄ = 1, ρ₁₂ = ρ₂₃ = ρ₃₄ = 0.8, ρ₁₃ = ρ₁₄ = ρ₂₄ = 0.5.

	${\widehat{\sigma }}_1$	${\widehat{\sigma }}_2$	${\widehat{\sigma }}_3$	${\widehat{\sigma }}_4$	${\widehat{\rho }}_{12}$	${\widehat{\rho }}_{23}$	${\widehat{\rho }}_{34}$	${\widehat{\rho }}_{13}$	${\widehat{\rho }}_{14}$	${\widehat{\rho }}_{24}$
Mean	0.936	0.928	0.959	0.948	0.824	0.842	0.845	0.525	0.516	0.516
SD	0.093	0.097	0.102	0.103	0.071	0.072	0.068	0.096	0.103	0.110
Mean($\widehat{se}$)	0.031	0.035	0.038	0.035	0.054	0.051	0.049	0.065	0.066	0.067

5 Results

In this section, I present the results of analyzing the multimodality fatigue data. I considered the beta mixture distribution for the percentage outcomes, since it is more popular than the simplex mixture distribution and has more empirical support in prior literature. I used the negative-binomial mixture distribution for count outcomes based on my simulation support in last section. A joint generalized regression model was fit for the 11 responses. The normalized time was the fixed-effect covariate, while each linear predictor function contained a random-effect variable to account for random cluster (subject) effects. The association among the responses were modeled through an unstructured covariance matrix. To compare the estimates, 11 univariate generalized models were fit for each response variable separately. Table 6 shows the parameter estimates, standard errors and p-values for the time effect obtained by the joint model with the estimated pseudolikelihood method, as well as obtained by the 11 separate univariate models. Very similar estimates and inference results were obtained for the fixed effects.

Table 6.

The parameter estimates, standard errors and p-values for the time effect obtained by fitting the joint model and the separate univariate models.

	Joint model			Univariate model
Response	Estimate	SE	p-Value	Estimate	SE	p-Value
FORCE	−1.613	0.279	<0.001*	−1.5280	0.284	<0.001*
FDPR	−2.786	0.490	<0.001*	−2.760	0.544	<0.001*
FDSR	−1.660	0.344	<0.001*	−1.620	0.347	<0.001*
EDR	−1.886	0.264	<0.001*	−1.678	0.268	<0.001*
FDPL	−0.339	0.265	0.201	−0.313	0.266	0.245
PMC	−0.169	0.386	0.662	−0.307	0.437	0.486
PSC	−0.273	0.373	0.464	−0.419	0.437	0.343
PFC	0.093	0.436	0.831	−0.034	0.444	0.940
CB	−0.846	0.578	0.144	−0.981	0.703	0.170
CG	0.135	0.470	0.775	0.031	0.517	0.953
SMA	−0.224	0.527	0.671	−0.302	0.592	0.612

^*The test is significant at the 0.05 level.

The null hypotheses of the tests were that the slope of time was equal to zero for each outcome, that is, β_1k = 0, k = 1, …, 11. Using approximate Wald-type tests, the statistical analyses showed significant decreases during the task performances for the responses, FORCE, FDP_R, FDS_R, ED_R, while all of the responses from fMRI and FDP_L from EMG showed no significant changes in the study. The outcomes from EMG for the two prime movers, FDS_R and FDP_R, and the antagonist, ED_R in the right arm followed a similar decreasing pattern as the FORCE. Each of four slope estimates are less than −1.5. It is not surprising that the slope estimate of the EMG outcome FDP_L in the left aim (the control muscle) was only −0.339 and was not significantly different from zero. Interesting results were found for the outcomes from fMRI: although most of the outcomes show slight declines during the task performances (except that PFC = 0.093 and CG = 0.135), none of them was significantly different from zero.

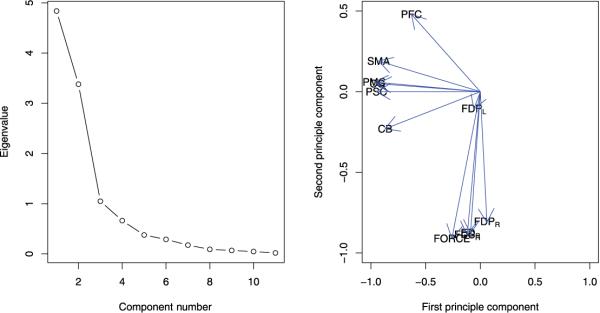
Table 7 presents the estimated correlation matrix. These correlation coefficients express the association among responses from different resources. To better understand the association of the responses, I performed a principal component analysis (PCA) on the correlation matrix directly. Figure 3 shows the graphical results from the PCA. The left panel is the scree plot that displays the eigenvalues of the correlation matrix in the order of component numbers. The first principal component accounts for as much of the variability in the data as possible, and each succeeding component accounts for as much of the remaining variability as possible. The right panel shows the first principle component score versus the second principle component score. In this reduced representation, I observed that the scales referring to the outcomes from EMG in the right arm and the force were grouped together. Oppositely, the scales referring to the outcomes from fMRI were far from the scale of the force although they were grouped together themselves. Unsurprisingly, the scale referring to FDP_L was standing along than other EMG outcomes.

Table 7.

The estimated correlation matrix of the random effects based on the joint model.

	Force	EMG				fMRI
	FORCE	FDPR	FDSR	EDR	FDPL	PMC	PSC	PFC	CB	CG	SMA
FORCE	1.000
FDPR	0.517	1.000
FDSR	0.827	0.724	1.000
EDR	0.805	0.622	0.666	1.000
FDPL	0.301	−0.013	0.178	0.260	1.000
PMC	0.154	−0.167	0.000	−0.008	0.099	1.000
PSC	0.242	−0.218	0.022	0.024	0.173	0.970	1.000
PFC	−0.442	−0.336	−0.462	−0.428	0.174	0.454	0.405	1.000
CB	0.512	−0.096	0.275	0.230	0.331	0.772	0.853	0.286	1.000
CG	0.094	−0.129	−0.059	−0.023	0.125	0.937	0.881	0.504	0.744	1.000
SMA	0.010	−0.342	−0.227	−0.027	0.135	0.906	0.878	0.592	0.658	0.832	1.000

Figure 3.

The graphical results for the principal component analysis (PCA) of the correlation matrix: the left panel displays the scree plot; the right panel shows that the first principle component score versus the second principle component score. The scales referring to the outcomes from electromyography (EMG) in the right arm and the force were grouped together, while the scales referring to the outcomes from functional magnetic resonance imaging (fMRI) were far from the scale of the force.

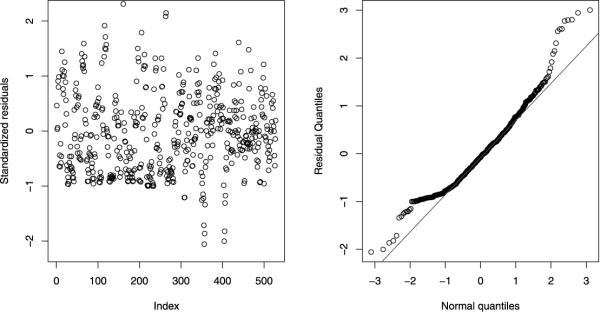
A residual analysis was performed for the fitted joint model. The standardized ordinary residuals were calculated based on the definition $r=(y-\mu )∕{\left(\widehat{\text{Var}}\left(y\right)\right)}^{1∕2}$ (McCullagh and Nelder, 1989; Ferrari Cribari-Neto, 2004). Figure 4 shows that the residual plots from the fitted joint model. The left panel displays the plot of the standardized residuals versus their index. A random pattern has been found, which indicates a reasonable fit for a joint model. The right panel shows the normal QQ plot for the residuals. The linearity of the points suggests that the data are close to normal. A few outliers are identified at the high end of the range. Otherwise, the joint model fit the data quite well. The predictive performance of the joint model could be further assessed, but it is beyond the focus of this paper. The tools developed Czado et al. (2009) will be useful for the evaluation.

Figure 4.

Residual plots for the joint model: The left panel shows the plot of the standardized residuals versus their index, and the right panel shows the normal QQ plot for the residuals.

My statistical analysis results for the fatigue study showed that the levels of the fMRI signals at the different ROIs were only negligibly affected by severe muscle fatigue, but by contrast there were significant reductions in the outcomes of the force and EMG with MVCs. The outcomes of the force and EMG were highly correlated, while no strong association was detected between fMRI and force outcomes. Several medical papers reported concordant findings as ours. Liu et al. (2005a) showed that fatigue induced by sustained or repetitive MVCs resulted in progressive declines in muscle and EMG signals, while the MVC fatigue had a minimal effect on EEG signals of the preparation phase but a more substantial effect on the signals of the sustained phase of the motor task. Liu et al. (2005b) reported that fMRI-measured brain activation level in the primary sensorimotor cortex was only minimally to moderately affected by severe muscle fatigue. Post et al. (2009) recently reported a study of motor fatigue using fMRI techniques. Their results suggested that, although the central nervous system changed its input to the relevant motor areas, this change was insufficient to overcome fatigue-related changes in the voluntary drive.

6 Discussion

I presented a joint model to analyze the multidimensional responses from multimodalities, which was motivated by the muscle fatigue study. A pseudolikelihood method within a GLMM framework was applied to the neuroscience data. The outcomes from multimodalities in neuroscience are often of multiple different natures. It is very important to specify a reasonable distribution based on the nature of the data when I model the data. As I have shown in simulations, a GLMM with specifying a suitable distribution has practical advantages for modeling data with special nature. The GLMMs appear more favorable than the linear regression models with certain transformation. The linear regression models with nonlinear transformed responses are usually difficult to interpret for investigators. Moreover, the joint model I discussed provides a feasible way to model the association among the multidimensional outcomes with different natures. The approach can be beneficial to multimodalities neuroscience studies.

In the analysis of the fatigue data, I only considered the random intercept model for the mean structure. I assumed the correlation between outcomes was constant over time, and the dispersion parameter for each outcome was constant. These assumptions were because the number of subjects and the number of time points in the study were relatively small, but the number of unknown estimates was quite large. My residual analysis showed that the proposed model fit well for the data. For other studies with sufficient samples, one may consider more complex models, such as random slope models. Multivariate hierarchical Bayesian modeling techniques can be an alternative to resolve the modeling of the multiple nonnormal responses. For multivariate models with complex mean and/or dispersion structures, Markov chain Monte Carlo methods could be implemented, but they may have problems in terms of both convergence and computational time. The recent advanced method, integrated nested Laplace approximation (INLA), could be potentially applied to solve the high-dimensional multivariate model. Using INLA and its simplified version, one can directly compute very accurate approximations to the posterior marginals in a complex Bayesian model (Rue et al., 2009). Recent papers to use INLA include Fong et al. (2010), Roos and Held (2011), Schroedle and Held (2011), Schroedle et al. (2011). Analyzing the multivariate neuroscience outcomes from multimodalities with INLA is of interest in my further research.